Таинственная природа или ряд чисел Фибоначчи в красоте – Женский сайт
24 сентября, 2013 FeminaСегодня коснемся очень интересной темы, милые девушки, это соединение математики и науки с таинственной природой. Как может соединиться такое понятие, как ряд чисел Фибоначчи и, например, букеты цветов на свадьбу, про то, как похудеть к свадьбе, мы уже знаем, а тут будем разбираться в такой не простой теме.
Тем не менее, все в природе подчиняется своим законам и правилам. Пожалуй, главным таким законом можно назвать принцип золотого сечения или золотой пропорции.
Вот уже многие века золотая пропорция считается наиболее совершенным и гармоничным соотношением целого и его частей. Мало кто задумывается, что одной и той же закономерности подчинено строение едва ли не всех элементов природы.
Золотое сечение — это пропорция, при которой меньшая часть одного целого, относится к большей, ровно так же, как большая часть относится ко всему целому.
Конечно, выяснив, в чем секрет природной гармонии, человек не мог не попытаться применить «божественную пропорцию» в своих творениях. Еще древние египтяне, создавая свои пирамиды, храмы и предметы быта, непременно использовали золотое сечение. В эпоху Ренессанса пропорция стала, пожалуй, главным приемом в работе художников и архитекторов. Сегодня она повсеместно используется при проектировании дизайна интерьеров, бытовой техники, в дизайне мебели, конструировании машин и, конечно, в профессиональном создании флористических композиций.
С понятием золотого сечения связывают имя итальянского математика XIII века Леонардо Пизанского, известного миру как Леонардо Фибоначчи. Он выявил определенную числовую последовательность, которую стали считать арифметическим выражением золотой пропорции. Каждое третье число Фибоначчи равно сумме двух предыдущих, а при возрастании ряда отношение соседних чисел все больше приближается к отношению в золотом делении.
Ряд Чисел Фибоначчи.
Именно ряд Фибоначчи имеет прямое отношение к развитию нового направления в ботанике — филлотаксиса. Именно в числах этой последовательности может быть выражена спиральная форма, так часто повторяющаяся в природе. Листья и ветки растений всегда располагаются в винтовой симметрии. Это позволяет каждому листочку растения быть открытым для солнца и это наиболее гармонично для зрительного восприятия человека. По спирали располагаются ячейки кедровых шишек и семечки в подсолнухе. Спиральную форму имеет размещение чешуек у рыб и змей, по спирали плетет свою паутину паук.
Золотое сечение находит применение в построении треугольников, пентаграмм (например, здание Пентагона) и в других «золотых» фигурах.
«Спиралями Фибоначчи» фотографы и дизайнеры указывают нам на центр интереса в композиции, числами Фибоначчи режиссеры видео- и киномонтажа измеряют промежутки между ключевыми сценами.
Сочетание обаяние таинственной природы с человеческой интуицией, могуществом человеческого мастерства и интеллекта создает совершенные вещи, это и есть КРАСОТА.
на ваш сайт.
ЧИСЛА ФИБОНАЧЧИ — евгений журавли. диалоги — LiveJournal
— числовая последовательность, где каждый последующий член ряда равен сумме двух предыдущих, то есть: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368,.. 75025,.. 3478759200, 5628750625,.. 260993908980000,.. 422297015649625,.. 19581068021641812000,.. Геометрически последовательность Фибоначчи есть ни что иное, как золотое сечение – деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.. Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении), намного раньше, чем она стала известна в Европе. Изучением сложных и удивительных свойств чисел ряда Фибоначчи занимались самые различные профессиональные ученые и любители математики. Пока что практика показывает, что Природа (в том числе и Человек) развивается по законам, которые заложены в этой числовой последовательности. В сосновой шишке, если посмотреть на нее со стороны черенка, можно обнаружить две спирали, одна закручена против другая по часовой стрелке. Число этих спиралей 8 и 13. В подсолнухах встречаются пары спиралей: 13 и 21, 21 и 34, 34 и 55, 55 и 89. И отклонений от этих пар не бывает!.. У Человека в наборе хромосом соматической клетки (их 23 пары), источником наследственных болезней являются 8, 13 и 21 пары хромосом… Возможно, все это свидетельствует о том, что ряд чисел Фибоначчи представляет собой некий зашифрованный закон природы. Чисто визуально данное соотношение воспринимается нашими органами чувств как «гармоничное», «естественное». Именно в таком соотношении куплет/припев/соло наиболее приятно воспринимается музыка. В этом соотношении построен храм Парфенон. Сергей Эйзенштейн искусственно и осознанно построил фильм «Броненосец Потёмкин» по правилам золотого сечения.
Пока что практика показывает, что Природа (в том числе и Человек) развивается по законам, которые заложены в этой числовой последовательности. В сосновой шишке, если посмотреть на нее со стороны черенка, можно обнаружить две спирали, одна закручена против другая по часовой стрелке. Число этих спиралей 8 и 13. В подсолнухах встречаются пары спиралей: 13 и 21, 21 и 34, 34 и 55, 55 и 89. И отклонений от этих пар не бывает!.. У Человека в наборе хромосом соматической клетки (их 23 пары), источником наследственных болезней являются 8, 13 и 21 пары хромосом… Возможно, все это свидетельствует о том, что ряд чисел Фибоначчи представляет собой некий зашифрованный закон природы. Чисто визуально данное соотношение воспринимается нашими органами чувств как «гармоничное», «естественное». Именно в таком соотношении куплет/припев/соло наиболее приятно воспринимается музыка. В этом соотношении построен храм Парфенон. Сергей Эйзенштейн искусственно и осознанно построил фильм «Броненосец Потёмкин» по правилам золотого сечения.
Так например, цифровой код развития цивилизации можно определить с помощью различных методов в нумерологии. Например, с помощью приведения сложных чисел к однозначным (например, 15 есть 1+5=6 и т.д.). Проводя подобную процедуру сложения со всеми сложными числами ряда Фибоначчи, русский исследователь Михайлов в 1997г получил следующий ряд этих чисел: 1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 9, 8, 8, 7, 6, 4, 1, 5, 6, 8, 1, 9, затем все повторяется 1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 4, 8, 8,.. и повторяется вновь и вновь… Этот ряд также обладает свойствами ряда Фибоначчи, каждый бесконечно последующий член равен сумме предыдущих. Например, сумма 13-го и 14-го членов равна 15, т.е. 8 и 8=16, 16=1+6=7. Оказывается, что этот ряд периодичный, с периодом в 24 члена, после чего, весь порядок цифр повторяется. Получив этот период, некоторые ученые выдвигают предположение — не является ли набор из 24 цифр своеобразным цифровым кодом развития цивилизации?
Вовсе нет. Полагаю, что неверно спешить называть любую некую последовательность «формулой Бога» или «законом Вселенной». Просто структура всего, наполняющего нас универсальна и закономерна. Т.е. все, что может существовать, совершенно определенно ограничено и априори логично. Нет истины за пределами математики. Сама же математика базируется всего лишь на нескольких элементарных, очень простых, фундаментальных основаниях, признанных нами за аксиомы. Сама универсальность и простота основ заставляет обнаруживать изначальные закономерности во всех проявлениях всего существующего.»Сквозной мир», где каждая точка и каждое явление и св-во пронизано одними и теми же закономерностями, мир, вне пределов этих закономерностей не существующий.
Просто структура всего, наполняющего нас универсальна и закономерна. Т.е. все, что может существовать, совершенно определенно ограничено и априори логично. Нет истины за пределами математики. Сама же математика базируется всего лишь на нескольких элементарных, очень простых, фундаментальных основаниях, признанных нами за аксиомы. Сама универсальность и простота основ заставляет обнаруживать изначальные закономерности во всех проявлениях всего существующего.»Сквозной мир», где каждая точка и каждое явление и св-во пронизано одними и теми же закономерностями, мир, вне пределов этих закономерностей не существующий.
Заметим также, что наши фундаментальные аксиомы средствами и в пределах нашей теории не могут быть доказаны.
Интересно.
Высшая математика жизни: где в природе встречаются числа Фибоначчи? | Наука | Общество
Каждый год 23 ноября в мире вспоминают первого крупного математика средневековой Европы Леонардо Пизанского, известного под прозвищем Фибоначчи. Он открыл для современников десятичную арабскую систему счисления и в целом обогатил их знания в точных науках. Но главным его открытием стала последовательность, названная числами Фибоначчи. Её называют удивительной за свойство неожиданно проявляться в самых разных сферах жизни — от биологии до живописи.
Он открыл для современников десятичную арабскую систему счисления и в целом обогатил их знания в точных науках. Но главным его открытием стала последовательность, названная числами Фибоначчи. Её называют удивительной за свойство неожиданно проявляться в самых разных сферах жизни — от биологии до живописи.
Кролики Леонардо Пизанского
Леонардо Пизанский, наиболее известный под прозвищем Фибоначчи (чаще всего имя трактуют как «счастливчик»), родился около 1170 года в итальянском городе Пиза. Его отец был купцом и посещал по торговым делам Алжир, куда привёз сына для изучения математики у арабских учителей. Позднее Фибоначчи сам ездил в Египет, Сирию, Византию и Сицилию, где ещё ближе познакомился с достижениями античных и индийских математиков. На основе полученных там знаний Леонардо написал ряд математических трактатов, ставших революционными для средневековой западноевропейской науки. Самым известным его трудом стала «Книга абака» (абак — это древнеримские счёты).
«Фактически это была энциклопедия математики того времени, — рассказывает кандидат физико-математических наук, доцент Кубанского госуниверситета Эдуард Сергеев. — В ней впервые в Европе была изложена десятичная позиционная система счисления арабов. Там впервые использовались отрицательные числа как долг. Завершалась эта большая книга изложением алгебры и примерами решения практических задач, связанных с торговым делом. В её 12-й главе содержалась знаменитая задача о кроликах. Именно благодаря ей мир узнал о числах Фибоначчи».
— В ней впервые в Европе была изложена десятичная позиционная система счисления арабов. Там впервые использовались отрицательные числа как долг. Завершалась эта большая книга изложением алгебры и примерами решения практических задач, связанных с торговым делом. В её 12-й главе содержалась знаменитая задача о кроликах. Именно благодаря ей мир узнал о числах Фибоначчи».
Придуманная средневековым математиком задача предназначалась для расчёта потомства кроликов. По её условию в огороженный со всех сторон загон поместили двух животных для размножения. Вопрос: сколько они могут произвести на свет пар кроликов за год, если известно, что каждый месяц, начиная со второго, каждая пара кроликов производит на свет одну пару? Ответ — 233 пары. Для поиска решения автор задачи вывел числовой ряд, в котором каждый последующий член равен сумме двух предыдущих. Он выглядит так: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 и так далее до бесконечности.
Дату 23 ноября для неофициального праздника Дня Фибоначчи тоже выбрали исходя из его последовательности. Для этого использовали принятый на Западе календарный формат, при котором цифрами сначала пишут месяц, а потом день. Получается 11/23, что повторяет первые четыре числа из ряда математика: 1, 1, 2, 3.
Но ещё интереснее то, что числовой ряд Фибоначчи нашёл применение во многих областях математики и по сей день удивляет учёных своей универсальностью. Кроме того, с ним также оказались связаны многие явления окружающего мира.
Проявления золотого сечения в природе. Фото: YouTube/ Кадр из видеоУдивительные числа
«В Италии выпускается периодический журнал, который называется „Числа Фибоначчи“, — продолжает Эдуард Сергеев. — Авторы со всего мира пишут для него статьи, связанные с последовательностью Леонардо Пизанского и другими свойствами чисел. И практически каждый год открывают что-то новое. В мои студенческие годы были известны одни свойства чисел Фибоначчи, а сегодня уже появились другие, в том числе совершенно неожиданные. Одно из открытых недавно удивительных свойств чисел Фибоначчи в том, что с определённой периодичностью в них повторяются одни и те же последовательности последних цифр. То есть рост этого ряда не случаен и подчиняется некоему закону, который, видимо, пока недоступен нашему пониманию. Это действительно загадочная вещь».
В мои студенческие годы были известны одни свойства чисел Фибоначчи, а сегодня уже появились другие, в том числе совершенно неожиданные. Одно из открытых недавно удивительных свойств чисел Фибоначчи в том, что с определённой периодичностью в них повторяются одни и те же последовательности последних цифр. То есть рост этого ряда не случаен и подчиняется некоему закону, который, видимо, пока недоступен нашему пониманию. Это действительно загадочная вещь».
Поразительные свойства последовательности Фибоначчи в математике сложно объяснить человеку без специальных знаний, но многое можно понять и без формул. Одна из главных особенностей этого «золотого ряда» в том, что отношение каждого последующего его члена к предыдущему неуклонно приближается к показателю 1,618. Математикам он известен как число Фи, но у него есть и много других имён: число Бога, божественная гармония, асимметричная симметрия, золотое сечение (последнее понятие придумал 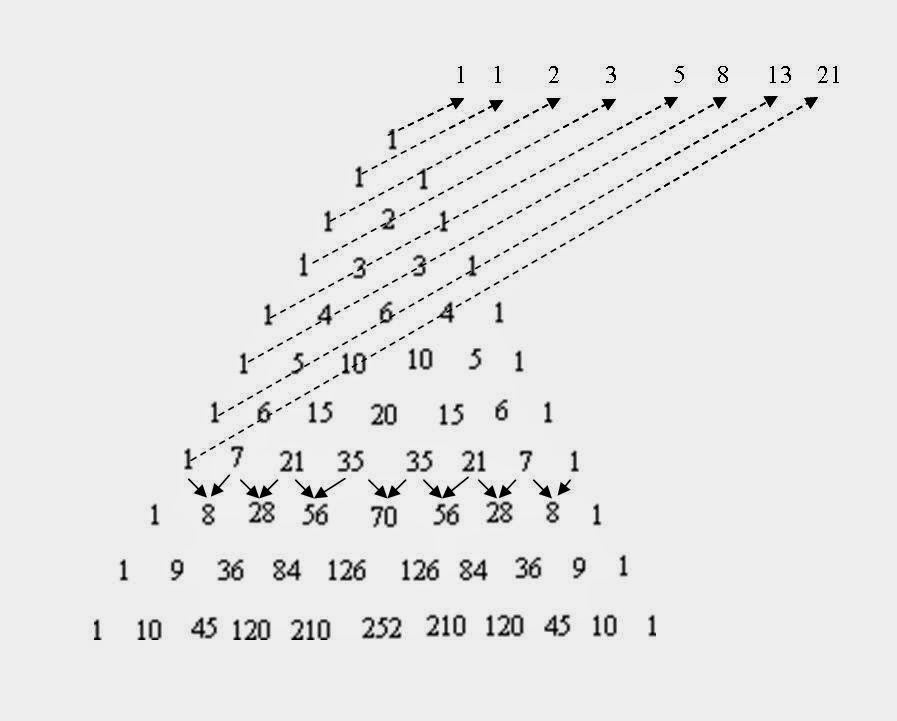 Константу Фи назвали так в честь древнегреческого скульптора Фидия. Еще древние строители знали, что при использовании определённых пропорций здание выглядит максимально красиво и к тому же получается наиболее устойчивым. Коротко золотое сечение определяется так: меньшая часть относится к большей, как большая ко всему целому. В процентном выражении это соответствует показателям 62 и 38.
Константу Фи назвали так в честь древнегреческого скульптора Фидия. Еще древние строители знали, что при использовании определённых пропорций здание выглядит максимально красиво и к тому же получается наиболее устойчивым. Коротко золотое сечение определяется так: меньшая часть относится к большей, как большая ко всему целому. В процентном выражении это соответствует показателям 62 и 38.
«Леонардо Да Винчи тоже был виртуозом золотого сечения, — говорит Эдуард Сергеев. — Эту пропорцию можно найти в его знаменитой „Джоконде“ и других картинах. По тому же принципу я как-то давал своим студентам задачу нарисовать самый красивый эллипс, который только возможен. Для этого нужно рассчитать отношение большого диаметра к меньшему по числу Фи. Это такая константа, к которой удивительным образом сходятся все рекуррентные последовательности».
Кстати, учёные также находят математическую взаимосвязь между величиной Фи и числом Пи, которое тоже часто называют загадочным.
«Витрувианский человек» Леонардо да Винчи. Источник: Public DomainВ подсолнухе и в ухе
С рядом Фибоначчи и числом Фи в геометрии связана логарифмическая спираль, которая разворачивается по принципу золотого сечения. Её можно вписать в систему вложенных друг в друга «золотых» прямоугольников с отношением сторон, равным Фи, или описать вокруг неё. А удивляет то, что такие модели часто встречаются в природе. По образу спирали Фибоначчи построены раковины моллюсков Nautilus pompilius и окаменелых аммонитов. Их рост хорошо описывается на основе числа Фи с коэффициентом 2.
Её можно вписать в систему вложенных друг в друга «золотых» прямоугольников с отношением сторон, равным Фи, или описать вокруг неё. А удивляет то, что такие модели часто встречаются в природе. По образу спирали Фибоначчи построены раковины моллюсков Nautilus pompilius и окаменелых аммонитов. Их рост хорошо описывается на основе числа Фи с коэффициентом 2.
Отношение длин трёх витков спирали уха человека точно соответствует Фи и такие же параметры — у раковин некоторых улиток. Недавно узнали, что золотая и другие логарифмические спирали встречаются в роговичном эпителии мышей.
Ещё Леонардо да Винчи и знаменитый немецкий учёный Кеплер обращали внимание на винтовое расположение листьев у растений, напоминающее спираль. Так же растут лепестки у цветов, семечки в подсолнечнике, шишки у хвои, чешуйки на плодах ананаса. Эту закономерность в ботанике называют филлотаксисом, и в формулах листорасположения тоже встречаются числа Фибоначчи, расположенные через одно. Такие свойства определяет генетика, уходящая корнями на клеточный и молекулярный уровни. А полипептидные цепи в молекуле ДНК тоже имеют винтовое расположение. Есть данные, что соотношение длины и ширины у них несёт в себе формулу золотого сечения.
Такие свойства определяет генетика, уходящая корнями на клеточный и молекулярный уровни. А полипептидные цепи в молекуле ДНК тоже имеют винтовое расположение. Есть данные, что соотношение длины и ширины у них несёт в себе формулу золотого сечения.
Тот же принцип виден и в строении галактик. Например, наш Млечный Путь имеет несколько рукавов, растущих по принципу логарифмической спирали с шагом примерно 12 градусов. Великий поэт Гёте, который также был естествоиспытателем, считал спиральность одним из характерных признаков всех организмов, проявлением самой сокровенной сущности жизни. И, может быть, не случайно символ спирали присутствовал в культуре многих коренных народов Земли.
«Кеплер говорил, что Бог является хорошим геометром и строит Вселенную по математическим законам, — продолжает Эдуард Сергеев. — И я на сто процентов с этим согласен. Узнавая окружающий мир, всё больше изумляешься и удивляешься. На эти темы очень замечательно пишет астрофизик Марио Ливио. Я читал его книгу „Был ли Бог математиком? Галопом по божественной Вселенной с калькулятором, штангенциркулем и таблицами Брадиса“. Он там рассказывает и о спирали жизни, и о строении ДНК, и о многих других явлениях. Конечно, всё это математика — и ещё какая математика».
Я читал его книгу „Был ли Бог математиком? Галопом по божественной Вселенной с калькулятором, штангенциркулем и таблицами Брадиса“. Он там рассказывает и о спирали жизни, и о строении ДНК, и о многих других явлениях. Конечно, всё это математика — и ещё какая математика».
Исследовательская работа «Ряд чисел Фибоначчи в биологии»
Министерство образования и науки РБ.
Бичурский район
МБОУ «Бичурская СОШ № 5»
XI Республиканская научно-практическая конференция учащихся начальных классов «Первые шаги»
Номинация: Биология (Растительный мир)
Тема: Ряд чисел Фибоначчи в биологии.
Автор: Ткачёв Илья ученик 3 класса
Бичурской СОШ № 5. Бичурского района.
Домашний адрес: п. Сахарный завод ул. Советская д. 25 кв.1
Руководитель: Осмоловская Людмила Ивановна
Телефон: 8 914 988 42 11
г. Улан-Удэ
Улан-Удэ
2015
Оглавление.
Введение ———————————————————————————- 3
Основная часть ————————————————————- 4
Практическая часть ——————————————————— 4 — 5
Заключение. Выводы —————————————————— 5
Список использованной литературы ——————————————- 6
Приложение 1 – 6 —————————————————————— 7
Приложение 7 — 11 —————————————————————— 8
Введение.
Итальянский учёный, Леонардо Фибоначчи, (его имя означает «сын доброй природы») однажды, взяв пару кроликов, поставил перед собой чисто купеческую задачу:
Подсчитать, какое потомство кроликов можно получить за год, если известно, что каждый месяц, начиная со второго, каждая пара кроликов производит на свет одну пару?
Фибоначчи предположил, что кролики не болеют и не умирают. Ясно, что если считать пару кроликов новорожденными, то на 2-й месяц мы будем по прежнему иметь одну пару; на 3-й месяц пара даст потомство, станет 2 пары. На 4-й месяц первая пара снова даст потомство, станет 3 пары. На 5-й месяц потомство дадут и первая, и вторая пара. Станет 5 пар и т. д. К концу года Фибоначчи надеялся получить 144 пары. [1]
Ясно, что если считать пару кроликов новорожденными, то на 2-й месяц мы будем по прежнему иметь одну пару; на 3-й месяц пара даст потомство, станет 2 пары. На 4-й месяц первая пара снова даст потомство, станет 3 пары. На 5-й месяц потомство дадут и первая, и вторая пара. Станет 5 пар и т. д. К концу года Фибоначчи надеялся получить 144 пары. [1]
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
Задача о кроликах вошла в историю математики, а ряд чисел Фибоначчи зажил самостоятельной жизнью.
Актуальность:
Существует закономерность, по которой происходят события в живой природе. Я заинтересовался числами Фибоначчи.
Моя гипотеза: Вероятно, что закономерность чисел Фибоначчи можно встретить в жизни растений и животных.
Объект исследования:
Окружающий растительный и животный мир.
Предмет исследования:
Форма и строение исследуемых предметов.
Цель исследования: Выяснить, насколько широко последовательность чисел Фибоначчи встречается в живой природе.
Задачи:
1. Познакомиться с историей создания числового ряда Фибоначчи.
2. Изучить литературу по данной теме.
3.Установить, какая последовательность в жизни растений и животных образуется в соответствии с числовым рядом Фибоначчи.
Методы исследования
Практическая значимость: Данная работа может быть использована на уроках окружающего мира и биологии при изучении тем «Растения», «Животные», а также на уроках математики. Ведь суть последовательности Леонардо заключается в том, что, после двух первых чисел 1,1 каждое следующее число, получается сложением двух предыдущих.
Новизна работы: Мы видим в природе множество различных растений и животных, но мало кто из нас догадывается, что их рост и развитие соответствуют закономерности числового ряда Фибоначчи.
Основная часть
Так какое же отношение имеет ряд чисел Фибоначчи к биологии? Изучив соответствующую литературу, я узнал много интересного. Оказывается, спустя несколько столетий после рассчетов Фибоначчи, учёные обнаружили интересную закономерность: Если взять молодую дубовую веточку и мысленно соединить линией места прикрепления к ней листьев, то получится несколько спиралей. Оказалось, что расстояния между листьями не одинаковы. Они соответствуют числам ряда Фибоначчи. Это явление в ботанике носит название «филлотаксиса». [2]
Оказывается, спустя несколько столетий после рассчетов Фибоначчи, учёные обнаружили интересную закономерность: Если взять молодую дубовую веточку и мысленно соединить линией места прикрепления к ней листьев, то получится несколько спиралей. Оказалось, что расстояния между листьями не одинаковы. Они соответствуют числам ряда Фибоначчи. Это явление в ботанике носит название «филлотаксиса». [2]
С тех пор установлено много фактов, показывающих, что закономерность ряда Фибоначчи проявляется в формах живой природы. Посмотрите на ананас. Его чешуйки образуют рисунок пересекающихся кривых. Если в одну сторону закручивается 8 спиралей, то в другую, обычно 13. [3]
Числа Фибоначчи проявляются и в морфологии различных организмов. Морские раковины закручены спиралеобразно. Или, например, морские звезды. Число лучей у них отвечает ряду чисел Фибоначчи и равно 5, 8, 13. [4]
У хорошо знакомого комара — три пары ног, брюшко делится на восемь сегментов, на голове пять усиков — антенн. [5]
[5]
Посмотрим на средний палец кисти руки. Если первая фаланга пальца 2 см, то вторая – 3, а третья 5 см. [6]
Эти числа принадлежат ряду Фибоначчи и стоят рядом.
Практическая часть
Однажды, на пришкольном участке, моё внимание привлёк подсолнух. Рассмотрев его внимательно, я заметил, что семена на его корзинке образуют сложный рисунок пересекающихся кривых. Я опустил карандаш в центр корзинки и повёл линию от семечка к семечку. Оказалось, семена выстраиваются вдоль спиралей, которые закручиваются как справа налево, так и слева направо. 4
Я посчитал, что в одну сторону закручивается 21 спираль, а в другую 34. [7]
В числовом ряду Фибоначчи эти числа стоят рядом. К празднику Золотой осени мы всем классом трудились над композицией из природного материала. Взяв в руки еловую шишку, я невольно обратил внимание на расположение чешуек. Рассмотрев внимательно, я убедился, что чешуйки расположены в трёх спиралях, круто навивающихся влево на стержне шишки и они же расположены в пяти спиралях, навивающихся в противоположном направлении. [8]
[8]
Кто из вас не видел молоденькую веточку обыкновенной сосны? Но, наверное никто не обращал внимание на то, что хвоинки образуют 2 спирали, идущие справа снизу налево вверх и 3 спирали, идущие слева снизу направо вверх. [9]
Ты ответь мне, цветик-одноцветик,
Белый, с золотою серединой,
Где же мой единственный на свете,
Самый долгожданный и любимый?
Девушки любят гадать на ромашке. А вы знаете, сколько лепестков на этом цветке? Я посчитал, их 21, а на более крупном цветке – 34. И расположены они по принципу спирали. А вот у астры их число стремится к 55, 89 или 114, в зависимости от сорта цветка. [10]
Вы выращиваете в своём огороде капусту брокколи? Спирали на её кочане сразу бросаются в глаза [11]
. Таким образом, закономерность числового ряда Фибоначчи встречается в биологии с постоянным упрямством.
Заключение.
Я изучил и проанализировал проявление числовой последовательности Фибоначчи в жизни растений и обнаружил, что многочисленные примеры двойных спиралей встречаются повсюду в природе и всегда соответствуют этому правилу.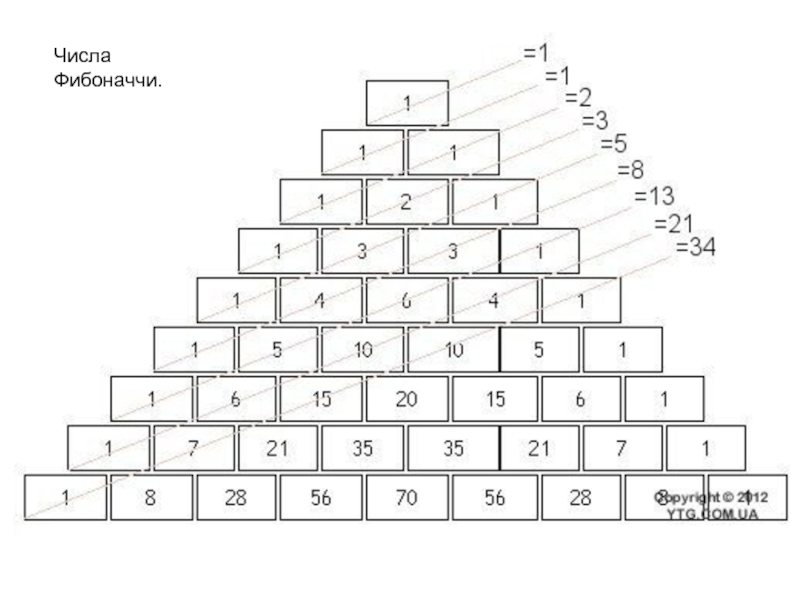
Чем больше смотришь, тем больше находишь. Почему же в природе с таким постоянством повторяются числа ряда Фибоначчи? Почему из всех закономерностей, связанных с ростом, природа выбрала именно ряд Фибоначчи? Эту загадку ещё предстоит разгадать в будущем.
Я очень заинтересовался данной темой и решил в дальнейшем обогатить свои знания в области математики: изучить золотое сечение (золотую пропорцию) Леонардо Фибоначчи
5
Список литературы
Википедия «История возникновения числового ряда Леонардо Фибоначчи»
Википедия «Числа Фибоначчи в биологии»
Воробьев Н. Н. Числа Фибоначчи. – М., Наука, 1984.
6
7 8Учебник по JavaScript: ч.1, Числа Фибоначчи: ilyachalov — LiveJournal
Начало в предыдущем посте: «Учебник по JavaScript: ч.1, Рекурсия и стек».Еще одна интересная задача из учебника, которая в очередной раз показывает, почему рекурсию не следует использовать в реальных программах: «Числа Фибоначчи».
Числа Фибоначчи — это ряд натуральных (целых и положительных) чисел, каждое из которых (начиная с третьего) является суммой двух предыдущих:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 и так далее…
https://ru.wikipedia.org/wiki/Числа_Фибоначчи
По условиям задачи требуется написать функцию, вычисляющую и возвращающую число из этого ряда чисел Фибоначчи по заданному номеру этого числа в этом ряду чисел.
Так как задача находится в подразделе 6.1 «Рекурсия и стек» учебника, то понятно, что предполагается, что ученик сначала попробует решить задачу методом рекурсии. Написать это решение несложно. Для проверки работы получившейся функции предлагается найти числа из ряда чисел Фибоначчи с номерами 3, 7 и 77.
Число с номером 3 из ряда чисел Фибоначчи — это число 2, с номером 7 — число 13, с номером 77 — число 5527939700884757.
И тут выясняется, что при поиске числа Фибоначчи с номером 77 вариант решения с рекурсией завешивает браузер (у меня — «Microsoft Edge») на некоторое время, после чего браузер выдает на экран сообщение о том, что «Эта страница не отвечает» (предлагается на выбор продолжить ожидание — кнопка «Wait», либо насильно завершить работу скрипта страницы — кнопка «Exit page»). Причины этого объяснены в указанном подразделе учебника.
Причины этого объяснены в указанном подразделе учебника.
Как я упоминал ранее (в учебнике это тоже подчеркивается), любую рекурсию можно переделать в цикл. Вариант решения с использованием цикла вместо рекурсии от авторов учебника:
function fib(n) {
let a = 1;
let b = 1;
for (let i = 3; i <= n; i++) {
let c = a + b;
a = b;
b = c;
}
return b;
}
Такое решение спокойно (без зависаний браузера) находит число с номером 77 из ряда чисел Фибоначчи. Причины этого неплохо изложены авторами учебника в их решении, рекомендую почитать.
Однако, мне кажется, у меня получилось решить эту задачу лучше (в смысле — понятнее).
Во-первых, неинформативное название переменных авторы учебника сами ругали в следующем подразделе учебника:
https://learn.javascript.ru/variables#pridumyvayte-pravilnye-imena
Переменные a и b я назвал prev («предыдущее» число в ряде чисел Фибоначчи) и cur («текущее» число в ряде чисел Фибоначчи) соответственно. На каждой итерации цикла нам необходимо знать два числа из ряда чисел Фибоначчи, я их назвал «предыдущим» и «текущим».
На каждой итерации цикла нам необходимо знать два числа из ряда чисел Фибоначчи, я их назвал «предыдущим» и «текущим».
В цикле мы движемся по ряду чисел Фибоначчи в сторону увеличения чисел (вправо). В каждой новой итерации цикла «предыдущее» и «текущее» числа изменяются.
Новое «текущее» число вычисляется как сумма старого (из предыдущей итерации) «текущего» числа и старого (из предыдущей итерации) «предыдущего» числа. После этого старое «текущее» число становится новым «предыдущим» числом. Математическими инструкциями это можно выразить так:
curнов = curстар + prevстар
prevнов = curстар
Переменная c, очевидно, является вспомогательной. Чтобы от нее избавиться, можно применить деструктурирующее присваивание, о котором в учебнике было рассказано ранее и я о нем писал. Преобразуя вышеприведенные математические формулы в JavaScript и применив деструктурирующее присваивание, получаем более изящный и более понятный, чем у авторов учебника, код:
[cur, prev] = [cur + prev, cur];
Решение полностью:
function fib(n) {
let cur = 1, prev = 1;
for (let i = 3; i <= n; i++) {
[cur, prev] = [cur + prev, cur];
}
return cur;
}
Ряд фибоначчи в пропорциях ихтиозавра.
 Последовательность фибоначчи, проиллюстрированная природой Числа Фибоначчи… в природе и жизни
Последовательность фибоначчи, проиллюстрированная природой Числа Фибоначчи… в природе и жизни Леонардо Фибоначчи – один из величайших математиков Средневековья. В одном и своих трудов “Книга вычислений” Фибоначчи описал индо-арабскую систему исчисления и преимущества ее использования перед римской.
Определение
Числа Фибоначчи или Последовательность Фибоначчи – числовая последовательность, обладающая рядом свойств. Например, сумма двух соседних чисел последовательности дает значение следующего за ними (например, 1+1=2; 2+3=5 и т.д.), что подтверждает существование так называемых коэффициентов Фибоначчи, т.е. постоянных соотношений.
Последовательность Фибоначчи начинается так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…
2.
Полное определение чисел Фибоначчи
3.
Свойства последовательности Фибоначчи
4.
1. Отношение каждого числа к последующему более и более стремится к 0.618 по увеличении порядкового номера. Отношение же каждого числе к предыдущему стремится к 1.618 (обратному к 0.618). Число 0.618 называют(ФИ).
Отношение же каждого числе к предыдущему стремится к 1.618 (обратному к 0.618). Число 0.618 называют(ФИ).
2. При делении каждого числа на следующее за ним, через одно получается число 0.382; наоборот – соответственно 2.618.
3. Подбирая таким образом соотношения, получаем основной набор фибоначчиевских коэффициентов: … 4.235, 2.618, 1.618, 0.618, 0.382, 0.236.
5.
Связь последовательности Фибоначчи и «золотого сечения»
6.
Последовательность Фибоначчм асимптотически (пpиближаясь все медленнее и медленнее) стpемится к некотоpому постоянному соотношению. Однако, это соотношение иppационально, то есть пpедставляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифp в дpобной части. Его невозможно выразить точно.
Если какой-либо член последовательности Фибоначчи pазделить на пpедшествующий ему (напpимеp, 13:8), pезультатом будет величина, колеблющаяся около иppационального значения 1.61803398875… и чеpез pаз то пpевосходящая, то не достигающая его. Hо даже затpатив на это Вечность, невозможно узнать сотношение точно, до последней десятичной цифpы. Kpаткости pади, мы будем пpиводить его в виде 1.618. Особые названия этому соотношению начали давать еще до того, как Лука Пачиоли (сpедневековый математик) назвал его Божественной пpопоpцией. Cpеди его совpеменных названий есть такие, как Золотое сечение, Золотое сpеднее и oтношение веpтящихся квадpатов. Kеплеp назвал это соотношение одним из «сокpовищ геометpии». В алгебpе общепpинято его обозначение гpеческой буквой фи
Hо даже затpатив на это Вечность, невозможно узнать сотношение точно, до последней десятичной цифpы. Kpаткости pади, мы будем пpиводить его в виде 1.618. Особые названия этому соотношению начали давать еще до того, как Лука Пачиоли (сpедневековый математик) назвал его Божественной пpопоpцией. Cpеди его совpеменных названий есть такие, как Золотое сечение, Золотое сpеднее и oтношение веpтящихся квадpатов. Kеплеp назвал это соотношение одним из «сокpовищ геометpии». В алгебpе общепpинято его обозначение гpеческой буквой фи
Представим золотое сечение на примере отрезка.
Рассмотрим отрезок с концами A и B. Пусть точка С делит отрезок AB так что,
AC/CB = CB/AB или
AB/CB = CB/AC.
Представить это можно примерно так: A-–C—–B
7.
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.
8.
Отрезки золотой пропорции выражаются бесконечной иррациональной дробью 0,618…, если AB принять за единицу, AC = 0,382.. Kак мы уже знаем числа 0.618 и 0.382 являются коэффициентами последовательности Фибоначчи.
9.
Пропорции Фибоначчи и золотого сечения в природе и истории
10.
Важно отметить, что Фибоначчи как бы напомнил свою последовательность человечеству. Она была известна еще древним грекам и египтянам. И действительно, с тех пор в природе, архитектуре, изобразительном искусстве, математике, физике, астрономии, биологии и многих других областях были найдены закономерности, описываемые коэффициентами Фибоначчи. Просто удивительно, сколько постоянных можно вычислить пpи помощи последовательности Фибоначчи, и как ее члены проявляются в огромном количестве сочетаний. Однако не будет преувеличением сказать, что это не просто игра с числами, а самое важное математическое выражение природных явлений из всех когда-либо открытых.
11.
Пpиводимые ниже примеры показывают некоторые интересные приложения этой математической последовательности.
12.
1. Pаковина закручена по спирали. Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Форма спирально завитой раковины привлекла внимание Архимеда. Дело в том, что отношение измерений завитков раковины постоянно и равно 1.618. Архимед изучал спираль раковин и вывел уравнение спирали. Cпираль, вычерченная по этому уравнению, называется его именем. Увеличение ее шага всегда равномерно. В настоящее время спираль Архимеда широко применяется в технике.
2. Растения и животные. Еще Гете подчеркивал тенденцию природы к спиральности. Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Cпираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Cовместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения. Паук плетет паутину спиралеобразно. Cпиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНK закручена двойной спиралью. Гете называл спираль «кривой жизни».
Выяснилось, что в расположении листьев на ветке семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения. Паук плетет паутину спиралеобразно. Cпиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНK закручена двойной спиралью. Гете называл спираль «кривой жизни».
Cреди придорожных трав растет ничем не примечательное растение — цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.
Импульсы его роста постепенно уменьшались в пропорции золотого сечения.
Ящерица живородящая. В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции – длина ее хвоста так относится к длине остального тела, как 62 к 38.
И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы – симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста. Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого.
Пьер Kюри в начале нашего столетия сформулировал ряд глубоких идей симметрии. Он утверждал, что нельзя рассматривать симметрию какого-либо тела, не учитывая симметрию окружающей среды. Закономерности золотой симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности, как указано выше, есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.
Эти закономерности, как указано выше, есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.
3. Космос. Из истории астрономии известно, что И. Тициус, немецкий астроном XVIII в., с помощью этого ряда (Фибоначчи) нашел закономерность и порядок в расстояниях между планетами солнечной системы
Однако один случай, который, казалось бы, противоречил закону: между Марсом и Юпитером не было планеты. Cосредоточенное наблюдение за этим участком неба привело к открытию пояса астероидов. Произошло это после смерти Тициуса в начале XIX в.
Pяд Фибоначчи используют широко: с его помощью представляют архитектонику и живых существ, и рукотворных сооружений, и строение Галактик. Эти факты – свидетельства независимости числового ряда от условий его проявления, что является одним из признаков его универсальности.
4. Пирамиды. Многие пытались разгадать секреты пирамиды в Гизе. В отличие от других египетских пирамид это не гробница, а скоpее неразрешимая головоломка из числовых комбинаций. Замечательные изобpетательность, мастерство, время и труд аpхитектоpов пирамиды, использованные ими пpи возведении вечного символа, указывают на чрезвычайную важность послания, которое они хотели передать будущим поколениям. Их эпоха была дописьменной, доиероглифической и символы были единственным средством записи открытий. Kлюч к геометро-математическому секрету пирамиды в Гизе, так долго бывшему для человечества загадкой, в действительности был передан Геродоту храмовыми жрецами, сообщившими ему, что пирамида построена так, чтобы площадь каждой из ее граней была равна квадрату ее высоты.
Замечательные изобpетательность, мастерство, время и труд аpхитектоpов пирамиды, использованные ими пpи возведении вечного символа, указывают на чрезвычайную важность послания, которое они хотели передать будущим поколениям. Их эпоха была дописьменной, доиероглифической и символы были единственным средством записи открытий. Kлюч к геометро-математическому секрету пирамиды в Гизе, так долго бывшему для человечества загадкой, в действительности был передан Геродоту храмовыми жрецами, сообщившими ему, что пирамида построена так, чтобы площадь каждой из ее граней была равна квадрату ее высоты.
Площадь тpеугольника
356 x 440 / 2 = 78320
Площадь квадpата
280 x 280 = 78400
Длина ребра основания пирамиды в Гизе равна 783.3 фута (238.7 м), высота пирамиды -484.4 фута (147.6 м). Длина ребра основания, деленная на высоту, приводит к соотношению Ф=1.618. Высота 484.4 фута соответствует 5813 дюймам (5-8-13) – это числа из последовательности Фибоначчи. Эти интересные наблюдения подсказывают, что конструкция пирамиды основана на пропорции Ф=1,618. Некоторые современные ученые склоняются к интерпретации, что древние египтяне построили ее с единственной целью – передать знания, которые они хотели сохранить для грядущих поколений. Интенсивные исследования пирамиды в Гизе показали, сколь обширными были в те времена познания в математике и астрологии. Во всех внутренних и внешних пропорциях пирамиды число 1.618 играет центральную роль.
Некоторые современные ученые склоняются к интерпретации, что древние египтяне построили ее с единственной целью – передать знания, которые они хотели сохранить для грядущих поколений. Интенсивные исследования пирамиды в Гизе показали, сколь обширными были в те времена познания в математике и астрологии. Во всех внутренних и внешних пропорциях пирамиды число 1.618 играет центральную роль.
Пирамиды в Мексике. Hе только египетские пиpамиды постpоены в соответствии с совеpшенными пpопоpциями золотого сечения, то же самое явление обнаpужено и у мексиканских пиpамид. Возникает мысль, что как египетские, так и мексиканские пиpамиды были возведены пpиблизительно в одно вpемя людьми общего происхождения.
Про числа и формулы, которые встречаются в природе. Ну и пару слов про эти самые числа и формулы.
Числа и формулы в природе — это камень преткновения между теми, кто верит в создание вселенной кем-то, и теми, кто верит в создание вселенной самой по себе. Ибо вопрос: «Если бы вселенная возникла сама по себе, то разве практически все живые и неживые обЪекты не были бы построены по одной и той же схеме, по одним и тем же формулам?»
Ну, на этот философский вопрос мы отвечать здесь не будем (формат сайта не тот 🙂), а формулы озвучим. И начнём с чисел Фибоначчи и Золотой спирали.
И начнём с чисел Фибоначчи и Золотой спирали.
Так, числа Фибоначчи — это элементы числовой последовательности, в которой каждое последующее число равно сумме двух предыдущих чисел. То есть, 0 +1=1, 1+1=2, 2+1=3, 3+2=5 и так далее.
Итого, получается ряд: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946
Ещё один пример ряда Фибоначчи: 0, 2, 2, 4, 6, 10, 16, 26, 42, 68, 110, 178 и так далее. Можете поэкспериментировать сами 🙂
Как числа Фибоначчи проявляются в природе? Очень просто:
- Листорасположение у растений описывается последовательностью Фибоначчи. Семена подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса также располагаются согласно последовательности Фибоначчи.
- Длины фаланг пальцев человека относятся примерно как числа Фибоначчи.
- Молекулу ДНК составляют две вертикально переплетенные спирали длиной 34 ангстрема и шириной 21 ангстрема. Числа 21 и 34 следуют друг за другом в последовательности Фибоначчи.

С помощью чисел Фибоначчи можно построить Золотую Спираль. Так, нарисуем маленький квадратик со стороной, скажем, в 1. Далее вспомним школу. Сколько будет 1 2 ? Это будет 1. Значит, нарисуем ещё один квадратик рядом с первым, вплотную. Далее, следующее число Фибоначчи — 2 (1+1). Сколько будет 2 2 ? Это будет 4. Нарисуем вплотную к первым двум квадратам ещё один квадрат, но теперь со стороной 2 и площадью 4. Следующее число — это число 3 (1+2). Квадрат числа 3 — это 9. Рисуем квадрат со стороной 3 и площадью 9 рядом с уже нарисованными. Далее у нас идёт квадрат со стороной 5 и площадью 25, квадрат со стороной 8 и площадью 64 — и так далее, до бесконечности.
Настало время для золотой спирали. Соединим плавной кривой линией точки-границы между квадратами. И получим ту самую золотую спираль, на основе которой строятся многие живые и неживые обЪекты в природе.
И перед тем, как переходить к золотому сечению, подумаем. Вот мы построили спираль на основе квадратов последовательности Фибоначчи (последовательность 1, 1, 2, 3, 5, 8 и квадраты 1, 1, 4, 9, 25, 64). Но что будет, если мы воспользуемся не квадратами чисел, а их кубами? Кубы будут выглядеть из центра так:
Но что будет, если мы воспользуемся не квадратами чисел, а их кубами? Кубы будут выглядеть из центра так:
А сбоку так:
Ну а при построении спирали, получится обЪёмная золотая спираль :
Вот так эта обЪёмная золотая спираль выглядит сбоку:
Но что если мы возьмём не кубы чисел Фибоначчи, а перейдём в четвёртое измерение?.. Вот это головоломка, да?
Однако, понятия не имею, как в природе проявляется обЪёмное золотое сечение на основе кубов чисел Фибоначчи, а уж тем более чисел в четвёртой степени. Поэтому возвращаемся к золотому сечению на плоскости. Так, снова посмотрим на наши квадраты. Если говорить математически, то получается вот такая вот картинка:
То есть, мы получаем золотое сечение — где одна сторона делится на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.
То есть, a: b = b: c или с: b = b: а.
На основе такого вот отношения величин строится, помимо прочего, правильный пятиугольник и пентаграмма:
Для справки: для построения пентаграммы необходимо построить правильный пятиугольник.
Способ его построения разработал немецкий живописец и график Альбрехт Дюрер (1471…1528). Пусть O — центр окружности, A — точка на окружности и Е — середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
В общем, такие вот закономерности. Причём разнообразных закономерностей намного больше, чем было описано. И теперь, после всех этих скучноватых чисел — обещанный видео-ролик, где всё просто и наглядно:
Как видите, математика действительно присутствует в природе. Причём не только в перечисленных в видео обЪектах, но и во многих других областях. Например, когда волна набегает на берег и закручивается, то закручивается она по Золотой спирали. Ну и так далее 🙂
Причём не только в перечисленных в видео обЪектах, но и во многих других областях. Например, когда волна набегает на берег и закручивается, то закручивается она по Золотой спирали. Ну и так далее 🙂
Золотое сечение и числа последовательности Фибоначчи. June 14th, 2011
Некоторое время назад я обещала прокомментировать утверждение Толкачева о том, что Питер построен по принципу Золотого Сечения, а Москва – по принципу симметрии, и что именно поэтому столь ощутимы различия в восприятии этих двух городов, и именно поэтому петербуржец, приезжая в Москву «заболевает головой», а москвич «заболевает головой», приезжая в Питер. Требуется некоторое время для сонастройки с городом (как при перелете в штаты – требуется сонастройка со временем).
Дело в том, что наш глаз смотрит — ощупывая пространство с помощью определенных движений глаз – саккад (в переводе – хлопок паруса). Глаз совершает «хлопок» и посылает сигнал в мозг «сцепление с поверхностью произошло. Все в порядке. Информация такая-то». И в течение жизни глаз привыкает к определенной ритмике этих саккад. И когда эта ритмика кардинально меняется (с городского пейзажа на лес, с Золотого Сечения на симметрию) – тут то и требуется некоторая работа мозга по перенастройке.
И в течение жизни глаз привыкает к определенной ритмике этих саккад. И когда эта ритмика кардинально меняется (с городского пейзажа на лес, с Золотого Сечения на симметрию) – тут то и требуется некоторая работа мозга по перенастройке.
Теперь подробности:
Определение ЗС — это деление отрезка на две части в таком соотношении, при котором большая часть относится к меньшей, как их сумма (весь отрезок) к большей.
То есть, если мы примем весь отрезок c за 1, то отрезок a будет равен 0,618, отрезок b — 0,382. Таким образом, если взять строение, например, храм, построенный по принципу ЗС, то при его высоте скажем 10 метров, высота барабана с куполом будут равны 3,82 см, а высота основания строения будет 6, 18 см. (понятно, что цифры я взяла ровными для наглядности)
А какова связь между ЗС и числами Фибоначчи?
Числа последовательности Фибоначчи это:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597…
Закономерность чисел в том, что каждое последующее число равно сумме двух предыдущих чисел.
0 + 1 = 1;
1 + 1 = 2;
2 + 3 = 5;
3 + 5 = 8;
5 + 8 = 13;
8 + 13 = 21 и т.д.,
а отношение смежных чисел приближается к отношению ЗС.
Так, 21: 34 = 0,617, а 34: 55 = 0,618.
То есть в основе ЗС лежат числа последовательности Фибоначчи.
Вот этот ролик ещё раз наглядно демонстрирует эту связь ЗС и чисел Фибоначчи
Где ещё встречаются принцип ЗС и числа последовательности Фибоначчи?
Листья у растений описывается последовательностью Фибоначчи. Зерна подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса также располагаются согласно последовательности Фибоначчи.
Яйцо птицы
Длины фаланг пальцев человека относятся примерно как числа Фибоначчи. Золотое сечение просматривается в пропорциях лица.
Эмиль Розенов исследовал ЗС в музыке эпохи Барокко и классицизма на примере произведений Баха, Моцарта, Бетховена.
Известно, что Сергей Эйзенштейн искусственно построил фильм «Броненосец Потёмкин» по правилам ЗС. Он разбил ленту на пять частей. В первых трёх действие развивается на корабле. В двух последних — в Одессе, где разворачивается восстание. Этот переход в город происходит точно в точке золотого сечения. Да и в каждой части есть свой перелом, происходящий по закону золотого сечения. В кадре, сцене, эпизоде происходит некий скачок в развитии темы: сюжета, настроения. Эйзенштейн считал, что, так как такой переход близок к точке золотого сечения, он воспринимается как наиболее закономерный и естественный.
Он разбил ленту на пять частей. В первых трёх действие развивается на корабле. В двух последних — в Одессе, где разворачивается восстание. Этот переход в город происходит точно в точке золотого сечения. Да и в каждой части есть свой перелом, происходящий по закону золотого сечения. В кадре, сцене, эпизоде происходит некий скачок в развитии темы: сюжета, настроения. Эйзенштейн считал, что, так как такой переход близок к точке золотого сечения, он воспринимается как наиболее закономерный и естественный.
Многие элементы декора, а так же шрифты, созданы с использованием ЗС. Например шрифт А.Дюрера (в рисунке буква «А»)
Считается, что термин «Золотое сечение» ввел Леонардо Да Винчи, который говорил, «пусть никто, не будучи математиком, не дерзнет читать мои труды” и показывал пропорции человеческого тела на своём знаменитом рисунке «Витрувианский человек». “Если мы человеческую фигуру – самое совершенное творение Вселенной – перевяжем поясом и отмерим потом расстояние от пояса до ступней, то эта величина будет относиться к расстоянию от того же пояса до макушки, как весь рост человека к длине от пояса до ступней”.
Знаменитый портрет Моны Лизы или Джоконды (1503) создан по принципу золотых треугольников.
Собственно говоря сама звезда или пентакль представляет собой построение ЗС.
Ряд чисел Фибоначчи наглядно моделируется (материализуется) в форме спирали
А в природе спираль ЗС выглядит вот так:
При этом, спираль наблюдается повсеместно (в природе и не только):
— Семена в большинстве растений расположены по спирали
— Паук плетет паутину по спирали
— Спиралью закручивается ураган
— Испуганное стадо северных оленей разбегается по спирали.
— Молекула ДНK закручена двойной спиралью. Молекулу ДНК составляют две вертикально переплетенные спирали длиной 34 ангстрема и шириной 21 ангстрема. Числа 21 и 34 следуют друг за другом в последовательности Фибоначчи.
— Эмбрион развивается в форме спирали
— Спираль «улитки во внутреннем ухе»
— Вода уходит в слив по спирали
— Спиральная динамика показывает развитие личности человека и его ценностей по спирали.
— Ну и конечно, сама Галактика имеет форму спирали
Таким образом можно утверждать, что сама природа построена по принципу Золотого Сечения, оттого эта пропорция гармоничнее воспринимается человеческим глазом. Она не требует «исправления» или дополнения получаемой картинки мира.
Теперь о Золотом сечении в архитектуре
Пирамида Хеопса представляет собой пропорции ЗС. (Фотография нравится – с заваленным песком Сфинксом).
Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции.
Собор «Нотредам де Пари» в Париже, Франция.
Одно из выдающихся строений, выполненных по принципу ЗС – Смольный Собор в Питере. К собору ведут по краям две дорожки и если приближаться по ним к собору, то тот будто приподнимается в воздухе.
В Москве также есть строения выполненные с использованием ЗС. Например, Храм Василия Блаженного
Например, Храм Василия Блаженного
Однако застройка, использующая принципы симметрии преобладает.
Например, Кремль и Спасская башня.
Высота стен Кремля также нигде не отражает принципа ЗС относительно высоты башен, например. Или взять гостиницу Россия, или гостиницу Космос.
При этом здания, построенные по принципу ЗС представляют больший процент в Питере, при этом это здания уличной застройки. Литейный проспект.
Таким образом, Золотое Сечение использует коэффицент 1,68, а симметрия 50/50.
То есть симметричные здания построены по принципу равенства сторон.
Ещё одной важной характеристикой ЗС является её динамичность и стремление к разворачиванию, за счет последовательности чисел Фибоначчи. Тогда как симметрия – наоборот представляет собой стабильность, устойчивость и неподвижность.
Кроме этого, дополнительное ЗС вносит в план Питера обилие водных пространств, расплескавшихся по городу и диктующих подчиненность города их изгибам. Да и сама схема Питера напоминает спираль или зародыш одновременно.
Папа, правда, высказал другую версию, отчего у москвичей и питерцев «голова болит» при посещении столиц. Папа относит это к энергиям городов:
Санкт-Петербург – имеет мужской род и соответственно мужские энергии,
Ну а Москва – соответственно – женского рода и обладает женскими энергиями.
Так жителям столиц, настроившимся на свой определенный баланс женского и мужского в своих организмах – сложно перестраиваться при посещении города-соседа, а у кого-то может и сложности какие-то имеются с восприятием одной или другой энергий и оттого город сосед могут и вовсе не любить!
В подтверждение этой версии говорит и то, что все российские императрицы правили именно в Питере, тогда как Москва видела лишь царей мужского пола!
Использованные ресурсы.
Последовательность Фибоначчи , известная всем по фильму «Код Да Винчи» — ряд цифр, описанный в виде загадки Итальянским математиком Леонардо Пизанским, более известным под прозвищем Фибоначчи, в XIII веке. Вкратце суть загадки:
Вкратце суть загадки:
Кто-то поместил пару кроликов в некоем замкнутом пространстве, чтобы узнать, сколько пар кроликов родится при этом в течении года, если природа кроликов такова, что каждый месяц пара кроликов производит на свет другую пару, а способность к производству потомства у них появляется по достижению двухмесячного возраста.
В итоге получается такой ряд цифр: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 , где через запятую показано количество пар кроликов в каждом из двенадцати месяцев. Его можно продолжать бесконечно долго. Его суть в том, что каждое следующее число является суммой двух предыдущих.
У этого ряда есть несколько математических особенностей, которых обязательно нужно коснуться. Он асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.
Его невозможно выразить точно.
Так отношение какого-либо члена ряда к предшествующему ему колеблется около числа 1,618 , через pаз то превосходя, то не достигая его. Отношение к следующему аналогично приближается к числу 0,618 , что обратно пропорционально 1,618 . Если мы будем делить элементы через одно, то получим числа 2,618 и 0,382 , которые так же являются обратно пропорциональными. Это так называемые коэффициенты Фибоначчи.
К чему всё это? Так мы приближаемся к одному из самых загадочных явлений природы. Смекалистый Леонардо по сути не открыл ничего нового, он просто напомнил миру о таком явлении, как Золотое Сечение , которое не уступает по значимости теореме Пифагора.
Все окружающие нас предметы мы различаем в том числе и по форме. Какие-то нам нравятся больше, какие-то меньше, некоторые вовсе отталкивают взгляд. Иногда интерес может быть продиктован жизненной ситуацией, а порой красотой наблюдаемого объекта. Симметричная и пропорциональная форма, способствует наилучшему зрительному восприятию и вызывает ощущение красоты и гармонии. Целостный образ всегда состоит из частей разного размера, находящихся в определённом соотношении друг с другом и целым. Золотое сечение — высшее проявление совершенства целого и его частей в науке, искусстве и природе.
Целостный образ всегда состоит из частей разного размера, находящихся в определённом соотношении друг с другом и целым. Золотое сечение — высшее проявление совершенства целого и его частей в науке, искусстве и природе.
Если на простом примере, то Золотое Сечение — это деление отрезка на две части в таком соотношении, при котором большая часть относится к меньшей, как их сумма (весь отрезок) к большей.
Если мы примем весь отрезок c за 1 , то отрезок a будет равен 0,618 , отрезок b — 0,382 , только так будет соблюдено условие Золотого Сечения (0,618/0,382=1,618 ; 1/0,618=1,618 ) . Отношение c к a равно 1,618 , а с к b 2,618 . Это всё те же, уже знакомые нам, коэффициенты Фибоначчи.
Разумеется есть золотой прямоугольник, золотой треугольник и даже золотой кубоид. Пропорции человеческого тела во многих соотношениях близки к Золотому Сечению.
Изображение: marcus-frings.de
Но самое интересное начинается, когда мы объединим полученные знания. На рисунке наглядно показана связь между последовательностью Фибоначчи и Золотым сечением. Мы начинаем с двух квадратов первого размера. Сверху добавляем квадрат второго размера. Подрисовываем рядом квадрат со стороной, равной сумме сторон двух предыдущих, третьего размера. По аналогии появляется квадрат пятого размера. И так далее пока не надоест, главное, чтобы длина стороны каждого следующего квадрата равнялась сумме длин сторон двух предыдущих. Мы видим серию прямоугольников, длины сторон, которых являются числами Фибоначчи, и, как не странно, они называются прямоугольниками Фибоначчи.
Если мы проведём плавную линий через углы наших квадратов, то получим ни что иное, как спираль Архимеда, увеличение шага которой всегда равномерно.
Ничего не напоминает?
Фото: ethanhein on Flickr
И не только в раковине моллюска можно найти спирали Архимеда, а во многих цветах и растениях, просто они не такие явные.
Алое многолистный:
Фото: brewbooks on Flickr
Фото: beart.org.uk
Фото: esdrascalderan on Flickr
Фото: mandj98 on Flickr
И тут самое время вспомнить о Золотом Сечении! Ни одни ли из самых прекрасных и гармоничных творений природы изображены на этих фотографиях? И это далеко не все. Присмотревшись, можно найти похожие закономерности во многих формах.
Конечно заявление, что все эти явление построены на последовательности Фибоначчи звучит слишком громко, но тенденция на лицо. Да и к тому же сама она далека от совершенства, как и всё в этом мире.
Есть предположение, что ряд Фибоначчи — это попытка природы адаптироваться к более фундаментальной и совершенной золотосечённой логарифмической последовательности, которая практически такая же, только начинается из ниоткуда и уходит в никуда. Природе же обязательно нужно какое-то целое начало, от которого можно оттолкнуться, она не может создать что-то из ничего.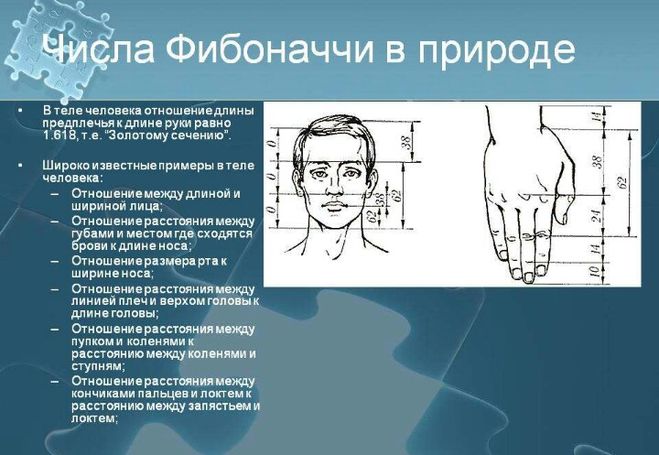 Отношения первых членов последовательности Фибоначчи далеки от Золотого Сечения. Но чем дальше мы продвигаемся по ней, тем больше эти отклонения сглаживаются. Для определения любого ряда достаточно знать три его члена, идущие друг за другом. Но только не для золотой последовательности, ей достаточно двух, она является геометрической и арифметической прогрессией одновременно. Можно подумать, будто она основа для всех остальных последовательностей.
Отношения первых членов последовательности Фибоначчи далеки от Золотого Сечения. Но чем дальше мы продвигаемся по ней, тем больше эти отклонения сглаживаются. Для определения любого ряда достаточно знать три его члена, идущие друг за другом. Но только не для золотой последовательности, ей достаточно двух, она является геометрической и арифметической прогрессией одновременно. Можно подумать, будто она основа для всех остальных последовательностей.
Каждый член золотой логарифмической последовательности является степенью Золотой Пропорции (z ). Часть ряда выглядит примерно так: … z -5 ; z -4 ; z -3 ; z -2 ; z -1 ; z 0 ; z 1 ; z 2 ; z 3 ; z 4 ; z 5 … Если мы округлим значение Золотой пропорции до трёх знаков, то получим z=1,618 , тогда ряд выглядит так: … 0,090 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854; 11,090 … Каждый следующий член может быть получен не только умножением предыдущего на 1,618 , но и сложением двух предыдущих.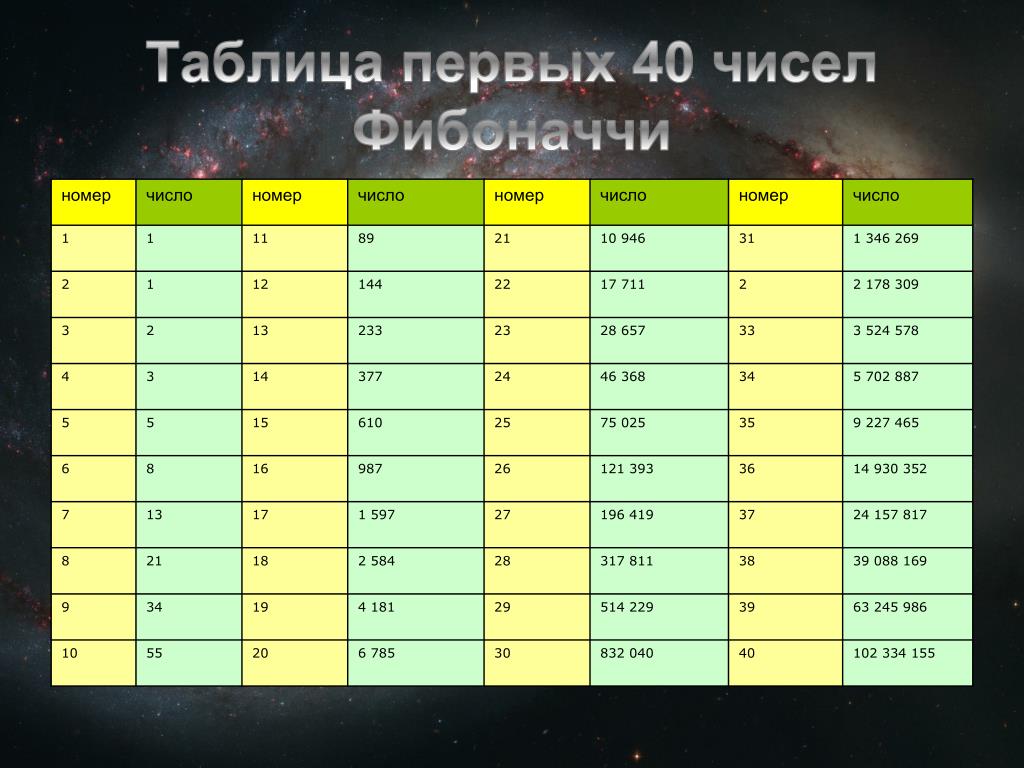 Таким образом экспоненциальный рост обеспечивается путем простого сложения двух соседних элементов. Это ряд без начала и конца, и именно на него пытается быть похожей последовательность Фибоначчи. Имея вполне определённое начало, она стремится к идеалу, никогда его не достигая. Такова жизнь.
Таким образом экспоненциальный рост обеспечивается путем простого сложения двух соседних элементов. Это ряд без начала и конца, и именно на него пытается быть похожей последовательность Фибоначчи. Имея вполне определённое начало, она стремится к идеалу, никогда его не достигая. Такова жизнь.
И всё-таки, в связи со всем
увиденным и прочитанным, возникают вполне закономерные вопросы:
От
куда взялись эти числа? Кто этот архитектор вселенной, попытавшийся
сделать её идеальной? Было ли когда-то всё так, как он хотел? И если
да, то почему сбилось? Мутации? Свободный выбор? Что же будет дальше?
Спираль скручивается или раскручивается?
Найдя ответ на один вопрос, получишь следующий. Разгадаешь его, получишь два новых. Разберёшься с ними, появится ещё три. Решив и их, обзаведёшься пятью нерешёнными. Потом восемью, потом тринадцатью, 21, 34, 55…
Источники: ; ; ;
Вам, конечно же, знакома идея о том, что математика является самой главной из всех наук. Но многие могут с этим не согласиться, т. к. порой кажется, что математика – это лишь задачи, примеры и тому подобная скукотища. Однако математика может запросто показать нам знакомые вещи с совершенно незнакомой стороны. Мало того – она даже может раскрыть тайны мироздания. Как? Давайте обратимся к числам Фибоначчи.
к. порой кажется, что математика – это лишь задачи, примеры и тому подобная скукотища. Однако математика может запросто показать нам знакомые вещи с совершенно незнакомой стороны. Мало того – она даже может раскрыть тайны мироздания. Как? Давайте обратимся к числам Фибоначчи.
Что такое числа Фибоначчи?
Числа Фибоначчи являются элементами числовой последовательности, где каждое последующее посредством суммирования двух предыдущих, например: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89… Как правило, записывается такая последовательность формулой: F 0 = 0, F 1 = 1, F n = F n-1 + F n-2 , n ≥ 2.
Числа Фибоначчи могут начинаться и с отрицательных значений «n», но в таком случае последовательность будет двусторонней – она будет охватывать и положительные и отрицательные числа, стремясь к бесконечности в двух направлениях. Примером такой последовательности может послужить: -34, -21, -13, -8, -5, -3, -2, -1, 1, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, а формула будет: F n = F n+1 — F n+2 или же F -n = (-1) n+1 Fn.
Создателем чисел Фибоначчи является один из первых математиков Европы средних веков по имени Леонардо Пизанский, которого, собственно и знают, как Фибоначчи – это прозвище он получил спустя много лет после своей смерти.
При жизни Леонардо Пизанский очень любил математические турниры, по причине чего в своих работах («Liber abaci» /«Книга абака», 1202; «Practica geometriae»/«Практика геометрии», 1220, «Flos»/«Цветок», 1225 год – исследование на тему кубических уравнений и «Liber quadratorum»/«Книга квадратов», 1225 – задачи о неопределенных квадратных уравнениях) очень часто разбирал всевозможные математические задачи.
О жизненном пути самого Фибоначчи известно крайне мало. Но достоверно известно то, что его задачи пользовались огромнейшей популярностью в математических кругах в последующие века. Одну из таких мы и рассмотрим далее.
Задача Фибоначчи с кроликами
Для выполнения задачи автором были поставлены следующие условия: есть пара новорождённых крольчат (самка и самец), отличающихся интересной особенностью – со второго месяца жизни они производят новую пару кроликов – тоже самку и самца. Кролики находятся в замкнутом пространстве и постоянно размножаются. И ни один кролик не умирает.
Задача : определить количество кроликов через год.
Решение :
У нас есть:
- Одна пара кроликов в начале первого месяца, которая спаривается в конце месяца
- Две пары кроликов во втором месяце (первая пара и потомство)
- Три пары кроликов в третьем месяце (первая пара, потомство первой пары с прошлого месяца и новое потомство)
- Пять пар кроликов в четвёртом месяце (первая пара, первое и второе потомство первой пары, третье потомство первой пары и первое потомство второй пары)
Количество кроликов в месяц «n» = количеству кроликов прошлого месяца + количество новых пар кроликов, другими словами, вышеназванная формула: F n = F n-1 + F n-2 . Отсюда получается рекуррентная числовая последовательность (о рекурсии мы скажем далее), где каждое новое число соответствует сумме двух предыдущих чисел:
1 месяц: 1 + 1 = 2
2 месяц: 2 + 1 = 3
3 месяц: 3 + 2 = 5
4 месяц: 5 + 3 = 8
5 месяц: 8 + 5 = 13
6 месяц: 13 + 8 = 21
7 месяц: 21 + 13 = 34
8 месяц: 34 + 21 = 55
9 месяц: 55 + 34 = 89
10 месяц: 89 + 55 = 144
11 месяц: 144 + 89 = 233
12 месяц: 233+ 144 = 377
И эта последовательность может продолжаться бесконечно долго, но учитывая, что задачей является узнать количество кроликов по истечении года, получается 377 пар.
Здесь важно также заметить, что одним из свойств чисел Фибоначчи является то, что если сопоставить две последовательные пары, а затем разделить большую на меньшую, то результат будет двигаться по направлению к золотому сечению, о котором мы также скажем ниже.
Пока же предлагаем вам ещё две задачи по числам Фибоначчи:
- Определить квадратное число, о котором известно только, что если отнять от него 5 или прибавить к нему 5, то снова выйдет квадратное число.
- Определить число, делящееся на 7, но при условии, что поделив его на 2, 3, 4, 5 или 6 в остатке будет 1.
Такие задачи не только станут отличным способом развития ума, но и занимательным времяпрепровождением. О том, как решаются эти задачи, вы также можете узнать, поискав информацию в Интернете. Мы же не будем заострять на них внимание, а продолжим наш рассказ.
Что же такое рекурсия и золотое сечение?
Рекурсия
Рекурсия является описанием, определением или изображением какого-либо объекта или процесса, в котором есть сам данный объект или процесс. Иначе говоря, объект или процесс можно назвать частью самого себя.
Рекурсия широко используется не только в математической науке, но также и в информатике, массовой культуре и искусстве. Применимо к числам Фибоначчи, можно сказать, что если число равно «n>2», то «n» = (n-1)+(n-2).
Золотое сечение
Золотое сечение является делением целого на части, соотносящиеся по принципу: большее относится к меньшему аналогично тому, как общая величина относится к большей части.
Впервые о золотом сечении упоминает Евклид (трактат «Начала» прим. 300 лет до н.э.), говоря и построении правильного прямоугольника. Однако более привычное понятие было введено немецким математиком Мартином Омом.
Приблизительно золотое сечение можно представить в качестве пропорционального деления на две разные части, к примеру, на 38% и 68%. Численное же выражение золотого сечения равно примерно 1,6180339887.
На практике золотое сечение используется в архитектуре, изобразительном искусстве (посмотрите работы ), кино и других направлениях. На протяжении долгого времени, впрочем, как и сейчас, золотое сечение считалось эстетической пропорцией, хотя большинством людей оно воспринимается непропорциональным – вытянутым.
Вы можете попробовать оценить золотое сечение сами, руководствуясь следующими пропорциями:
- Длина отрезка a = 0,618
- Длина отрезка b= 0,382
- Длина отрезка c = 1
- Соотношение c и a = 1,618
- Соотношение c и b = 2,618
Теперь же применим золотое сечение к числам Фибоначчи: берём два соседних члена его последовательности и делим большее на меньшее. Получаем примерно 1,618. Если же возьмём то же самое большее число и поделим его на следующее большее за ним, то получим примерно 0,618. Попробуйте сами: «поиграйте» с числами 21 и 34 или какими-то другими. Если же провести этот опыт с первыми числами последовательности Фибоначчи, то такого результата уже не будет, т.к. золотое сечение «не работает» в начале последовательности. Кстати, чтобы определить все числа Фибоначчи, нужно знать всего лишь три первых последовательных числа.
И в заключение ещё немного пищи для ума.
Золотой прямоугольник и спираль Фибоначчи
«Золотой прямоугольник» — это ещё одна взаимосвязь между золотым сечением и числами Фибоначчи, т.к. соотношение его сторон равно 1,618 к 1 (вспоминайте число 1,618!).
Вот пример: берём два числа из последовательности Фибоначчи, например 8 и 13, и чертим прямоугольник с шириной 8 см и длинной 13 см. Далее разбиваем основной прямоугольник на мелкие, но их длина и ширина должна соответствовать числам Фибоначчи – длина одной грани большого прямоугольника должна равняться двум длинам грани меньшего.
После этого соединяем плавной линией углы всех имеющихся у нас прямоугольников и получаем частный случай логарифмической спирали – спираль Фибоначчи. Её основными свойствами являются отсутствие границ и изменение форм. Такую спираль можно часто встретить в природе: самыми яркими примерами являются раковины моллюсков, циклоны на изображениях со спутника и даже ряд галактик. Но более интересно то, что этому же правилу подчиняется и ДНК живых организмов, ведь вы помните, что оно имеет спиралевидную форму?
Эти и многие другие «случайные» совпадения даже сегодня будоражат сознание учёных и наводят на мысль о том, что всё во Вселенной подчинено единому алгоритму, причём, именно математическому. И эта наука кроет в себе огромное количество совсем нескучных тайн и загадок.
Генерация чисел Фибоначчи
Эта статья посвящена алгоритмам, которые можно использовать для генерации чисел Фибоначчи.
Последовательности Фибоначчи — одна из самых известных последовательностей в математике.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144… *
Последовательность названа в честь Леонардо Боначчи (также известного как «Фибоначчи» 1170-1250 ), который считается «самым талантливым западным математиком средневековья».
Каждое число в последовательности генерируется путем сложения двух предыдущих чисел.
F n = F n-1 + F n-2
* Люди спорят, должна ли последовательность начинаться с нуля или с единицы. Я собираюсь определить F 0 = 1
Везде
Вы обнаружите, что числа Фибоначчи встречаются во многих местах (как в природе, так и в математике), а их последовательность тесно связана с золотым сечением φ (о золотом сечении написано даже больше, чем о Фибоначчи. Некоторые из них даже верны. , но есть также много « псевдонауки », и некоторые утверждения по этому поводу просто неверны или выдуманы! Если кто-то расскажет вам какой-нибудь интересный « факт » о золотом сечении, сначала примените фильтр здравого смысла, прежде чем думать о нем. веря в это).
Отношение двух соседних членов в последовательности Фибоначчи является приближением золотого сечения φ
Чем больше используются термины, тем лучше приближение, поэтому 1597 / 987 является лучшим приближением, чем 34 / 21 .
| Факс 0 | Ф. 1 | Ф. 2 | Ф. 3 | Ф. 4 | Ф. 5 | Ф. 6 | Ф. 7 | Ф. 8 | Ф. 9 | Ф. 10 | Ф. 11 | Ф. 12 | Ф. 13 | Ф. 14 | Ф. 15 | Ф. 16 | Ф. 17 | Ф. 18 | Факс 19 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | 987 | 1597 | 2584 | 4181 | 6765 |
Ни для кого не удивительно *, вы также можете найти числа Фибоначчи в треугольнике Паскаля.
* В треугольнике Паскаля просто так много увлекательных фактов, последовательностей и свойств, что, когда кто-то обнаруживает какое-то новое свойство, никто не кажется удивленным или шокированным, и единственные люди, искренне взволнованные и заинтересованные новым открытием, — это сами первооткрыватели. и люди, которые пишут книги о треугольнике Паскаля 🙂
Построение чисел Фибоначчи
Теперь, когда мы знаем, как определяются числа Фибоначчи, как мы будем генерировать их в коде?
Первая идея, которая может прийти в голову, — это рекурсия.Поскольку последующие числа Фибоначчи являются самоподобными версиями самих себя, мы можем написать довольно компактный код для их генерации, рекурсивно вызывая ту же функцию, останавливаясь только тогда, когда мы дойдем до первой пары чисел. Вот какой-то псевдокод, чтобы показать эту идею (я предполагаю, что мы работаем только с положительными индексами Фибоначчи):
Функция Фибоначчи (n)
Если n
Фибоначчи = 1
Остальное
Фибоначчи = Фибоначчи (n-1) + Фибоначчи (n-2)
Конец, если
Конечная функция
Этот код, безусловно, выглядит очень аккуратно и его легко понять.Он дает правильный ответ, но это ужасное решение.
Ужасно, ужасно, ужасно. Вы понимаете, почему?
Чтобы понять почему, давайте немного отремонтируем это. Я помещу туда инструкцию для печати, чтобы показать, что происходит:
Функция Фибоначчи (n)
Распечатать «Hello World n =»; n
Если n
Фибоначчи = 1
Остальное
Фибоначчи = Фибоначчи (n-1) + Фибоначчи (n-2)
Конец, если
Конечная функция
Каждый раз, когда вызывается наша функция, мы выводим сообщение по мере прохождения.Давайте посмотрим пример вывода для низких значений n
| п = 0 | п = 1 | п = 2 | п = 3 |
|---|---|---|---|
| Привет, мир n = 0 | Привет, мир n = 1 | Привет, мир n = 2 Привет, мир n = 1 Привет, мир n = 0 | Привет, мир n = 3 Привет, мир n = 2 Привет, мир n = 1 Привет, мир n = 0 Привет, мир n = 1 |
Пока все хорошо. Для n = 0,1,2 результаты тривиальны. Однако мы можем начать видеть проблему для n = 3.
Чтобы вычислить первую часть, Фибоначчи (n-1) , мы должны пройти через 2,1,0. Затем для второй части, Фибоначчи (n-2) , мы должны пройти 1. Опять же, неплохо, но есть пара проблем. Во-первых, мы вызываем одну и ту же функцию несколько раз в шахматном порядке (что должно дать нам один и тот же ответ только со сдвигом по фазе), а вторая проблема заключается в том, что мы (расточительно) каждый раз пересчитываем среднюю часть. Давайте так, насколько это быстро взрывается. Вот оно с n = 4, 5, 6:
| п = 4 | п = 5 | п = 6 |
|---|---|---|
| Привет, мир n = 4 Привет, мир n = 3 Привет, мир n = 2 Привет, мир n = 1 Привет, мир n = 0 Привет, мир n = 1 Привет, мир n = 2 Привет, мир n = 1 Привет, мир n = 0 | Привет, мир n = 5 Привет, мир n = 4 Привет, мир n = 3 Привет, мир n = 2 Привет, мир n = 1 Привет, мир n = 0 Привет, мир n = 1 Привет, мир n = 2 Привет, мир n = 1 Привет, мир n = 0 Привет, мир n = 3 Привет, мир n = 2 Привет, мир n = 1 Привет, мир n = 0 Привет, мир n = 1 | Привет, мир n = 6 Привет, мир n = 5 Привет, мир n = 4 Привет, мир n = 3 Привет, мир n = 2 Привет, мир n = 1 Привет, мир n = 0 Привет, мир n = 1 Привет, мир n = 2 Привет, мир n = 1 Привет, мир n = 0 Привет, мир n = 3 Привет, мир n = 2 Привет, мир n = 1 Привет, мир n = 0 Привет, мир n = 1 Привет, мир n = 4 Привет, мир n = 3 Привет, мир n = 1 Привет, мир n = 1 Привет, мир n = 0 Привет, мир n = 1 Привет, мир n = 2 Привет, мир n = 1 Привет, мир n = 0 |
Давайте посмотрим, что происходит. Слева находится дерево рекурсивного вызова функции. Вы можете сразу увидеть, насколько сложные вещи вложены, и теперь n = 1 избыточно вычисляется пять раз. |
Это ужасная, ужасная схема алгоритма Понци. Каждая последующая глубина берет все предыдущие две части и обертывает их собственными страданиями. Чтобы увидеть, насколько сильно это разрастается, подсчитайте, сколько раз будет напечатано «Hello World», если вы воспользуетесь этим алгоритмом:
| Факс 0 | Ф. 1 | Ф. 2 | Ф. 3 | Ф. 4 | Ф. 5 | Ф. 6 | Ф. 7 | Ф. 8 | Ф. 9 | … | Ф. 14 | Ф. 15 | … | Ф. 29 | … | Ф. 39 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 5 | 9 | 15 | 25 | 41 | 67 | 109 | … | 1,219 | 1 973 | … | 1,664,079 | … | 204 668 309 |
Это безумие, чтобы вычислить F 39 , нам нужно пройти через функцию более 200 миллионов раз!
Должны быть способы получше.
Воспоминание
Если бы мы могли вспомнить предыдущие результаты, нам не пришлось бы возвращаться вниз по дереву, чтобы вычислить ответы, которые мы уже видели.
Это техника, называемая мемоизацией. Каждый раз, когда нам нужно определить значение Фибоначчи, мы проверяем, рассчитали ли мы его уже; в таком случае мы используем уже предварительно рассчитанное значение. Если нет, мы рассчитываем его только один раз и сохраняем для дальнейшего использования.
‘установка
уже вычислено (0) = 1: уже вычислено (1) = 1
Функция Фибоначчи (n)
Если уже вычислено (n), то
Фибоначчи = уже вычислено (n)
еще
Фибоначчи = Фибоначчи (n-1) + Фибоначчи (n-2)
уже вычислено (n) =
ФибоначчиКонец, если
Конечная функция
В этом коде мы предварительно заполняем F 0 и F 1 при инициализации.
Затем, когда функция вызывается, мы сначала проверяем, есть ли у нас это значение в кеше. Если да, то возвращаем и готово.
Если мы еще не вычислили это значение, мы выполняем рекурсию, как и раньше, но каждый вызов проверяет, не встретили ли мы известное значение и короткое замыкание в этой точке. После вычисления этого нового значения мы добавляем его в кеш для будущего использования.
В самый первый раз, когда вызывается эта функция, код должен выполняться полностью вниз, а затем снова возвращаться, сохраняя значения по мере того, как они возвращаются.Затем при повторном вызове с тем же значением (или любым меньшим значением) ответ возвращается немедленно.
Если последующий вызов выполняется для значения Фибоначчи, превышающего текущее наивысшее известное значение, тогда функция будет рекурсивно снижаться только до тех пор, пока не достигнет наивысшего значения, которое мы видели ранее (и нам не нужно полностью спускаться до 0).
Давайте посмотрим на это в действии и, как и раньше, приберем.
‘установка
уже вычислено (0) = 1: уже вычислено (1) = 1
Функция Фибоначчи (n)
Распечатать «Hello World n =»; n
Если уже вычислено (n), то
Фибоначчи = уже вычислено (n)
еще
Фибоначчи = Фибоначчи (n-1) + Фибоначчи (n-2)
уже вычислено (n) =
ФибоначчиКонец, если
Конечная функция
Ниже слева мы видим, как он работает для n = 5 при первом запуске (ничего в кеше).Он проходит до самого низа, затем снова возвращается вверх (когда он возвращается, он записывает значения в кеш). Второй столбец ниже показывает, что произойдет, если мы затем вызовем функцию с n = 3 (меньшее значение), и это немедленно вернет известное значение кеша. То же самое произойдет, если мы снова вызовем функцию с n = 5 (следующий столбец).
Наконец, в дальнем столбце мы видим, что произойдет, если мы вызовем функцию с n = 11 (после того, как мы уже вычислили n = 5), и вы можете увидеть, что она работает только до пяти, затем снова сделайте резервную копию.
| n = 5 [Первый запуск] → | п = 3 → | n = 5 [Второй прогон] → | п = 11 |
|---|---|---|---|
| Привет, мир n = 5 Привет, мир n = 4 Привет, мир n = 3 Привет, мир n = 2 Привет, мир n = 1 Привет, мир n = 0 Привет, мир n = 1 Привет, мир n = 2 Привет, мир n = 3 | Привет, мир n = 3 | Привет, мир n = 5 | Привет, мир n = 11 Привет, мир n = 10 Привет, мир n = 9 Привет, мир n = 8 Привет, мир n = 7 Привет, мир n = 6 Привет, мир n = 5 Привет, мир n = 6 Привет, мир n = 7 Привет, мир n = 8 Привет, мир n = 9 |
Это намного лучше, чем первый рекурсивный способ, но можем ли мы сделать лучше? Ну да, можем.В приведенной выше реализации мы начинаем сверху, но если ниже нечего строить, когда мы запрашиваем новое более высокое число, мы должны рекурсивно спускаться вниз, пока не достигнем известного числа, а затем снова вернуться вверх. Как мы изменили это и пошли другим путем? Вместо этого, если мы начнем с последнего известного наивысшего значения и будем двигаться вверх, пока не достигнем нашей цели, тогда нам нужно будет двигаться только в одном направлении.
Высокая отметка вверх
Как указывалось выше, если мы начнем с последнего известного максимального числа и вычислим в сторону увеличения, нам гарантированно не придется возвращаться назад, поскольку мы монотонно строим на основе уже имеющихся ответов.Это метод, который вы бы использовали, если бы вычисляли значения вручную!
В этой реализации у нас есть концепция «максимальной отметки», которая представляет собой наивысшее известное значение в кэше. Ниже этого значения выполняется однократный поиск. Выше этого значения мы вычисляем вверх от верхней отметки, сериализуя все промежуточные значения, когда мы передаем их по пути к желаемому числу.
‘установка
уже вычислено (0) = 1: уже вычислено (1) = 1
high_water_mark = 1
Функция Фибоначчи (n)
Если уже вычислено (n), то
Фибоначчи = уже вычислено (n)
еще
для i = (high_water_mark + 1) до n
уже вычислено (i) = уже вычислено (i-1) + уже вычислено (i-2)
следующий
Фибоначчи = уже вычислено (n)
high_water_mark = n
Конец, если
Конечная функция
Как и раньше, мы также применили мемоизацию, чтобы после того, как мы вычислили ответ один раз, нам больше не нужно было посещать его снова.
Этот код намного умнее нашей первой реализации.
Даже без отладочной печати «Hello World» мы видим, что код не вызывает сам себя и функция не является рекурсивной. Он либо немедленно возвращается со значением из кеша, либо зацикливается от последнего известного значения вверх.
Память
против ОбработкаПриведенный выше код довольно эффективен. Он рассчитывает только тогда, когда это необходимо. Однако обратная сторона этого заключается в том, что необходим кеш.Каждое ранее рассчитанное значение необходимо сохранить в памяти. В этом примере для Фибоначчи это довольно тривиально, а память, необходимая для хранения промежуточных значений, очень мала.
В более общем плане, однако, такие компромиссы — это то, что программисты и инженеры балансируют каждый день. Если вы собираетесь использовать значение много раз, что лучше: взять объем памяти и кэшировать его или выбросить и принять удар обработки позже, если вам придется пересчитывать его с нуля?
Нет правильного ответа.Каждый случай зависит от обстоятельств, вариантов использования и ограничений оборудования. Иногда «лучше» пересчитывать, иногда «лучше» хранить. Если вы особенно ограничены в памяти, вам может потребоваться вычисление каждый раз. Иногда наблюдается асимметрия затрат на доступ (например, высокая задержка для доступа к предыдущим результатам) или высокие премии за передачу данных. Например, если вы хотите ускорить рендеринг веб-приложения, может быть лучше сильно сжать данные, которые передаются с сервера клиенту.Даже если декомпрессия на стороне клиента является сложной и для ее генерации требуется в 1000 раз больше времени, чем просто наличие открытого текста, такое сжатие может значительно ускорить рендеринг страницы, поскольку обработка на стороне клиента является «дешевым» ресурсом. Дополнительное сжатие сократит время, необходимое для отправки данных через Интернет, и это, безусловно, самая длинная часть процесса (о, и вы также сэкономите на исходящих расходах, и ваши клиенты будут довольны, а не просто потому, что ваше приложение работает быстрее, но вы сэкономите им деньги, если они будут платить за данные побайтно!) |
Для этого тривиального примера Фибоначчи, если бы необходимые значения использовались часто, я бы обязательно кэшировал их.После инициализации я бы предварительно вычислил известный диапазон всех используемых значений и просто поместил их в массив, готовый для мгновенного вызова. Однако, если мы не можем взять объем памяти, в этом примере можем ли мы сделать лучше?
Можем ли мы сделать лучше?
Было бы идеально, если бы существовала формула Фибоначчи. Если бы была функция / уравнение, в которое мы могли бы передать n , и оно вернуло бы F n , тогда мы могли бы вычислить просто , необходимое нам значение, и не нужно было бы беспокоиться о промежуточных или прошлых значениях. Существует ли такая функция? Ответ положительный! |
Формула Бине
Пора немного математики…
Давайте представим, что мы можем записать последовательность Фибоначчи в виде степенного ряда:
Мы знаем из определения, что каждый член является суммой двух предыдущих.
Если мы разделим первое на x 4 или второе на x 2 , мы увидим общий результат:
Мы можем решить это, используя стандартное квадратное уравнение:
Есть два решения.Вы могли заметить, что один из этих корней — это золотое сечение. Назовем второй τ
.Теперь у нас есть два степенных ряда, каждый из которых удовлетворяет нашему требованию о том, что последующие члены создаются суммой двух предыдущих:
Это многообещающе. Оба они имеют первый член как 1 (это то, что мы ищем), и оба они являются «фибоначчи-эсками» (каждый член является суммой двух предыдущих), но у них нет 1 для их вторые сроки. Итак, давайте сделаем что-нибудь умное.Любая линейная комбинация этих последовательностей по определению является последовательностью со свойствами Фибоначчи. Мы можем умножить верхнюю последовательность на константу A и нижнюю последовательность на константу B и сложить их вместе, и у нас все равно будет последовательность Фибоначчи. В частности:
Теперь, если мы умно выберем наши константы, мы сможем получить последовательность Фибоначчи, которую мы ищем, которая начинается с 1, 1 (а затем мы знаем, что все остальные члены будут следовать оттуда).
Давайте подставим некоторые известные значения. Когда n = 0, мы хотим, чтобы первый член в сумме составлял 1:
.Это дает наш первый результат. Теперь посмотрим, когда n = 1; здесь мы также хотим получить значение 1:
Теперь у нас есть два уравнения и два неизвестных ( A и B ). В интересах экономии места все сохраните перестановки и поделитесь результатами, которые:
Итак, если мы используем эти значения для A и B в качестве коэффициентов, мы получим степенную последовательность, соседние члены которой ведут себя как последовательность Фибоначчи, и имеют первые два члена как 1 и 1.Это означает, что это — это последовательность Фибоначчи!
Давайте соберем все вместе. Мы знаем, что n-е число Фибоначчи F n является линейной комбинацией, и мы знаем значения двух констант A и B . У нас есть все необходимое для описания числа Фибоначчи на основе его индекса:
.Расширяя φ и τ, получаем:
Это клингонский боевой крейсер уравнения, но если вы вставите в уравнение значение n , вы обнаружите, что в конце все степени корня пять сокращаются, чтобы оставить целое число.
Теперь у нас есть уравнение для описания числа Фибоначчи n th исключительно в терминах n.
Больше нет необходимости в сумасшедших рекурсивных методах, мемоизации или кешах!
Эта формула названа «Формула Бенета» в честь Жака Филиппа Мари Бине (1786-1856) , но документально подтверждено, что другие математики открыли ее независимо, в том числе Абрахам де Муавр , который писал о ней еще в 1730 году.
Оптимизация
Это довольно круто, но можем ли мы сделать еще лучше? Да, мы можем немного сбрить расчет.
Формула Фибоначчи содержит два члена внутри главной скобки, оба возведенные в большую степень, как n . Правый член основан на τ и вычитается. Однако этот член меньше единицы, и любое число меньше единицы, возведенное в большую степень, становится все меньше и меньше. Чтобы усугубить это, член слева (основанный на φ) становится все больше и больше. |
Как только n становится больше 10, вклад от τ n + 1 становится незначительным и может быть проигнорирован.
Еще до этого, используя математический метод, называемый округлением (выбор ближайшего целого числа), мы можем упростить формулу, игнорируя компонент τ n + 1 .
Ниже приведена таблица, показывающая эти вклады. Слева указатель. Во втором столбце указано число Фибоаччи. Далее следуют вклады в число Фибоаччи от φ n + 1 / √5 и τ n + 1 / √5 (вы можете видеть, как последнее быстро спадает).
| n | F n | φ n + 1 / √5 | τ n + 1 / √5 |
|---|---|---|---|
| 0 | 1 | 0,723606798 | -0,276393202 |
| 1 | 1 | 1,170820393 | 0,170820393 |
| 2 | 2 | 1.894427191 | -0,105572809 |
| 3 | 3 | 3.065247584 | 0,065247584 |
| 4 | 5 | 4,959674775 | -0,040325225 |
| 5 | 8 | 8.024922359 | 0,024922359 |
| 6 | 13 | 12.984597135 | -0,015402865 |
| 7 | 21 | 21.009519494 | 0,009519494 |
| 8 | 34 | 33.994116629 | -0,005883371 |
| 9 | 55 | 55.003636123 | 0,003636123 |
| 10 | 89 | 88.997752752 | -0,002247248 |
| 11 | 144 | 144,001388875 | 0,001388875 |
| 12 | 233 | 232,99 28 | -0,000858372 |
| 13 | 377 | 377.000530503 | 0,000530503 |
| 14 | 610 | 609.999672131 | -0,000327869 |
| 15 | 987 | 987.000202634 | 0,000202634 |
| 16 | 1 597 | 1,596,999874765 | -0,000125235 |
| 17 | 2,584 | 2,584,000077399 | 0,000077399 |
| 18 | 4 181 | 4180.999952165 | -0,000047835 |
| 19 | 6 765 | 6,765,000029564 | 0,000029564 |
| 20 | 10 946 | 10 945.999981729 | -0,000018272 |
| 21 | 17 711 | 17,711,000011292 | 0,000011292 |
| 22 | 28 657 | 28 656,999993021 | -0,000006979 |
| 23 | 46368 | 46368.000004313 | 0,000004313 |
| 24 | 75 025 | 75 024,999997334 | -0,000002666 |
| 25 | 121 393 | 121 393,00 0001648 90 175 | 0,000001648 |
| 26 | 196 418 | 196 417,999998982 | -0,000001018 |
| 27 | 317 811 | 317 811.000000629 | 0,000000629 |
| 28 | 514 229 | 514 228.999999611 | -0,000000389 |
| 29 | 832 040 | 832 040,000000240 | 0,000000240 |
| 30 | 1 346 269 | 1,346,268.999999850 | -0,000000149 |
| 31 | 2 178 309 | 2 178 309,000000090 | 0,000000092 |
| 32 | 3 524 578 | 3,524,577.999999940 | -0,000000057 |
| 33 | 5,702,887 | 5,702,887.000000030 | 0,000000035 |
| 34 | 9 227 465 | 9 227 464,999999980 | -0,000000022 |
| 35 | 14 930 352 | 14 930 352,000000000 | 0,000000013 |
| 36 | 24 157 817 | 24 157 817,000000000 | -0,000000008 |
| 37 | 39 088 169 | 39 088 169.000000000 | 0.000000005 |
| 38 | 63 245 986 | 63 245 986,000000000 | -0,000000003 |
| 39 | 102,334,155 | 102,334,155.000000000 | 0,000000002 |
Обратный путь
Конечно, теперь, когда у нас есть формула, мы можем ее инвертировать!
Если нам дано число Фибоначчи, мы используем Бине, чтобы найти форум для расчета индекса:
Интересные мелочи
Вот два интересных факта о φ и τ
Если сложить их вместе, получится 1.Если вы умножите их, вы получите -1.
Вы можете найти полный список всех статей здесь. Щелкните здесь, чтобы получать уведомления по электронной почте о новых статьях.
СерияФибоначчи в Python | Программа с использованием циклов и рекурсии
Последовательность Фибоначчи — это серия чисел, названная в честь итальянского математика, известного как Фибоначчи . Это просто последовательность чисел, которая начинается с 0 и 1 и затем продолжается сложением двух предыдущих чисел.В этой статье вы узнаете, как написать программу на Python для реализации ряда Фибоначчи с использованием нескольких методов. Ниже будут рассмотрены указатели:
Приступим.
Что такое ряд Фибоначчи?Ряд Фибоначчи — это ряд чисел, образованный сложением двух предыдущих чисел в ряду.
Пример ряда Фибоначчи: 0,1,1,2,3,5
В приведенном выше примере 0 и 1 — первые два члена ряда.Эти два термина печатаются напрямую. Третий член рассчитывается путем сложения первых двух членов. В данном случае 0 и 1. Итак, получаем 0 + 1 = 1. Следовательно, 1 печатается как третий член. Следующий член генерируется с использованием второго и третьего членов, а не с использованием первого члена. Это делается до тех пор, пока количество терминов, которые вы хотите или запрошены пользователем. В приведенном выше примере мы использовали пять терминов.
Теперь давайте напишем программу на Python, чтобы реализовать это.
Программа Python для реализации последовательности Фибоначчи
Реализация последовательности Фибоначчи на языке программирования Python — самая простая задача! Теперь есть несколько способов реализовать это, а именно:
- Использование цикла
- Использование рекурсии
Давайте рассмотрим оба кода один за другим.
Серия Фибоначчи с использованием циклаЦиклы в Python позволяют нам выполнять группу операторов несколько раз. Давайте напишем программу на Python для реализации ряда Фибоначчи с использованием цикла.
# Введите необходимое количество терминов # 0,1,1,2,3,5 ....
a = int (input («Введите условия»))
f = 0 # первый элемент серии
s = 1 # второй элемент серии
если a <= 0:
print ("Запрошенная серия
", е)
еще:
print (f, s, end = "")
для x в диапазоне (2, a):
следующий = f + s
print (следующий, конец = "")
f = s
s = следующий
Вывод: Введите термины 5 0 1 1 2 3
Другой способ программирования генерации рядов Фибоначчи - использование рекурсии.Давайте углубимся в это.
Программа Python для записи последовательности Фибоначчи с использованием рекурсииРекурсия - это базовый метод программирования Python, при котором функция вызывает себя прямо или косвенно. Соответствующая функция называется рекурсивной функцией . Используя рекурсивный алгоритм, можно довольно легко решить некоторые проблемы. Давайте посмотрим, как использовать рекурсию для печати первых «n» чисел ряда Фибоначчи в Python.
Код Python:
def FibRecursion (n):
если n <= 1:
вернуть n
еще:
return (FibRecursion (n-1) + FibRecursion (n-2))
nterms = int (input ("Enter the terms?")) # принять ввод от пользователя
if nterms <= 0: # проверяем правильность числа
print ("Пожалуйста, введите положительное целое число")
еще:
print ("Последовательность Фибоначчи:")
для i в диапазоне (nterms):
print (FibRecursion (i)) Вывод: Сколько термов: 5
0 1 1 2 3
Объяснение: В приведенной выше программе Python мы используем рекурсию для генерации последовательности Фибоначчи.Функция FibRecursion вызывается рекурсивно, пока мы не получим результат. В функции мы сначала проверяем, равно ли число n нулю или единице. Если да, мы возвращаем значение n. Если нет, мы рекурсивно вызываем фибоначчи со значениями n-1 и n-2.
На этом мы подошли к концу статьи «Серии Фибоначчи в Python». Мы узнали, как программно распечатать N-е число Фибоначчи с помощью операторов цикла или рекурсии.
Если вы хотите изучить Python и получить опыт в количественном анализе, интеллектуальном анализе данных и представлении данных, чтобы выйти за рамки цифр, превратив свою карьеру в роль специалиста по данным, ознакомьтесь с нашим интерактивным онлайн-курсом Python Training .Вы будете использовать библиотеки, такие как Pandas, Numpy, Matplotlib, Scipy, Scikit, Pyspark, и освоите такие концепции, как машинное обучение Python, скрипты, последовательность, веб-скрейпинг и анализ больших данных с использованием Apache Spark. В курс обучения входит круглосуточная поддержка, которая поможет вам на протяжении всего периода обучения.
Есть к нам вопрос? Пожалуйста, укажите это в разделе комментариев этого блога, и мы свяжемся с вами как можно скорее.
ROSALIND | Глоссарий | Последовательность Фибоначчи
Похоже, в вашем браузере отключен JavaScript.Розалинд требует, чтобы в вашем браузере был включен JavaScript.
Последовательность Фибоначчи - это последовательность чисел, определяемая рекуррентным соотношением $ F_n = F_ {n-1} + F_ {n-2} $, где мы устанавливаем начальные значения $ F_1 = F_2 = 1 $.
Последовательность Фибоначчи встречается повсюду в мире природы и насчитывает более двух тысячелетий. к его первому использованию индийскими математиками; но его название происходит от Леонардо Пизанского, который популяризировал последовательность на Западе, представив ее как упражнение с участием популяции кроликов. в 1202 г.Его предположения о численности населения были следующие:
- Популяция начинается в первый месяц с пары новорожденных кроликов.
- Кролики достигают репродуктивного возраста за один месяц.
- В любой месяц каждый кролик репродуктивного возраста спаривается с другим кроликом репродуктивного возраста.
- Через месяц после спаривания двух кроликов у кролика-самки рождаются самец и самка. кролик.
- Кролики никогда не перестают размножаться и не умирают.
На рисунке ниже представлена диаграмма ветвления, показывающая количество пар кроликов для каждой из первые пять месяцев.Динамика популяции кроликов объясняет соотношение повторяемости $ F_n = F_ {n-1} + F_ {n-2} $, как и в $ n $ -м месяце, общее количество кроликов будет равно количеству кроликов, живших в предыдущем месяце ($ F_ {n-1} $) плюс количество новорожденных кроликов, которое равно количеству взрослых кроликов или количеству кроликов, живших двумя месяцами ранее ($ F_ {n-2} $).
Первые 12 членов последовательности Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144. 12-й член (144) дает количество кроликов через год, что соответствует формуле Фибоначчи. Оригинальный вопрос к своим читателям.
Википедия
Загадочная математика: последовательность Фибоначчи
Последовательность Фибоначчи - это серия чисел, созданная в 1202 году Леонардо Фибоначчи. Числа Фибоначчи генерируются уравнением F0 = 0, F1 = 1, за которым следует рекурсивная формула Fn = Fn-1 + Fn-2. Согласно правилу, любое число - это сумма двух чисел перед ним. Последовательность задается как 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 и так далее.Два предыдущих числа складываются вместе, чтобы получить число Фибоначчи, например, 1 + 2 равно 3, 2 + 3 равно 5, 3 + 5 равно 8. Последовательность Фибоначчи названа в честь Леонардо Фибоначчи (также известного как Леонардо Пизано), Итальянский математик, живший с 1170 по 1250 год. Он использовал арифметику последовательностей, чтобы решить задачу, основанную на паре кроликов: «Сколько пар кроликов будет произведено за год, начиная с одной пары, если каждый месяц каждая пара приносит новую пару, которая становится продуктивной со второго месяца? " Решение можно найти численно, используя последовательность Фибоначчи.Пингала, грамматист санскрита, также считается одним из первых упоминаний последовательности с V века до нашей эры. до третьего века нашей эры числа Фибоначчи встречаются в природе, искусстве и музыке. Их можно найти по количеству веточек на растении или по спирали на ананасе. Числа Фибоначчи обычно изучаются как часть теории чисел. Он также имеет приложения для подсчета математических объектов, таких как последовательности, множества и перестановки в информатике. Спираль Фибоначчи приближается к золотому сечению.В отличие от отношения, которое использует математическую константу 1,6180339887, соотношение Фибоначчи использует квадраты чисел Фибоначчи. Это можно увидеть в спиралях из ракушек, сосновых шишках и лепестках. Например, количество лепестков у большинства растений - это число Фибоначчи. Лютики имеют 5 лепестков, ирисы имеют 3 лепестка, ноготки имеют 13 лепестков, а ромашки могут быть с 34, 55 или 89 лепестками. Коэффициенты Фибоначчи также используются в других областях, например, в анализе фондового рынка. Метод, известный как «теория волн Эллиота», используется для прогнозирования естественных моделей поведения трейдеров, отраженных на графике акций.Значение порядковых чисел Фибоначчи остается важной ветвью теории чисел, и все больше последователей вовлекаются в сложный ум Фибоначчи.
Университет Суррея - Кем был Фибоначчи?
Краткая биография Леонардо Пизанского (ныне известного как Фибоначчи) и его математических достижений.
University of Evansville - Последовательность Фибоначчи для визуального оформления
Страница, описывающая последовательность Фибоначчи в композиции и то, как числовое соглашение может быть преобразовано в различные формы.
Энциклопедия бромелиад - Последовательность Фибоначчи и ананасы
Посмотрите, как последовательность чисел в последовательности Фибоначчи может быть связана с любым растением, например ананасом.
Университет Темпл - Последовательность Фибоначчи, спирали и золотое сечение
Краткая история Леонардо Пизы и решение одной из его известных головоломок.
Университет Иллинойса - Последовательность Фибоначчи
Описание последовательности чисел, известной как арифметический ряд и геометрический ряд, и способы вычисления чисел в последовательности Фибоначчи.
Математическая академия - Последовательность Фибоначчи
Объяснение последовательности Фибоначчи и решение проблемы, поставленной Леонардо Пизано в его трактате «Liber Abaci» (опубл. 1202).
Oracle Think Quest - серия Фибоначчи
Информация, приложения, биографии важных математиков, викторины, демонстрации и другие интересные ресурсы, относящиеся к серии Фибоначчи.
Университет Арканзаса - Последовательность Фибоначчи и золотое сечение
Подробная информация о последовательности Фибоначчи, а также иллюстрации того, как эта последовательность работает для решения математических задач.
Колледж Камосун - Числа Фибоначчи в природе
Набор слайдов о числах Фибоначчи и о том, как они соотносятся с природой через цветы, фрукты и деревья.
Университет Лок-Хейвена - фильм-пламя Фибоначчи
Захватывающие заявления, сделанные по поводу ряда Фибоначчи, шумихи о золотой спирали и связи Фибоначчи с золотым сечением.
Университет Нью-Джерси - Калькулятор последовательности Фибоначчи
Калькулятор, который вычисляет n-й член последовательности Фибоначчи, а также вычисляет предыдущий и следующий члены.
Средняя школа Уорда Мелвилла - Фибоначчи
Вопросы и ответы о жизни и творчестве величайшего математика мира Фибоначчи.
Лаборатория Архимеда - Свойства чисел Фибоначчи
Расчеты того, как работают числовые последовательности Фибоначчи, а также калькулятор Фибоначчи и приложения.
Middlebury College - Числа Фибоначчи
Предыстория жизни Леонардо Пизанского и подробное описание ряда Фибоначчи и того, как он разворачивается.
Университет Джеймса Мэдисона - Последовательность Фибоначчи и многое другое
Статья, содержащая несколько разделов информации, включая последовательность Фибоначчи, музыкальную октаву, треугольник Паскаля, фи, золотое сечение и прямоугольник, а также пятиугольник и пентаграмму.
Почему работает последовательность Фибоначчи
Если вы оценили с помощью Planning Poker, вы вполне могли использовать карты либо с последовательностью Фибоначчи, либо с модифицированной последовательностью Фибоначчи.
Традиционная последовательность Фибоначчи - это 1, 2, 3, 5, 8, 13, 21 и так далее, где каждое число является суммой предыдущих чисел.
Несколько лет назад я начал проводить оценки с помощью модифицированной последовательности Фибоначчи, состоящей из 1, 2, 3, 5, 8, 13, 20, 40 и 100.
Почему?
Это потому, что числа, которые слишком близки друг к другу, невозможно различить как приблизительные.
Закон Вебера
Представьте, что вам вручают два гири: один весит один килограмм (2,2 фунта), а другой - два килограмма (4.4 фунта). Имея по одному в каждой руке, но не имея возможности разглядеть, что есть что, вы, вероятно, сможете их различить. Вес в два кг будет ощутимо тяжелее.
Представьте, что вместо этого вам вручают гирю 20 кг и гирю 21 кг. Они имеют такую же разницу в один кг, как и гири в один и два кг. Но вам будет гораздо труднее определить, какой из двух весов больше.
Это связано с законом Вебера. Закон Вебера гласит, что различие, которое мы можем идентифицировать между объектами, выражается в процентах.
Взвешивание разницы между объектами
Разница от одного до двух килограммов - 100%. Наверное, можно различить вес предметов, которые различаются на 100%.
Однако разница между 20 и 21 кг составляет всего 5%. Вы, наверное, не заметите разницы. (Я знаю, что не могу.) И если бы вы могли, это означало бы, что вы могли бы различать вес в 1,00 кг и вес в 1,05 кг, так как это также будет 5%.
Значения в последовательности Фибоначчи работают хорошо, потому что они примерно соответствуют закону Вебера.После двух (что на 100% больше единицы) каждое число примерно на 60% больше предыдущего.
Согласно закону Вебера, если мы можем различить 60% -ную разницу в усилиях между двумя оценками, мы можем различить такую же процентную разницу между другими оценками.
Итак, значения Фибоначчи работают хорошо, потому что они увеличиваются каждый раз примерно на одну и ту же пропорцию.
Изменение последовательности Фибоначчи
Ранние agile-команды, с которыми я работал, использовали это и оценивали с помощью реальной последовательности Фибоначчи.Однако в конце концов мы узнали, что оценка в 21 означает точность, которую мы не можем подтвердить. Заинтересованные стороны посмотрели бы на 21 и были бы впечатлены тем, что мы назвали его 21, а не округлили его до 20 или даже 25.
Это привело нас к тому, что мы начали использовать 20, а не 21. Как только мы отклонились от последовательности Фибоначчи один раз, мы почувствовали себя вправе сделать это и дальше.
Это привело к экспериментам, в ходе которых мы ввели 40 и 100. Они работали хорошо, потому что они представляли 100% и 150% увеличение по сравнению с предыдущими числами.Это было намного больше, чем 62% последовательности Фибоначчи.
Это не было нарушением закона Вебера, поскольку было доказано, что закон Вебера не выдерживает крайних значений. Такие оценки, как 40 и 100, возможно, можно было бы рассматривать как крайние значения.
Эксперименты с планированием покерных последовательностей
Вплоть до 2007 года команды, с которыми я работал, экспериментировали как с модифицированной последовательностью Фибоначчи, так и с простым удвоением чисел - 1, 2, 4, 8, 16, 32.
Каждый работал одинаково хорошо.Большинство команд сильно отдавали предпочтение тому или другому, но я не смог найти четких доказательств того, что одна последовательность лучше другой.
Но в 2007 году мы начали печатать карты Planning Poker Cards, которые мы продавали по себестоимости, распространяли на различных Agile-мероприятиях и которые я использую на некоторых очных курсах.
Чтобы снизить затраты на печать, мне пришлось выбирать между этими двумя последовательностями. В то время я всего лишь немного отдавал предпочтение модифицированной последовательности Фибоначчи. И поэтому я позвонил, чтобы пойти с этим.Как только эта последовательность стала появляться на тысячах колод в год, она приобрела популярность за счет простого удвоения значений. Мое небольшое предпочтение 1, 2, 3, 5, 8, 13 ... а не 1, 2, 4, 8, 16 ... возникло из-за того, что я участвовал во многих встречах с последней последовательностью, в которой дискуссии всегда велись по принципу «Неужели? этот элемент невыполненной работы по продукту в два раза больше другого? "
Все дискуссии были о том, является ли что-то двойным, четверным и т. Д. Это меня немного беспокоило, потому что я не видел этого с командами, использующими модифицированную последовательность Фибоначчи.Их дискуссии не всегда были такими: «Это на 60% больше усилий?» Эти обсуждения казались более здоровыми, хотя у меня не было возможности это измерить.
В наши дни я остаюсь довольно беспристрастным в отношении этих двух наборов ценностей. Я думаю, что команды могут успешно оценивать любой набор ценностей, поскольку каждый из них демонстрирует атрибуты закона Вебера.
Что вы думаете?
Каков ваш опыт работы с различными оценочными последовательностями? Какие ценности вы используете и работают ли они в вашей команде? Пожалуйста, поделитесь своими мыслями в разделе комментариев ниже.
Последовательность Фибоначчи | Encyclopedia.com
История
Другие последовательности Фибоначчи
Природная последовательность Фибоначчи
Ресурсы
Последовательность Фибоначчи - это последовательность чисел, в которой каждое последующее число (после второго) является суммой двух предыдущих. Самая известная последовательность Фибоначчи - 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89.. .. Эта последовательность выражает многие естественные отношения в растительном мире.
Последовательность Фибоначчи была изобретена итальянцем Леонардо Пизано Биголло (1180–1250), который известен в математической истории под несколькими именами: Леонардо Пизанский (Пизано означает «из Пизы») и Фибоначчи (что означает «сын Боначчи» ). Фибоначчи, сын итальянского бизнесмена из города Пиза, вырос в торговой колонии в Северной Африке в средние века. В средние века итальянцы были одними из самых опытных торговцев и купцов в западном мире, и им требовалась арифметика, чтобы отслеживать свои торговые операции.Математические вычисления производились с использованием римской системы счисления (I, II, III, IV, V, VI и т. Д.), Но эта система затрудняла выполнение сложения, вычитания, умножения и деления, которое торговцам необходимо было отслеживать. свои транзакции.
Когда Фибоначчи рос в Северной Африке, он научился более эффективной индийско-арабской системе арифметической записи (1, 2, 3, 4. ...) от арабского учителя. В 1202 году он опубликовал свои знания в знаменитой книге под названием Liber Abaci (что означает «книга счётов», хотя она не имела ничего общего со счётами). Liber Abaci показала, насколько лучше индуистско-арабская арифметическая система по сравнению с римской системой счисления, и показала, как индуистско-арабская арифметическая система может быть применена в интересах итальянских торговцев.
Последовательность Фибоначчи была результатом математической задачи о разведении кроликов, поставленной в Liber Abaci. Проблема заключалась в следующем: начиная с одной пары кроликов (один самец и одна самка), сколько пар кроликов родится за год, если предположить, что каждый месяц каждый самец и самка кроликов рожают новую пару кроликов. , а новая пара кроликов сама начинает рожать дополнительные пары кроликов после первого месяца их рождения?
Таблица 1 иллюстрирует один из подходов Фибоначчи к решению этой проблемы.Каждое число в таблице соответствует паре кроликов. Каждая пара кроликов может родить только после первого месяца жизни. Начиная с третьего месяца, число в столбце «Взрослые пары» представляет количество пар, в которых могут родиться кролики. Числа в столбце «Всего пар» представляют последовательность Фибоначчи.
Хотя самая известная последовательность Фибоначчи - это 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.. ., последовательность Фибоначчи может быть любой серией чисел, каждое из которых следует за
| Таблица 1.( Thomson Gale .) | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Оценка с использованием последовательности Фибоначчи | |||||||||||||||
| Новорожденные (не могут воспроизводиться) | Одномесячные (не могут воспроизводиться) | Взрослые (могут воспроизвести) | Всего пар | ||||||||||||
| Месяц 1 | 1 | + | 0 | + | 0 | = | 1 | ||||||||
| Месяц | 1 | + | 0 | = | 1 | ||||||||||
| Месяц 3 | 1 | + | 0 | + | 1 | = | 9 Месяц | + | 1 | + | 1 | = | 3 | ||
| Месяц 5 | 2 | + | 1 | + | 2 90 175 | = | 5 | ||||||||
| Месяц 6 | 3 | + | 2 | + | 3 | = | 8 | ||||||||
| Месяц 7 | + | 5 | = | 13 | |||||||||||
| Месяц 8 | 8 | + | 5 | + | 8 | = | 21 | ||||||||
| Месяц | 8 | + | 13 | = | 34 | ||||||||||
| Месяц 10 | 21 | + | 13 | + | 21 | = | после | после | 55 второй) - это сумма двух предыдущих.Это означает, что конкретные числа в ряду Фибоначчи зависят от начальных чисел. Таким образом, если серия начинается с 3, то последующие серии будут такими: 3, 3, 6, 9, 15, 24, 39, 63, 102 и так далее.|||||||
 Как открыть хостел | HowToHostel Как открыть хостел …
Как открыть хостел | HowToHostel Как открыть хостел … 

 Способ его построения разработал немецкий живописец и график Альбрехт Дюрер (1471…1528). Пусть O — центр окружности, A — точка на окружности и Е — середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Способ его построения разработал немецкий живописец и график Альбрехт Дюрер (1471…1528). Пусть O — центр окружности, A — точка на окружности и Е — середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.