Последовательность фибоначчи от 1 до 500 с: циклом и рекурсией. Язык Python

Уровни Фибоначчи. Что это и как их использовать в трейдинге

Золотое сечение или с чего все начиналось

Те, кого интересует сугубо прикладной аспект данных инструментов, могут пропустить этот раздел — экскурс в историю чисел Фибоначчи, а также их появления в трейдинге.

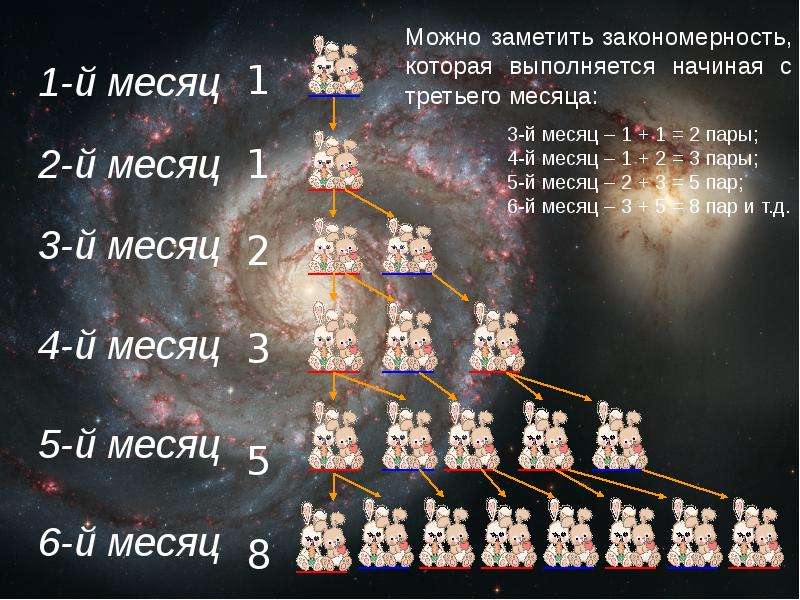
Последовательность Фибоначчи была хорошо известна еще в древней Индии, где применялась в стихосложении. Но имя свое она получила благодаря европейскому математику XII века Леонардо Пизанскому, более известному по псевдониму Фибоначчи. Фибоначчи, помимо других многочисленных математических задач, подробно исследовал и описал эту последовательность в труде «Liber Abaci» («Книга Абака» или «Книга об Абаке»). Последовательность эта представляет из себя бесконечный ряд чисел, каждый следующий член которого равен сумме двух предыдущих:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 …

У этого ряда есть много замечательных математических особенностей, но главным является то, что отношение члена ряда к предыдущему стремится к знаменитому «Золотому сечению» — числу 1,618. Это число известно с античных времен и впервые встречается в «Началах» Евклида (около 300 лет до н. э.), где применялось для построения правильного пятиугольника.

Золотое сечение считается наиболее гармоничной пропорцией отношения целого к части. Магическим образом число 1,618 очень часто встречается в природных формах, напрямую не имеющих ничего общего между собой. Эту пропорцию можно заметить в раковинах улиток, расстоянии между листьями на ветке, форме спиралей галактик и даже в среднестатистическом соотношении частей тела человека.

Белорусский ученый Эдуард Сороко, который изучал формы золотых сечений в природе, отмечал, что все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм — это закручивание по спирали.

В музыкальных произведениях, стихотворениях и художественных произведениях также встречается пропорция 1,618.

Идея искать золотое сечение в графиках биржевых котировок принадлежала американскому инженеру и управленцу Ральфу Hельсону Эллиотту, который увлекся анализом цен после серьезной болезни в начале 1930х гг. Эллиотт изучал годовые, месячные, недельные, дневные, часовые и получасовые графики различных фондовых индексов, охватывающих 75-летнюю историю поведения рынка. В процессе исследования он заметил, что движения индексов подчинены определенным ритмам — волнам, в пропорциях которых прослеживаются те самые 1,618. Эллиот написал на эту тему ряд трудов, самым масштабным из которых стала книга «Закон природы — секрет вселенной» (англ. Nature’s Law — The Secret of the Universe)», в которую он включил все свои наработки, касающиеся теории волн и соотношения Фибоначчи.

После Эллиота многие трейдеры и исследователи рынка искали различные применения числам Фибоначчи в биржевой торговле. Развитие вычислительной техники позволило аналитикам далеко продвинуться в этом направлении. Современные трейдеры активно используют инструменты, основанные на данном математическом.

Уровни Фибоначчи в биржевой торговле

Пожалуй, самый распространенный терминал для торговли на российском фондовом рынке Quik предлагает пользователю четыре инструмента, основанных на последовательности Фибоначчи. Это уровни, веер, дуги и временные зоны Фибоначчи. Начнем с самых популярных — уровней.

Одним из самых старых и надежных инструментов трейдера являются широко распространенные уровни поддержки и сопротивления. Участникам рынка нужны ценовые ориентиры, чтобы понять, выгодно ли покупать сейчас, не пора ли продавать и где цена может сменить свое направление. Однако не всегда удается точно определить, какой уровень отработает, а какой цена даже не заметит. Как раз эту проблему помогают решить уровни Фибоначчи.

Определение уровней коррекции

По правилам, инструмент «Уровни Фибоначчи» растягивается от начала тренда к его окончанию (на самом деле, если вы растянете уровни наоборот от конца к началу, в Quik разницы не будет). Если растянуть его таким образом, то получившиеся уровни станут возможными целям для коррекции. От этих уровней можно входить по тренду, либо использовать в качестве цели в контр-трендовых сделках.

На примере графика акций «Норильского никеля» хорошо видно, как четко были отработаны уровни 23,6 и 38,2. Причем тут есть особенность: если уровень Фибоначчи совпадает с уровнем на графике, как в данном примере, то вероятность, что он будет отработан, становится очень высокой. Еще лучше, если при этом он будет расположен на круглом числе.

Стоит сразу оговорить ограничение применения. Данный инструмент применяется только при наличии явно выраженного тренда. Если применять его на инструменте, который движется внутри боковика, то уровни отрабатываются очень «грязно», и вряд ли их использование принесет вам прибыль в долгосрочной перспективе.

Движение по Русгидро происходило внутри флэта с большим откатом. В этом случае уровень 23,6 отработал очень «грязно», и цена могла много раз зацепить стоп-заявку.

Также, уровни становятся более «грязными», когда фаза коррекции затягивается. Однако и в этом случае уровни коррекции по Фибоначчи могут оставаться актуальными, причем могут работать в том числе и зеркально.

Еще одним способом применения коррекционных уровней может быть торговля откатов. Когда инструмент делает быстрое движение к значимому уровню, от которого высока вероятность отката, коррекционный уровень 38,2 может показать вам потенциал, до которого можно держать позицию.

Что касается таймфреймов, применять инструмент стоит в диапазоне таймфреймов М15 — D1.

Определение волн Эллиота

Часто уровни Фибоначчи используются в связке с волновой теорией Эллиота. Согласно этой теории, любое трендовое движение по финансовому инструменту можно разложить на пять волн: три основных (импульсных) по тренду и две коррекционных против тренда. Импульсные волны нумеруются как первая, третья и пятая, а коррекционные, в свою очередь, вторая и четвертая.

Любое коррекционное движение тоже можно разложить, но только на три волны. Все внутренние волны также раскладываются по принципу фрактала (фрактал — самоподобная структура). Наглядно этот процесс представлен на рисунке ниже.

Понимание, какую волну формирует цена сейчас, дает возможность предположить, куда она пойдет далее. Самой интересной для трейдеров является третья волна. Она считается самой длинной и самой быстрой. Идеальная сделка с использованием теории Эллиота — это войти в сделку в конце второй волны и выйти из неё в конце третьей.

Согласно теории, высота 3-й волны относится к 1-й, как 1,618. Значит, если мы видим уже сформировавшиеся 1-ю и 2-ю волны, то мы можем рассчитать длину 3-й, используя уровни Фибоначчи. Для этого в некоторых терминалах специально предусмотрен инструмент «расширение Фибоначчи». Строится он по трем точкам: начало первой волны, конец первой волны и конец второй волны. (главное соблюсти эти точке на ценовой шкале по вертикали. По горизонтали положение точек не так важно). На экране появятся уровни Фибоначчи, и уровень с отметкой 1,618 будет отмечать расчетный конец третьей волны.

В терминале Quik инструмента «расширение Фибоначчи» нет. Но его можно заменить обычными уровнями Фибоначчи. Для этого нужно растянуть их так, чтобы 0 был на начале первой волны, а 100 на её окончании. А потом просто перетащить всю конструкцию так, чтобы 0 оказался в конце второй волны.

Хочется отметить, что не всегда конец третьей волны приходится на уровень 1,618. Довольно часто цена немного не доходит или немного опережает эту отметку.

Помимо определения длины третьей волны, ряд специалистов предлагали способы определения и других волн. В книге Б. Вильямса «Торговый хаос» предлагается следующая система определения длин волн:

1 волна — определяется по факту формирования

2 волна — чаще всего заканчивается на уровнях коррекции 50,0 и 61,8.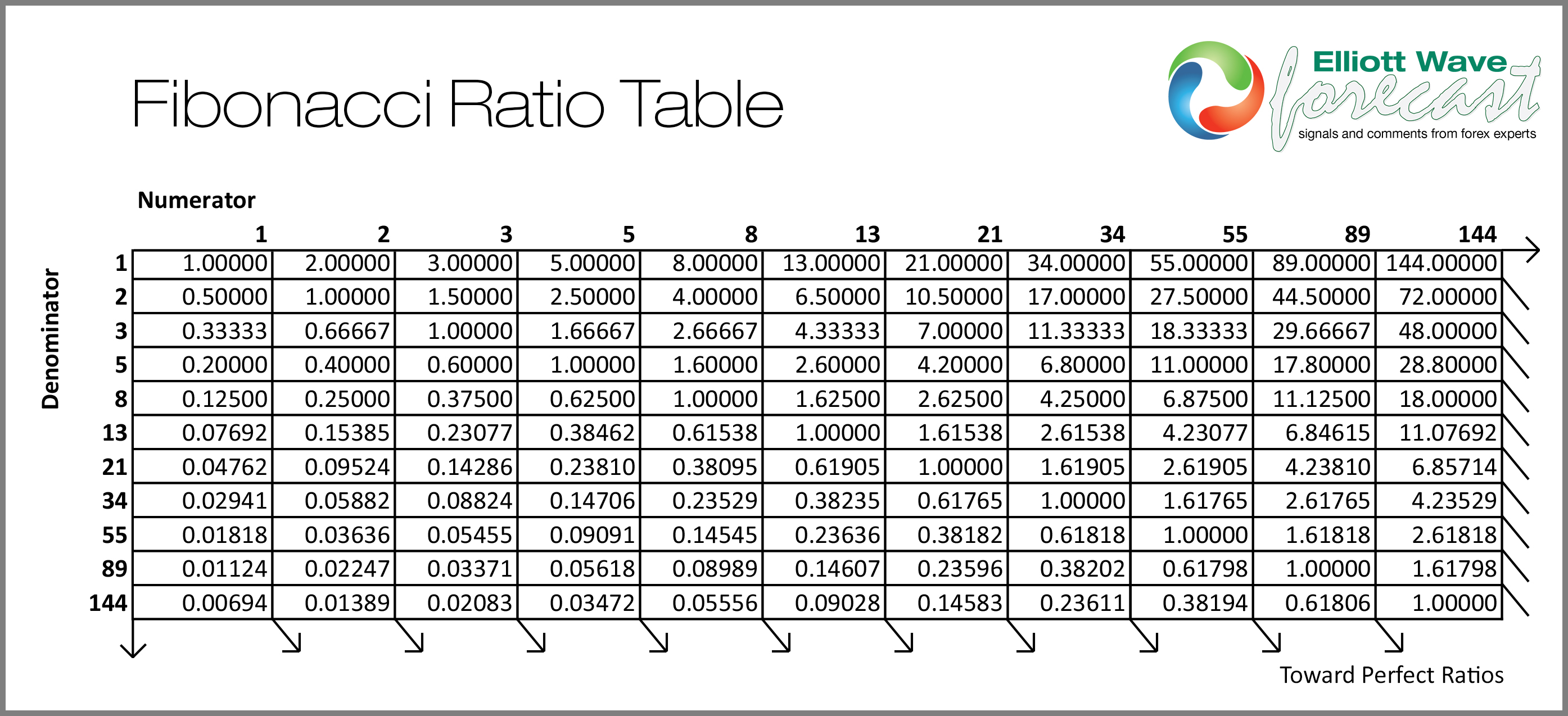

3 волна — составляет от 1 до 1,618 от длины первой волны.

4 волна — чаще всего заканчивается между уровнями коррекции 38,2 и 50,0 и чаще всего выглядит в виде бокового движения.

5 волна — составляет от 61,8% до 100% от диапазона между началом первой волны и концом третьей.

Рассмотрим на примере графика Россетей. Зеленым отмечены импульсные волны, а красным — коррекционные.

Самым сложным в применении волн Эллиота является вопрос: «В какой волне цена находится сейчас?» Консенсуса по поводу того, как определить точку отсчета первой волны у адептов волновой теории нет по сей день и, возможно, так и не будет.

С практической точки зрения наиболее эффективным является подход: «Не уверен — не торгуй». На некоторых инструментах в определенной фазе волны прорисовываются очень четко и легко идентифицируются. На других же, выделить волны практически невозможно. Необходимо путем регулярного наблюдения отыскивать среди всего многообразия инструментов те, которые ходят понятным для вас образом, и торговать только их. А как только волны начинают ломаться, переходить на другой инструмент.

Очень важно не зацикливаться на одной ценной бумаге, пытаясь отыскать волны там, где их нет. Кроме того, торговая система обязательно должна включать в себя план на случай негативного стечения событий. Стоп—лосс должен обеспечивать соотношение риск/прибыль не менее 1/2.

Веер Фибоначчи

Как и уровни, этот инструмент, может использоваться для определения точек, где завершится коррекция. Алгоритм, по которому строятся лучи веера достаточно простой. Если провести вертикальную линию через точку окончания трендового движения, то лучи будут проходить через точки пересечения этой линии с соответствующими уровнями Фибоначчи. В большинстве терминалов этот алгоритм представлен в виде готового инструмента, который растягивается от начальной точки трендового движения к её концу. Лучи веера, в таком случае, будут показывать возможные окончания коррекции, где можно открывать позицию по тренду.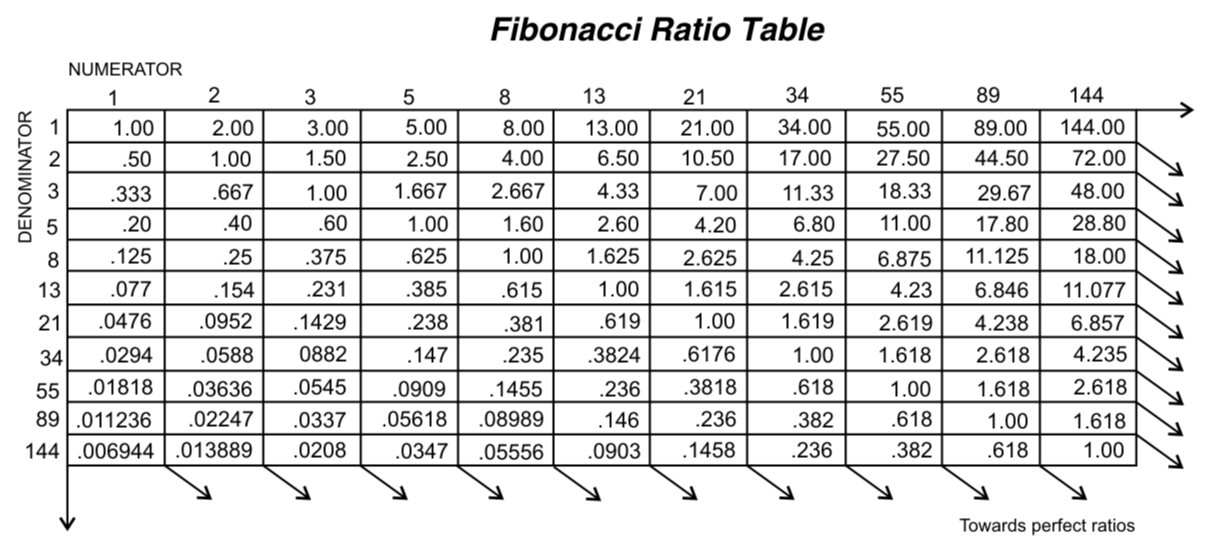

По умолчанию в инструменте могут быть разные настройки, но наиболее распространенными являются настройки лучей 38,2; 50,0; 61,8. В Quik их можно задать следующим образом: щелчок правой кнопкой мыши по вееру -> редактировать -> в разделе «Уровни Фибоначчи» задаете нужные значения.

Веер рекомендуется использовать в связке с другими методами определения длины коррекции. Построение веера имеет погрешность в зависимости от масштаба и таймфрейма, что может привести к неверной трактовке сигналов.

Дуги Фибоначчи

В отличие от предыдущих инструментов, дуги примечательны тем, что они учитывают еще и временной фактор. Это позволяет трейдеру не только предположить, как поведет себя цена, но и в какой момент это произойдет.

Дуги Фибоначчи строятся следующим образом: сначала между началом и концом тренда строится прямая. Затем строятся три дуги с центром в конце пересекающие прямую на уровнях Фибоначчи 38,2%, 50% и 61,8%. В большинстве терминалом дуги, точно так же реализованы в виде отдельного инструмента.

Дуги Фибоначчи очень сильно зависят от масштаба графика. Наиболее подходящий масштаб можно выбрать проанализировав эффективность инструмента на истории. Так же, как и веер рекомендуется использовать дуги совместно с другими методами технического анализа.

Временные зоны Фибоначчи

В основе временных зон Фибоначчи положена одноименная последовательность чисел 0, 1, 1, 2, 3, 5, 8, 13, 21… Исходной точкой для построения выбирается локальный максимум или минимум. Вторая точка позволит определить длину единичного интервала. На графике появятся вертикальные линии с шагом, соответствующем последовательности чисел Фибоначчи в единичном интервале.

Вертикальные линии помогают идентифицировать моменты времени, когда стоит ожидать разворота. При нахождении цены в районе очередной линии необходимо использовать другие индикаторы и сигналы для поиска точки входа против движения. Можно, например, комбинировать временные зоны с веером или уровнями Фибоначчи.

Другие инструменты

Помимо представленных способов использования чисел Фибоначчи в торговле придумана еще масса вариантов: спираль Фибоначчи, канал Фибоначчи, клин Фибоначчи и т. д. Они немного отличаются по методам построения и внешнему виду, но суть их одна — определение длины коррекции. Вы можете выбрать наиболее подходящие для себя инструменты и пополнить ими свой торговый арсенал.

Книги, которые можно прочитать на эту тему

В книге А. Фроста и Р. Пректера «Волновой принцип Эллиота» можно ознакомиться с основными принципами волновой теории Эллиота в её классическом виде.

В книге Б. Мендельброта и Р. Хадсона «(Не)послушные рынки» можно прочесть о современном взгляде на ритмы финансовых рынков и фрактальной структуре изменения цен.

В книге Б. Вильямса «Торговый хаос» можно подробнее ознакомиться с методом подсчета волн, кратко изложенном в данном материале.

В книге Р. Фишеpа «Последовательность Фибоначчи: приложения и стратегии для трейдеров» изложен еще один взгляд на использование уровней Фибоначчи при подсчете волн.

Открыть счет

БКС Экспресс

Как написать последовательность Фибоначчи?

Я нашел этот вопрос, пытаясь получить самую короткую Pythonic-генерацию этой последовательности (позже я понял, что видел подобное в предложении по расширению Python ), и я не заметил, чтобы кто-то еще предлагал мое конкретное решение (хотя главный ответ приближается, но все же менее элегантно), так что вот оно, с комментариями, описывающими первую итерацию, потому что я думаю, что это может помочь читателям понять:

def fib():
    a, b = 0, 1
    while True:            
        yield a            
        a, b = b, a + b    

и использование:

for index, fibonacci_number in zip(range(10), fib()):
     print('{i:3}: {f:3}'. format(i=index, f=fibonacci_number))

печатает:

  0:   0
  1:   1
  2:   1
  3:   2
  4:   3
  5:   5
  6:   8
  7:  13
  8:  21
  9:  34
 10:  55

(Для целей атрибуции я недавно заметил аналогичную реализацию в документации Python по модулям, даже с использованием переменных aи b, которые, как я припоминаю, видел перед написанием этого ответа. Но я думаю, что этот ответ демонстрирует лучшее использование языка.)

Интернет Энциклопедия целочисленных последовательностей определяет последовательность Фибоначчи рекурсивно

F (n) = F (n-1) + F (n-2) с F (0) = 0 и F (1) = 1

Кратко определить это рекурсивно в Python можно следующим образом:

def rec_fib(n):
    '''inefficient recursive function as defined, returns Fibonacci number'''
    if n > 1:
        return rec_fib(n-1) + rec_fib(n-2)
    return n

Но это точное представление математического определения невероятно неэффективно для чисел, намного превышающих 30, потому что каждое вычисляемое число должно также вычисляться для каждого числа ниже него. Вы можете продемонстрировать, насколько он медленный, используя следующее:

for i in range(40):
    print(i, rec_fib(i))

Его можно запоминать для повышения скорости (в этом примере используется тот факт, что аргумент ключевого слова по умолчанию является одним и тем же объектом каждый раз при вызове функции, но обычно вы не будете использовать изменяемый аргумент по умолчанию именно по этой причине):

def mem_fib(n, _cache={}):
    '''efficiently memoized recursive function, returns a Fibonacci number'''
    if n in _cache:
        return _cache[n]
    elif n > 1:
        return _cache.setdefault(n, mem_fib(n-1) + mem_fib(n-2))
    return n

Вы обнаружите, что мемоизированная версия работает намного быстрее и быстро превысит вашу максимальную глубину рекурсии, прежде чем вы даже сможете подумать о том, чтобы встать для кофе. Вы можете визуально увидеть, насколько это быстрее, сделав следующее:

for i in range(40):
    print(i, mem_fib(i))

(Может показаться, что мы можем просто сделать следующее, но на самом деле это не позволяет нам воспользоваться кешем, потому что он вызывает себя до вызова setdefault.)

def mem_fib(n, _cache={}):
    '''don't do this'''
    if n > 1:  
        return _cache.setdefault(n, mem_fib(n-1) + mem_fib(n-2))
    return n

Рекурсивно определенный генератор:

Изучая Haskell, я наткнулся на эту реализацию в Haskell:

fib@(0:tfib) = 0:1: zipWith (+) fib tfib

На данный момент я думаю, что ближе всего к этому в Python я могу подойти:

from itertools import tee

def fib():
    yield 0
    yield 1
    
    f, tf = tee(fib()) 
    next(tf)
    for a, b in zip(f, tf):
        yield a + b

Это демонстрирует:

[f for _, f in zip(range(999), fib())]

Однако он может доходить только до предела рекурсии. Обычно 1000, тогда как версия Haskell может доходить до сотен миллионов, хотя для этого используются все 8 ГБ памяти моего ноутбука:

> length $ take 100000000 fib 
100000000

Использование итератора для получения n-го числа Фибоначчи

Комментатор спрашивает:

Вопрос к функции Fib (), основанной на итераторе: что делать, если вы хотите получить n-е, например 10-е число fib?

В документации itertools есть рецепт для этого:

from itertools import islice

def nth(iterable, n, default=None):
    "Returns the nth item or a default value"
    return next(islice(iterable, n, None), default)

и сейчас:

>>> nth(fib(), 10)
55

Фибоначчиева система счисления — Задачи

Как известно, последовательность Фибоначчи начинается с двух чисел 0 и 1 и каждый последующий член последовательности получается как сумма двух предыдущих.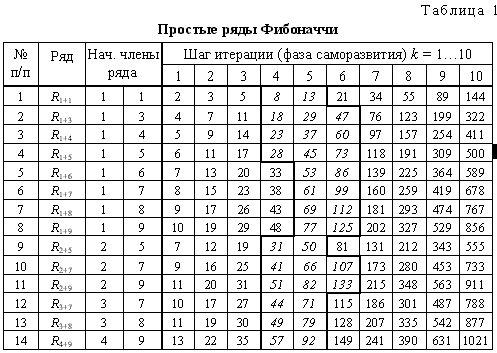 Например, третий член последовательности это 1 (1=1+0), четвёртый — 2 (2=1+1), пятый — 3 (3=2+1) и т.д.

Рисунок 1 — Первые числа последовательности Фибоначчи

Эта последовательность проявляется очень часто и в нашей жизни и в природе и имеет большое значение. А знаете ли Вы, что все положительные целые числа можно представить как сумму чисел из последовательности Фибоначчи? Более того, все натуральные числа можно представить при помощи последовательности Фибоначчи, причём без повторений. Например: 13 может быть представлено из указанного множества как {13}, {5,8} или {2,3,8} а 17 представлено как {1,3,13} или {1,3,5,8}. Так как все числа обладают этим свойством (может у Вас есть желание доказать это?), то этот набор является хорошим способом для использования в качестве «базы» (основания системы счисления) для представления чисел. Но, как мы видели выше, некоторые числа могут быть представлены более чем одним способом суммой чисел из последовательности Фибоначчи. Как нам выйти из этой ситуации? Очень просто! Для этого достаточно наложить ограничение, что для предоставления числа нельзя использовать два соседних элемента из последовательности Фибоначчи! Это ограничение объясняется тем, что сумма двух соседних членов последовательности Фибоначчи сама является членом последовательности Фибоначчи.

Теперь, когда мы знаем всё изложенное выше, мы можем предложить хороший способ предоставления любого целого положительного числа. Для этого мы будем использовать двоичную последовательность (только нулей и единиц). Например, 17 = 1 + 3 + 13 (мы должны помнить, что нельзя использовать два последовательных числа Фибоначчи). Будем использовать ноль в записи, если очередное число из последовательности Фибоначчи не используется, и единицу для тех что используются. Тогда, 17 = 100101 (ведущие нули должны быть опущены). На рисунке 2 подробно показано, как получена эта запись и что означают нули и единицы в приведённой выше записи. Для лучшего понимания этой схемы обратим внимание на тот факт, что не использование двух соседних чисел Фибоначчи означает, что двоичная последовательность не будет иметь двух подряд идущих единиц. Используя приведённое представление числа, мы будем говорить, что мы используем Фибоначчиеву систему счисления и записывать его как 17 = 100101 (fib).

Рисунок 2 — Объяснение представления числа 17 в Фибоначчиевой системе счисления

Ваша задача состоит в записи заднного десятичного числа в Фибоначчиевой системе счисления.

Входные данные

В первой строке входных данных задано единственное натуральное число N, указывающее на количество примеров в тесте (1 ≤ N ≤ 500).

Следующие N строк содержат по одному положительному целому числу, не превышающему 100 000 000. Числа могут быть поданы в произвольном порядке.

Выходные данные

Вы должны вывести по одной строке для каждого из N чисел, полученных во входных данных, в следующем формате: «DEC_BASE = FIB_BASE (fib)«. DEC_BASE это заданное оригинальное число в десятичной системе счисления, а FIB_BASE соответственно — его представление в Фибоначчиевой системе счисления. Образец вывода приведён в примере выходных данных.

Лимит времени 1 секунда

Лимит использования памяти 64 MiB

Как написать последовательность Фибоначчи? — CodeRoad

Я нашел этот вопрос, пытаясь получить самую короткую Питоническую генерацию этой последовательности (позже осознав, что видел похожую в предложении по улучшению Python), и я не заметил, чтобы кто-то еще придумал мое конкретное решение (хотя верхний ответ близок, но все же менее элегантен), так что вот он, с комментариями, описывающими первую итерацию, потому что я думаю, что это может помочь читателям понять, что это такое.:

def fib():
    a, b = 0, 1
    while True:            # First iteration:
        yield a            # yield 0 to start with and then
        a, b = b, a + b    # a will now be 1, and b will also be 1, (0 + 1)

и использование:

for index, fibonacci_number in zip(range(10), fib()):
     print('{i:3}: {f:3}'.format(i=index, f=fibonacci_number))

печать:

  0:   0
  1:   1
  2:   1
  3:   2
  4:   3
  5:   5
  6:   8
  7:  13
  8:  21
  9:  34
 10:  55

(Для целей атрибуции я недавно заметил аналогичную реализацию в документации Python по модулям, даже используя переменные a и b, которые, как я теперь вспоминаю, я видел перед написанием этого ответа. Но я думаю, что этот ответ демонстрирует лучшее использование языка.)

Онлайн энциклопедия целочисленных последовательностей определяет последовательность Фибоначчи рекурсивно как

F (n) = F (n-1) + F (n-2) с F (0) = 0 и F (1) = 1

Кратко определить это рекурсивно в Python можно следующим образом:

def rec_fib(n):
    '''inefficient recursive function as defined, returns Fibonacci number'''
    if n > 1:
        return rec_fib(n-1) + rec_fib(n-2)
    return n

Но это точное представление математического определения невероятно неэффективно для чисел, намного превышающих 30, потому что каждое вычисляемое число должно также вычисляться для каждого числа ниже него. Вы можете продемонстрировать, насколько это медленно, используя следующее:

for i in range(40):
    print(i, rec_fib(i))

Его можно запомнить для повышения скорости (в этом примере используется тот факт, что аргумент ключевого слова по умолчанию является одним и тем же объектом каждый раз, когда вызывается функция, но обычно вы не используете изменяемый аргумент по умолчанию именно по этой причине):

def mem_fib(n, _cache={}):
    '''efficiently memoized recursive function, returns a Fibonacci number'''
    if n in _cache:
        return _cache[n]
    elif n > 1:
        return _cache.setdefault(n, mem_fib(n-1) + mem_fib(n-2))
    return n

Вы обнаружите, что записанная версия намного быстрее и быстро превысит вашу максимальную глубину рекурсии, прежде чем вы даже подумаете о том, чтобы встать за кофе. Вы можете увидеть, насколько это быстрее визуально, сделав это:

for i in range(40):
    print(i, mem_fib(i))

(Может показаться, что мы можем просто сделать следующее, Но на самом деле это не позволяет нам воспользоваться преимуществами кэша, потому что он вызывает себя до вызова setdefault.)

def mem_fib(n, _cache={}):
    '''don't do this'''
    if n > 1:  
        return _cache.setdefault(n, mem_fib(n-1) + mem_fib(n-2))
    return n

Рекурсивно определенный генератор:

Поскольку я изучал Haskell, я наткнулся на эту реализацию в Haskell:

fib@(0:tfib) = 0:1: zipWith (+) fib tfib

Самое близкое, что я думаю, что могу получить к этому в Python на данный момент, это:

from itertools import tee

def fib():
    yield 0
    yield 1
    # tee required, else with two fib()'s algorithm becomes quadratic
    f, tf = tee(fib()) 
    next(tf)
    for a, b in zip(f, tf):
        yield a + b

Это демонстрирует это:

[f for _, f in zip(range(999), fib())]

Однако он может доходить только до предела рекурсии.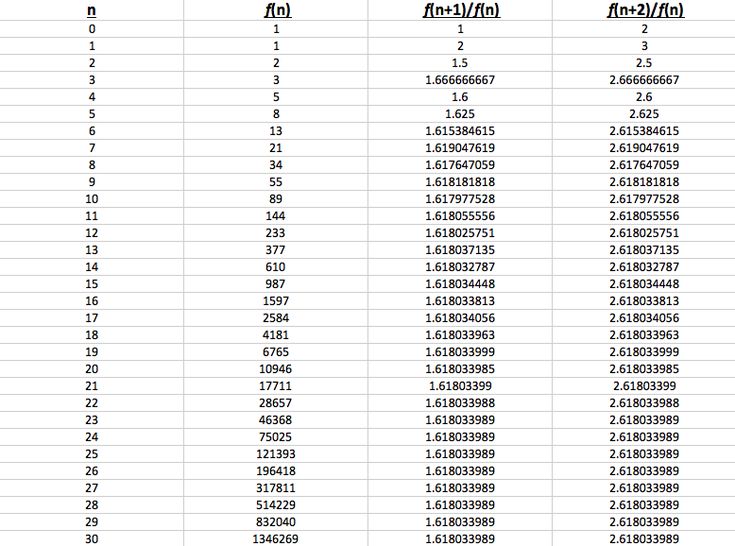 Обычно 1000, в то время как версия Haskell может доходить до 100 миллионов, хотя для этого она использует все 8 GB памяти моего ноутбука:

> length $ take 100000000 fib 
100000000

Использование итератора для получения n-го числа Фибоначчи

Комментатор спрашивает:

Вопрос для функции Fib(), основанной на итераторе: что делать, если вы хотите получить N-е, например 10-е число fib?

В документации itertools есть рецепт для этого:

from itertools import islice

def nth(iterable, n, default=None):
    "Returns the nth item or a default value"
    return next(islice(iterable, n, None), default)

а теперь:

>>> nth(fib(), 10)
55

Числа Фибоначчи в фотографии

Многие фотографы при съемке используют правило третей для построения композиции. Но этому правилу есть альтернатива, которая поможет вам еще больше усовершенствовать ваши фотографии. Речь идет о числах Леонарда Фибоначчи. Он заметил, что в природе существуют некие пропорции, которые особенно приятны для взгляда человека.

И эти пропорции широко использовались как в прошлом, например в архитектуре (Парфенон), в живописи (Мона Лиза, Тайная Вечеря) и т.д., так и сейчас многие дизайнеры придерживаются пропорций 1:1.618. Эти пропорции также называются золотым сечением, которое дает много возможностей для композиционного построения снимка, благодаря чему снимок выглядит так, что на подсознательном уровне человек постоянно хочет на него смотреть и любоваться.

Чтобы понять, что такое последовательность Фибоначчи предлагаю посмотреть этот замечательный видеоролик.

Ниже представлены фотографии, которые сделаны с применением пропорций Фибоначчи.

На снимке выше более выделяющийся глаз лошади расположена на пересечении линий согласно пропорций Фибоначчи. Если бы и придерживался правила третей, голова лошади была бы расположена ближе к краю снимка. На этом же снимке голова и не в центре и не с краю.

На следующей фотографии голова расположена так, что глаз находится ровно в центре спирали.

На этой фотографии из Key West горизонт пересекается с верхней линией сетки. Благодаря этому на фотографии гармонично расположены и церковь и улица и небо.

На этом снимке сетка Фибоначчи также помогает удачно скомпоновать кадр. Двери заключены между вертикальными линиями и горизонтальной, благодаря этому в кадре присутствует достаточное количество потолка, который ведет взгляд зрителя к двери.

Ниже представлены еще несколько снимков, сделанных при помощи золотого сечения.

В заключение хотелось бы сказать, что вы можете с успехом продолжать пользоваться правилом третей, но если вы добавите в свои снимки и правило золотого сечения, вы сможете разнообразить свои снимки и сделать их еще более совершенными и гармоничными.

Смотрите так же Правило третей

Автор: James Brandon

Перевод: Елена Вилкойть

Калькулятор Фибоначчи

Многие трейдеры предпочитают технический анализ. Однако в этом случае можно упустить из виду некоторые важные данные и информацию. Технический анализ не учитывает такие факторы как политическая нестабильность, важные макроэкономические и политические события и другие данные, которые могут оказать сильное влияние на валютные тренды..

К сожалению, еще не придумано торговых инструментов или методик, которые всегда работали бы со 100%-ным результатом.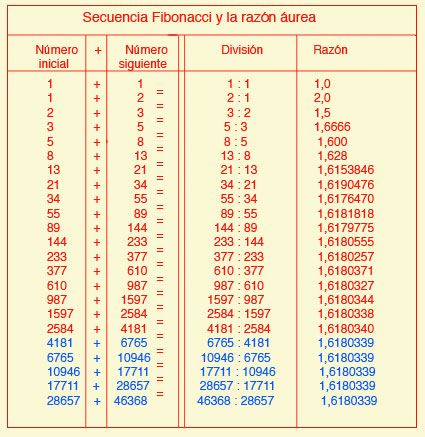 Методы технического анализа, применяемые для интерпретации движений рынка, всецело основаны на чисто математическом анализе.Если эти расчеты оказываются неверными, рынок поворачивается против вас. Никогда не стоит тешить себя надеждой, что тренд обещает вам гарантированную прибыль. – но нельзя и игнорировать тренд как нечто несущественное. Подходите к последовательности уровней Фибоначчи как к стратегии, которая сработает в вашупользуr, когда тренд уже движется в выгодном для вас направлении. Эта стратегия поможет вам выбрать оптимальные точки входа в рынок и выхода из него. Кроме того, вы можете использовать уровни расширения, чтобы предположить, каких уровней может в конечном итоге достичь цена.

Ключевыми уровнями Фибоначчи принято считать 38.2%, 50% и 61.8%. Эти уровни оказывают наибольшееare сопротивление и поддержку при изменениях курса. С помощью уровней Фибоначчи можно определить не только возможные цели коррекции, но и возможные цели в случае продолжения тренда. На графике снизу видно, что уровни зажаты между точками 1,2 и 3. Учитывая характер тренда – в нашем примере он восходящий, — расширение также будет происходить в восходящем направлении. Обратите внимание на то, что эти уровни находятся выше текущей цены, указывая на вероятные области фиксации прибыли. В данном примере, работая с расширением 100, можно было бы получить неплохую прибыль. Мы рекомендуем вам практиковать различные стратегии и оттачивать навыки в этой области. Например, вы можете посмотреть на график и продумать свой путь к прибыли, что вам придется делать довольно быстро в режиме реального времени. Ниже приведен пример уровней расширения при восходящем тренде. Вы также можете найти примеры того, как стратегия работает при нисходящем тренде, поскольку тот же принцип применяется при восходящем и нисходящем трендах.

Российский рынок ждет деталей санкций в красной зоне

Отечественные индексы показывают отрицательную динамику в первой половине сессии четверга на фоне ожидаемого сегодня оглашения деталей новых санкций в отношении России. По информации Reuters, 30 организаций внесут в черный список, а 10 отечественных дипломатов будут высланы из США в связи с обвинениями о вмешательстве России в выборы в США, а также потенциальной причастностью к кибератакам на ряд американских компаний. Кроме того, ожидается, что США объявит о новых ограничениях для американских финансовых институтов в отношении торговли инструментами, привязанными к российскому суверенному долгу.

Рубль отреагировал на скорые санкции приличным снижением относительно доллара и евро: к 12:00 мск пара окрепла на 1,04%, до 76,6617, а ушла в плюс на 1,02%, до 91,8682. к 12:00 мск снизился на 0,62%, до 3554,73 пункта. Индекс потерял 1,98% и упал до 1460,57 пункта.

Среди важных корпоративных событий на сегодня отметим публикацию операционных результатов «Детского мира (MCX:)» и «Группы ПИК (MCX:)» за I квартал 2021 года. Кроме того, дивиденды за 2020 год на заседании совета директоров обсудят банк «Авангард» и «Трубная металлургическая компания (MCX:)», а наблюдательный совет «Якутской топливно-энергетической компании» соберется для решения по дивидендам за I квартал 2021 года.

Касательно сегодняшней макростатистики по РФ, отметим публикацию мартовских данных по промышленному производству (консенсус −1% г/г). В глобальном разрезе инвесторы будут следить за количеством первичных обращений за пособиями по безработице (консенсус 700 тыс.), мартовскими розничными продажами (консенсус 5,9% м/м) и мартовским промышленным производством (консенсус 2,8% м/м) в США.

В лидерах роста к середине дня оказались акции АЛРОСы (+2,01%), РУСАЛа (MCX:) (+2,22%), а также «Полиметалла (MCX:)» (+0,99%), «Северстали (MCX:)» (+1,07%), «ФосАгро (MCX:)» (+1,01%) и НЛМК (MCX:) (+0,77%). Сильнее других подешевели бумаги Mail.ru Group (−1,31%), АФК «Система» (−1,27%), «Газпрома (MCX:)» (−1,27%) и «Сбера» (−1,17%).

С технической точки зрения, на дневном графике Индекс МосБиржи продолжает торговаться в рамках восходящего тренда, который на фоне неблагоприятного новостного фона окажет поддержку в диапазоне 3480-3500 пунктов.

Индекс МосБиржи

Растущая нефть и отчеты банков помогли DJIA обновить максимумы

В среду, 14 апреля, ведущие американские фондовые индексы показали смешанную динамику. Статистика по запасам сырой нефти от EIA толкнула вверх котировки черного золота и акции нефтегазового сектора, а финансовые гиганты Goldman Sachs, Wells Fargo (NYSE:) и JP Morgan Chase накануне открыли сезон корпоративных отчетностей за I квартал текущего года хорошими результатами. На таком фоне рынок ротировался из акций технологического сектора, потянувшего вниз и S&P 500.

Опубликованная EIA статистика по нефтяным запасам показала, что на минувшей неделе резервы черного золота упали на 5,9 млрд баррелей при консенсусе снижения на 2,9 млрд баррелей. Экспорт сырой нефти из США также резко упал, составив почти 6,0 млн баррелей за неделю, закончившуюся 9 апреля. Котировки майских фьючерсов на на таком фоне за день подскочили на 4,49%, до $62,88 за баррель.

По результатам торговой сессии индекс широкого рынка снизился на 0,41% до 4124,66 пункта. Индикатор голубых фишек закрылся в плюсе на 0,16% на отметке 33 730,89 пункта. Индекс высокотехнологичных отраслей NASDAQ Composite полегчал на 0,99%, до 13 857,84 пункта. Отметим, что Dow Jones Industrial Average в ходе торгов обновил исторический максимум.

Отраслевой индекс S&P 500 Energy показал наилучшую динамику в ходе торговой сессии, поднявшись на 2,91%, до 371,78 пунктов. Больше остальных выросли бумаги Diamondback Energy (+6,05%), Nov (+5,91%), EOG Resources (NYSE:) (+5,28%), Occidental Petroleum (NYSE:) (+5,19%), Pioneer Natural Resources (NYSE:) (+5,09%) и APA (+4,98%).

Акции Goldman Sachs и Wells Fargo выросли на 2,34% и 5,53% соответственно на фоне выдающихся результатов в первом отчетном квартале 2021 года. Чистая прибыль Goldman Sachs подскочила до $6,7 млрд, что почти в 6 раз превысило результат I квартала 2020 года. Одним из факторов роста стал бум SPAC, который помог Goldman получить значительные комиссионные: доходы от инвестиционного банкинга возросли на 73%, до $3,77 млрд. Wells Fargo по итогам I квартала зафиксировал чистую прибыль на отметке $4,74 млрд, что эквивалентно росту на 626% г/г. CEO Wells Fargo Чарли Шарф прокомментировал, что результаты включают в том числе сокращение резервов по кредитам на $ 1,6 млрд и отражают общее восстановление американской экономики.

Акции военно-промышленной корпорации Lockheed Martin (NYSE:) окрепли на 0,4% в ходе торгов. Среди прочих фаворитов торгов отметим Freeport-McMoRan (+7,89%), Lincoln National (+2,46%), Albemarle (+2,93%), NetApp (+2,65%), LyondellBasell (+2,27%).

Акции JPMorgan Chase в ходе торгов снизились на 1,87%, несмотря на то, что прибыль крупнейшего банка США за I квартал подскочила почти на 400% г/г. Причиной стало выделение более $5 млрд в резервы для покрытия дефолтов по кредитам и займам, связанных с воздействием пандемии COVID-19.

Наименее удачно торговая сессия сложилась также для Discovery (−4,95%), Tesla (NASDAQ:) (−3,95%), Twitter (−3,74%), PayPal (−2,98%), Caesars Entertainment (−2,57%), NVIDIA (NASDAQ:) (−2,57%).

S&P 500

На дневном графике S&P 500 остается в пределах восходящего канала, торгуясь вблизи верхней полосы Боллинджера. Стохастический осциллятор находится вблизи отметки 100, что также указывает на перегретость индекса. В связи с этим потенциал дальнейшего роста выглядит ограниченным, поддержку индекс найдет в диапазоне 4000-4080 пунктов.

S&P 500

Индексы Европы показывают умеренный рост в начале торговой сессии

Фондовые площадки Европы показывают умеренную растущую динамику в первой половине торгов четверга. К 12:00 мск немецкий вырос на 0,4%, британский поднялся на 0,45%, а французский стал тяжелее на 0,29%. Сводный фондовый индекс региона окреп на 0,37%, до 438,2 пункта.

Сегодня были опубликованы данные по мартовскому уровню инфляции в группе стран Еврозоны: Франция — 0,6% м/м (консенсус 0,6% м/м), Италия — 0,3% м/м (консенсус 0,3% м/м), Германия — 0,5% м/м (консенсус 0,5% м/м).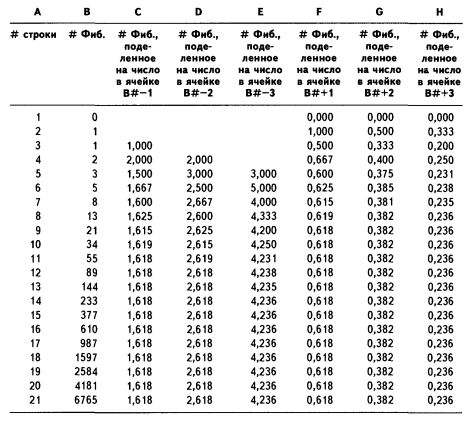

Акции крупнейшей в мире пивоваренной компании Anheuser Busch Inbev (BR:) оказались в числе лидеров сессии к середине торгов (+4,39%), добравшись до отметки €56,85. Это произошло на фоне получения акциями компании новой целевой цены €74 и рекомендации «выше рынка» от аналитиков Barclays (LON:).

Акции швейцарской электротехнической компании Abb подросли на 3,45% после поднятия прогноза менеджмента по годовой выручке в 2021 году. В четверг компания объявила, что по итогам первого квартала было зафиксировано увеличение выручки на 11% г/г, до €6,9 млрд. Теперь рост продаж в 2021 году ожидается на 5 и более процентов г/г.

Среди лидеров торгов на площадках Европы также выделим Publicis Groupe (PA:) (+3,65%), Deutsche Wohnen (+3,56%), Travis Perkins (LON:) (+3,23%), Nestle (+2,78%) и Kingfisher (LON:) (+3,35%). Наименее удачно торговая сессия складывается для Legal & General (LON:) Group (−4,03%), TechnipFMC (−3,25%), St. James’s Place (−2,69%), Siemens Energy (−2,12%) и Standard Life (LON:) Aberdeen (−1,72%).

DAX

С точки зрения теханализа, на дневном графике DAX остается у верхней границы среднесрочного восходящего канала. Стохастический осциллятор указывает на некоторую перекупленность индекса, что ограничивает потенциал дальнейшего роста. Поддержка обеспечивается диапазоном 15 000-15 165 пунктов.

Dax

Китайские фондовые рынки закрылись в красной зоне в ожидании данных по ВВП

В четверг китайские фондовые рынки закрылись на отрицательной территории. На рынке превалируют опасения дальнейшего серьезного ужесточения кредитно-денежной политики со стороны Народного Банка Китая, которое может стартовать после выхода в пятницу данных по ВВП страны за I квартал 2021 года. Экономисты, опрошенные Bloomberg, ожидают, что экономика Китая выросла на внушительные 18,6% г/г за первые три месяца текущего года. Многие инвесторы полагают, что в случае хорошей статистики ЦБ Китая приступит к «охлаждению» экономики. Отметим, что помимо ВВП завтра будут опубликованы мартовские данные по розничным продажам и промышленному производству в стране.

По итогам торгов индекс голубых фишек CSI 300 снизился на 0,64%, до 4948,97 пункта. Индекс высокотехнологичных компаний ChiNext полегчал на 0,53% и закрылся на уровне 2868,24 пункта. Гонконгский индекс финишировал в минусе на 0,37% на отметке 28 793,14 пункта.

К 12:00 мск на валютном рынке пара окрепла на 0,01%, до 6,5295, тогда как курс подрос на 0,02%, до 6,5307. Котировки валютной пары поднялись на 0,03% до 7,7674. Доходность 10-летних китайских государственных облигаций в четверг укрепилась на 2,3 б. п. до 3,191%.

Напряжение на рынках возросло после вчерашней публикацией ЦБ Китая о расширении масштабов стресс-тестов, проводимых регулятором: в этом году они охватят все 4 024 банка страны на фоне увеличения объемов кредитования в ряде секторов экономики. Группа акций финансового сектора Поднебесной отреагировала на новость заметным снижением: Industrial Bank (−4,1%), Industrial and Commercial Bank of China (−1,63%), China Construction Bank (−1,22%).

В числе лидеров на сегодняшних торгах оказались акции производителя автомобильных запчастей Beijing Wkw Automotive Parts (+10,03%). Это произошло на фоне заявления компании о том, что чистая прибыль за I квартал, как ожидается, вырастет на 3982-5238% из-за низкой базы годом ранее.

Акции автопроизводителя Qingling Motors также подросли в ходе сессии четверга (+9,27%). Накануне компания объявила о запуске совместного с Bosch предприятия Bosch Hydrogen Powertrain Systems. Предприятие будет разрабатывать, собирать и продавать системы топливных элементов в Китае. Выход на рынок запланирован в период с конца 2022 года по начало 2023 года.

Акции производителя сельскохозяйственной продукции New Hope Liuhe стали одними из неудачников торговой сессии (−3,26%). Компания ожидает, что ее чистая прибыль за первый квартал снизится на 88,9-92,6% г/г по причине неблагоприятной конъюнктуры на рынке свинины и возросших операционных расходов.

Акции China Biologic Products Holdings показали минимальный рост на 0,02%. Среди компаний-лидеров сегодняшней сессии также отметим Jiangxi Copper (+7,43%), LONGi Green Energy Technology (+5,91%), Montage Technology (+3,88%), CK Asset Holdings (+2,23%) и CNOOC (+1,61%).

Наименее удачно торговая сессия сложилась также для Chengdu Kanghong Pharmaceutical Group (−7,93%), Offcn Education Technology (−4,78%), Jiangsu Hengrui Medicine (−3,91%), Galaxy Entertainment (−2,43%), WuXi Biologics (−2,06%).

CSI 300

С точки зрения теханализа, CSI 300 торгуется в нижней части канала Боллинджера. Поддержку индексу в случае коррекции при сохранении негативного новостного фона окажет уровень 4900, а ближайшим сопротивлением выступит отметка 5020 пунктов.

CSI 300

Цена преодолела отметку $66 после выхода данных о запасах нефти в США

Сегодня цены на нефть корректируются после роста почти на 5% по итогам вчерашних торгов. Поводом для оптимизма стало существенное сокращение запасов нефти в США, а также улучшенные прогнозы по нефтяному спросу от Международного энергетического агентства. Однако в том же отчете МЭА говорилось и о том, что из-за растущих объемов добычи как в странах ОПЕК+, так и за периметром альянса, цены на нефть в ближайшие месяцы могут оказаться под давлением.

К 11:53 мск июньские фьючерсы на нефть марки Brent снижаются на 0,44% и находятся у отметки $66,29, а майские фьючерсы на нефть марки WTI торгуются в минусе на 0,43% на уровне $62,28.

Вчера участники рынка весьма позитивно восприняли данные от агентства EIA по запасам нефти в США. По итогам предыдущей недели запасы сырой нефти в стране сократились на 5,889 млн баррелей в сравнении со снижением на 3,522 млн баррелей неделей ранее и консенсус-прогнозом в −2,889 млн баррелей.

Помимо этого, было зафиксировано сокращение запасов дистиллятов: показатель снизился на 2,083 млн, тогда как аналитики ожидали роста на 0,971 млн баррелей.

Вместе с тем запасы бензина выросли на прошлой неделе на 0,309 млн баррелей, что, однако оказалось ниже консенсус-прогноза в +0,786 млн баррелей.

Также вчера обновленные прогнозы по спросу на нефть представило Международное энергетическое агентство. Согласно оценкам МЭА, мировой спрос в текущем году увеличится на 5,7 млн б/с, до 96,7 млн б/с, что на 230 тыс. б/с выше предыдущего прогноза.

В то же время МЭА отмечает сохраняющиеся риски со стороны спроса, связанные с неблагоприятной пандемической обстановкой в ряде крупных стран, особенно в Индии и Бразилии. В совокупности на эти две страны приходится порядка 8% мирового потребления нефти, и ухудшение ситуации с коронавирусом может ощутимо сказаться на спросе на нефть с их стороны.

Также МЭА не исключает, что нефтяные цены могут оказаться под давлением в ближайшие месяцы на фоне растущей нефтедобычи в результате ослабления квот со стороны ОПЕК+ и роста добычи в других странах. В докладе отмечается, что по итогам марта мировое предложение выросло на 1,7 млн б/с за счет восстановления добычи в США и увеличения объемов добываемой нефти в странах ОПЕК+. Таким образом, в скором времени рынок нефти перейдет от состояния дефицита к балансу, что может стать препятствием для дальнейшего роста нефтяных цен.

Нефть Brent

Цена нефти марки Brent пробила вверх линию 50-дневной скользящей средней и консолидируется вблизи уровня вчерашнего закрытия. Стохастические линии направлены вверх, что все еще благоприятно для роста котировок.

Brent

Цены цветных металлов растут на торгах в четверг. По состоянию на 11:53 мск котировки золота прибавляют 0,65% и находятся у отметки $1747,2 за тройскую унцию.

Золото (GC)

Цена продолжает консолидироваться под уровнем $1750 над линией 50-дневной скользящей средней. Стохастические линии находятся вблизи зоны перекупленности, однако направлены вверх, что может указывать на возможность еще одной попытки протестировать отметку $1750.

Золото

Александр Ковалев, аналитик ГК «ФИНАМ»

Что такое ретрейсменты Фибоначчи и соотношения Фибоначчи?

Уровни коррекции Фибоначчи популярны среди технических трейдеров. Они основаны на ключевых числах, определенных математиком Леонардо Фибоначчи в 13 веке. Последовательность чисел Фибоначчи не так важна, как математические отношения, выраженные в виде отношений, между числами в ряду.

В техническом анализе коррекция Фибоначчи создается путем взятия двух крайних точек (обычно пика и впадины) на графике акций и деления вертикального расстояния на ключевые соотношения Фибоначчи, равные 23.6%, 38,2%, 50%, 61,8% и 100%.

После определения этих уровней рисуются горизонтальные линии, которые используются для определения возможных уровней поддержки и сопротивления.

Ключевые выводы

• Уровни коррекции Фибоначчи — популярные инструменты, которые трейдеры могут использовать для построения линий поддержки, определения уровней сопротивления, размещения стоп-лоссов и установки целевых цен.
• Восстановление Фибоначчи создается путем взятия двух крайних точек на графике акций и деления вертикального расстояния на ключевые соотношения Фибоначчи, равные 23.6%, 38,2%, 50%, 61,8% и 100%.
Уровни коррекции Фибоначчи
• страдают теми же недостатками, что и другие универсальные торговые инструменты, поэтому их лучше всего использовать вместе с другими индикаторами.

Как работают соотношения Фибоначчи

Прежде чем мы сможем понять, почему были выбраны эти соотношения, давайте рассмотрим числовой ряд Фибоначчи.

Последовательность чисел Фибоначчи выглядит следующим образом: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т. Д. Каждый член в этой последовательности представляет собой просто сумму двух предыдущих сроки, и последовательность продолжается бесконечно.Одна из замечательных характеристик этой числовой последовательности состоит в том, что каждое число примерно в 1,618 раза больше предыдущего. Эта общая взаимосвязь между каждым числом в серии является основой соотношений, используемых техническими трейдерами для определения уровней восстановления.

Ключевое соотношение Фибоначчи 61,8% находится путем деления одного числа в ряду на число, которое следует за ним. Например, 21, разделенное на 34, равно 0,6176, а 55, разделенное на 89, равняется примерно 0.61798.

Соотношение 38,2% определяется путем деления числа в ряду на число, расположенное в двух точках справа. Например, 55, разделенное на 144, примерно равно 0,38194.

Соотношение 23,6% находится путем деления одного числа в ряду на число, которое находится на три знака вправо. Например, деление 8 на 34 дает примерно 0,23529.

Восстановление Фибоначчи и прогнозирование цен на акции

По неизвестным причинам эти отношения Фибоначчи, кажется, играют роль на фондовом рынке, как и в природе.Технические трейдеры пытаются использовать их для определения критических точек, в которых динамика цены актива может развернуться.

Уровни коррекции Фибоначчи — наиболее широко используемый из всех торговых инструментов Фибоначчи. Отчасти это связано с их относительной простотой, а отчасти с их применимостью практически к любому торговому инструменту. Их можно использовать для построения линий поддержки, определения уровней сопротивления, размещения стоп-ордеров и установки целевых цен. Коэффициенты Фибоначчи могут даже выступать в качестве основного механизма в стратегии торговли против тренда.

Уровни коррекции Фибоначчи — это горизонтальные линии, которые указывают возможные местоположения уровней поддержки и сопротивления. Каждый уровень связан с одним из вышеуказанных соотношений или процентов. Он показывает, насколько цена откатилась от предыдущего движения. Направление предыдущего тренда, вероятно, сохранится. Однако цена актива обычно восстанавливается до одного из указанных выше соотношений до того, как это произойдет.

На следующем графике показано, как появляется коррекция Фибоначчи. Большинство современных торговых платформ содержат инструмент, который автоматически рисует горизонтальные линии. Обратите внимание, как цена меняет направление по мере приближения к уровням поддержки и сопротивления.

  >>> def fib_to (n):
... fibs = [0, 1]
... для i в диапазоне (2, n + 1):
... fibs.append (fibs [-1] + fibs [-2])
... вернуть выдумки
...
  

  >>> fib_to (20)
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765]
  

  >>> fib_to (40) [17]
1597
  

  >>> def fib (n, computed = {0: 0, 1: 1}):
... если n не вычислено:
... вычислено [n] = fib (n-1, вычислено) + fib (n-2, вычислено)
... вернуть вычисленное [n]
  

  >>> fib (400)
176023680645013966468226945392411250770384383304492191886725992896575345044216019675
  

  импорт функциональных средств

@ functools.lru_cache (Нет)
def fib (n):
    если n <2:
        вернуть n
    вернуть fib (n-1) + fib (n-2)
  

  >>> def fib (n):
... а, Ь = 0, 1
... для _ в диапазоне (n):
... а, Ь = Ь, а + Ь
... вернуть
  

  def fib ():
    а, Ь = 0, 1
    while True: # Первая итерация:
        yield a # yield 0 для начала, а затем
        a, b = b, a + b # a теперь будет 1, а b также будет 1, (0 + 1)
  

  для индекса, fibonacci_number в zip (диапазон (10), fib ()):
     print ('{i: 3}: {f: 3}'.формат (i = индекс, f = fibonacci_number))
  

  0: 0
  1: 1
  2: 1
  3: 2
  4: 3
  5: 5
  6: 8
  7: 13
  8: 21
  9: 34
 10: 55
  

  def rec_fib (n):
    '' 'неэффективная рекурсивная функция, как определено, возвращает число Фибоначчи' ''
    если n> 1:
        вернуть rec_fib (n-1) + rec_fib (n-2)
    вернуть n
  

  для i в диапазоне (40):
    print (я, rec_fib (я))
  

  def mem_fib (n, _cache = {}):
    '' 'эффективно запоминаемая рекурсивная функция, возвращает число Фибоначчи' ''
    если n в _cache:
        return _cache [n]
    elif n> 1:
        вернуть _cache.setdefault (n, mem_fib (n-1) + mem_fib (n-2))
    вернуть n
  

  для i в диапазоне (40):
    print (я, mem_fib (я))
  

  def mem_fib (n, _cache = {}):
    '' 'не делай этого' ''
    если n> 1:
        вернуть _cache.setdefault (n, mem_fib (n-1) + mem_fib (n-2))
    вернуть n
  

  fib @ (0: tfib) = 0: 1: zipWith (+) fib tfib
  

  от itertools import tee

def fib ():
    выход 0
    выход 1
    # требуется тройник, иначе с двумя алгоритмами fib () становится квадратичный
    f, tf = тройник (fib ())
    следующий (tf)
    для a, b в zip (f, tf):
        дать a + b
  

  [f для _, f в zip (диапазон (999), fib ())]
  

 > length $ take 100000000 fib
100000000
  

  из itertools import islice

def nth (итерабельность, n, по умолчанию = None):
    «Возвращает n-й элемент или значение по умолчанию»
    return next (islice (iterable, n, None), по умолчанию)
  

  >>> nth (fib (), 10)
55
  

 # прогнозирование последовательности Фибоначчи с помощью линейной регрессии 
 import pandas as pdfibonacci = pd.DataFrame ([[1, 1, 2], 
 [2, 1, 3], 
 [3, 2, 5], 
 [5, 3, 8], 
 [8, 5, 13] 
]) fibonacci .columns = [0, 1, 2] 
 fibonacci.iloc [0] 
 fibonacci 

 импортировать numpy как np 
 из sklearn. linear_model import LinearRegressionreg = LinearRegression (). fit (fibonacci [[0, 1]], fibonacci [2]) 
 reg.score (fibonacci [[0, 1]], fibonacci [2]) 

 # с любыми двумя числами модель вернет их сумму, полученную из обучающих данных. 
 def pred (x): 
 return reg.pred (np.array ([x])) 

 list1 = [0, 1] 

 для k в диапазоне (25): 
 # результаты предсказания np для 1 + 1 могут быть 1.999999: преобразовано в int, оно становится единицей. Я использую rint, чтобы округлить его до ближайшего numpy int, а затем преобразовать его в int 
 list1.append (int (np.rint (pred ([list1 [k], list1 [k + 1]])))) 
 print (list1) 

 [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657 , 46368, 75025, 121393]