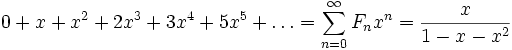Числа Фибоначчи в Европе популяризовал Леонардо Пизанский (по прозвищу Фибоначчи – сын Боначчи), в задаче о кроликах:
Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый день января. Эта пара кроликов производит новую пару кроликов (самку и самца) в первый день февраля и затем в первый день каждого следующего месяца. Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов. Возникает вопрос: сколько пар кроликов будет в огороженном месте через год, то есть через 12 месяцев с начала размножения.
Оказывается, число кроликов по месяцам описывается последовательностью
1, 2, 3, 5, 8, 13,…
В ней каждое число равно сумме двух предыдущих. Условия задачи все равно нереалистичны, так что можно не стесняться: предположить, что кролики бессмертны, и продолжить последовательность до бесконечности:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, ….
Есть свидетельства, что последовательность задолго до Леонардо была известна в Индии, и что в честь Фибоначчи ее назвал Эдуард Люка.
Про экспоненциальный рост
Как мы видим, последовательность очень быстро растет (экспоненциально, как последовательность степеней). Примерно как 1, 2, 4, 8, 16, 32, … или 1, 10, 100, 1000, … (тоже экспоненциальный рост.) Экспоненциальный рост вообще встречается в природе и в приложениях: так растут популяции, капиталы в банке, число радиоактивных атомов и число зерен на шахматной доске (Вы же помните легенду про жадного султана и бедного изобретателя шахмат ;))
В природе экспоненциальный рост имеет место лишь приблизительно и только в некоторых пределах.
Красивые фотографии
Последовательности в природе, напоминающие Фибоначчи, тоже похожи на Фибоначчи только приблизительно и в некоторых пределах. Широко известны примеры из мира растений: семена подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса. Видимо, здесь задействован один механизм (я скопировала первую попавшуюся картинку из интернета):
Отчасти популярность чисел Фибоначчи связана с такими красивыми картинками. В интернете их полным-полно.
А вот скажем, закон радиоактивного распада не менее поразителен, история его открытия драматична, человечество поставило его себе на службу… но он не так популярен в СМИ. Нет для него таких красивых картинок, да и описывается он дифференциальным уравнением, а любителей дифференциальных уравнений меньше, чем любителей красивых картинок.
В математике
В математике бывают объекты, которые задаются очень просто, но показывают удивительно сложные и многогранные связи между своими компонентами. Например: треугольник в планиметрии, конические сечения, треугольник Паскаля, простые числа, … Они завораживают нас как картинки в калейдоскопе. Чуть повернешь – и открываются новые узоры, новые свойства. Числа Фибоначчи –один из таких объектов. Каждый математик на пути в науку их обязательно встречал.
Чтобы перечислить все их удивительные свойства, нужна отдельная книга (и кстати, выходит журнал с таким названием, посвященный одним только числам Фибоначчи). Скажу только, что отношение каждого числа Фибоначчи к предыдущему приближает золотое сечение, и чем числа больше, тем приближение лучше.
Почему же математики выделили числа Фибоначчи в отдельную группу чисел
Потому что любят все классифицировать и раскладывать по полочкам. Раз есть объект – надо дать ему название. На сайте https://oeis.org/A000045 , где собраны большинство последовательностей чисел, встречающихся в математике, последовательность Фибоначчи идет под номером 45. Она вовсе не такая уж исключительная, кроме неё на этом сайте собрано около трети миллиона последовательностей. Каждая из них тоже представляет собой «отдельную группу чисел».
Специалист по теории чисел Леопольд Кронекер считал, что только одна из них создана Богом (и это вовсе не последовательность Фибоначчи, а другая, на сайте ее номер 27), а остальные – дело рук человеческих.
В целом журналисты несколько преувеличивают значимость чисел Фибоначчи: они, безусловно, прекрасны, но стоят в одном ряду с многими другими не менее прекрасными и полезными математическими объектами.
Число Бога, числа Фибоначчи, Золотое Сечение
Во вселенной еще много неразгаданных тайн, некоторые из которых ученые уже смогли определить и описать.
Первая тысяча знаков значения Φ
1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362
Числа Фибоначчи и золотое сечение составляют основу разгадки окружающего мира, построения его формы и оптимального зрительного восприятия человеком, с помощью которых он может ощущать красоту и гармонию.
Принцип определения размеров золотого сечения лежит в основе совершенства целого мира и его частей в своей структуре и функциях, его проявление можно видеть в природе, искусстве и технике. Учение о золотой пропорции было заложено в результате исследований древними учеными природы чисел.
Свидетельства использования древними мыслителями золотой пропорции приведены в книге Эвклида «Начала», написанной еще в 3 в. до н.э., который применял это правило для построения правильных 5-угольников. У пифагорейцев эта фигура считается священной, поскольку является одновременно симметричной и асимметричной. Пентаграмма символизировала жизнь и здоровье.

Числа Фибоначчи
Знаменитая книга Liber abaci математика из Италии Леонардо Пизанского, который в последующем стал известен, как Фибоначчи, увидела свет в 1202 г. В ней учены


Леонардо Фибоначчи (также Леонардо Пизанский) считается первым европейским «специалистом-математиком» средневековья. Он занимался главным образом теоретико-числовыми проблемами, в которых указанные им методы решения выходили за рамки знания арабского языка, а также греческого культурного круга.
О жизни Фибоначчи известно не так уж и много. Он жил примерно с 1170 по 1250 год и происходил из уважаемой купеческой семьи. Его отец был консульским работником Пизанской Республики в Тунисе, он нанял мавра для обучения мальчика, и благодаря этому молодой Леонардо был ознакомлен с математическими достижениями арабов. Позже Фибоначчи в качестве коммерческого представителя своего родного города отправился в Египет, Сирию, Грецию, Сицилию и другие страны. Он воспользовался этой возможностью, чтобы изучить научные достижения этих народов и приобрести их самостоятельно. Таким образом, два культурных круга слились в Леонардо.
Это также объясняет, почему он стал известен под двумя именами: с одной стороны, следуя итальянской традиции, он оставил после Леонардо название своего родного города, т.е. Леонардо Пизанский. С другой стороны, он добавил слово «сын» и имя отца (Боначчи) согласно арабскому обычаю, «filius Bonacci («сын Боначчи»)» было сокращено до Фибоначчи, под этим именем он и вошел в историю математики.
Вклад Фибоначчи в арифметику — Книга абака (Liber abaci)
В Европе математика пришла в упадок после падения греческой культуры. Сначала индейцы положили начало новому расцвету с развитием платежных систем и арифметики, а затем арабы, которые продвинулись в развитии с установлением плоскостной и пространственной тригонометрии. Ситуация была такова, что знания необходимо было распространять в Европе, и никто не был лучше подготовлен для этого, чем Фибоначчи, который освоил и расширил все эти познания.
В 1202 году была опубликована его работа «Liber abaci» (Книга абака), состоящая из 15 разделов, первое европейское общее представление арифметики. Леонардо Пизанский в своём труде вводит индо-арабские цифры, тут же описывает алгоритм умножения (который в новой системе во много раз проще, чем в старой, римской) и показывает, как преобразовать числа из старой системы в новую. Это была трудная задача, потому что было широко распространено недоверие к этим цифрам. В 1299 году городские отцы во Флоренции запретили их использование.

 Книга абака (Liber abaci)
Книга абака (Liber abaci)О Фибоначчи рассказывается следующая история: В 1225 году в Пизе был конкурс по расчетам. Участникам пришлось решать сложные задачи. Одной из таких задач было:
Найти (рациональное) квадратное число, которое, будучи увеличено или уменьшено на 5, вновь даёт (рациональные) квадратные числа.
Фибоначчи нашел решение и вышел из конкурса победителем. Леонардо попросил присутствовавшего на конкурсе императора Фридриха II содействовать распространению арабских цифр. Фридрих II обещал, но даже он не смог это исполнить. Понадобилось время до 1494 года, чтобы Медичи полностью перешли на арабские цифры. Тем не менее, книга Фибоначчи внесла свой вклад в их распространение и переход к десятичной системе счисления.
В принципе, «Liber abaci» резюмировала, систематизировала и обогатила все математические знания того времени, и эта работа не была превзойдена на протяжении длительного времени. В ней можно найти правила деления на 2, 3, 5 и 9, методы определения наименьшего общего кратного, для которого ранее просто использовалось произведение чисел. Кроме того, представлены методы решения задач с пропорциями, решения задач со смещением, показаны способы решения систем уравнений (до семи неизвестных), продемонстрированы решения уравнений более высокой степени. Наконец, описаны методы аппроксимации для кубических корней, в которых происходит итерация.
В 1220 году последовала вторая работа Фибоначчи «Практика геометрии» — это термин, используемый средневековыми землемерами, известными в наше время как геодезисты. Фибоначчи написал для этих ремесленников «De practica geometrie», подходящее дополнение к Liber abbaci.
В 1225 году была издана «Книга квадратов» (Liber quadratorum).
В ней рассматривается несколько вопросов теории чисел, среди которых индуктивный метод нахождения пифагоровых троек.
Последовательность Фибоначчи (числа Фибоначчи)
Фибоначчи перенял большую часть своей работы от предшественников, он не только систематизировал, но и обогатил ее. Его имя до сих пор ассоциируется с одним открытием. Отправной точкой для этого была изначально странно выглядящая проблема:
- Одна пара кроликов рождает новую пару каждый месяц
- Каждая новая пара создает новую пару каждый месяц со второго месяца
- За это время не было ни одной смерти
В первом месяце есть только одна пара, во втором — уже две пары. В третьем месяце добавляется новая пара из первой пары, а в четвертом — новая пара из первой и второй пары, так что всего их пять. Это приводит к следующей последовательности: 1; 2; 3; 5; …
Если поместить 1 перед первым элементом в качестве дополнительного элемента, то получится так называемая последовательность Фибоначчи (числа Фибоначчи):


Каждый элемент является суммой двух предыдущих. Это первая известная рекурсивно определенная последовательность. Фибоначчи изучил эту последовательность и обнаружил много замечательных свойств, таких как:
Сумма первых n членов равна числу Фибоначчи — 1
(например: 1 + 1 + 2 + 3 + 5 + 8 = 21 — 1)
Сумма квадратов двух соседних чисел Фибоначчи снова приводит к числу Фибоначчи.
(например: 32 + 52 = 34).
Только намного позже оказалось, что эта последовательность играет важную роль в других математических задачах, таких как золотое сечение и треугольник Паскаля, и что, например, разветвления деревьев, как правило, следуют этому закону.
Золотое сечение. Последовательность Фибоначчи в природе
Золотое сечение можно найти, разделив линию на две части. Меньшая часть должна быть в той же пропорции, что и большая часть к общей длине линии. Если вычислить это соотношение, получится иррациональное число, которое и является числом золотого сечения, обозначается φ(Фи) и составляет примерно 1.6180339887.

 Геометрическое изображение золотой пропорции.
Геометрическое изображение золотой пропорции.Существует очень интересная деталь чисел Фибоначчи. Если разделить какое-либо число в последовательности на предыдущие, то всегда получается значение, которое равно числу золотого сечения.
Золотой прямоугольник имеет стороны, которые соответствуют золотой пропорции; их пропорция друг к другу составляет 1:1,618,
Серия золотых прямоугольников создает форму золотой спирали.

 Золотой прямоугольник
Золотой прямоугольникЗолотой треугольник представляет собой равнобедренный треугольник, который имеет две равные стороны, находящиеся в золотом сечении к третьей стороне.

 Золотой треугольник
Золотой треугольникМногие крупные компании используют золотые пропорции в дизайне логотипов.

 Золотое сечение в логотипах
Золотое сечение в логотипахЗолотое сечение можно найти как в природе, так и в искусстве: многие растения растут в духе золотого сечения, даже человеческое лицо можно разделить в соответствии с пропорциями «золотой спирали». Поэтому вездесущая пропорция также называется «Божественной пропорцией».

 Золотая пропорция в природе
Золотая пропорция в природеФибоначчи повсюду! — Мастерок.жж.рф — LiveJournal
Итак, мы выяснили с вами Кто такой Фибоначчи, а теперь давайте рассмотрим вот такой феномен.
Оказывается Фибоначчи повсюду!
На самом деле эти числа были известны задолго до Фибоначчи ещё в древней Индии, где они использовались в метрическом стихосложении.
Леонардо Фибоначчи первым ввёл эту числовую последовательность в западноевропейской математической науке в своей важной книге «Liber Abaci» («Книга абака») в 1202 году. Он использовал эту последовательность чисел, когда пытался объяснить рост популяции кроликов.
Фибоначчи рассматривает гипотетическую ситуацию, когда в поле появляется пара кроликов. Они спариваются в конце месяца и в конце второго месяца самка производит еще одну пару. Кролики никогда не умирают, спариваются ровно через месяц, и самки всегда производят пару (один самец, одна самка). Вопрос, который поставил Фибоначчи был следующим: сколько пар будет через один год? Если посчитать, то окажется, что количество пар в конце N-го месяца равно Fn или N-му числу Фибоначчи. Таким образом, количество пар кроликов через 12 месяцев будет F12 или 144.
Числа Фибоначчи и золотое сечение
Как известно, последовательность Фибоначчи начинается с 1 и 1, после чего каждое новое число является результатом сложения двух предыдущих чисел:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Если разделить два последовательных числа в этом ряду, например 144/89, в конечном итоге получится число 1,618, которое называется «Золотое число» или «Золотое сечение».
Последовательное приближение соотношения двух соседних чисел ряда Фибоначчи к Золотому сечению.
Пропорция золотого сечения считается эстетически приятной и из-за этого многие художники и архитекторы, в том числе Сальвадор Дали и Ле Корбюзье использовали её в своих работах.
Последовательность Фибоначчи и Золотое сечение тесно взаимосвязаны. Отношение последовательных чисел Фибоначчи сходится и приближается к золотому сечению, а выражение замкнутой формулы для последовательности Фибоначчи включает Золотое сечение.
Золотой прямоугольник (розовый) с длинной стороной a и короткой стороной b, и находящийся рядом с ним квадрат со стороной длиной a, создадут подобный золотой прямоугольник с длинной стороной а + b и короткой стороной a. Это изобажение иллюстрирует взаимосвязь отношений (a+b)/a = a/b.
Спираль Фибоначчи или золотая спираль — это последовательность соединенных четвертей окружностей, вписанных внутри массивов квадратов со сторонами равными числам Фибоначчи. Квадраты идеально подходят друг к другу из-за природы последовательности Фибоначчи, в которой следующее число равно сумме двух перед ним (см.предыдущий рисунок). Любые два последовательных числа Фибоначчи имеют отношение, очень близкое к золотому сечению, которое составляет примерно 1.618034. Чем больше пара чисел Фибоначчи, тем ближе это приближение. Спираль и результирующий прямоугольник называются золотым прямоугольником.
Почему эта последовательность настолько уникальна
Числа Фибоначчи описывают различные явления в искусстве, музыке и природе. Числа спиралей на большинстве шишек и ананасах равны числам Фибоначчи. Расположение листьев и ветвей на стеблях многих растений соответствуют числам Фибоначчи. На пианино количество белых (8) клавиш и черных (5) клавиш в каждой октаве (13) являются числами Фибоначчи. Длины и ширины много прямоугольных предметов, таких как учетные карточки, окна, игральные карты и пр. соответствуют последовательным числам ряда Фибоначчи.
Числа Фибоначчи в природе
Подсолнухи являются отличными примерами последовательности Фибоначчи, потому что семена в центре цветка организованы в два набора спиралей — короткие, идущие по часовой стрелке от центра, и более длинные — против часовой стрелки. Если считать спирали последовательно, то, видимо, всегда найдутся числа Фибоначчи.
Последовательность Фибоначчи можно также увидеть в форме или разделении ветвей дерева. Основной ствол будет расти до тех пор, пока он не создаст ветвь, которая создает две точки роста. Затем один из новых стеблей разветвляется на два, в то время как другой находится в состоянии покоя. Такая картина ветвления повторяется для каждого из новых стеблей. Корневая система и даже водоросли также демонстрируют эту закономерность.
Вот еще несколько примеров, где вы можете найти спираль Фибоначчи в природе.
Неудивительно, что спиральные галактики также следуют знакомой схеме Фибоначчи. Млечный Путь имеет несколько спиральных рукавов, каждый из которых представляет логарифмическую спираль около 12 градусов.
Числа Фибоначчи в теле человека
Есть много примеров соотношений частей тела человека на основе последовательности Фибоначчи, например рука и, в частности, кости пальца.
Каждая кость указательного пальца, от кончика до основания запястья, больше предыдущей примерно на коэффициент Фибоначчи 1,618, что соответствует числам Фибоначчи 2, 3, 5 и 8.
Числа Фибоначчи в биржевой торговле
Последовательность Фибоначчи является инструментом технического анализа, используемым профессиональными трейдерами в сочетании с другими инструментами для расчета прогноза потенциального конца коррекции, принимая процент от предыдущего движения.
Считается, что во время мощного рыночного движения, цены могут откатываться на 23,6% (это соответствует отношению числа ряда Фибоначчи на позиции N к числу на позиции N+3), 38,2% (соответствует отношению числа ряда Фибоначчи на позиции N к числу на позиции N+2) или 50% (половина). Эти уровни коррекции Фибоначчи считаются «нормальными». Если же цена падает на 61,2% (отношение двух соседних чисел ряда Фибоначчи — позиции N и N+1) и более, то это серьезный сигнал вероятного разворота тренда.
Числа Фибоначчи в фотографии и искусстве
В фотографии сетка фи (phi) является интерполяцией спирали Фибоначчи и в наши дни считается фундаментальным методом для создания приятной композиции в кадре. Цель состоит в том, чтобы выровнять объект по линиям, созданным спиралью, или использовать её в качестве разделителя для создания правильного ощущения кадра.
Сетка фи (красные линии) и спираль Фиббоначи в кадре.
Имеется много примеров, когда последовательность Фибоначчи появляется вокруг нас, и мы не обращаем внимания на это математическое чудо, которое кажется таинственным фактором, приносящим универсальную форму гармонии элементам математического музыкального искусства природы.
Может именно из-за этого Дональд Трамп был избран президентом? (шутка):
И еще немного фундаментального числа!
[источники]Источники:View story at Medium.com
Это копия статьи, находящейся по адресу http://masterokblog.ru/?p=47272.
Чи́сла Фибона́ччи — элементы числовой последовательности
- 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS)
в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (или Фибоначчи) [1].
Более формально, последовательность чисел Фибоначчи 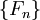 задается рекуррентным соотношением:
задается рекуррентным соотношением:
Иногда числа Фибоначчи рассматривают и для неположительных номеров n как двусторонне бесконечную последовательность, удовлетворяющую основному соотношению. Члены с такими номерами легко получить с помощью эквивалентной формулы «назад»: Fn = Fn + 2 − Fn + 1:
| n | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fn | −55 | 34 | −21 | 13 | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Легко видеть, что F − n = ( − 1)n + 1Fn. Для чисел Фибоначчи с отрицательными индексами остаются верными большинство нижеприведённых свойств.
Происхождение
Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении), намного раньше, чем она стала известна в Европе.
Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».
На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что:
- В «нулевом» месяце, имеется пара кроликов (0 новых пар).
- В первом месяце, первая пара производит на свет другую пару (1 новая пара).
- Во втором месяце, обе пары кроликов порождают другие пары и первая пара погибает (1 новая пара).
- В третьем месяце, вторая пара и две новые пары порождают в общем три новые пары, а старая вторая пара погибает (2 новые пары).
Закономерным является тот факт, что каждая пара кроликов порождает ещё две пары на протяжении жизни, а затем погибает.
Пусть популяция за месяц n будет равна F(n). В это время, только кролики которые жили в месяце n-2 являются способными к размножению и производят потомков, тогда F(n-2) пар прибавится к текущей популяции F(n-1). Таким образом общее количество пар будет равно F(n) = F(n — 1) + F(n — 2).
Формула Бине
Формула Бине выражает в явном виде значение Fn как функцию от n:
 ,
,
где 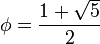 — золотое сечение. При этом
— золотое сечение. При этом 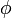 и
и 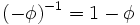 являются корнями квадратного уравнения
являются корнями квадратного уравнения 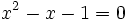 .
.
Из формулы Бине следует, что для всех 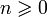 , Fn есть ближайшее к
, Fn есть ближайшее к 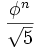 целое число, то есть
целое число, то есть 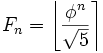 . В частности, справедлива асимптотика
. В частности, справедлива асимптотика 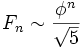 .
.
Тождества
И более общие формулы:
- Числа Фибоначчи представляются значениями континуант на наборе единиц:
 , то есть
, то есть
 , а также
, а также  ,
,
- где матрицы имеют размер
 , i — мнимая единица.
, i — мнимая единица.
Свойства
- Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. (Fm,Fn) = F(m,n). Следствия:
- Fm делится на Fn тогда и только тогда, когда m делится на n (за исключением n = 2). В частности, Fm делится на F3 = 2 (то есть является чётным) только для m = 3k; Fm делится на F4 = 3 только для m = 4k; Fm делится на F5 = 5 только для m = 5k и т. д.
- Fm может быть простым только для простых m (с единственным исключением m = 4) (например, число 233 простое, и индекс его, равный 13, также прост). Обратное не верно, первый контрпример —
 . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
. Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
 .
.
- В 1964 Дж. Кон (J. H. E. Cohn) доказал, что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12: F0 = 02 = 0, F1 = 12 = 1, F2 = 12 = 1, F12 = 122 = 144. При этом для n=0,1,12 верно утверждение Fn = n2.
- Множество чисел Фибоначчи совпадает с множеством положительных значений многочлена
z(x,y) = 2xy4 + x2y3 − 2x3y2 − y5 − x4y + 2y,
на множестве неотрицательных целых чисел x и y [2].
- Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
- Последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом 60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом 300, последние три цифры — с периодом 1500, последние четыре — с периодом 15000, последние пять — с периодом 150000 и т. д.
Вариации и обобщения
В других областях
- В природе
- Расстояния между листьями (или ветками) на стволе растения относятся примерно как числа Фибоначчи.
- В культуре
См. также
Литература
Ссылки
Примечания
- ↑ [1] БСЭ]
- ↑ P. Ribenboim, The New Book of Prime Number Records, Springer, 1996, p. 193.
Wikimedia Foundation. 2010.
Ряд Фибоначчи — это… Что такое Ряд Фибоначчи?
Чи́сла Фибона́ччи — элементы числовой последовательности
- 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS)
в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (или Фибоначчи) [1].
Более формально, последовательность чисел Фибоначчи 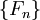 задается рекуррентным соотношением:
задается рекуррентным соотношением:
Иногда числа Фибоначчи рассматривают и для неположительных номеров n как двусторонне бесконечную последовательность, удовлетворяющую основному соотношению. Члены с такими номерами легко получить с помощью эквивалентной формулы «назад»: Fn = Fn + 2 − Fn + 1:
| n | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fn | −55 | 34 | −21 | 13 | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Легко видеть, что F − n = ( − 1)n + 1Fn. Для чисел Фибоначчи с отрицательными индексами остаются верными большинство нижеприведённых свойств.
Происхождение
Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении), намного раньше, чем она стала известна в Европе.
Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».
На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что:
- В «нулевом» месяце, имеется пара кроликов (0 новых пар).
- В первом месяце, первая пара производит на свет другую пару (1 новая пара).
- Во втором месяце, обе пары кроликов порождают другие пары и первая пара погибает (1 новая пара).
- В третьем месяце, вторая пара и две новые пары порождают в общем три новые пары, а старая вторая пара погибает (2 новые пары).
Закономерным является тот факт, что каждая пара кроликов порождает ещё две пары на протяжении жизни, а затем погибает.
Пусть популяция за месяц n будет равна F(n). В это время, только кролики которые жили в месяце n-2 являются способными к размножению и производят потомков, тогда F(n-2) пар прибавится к текущей популяции F(n-1). Таким образом общее количество пар будет равно F(n) = F(n — 1) + F(n — 2).
Формула Бине
Формула Бине выражает в явном виде значение Fn как функцию от n:
 ,
,
где 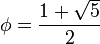 — золотое сечение. При этом
— золотое сечение. При этом 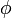 и
и 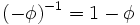 являются корнями квадратного уравнения
являются корнями квадратного уравнения 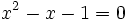 .
.
Из формулы Бине следует, что для всех 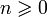 , Fn есть ближайшее к
, Fn есть ближайшее к 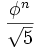 целое число, то есть
целое число, то есть 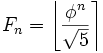 . В частности, справедлива асимптотика
. В частности, справедлива асимптотика 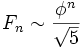 .
.
Тождества
И более общие формулы:
- Числа Фибоначчи представляются значениями континуант на наборе единиц:
 , то есть
, то есть
 , а также
, а также  ,
,
- где матрицы имеют размер
 , i — мнимая единица.
, i — мнимая единица.
Свойства
- Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. (Fm,Fn) = F(m,n). Следствия:
- Fm делится на Fn тогда и только тогда, когда m делится на n (за исключением n = 2). В частности, Fm делится на F3 = 2 (то есть является чётным) только для m = 3k; Fm делится на F4 = 3 только для m = 4k; Fm делится на F5 = 5 только для m = 5k и т. д.
- Fm может быть простым только для простых m (с единственным исключением m = 4) (например, число 233 простое, и индекс его, равный 13, также прост). Обратное не верно, первый контрпример —
 . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
. Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
 .
.
- В 1964 Дж. Кон (J. H. E. Cohn) доказал, что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12: F0 = 02 = 0, F1 = 12 = 1, F2 = 12 = 1, F12 = 122 = 144. При этом для n=0,1,12 верно утверждение Fn = n2.
- Множество чисел Фибоначчи совпадает с множеством положительных значений многочлена
z(x,y) = 2xy4 + x2y3 − 2x3y2 − y5 − x4y + 2y,
на множестве неотрицательных целых чисел x и y [2].
- Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
- Последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом 60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом 300, последние три цифры — с периодом 1500, последние четыре — с периодом 15000, последние пять — с периодом 150000 и т. д.
Вариации и обобщения
В других областях
- В природе
- Расстояния между листьями (или ветками) на стволе растения относятся примерно как числа Фибоначчи.
- В культуре
См. также
Литература
Ссылки
Примечания
- ↑ [1] БСЭ]
- ↑ P. Ribenboim, The New Book of Prime Number Records, Springer, 1996, p. 193.
Wikimedia Foundation. 2010.
Загрузка…
Числа Фибоначчи и золотое сечение
Последовательность Фибоначчи это не что иное, как ряд чисел, в котором каждое следующее число равно сумме предыдущих двух. Эта последовательность названа в честь европейского математика XII века Леонардо Пизанского, известного под псевдонимом Фибоначчи. Разумеется, Фибоначчи был известен и по другим математическим достижениям, но свою работу над «числами Фибоначчи» он описал в книгах «Liber Abaci» («Книга Абака» или «Книга об Абаке»). Сама последовательность Фибоначчи представляет собой бесконечный ряд чисел, где, как уже было сказано ранее, каждое новое число является суммой предыдущих двух:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 …
Первое число 0, второе число 1 и тут уже включается математика. Чтобы определить третье число, необходимо сложить первые два – получаем число «1» (0+1=1), четвертое число – это сумма второго и третьего числа (1+1=2), т.е. «2». Пятое число – сумма третьего и четвертного числа, т.е. 1+2=3. И так до бесконечности.
Ряд чисел Фибоначчи имеет много математических особенностей, но главным является то, что отношение каждого члена ряда к предыдущему члену стремится к «Золотому сечению» — числу 1.618. Впервые это число встречается в «Началах» Эвклида, где применялось для построения правильного пятиугольника (около 300 лет до нашей эры).
Буквально, если взять любое число из ряда Фибоначчи и разделить его на предыдущее, а результат округлить в бОльшую сторону, то получим число 1.618. Например, 144/89= 1.61797, округлив мы получим те самые 1.618.
Золотое сечение является самой гармоничной пропорцией целого числа к его части. Число 1.618 постоянно встречается в природных формах, которые не имеют ничего общего между собой. Например, в расположении листиков у растений, форме раковин улиток, фалангах пальцев человека, расположении звезд в спиралях галактик, форме цветков у растений, вихрях тайфунов и т.д..
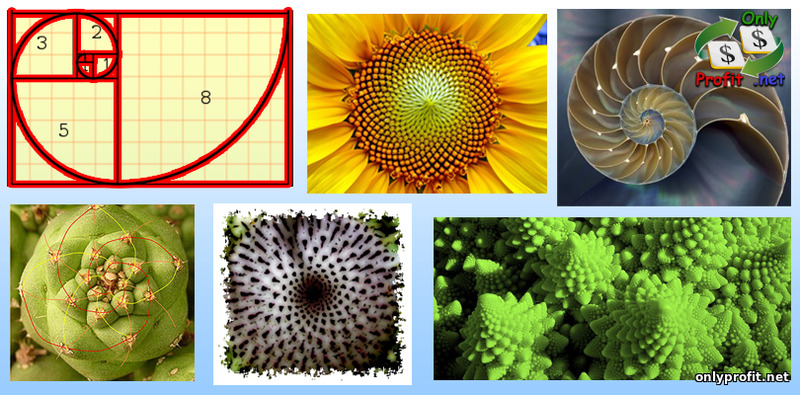
Золотое сечение (число 1.618) так же встречается в музыке, литературе, живописи. В 19-ом веке, ученные признали золотое сечение эталоном гармонии пропорций в природе.
В начале 1930-х годов, американский инженер и управленец Ральф Нельсон Эллиотт задумался о поисках золотого сечения в графиках биржевых котировок. Работа Эллиотта заключалась в анализе годовых, месячных, недельных, дневных, часовых и получасовых графиков различных фондовых индексов, имеющих историю более 75 лет поведения рынка. Впоследствии, Эллиотт заметил, что все движения цены на рынках были подчинены определенным законам — волнам, в которых так же просматривалось число 1.618. На основе этих наблюдений была написана книга «Закон природы – секрет вселенной» (Nature’s Law – The Secret of the Universe), в которой он описал все свои наработки по теории волн и соотношении чисел Фибоначчи.
Эллиотт положил начало целому учению, но он только стал первым. Со временем, многие трейдеры стали так же обращать свое внимание на закономерности цены и находить в них золотое сечение. Развитие вычислительной техники позволило очень сильно углубить знания в этой теме. Это привело к тому, что очень многие современные трейдеры стали использовать инструменты, созданные на основе чисел Фибоначчи.
Уровни Фибоначчи: уровни коррекции (ретрейсмента) Фибоначчи
Уровни коррекции (ретрейсмента) Фибоначчи выглядят следующим образом:0.236, 0.382, 0.500, 0.618, 0.764
Для чего нужны эти уровни в торговле? Они выступают, как уровни поддержки и сопротивления, а измеряют величину отката цены во время трендовых движений. Высока вероятность, что именно от этих уровней цена продолжит двигаться в сторону текущего тренда.
К счастью, нет никакой необходимости рассчитывать дроби самостоятельно, поэтому все за нас сделают инструменты, встроенные в живой график или любой терминал Meta Trader 4 (уровни Фибоначчи). Нужно лишь правильно нанести эти уровни на график.
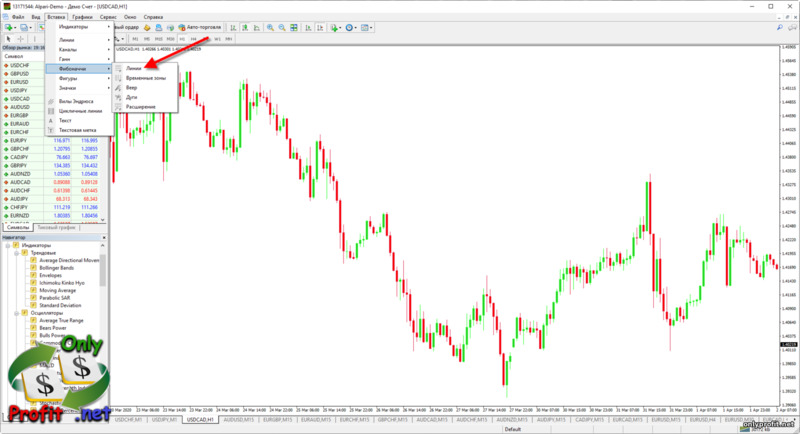
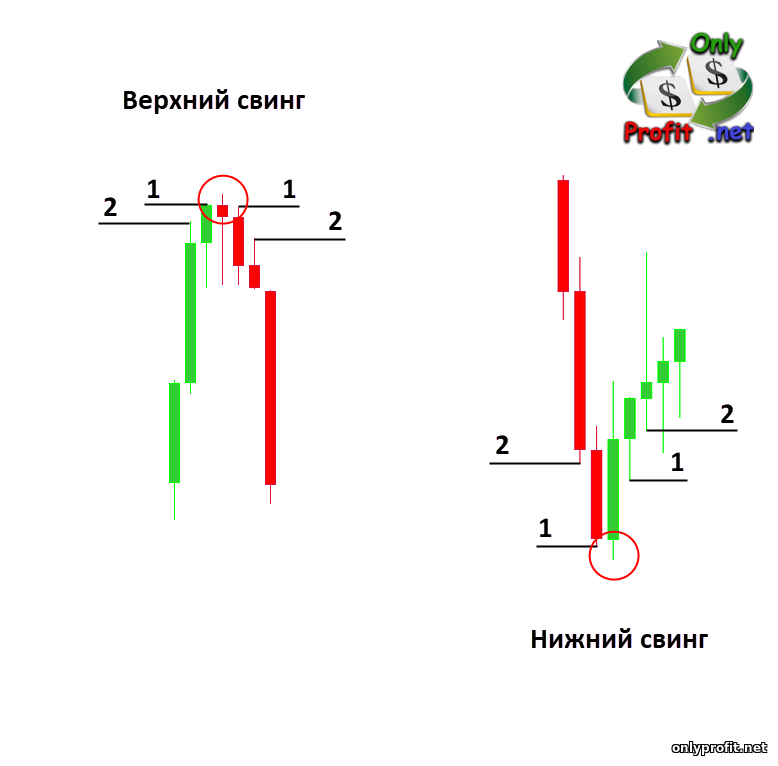
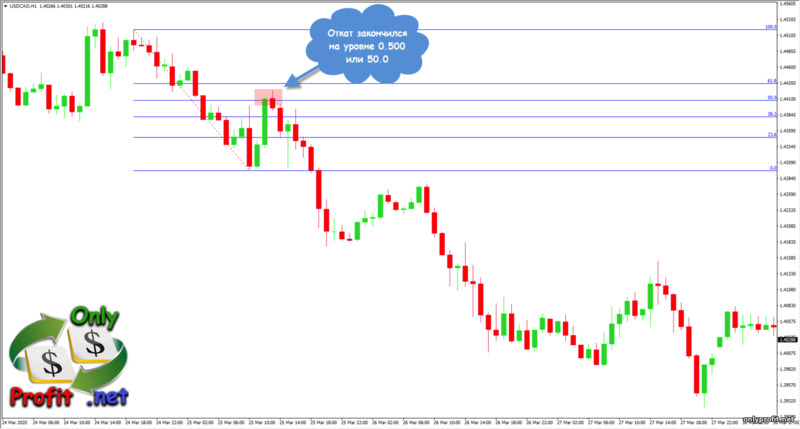
Уровни Фибоначчи в тренде вверх
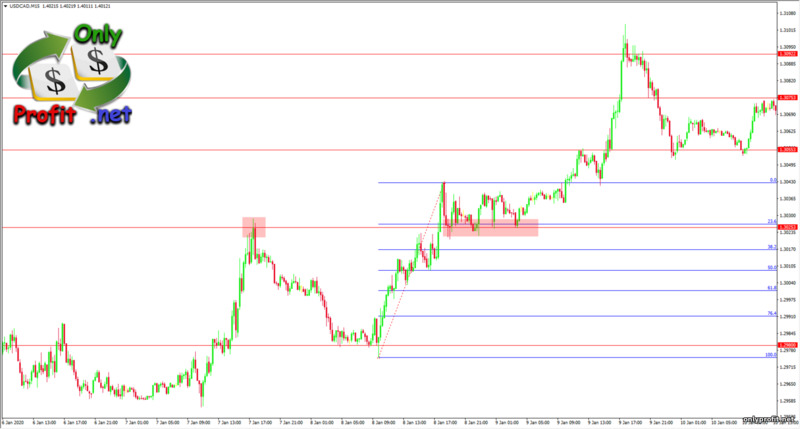
Для восходящего тренда мы растягиваем уровни Фибоначчи от нижнего свинга, означающего начало трендового импульса, до верхнего свинга, после которого начался откат цены: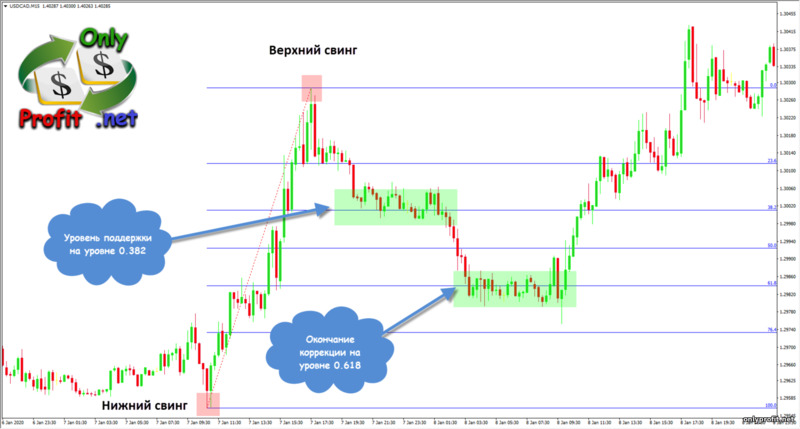
В данном примере, цена отреагировала на уровень Фибоначчи 0.382 – возник боковой канал, после которого цена опустилась до уровня 0.618 – он и стал точкой разворота цены и продолжения тренда.
$IMAG7$
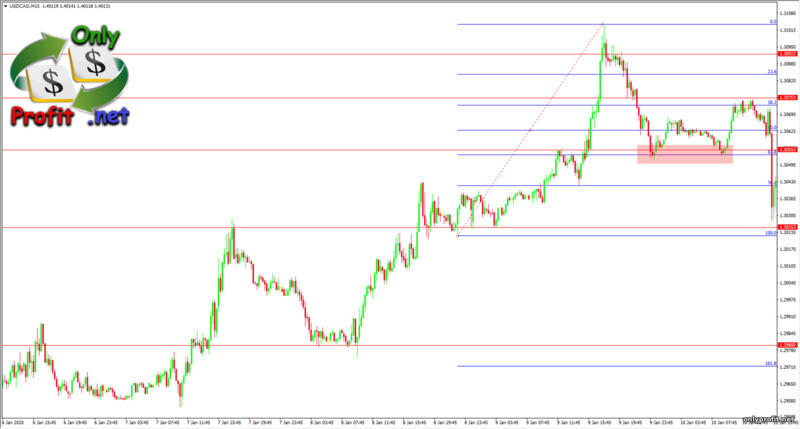
Вот еще один пример – в данном случае, тренд продолжился от уровня 0.382. Обратите внимание – этот уровень являлся уровнем поддержки и сопротивления в прошлом нисходящем тренде. Совпадение? Я бы так не сказал.Уровни Фибоначчи в тренде вниз
В нисходящем тренде мы растягиваем уровни Фибоначчи сверху вниз (от верхнего свинга до нижнего свинга) и слева направо: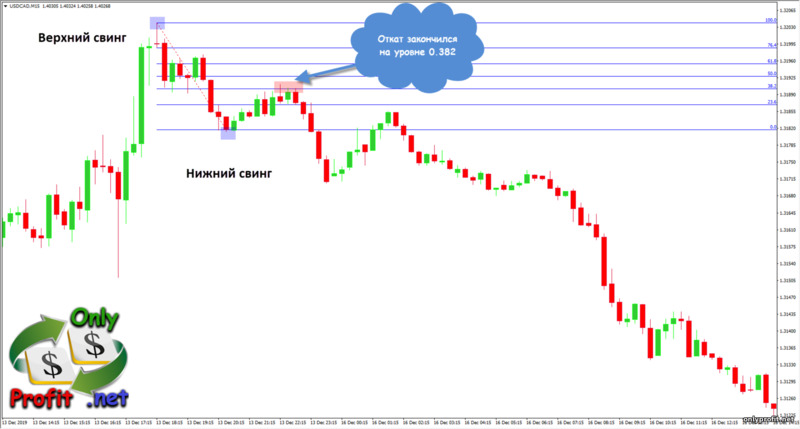
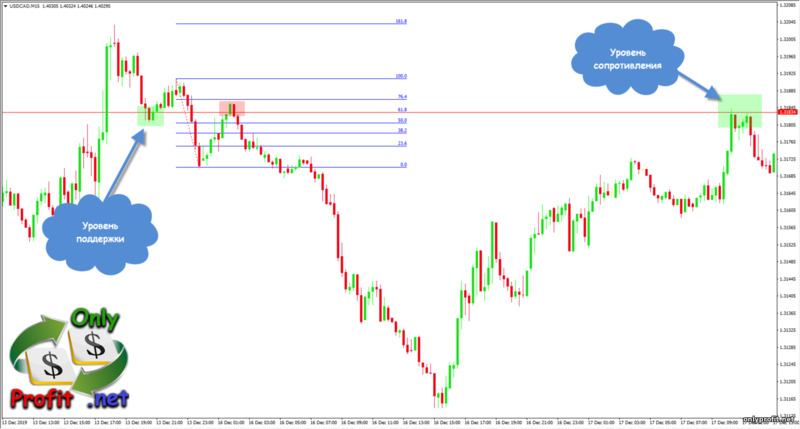
Уровни Фибоначчи на разворотах тренда
Всегда ли работают уровни Фибоначчи? Разумеется, нет. Например, возьмем ситуацию разворота трендового движения: был нисходящий тренд, а стал восходящий.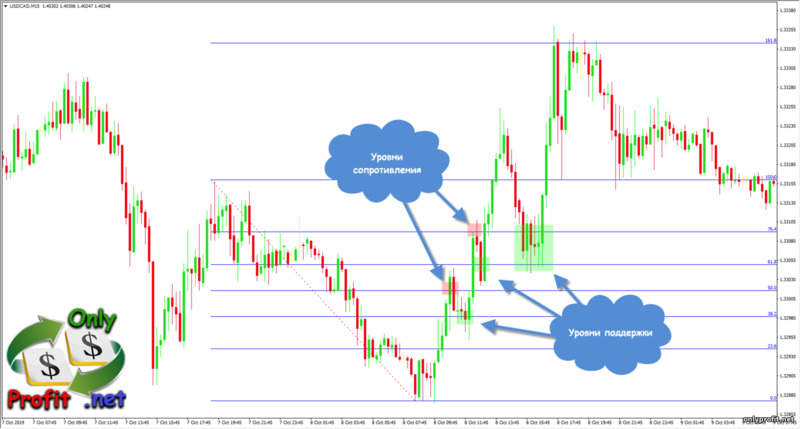
Стоит понимать, что уровни Фибоначчи – это не какой-то 100% торговый метод, а просто инструмент, который показывает возможные точки разворота. Т.е. нет никаких гарантий, есть только вероятность. Поэтому даже к золотому сечению и уровням Фибоначчи стоит относиться с осторожностью.
В каких-то случаях уровни коррекции будут разворачивать цену, в каких-то случаях цена их даже не заметит, хотите вы этого или нет. В торговле вообще нет ничего 100%, пора бы давно с этим смириться. Но вероятность верного прогноза мы всегда можем увеличить.
Уровни Фибоначчи и уровни поддержки и сопротивления
Немного ранее мы уже разобрали пару примеров, где горизонтальные уровни поддержки и сопротивления совпадали с уровнями Фибоначчи. Одно прекрасно подтверждает другое – сила уровня растет, т.к. разные участники рынка используют разные инструменты, но, в данном случае, их мнения совпадут, пусть основаны они на разной информации.Что же, давайте добавим на график уровни поддержки и сопротивления, а потом посмотрим, как же уровни Фибоначчи помогают определить сильные уровни цены:
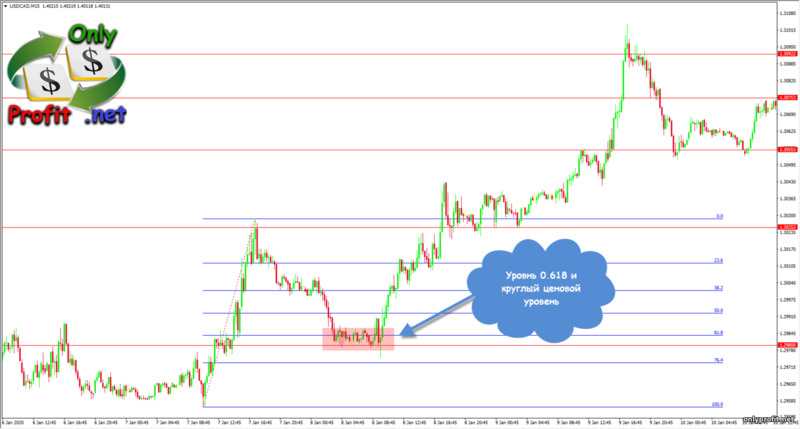
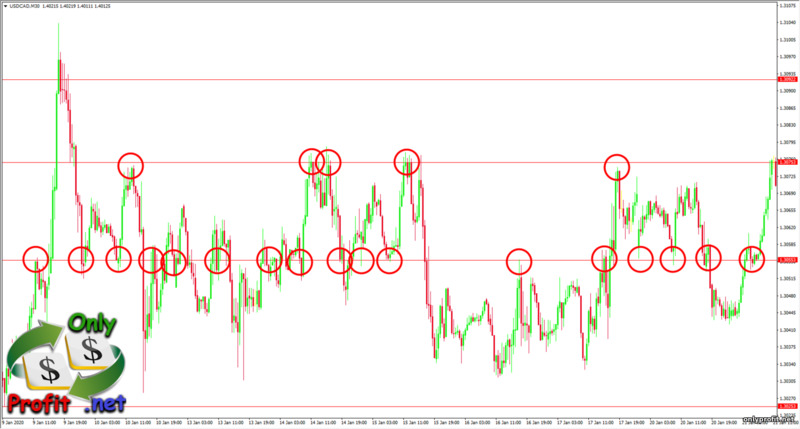
Какой вывод из всего этого можно сделать? Уровни Фибоначчи прекрасно работают с уровнями поддержки и сопротивления. Более того, эти инструменты прекрасно дополняют друг друга и усиливают вероятность верного прогноза. Стоит ли использовать уровни Фибоначчи, скажем, для торговли по Price Action? Однозначно, да!
Уровни Фибоначчи и линия тренда
Линия тренда, как и горизонтальные уровни поддержки и сопротивления, способна указать разворот цены, а значит, совместима с уровнями Фибоначчи. Если во время тренда нанести линию тренда, а после нанести уровни Фибоначчи, то их пересечение станет сильной точкой, от которой, с большой вероятностью, развернется цена во время коррекции: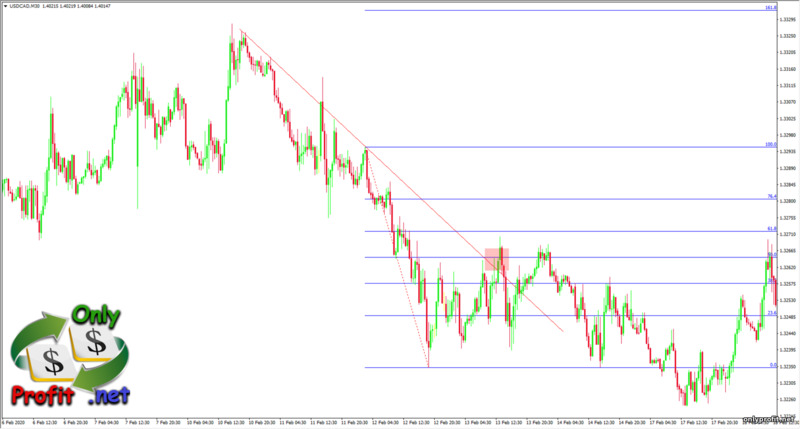
Аналогично можно использовать скользящие средние, как динамические уровни поддержки и сопротивления, совместно с уровнями Фибоначчи:
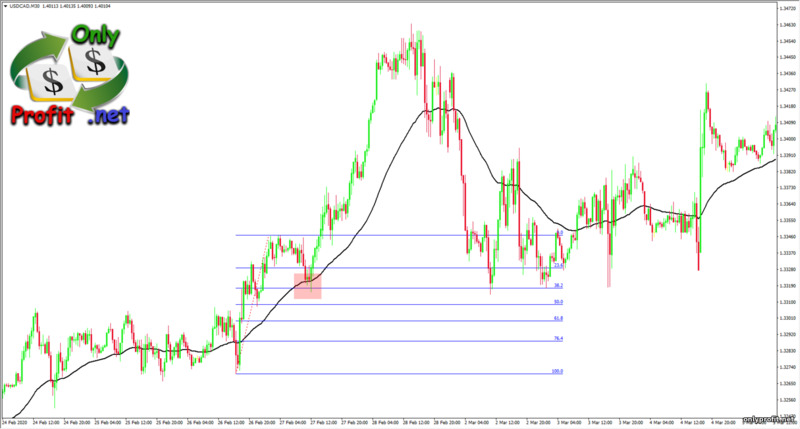
Уровни Фибоначчи и японские свечи (разворотные паттерны Price Action)
Немного ранее я не просто так упомянул Price Action – уровни Фибоначчи очень хорошо сочетаются с разворотными паттернами Прайс Экшен, так что, если позволяют знания, то внимательно присмотритесь к ценовому графику и вы найдете точки разворота цены: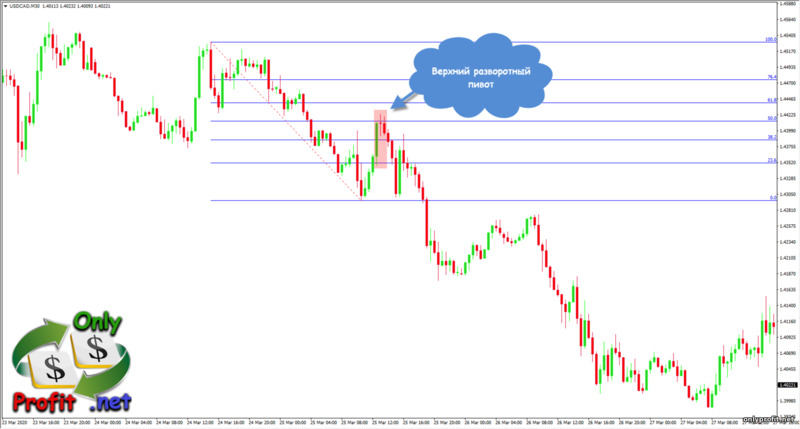
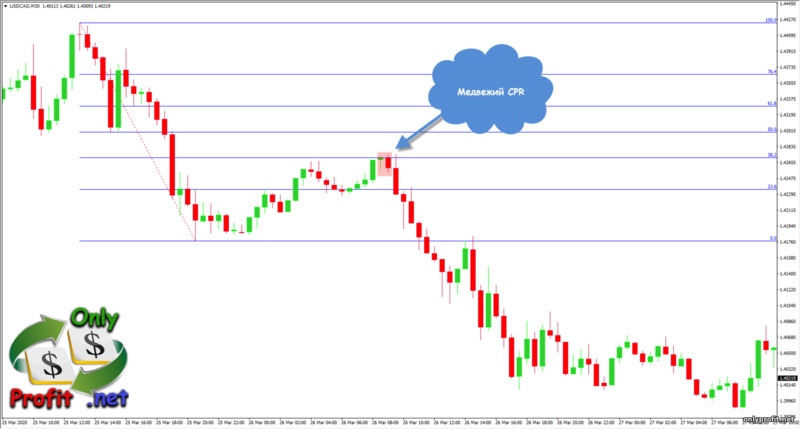
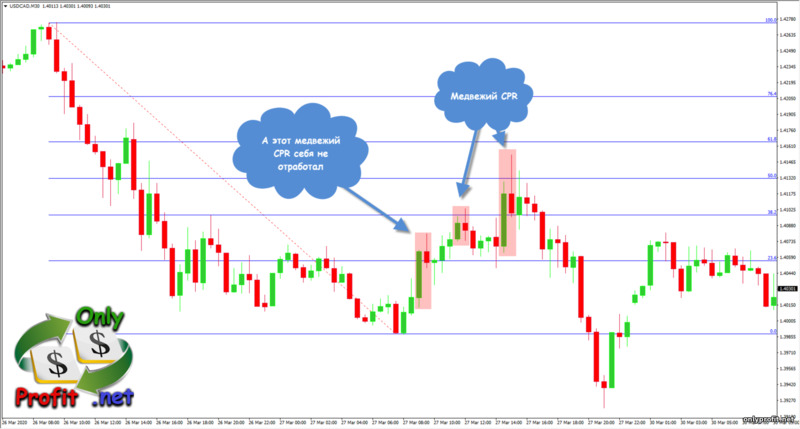
А вот и любимый паттерн многих трейдеров бинарных опционов и рынка Forex – буратино:
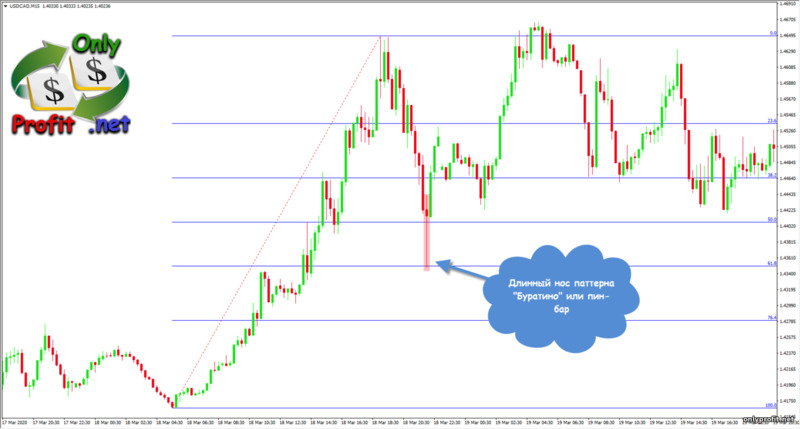
Как вы уже поняли, совмещать паттерны Price Action с уровнями Фибоначчи – замечательная идея, а если подкрепить все это дело уровнями поддержки и сопротивления, а так же скользящими средними и линиями тренда, то успех гарантирован!
Уровни расширения Фибоначчи
Уровни расширения Фибоначчи – это уровни:0, 0.382, 0.618, 1.000, 1.382, 1.618
Уровни расширения – это уровни, показывающие, до какого значения вероятнее всего дойдет цена в трендовых движениях, после окончания отката. Для начала, нам нужно нанести на график уровни Фибоначчи:
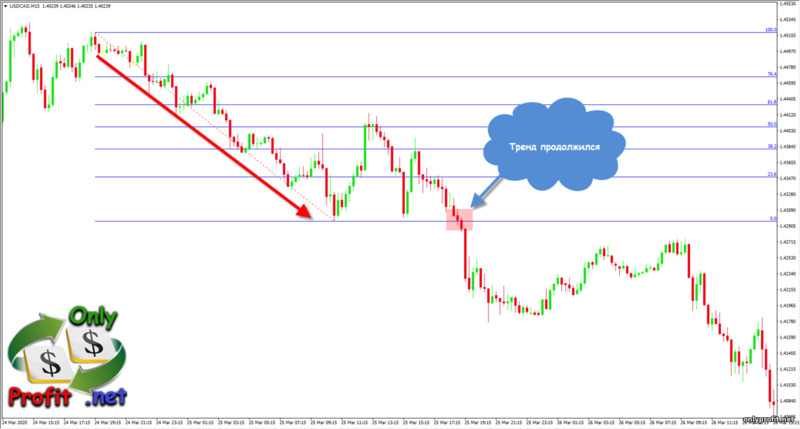
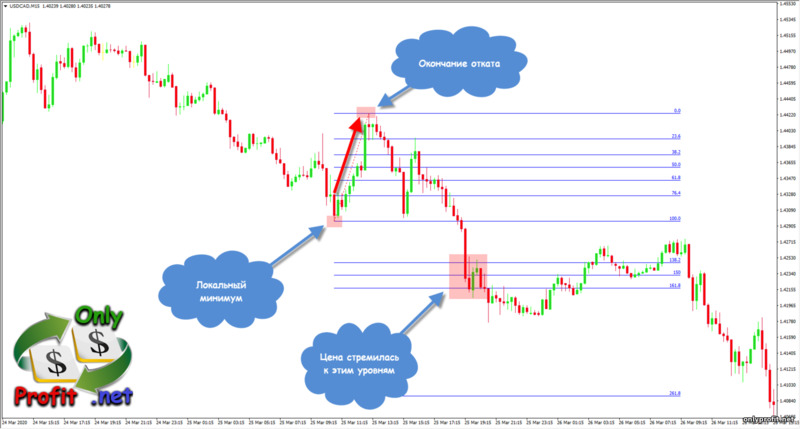
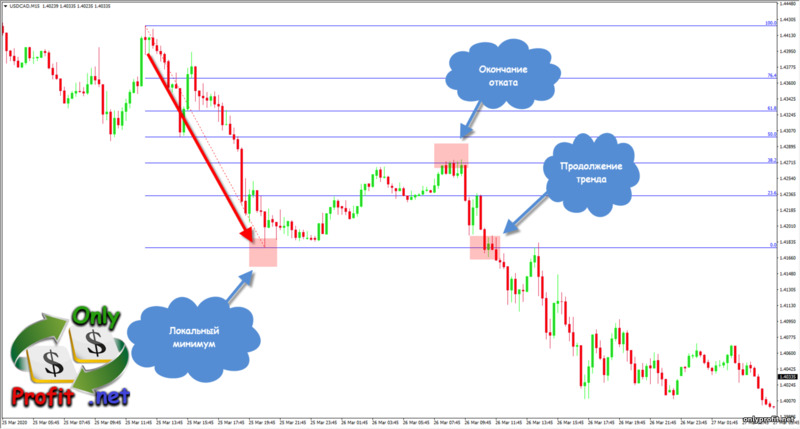
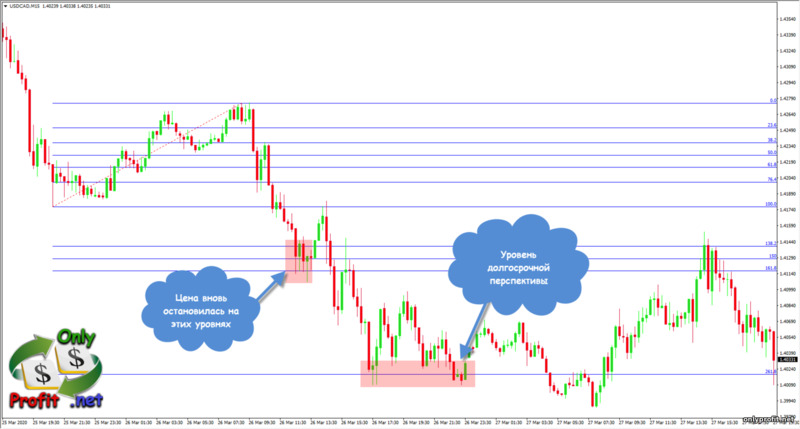
Уровни расширения цены нужны для того, чтобы понять, какой силой обладает трендовое движение. Опираясь на силу отката, можно предположить, как далеко уйдет цена после продолжения тренда.
Так же стоит учитывать, что уровни расширения Фибоначчи, как и уровни коррекции, могут указывать на сильные уровни поддержки и сопротивления. Разумеется, все эти уровни нужно фильтровать чем-то более сильным, чем обычный набор чисел золотого сечения (например, горизонтальными уровнями поддержки и сопротивления). В таком случае, ценовой график позволит вам понять, на какие уровни стоит обратить свое внимание и где ждать возможного отката цены.
Уровни Фибоначчи и волны Эллиотта
Очень часто уровни Фибоначчи используют совместно с волновой теорией Эллиотта. Согласно этой теории, любое трендовое движение цены можно разложить на пять волн – три трендовых импульса и два отката. Трендовые импульсы нумеруются цифрами 1, 3 и 5, а волны коррекции, соответственно, цифрами 2 и 4.В свою очередь, любой трендовый импульс можно так же разложить на 5 волн (3 трендовых импульса и 2 отката), а откаты можно разложить только на три волны (сложные откаты). В теории этот процесс выглядит следующим образом:
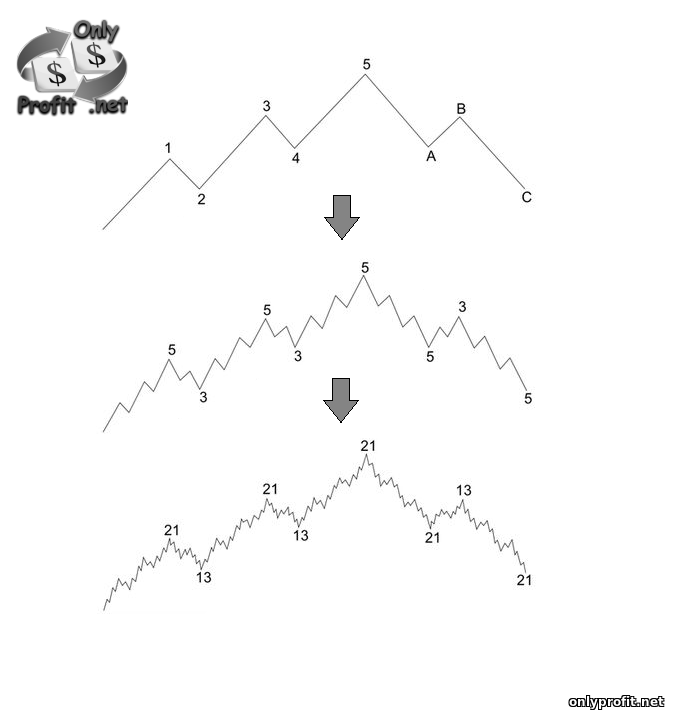
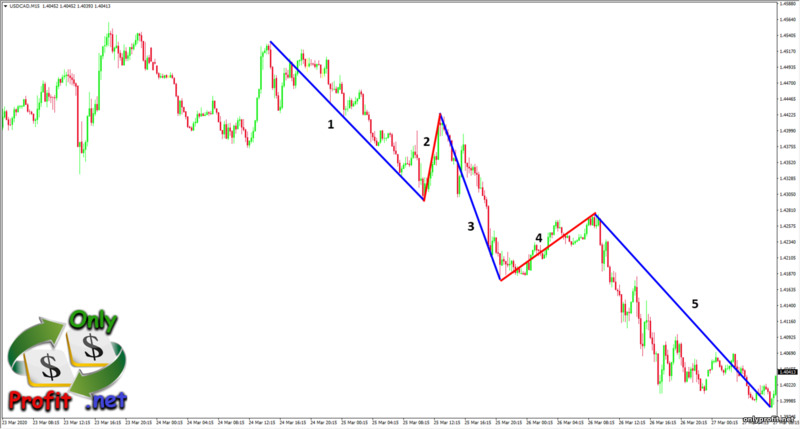
Согласно теории Эллиотта, длина третьей волны относится к первой волне как 1.618 (золотое сечение), что дает нам возможность рассчитать длину третьей волны после формирования первой и второй волн. Для этого нам понадобятся все те же уровни расширения Фибоначчи, а так же найти первую и вторую волну. С первой волной проблем возникнуть не должно:
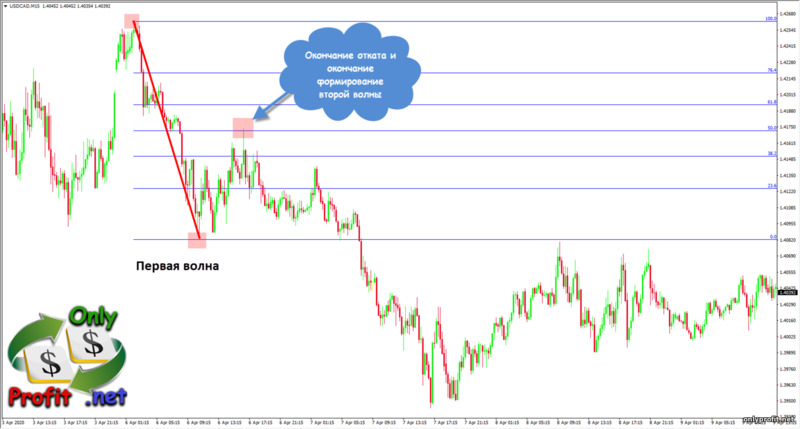
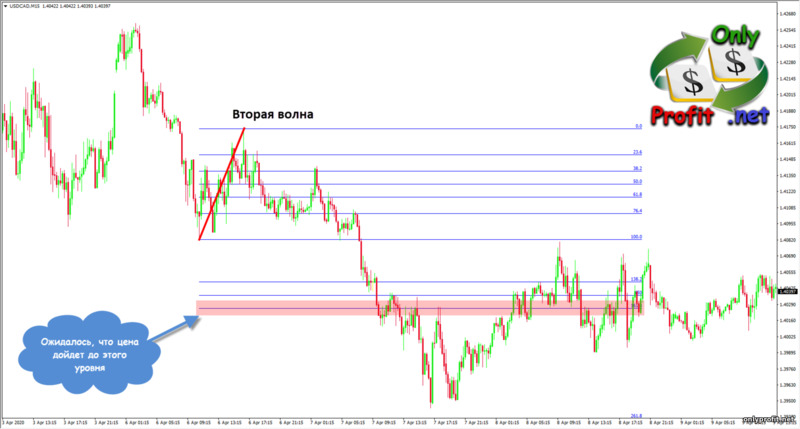
Кроме определения третьей волны, специалисты предлагали различные способы определения других волн. Например, в книге «Торговый хаос» (Билл Вильямс) предлагается следующий метод:
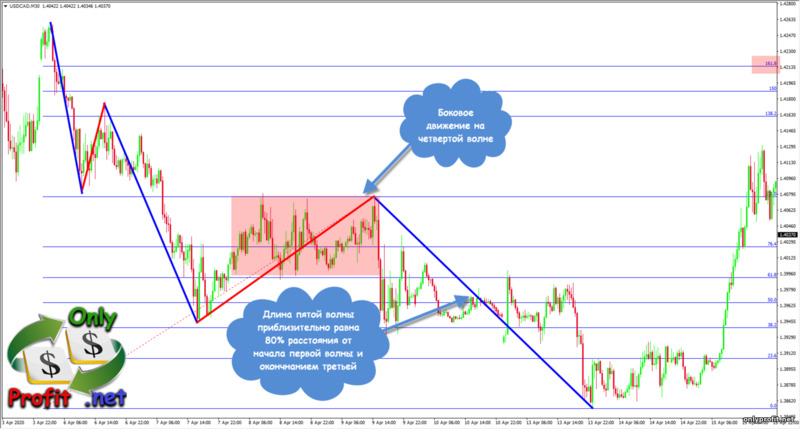
- Первую волну определяем по факту формирования
- Вторая волна, чаще всего, заканчивается на уровнях коррекции Фибоначчи 0.382 и 0.500
- Третья волна составляет от 1 до 1.618 длинны первой волны
- Четвертая волна чаще всего выглядит в форме бокового движения и редко заканчивается выше уровней 0.382 и 0.500
- Длина пятой волны составляет от 61.8% до 100% длины диапазона от начала первой волны до окончания третьей волны
Веер Фибоначчи в трейдинге
Веер Фибоначчи, как и уровни Фибоначчи, способен определять уровни коррекции цены. Принцип работы все тот же – веер растягивается между двумя точками: начало трендового импульса и начало отката.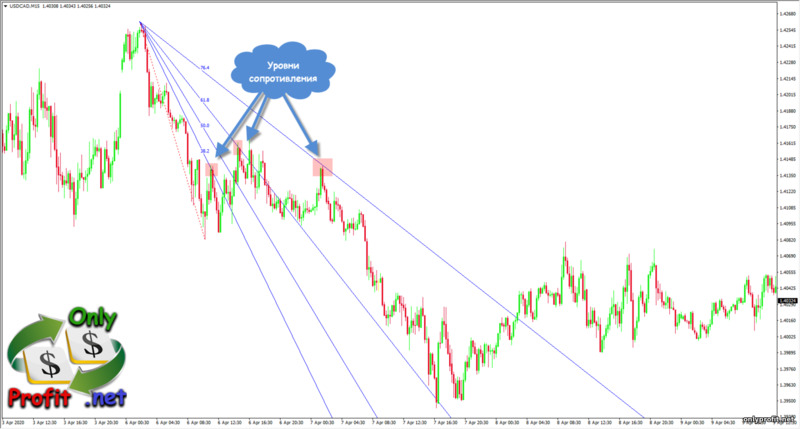
В стандартной версии веера Фибоначчи только три уровня: 0.382, 0.500 и 0.618. Они являются самыми сильными и значимыми уровнями, но если вам необходимо, то вы всегда можете добавить и дополнительные уровни – они такие же, как и у горизонтальных уровней Фибоначчи (например, 0.764).
Дуги Фибоначчи в трейдинге
Дуги Фибоначчи, в отличие от веера и горизонтальных уровней, учитывают еще один важный фактор – время. Это позволяет определить не только силу возможного отката, но и то, когда он закончится.Построение дуг Фибоначчи производится следующим образом:
- От начала трендового импульса до начала отката протягивается линия (все, как и в случае с уровнями и веером Фибоначчи)
- Инструмент формирует на графике три дуги
- Каждая дуга (расположен под или над точкой окончания отката) будет равна уровням 0.382, 0.500 и 0.618
- Сами дуги будут указывать на время, за которое откат, вероятнее всего, будет завершен
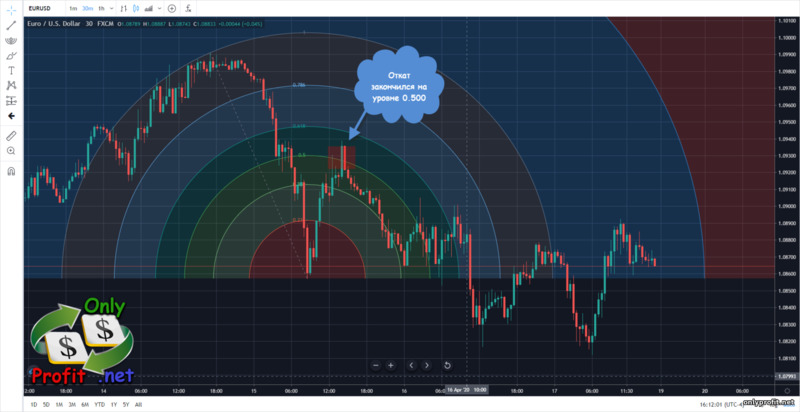
Временные зоны Фибоначчи в трейдинге
Временные зоны Фибоначчи основаны на последовательности Фибоначчи (0, 1, 1, 2, 3, 5, 8…). Они растягиваются от локального минимума или максимума до следующего локального максимума или минимума. На график наносятся вертикальные уровни, которые, в теории, помогут определить время разворотов цены: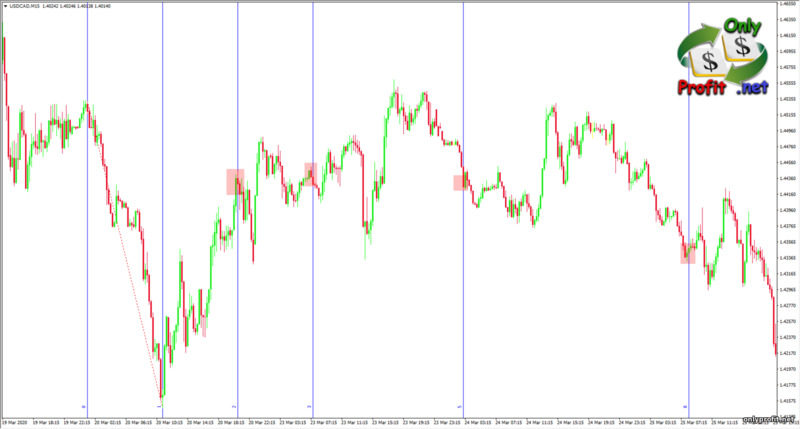
Использование уровней Фибоначчи в своей торговле
Уровни Фибоначчи – это дополнительный инструмент технического анализа, который позволяет определить предполагаемые зоны поддержки и сопротивления. Использовать сетку Фибоначчи стоит с : Что же касается самых важных уровней коррекции Фибоначчи, то это:- 0.382 (38.2%)
- 0.500 (50%)
- 0.618 (61.8%)
К важным уровням расширения Фибоначчи стоит отнести такие уровни, как:
- 1.000 (100%)
- 1.382 (138.2%)
- 1.500 (150%)
- 1.618 (161.8%)
Так же, уровни Фибоначчи очень плотно связанны с волновой теорией Эллиотта. Все это не так просто, как хотелось бы (особенно, для начинающих трейдеров). Но у вас всегда есть выбор – использовать или нет эти инструменты технического анализа. Забавно, что среди начинающих трейдеров и профессионалов всегда есть те, кто «не может жить» без золотого сечения, а есть те, кто его использовать не собирается вообще.
Что такое последовательность Фибоначчи?
Последовательность Фибоначчи — одна из самых известных формул в математике.
Каждое число в последовательности является суммой двух чисел, которые предшествуют ему. Итак, последовательность идет: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Математическое уравнение, описывающее его: Xn + 2 = Xn + 1 + Xn
Основа школьных и старших классов, его называют «секретный код природы» и «универсальное правило природы». Говорят, что он управляет размерами всего: от Великой пирамиды в Гизе до легендарной морской раковины, которая, вероятно, украшала обложку вашего школьного учебника по математике.
И шансы, что почти все, что вы знаете об этом, неверны.
Рассеянная история
Итак, какова реальная история этой знаменитой последовательности?
Многие источники утверждают, что он был впервые обнаружен или «изобретен» Леонардо Фибоначчи. Итальянский математик, который родился около 1170 г. н.э., первоначально был известен как Леонардо из Пизы, сказал Кит Девлин, математик из Стэнфордского университета. Только в 19 веке историки придумали прозвище Фибоначчи (что означает «сын клана Боначи»), чтобы отличить математику от другого знаменитого Пизанского Леонардо, сказал Девлин.[Большие числа, которые определяют Вселенную]
Но Леонардо из Пизы на самом деле не обнаружил последовательность, сказал Девлин, который также является автором «В поисках Фибоначчи: поиски, чтобы заново открыть забытого математического гения, который изменил мир» (Принстон Университетская пресса, 2017). Древние санскритские тексты, которые использовали индуистско-арабскую систему счисления, впервые упоминают об этом, и те, которые предшествуют Леонардо Пизанскому на века.
«Это было всегда», — сказал Девлин в интервью Live Science.
Тем не менее, в 1202 году Леонардо из Пизы опубликовал большой том «Liber Abaci,» математическая «кулинарная книга о том, как делать вычисления», — сказал Девлин.Девлин сказал, что «Liber Abaci», написанная для торговцев, выложила арабо-индуистскую арифметику, полезную для отслеживания прибылей, убытков, остатков по кредитам и так далее, сказал Девлин.
В одном месте книги Леонардо из Пизы представляет последовательность с проблемой, касающейся кроликов. Проблема заключается в следующем: начать с самца и самки кролика. Через месяц они созревают и производят помет с другим кроликом мужского и женского пола. Месяц спустя эти кролики размножаются и выходят — как вы уже догадались — еще один самец и самка, которые также могут спариваться через месяц.(Не обращайте внимания на невероятно невероятную биологию.) Через год, сколько у вас будет кроликов? Ответ, оказывается, 144 — и формула, используемая для получения этого ответа, — это то, что сейчас известно как последовательность Фибоначчи. [11 самых красивых математических уравнений]
«Liber Abaci» впервые представила последовательность в западном мире. Но после нескольких скудных параграфов о разведении кроликов Леонардо из Пизы никогда не упоминал эту последовательность снова. Фактически, это было главным образом забыто до 19-ого столетия, когда математики работали больше о математических свойствах последовательности.В 1877 году французский математик Эдуард Лукас официально назвал проблему кролика «последовательностью Фибоначчи», сказал Девлин.
Последовательность Фибоначчи и золотое сечение — красноречивые уравнения, но они не так волшебны, как могут показаться. (Изображение предоставлено: Shutterstock)Воображаемое значение
Но каково значение последовательности Фибоначчи? Помимо того, что это аккуратный учебный инструмент, он обнаруживается в нескольких местах на природе. Однако, по словам Девлина, это не какой-то секретный код, управляющий архитектурой вселенной.
Это правда, что последовательность Фибоначчи тесно связана с тем, что сейчас известно как золотое сечение (которое даже не является истинным отношением, потому что это иррациональное число). Проще говоря, отношение чисел в последовательности, когда последовательность стремится к бесконечности, приближается к золотому отношению, которое составляет 1.6180339887498948482 … Оттуда математики могут вычислить то, что называется золотой спиралью, или логарифмическую спираль, коэффициент роста которой равен золотое сечение. [9 самых массовых чисел в истории]
Золотое сечение действительно отражает некоторые виды роста растений, сказал Девлин.Например, спиральное расположение листьев или лепестков на некоторых растениях следует золотому сечению. Сосновые шишки демонстрируют золотую спираль, как и семена подсолнуха, согласно «Филлотаксису: системное исследование морфогенеза растений» (Cambridge University Press, 1994). Но есть столько же растений, которые не следуют этому правилу.
«Это не« единственное правило Бога »для растущих вещей, скажем так», — сказал Девлин.
И, пожалуй, самый известный пример из всех, морская ракушка, известная как наутилус, на самом деле не выращивает новые клетки в соответствии с последовательностью Фибоначчи, сказал он.
Когда люди начинают устанавливать связь с человеческим телом, искусством и архитектурой, связи с последовательностью Фибоначчи переходят от незначительных к совершенно вымышленным.
«Нужна большая книга, чтобы документировать всю дезинформацию о золотом сечении, большая часть которой — просто повторение одних и тех же ошибок разными авторами», — писал математик Джордж Марковский, который тогда работал в университете штата Мэн. в 1992 году в журнале колледжа математики.
Большая часть этой дезинформации может быть приписана книге 1855 года немецкого психолога Адольфа Цейзинга.Цейзинг утверждал, что пропорции человеческого тела основаны на золотом сечении. Золотое сечение прорастало «золотые прямоугольники», «золотые треугольники» и всевозможные теории о том, где возникают эти знаковые измерения. С тех пор люди говорят, что золотое сечение можно найти в измерениях Пирамиды в Гизе, Парфенона, «Витрувианского человека» Леонардо да Винчи и комплекса зданий эпохи Возрождения. По словам Девлина, всеобщее утверждение о том, что это соотношение является «исключительно приятным» для человеческого глаза, было высказано некритически.
Все эти утверждения, когда они проверены, измеримы ложно, сказал Девлин.
«Мы хорошие распознаватели образов. Мы можем видеть шаблон независимо от того, есть он или нет», — сказал Девлин. «Это все просто желаемое за действительное».
,Не часто кто-то предполагает, что знание математики может сделать вас вечеринкой, но это именно то, что я собираюсь сделать. Да, своевременная доставка нескольких забавных фактов о знаменитой последовательности Фибоначчи может просто заставить ваших друзей требовать большего, потому что это действительно круто. Итак, без дальнейших церемоний, давайте продолжим наше исследование последовательностей, которые мы начали несколько статей назад, перейдя прямо к разговору о знаменитой последовательности Фибоначчи.
Обзор математических последовательностей
Как мы уже говорили, математические последовательности — это довольно простые вещи — это просто списки чисел, упорядоченные в определенном порядке. Количество последовательностей, которые можно записать, бесконечно, так как подойдет любой случайный список чисел. Но некоторые типы последовательностей решительно неслучайны, одним из которых является геометрическая последовательность. В такой последовательности каждый элемент получается из предыдущего, умножая его на одно и то же фиксированное число. Например: 2, 4, 8, 16, 32 — это геометрическая последовательность, в которой каждый последующий элемент получается путем умножения предыдущего на 2.
Экспоненциальный рост населения
В прошлой статье я использовал эту конкретную последовательность, чтобы описать, как могут расти популяции. Начиная с одной пары организмов, которые производят одну дополнительную пару потомков в каждом репродуктивном цикле, число организмов будет расти как: 2, 4, 8, 16, 32 и так далее. Еще через несколько поколений эта последовательность предсказывает, что популяция станет очень большой, очень быстро. Но действительно ли этот тип последовательности описывает природу?
Ну, это зависит.Этот тип роста — так называемый геометрический или экспоненциальный рост — может фактически иметь место в некоторых ситуациях. Но даже если геометрический рост происходит какое-то время, он не может длиться вечно, поскольку быстро размножающиеся организмы в конечном итоге истощают свои ресурсы — будь то еда или доступное жизненное пространство — в этот момент их число должно перестать расти в геометрической прогрессии. Но разве это единственная проблема с описанием роста населения как геометрической последовательности?
Страницы
.чисел Фибоначчи (0,1,1,2,3,5,8,13, …)
Последовательность Фибоначчи представляет собой последовательность чисел, где каждое число сумма двух предыдущих чисел, кроме первых двух чисел, которые 0 и 1.
формула последовательности Фибоначчи
Например:
F 0 = 0
F 1 = 1
F 2 = F 1 + F 0 = 1 + 0 = 1
F 3 = F 2 + F 1 = 1 + 1 = 2
F 4 = F 3 + F 2 = 2 + 1 = 3
F 5 = F 4 + F 3 = 3 + 2 = 5
,..
Золотое сечение сходимости
Соотношение двух последовательных чисел Фибоначчи сходится к золотое сечение:
φ — это золотое сечение = (1 + √5) / 2 ≈ 1.61803399
Таблица последовательности Фибоначчи
| n | F n |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
| 9 | 34 |
| 10 | 55 |
| 11 | 89 |
| 12 | 144 |
| 13 | 233 |
| 14 | 377 |
| 15 | 610 |
| 16 | 987 |
| 17 | 1597 |
| 18 | 2584 |
| 19 | 4181 |
| 20 | 6765 |
Калькулятор последовательности Фибоначчи
TBD
C код функции Фибоначчи
двойная Фибоначчи (без знака int n)
{
двойной f_n = n;
двойной f_n1 = 0.0;
двойной f_n2 = 1,0;
if (n> 1) {
для (int к = 2; к <= п; k ++) {
f_n = f_n1 + f_n2;
f_n2 = f_n1;
f_n1 = f_n;
}
}
return f_n;
}
,n) вместо O (logn)? Переполнение стека- Товары
- Клиенты
- Случаи использования
- Переполнение стека Публичные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимать технический талант
- реклама Связаться с разработчиками по всему миру
 Как открыть хостел | HowToHostel Как открыть хостел …
Как открыть хостел | HowToHostel Как открыть хостел … 
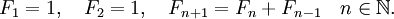
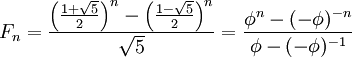 ,
,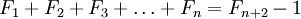
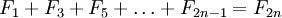
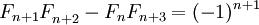

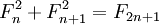
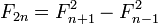
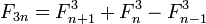
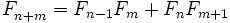
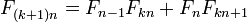
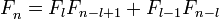
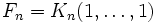 , то есть
, то есть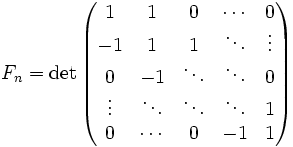 , а также
, а также 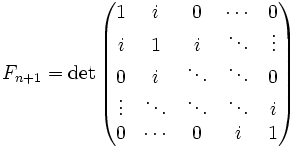 ,
,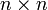 , i — мнимая единица.
, i — мнимая единица.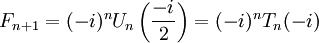
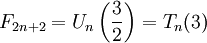
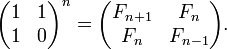
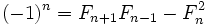
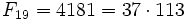 . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.
. Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.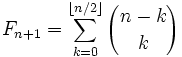 .
.