Последовательность фибоначчи это – Числа Фибоначчи: ищем секрет мироздания

Что такое числа Фибоначчи и уровни Фибоначчи

Последовательность Фибоначчи это набор чисел, который постоянно встречается в окружающей нас природе. Открытие этого явления приписывают математику 13-го века, Леонардо Фибоначчи.

В данной последовательности каждый член равен сумме двух предыдущих:

N(i)=N(i-1)+N(i-2)

Используя эту формулу, и предполагая, что первые две цифры ноль и единица, можно вычислить первые десять чисел последовательности следующим образом:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 2

2 + 1 = 3

3 + 2 = 5

5 + 3 = 8

8 + 5 = 13

13 + 8 = 21

21 + 13 = 34

Таким образом, первые десять чисел в последовательности Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34.

Количество лепестков на цветах часто совпадает с числами Фибоначчи, особенно 3, 5 и 8. Некоторые ромашки имеют 13 и 21 лепестков.

Коэффициенты Фибоначчи

Из последовательности Фибоначчи выводится ряд коэффициентов имеющих особое значение для трейдеров.

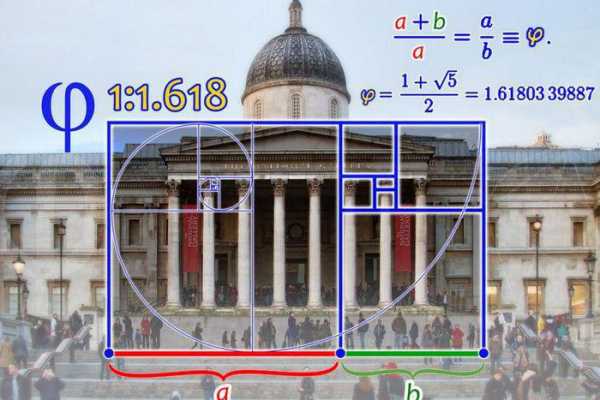
Наиболее важным коэффициентом Фибоначчи является отношение очередного члена последовательности к следующему члену. Это соотношение практически одинаково для любых двух последовательно идущих членов и стремится к величине 0,618 или 61,8%. Это соотношение называют «золотой серединой» или «золотым сечением». Золотое сечение также имеет широкое распространение в природе, в частности пропорции человеческого тела, очень близки к нему. В трейдинге значение 61,8% является наиболее надежным уровнем прогнозирования отката. Например:

        8 разделить на 13 = 0,615 = 61,5%

        13 разделить на 21 = 0,619 = 61,9%

        21 разделить на 34 = 0.617 = 61,7%

Два других коэффициента Фибоначчи часто используемые трейдерами это 38,2% и 23,6%. Эти два коэффициента считаются менее надежными, но также применяются в техническом анализе.

Отношение 38,2% получают путем деления любого члена последовательности на число стоящее через один разряд вправо. Например:

        8 делится на 21 = 0,380 = 38,0%

        144 делится на 377 = 0,381 = 38,1%

        6765 делится на 17 716 = 0,381 = 38,1%

Аналогичным образом, отношение 23,6% получается делением любого члена последовательности на число через два разряда вправо:

        5 делится на 21 = 0,238 = 23,8%

        34 разделить на 144 = 0,236 = 23,6%

        6765 делится на 28 667 = 0,235 = 23,5%

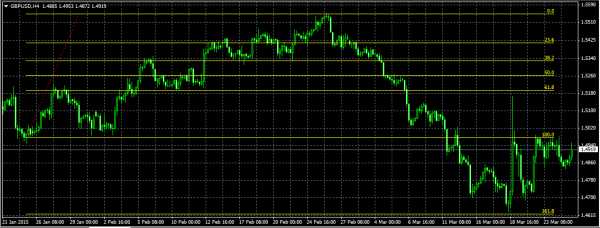Кликните по рисунку для увеличения

www.azbukatreydera.ru

Ряд Фибоначчи — это… Что такое Ряд Фибоначчи?

Чи́сла Фибона́ччи — элементы числовой последовательности

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS)

в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (или Фибоначчи) ^[1].

Более формально, последовательность чисел Фибоначчи задается рекуррентным соотношением:

Иногда числа Фибоначчи рассматривают и для неположительных номеров n как двусторонне бесконечную последовательность, удовлетворяющую основному соотношению. Члены с такими номерами легко получить с помощью эквивалентной формулы «назад»: F_n = F_{n + 2} − F_{n + 1}:

n	−10	−9	−8	−7	−6	−5	−4	−3	−2	−1	0	1	2	3	4	5	6	7	8	9	10
Fn	−55	34	−21	13	−8	5	−3	2	−1	1	0	1	1	2	3	5	8	13	21	34	55

Легко видеть, что F _{− n} = ( − 1)^{n + 1}F_n. Для чисел Фибоначчи с отрицательными индексами остаются верными большинство нижеприведённых свойств.

Происхождение

Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении), намного раньше, чем она стала известна в Европе.

Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».

На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что:

• В «нулевом» месяце, имеется пара кроликов (0 новых пар).
• В первом месяце, первая пара производит на свет другую пару (1 новая пара).
• Во втором месяце, обе пары кроликов порождают другие пары и первая пара погибает (1 новая пара).
• В третьем месяце, вторая пара и две новые пары порождают в общем три новые пары, а старая вторая пара погибает (2 новые пары).

Закономерным является тот факт, что каждая пара кроликов порождает ещё две пары на протяжении жизни, а затем погибает.

Пусть популяция за месяц n будет равна F(n). В это время, только кролики которые жили в месяце n-2 являются способными к размножению и производят потомков, тогда

F(n-2) пар прибавится к текущей популяции F(n-1). Таким образом общее количество пар будет равно F(n) = F(n — 1) + F(n — 2).

Формула Бине

Формула Бине выражает в явном виде значение F_n как функцию от n:

,

где  — золотое сечение. При этом и являются корнями квадратного уравнения .

Из формулы Бине следует, что для всех , F_n есть ближайшее к целое число, то есть . В частности, справедлива асимптотика .

Тождества

И более общие формулы:

• Числа Фибоначчи представляются значениями континуант на наборе единиц: , то есть

, а также ,

где матрицы имеют размер ,

i — мнимая единица.

Свойства

• Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. (F_m,F_n) = F_(m,n). Следствия:
  • F_m делится на F_n тогда и только тогда, когда m делится на n (за исключением n = 2). В частности, F_m делится на F₃ = 2 (то есть является чётным) только для m = 3k; F_m делится на F₄ = 3 только для m = 4k; F_m делится на F₅ = 5 только для m = 5k и т. д.
  • F_m может быть простым только для простых
    m (с единственным исключением m = 4) (например, число 233 простое, и индекс его, равный 13, также прост). Обратное не верно, первый контрпример — . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.

.

• В 1964 Дж. Кон (J. H. E. Cohn) доказал, что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12: F₀ = 0² = 0, F₁ = 1² = 1, F₂ = 1² = 1, F₁₂ = 12² = 144. При этом для n=0,1,12 верно утверждение F_n = n².

• Множество чисел Фибоначчи совпадает с множеством положительных значений многочлена
      z(x,y) = 2xy⁴ + x²y³ − 2x ³y² − y⁵ − x⁴y + 2y,
  на множестве неотрицательных целых чисел x и y ^[2].

• Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.

• Последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом 60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом 300, последние три цифры — с периодом 1500, последние четыре — с периодом 15000, последние пять — с периодом 150000 и т. д.

Вариации и обобщения

В других областях

В природе

• Расстояния между листьями (или ветками) на стволе растения относятся примерно как числа Фибоначчи.

В культуре

См. также

Литература

Ссылки

Примечания

1. ↑ [1] БСЭ]
2. ↑ P. Ribenboim, The New Book of Prime Number Records, Springer, 1996, p. 193.

Wikimedia Foundation. 2010.

dic.academic.ru

Числа Фибоначчи и золотое сечение: взаимосвязь

Во вселенной еще много неразгаданных тайн, некоторые из которых ученые уже смогли определить и описать. Числа Фибоначчи и золотое сечение составляют основу разгадки окружающего мира, построения его формы и оптимального зрительного восприятия человеком, с помощью которых он может ощущать красоту и гармонию.

Золотое сечение

Принцип определения размеров золотого сечения лежит в основе совершенства целого мира и его частей в своей структуре и функциях, его проявление можно видеть в природе, искусстве и технике. Учение о золотой пропорции было заложено в результате исследований древними учеными природы чисел.

В основе его лежит теория о пропорциях и соотношениях делений отрезков, которое было сделано еще древним философом и математиком Пифагором. Он доказал, что при разделении отрезка на две части: X (меньшую) и Y (большую), отношение большего к меньшему будет равно отношению их суммы (всего отрезка):

X : Y = Y : X+Y.

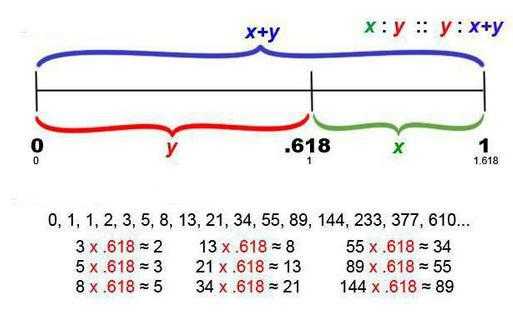
В результате получается уравнение: х² – х – 1=0, которое решается как х=(1±√5)/2.

Если рассмотреть соотношение 1/х, то оно равно 1,618…

Свидетельства использования древними мыслителями золотой пропорции приведены в книге Эвклида «Начала», написанной еще в 3 в. до н.э., который применял это правило для построения правильных 5-угольников. У пифагорейцев эта фигура считается священной, поскольку является одновременно симметричной и асимметричной. Пентаграмма символизировала жизнь и здоровье.

Числа Фибоначчи

Знаменитая книга Liber abaci математика из Италии Леонардо Пизанского, который в последующем стал известен, как Фибоначчи, увидела свет в 1202 г. В ней ученый впервые приводит закономерность чисел, в ряду которых каждое число является суммой 2-х предыдущих цифр. Последовательность чисел Фибоначчи заключается в следующем:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 и т.д.

Также ученый привел ряд закономерностей:

• Любое число из ряда, разделенное на последующее, будет равно значению, которое стремится к 0,618. Причем первые числа Фибоначчи не дают такого числа, но по мере продвижения от начала последовательности это соотношение будет все более точным.
• Если же поделить число из ряда на предыдущее, то результат устремится к 1,618.
• Одно число, поделенное на следующее через одно, покажет значение, стремящееся к 0,382.

Применение связи и закономерностей золотого сечения, числа Фибоначчи (0,618) можно найти не только в математике, но и в природе, в истории, в архитектуре и строительстве и во многих других науках.

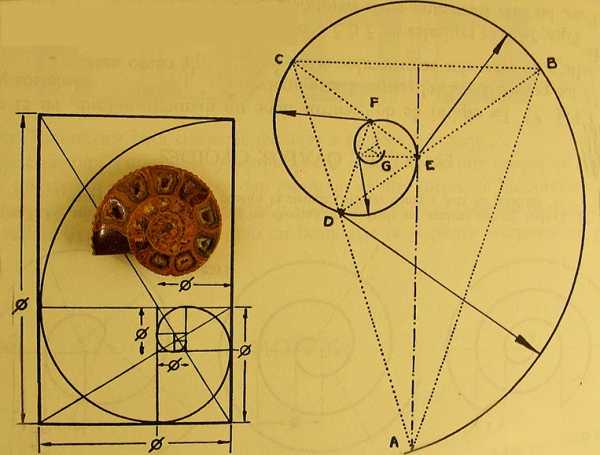
Спираль Архимеда и золотой прямоугольник

Спирали, очень распространенные в природе, были исследованы Архимедом, который даже вывел ее уравнение. Форма спирали основана на законах о золотом сечении. При ее раскручивании получается длина, к которой можно применить пропорции и числа Фибоначчи, увеличение шага происходит равномерно.

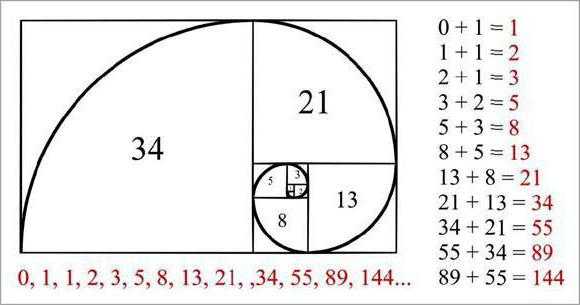
Параллель между числами Фибоначчи и золотым сечением можно увидеть и построив «золотой прямоугольник», у которого стороны пропорциональны, как 1,618:1. Он строится, переходя от большего прямоугольника к малым так, что длины сторон будут равны числам из ряда. Построение его можно сделать и в обратном порядке, начиная с квадратика «1». При соединении линиями углов этого прямоугольника в центре их пересечения получается спираль Фибоначчи или логарифмическая.

История применения золотых пропорций

Многие древние памятники архитектуры Египта возведены с использованием золотых пропорций: знаменитые пирамиды Хеопса и др. Архитекторы Древней Греции широко использовалиих их при возведении архитектурных объектов, таких как храмы, амфитеатры, стадионы. Например, были применены такие пропорции при строительстве античного храма Парфенон, театра Диониса (Афины) и других объектов, которые стали шедеврами древнего зодчества, демонстрирующими гармонию, основанную на математической закономерности.

В более поздние века интерес к золотому сечению поутих, и закономерности были забыты, однако опять возобновился в эпоху Ренессанса вместе с книгой францисканского монаха Л. Пачоли ди Борго «Божественная пропорция» (1509 г.). В ней были приведены иллюстрации Леонардо да Винчи, который и закрепил новое название «золотое сечение». Также были научно доказаны 12 свойств золотой пропорции, причем автор рассказывал о том, как проявляется она в природе, в искусстве и называл ее «принципом построения мира и природы».

Витрувианский человек Леонардо

Рисунок, которым Леонардо да Винчи в 1492 г. проиллюстрировал книгу Витрувия, изображает фигуру человека в 2-х позициях с руками, разведенными в стороны. Фигура вписана в круг и квадрат. Этот рисунок принято считать каноническими пропорциями человеческого тела (мужского), описанными Леонардо на основе изучения их в трактатах римского архитектора Витрувия.

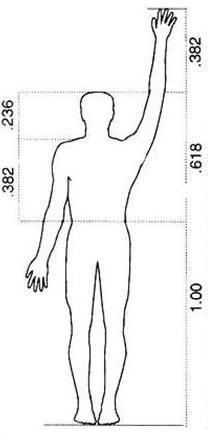
Центром тела как равноудаленной точкой от конца рук и ног считается пупок, длина рук приравнивается к росту человека, максимальная ширина плеч = 1/8 роста, расстояние от верха груди до волос = 1/7, от верха груди до верха головы =1/6 и т.д.

С тех пор рисунок используется в виде символа, показывающего внутреннюю симметрию тела человека.

Термин «Золотое сечение» Леонардо использовал для обозначения пропорциональных отношений в фигуре человека. Например, расстояние от пояса до ступней ног соотносится к аналогичному расстоянию от пупка до макушки так же, как рост к первой длине (от пояса вниз). Эти вычисление делается аналогично соотношению отрезков при вычислении золотой пропорции и стремится к 1,618.

Все эти гармоничные пропорции часто используются деятелями искусства для создания красивых и впечатляющих произведений.

Исследования золотого сечения в 16-19 веках

Используя золотое сечение и числа Фибоначчи, исследовательскую работу по вопросу о пропорциях продолжают уже не одно столетие. Параллельно с Леонардо да Винчи немецкий художник Альбрехт Дюрер также занимался разработкой теории правильных пропорций тела человека. Для этого им даже был создан специальный циркуль.

В 16 в. вопросу о связи числа Фибоначчи и золотого сечения были посвящены работы астронома И. Кеплера, который впервые применил эти правила для ботаники.

Новое «открытие» ожидало золотое сечение в 19 в. с опубликованием «Эстетического исследования» немецкого ученого профессора Цейзига. Он возвел эти пропорции в абсолют и объявил о том, что они универсальны для всех природных явлений. Им были проведены исследования огромного количества людей, вернее их телесных пропорций (около 2 тыс.), по итогам которых сделаны выводы о статистических подтвержденных закономерностях в соотношениях различных частей тела: длины плеч, предплечий, кистей, пальцев и т.д.

Были исследованы также предметы искусства (вазы, архитектурные сооружения), музыкальные тона, размеры при написании стихотворений — все это Цейзиг отобразил через длины отрезков и цифры, он же ввел термин «математическая эстетика». После получения результатов выяснилось, что получается ряд Фибоначчи.

Число Фибоначчи и золотое сечение в природе

В растительном и животном мире существует тенденция к формообразованию в виде симметрии, которая наблюдается в направлении роста и движения. Деление на симметричные части, в которых соблюдаются золотые пропорции, — такая закономерность присуща многим растениям и животным.

Природа вокруг нас может быть описана с помощью чисел Фибоначчи, например:

• расположение листьев или веток любых растений, а также расстояния соотносятся с рядом приведенных чисел 1, 1, 2, 3, 5, 8, 13 и далее;
• семена подсолнуха (чешуя на шишках, ячейки ананаса), располагаясь двумя рядами по закрученным спиралям в разные стороны;
• соотношение длины хвоста и всего тела ящерицы;
• форма яйца, если провести линию условно через широкую его часть;
• соотношение размеров пальцев на руке человека.

И, конечно, самые интересные формы представляют закручивающиеся по спирали раковины улиток, узоры на паутине, движение ветра внутри урагана, двойная спираль в ДНК и структура галактик — все они включают в себя последовательность чисел Фибоначчи.

Использование золотого сечения в искусстве

Исследователи, занимающиеся поиском в искусстве примеров использования золотого сечения, подробно исследуют различные архитектурные объекты и произведения живописи. Известны знаменитые скульптурные работы, создатели которых придерживались золотых пропорций, — статуи Зевса Олимпийского, Аполлона Бельведерского и Афины Парфенос.

Одно из творений Леонардо да Винчи — «Портрет Моны Лизы» — уже многие годы является предметом исследований ученых. Ими было обнаружено, что композиция работы целиком состоит из «золотых треугольников», объединенных вместе в правильный пятиугольник-звезду. Все работы да Винчи являются свидетельством того, насколько глубоки были его познания в строении и пропорциях тела человека, благодаря чему он и смог уловить невероятно загадочную улыбку Джоконды.

Золотое сечение в архитектуре

В качестве примера ученые исследовали шедевры архитектуры, созданные по правилам «золотого сечения»: египетские пирамиды, Пантеон, Парфенон, Собор Нотр-Дам де Пари, храм Василия Блаженного и др.

Парфенон — одно из красивейших зданий в Древней Греции (5 в. до н.э.) — имеет 8 колонн и 17 по разным сторонам, отношение его высоты к длине сторон равно 0,618. Выступы на его фасадах сделаны по «золотому сечению» (фото ниже).

Одним из ученых, который придумал и успешно применял усовершенствование модульной системы пропорций для архитектурных объектов (так называемый «модулор»), — был французский архитектор Ле Корбюзье. В основу модулора положена измерительная система, связанная с условным делением на части человеческого тела.

Русский архитектор М. Казаков, построивший несколько жилых домов в Москве, а также здания сената в Кремле и Голицынской больницы (сейчас 1-я Клиническая им. Н. И. Пирогова), — был одним из архитекторов, которые использовали при проектировании и строительстве законы о золотом сечении.

Применение пропорций в дизайне

В дизайне одежды все модельеры делают новые образы и модели с учетом пропорций человеческого тела и правил золотого сечения, хотя от природы не все люди имеют идеальные пропорции.

При планировании ландшафтного дизайна и создании объемных парковых композиций с помощью растений (деревьев и кустарников), фонтанов и малых архитектурных объектов также могут применяться закономерности «божественных пропорций». Ведь композиция парка должна быть ориентирована на создание впечатления на посетителя, который свободно сможет ориентироваться в нем и находить композиционный центр.

Все элементы парка находятся в таких соотношениях, чтобы с помощью геометрического строения, взаиморасположения, освещения и света, произвести на человека впечатление гармонии и совершенства.

Применение золотого сечения в кибернетике и технике

Закономерности золотого сечения и чисел Фибоначчи проявляются также в переходах энергии, в процессах, происходящих с элементарными частицами, составляющих химические соединения, в космических системах, в генной структуре ДНК.

Аналогичные процессы происходят и в организме человека, проявляясь в биоритмах его жизни, в действии органов, например, головного мозга или зрения.

Алгоритмы и закономерности золотых пропорций широко используются в современной кибернетике и информатике. Одна из несложных задач, которую дают решать начинающим программистам, — написать формулу и определить, сумму чисел Фибоначчи до определенного числа, используя языки программирования.

Современные исследования теории о золотой пропорции

Начиная с середины 20 века, интерес к проблемам и влиянию закономерностей золотых пропорций на жизнь человека, резко возрастает, причем со стороны многих ученых различных профессий: математиков, исследователей этноса, биологов, философов, медицинских работников, экономистов, музыкантов и др.

В США с 1970-хгодов начинает выпускаться журнал The Fibonacci Quarterly, где публикуются работы на эту тему. В прессе появляются работы, в которых обобщенные правила золотого сечения и ряда Фибоначчи используют в различных отраслях знаний. Например, для кодирования информации, химических исследований, биологических и т.д.

Все это подтверждает выводы древних и современных ученых о том, что золотая пропорция многосторонне связана с фундаментальными вопросами науки и проявляется в симметрии многих творений и явлений окружающего нас мира.

fb.ru

Числа фибоначчи — это… Что такое Числа фибоначчи?

Числа Фибоначчи — Числа Фибоначчи  элементы числовой последовательности 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, … (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух… …   Википедия

Числа Фибоначчи — последовательность целых чисел, заданная с помощью рекуррентного соотношения: каждое последующее равно сумме двух предыдущих. Последовательность чисел Фибоначчи начинается так: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233. Леонардо Фибоначчи… …   Судьба эпонимов. Словарь-справочник

Фибоначчи — (Fibonacci) Фибоначчи первый крупный математик средневековой Европы Десятичная система счисления, арабские цифры, числа, последовательность, уровни, ряд, линии и спираль Фибоначчи Содержание >>>>>>>>> …   Энциклопедия инвестора

Фибоначчи числа — Числа Фибоначчи  элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух предыдущих чисел. Название по… …   Википедия

Числа Фиббоначчи — Числа Фибоначчи  элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух предыдущих чисел. Название по… …   Википедия

Числа Фибоначи — Числа Фибоначчи  элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух предыдущих чисел. Название по… …   Википедия

Фибоначчи — Леонардо Пизанский Leonardo Pisano Дата рождения: ок. 1170 года …   Википедия

Фибоначчи числа —         элементы числовой возвратной последовательности (См. Возвратная последовательность) 1, 1, 2, 3, 5, 8,… (ряда Фибоначчи), в которых каждый последующий член равен сумме двух предыдущих. Название по имени средневекового математика Леонардо …   Большая советская энциклопедия

Числа трибоначчи — Числа трибоначчи  последовательность целых чисел , заданная с помощью линейного рекуррентного соотношения: . Название является вариацией «чисел Фибоначчи»  с добавкой «три» (лат. tri ), обозначающей количество суммируемых чисел.… …   Википедия

Числа Люка — Не следует путать с последовательностями Люка. Числа Люка задаются рекуррентной формулой с начальными значениями и . Последовательность чисел Люка начинается так: 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, … (последовательность A000032 в… …   Википедия

dic.academic.ru

Последовательность Фибоначчи, проиллюстрированная природой (GreenWord.ru)

Последовательность Фибоначчи, известная всем по фильму «Код Да Винчи» — ряд цифр, описанный в виде загадки Итальянским математиком Леонардо Пизанским, более известным под прозвищем Фибоначчи, в XIII веке. Вкратце суть загадки:

Кто-то поместил пару кроликов в некоем замкнутом пространстве, чтобы узнать, сколько пар кроликов родится при этом в течении года, если природа кроликов такова, что каждый месяц пара кроликов производит на свет другую пару, а способность к производству потомства у них появляется по достижению двухмесячного возраста.

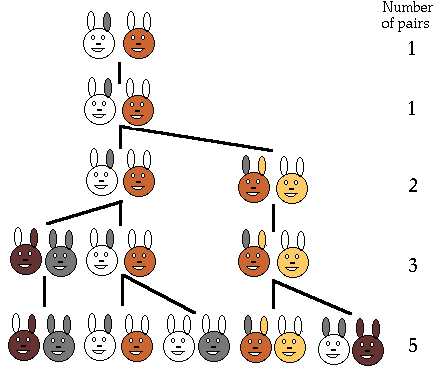
В итоге получается такой ряд цифр: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, где через запятую показано количество пар кроликов в каждом из двенадцати месяцев. Его можно продолжать бесконечно долго. Его суть в том, что каждое следующее число является суммой двух предыдущих.

У этого ряда есть несколько математических особенностей, которых обязательно нужно коснуться. Он асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.

Так отношение какого-либо члена ряда к предшествующему ему колеблется около числа 1,618, через pаз то превосходя, то не достигая его. Отношение к следующему аналогично приближается к числу 0,618, что обратно пропорционально 1,618. Если мы будем делить элементы через одно, то получим числа 2,618 и 0,382, которые так же являются обратно пропорциональными. Это так называемые коэффициенты Фибоначчи.

К чему всё это? Так мы приближаемся к одному из самых загадочных явлений природы. Смекалистый Леонардо по сути не открыл ничего нового, он просто напомнил миру о таком явлении, как Золотое Сечение, которое не уступает по значимости теореме Пифагора.

Все окружающие нас предметы мы различаем в том числе и по форме. Какие-то нам нравятся больше, какие-то меньше, некоторые вовсе отталкивают взгляд. Иногда интерес может быть продиктован жизненной ситуацией, а порой красотой наблюдаемого объекта. Симметричная и пропорциональная форма, способствует наилучшему зрительному восприятию и вызывает ощущение красоты и гармонии. Целостный образ всегда состоит из частей разного размера, находящихся в определённом соотношении друг с другом и целым. Золотое сечение — высшее проявление совершенства целого и его частей в науке, искусстве и природе.

Если на простом примере, то Золотое Сечение — это деление отрезка на две части в таком соотношении, при котором большая часть относится к меньшей, как их сумма (весь отрезок) к большей.

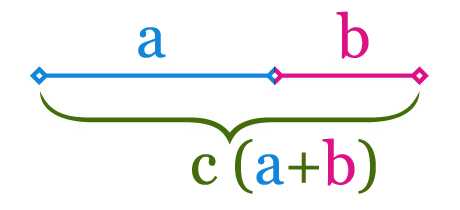
Если мы примем весь отрезок c за 1, то отрезок a будет равен 0,618, отрезок b — 0,382, только так будет соблюдено условие Золотого Сечения (0,618/0,382=1,618; 1/0,618=1,618). Отношение c к a равно 1,618, а с к b 2,618. Это всё те же, уже знакомые нам, коэффициенты Фибоначчи.

Разумеется есть золотой прямоугольник, золотой треугольник и даже золотой кубоид. Пропорции человеческого тела во многих соотношениях близки к Золотому Сечению.

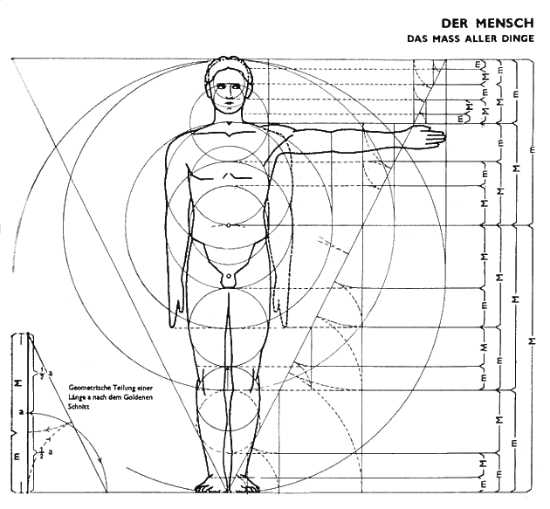
Изображение: marcus-frings.de

Но самое интересное начинается, когда мы объединим полученные знания. На рисунке наглядно показана связь между последовательностью Фибоначчи и Золотым сечением. Мы начинаем с двух квадратов первого размера. Сверху добавляем квадрат второго размера. Подрисовываем рядом квадрат со стороной, равной сумме сторон двух предыдущих, третьего размера. По аналогии появляется квадрат пятого размера. И так далее пока не надоест, главное, чтобы длина стороны каждого следующего квадрата равнялась сумме длин сторон двух предыдущих. Мы видим серию прямоугольников, длины сторон, которых являются числами Фибоначчи, и, как не странно, они называются прямоугольниками Фибоначчи.

Если мы проведём плавную линий через углы наших квадратов, то получим ни что иное, как спираль Архимеда, увеличение шага которой всегда равномерно.

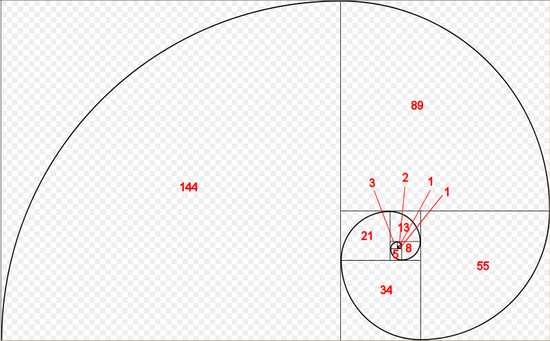
Ничего не напоминает?

Фото: ethanhein on Flickr

И не только в раковине моллюска можно найти спирали Архимеда, а во многих цветах и растениях, просто они не такие явные.

Алое многолистный:

Фото: brewbooks on Flickr

Броколи романеско:

Фото: beart.org.uk

Подсолнечник:

Фото: esdrascalderan on Flickr

Сосновая шишка:

Фото: mandj98 on Flickr

А если взглянуть чуть подальше, то можно разглядеть ряд Фибоначчи в недосягаемых галактиках.

И тут самое время вспомнить о Золотом Сечении! Ни одни ли из самых прекрасных и гармоничных творений природы изображены на этих фотографиях? И это далеко не все. Присмотревшись, можно найти похожие закономерности во многих формах.

Конечно заявление, что все эти явление построены на последовательности Фибоначчи звучит слишком громко, но тенденция на лицо. Да и к тому же сама она далека от совершенства, как и всё в этом мире.

Есть предположение, что ряд Фибоначчи — это попытка природы адаптироваться к более фундаментальной и совершенной золотосечённой логарифмической последовательности, которая практически такая же, только начинается из ниоткуда и уходит в никуда. Природе же обязательно нужно какое-то целое начало, от которого можно оттолкнуться, она не может создать что-то из ничего. Отношения первых членов последовательности Фибоначчи далеки от Золотого Сечения. Но чем дальше мы продвигаемся по ней, тем больше эти отклонения сглаживаются. Для определения любого ряда достаточно знать три его члена, идущие друг за другом. Но только не для золотой последовательности, ей достаточно двух, она является геометрической и арифметической прогрессией одновременно. Можно подумать, будто она основа для всех остальных последовательностей.

Каждый член золотой логарифмической последовательности является степенью Золотой Пропорции (z). Часть ряда выглядит примерно так: … z^-5; z^-4; z^-3; z^-2; z^-1; z⁰; z¹; z²; z³; z⁴; z⁵ … Если мы округлим значение Золотой пропорции до трёх знаков, то получим z=1,618, тогда ряд выглядит так: … 0,090 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854; 11,090 … Каждый следующий член может быть получен не только умножением предыдущего на 1,618, но и сложением двух предыдущих. Таким образом экспоненциальный рост обеспечивается путем простого сложения двух соседних элементов. Это ряд без начала и конца, и именно на него пытается быть похожей последовательность Фибоначчи. Имея вполне определённое начало, она стремится к идеалу, никогда его не достигая. Такова жизнь.

И всё-таки, в связи со всем увиденным и прочитанным, возникают вполне закономерные вопросы:
От куда взялись эти числа? Кто этот архитектор вселенной, попытавшийся сделать её идеальной? Было ли когда-то всё так, как он хотел? И если да, то почему сбилось? Мутации? Свободный выбор? Что же будет дальше? Спираль скручивается или раскручивается?

Найдя ответ на один вопрос, получишь следующий. Разгадаешь его, получишь два новых. Разберёшься с ними, появится ещё три. Решив и их, обзаведёшься пятью нерешёнными. Потом восемью, потом тринадцатью, 21, 34, 55…

Источники: 1; 2; 3; 4

greenword.ru

Число Фибоначчи — это… Что такое Число Фибоначчи?

Чи́сла Фибона́ччи — элементы числовой последовательности

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS)

в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (или Фибоначчи) ^[1].

Более формально, последовательность чисел Фибоначчи задается рекуррентным соотношением:

Иногда числа Фибоначчи рассматривают и для неположительных номеров n как двусторонне бесконечную последовательность, удовлетворяющую основному соотношению. Члены с такими номерами легко получить с помощью эквивалентной формулы «назад»: F_n = F_{n + 2} − F_{n + 1}:

n	−10	−9	−8	−7	−6	−5	−4	−3	−2	−1	0	1	2	3	4	5	6	7	8	9	10
Fn	−55	34	−21	13	−8	5	−3	2	−1	1	0	1	1	2	3	5	8	13	21	34	55

Легко видеть, что F _{− n} = ( − 1)^{n + 1}F_n. Для чисел Фибоначчи с отрицательными индексами остаются верными большинство нижеприведённых свойств.

Происхождение

Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении), намного раньше, чем она стала известна в Европе.

Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».

На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что:

• В «нулевом» месяце, имеется пара кроликов (0 новых пар).
• В первом месяце, первая пара производит на свет другую пару (1 новая пара).
• Во втором месяце, обе пары кроликов порождают другие пары и первая пара погибает (1 новая пара).
• В третьем месяце, вторая пара и две новые пары порождают в общем три новые пары, а старая вторая пара погибает (2 новые пары).

Закономерным является тот факт, что каждая пара кроликов порождает ещё две пары на протяжении жизни, а затем погибает.

Пусть популяция за месяц n будет равна F(n). В это время, только кролики которые жили в месяце n-2 являются способными к размножению и производят потомков, тогда F(n-2) пар прибавится к текущей популяции F(n-1). Таким образом общее количество пар будет равно F(n) = F(n — 1) + F(n — 2).

Формула Бине

Формула Бине выражает в явном виде значение F_n как функцию от n:

,

где  — золотое сечение. При этом и являются корнями квадратного уравнения .

Из формулы Бине следует, что для всех , F_n есть ближайшее к целое число, то есть . В частности, справедлива асимптотика .

Тождества

И более общие формулы:

• Числа Фибоначчи представляются значениями континуант на наборе единиц: , то есть

, а также ,

где матрицы имеют размер , i — мнимая единица.

Свойства

• Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. (F_m,F_n) = F_(m,n). Следствия:
  • F_m делится на F_n тогда и только тогда, когда m делится на n (за исключением n = 2). В частности, F_m делится на F₃ = 2 (то есть является чётным) только для m = 3k; F_m делится на F₄ = 3 только для m = 4k; F_m делится на F₅ = 5 только для m = 5k и т. д.
  • F_m может быть простым только для простых m (с единственным исключением m = 4) (например, число 233 простое, и индекс его, равный 13, также прост). Обратное не верно, первый контрпример — . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.

.

• В 1964 Дж. Кон (J. H. E. Cohn) доказал, что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12: F₀ = 0² = 0, F₁ = 1² = 1, F₂ = 1² = 1, F₁₂ = 12² = 144. При этом для n=0,1,12 верно утверждение F_n = n².

• Множество чисел Фибоначчи совпадает с множеством положительных значений многочлена
      z(x,y) = 2xy⁴ + x²y³ − 2x³y² − y⁵ − x⁴y + 2y,
  на множестве неотрицательных целых чисел x и y ^[2].

• Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.

• Последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом 60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом 300, последние три цифры — с периодом 1500, последние четыре — с периодом 15000, последние пять — с периодом 150000 и т. д.

Вариации и обобщения

В других областях

В природе

• Расстояния между листьями (или ветками) на стволе растения относятся примерно как числа Фибоначчи.

В культуре

См. также

Литература

Ссылки

Примечания

1. ↑ [1] БСЭ]
2. ↑ P. Ribenboim, The New Book of Prime Number Records, Springer, 1996, p. 193.

Wikimedia Foundation. 2010.

dic.academic.ru

Числа Фибоначчи — это… Что такое Числа Фибоначчи?

Чи́сла Фибона́ччи — элементы числовой последовательности

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, … (последовательность A000045 в OEIS)

в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (известного как Фибоначчи)^[1]. Иногда число 0 не рассматривается как член последовательности.

Более формально, последовательность чисел Фибоначчи задается линейным рекуррентным соотношением:

Иногда числа Фибоначчи рассматривают и для отрицательных номеров n как двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. При этом члены с отрицательными индексами легко получить с помощью эквивалентной формулы «назад»: :

n	−10	−9	−8	−7	−6	−5	−4	−3	−2	−1	0	1	2	3	4	5	6	7	8	9	10
	−55	34	−21	13	−8	5	−3	2	−1	1	0	1	1	2	3	5	8	13	21	34	55

Легко заметить, что .

Происхождение

Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении), намного раньше, чем она стала известна в Европе.

Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».

На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что:

• В «нулевом» месяце имеется пара кроликов (1 новая пара).
• В первом месяце первая пара производит на свет другую пару (1 новая пара).
• Во втором месяце обе пары кроликов порождают другие пары и первая пара погибает (2 новые пары).
• В третьем месяце вторая пара и две новые пары порождают в общем три новые пары, а старая вторая пара погибает (3 новые пары).

Закономерным является тот факт, что каждая пара кроликов порождает ещё две пары на протяжении жизни, а затем погибает.

Пусть популяция за месяц будет равна . В это время только те кролики, которые жили в месяце , являются способными к размножению и производят потомков, тогда пар прибавится к текущей популяции . Таким образом общее количество пар будет равно:

Формула Бине

Формула Бине выражает в явном виде значение как функцию от n:

,

где  — золотое сечение. При этом и являются корнями характеристического уравнения .

Из формулы Бине следует, что для всех , есть ближайшее к целое число, то есть . В частности, при справедлива асимптотика .

Формула Бине может быть аналитически продолжена следующим образом:

При этом соотношение выполняется для любого комплексного числа z.

Тождества

Геометрическое доказательство формулы для суммы квадратов первых n чисел Фибоначчи^[2].

И более общие формулы:

• Числа Фибоначчи представляются значениями континуант на наборе единиц: , то есть

, а также ,

где матрицы имеют размер , i — мнимая единица.

Свойства

• Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. . Следствия:

• Последовательность чисел Фибоначчи является частным случаем возвратной последовательности, её характеристический многочлен имеет корни и .
• Отношения являются подходящими дробями золотого сечения и, в частности,
• Суммы биномиальных коэффициентов на диагоналях треугольника Паскаля являются числами Фибоначчи ввиду формулы

  .

• В 1964 году Дж. Кон (J. H. E. Cohn) доказал,^[3] что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12:

  , , , .

• Производящей функцией последовательности чисел Фибоначчи является:

• Множество чисел Фибоначчи совпадает с множеством неотрицательных значений многочлена

на множестве неотрицательных целых чисел x и y.^[4]

• Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
• Период чисел Фибоначчи по модулю натурального числа n называется периодом Пизано и обозначается π(n). Периоды Пизано π(n) образуют последовательность:

  1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, 24, 36, … (последовательность A001175 в OEIS)

  • В частности, последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом π(10)=60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом π(100)=300, последние три цифры — с периодом π(1000)=1500, последние четыре — с периодом π(10000)=15000, последние пять — с периодом π(100000)=150000 и т. д.
• Натуральное число N является числом Фибоначчи тогда и только тогда, когда или является квадратом.^[5]
• Не существует арифметической прогрессии длиной больше 3, состоящей из чисел Фибоначчи.^[6]
• Число Фибоначчи равно количеству кортежей длины n из нулей и единиц, в которых нет двух соседних нулей. При этом равно количеству таких кортежей, начинающихся с нуля, а — начинающихся с единицы.

Вариации и обобщения

В других областях

Следует отметить, что существует мнение, что почти все утверждения, находящие числа Фибоначчи в природных и исторических явлениях, неверны — это распространенный миф, который почти всегда оказывается неточной подгонкой под желаемый результат^[7][8].

В природе

В культуре

• Американский писатель-фантаст Дэн Браун в книге «Код да Винчи» описал анаграмму на основе последовательности Фибоначчи.
• Светящиеся числа Фибоначчи от 1 до 55 прикреплены на дымовой трубе Turku Energia в Турку^[14] и главном вокзале Цюриха^[15].
• В фильме «Двадцать одно» (англ. 21) последовательность Фибоначчи представлена в виде надписи на торте.
• «Ряд Фибоначчи» — дополнительное название песни 2012 года «Новый сигнал из космоса» российской рок-группы «Сплин».
• В java-игре Doom RPG для мобильных телефонов в «Проходе» после прохождения 7 сектора есть секретная дверь, кодом которой являются числа Фибоначчи
• Числам Фибоначчи посвящён один их шуточных лимериков Джеймса Линдона^[16]:

     Плотная пища жён Фибоначчи
     Только на пользу им шла, не иначе.
     Весили жёны, согласно молве,
     Каждая — как предыдущие две.

См. также

Примечания

Литература

Ссылки

dic.academic.ru