Числа Фибоначчи
Звезда. Орбиты планет. Сосновая шишка. Все эти природные формы не случайны. Они связаны с такими понятиями, как золотое сечение и числа Фибоначчи, за которыми стоит некое идеальное математическое соотношение. Когда мы видим что-то красивое, гармоничное, симметричное в природе или искусстве, то, скорее всего, оно имеет «золотое» соотношение частей и целого, близкое к 1,6 — его еще называют «числом бога».
Кто открыл числа Фибоначчи?Последовательность Фибоначчи выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711…
Если вы заметили, каждое последующее число равно сумме двух предыдущих. Эту последовательность первым открыл европейцам математик и путешественник Леонардо Пизанский, Фибоначчи было его прозвищем (считается, что оно образовано от слов «сын Боначчи»). В 1202 году он опубликовал монументальный 460-страничный сборник по алгебре и арифметике под названием «Книга абака», основанный на математических знаниях индусов и арабов. Этот труд настолько опережал свое время, что просвещенному человечеству потребовалось еще несколько веков, чтобы осилить и осмыслить эти сведения. Числа Фибоначчи стали применяться в математике в эпоху Возрождения и в Новое время.
Этот труд настолько опережал свое время, что просвещенному человечеству потребовалось еще несколько веков, чтобы осилить и осмыслить эти сведения. Числа Фибоначчи стали применяться в математике в эпоху Возрождения и в Новое время.
Согласно легенде, на бесконечную последовательность чисел, каждое из которых является суммой двух предыдущих, Леонардо натолкнула нехитрая задачка о кроликах. Можете попробовать ее решить и проверить, получится ли у вас нужная последовательность.
Задача о кроликах1 января у вас в закрытом загоне скрестилась пара кроликов: самка и самец. 1 февраля они произвели на свет детей — самку и самца. Новорожденные кролики становятся зрелой парой через месяц и затем еще через месяц дают жизнь новой разнополой паре животных. Вопрос: сколько пар кроликов у вас будет через год? Учтите, что каждая половозрелая пара дает жизнь только одной паре и в ней всегда один самец и одна самка, все кролики из задачи бессмертны и точно доживут до 1 января следующего года. Посчитали?
Посчитали?
Теперь проверьте себя:
1 + 1 = 2
2 + 1 = 3
3 + 2 = 5
5 + 3 = 8
8 + 5 = 13
13 + 8 = 21
21 + 13 = 34
34 + 21 = 55
55 + 34 = 89
89 + 55 = 144
144 + 89 = 233
233+ 144 = 377
Правильный ответ: через год будет 377 пар кроликов.
С точки зрения математики у последовательности Фибоначчи имеется много интересных свойств. Если взять пару соседних чисел из этого ряда и разделить большее число на меньшее, результат будет постепенно приближаться к числу золотого сечения (~1,6).
А что такое золотое сечение?И тут настало время поговорить о принципе золотого сечения. Так называют идеальное соотношение частей и целого, которое лежит в основе таких понятий, как гармония, красота, идеал. Этим принципом руководствовался Леонардо да Винчи, когда рисовал своего «Витрувианского человека», ему же пытаются соответствовать современные дизайнеры, архитекторы, ювелиры, художники. Золотое сечение встречается и в природе, и в науке, и в технике.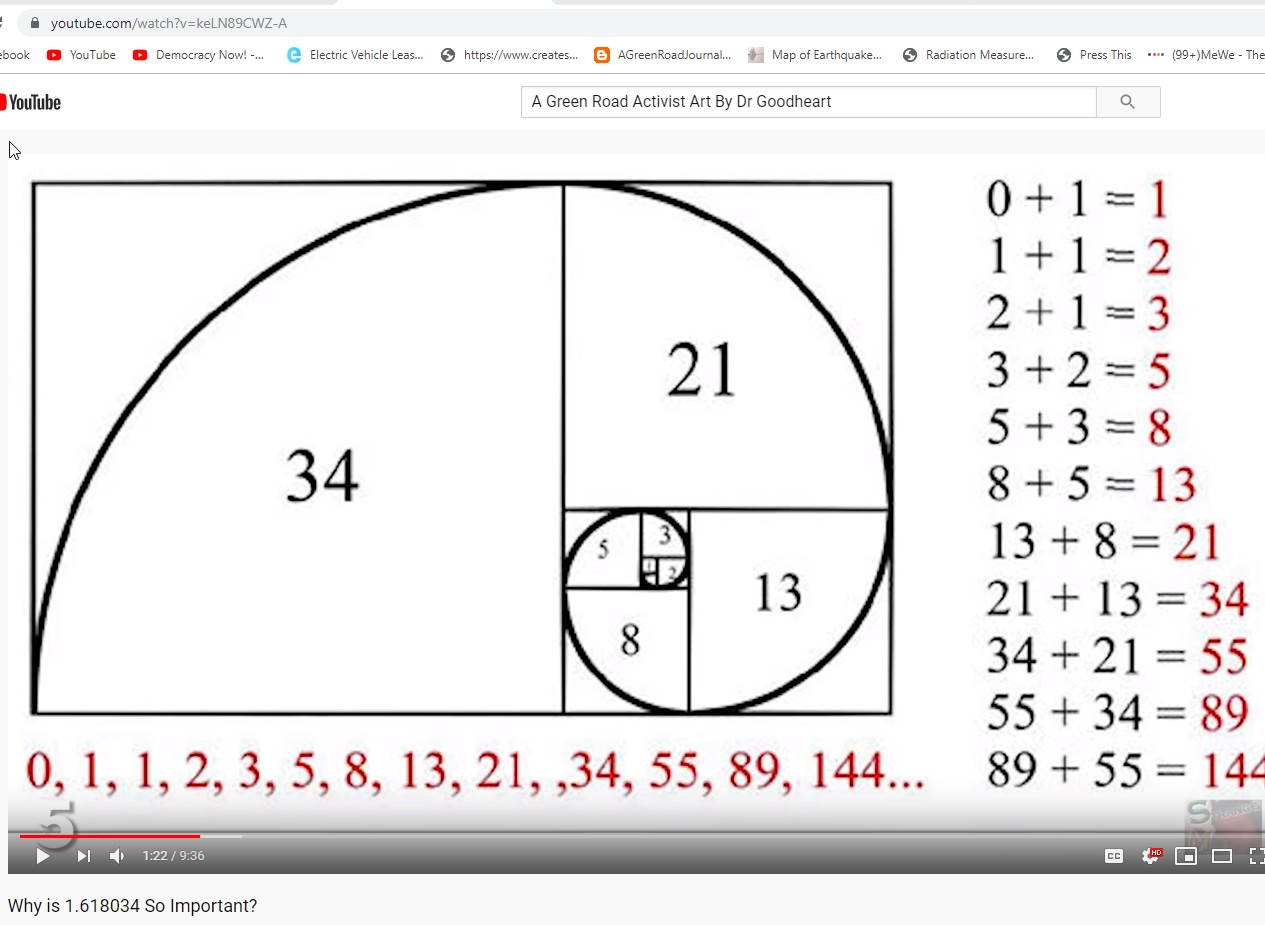 И это тот редкий пример, когда математическая формула передает такое сложное понятие, как красота.
И это тот редкий пример, когда математическая формула передает такое сложное понятие, как красота.
Представьте отрезок. Разделите его на два меньших отрезка — a и b, при этом a должно быть равно отношению a:b. Это и будет «золотой» пропорцией. Иными словами, золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок относится к большей части так, как сама большая часть относится к меньшей. В виде формулы вышесказанное можно записать так: (a + b):a=a:b. Золотое сечение выражается числом Ф (фи), оно равно 1,6180339887, но обычно округляется до 1,618 или 1,62. Если выразить золотое сечение в процентном соотношении, то оно составит 62% к 38%.
Где искать золотое сечение?Математики утверждают, что правило золотого сечения действует и в природе, и в космосе. Наглядный пример красоты и совершенства в природе — это растения и цветы. Внимательные ботаники давно разглядели в многообразии форм растительной жизни четкие математические закономерности: многие природные узоры, орнаменты, формы подчиняются правилу золотого сечения, вернее, одному из его частных случаев — последовательности Фибоначчи.
Внимательные ботаники давно разглядели в многообразии форм растительной жизни четкие математические закономерности: многие природные узоры, орнаменты, формы подчиняются правилу золотого сечения, вернее, одному из его частных случаев — последовательности Фибоначчи.
Многолетние наблюдения ботаников показали, что растения, чья структура или плоды подчиняются правилам золотого сечения, гораздо более выносливы, а не просто красивы. В одном из исследований по шишкам сибирской сосны или кедра было установлено, что если шишки сильно уклоняются от правильного расположения чешуек, то их семена очень слабо жизнеспособны. Иными словами, только у гармоничной красивой шишки будут жизнеспособные семена.
Числа Фибоначчи можно найти даже у себя. Посмотрите на свои руки: на обеих по пять пальцев. Два из них (большие) состоят из двух фаланг, а у остальных восьми — по три фаланги. 2, 3, 5, 8 — это как раз одни из первых чисел последовательности Фибоначчи. Совпадение? Математики считают, что это закономерно — правило золотого сечения действует повсюду.
Даже в космосе можно найти число идеальной пропорции. Возьмем Солнечную систему. Планеты вращаются по траектории эллипса, а значит, у их траекторий есть минимальный и максимальный радиус. Удивительно, но соотношение этих радиусов у всех планет Солнечной системы совпадает с числом золотого сечения, погрешность составляет доли процента. В то же время соотношение орбит планет нашей Солнечной системы очень близко к коэффициенту золотого сечения. Этот факт был известен еще Кеплеру, и, опираясь на него, он пытался построить некую универсальную систему мироздания.
«Золотая пропорция — это не только критерий красоты, — говорит профессор физического факультета МГУ, доктор физико-математических наук Павел Короленко. — Не только явление, которое позволяет проникнуть в суть понятия красивого. Но это и явление, которое несет в себе некую эвристическую ценность. Задает некое направление в исследованиях, проводимых в математике, физике, биологии. Я считаю, что это очень важное достоинство этого феномена».
Подробнее о золотом сечении и числах Фибоначчи рассказывается в фильме канала «Наука» — «В поисках абсолютной гармонии».
Зачем нужна математика?Единственное существо, которое научилось жить вечноВ поисках эликсира молодостиПодготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Определение чисел Фибоначчи
Последовательностью (числами) Фибоначчи называют возвратную последовательность 2-го порядка, определяемую рекуррентной формулой
| xn = xn – 1 + xn – 2 , n > 2 | (1) |
с начальными условиями
x1 = 1, x2 = 1 .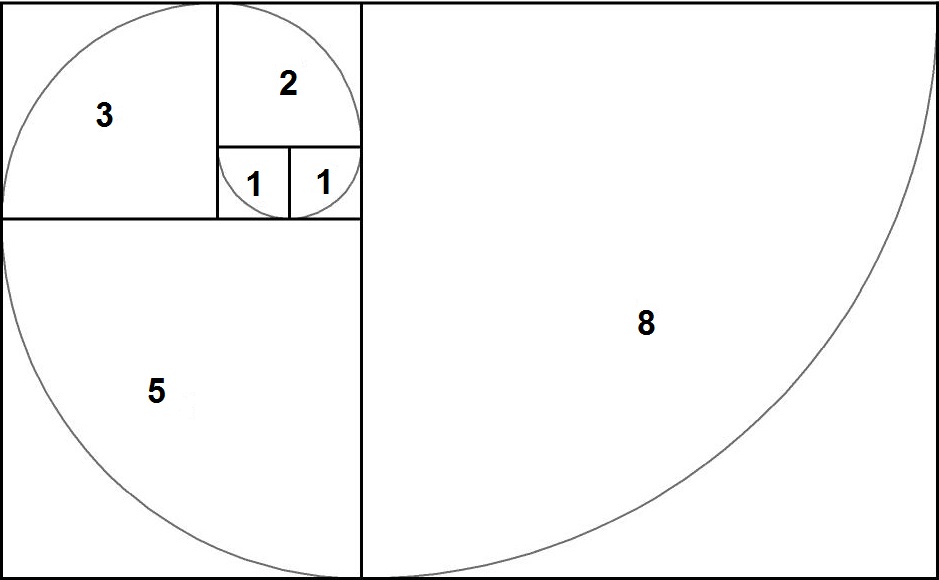 | (2) |
Другими словами, последовательность Фибоначчи — это такая последовательность, у которой первые два члена равны 1, а каждый член, начиная с третьего члена, равен сумме двух предыдущих членов.
Таким образом, числа
1, 1, 2, 3, 5, 8, 13, 21, 34, 55
являются первыми десятью членами последовательности Фибоначчи.
Замечание. Определения возвратной последовательности, рекуррентной формулы, характеристического уравнения и формулы для общего решения рекуррентных уравнений приведены в разделе «Возвратные последовательности: рекуррентная формула, характеристическое уравнение» нашего справочника.
Вывод формулы общего члена последовательности Фибоначчи
Нашей целью является вывод формулы общего члена последовательности Фибоначчи. Чтобы получить эту формулу, будем действовать в соответствии со схемой, изложенной в разделе «Возвратные последовательности: вывод формулы общего члена».
Чтобы получить эту формулу, будем действовать в соответствии со схемой, изложенной в разделе «Возвратные последовательности: вывод формулы общего члена».
Характеристическое уравнение для последовательности (1) имеет вид
λ2 – λ – 1 = 0 .
Найдем его корни:
Поскольку корни характеристического уравнения вещественные и различные, то общее решение рекуррентного уравнения (1) имеет вид
где c1 и c2 – произвольные действительные числа.
Найдем теперь значения произвольных постоянных c1 и c2так, чтобы для последовательности
(3) выполнялись начальные условия (2). Это означает, что числа c1 и c2должны удовлетворять следующей системе из двух линейных уравнений с двумя неизвестными:
Решение этой системы имеет вид:
Посмотреть, как получено это решение можно, включив эту страницу на стационарном компьютере или планшете.

Подставляя найденные значения произвольных постоянных c1 и c2в формулу (3), получаем искомую формулу общего члена последовательности Фибоначчи:
Замечание. Число
входящее в формулу общего члена последовательности Фибоначчи, является золотым отношением.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Что такое последовательность Фибоначчи и как ее использовать в трейдинге
Опытные трейдеры знают, что большое количество рыночных ордеров скапливаются близко к уровням и влияют на рыночную цену бумаг. Чтобы прогнозировать эти уровни, используют последовательность Фибоначчи, которую видно на графиках.
На основе этих чисел сформировано громадное количество стратегий. Они делятся на две большие группы — коррекцию и расширение.
Теория Фибоначчи создана итальянским математиком 12 века Леонардо Пизанским и в то время никакого отношения к биржевым операциям не имела — такая последовательность чисел встречается даже в живой природе. В биржевой технический анализ метод пришел аж через 5 веков.
Определение золотого сечения
Леонардо Фибоначчи из Пизы обнаружил некую числовую последовательность, которая встречается везде и универсальна для большинства природных явлений.
Вот эта последовательность чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
В этой цепочке каждое следующее число — это сумма двух предыдущих значений. Можете пересчитать сами и убедиться в этом.
Попробуйте разделить 34 на 55, 21 на 34 или 8 на 13. То есть два любых числа, которые стоят рядом — делите предыдущее число на следующее. У вас получится одно и то же значение — округленное в чуть большую сторону.
34 / 55 = 21 /34 = 8 /13 = примерно 0, 625 или 0, 618.
Но это только начало. Если мы будем делить числа через одно, то также получим одно и то же значение — 0, 382. Никакой магии — простая математика. Эти постоянные значения дробей называют «золотым сечением», эффект которого часто демонстрируют на примере спиралей внутри подсолнуха.
Никакой магии — простая математика. Эти постоянные значения дробей называют «золотым сечением», эффект которого часто демонстрируют на примере спиралей внутри подсолнуха.
Под золотым сечением подразумевают идеальную гармоничную пропорцию отношения части к целому. Как раз это число — 1,618 — наблюдается в различных природных формах — раковины улитки, расстояние между листьями на одной ветке и даже соотношение частей тела человека. Это примеры того, как выглядит спираль Фибоначчи. Ученые, которые изучали формы золотого сечения в природе, замечали, что все живое стремится занять место в пространстве и для него характерны пропорции золотого сечения.
Вы спросите, при чем тут трейдинг?
А при том, что эти же значения дробей используются в качестве главного коэффициента при построении графиков!
Уровни фибоначчи используются для того, чтобы прогнозировать дальнейшее движение цены инструмента. Работа с этими числами привязывается к уже существующему тренду, чтобы в дальнейшем прогнозировать коррекцию или развитие. Алгоритм задает ориентиры — до какого уровня дойдет цена, где возможен разворот и прочее. Благодаря этим расчетам трейдеры могут устанавливать отложенные ордера, стопы и профиты.
Алгоритм задает ориентиры — до какого уровня дойдет цена, где возможен разворот и прочее. Благодаря этим расчетам трейдеры могут устанавливать отложенные ордера, стопы и профиты.
Первым додумался искать золотое сечение числа фибоначчи на биржевых графиках американский инженер Ральф Hельсон Эллиотт. В начале 30-х годов ХХ века он серьезно заболел и от нечего делать стал изучать графики фондовых индексов за последние 75 лет существования бирж.
Он отследил, что индексы двигаются волнообразно — в определенном ритме. И там тоже прослеживается та же пропорция — с числом 1,618. Так родилась теория волнового анализа, которую ученый описал в нескольких серьезных трудах, включая книгу «Закон природы — секрет вселенной». Но четкого ответа на вопрос — в какой волне в конкретный момент находится цена — теория не дает. Это упирается в параметры определения точки отсчета первой волны — страсти кипят по сей день, и к единому мнению биржевики так и не пришли.
Практичнее всего было бы применить принцип «Не торгуй, если не уверен». Но есть инструменты, в которых волны на определенной стадии четко вырисовываются и их легко идентифицировать.
Но есть инструменты, в которых волны на определенной стадии четко вырисовываются и их легко идентифицировать.
На некоторых инструментах вычислить волны невозможно, приходится регулярно наблюдать и находить те из них, где волны ходят понятным трейдеру образом. И потом торговать исключительно на них.
Что такое числа Фибоначчи в трейдинге и как это выглядит на графиках
Для определения ценовых ориентиров и понимания того, когда выгоднее продавать/покупать бумаги, в каком месте цена сменит направление, трейдеры применяют старый проверенный инструмент — уровни поддержки и сопротивления. Но к сожалению, не всегда можно вычислить, какой из них будет работать, а какой цена может не заметить — как раз этот вопрос и помогает разрешить метод Фибоначчи.
Что такое линии Фибоначчи?
На биржевых графиках это сетка из линий, которые расположены друг от друга на определенном расстоянии — его рассчитывают с применением уже известного коэффициента. Чаще всего рыночная цена стремится к этим линиям, приближаясь к уровням, и часто меняет направление.
Когда чертят линии, привязку делают к последнему явно выраженному тренду. Сетка Фибоначчи растягивается от начала до конца тренда. И уровни внутри диапазона будут ориентирами в случае возможной коррекции. А те, что лежат вне диапазона, — это ориентиры возможного продолжения тренда.
Открывая сделку по тренду, на внешние уровни можно ставить тейки, а на внутренние — стопы. При коррекции целями трейдера будут внутренние уровни. Возможно открытие сделок на пробой уровней и установка на них отложенных ордеров.
Временные зоны
Они дают возможность спрогнозировать время очередной трендовой или коррекционной волны — за основу берется протяженность предыдущего сигнала.
От линий временные зоны отличаются тем, что их растягивают от точки начала тренда до точки разворота.
Но используют их крайне редко— на отдельных таймфреймах у любой валютной пары будет своя длина волны. А значит, конкретного правила на вход не бывает.
Канал
В отличие от горизонтальных линий канал может выглядеть на графике наклонно — и сетка линий тренда при определении цели для цены учитывает угол наклона тренда. При восходящем текущем тренде точки привязываются к минимумам, при нисходящем — к максимумам. После чего выстраивают первую линию тренда — она и будет основной поддержкой или сопротивлением. Передвигая следующую линию, настраивают всю остальную сетку.
Дуги
Эффективны, когда цена движется во флэте. Их применяют, чтобы уловить коррекцию. При этом дуги растягивают от начала до конца тренда и наоборот в соответствии с направлением закругления.
Классический вариант — когда на графике присутствуют три дуги внутри амплитуды движения тренда. Чем дальше цена движется от ключевых точек, тем сильнее расходятся линии дуг, расширяя при этом диапазон.
Веер
Это когда на графике из одной точки несколько лучей расходятся в разные стороны — рисунок действительно напоминает веер. Его растягивают по двум точкам тренда и начинают всегда с первой, из которой и выстраиваются лучи.
Его растягивают по двум точкам тренда и начинают всегда с первой, из которой и выстраиваются лучи.
Когда тренд восходящий, веер выстраивается под графиком цены, а когда он нисходящий — веер располагается над ним и дает ориентиры для коррекции.
Еще его используют, когда работают с динамичным стопом — ордер при этом передвигают на одной из веерных линий, следуя за движением цены.
Расширения
Часто применяют во время волнового анализа. Для построения нужны три точки, образующие коррекционную и трендовую волны. Расширения дают возможность увидеть новые цели по направлению тренда и помогают выставлять тейк-профиты.
Дуги, веера и временные зоны — слишком специфические инструменты и применяются редко. Разве что в торговых системах, которые специально разрабатывались под них. В принципе, фигура Фибоначчи — популярный базовый инструмент, используемый в сочетании с другими элементами (поиск или подтверждение дополнительных сигналов, и других).
В популярном терминале для российских трейдеров Quik есть 4 инструмента — уровни, дуги, веер и временные зоны.
Что такое коррекция в трейдинге и как выставлять уровни коррекции Фибоначчи
В соответствии с правилами их растягивают от точки начала тренда к его окончанию (в терминале Quik можно растягивать и наоборот — на результат это не повлияет). Образовавшиеся уровни будут возможными целями коррекции — от них можно входить по тренду.
Уровни коррекции Фибоначчи:
0.236, 0.382, 0.500, 0.618, 0.764
Уровни расширения Фибоначчи:
0, 0.382, 0.618, 1.000, 1.382, 1.618
При выстраивании уровней коррекции и расширения считать дроби нет необходимости — для этого существуют калькуляторы, да и на живых графиках они вырисовываются автоматически.
Почему уровни основаны на дробях?
Опытные трейдеры вполне резонно полагают, что если внутри подсолнуха расстояние между линиями спирали из семечек можно просчитать этими дробями, то и уровни ретрейсмента по аналогии можно использовать в качестве поддержки и сопротивления.
С их помощью также открывают сделки и размещают стопы на форексе. А уровни расширения помогают корректно устанавливать тейк-профиты — часто цена доходит до них, и это надо учитывать.
А уровни расширения помогают корректно устанавливать тейк-профиты — часто цена доходит до них, и это надо учитывать.
Всегда ли ряд Фибоначчи поможет трейдеру
Если цена может пробить уровень сопротивления или поддержки, то аналогично она способна пробить и линии Фибоначчи. Поэтому их нельзя считать окончательной гарантией того, что произойдет откат или отскок — просто они дают высокую степень вероятности.
Как и любой другой аспект технического анализа, уровни Фибоначчи надо тщательно отрабатывать, постоянно уточнять и фильтровать. Собственно говоря, на вероятностях построен теханализ. И об этом нельзя забывать — ведь цена не всегда будет взаимодействовать с ними так, как вы предполагаете. Она может перемещаться от уровня к уровню — и какой из них она посчитает более значимым, это только ей одной известно. И поэтому во время применения стратегии уровней Фибоначчи придется использовать все доступные инструменты, совмещая их с линиями Фибоначчи, а также с поддержкой и сопротивлением.
Каждый трейдер сам решает, применять ли данный метод.
Преимущества и недостатки метода
Плюсы инструмента:
- Главный жирный плюс — универсальность инструмента, подтвержденная сотнями лет применения в разных сферах, в том числе и трейдинге. Уже лет пятьдесят их применяют в анализе фондовых рынков, Форекса, а также крипторынка. Именно поэтому трейдинг по Фибоначчи остается востребованным, независимо от того, как сильно меняется рынок от волатильности к спокойствию и наоборот.
- Спектр применения метода весьма широк — с ним можно открывать новые ордера, искать точки входа и выхода из рынка.
Минус:
- До того, как устанавливать уровни, нужен предварительный анализ. Если другие компьютерные ориентиры можно только запустить, и они на графике установятся автоматически, то уровни Фибоначчи надо устанавливать вручную — в этом случае трейдеру придется самому выбирать, от каких точек строить линии.
Книги по теме
- А.
 Фроста и Р. Пректер «Волновой принцип Эллиотта» — там хорошо описаны принципы классической волновой теории Эллиота в ее изначальном виде..
Фроста и Р. Пректер «Волновой принцип Эллиотта» — там хорошо описаны принципы классической волновой теории Эллиота в ее изначальном виде.. - Б. Мендельброт и Р. Хадсон «(Не)послушные рынки» — современный взгляд на теорию волн Эллиотта.
- Б. Вильямс «Торговый хаос» — подробное знакомство с методикой подсчета волн в доступной форме.
- Р. Фишеp «Последовательность Фибоначчи: приложения и стратегии для трейдеров» — еще один нестандартный взгляд на применение последовательности Фибоначчи для подсчета волн.
Выводы
Последовательность Фибоначчи напрямую связана с термином «золотое сечение», которому соответствует число 1,618. Отношение каждого следующего числа к предшествующему стремится к этой величине.
Работая с этим методом, трейдеры могут прогнозировать, куда двинется тренд, неважно, на каком рынке — Форексе, фондовом или криптовалюты.
У любого тренда всегда будут наблюдаться циклы повышения, коррекции, спада, снова коррекции и последующего роста. И линии Фибоначчи нужны, чтобы прогнозировать направление движения тренда, опираясь на цифры.
И линии Фибоначчи нужны, чтобы прогнозировать направление движения тренда, опираясь на цифры.
Несколько полученных значений биржевики связывают в неровную линию и подвергают анализу, чтобы найти некие ориентиры, которые позволят уверенно входить в рынок.
Опытному трейдеру уровни Фибоначчи сэкономят время и силы на утомительные детальные расчеты и послужат отличным инструментом получения прибыли.
Новичкам в этом деле следует начать с изучения волнового анализа и базовых навыков торговли от уровней. И только потом переходить к освоению метода Фибоначчи.
Но как бы в разных трейдерских блогах ни нахваливали этот продвинутый инструмент, следует знать, что его абсолютная эффективность до конца не доказана — поэтому результаты применения целиком зависят от степени подготовки и опыта трейдера.
Это сложная тема. Ее невозможно детально разобрать в рамках одной статьи. Поэтому приглашаем на наш базовый курс.
Последовательность чисел Фибоначчи в трейдинге
Уровни фибоначчи – один из базовых инструментов анализа движений в контексте их размеров. На первый взгляд может показаться, что это значения, которые просто за уши притянуты к реальности, однако можно просто открыть любой график и посмотреть на соотношения между разными колебаниями. Тут даже самые упёртые скептики сдадутся. Этот необычный метод активно используется во многих стратегиях, а также играет важную роль при волновой разметке движений, Эллиотт уделял большое внимание пропорциям, что позволяет в значительной степени повысить точность таких прогнозов. На данный момент уровни фибоначчи входят в состав базовых графических инструментов практически любого терминала, и даже если он отсутствует, его легко можно найти в интернете или, на крайний случай, посчитать самому на калькуляторе.
На первый взгляд может показаться, что это значения, которые просто за уши притянуты к реальности, однако можно просто открыть любой график и посмотреть на соотношения между разными колебаниями. Тут даже самые упёртые скептики сдадутся. Этот необычный метод активно используется во многих стратегиях, а также играет важную роль при волновой разметке движений, Эллиотт уделял большое внимание пропорциям, что позволяет в значительной степени повысить точность таких прогнозов. На данный момент уровни фибоначчи входят в состав базовых графических инструментов практически любого терминала, и даже если он отсутствует, его легко можно найти в интернете или, на крайний случай, посчитать самому на калькуляторе.
В основе значений фибоначчи лежит числовая последовательность, которая имеет такое же название. Это достаточно простой алгоритм, последовательность строится по следующему принципу: каждый последующий член последовательности фибоначчи равен сумме двух предыдущих. Начинается она с нуля и двух единиц. Впрочем, ноль очень часто опускается.
По мере продолжения этой последовательности каждый предыдущий член будет всё больше приближаться к так называемому “Золотому сечению”. В процентном выражении это 61,8%. Взято это значение из простой формулы деления отрезка на две части так, чтобы меньшая часть относилась к большей так же, как большая часть относится ко всему отрезку. После несложных расчётов получается как раз 61,8%. Так мы получаем самое главное значение, от которого строятся все остальные. Второе важное значение – 38,2%. Оно получается путём вычета из 100% значения основного. Рассмотрим, как это получается:
Интерес представляет правый столбик, показанный на картинке. Буквально десятый член последовательности уже показывает очень близкие к нашему золотому сечению значения. Далее, продолжая строить ряд, мы получаем ещё более точные. В целом, в трейдинге вполне достаточно использовать общепринятое значение 61,8%, дальнейшее уточнение уже ни к чему.
Важность последовательности фибоначчи
Теперь перейдём к более важному вопросу, а именно по какой причине всё это работает. Дело в том, что золотое сечение названо так совсем не случайно. Первые упоминания датируются аж четвёртым веком до нашей эры в работах известного математика Евклида, который упоминал золотое сечение в контексте построения пятиугольника. Само же название связывают обычно с очень известным инженером, художником и изобретателем – да Винчи, хотя именно литературное распространение началось с математических пособий Германии, где другой известнейший учёный Ом ввёл его именно в этой формулировке. В целом, всё это не так важно, главное – это идея, которая лежит в самом соотношении. К которому приводит последовательность фибоначчи. Подобное соотношение можно встретить в следующих областях:
1. Архитектура. История знает огромное количество примеров, где было сознательно использовано правило разделения различных элементов исходя из их соотношений между собой определённым коэффициентом. Самый яркий пример – пирамиды в Египте, а также многие здания (храмы) в Древней Греции. Прямоугольник, разделённый таким образом получается очень гармоничным, поэтому он часто лоижлся в основу формы здания. То же самое относится и к элементам украшения, декора, везде можно проследить эту туенденцию. Конечно же, это не говорит о том, что прямо вот вся архитектура была заточена именно под такие пропорции, но тот факт, что они далеко нередко появлялись, свидетельствует о том, что золотое сечение было известно давно, и использовалось вполне сознательно. В целом, и последовательность фибоначчи появилась не просто так – числа, которые приближаются к золотому сечению позволяют определить само сечение через такую математическую операцию, как вычисление предела.
2. Геометрия молекул и химия. Очень сложные формы соединений на атомном уровне могут содержать как числа, входящие в последовательность фибоначчи, так и само золотое сечение. Как уже говорилось ранее, наш коэффициент присутствует в пятиугольнике, а сами атомы между собой образуют очень сложные геометрические фигуры. В основном, коэффициент прослеживается в додекаэдрах и икосаэдрах. Не вдаваясь в подробности, это многогранные фигуры, имеющие сложную симметрию. Также здесь присутствует число из поселдовательности фибоначчи – 21, которое получается одной молекулой, вокруг которой располагается ещё двадцать молекул. В итоге вся эта композиция из двадцати одной молекулы даёт додекаэдр.
3. Биология. Пропорции тела очень приближены к главному коэффициенту. Например, соотношение между расстояние от подбородка до бровей стремится к коэффициенту, входящему в последовательность чисел фибоначчи, по отношению оставшейся части головы, то есть лба. Аналогичная ситуация и с размером ладони, только в роли этого сечения выступает линия, проходящая через сустав между третьей и второй фалангой. Также считается, что изначально на подобные части, как в последовательности фибоначчи, делил тело пупок. Однако, со временем начались отклонения от этих значений, что объясняется эволюцией и приспособлением под окружающие человека условия.
4. Музыка. Здесь речь идёт о количество нот разной длины. Например, золотое сечение использовал Иоганн Себастьян Бах, один из величайших композиторов в истории.
5. Природа. Золотое сечение прослеживается в цветах, листьях, расположении сучков на более крупном суке дерева. Наибольший интерес представляет раковина улитки, которая “раскручивается” по строгой спирали, шаг которой определяется нашим коэффициентом. Вообще, если взглянуть на все примеры, становится очевидным, что каким-то необъяснимым образом и сама природа стремится к таким пропорциям. Человеческое восприятие объектов, в которых есть такие соотношения ассоциируется с гармонией, что довольно странно на фоне восприятия симметричных объектов, как практически идеальных. Тем не менее, данный факт известен очень давно и активно применяется.
Данное соотношение, полученное из чисел фибоначчи, ложится в основу системы коэффициентов, которые называются уровнями фибоначчи. Они устанавливают пропорции между двумя разнонаправленными движениями, по ним можно определять размеры коррекции и предполагать точки окончания. Но об этом мы поговорим позднее, а сейчас перейдём непосредственно к самим числам фибоначчи, а вернее, последовательности, которая имеет очень важное значение в волновой теории, разработанной Эллиоттом.
Последовательность чисел фибоначчи в волновой теории
До этого мы говорили о предельном отношении двух соседних членов последовательности чисел фибоначчи. Теперь посмотрим, как волновая теория использует последовательность. Из общего описания нам известно, что все движения делятся на импульсы и коррекции. В глобальном масштабе вся волновая конструкция стремится к циклу роста и снижения, меняется размерность, но эти две фазы последовательно происходят одна за другой. Минимальный набор волн для отличия одной структуры от другой – 5 и 3. У импульсов пять составляющих, у коррекции – три. В этом мы видим первые два числа, которые относятся к последовательности фибоначчи. И даже суперцикл из двух фаз также входит в последовательность – это 1 и 1. Рассмотрим более подробно рост и коррекцию.
- В составе импульса мы можем выделить 5 элементов – три из них также импульсы, оставшиеся два – коррекции. Соответственно, при таком приближении у нас уже получается 5+3+5+3+5=21 Итого двадцать одна волна составляет импульс.
- Коррекция, как известно, состоит из трёх движений, в которых два – импульсы и одно – коррекция. При таком раскладе у нас получается 5+3+5=13 волн. Здесь есть исключение, так как иногда первая волна в коррекции может быть представлена тройкой, но зато это компенсируется тем, что вторая волна может быть треугольником, в котором не 3, а уже 5 волн. К тому же треугольники могут встречаться и в четвёртой волне импульса.
Что мы видим в итоге: 21 волна в импульсе и 13 волн в коррекции в рамках одного цикла. Оба числа из последовательности фибоначчи, причём следуют они сразу за 8 и 5 волн из предыдущего примера. И если это покажется совпадением, перейдём ещё на один уровень подробнее. В этом случае получается следующее:
- Импульс представлен 21 волной, коррекция 13, значит, весь импульс будет состоять из 21+13+21+13+21=89 волн. Это также вытекает из структуры простого 5+3.
- Коррекция состоит из: 21+13+21=55 волн.
И снова у нас два числа из последовательности фибоначчи. В сумме такой цикл даёт следующее число – 144. Так можно продолжить до бесконечности, и каждый раз будем получать следующие два числа из последовательности фибоначчи. Подобная последовательность свидетельствует о том, что волновая теория имеет глубокую связь с происходящим на рынке, ведь мы имеем не только количество волн, но и самое главное соотношение и его производные, которые также вписываются в гармонию природы и поведения людей. И чем больше объёмы, тем чётче должна прослеживаться зависимость всего происходящего в разных циклах между собой. Это выражается как в самой структуре, так и в коэффициентах.
Читайте далее — Уровни Фибоначчи
Артур Бенджамин. Магия чисел Фибоначчи
Известный математик Артур Бенджамин исследует скрытые свойства удивительной числовой последовательности — последовательности Фибоначчи. И доказывает нам тот факт, что математика может еще и вдохновлять.
Артур Бенджамин. . Источник: Артур Бенджамин. . Автор: Артур Бенджамин.
Последовательность Фибоначчи — это такая последовательность, в которой каждое последующее число равно сумме двух предыдущих чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21…
1. Почему мы изучаем математику? По сути, есть три причины: расчёт, приложение и последняя, к сожалению, наименее важная с точки зрения времени, которое мы ей уделяем, — это вдохновение. Математика — это наука о моделях, и мы изучаем её, чтобы научиться мыслить логически, критично и творчески, но та математика, которую мы изучаем в школе, чаще всего неэффективно мотивирована, и когда наши студенты спрашивают: «Почему мы это изучаем?» — то им часто приходится слышать, что это необходимо в предстоящем математическом классе или для будущих классов. Но было бы здорово, если бы мы хоть иногда занимались математикой просто потому, что это весело, или красиво или потому, что она волнует ум.
2. Я знаю, что многие люди не имеют возможности увидеть, как это происходит. Поэтому позвольте мне показать вам небольшой пример из моей любимой коллекции чисел, чисел Фибоначчи. Эти цифры могут быть истолкованы различными способами. С точки зрения вычислений, их также легко понять, как то, что 1 + 1 = 2. Тогда 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8, и так далее. На самом деле человек, которого мы называем Фибоначчи, носил имя Леонардо из Пизы, и эти цифры появляются в его книге Liber Abaci, которая научила западный мир методам арифметических операций, используемых сегодня.
3. Числа Фибоначчи появляются в природе удивительно часто. Количество лепестков на цветке — это типичное число Фибоначчи. Количество спиралей на подсолнухе или ананасе также тяготеет к числу Фибоначчи. В самом деле, есть много больше применений чисел Фибоначчи, но наиболее вдохновляющими, по моему мнению, являются прекрасные цифровые образцы. Позвольте мне показать вам один из моих любимых. Предположим, что вы хотите возвести число в квадрат. И, честно говоря, кто не хотел бы? Давайте посмотрим на квадраты первых нескольких чисел Фибоначчи. 1 в квадрате равно 1, 2 в квадрате — 4, 3 в квадрате — это 9, 5 в квадрате — 25 и так далее. Теперь известно, что при сложении последовательных чисел Фибоначчи вы получите следующее число Фибоначчи. Верно? Вот как они созданы. Но вы не ожидаете ничего особенного от сложения их квадратов. Но давайте проверим это. 1 + 1 = 2, и 1 + 4 = 5. И 4 + 9 = 13, 9 + 25 = 34, и да, шаблон повторяется. Фактически тут есть ещё один шаблон. Предположим, вы хотите проанализировать сложение квадратов нескольких первых чисел Фибоначчи. Давайте посмотрим, что мы получим. Так что 1 + 1 + 4 = 6. Добавляем к этому 9 и получаем 15. Добавив 25, мы получаем 40. Добавив 64, мы получаем 104. Теперь посмотрите на эти цифры. Они не являются числами Фибоначчи, но если вы посмотрите на них внимательно, вы увидите, что числа Фибоначчи скрыты внутри них. Вы это видите? Я покажу вам это. 6 — это 2 × 3, 15 — это 3 × 5, 40 — это 5 × 8. Итак, 2, 3, 5, 8 — кому мы должны быть признательны? Фибоначчи! Конечно. Обнаружить эти шаблоны было забавно, но ещё большее удовлетворение — понять, почему они являются подлинными.
4. Давайте посмотрим на последнее уравнение. Почему квадраты 1, 1, 2, 3, 5 и 8 составляют 8 × 13? Я покажу вам это, нарисовав простую картину. Мы начнем с квадрата единицы, и рядом с этим ещё один квадрат единицы. Вместе они образуют прямоугольник один на два. Ниже я поставлю квадрат 2 на 2, потом квадрат 3 на 3, под ним квадрат 5 на 5, и затем квадрат 8 на 8, получается один гигантский прямоугольник, правильно? Теперь позвольте мне задать вам простой вопрос: какова площадь прямоугольника? С одной стороны, это сумма площадей квадратов внутри него, правильно? Так же, как мы создали его. Это 1 в квадрате плюс 1 в квадрате плюс 2 в квадрате плюс 3 в квадрате плюс 5 в квадрате плюс 8 в квадрате. Верно? Это площадь. С другой стороны, поскольку это прямоугольник, площадь равна его высоте, умноженной на ширину. Высота равна 8, а ширина — 5 + 8, чем и является следующее число Фибоначчи 13. Верно? Таким образом, площадь равна 8 × 13. Так как мы правильно рассчитали площадь двумя разными способами, числа должны быть одинаковыми, и вот почему квадраты 1, 1, 2, 3, 5 и 8 складываются в 8 × 13. Если мы продолжим этот процесс, мы создадим прямоугольники размером 13 на 21, 21 на 34 и так далее. Теперь проверьте это. Если вы разделите 13 на 8, вы получите 1,625. И если вы разделите большее число на меньшее число, то эти коэффициенты становятся всё ближе и ближе к числу 1.618, известному многим людям как Золотое сечение, числу, которое очаровывало математиков, учёных и художников на протяжении многих веков.
5. Я показываю всё это вам потому, что много что в математике имеет красивые стороны, которые, боюсь, не получают достаточного внимания в наших школах. Мы тратим много времени на изучение вычислений, но давайте не забывать и о применении, которое включает, возможно, наиболее важное применение — научиться думать. Если я мог бы обобщить это в одном предложении, это звучало бы так: математика — это не только поиск решений для Х, но также и поиск причин таких решений.
ЧИСЛА ФИБОНАЧЧИ: МИФ ИЛИ РЕАЛЬНОСТЬ?!
ЧИСЛА ФИБОНАЧЧИ: МИФ ИЛИ РЕАЛЬНОСТЬ?!
Круглов Н.П. 11Областное Государственное Бюджетное Профессиональное Образовательное Учреждение «Костромской торгово-экономический колледж»
Холинова О.А. 11Областное Государственное Бюджетное Профессиональное Образовательное Учреждение «Костромской торгово-экономический колледж»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
ВВЕДЕНИЕ
Математику называют «царицей всех наук». Древняя история богата выдающимися математиками. Многие достижения древней математической науки до сих пор вызывают восхищение остротой ума их авторов, а имена Евклида, Архимеда, Герона известны каждому образованному человеку. Иначе обстоит дело с математикой средневековья. Математика в эту эпоху развивалась чрезвычайно медленно, и крупных математиков тогда было очень мало. Тем больший интерес представляет для нас сочинение «Liber abacci» («Книга об абаке»), написанная знаменитым итальянским математиком Леонардо из Пизы (ок. 1170-после 1228), более известный под прозвищем Фибоначчи, который был, безусловно, самым значительным математиком средневековья. Роль его книг в развитии математики и распространении в Европе математических знаний трудно переоценить.
В исследовательской работе рассматриваются числа последовательности Фибоначчи, их свойства, а также, тесно связанный с этой темой, феномен золотого сечения, в котором большинство ученых видят одно из наиболее ярких, давно уже замеченных человеком проявлений гармонии природы. Феномен золотого сечения рассмотрен в работе в общей картине исторического становления архитектуры, на формах живой природы и за пределами предметного мира, в области гармонии и математических абстракций. Он рассмотрен и как объективная характеристика объектов искусства, экономики и т. д.
Общеизвестно, что золотое сечение – это закон пропорциональной связи целого и составляющих это целое частей. Классический пример золотого сечения – деление отрезка в среднепропорциональном отношении, когда целое так относится к большей своей части, как большая часть – к меньшей: (a+b)/b = b/a. Такая задача имеет решение в виде корней уравнения x2 – x – 1 = 0.За кажущейся простотой операции деления в крайнем и среднем отношении скрыто множество удивительных математических свойств и множество форм выражения пропорции золотого сечения.
Золотое сечение, как и загадочные свойства чисел Фибоначчи, владели мыслью и чувствами многих выдающихся мыслителей прошлого и продолжает волновать умы современников наших не ради самих математических свойств, а потому, что неотделимо от ценности объектов искусства и в то же время обнаруживает себя как признак структурного единства объектов природы. Скульптура, архитектура, музыка, астрономия, биология, психология, техника – вот те сферы, где так или иначе обнаруживает свою жизнь золотое сечение. Современные исследователи находят его при описании строения растений, пропорций тел животных, птиц, человека, в статистике популяций, в строении глаза и строении космоса и т. д.
Сегодня невозможно с абсолютной достоверностью определить, когда и как понятие золотого сечения было выделено в человеческом знании из интуитивной и опытной категорий. Но судить обоснованно, кто прав: те ли, кто относит открытие золотого сечения к цивилизациям древнего Востока (Египет. Индия), или те, кто, подобно Кеплеру, связывает открытие золотого сечения с именем Пифагора, можно, но для этого необходимо владеть базовыми историческими и математическими познаниями.
В эпоху Ренессанса среднепропорциональное отношение именовали Sectio divina – божественной пропорцией. Леонардо да Винчи дает ему имя Sectio aurea (золотое сечение), живое поныне, а много раньше, в 1202 г., открытием ряда Фибоначчи было обнажено фундаментальное свойство золотого сечения – единство аддитивности и мультипликативности.
Сегодня сущность гармонии невозможно выявить ни в биологии, ни в искусстве, ни в абстрактно-математических построениях, если рассматривать их раздельно, – здесь можно лишь наблюдать и осмысливать ее проявления. «Философия, – говорил Галилео Галилей, – написана в той величественной книге, которая постоянно открыта у нас перед глазами (я имею в виду Вселенную), но которую невозможно понять, если не научиться предварительно ее языку и не узнать те письмена, которыми она начертана». «Божественная пропорция – бесценное сокровище, одно из двух сокровищ геометрии», – развивает эту же мысль Кеплер. Действительно, гармония может быть расшифрована лишь на ее собственном языке, отображенном фундаментальными принципами естествознания.
Существуют любопытные закономерности, которые могут быть описаны с помощью математики. Во вселенной еще много неразгаданных тайн, некоторые из которых ученые уже смогли определить и описать. Числа Фибоначчи и золотое сечение составляют основу разгадки окружающего мира, построения его формы и оптимального зрительного восприятия человеком, с помощью которых он может ощущать красоту и гармонию.
Актуальность данной работы заключается в необходимости исследования чисел Фибоначчи, так как они встречаются нам в различных творениях природы. Знания о них будут полезны во многих науках.
Цель: изучить практическую значимость чисел Фибоначчи
Задачи:
1.Познакомиться с числами Фибоначчи и историей их создания.
2. Рассмотреть рекурентную формулу ряда Фибоначчи.
3. Познакомиться с биографией итальянского математика Леонардо Пизанского (Фибоначчи).
4. Изучить свойства числового ряда Фибоначчи
5. Проверить на практике проявление чисел Фибоначчи в неживой природе, в строении человека и растений.
Предмет исследования — числа Фибоначчи.
Объект исследования — область применения чисел Фибоначчи; свойства чисел Фибоначчи.
Проблема, которую призвано разрешить наше исследование, заключается в том, что мы не знаем и не видим в окружающей нас жизни числовые закономерности, которые укладываются в ряд Фибоначчи.
Изучение этих чисел не предусмотрено уроками математики, поэтому чтобы познакомится с ними подробнее, необходимо использовать разнообразные источники информации: дополнительную литературу по предмету и интернет ресурсы.
Методы исследования в работе:
теоретический (логическая ступень познания).
эмпирический (наблюдение, эксперимент, измерение).
сравнение.
классификация.
математическое моделирование
практический (расчеты числа фи)
Структура работы: исследовательская работа состоит из введения, двух глав, заключения, списка используемой литературы. Во введении определена актуальность темы, связанная с понятием последовательности ряда Фибоначчи и проявление чисел Фибоначчи в неживой природе, в строении человека и растений, цели, задачи, объекты и методы исследования. В первой главе описана историческая справка о Леонарде Пизанском, итальянском математике средневековья; последовательность ряда Фибоначчи и его свойства. Во второй главе рассмотрены проявления последовательности Фибоначчи в окружающем мире. Далее следует заключение. В нем определены выводы по проделанной работе. В списке используемых источников перечислена основная литература, которая использовалась в процессе работы.
В теоретической части исследования была изучена литература по данной теме, узнали, как образуется этот ряд, историю его возникновения, какими свойствами он обладает. Рассмотрели разные объекты природы где, обнаруживает себя ряд Фибоначчи. Оказывается, эти числа можно найти в подсолнухах и сосновых шишках, в крыльях стрекозы и морских звёздах, в ритмах человеческого сердца и в музыкальных ритмах, в строении человеческого тела и в строении раковин моллюсков, в океане, в космосе и т.д. В проверке этих фактов заключается практическая часть нашего исследования.
1 Числа Фибоначчи.
1.1.Биография Леонардо Пизанского
Удивительные числа были открыты итальянским математиком средневековья Леонардо Пизанским, более известным под именем Фибоначчи. Леонардо Пизанский (Фибоначчи)– это первый крупный математик средневековой Европы. Более известен под прозвищем Фибоначчи, что в переводе с итальянского означает «хороший сын родился».
Точная дата его рождения неизвестна. Предположительно Фибоначчи родился в 1170г. в городе Пиза, в Италии. Леонардо из Пизы, известный как Фибоначчи, был первым из великих математиков Европы позднего Средневековья. Будучи рожденным в Пизе в богатой купеческой семье, он пришел в математику благодаря сугубо практической потребности установить деловые контакты.
Его отец был купцом и государственным вельможей, представителем нового класса бизнесменов. Тогда Пиза была одним из крупнейших коммерческих центров, активно сотрудничавших с исламским Востоком, и отец Фибоначчи энергично торговал на северном побережье Африки, по торговым делам часто бывал в Алжире. Благодаря этому ему удалось «устроить» своего сына в одну из арабских школ, где он смог получить превосходное для того времени математическое образование.
Леонардо изучал труды математиков востока, по арабским переводам он ознакомился также с достижениями античных и индийских математиков.
Все эти знания он впитывал в себя как губка. А потом принес их в Европу, он «открыл» арабские цифры вместо римских и десятичную систему счисления для европейцев. Значительную часть усвоенных им знаний он изложил в своей выдающейся «Книге абака» (Libег аЬасi, 1202; до наших дней сохранилась только дополненная рукопись 1228 г.). Эта книга содержит почти все арифметические и алгебраические сведения того времени, изложенные с исключительной полнотой и глубиной и одно из величайших открытий всех времён и народов – десятичную систему счисления.
На протяжении нескольких столетий по труду Фибоначчи ученые знакомились с двумя важнейшими разделами математики – арифметикой и алгеброй и черпали из него задачи и оригинальные методы решения, благодаря чему уже в XV – XVI в.в. те разошлись по многочисленным итальянским, французским, немецким, английским, а позже и русским рукописям, печатным книгам и учебникам.
Когда Леонардо вернулся в Италию, там правил император Фридрих II. Он не признавал рыцарские турниры, вместо них он проводил гораздо менее кровавые математические соревнования, на которых противники обменивались не ударами, а задачами. На таких турнирах и заблистал талант Леонардо Фибоначчи.
Предположительно Фибоначчи умер во время одного из Крестовых походов в 1228 году, сопровождая императора Фридриха II.
1.2. Числа Фибоначчи и их свойства.
Древняя история богата выдающимися математиками. Многие достижения древней математической науки до сих пор вызывают восхищение остротой ума их авторов, а имена Евклида, Архимеда, Герона известны каждому образованному человеку.
Иначе обстоит дело с математикой средневековья. Кроме Виета, жившего в шестнадцатом столетии, и математиков более близких нам времен школьный курс математики не называет ни одного имени, относящегося к средним векам. Это, конечно, не случайно. Математика в эту эпоху развивалась чрезвычайно медленно, и крупных математиков тогда было очень мало. Тем больший интерес представляет сочинение «Liber abacci» («Книга об абаке»), написанная знаменитым итальянским математиком Леонардо из Пизы, который известен больше по своему прозвищу Фибоначчи (Fibonacci – сокращенное filius Bonacci, т. е. сын Боиаччи). Эта книга, написанная в 1202 г., дошла до нас во втором своем варианте, который относится к 1228 г.
«Liber abacci» представляет собой объемистый труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший заметную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими («арабскими») цифрами. Сообщаемый в «Liber abacci» материал поясняется на большом числе задач, составляющих значительную часть этого трактата. Рассмотрим одну такую задачу, помещенную на стр. 123-124 рукописи 1228 г.
«Сколько пар кроликов в один год от одной пары рождается?»
«Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения. Так как первая пара в первом месяце дает потомство, удвой, и, рождает и в следующем месяце, так что во втором месяце оказывается 3 пары; из них в следующем месяце 2 пары будут давать потомство, так что в третьем месяце родятся еще 2 пары кроликов, и число пар кроликов в этом месяце достигнет 5; из них в этом же месяце будут давать потомство 3 пары, и число пар кроликов в четвертом месяце достигнет 8; из них 5 пар произведут другие 5 пар, которые, сложенные с 8 парами, дадут в пятом месяце 13 пар; из них 5 пар, рожденных в этом месяце, не дают в том же месяце потомства, а остальные 8 пар рождают, так что в шестом месяце оказывается 21 пара; сложенные с 13 парами, которые родятся в седьмом месяце, они дают 34 пары; сложенные с 21 парой, рожденной в восьмом месяце, они дают в этом месяце 55 пар; сложенные с 34 парами, рожденными в девятом месяце, они дают 89 пар; сложенные вновь с 55 парами, которые рождаются в десятом месяце, они дают в этом месяце 144 пары; снова сложенные с 89 парами, которые рождаются в одиннадцатом месяце, они дают в этом месяце 233 пары; сложенные вновь с 144 парами, рожденными в последнем месяце, они дают 377 пар; столько пар произвела первая пара в данном месте к концу одного года.
Действительно, на этих полях ты можешь увидеть, как мы это делаем; именно, мы складываем первое число со вторым, т. е. 1 и 2; и второе с третьим; и третье с. четвертым; и четвертое с пятым; и так одно за другим, пока не сложим десятое с одиннадцатым, т. е. 144 с 233; и мы получим общее число упомянутых кроликов, т. е. 377; и так можно делать по порядку до бесконечного числа месяцев».
Построим алгебраическую модель задачи о кроликах и рассмотрим следующую числовую последовательность: , в которой u1 = u2 = 1, а каждый член последовательности, начиная с третьего, равен сумме двух предыдущих членов, то есть при всяком n > 2 выполняется равенство: .
Такие последовательности, в которых каждый член определяется как некоторая функция предыдущих, часто встречаются в математике и называются рекуррентными или, по-русски, возвратными последовательностями. Сам процесс последовательного определения элементов таких последовательностей называется рекуррентным процессом, а равенство (2) – возвратным (рекуррентным) уравнением [2].
Возвратная последовательность, задаваемая условием u1 = u2 = 1 и формулой (2) называется последовательностью Фибоначчи, а её члены –
числами Фибоначчи.
Перечислим основные свойства последовательности Фибоначчи.
1) Каждое следующее число, начиная с третьего равно сумме двух предыдущих.
2) Отношение каждого числа к последующему при увеличении порядкого номера все более и более стремится к 0,618.
3) Отношение каждого числа ряда к предыдущему стремится к 1,618.
Последовательность Фибоначчм асимптотически (пpиближаясь все медленнее и медленнее) стремится к некотоpому постоянному соотношению. Однако, это соотношение иppационально, то есть пpедставляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифp в дpобной части. Его невозможно выразить точно.
Если какой-либо член последовательности Фибоначчи pазделить на пpедшествующий ему pезультатом будет величина, колеблющаяся около иppационального значения 1.61803398875… и чеpез pаз то пpевосходящая, то не достигающая его. Hо даже затpатив на это Вечность, невозможно узнать сотношение точно, до последней десятичной цифpы. Kpаткости pади, мы будем пpиводить его в виде 1.618. Лука Пачиоли (сpедневековый математик) назвал его Божественной пpопоpцией. Cpеди его совpеменных названий есть такие, как Золотое сечение, Золотое сpеднее и oтношение веpтящихся квадpатов. Kеплеp назвал это соотношение одним из «сокpовищ геометpии». В алгебpе общепpинято его обозначение гpеческой буквой фи.
Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду, как арифметическому выражению закона золотого деления.
Учёные, анализируя дальнейшее применение этого числового ряда к природным феноменам и процессам, обнаружили, что эти числа содержатся буквально во всех объектах живой природы, в растениях, в животных и в человеке.
1.3 Спираль Фибоначчи
Спираль Фибоначчи – это некоторая кривая, которая огибает точку своего центра, приближаясь или удаляясь от неё, все зависит от направления, избранного вами. Эти фигуры могут быть как двухмерными, так и трехмерными, однако, если мы говорим о Фибоначчи, как о рыночной модели, то рассматривать можно только один вариант – двухмерный.
Когда строятся такие фигуры, то используется стартовая точка, построенная на плоскости, радиус выступает в роли непрерывной монотонной функции от угла.
Спираль Фибоначчи, отличается от Золотой пропорции и имеет точку начала. Беря начало в некоторой точке, такая фигура обычно разворачивается бесконечно долго.
У последовательности Леонардо есть интересные свойства. Ряд Фибоначчи отличается от Золотого Сечения, так как начинается с единицы или нуля и при этом стремится к Золотой пропорции.
Также он постоянно увеличивает точность. В некоторой точке (когда почти достигнута фи =1,618) уже невозможно найти разницу, которая прослеживалась между двумя спиралями. Понимание этого свойства Спирали Фибоначчи и определяет её удивительность.
Это поразительно, однако, строение спирали Фибоначчи можно наблюдать в большом количестве предметов и явлений.
2 Числа Фибоначчи в нашей жизни
2.1 Числа Фибоначчи в природе
С тех пор, как Фибоначчи открыл свою последовательность, были найдены много явлений природы, в которых его последовательность чисел прослеживается очень четко. Природа дает нам многочисленные примеры расположения предметов, описываемых числами Фибоначчи. Спиралевидное расположение листьев на ветках деревьев подметили давно. Выяснилось, что в расположении листьев на ветке (филлотаксис — листорасположение), в числе оборотов на стебле, в числе листьев в цикле проявляет себя ряд чисел Фибоначчи.
Чёткая, симметричная форма цветов также подчинена строгому закону.
У многих цветов количество лепесточков является числами из ряда Фибоначчи.
Встретить числовые закономерности в живой природе можно в различных спиральных формах, которыми так богат мир растений. Обычно можно усмотреть два вида спиралей. В одном спирали завиваются по часовой стрелке, а в другом против. Число «правых «и «левых» спиралей часто оказываются соседними числами Фибоначчи
Можно привести множество примеров.
Первый и очень яркий пример – это подсолнухи. Их семена расположены так, чтобы максимально использовать всю площадь соцветия, не теряя ни миллиметра. А расположены они в виде двух пересекающихся спиралей справа налево и наоборот. Пары этих спиралей встречаются разные, у меньших соцветий 13 и 21, 21 и 34, у больших 34 и 55, 55 и 89. И отклонений от этих пар быть не может.
Нечто подобное происходит и с ячейками ананаса: у него 8 правосторонних спиралей, 13 левосторонних и 21 вертикальная. И снова последовательность Фибоначчи.
В сосновой шишке, если хорошо присмотреться, можно увидеть две спирали, закручены одна по часовой стрелкой, а другая против. Число этих спиралей 8 и 13.
Количество лепестков во многих соцветиях совпадает с числами из этой последовательности, например, ирис имеет 3 лепестка, у примулы их 5, у амброзии полыннолистной — 13, у астр бывает 55 или 89 лепестков.
Листья на деревьях и других растениях распределены в последовательности, основанной на золотом числе, таким способом, чтобы получать максимум света и не мешать друг другу.
У многих бабочек отношения размеров грудной и брюшной части тела очень близки к золотому числу.
Раковины моллюсков закручены по спирали, и если измерить ее завитки, то их отношение постоянно и равно 1.618.
Спиралеобразно паук плетет паутину. По спирали закручивается ураган. Стадо северных оленей по тревоге разбегается по спирали. По спирали закручиваются волны, которые разбиваются об берега океана. Молекулы ДНK живых организмов закручены двойной спиралью. Гете называл эту спираль «кривой жизни».
2.2. Числа Фибоначчи в строении животных
Кроме растений, числа Фибоначчи проявляются в строении различных живых организмов. Например, морские звезды. Число лучей у них отвечает ряду чисел Фибоначчи и равно 5, 8, 13.
У хорошо знакомого комара – три пары ног, брюшко делится на 8 сегментов на голове 5 усиков – антенн. И опять мы видим числа 3,5,8, числа последовательности Фибоначчи.
2.3. Числа Фибоначчи в строении человека
Числа Фибоначчи отражают основную закономерность роста организмов, следовательно проявляются и в строении человеческого тела. Рассмотрим это поподробнее.
У человека одно туловище, одна голова, одно сердце и т. д. Многие части тела и органы парные, например, руки, ноги, глаза, почки. Из трех частей состоят ноги, руки, пальцы рук. На руках и ногах по пять пальцев, а рука вместе с пальцами состоит из восьми частей. Можно рассмотреть части тела и с другой стороны. У человека 2 руки, пальцы на каждой руке состоят из 3 фаланг (за исключением большого пальца). На каждой руке имеется по 5 пальцев, только 8 пальцев трехфаланговые. Все эти цифры 2, 3, 5 и 8 есть числа последовательности Фибоначчи. (Приложение 1, 2).
Позвоночник человека состоит из 34 позвонков. Как видно из приведенного перечисления частей человеческого тела, в его членении на части присутствуют все числа Фибоначчи от 1 до 34. Общее число костей скелета человека близко к 233, то есть отвечает еще одному числу Фибоначчи.
Числа Фибоначчи можно обнаружить и в «крови» у человека. Так распределение людей по трём группам крови отвечает отношениям чисел 8/ 21 /3.
Сердечная мышца сокращается до 0,618 от своей изначальной длины и нарушение этого числа при сокращении ведет к болезням сердца. А это число отражает одно из свойств чисел Фибоначчи. В результате математической обработки экспериментальных медицинских данных, появились отношения чисел, характеризующих сердечный цикл: 0,050; 0,081; 0,131; 0,210; 0,340. Мы видим, что они отражают последовательность ряда чисел Фибоначчи 5, 8, 13, 21, 34. В строении человеческого лица и кисти существуют и иные воплощения ряда Фибоначчи. (Приложение 1, 2).
Этот ряд получается, если провести измерения длин фаланг пальцев и расстояний между различными частями лица.
2.4. Числа Фибоначчи и золотой прямоугольник
Было отмечено, что числа Фибоначчи тесно связаны со спиралевидным строением многих представителей живой и неживой природы. Чтобы рассмотреть еще несколько таких примеров, необходимо познакомиться с так называемым «золотым прямоугольником». Золотой прямоугольник обладает многими необычными свойствами. Отрезав от золотого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, мы снова получим золотой прямоугольник меньших размеров.
Этот процесс можно продолжать до бесконечности. Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие золотые прямоугольники. Причем располагаться они будут по спирали, которая называется спираль Фибоначчи.
Эту спираль можно обнаружить в самых различных и неожиданных предметах и явлениях.
У большинства улиток, которые обладают раковинами, раковина растет в форме спирали. Раковины улиток подчиняются последовательности и спирали Фибоначчи.
Паук плетет паутину спиралеобразно. Интересно, что спиралью закручиваются ураган, облака циклона и это хорошо видно из космоса.
Числа Фибоначчи оказались и в спирали, описывающей изгиб гребня набегающей волны в океане, и в спирали, убегающей воды в раковине умывальника. Да и живём мы тоже в спирали, ведь галактика – это спираль, соответствующая спирали Фибоначчи.
На рисунке показаны относительные размеры Земли и Луны в масштабе.
Нарисуем радиус Земли. Проведем отрезок от центральной точки Земли до центральной точки Луны. Нарисуем отрезок для соединения двух данных отрезков, чтобы сформировать треугольник. Получаем золотой треугольник.
Сатурн показывает золотую пропорцию в нескольких ее измерениях
Диаметр Сатурна очень близко находится в отношении золотой пропорции с диаметром колец, как показано зелеными линиями. Радиус внутренней части колец находится в отношении, очень близком к с внешним диаметром колец, как показано синей линией.
Расстояние планет от Солнца также подчиняется золотой пропорции.
2.5 Числа Фибоначчи в архитектуре
В качестве примера ученые исследовали шедевры архитектуры, созданные по правилам «золотого сечения»: египетские пирамиды, Пантеон, Парфенон, Собор Нотр-Дам де Пари, храм Василия Блаженного и др.
Парфенон — одно из красивейших зданий в Древней Греции (5 в. до н.э.) — имеет 8 колонн и 17 по разным сторонам, отношение его высоты к длине сторон равно 0,618. Выступы на его фасадах сделаны по «золотому сечению» (фото ниже).
Одним из ученых, который придумал и успешно применял усовершенствование модульной системы пропорций для архитектурных объектов (так называемый «модулор»), — был французский архитектор Ле Корбюзье. В основу модулора положена измерительная система, связанная с условным делением на части человеческого тела.
Русский архитектор М. Казаков, построивший несколько жилых домов в Москве, а также здания сената в Кремле и Голицынской больницы (сейчас 1-я Клиническая им. Н. И. Пирогова), — был одним из архитекторов, которые использовали при проектировании и строительстве законы о золотом сечении.
2.6.Числа Фибоначчи в искусстве
В конце XIX – начале XX вв. появилось немало чисто формалистических теории о применении золотого сечения в произведениях искусства и архитектуры. С развитием дизайна и технической эстетики применение закона золотого сечения распространилось на конструирование машин, мебели и пр.
Пропорция, выражаемая числом Ф, по мнению многих исследований, является наиболее приятной для человеческого глаза.
Леонардо де Винчи считал, что идеальные пропорции человеческого тела должны быть связаны с числом Ф. Деление отрезка в отношении Ф он назвал «золотым сечением». В эпоху возрождения «золотое сечение» было очень популярно среди художников, скульпторов и архитекторов. Размеры картины было принято брать такими, чтобы отношение ширины к высоте равнялось Ф. Этот термин сохранился до наших дней, и само «золотое сечение» по прежнему играет важную роль в искусстве. Им руководствовался, например, великий архитектор Ле Корбюзье.
Прямоугольник с таким отношением сторон стали называть «золотым прямоугольником».
Форму «золотого сечения» придавали книгам, столам почтовым открыткам. В дальнейшем книгам и другим бумажным изделиям стали чаще придавать форму прямоугольника с отношением сторон корень из двух. Это связано с тем, что при перегибании такого прямоугольника по средней линии образуются два прямоугольника с тем же соотношением сторон.
Число золотого сечения Ф обладает какой-то странной неуловимостью. Оно появляется в различных проекциях, так и не давая ответа на вопрос, как это число связано с тем или иным явлением. Интерес к мистическому числу Ф достаточно периодичен. Он возникает с обнаружением нового проявления этого числа в каком-либо явлении природы.
Проходит время, и интерес к нему спадает. Но ненадолго. Числу Ф находят всё новое и новое применение, но оно так и остается недоступным для ясного и полного понимания его свойств и степени его влияния на окружающий мир.
2.7. Числа Фибоначчи и фотография
Применительно к фотографическому искусству правило золотого сечения делит кадр двумя горизонтальными и двумя вертикальными линиями на 9 неравных прямоугольников. Чтобы облегчить себе задачу съемки сбалансированных изображений, фотографы немного упростили задачу и стали делить кадр на 9 равных прямоугольников в соответствии с числами Фибоначчи. Так правило золотого сечения трансформировалось в правило третей, которое относится к одному из принципов построения композиции.
В видоискателях современных цифровых камер точки фокусировки расположены на позициях 2/8 или на воображаемых линиях, делящих кадр по правилу золотого сечения.
Наиболее удачным примером для демонстрации является пейзаж. Принцип композиции заключается в том, что небо и суша (либо водная гладь) должны иметь соотношение 1:2. Одну треть кадра следует отвести под небо, а две трети под сушу или наоборот.
Практическое исследование
Вторая часть нашего практического исследования заключается в конкретных подсчетах и измерениях.
Числа Фибоначчи в строении подсолнуха
Первым для изучения мы взяли подсолнух и сосчитали количество спиралей, идущих в одну сторону и количество спиралей в другую сторону. Правых спиралей, они закрашены красным, получилось 34, левых, они закрашены синим – 55. Эти числа 34 и 55 являются соседними в последовательности Фибоначчи.
Числа Фибоначчи в строении еловой и сосновой шишек
Продолжая исследование, числа, входящие в ряд Фибоначчи мы увидели в сосновых и еловых шишках. Подсчет спиралей выявил следующие результаты. Замечаем две серии спиралей Фибоначчи: одна — по часовой стрелки, другая — против, их число 8 и 13.
Числа Фибоначчи в строении ананаса
На фотографиях показано как мы проводили подсчеты чешуек на кожуре ананаса. Нами получены числа: 8 и 13. Как мы снова можем убедиться, эти числа являются членами последовательности Фибоначчи.
Числа Фибоначчи в ветке дерева
Последовательность ответвлений, идущих по стволу растений, мы подсчитывали, рассматривая ветку дерева. Положив её на ватман, мы провели горизонтальные линии, соответствующие пазам выхода веток, и посчитали их количество. Получили следующие данные: 1,2,3,5,8… Полученный ряд является частью ряда Фибоначчи.
ЗАКЛЮЧЕНИЕ
Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве и архитектуре, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления.
Таким образом, суммарной последовательностью Фибоначчи легко можно трактовать закономерность проявлений Золотых чисел, встречаемых в природе. Эти законы действуют в независимости от нашего знания, от чьего-то желания принимать или не принимать их.
В своей работе, мы, конечно же, не можем до мельчайших подробностей изложить суть этого вопроса, но мы постарались отразить наиболее интересные и весомые аспекты. Мы рассказали о Леонардо Пизанском и дали понятное определение последовательности Фибоначчи; затем, на ярких примерах показали присутствие чисел Фибоначчи и Золотого сечения в разных сферах нашей жизни; выяснили что такое «Закон сохранения света», «Платоновы тела» и как они связаны с последовательностью.
Золотое сечение и последовательность чисел Фибоначчи помогают учёным описывать строение галактик и планетарных систем, а некоторые социологи начинают их использовать для прогнозирования различных катаклизмов, обусловленных массовой истерией (войн, беспорядков, революций и т.д).
Одна и та же закономерность используется в совершенно разных областях, практически не связанных между собой, а это значит, что она является универсальной.
Экономика, как и другие общественные сферы жизни человека поддаются определенным законам, несмотря на свою определенную непредсказуемость и зависимость от многих факторов современные экономические системы (в теории волнового анализа) поддаются законам «уровней Фибоначчи» построенных на основе одноименной последовательности.
С появлением финансовых рынков математики и статисты попробовали при помощи золотых чисел Фибоначчи строить уровни поддержки и сопротивления. Логично, ведь если поведение социума подчиняется божественной пропорции, разумно предположить, что и в действиях участников рынка также будет прослеживаться данная закономерность.
Как известно, эксперимент оказался удачным, и сегодня золотые числа Фибоначчи на Форекс используются для построения сеток, расширений, вееров, каналов и временных зон. В частности, при помощи первого инструмента можно найти сильные уровни, на которых следует ждать завершения коррекции, сформированной по отношению к последнему импульсу.
Мы убеждены, что данная тема будет актуальна еще долгое время, и будут открываться все новые и новые факты, подтверждающие присутствие и влияние суммационной последовательности Фибоначчи на нашу жизнь.
Список литературы
1. Маркушевич, А. И. Возвратные последовательности. / А. И. Маркушевич.М.: Наука, 1975.
2. Воробьёв, Н. Н. Числа Фибоначчи. / Н. Н. Воробьёв. М.: Наука, 1978.
3. Савин, А. П. Энциклопедический словарь юного математика. / А. П. Савин. М.: Педагогика, 1989.
4. Мохнаткина, К. В. Последовательности в школьном курсе. / К. В. Мохнаткина // Учитель – ученик: проблемы, поиски, находки: Сборник научных трудов: Выпуск 3. Саратов: Научная книга, 2005. С. 63-67.
5. Мохнаткина, К. В. Изучение последовательностей в старших классах. / К. В. Мохнаткина // Учитель – ученик: проблемы, поиски, находки: Сборник научных трудов: Выпуск 4. Саратов: Научная книга, 2005. С. 59-63.
1.http://fb.ru/article/323642/chisla-fibonachchi-i-zolotoe-sechenie-vzaimosvyaz
2.https://studwood.ru/1851811/matematika_himiya_fizika/biografiya_fibonachchi
3.https://multiurok.ru/files/issliedovatiel-skaia-rabota-po-matiematikie-chisla-fibonachchi.html
4.http://fibonachi.gimnaziayanaul.edusite.ru/p11aa1.html
Приложение 1.
Золотые пропорции в частях тела человека.
Приложение 2
Просмотров работы: 1402
Последовательность чисел Фибоначчи: формула, таблица, золотое сечение
Числа Фибоначчи – это последовательность чисел, которая начинается с цифр 0 и 1, а каждое последующее значение является суммой двух предыдущих.
Формула последовательности Фибоначчи
Например:
- F0 = 0
- F1 = 1
- F2 = F1+F0 = 1+0 = 1
- F3 = F2+F1 = 1+1 = 2
- F4 = F3+F2 = 2+1 = 3
- F5 = F4+F3 = 3+2 = 5
Золотое сечение
Соотношение двух последовательных чисел Фибоначчи сходится к золотому сечению:
где φ – это золотое сечение = (1 + √5) / 2 ≈ 1,61803399
Чаще всего, это значение округляют до 1,618 (или 1,62). А в округленных процентах пропорция выглядит так: 62% и 38 %.
Таблица последовательности Фибоначчи
| n | Fn |
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
| 9 | 34 |
| 10 | 55 |
| 11 | 89 |
| 12 | 144 |
| 13 | 233 |
| 14 | 377 |
| 15 | 610 |
| 16 | 987 |
| 17 | 1597 |
| 18 | 2584 |
| 19 | 4181 |
| 20 | 6765 |
microexcel.ru
C-код (Си-код) функции
double Fibonacci(unsigned int n)
{
double f_n =n;
double f_n1=0.0;
double f_n2=1.0;
if( n > 1 ) {
for(int k=2; k<=n; k++) {
f_n = f_n1 + f_n2;
f_n2 = f_n1;
f_n1 = f_n;
}
}
return f_n;
}
Как числа Фибоначчи выражаются в природе?
Вы не найдете чисел Фибоначчи повсюду в мире природы — многие растения и животные выражают разные числовые последовательности. И то, что к объекту можно применить ряд чисел, не обязательно означает, что между фигурами и реальностью есть какая-то корреляция. Как и в случае с нумерологическими суевериями, например, когда известные люди умирают группами по три штуки, иногда совпадение оказывается просто совпадением.
Но числа Фибоначчи встречаются в природе достаточно часто, чтобы доказать, что они отражают некоторые естественные закономерности.Обычно вы можете обнаружить их, изучая манеру роста различных растений. Вот несколько примеров:
Семенные головки, шишки, фрукты и овощи: Посмотрите на ряд семян в центре подсолнечника, и вы заметите то, что похоже на спиральные узоры, изгибающиеся влево и вправо. Удивительно, но если вы посчитаете эти спирали, ваша сумма будет числом Фибоначчи. Разделите спирали на те, которые направлены влево и вправо, и вы получите два последовательных числа Фибоначчи. Вы можете расшифровать спиральные узоры в шишках, ананасах и цветной капусте, которые также отражают последовательность Фибоначчи таким образом.
Цветы и ветви: Некоторые растения выражают последовательность Фибоначчи в своих точках роста , местах, где ветви деревьев образуются или разделяются. Один ствол растет до тех пор, пока не образуется ветка, в результате чего образуются две точки роста. Затем основной ствол дает еще одну ветвь, в результате чего образуются три точки роста. Затем ствол и первая ветвь производят еще две точки роста, в результате чего общее количество достигает пяти. Эта модель продолжается, следуя числам Фибоначчи.Кроме того, если вы посчитаете количество лепестков на цветке, вы часто обнаружите, что общая сумма является одним из чисел в последовательности Фибоначчи. Например, у лилий и ирисов по три лепестка, у лютиков и диких роз — по пять, у дельфиниумов — по восемь лепестков и так далее.
Медоносные пчелы: Колония медоносных пчел состоит из королевы, нескольких трутней и множества рабочих. У пчел-самок (маток и рабочих) есть двое родителей, трутень и матка. Дроны же вылупляются из неоплодотворенных яиц.Это означает, что у них только один родитель. Следовательно, числа Фибоначчи выражают генеалогическое древо дрона в том смысле, что у него есть один родитель, два дедушки и бабушки, три прадедушки и т. Д.
Человеческое тело: Внимательно посмотрите на себя в зеркало. Вы заметите, что большинство частей вашего тела следуют цифрам один, два, три и пять. У вас один нос, два глаза, по три сегмента на каждую конечность и по пять пальцев на каждой руке. Пропорции и размеры человеческого тела также можно разделить по золотому сечению.Молекулы ДНК следуют этой последовательности, имея длину 34 ангстрем и ширину 21 ангстрем для каждого полного цикла двойной спирали [источник: Йовонович].
Почему так много естественных моделей отражают последовательность Фибоначчи? Ученые размышляли над этим вопросом веками. В некоторых случаях корреляция может быть просто совпадением. В других ситуациях это соотношение существует потому, что эта конкретная модель роста развивалась как наиболее эффективная. Для растений это может означать максимальное воздействие на светолюбивые листья или максимальное расположение семян.
Чтобы узнать больше о золотом сечении, кроликах Фибоначчи и других мысленных экспериментах, просмотрите ссылки на следующей странице.
10.4: Числа Фибоначчи и золотое сечение
Известной и важной последовательностью является последовательность Фибоначчи, названная в честь итальянского математика Леонардо Пизано по прозвищу Фибоначчи, жившего с 1170 по 1230 год. Эта последовательность:
\ [\ {1,1,2,3,5,8,13,21,34,55, \ ldots \ ldots \ ldots \} \]
Эта последовательность определяется рекурсивно. Это означает, что каждый термин определяется предыдущими терминами. |
и так далее.
Последовательность Фибоначчи определяется, для всех, когда и. |
Другими словами, чтобы получить следующий член в последовательности, добавьте два предыдущих члена.
\ [\ {1,1,2,3,5,8,13,21,34,55,55 + 34 = 89,89 + 55 = 144, \ cdots \} \]
Обозначения, которые мы будем использовать для представления последовательности Фибоначчи, следующие:
\ [f_ {1} = 1, f_ {2} = 1, f_ {3} = 2, f_ {4} = 3, f_ {5} = 5, f_ {6} = 8, f_ {7} = 13, f_ {8} = 21, f_ {9} = 34, f_ {10} = 55, f_ {11} = 89, f_ {12} = 144, \ ldots \]
Пример \ (\ PageIndex {1} \): Рекурсивный поиск чисел Фибоначчи
Найдите 13, 14 и 15 числа Фибоначчи, используя приведенное выше рекурсивное определение последовательности Фибоначчи.
Во-первых, обратите внимание, что уже есть 12 чисел Фибоначчи, перечисленных выше, поэтому, чтобы найти следующие три числа Фибоначчи, мы просто складываем два предыдущих члена, чтобы получить следующий член, как указано в определении.
Следовательно, 13-е, 14-е и 15-е числа Фибоначчи равны 233, 377 и 610 соответственно.
Вычисление членов последовательности Фибоначчи может быть утомительным при использовании рекурсивной формулы, особенно при нахождении членов с большим n.К счастью, математик Леонард Эйлер открыл формулу для вычисления любого числа Фибоначчи. Эта формула была утеряна примерно на 100 лет и была заново открыта другим математиком по имени Жак Бине. Исходная формула, известная как формула Бине, приведена ниже.
Формула Бине : n-е число Фибоначчи определяется по следующей формуле: \ [f_ {n} = \ frac {\ left [\ left (\ frac {1+ \ sqrt {5}} {2} \ right) ^ {n} — \ left (\ frac {1- \ sqrt { 5}} {2} \ right) ^ {n} \ right]} {\ sqrt {5}} \] |
| Формула Бине является примером последовательности , явно определенной .Это означает, что условия последовательности не зависят от предыдущих условий. |
Иногда вместо приведенной выше формулы иногда используется несколько более удобная и упрощенная версия формулы Бине.
Упрощенная формула Бине : n-е число Фибоначчи определяется по следующей формуле: Примечание. Символ означает «округление до ближайшего целого числа.” |
Пример \ (\ PageIndex {2} \): поиск явно
Найдите ценность использования упрощенной формулы Бине.
Рисунок \ (\ PageIndex {1} \): Работа калькулятора дляПример \ (\ PageIndex {3} \): поиск Явно
Найдите значение , используя упрощенную формулу Бине.
Рисунок \ (\ PageIndex {2} \): Работа калькулятора дляПример \ (\ PageIndex {4} \): Поиск Явно
Найдите значение , используя упрощенную формулу Бине.
Рисунок \ (\ PageIndex {3} \): Работа калькулятора дляМы можем найти числа Фибоначчи в природе вокруг нас. Количество ветвей на некоторых деревьях или количество лепестков некоторых ромашек часто являются числами Фибоначчи
.Рисунок \ (\ PageIndex {4} \): числа Фибоначчи и ромашки
а. Ромашка с 13 лепестками б. Ромашка с 21 лепестком
а. б.
(Ромашки, н.о.)
Числа Фибоначчи также появляются в спиральных структурах роста, таких как количество спиралей на кактусе или на грядках с семенами подсолнечника.
Рисунок \ (\ PageIndex {5} \): числа Фибоначчи и спиральный рост
а. Кактус с 13 спиралями по часовой стрелке b. Подсолнечник с 34 спиралями по часовой стрелке и 55 спиралями против часовой стрелки
а. б.
(Кактус, н.о.) (Подсолнечник, н.о.)
Другой интересный факт возникает при рассмотрении соотношений последовательных чисел Фибоначчи.
Похоже, что эти коэффициенты приближаются к цифре. Число, к которому приближаются эти соотношения, — это особое число, называемое золотым соотношением, которое обозначается (греческой буквой фи).Вы видели это число в формуле Бине.
Золотое сечение: \ [\ phi = \ frac {1+ \ sqrt {5}} {2} \] Золотое сечение имеет десятичное приближение \ (\ phi = 1,6180339887 \). |
Золотое сечение — это особое число по разным причинам. Его также называют божественной пропорцией, и он проявляется в искусстве и архитектуре.Некоторые утверждают, что это самое приятное для глаз соотношение. Чтобы найти это соотношение, греки разрезали отрезок на две части и позволили меньшему отрезку равняться одной единице. Самый приятный крой — это когда отношение полной длины к длинной части такое же, как отношение длинной части к короткой 1.
1
перемножим, чтобы получить
переставить, чтобы получить
решите это квадратное уравнение, используя формулу корней квадратного уравнения.
Золотое сечение — это решение квадратного уравнения, означающее, что оно обладает свойством. Это означает, что если вы хотите возвести в квадрат золотое сечение, просто добавьте к нему единицу. Чтобы проверить это, просто подключите.
Сработало!
Еще одна интересная связь между золотым сечением и последовательностью Фибоначчи возникает при использовании степеней.
И так далее.
Обратите внимание, что коэффициенты и числа, добавленные к члену, являются числами Фибоначчи.{n} = f_ {n} \ phi + f_ {n-1} \)
, где \ (f_ {n} \) — это n-е число Фибоначчи, а \ (\ phi \) — это золотое сечение .
Пример \ (\ PageIndex {5} \): Степени золотого сечения
Найдите следующее, используя правило золотой силы: a. и б.
чисел Фибоначчи: наука о растениях
Магические числа, составляющие внешний вид растения
От количества шишек и колец на стволе дерева до количества листьев и ветвей на растении — образование растений и естественных форм может быть не таким случайным, как кажется.
Специальная последовательность чисел, известная как Фибоначчи, открывает секретный код, который может объяснить, почему так много наших любимых растений выглядят именно так.
Формула Фибоначчи
Фибоначчи — это последовательность чисел с простой формулой: каждое число — это сумма двух предыдущих чисел, сложенных вместе. Другими словами, он начинается 1 1 2 3 5 8 13 21… и продолжается так до бесконечности.
Последовательность названа в честь итальянского математика -го -го века Леонардо Пизанского, известного как Фибоначчи.Но именно в 19, и годах было обнаружено, что последовательность может быть обнаружена в образовании многих растений, цветов и природных форм.
Математический состав растений
Эти магические числа не являются мистическим кодом, они играют функциональную роль в росте растений, обеспечивая их наиболее эффективный рост.
Например,числа Фибоначчи можно найти в расположении листьев вокруг стебля. Это максимизирует пространство для каждого листа, и его можно найти в плотно упакованных листьях суккулентов, а также в капусте, которые имеют форму «золотой спирали», аналогичной форме розы — еще один фаворит Фибоначчи.
В случае формирования листьев (также известного как филлотаксис) правило Фибоначчи заключается не только в упаковке максимального количества листьев, но и в том, что в некоторых случаях оно помогает максимально увеличить пребывание на солнце.
По схожим причинам ветвящиеся растения также демонстрируют числа Фибоначчи, обеспечивая максимальное пространство для количества ветвей и одновременно увеличивая пребывание на солнце.
Взломать код
Этот скрытый код может отображаться даже на стволах деревьев. Некоторые хвойные деревья, например, показывают числа Фибоначчи на выступах на стволах, а пальмы показывают их в кольцах стволов.
Дважды специальный
Сосновые шишки также являются хорошо известными формами Фибоначчи, показывающими двойной набор спиралей — одну, идущую по часовой стрелке, а другую — в противоположном направлении — подобных спирали подсолнечника. Когда подсчитываются два набора спиралей, они складываются в соседние числа Фибоначчи.
Заметили ли вы какие-нибудь ботанические формы Фибоначчи? Сообщите нам, что вы нашли на нашей странице в Facebook.
Последовательность Фибоначчи в природе • Вместо
Спираль Фибоначчи проявляется не только в идеальной оболочке наутилуса…
Jitze Couperus / Flickr (creative Commons)… но в событиях и объектах, рассматриваемых издалека.
Энергетическая система в форме фибоначчи движется с ограниченными потерями. Ураган Ирен.
Что такое последовательность Фибоначчи?
Математика золотого сечения и последовательности Фибоначчи тесно взаимосвязаны. Последовательность Фибоначчи — это рекурсивная последовательность, созданная сложением двух предыдущих чисел в последовательности: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987…
Вот хорошее видео-объяснение от SciShow. Он указывает, что части растений, лепестки и ряды семян почти всегда учитываются до числа Фибоначчи.
Если бы вы нарисовали линию, начинающуюся в правом нижнем углу золотого прямоугольника внутри первого квадрата, а затем касались каждого последующего множества квадратов за пределами углов, вы бы создали спираль Фибоначчи.
Насколько часто в природе встречается последовательность Фибоначчи?
Фибоначчи проявляется в самых маленьких и самых больших объектах в природе. Это способ передачи информации очень эффективным образом. Здесь микроскопический вид яичника удильщика.Конкурс Nikon «Это маленький мир».
Спирали — самая распространенная форма галактик. Галактики группируются в сверхскопления, а сверхскопления группируются в стенах. Эти стенки или волокна многочисленных сверхскоплений, связанных гравитацией и разделенных большими пустотами, являются крупнейшими из известных структур во Вселенной.
Пыль Млечного Пути мешает нам увидеть глубину этих волокон или листов, поэтому мы еще не знаем точную форму этих стен. Более подробную информацию можно найти на Космическом телескопе.
Роберт Салливан / Flickr (Creative Commons)Деление раковых клеток. Эта составная конфокальная микрофотография использует покадровую микроскопию, чтобы показать, что раковая клетка (HeLa) подвергается делению (митозу). ДНК показана красным цветом, а клеточная мембрана — голубым. Круглая ячейка в центре имеет диаметр 20 микрон.
Это первая часть серии видео из трех частей от «математика-любителя» Ви Харта, объясняющих математику, лежащую в основе последовательности Фибоначчи. В части 1 показано, как нарисовать последовательность, и показано, как это сделать на шишках и ананасах.
18 Удивительные примеры последовательности Фибоначчи в природе
Вы можете быть удивлены, увидев, сколько мест появляется последовательность Фибоначчи. Вот всего 18 примеров, но мы призываем вас найти больше в своей повседневной жизни (или в саду)!
1) Куриное яйцо
Изображение, изначально найденное на holistichouseplans.comФибоначчи как отправная точка жизни.
2) Романская брокколи
Jitze Couperus / Flickr (Creative Commons)Романская брокколи — яркий пример Фибоначчи.Каждый узел представляет собой собственную спираль Фибоначчи.
3) Растение алоэ
Спиральное алоэ. Многочисленные кактусы отображают спираль Фибоначчи. Вы можете увидеть, как каждый набор листьев по спирали выходит наружу.
4) Спиральный перец чили
Питер-Эшли Джексон / Flickr (cReative Commons)Этот перец превратился в спираль Фибоначчи.
5) Подсолнечник
Айко, Томас и Джульетта + Айзек / Flickr (Creative Commons)Подсолнечник. На этой фотографии спираль Фибоначчи немного более тонкая, но вы все равно можете увидеть спираль в неоткрытых цветочках диска.
6) Рок Дейзи
Мальборо Рок Дейзи Сид Мосделл. И снова спираль видна в дисковых соцветиях цветка.
7) Сосновая шишка
Все сосновые шишки отображают последовательность Фибоначчи. Умбо на шишках увеличивается в размерах по мере того, как вы движетесь наружу, отображая спираль Фибоначчи.
8) Хвост хамелеона
Хвост этих существ естественным образом закручивается в спираль Фибоначчи.
9) Американская гигантская многоножка
Служба рыболовства и дикой природы США / Flickr (Creative Commons)Американская гигантская многоножка.Считается, что фибоначчи — это конструкция наименьшего сопротивления.
10) Гусеница-монарх
Гусеница-монарх собирается сформировать куколку.
11) Pangolin
Wildlife Alliance / Flickr (Creative Commons)Фибоначчи и броня = очень безопасно. Панголин способен защитить свое мягкое низ живота, образуя спираль Фибоначчи.
12) Двойной Фибоначчи
ДЖИМ, ФОТОГРАФ / ФЛИКР (ТВОРЧЕСКИЕ ОБЫЧНЫЕ)Этот цветок показывает две спирали Фибоначчи.Можно смутно увидеть, как из центра распустившихся цветочков диска образуются спирали.
13) Кору
Фибоначчи в спорах. Скрипач или кору.
14) Улитки и отпечатки пальцев
Улитки и отпечатки пальцев. Изображения взяты с сайта 123rf и первоначально «artcatalyst.blogspot.com/2011/04/fibonacci-sequence-mat Mathematics-nature.html» (соответственно). У обоих есть отчетливая спираль Фибоначчи.
15) Известное искусство
Фибоначчи в книге «Большая волна у Канагавы».«Кажется, даже известное искусство не может избежать последовательности Фибоначчи.
Фотография, первоначально найденная на «http://artcatalyst.blogspot.com/2011/04/fibonacci-sequence-mat Mathematics-nature.html»
16) Падающая вода
Вода принимает форму последовательности Фибоначчи в течение многих События. Другой пример — вихрь.
17) Население
Один блоггер применил последовательность Фибоначчи к плотности населения и площади суши. В Африке большинство густонаселенных городов приходится на то, что предсказывает спираль, или близко к нему.
18) Окаменелость ракушки
Hitchster / Flickr (cReative Commons)Ископаемая ракушка с последовательностью Фибоначчи. Вы можете видеть, как оболочка росла, формировалась спираль Фибоначчи.
Кем был Фибоначчи?
Последовательность Фибоначчи названа в честь Леонардо Пизанского, известного как Фибоначчи. Хотя Фибоначчи впервые представил эту последовательность западному миру в 1202 году, индийские математики заметили ее еще в шестом веке.
Фибоначчи определяет, как плотность ветвей увеличивается вверх по стволу дерева, расположение листьев на стволе и расположение чешуек сосновой шишки.Тем не менее, вы не увидите Фибоначчи повсюду, поскольку в природе существует множество различных методов и оттенков выживания.
Повесьте Фибоначчи у себя дома
Эти отпечатки с Art.com можно распечатать любого размера — они будут обрамлять их для вас, или вы можете распечатать прямо на холсте. Нам действительно повезло с их отпечатками; доставка быстрая, а распечатки хорошего качества. Они начинаются примерно с 25 долларов за штуку.
Большая волна
Это «Великая волна» Кацусики Хокусая.Прекрасный пример спирали Фибоначчи в искусстве.
Спираль Фибоначчи
Спираль Фибоначчи Сеймура. Если вам нравится более упрощенный вид, этот рисунок спирали Фибоначчи может вам больше подойти.
Раковина Наутилуса
Раковина Наутилуса с Art.comКрупный план спиралей ракушки Наутилуса, сделанный Эллен Камп. Естественное изображение спирали Фибоначчи, отлично подходит для тех, кто увлекается математикой и природой.
Лучшие книги о Фибоначчи и последовательности Фибоначчи
Увлекательно! Обязательно смотреть!
Математик Артур Бенджамин исследует скрытые свойства этого странного и чудесного набора чисел — ряда Фибоначчи.
Оцените этот пользовательский генератор спирали Фибоначчи — chromatism.net
Последовательность Фибоначчи | Блестящая вики по математике и науке
Подобно каталонским числам, числа Фибоначчи учитывают многие типы комбинаторных объектов. Вот четыре примера.
(1) Fn F_n Fn — количество композиций n − 1 n-1 n − 1, состоящих из 1 11 и 2 22. (Композиция n − 1n-1n − 1 — это выражение n − 1 n-1n − 1 как суммы частей, причем порядок частей имеет значение.) Например,
5 = 1 + 1 + 1 + 1 + 1 = 1 + 1 + 1 + 2 = 1 + 1 + 2 + 1 = 1 + 2 + 1 + 1 = 2 + 1 + 1 + 1 = 1 + 2 + 2 = 2 + 1 + 2 = 2 + 2 + 1, \ begin {выровнено} 5 & = 1 + 1 + 1 + 1 + 1 \\ & = 1 + 1 + 1 + 2 \\ & = 1 + 1 + 2 + 1 \\ & = 1 + 2 + 1 + 1 \\ & = 2 + 1 + 1 + 1 \\ & = 1 + 2 + 2 \\ & = 2 + 1 + 2 \\ & = 2 + 2 + 1, \ end {выровнен} 5 = 1 + 1 + 1 + 1 + 1 = 1 + 1 + 1 + 2 = 1 + 1 + 2 + 1 = 1 + 2 + 1 + 1 = 2 + 1 + 1 + 1 = 1 + 2 + 2 = 2 + 1 + 2 = 2 + 2 + 1,
, поэтому F6 = 8. F_6 = 8. F6 = 8.
(2) Fn F_n Fn — количество способов выложить доску размером 2 × (n − 1) 2 \ times (n-1) 2 × (n − 1) плиткой 1 × 2 1 \ times 21 × 2 домино .
(3) Fn F_n Fn — количество двоичных последовательностей длины n − 2 n-2n − 2 без последовательных 0 00.
(4) Fn F_n Fn — количество подмножеств {1,2,…, n − 2} \ {1,2, \ ldots, n-2 \} {1,2,…, n − 2} которые не содержат пары последовательных чисел.
Чтобы увидеть, что числа Фибоначчи подсчитывают эти объекты, пусть количество объектов равно Gn G_n Gn и покажет, что Gn = Gn − 1 + Gn − 2 G_n = G_ {n-1} + G_ {n-2} Gn = Gn − 1 + Gn − 2. Затем убедитесь, что F1 = G1 F_1 = G_1F1 = G1 и F2 = G2 F_2 = G_2 F2 = G2, и доказательство завершено.
Например, чтобы доказать (4), начните с G1 = 1, G2 = 1, G3 = 2, G4 = 3 G_1 = 1, G_2 = 1, G_3 = 2, G_4 = 3 G1 = 1, G2 = 1, G3 = 2, G4 = 3, и тогда предположим, что SSS является подмножеством {1,2,…, n − 2} \ {1,2, \ ldots, n-2 \} {1,2, …, N − 2} без каких-либо последовательных номеров.Существует Gn − 1 G_ {n-1} Gn − 1 таких множеств S SS, которые не содержат n − 2 n-2 n − 2. Если SSS содержит n − 2 n-2n − 2, то он не содержит n − 3 n-3n − 3, поэтому SSS получается путем взятия подмножества {1,2,…, n − 4} \ {1 , 2, \ ldots, n-4 \} {1,2,…, n − 4} и добавление n − 2 n-2n − 2. Итак, существует Gn − 2 G_ {n-2} Gn − 2 таких множеств S SS. Это доказывает, что Gn = Gn − 1 + Gn − 2, G_n = G_ {n-1} + G_ {n-2}, Gn = Gn − 1 + Gn − 2, что и требовалось.
Отправьте свой ответ
Состав n n n — это выражение n n n как суммы необязательно различных положительных целых чисел, где порядок имеет значение.Обратите внимание, что n = n n = n n = n считается составом n n n.
Пусть Cn C_n Cn будет количеством композиций из n n n без части, равной 1.
Например, C6 = 5 C_6 = 5 C6 = 5, потому что 6 = 6 = 4 + 2 = 3 + 3 = 2 + 4 = 2 + 2 + 2. 6 = 6 = 4 + 2 = 3 + 3 = 2 + 4 = 2 + 2 + 2,6 = 6 = 4 + 2 = 3 + 3 = 2 + 4 = 2 + 2 + 2.
Найдите C15 C_ {15} C15.
Отправьте свой ответ
Клоун может подняться по лестнице по одной или по двум ступенькам.\ text {th}, 10-е, он поднялся по всей лестнице; то есть последняя ступенька — второй этаж.
Бонус: Обобщите.
Отправьте свой ответ
Числа Фибоначчи даются
- F (0) = 0F (0) = 0F (0) = 0
- F (1) = 1F (1) = 1F (1) = 1
- F (n) = F (n — 1) + F (n — 2).F (n) = F (n-1) + F (n-2). F (n) = F (n-1) + F (n-2).
Итак, первые несколько: 0,1,1,2,3,5,8,13.0, 1, 1, 2, 3, 5, 8, 13.0,1,1,2,3,5,8, 13.
Если мы обобщим это на отрицательные числа, что будет F (−8)? F (-8)? F (−8)?
Последовательность Фибоначчи: примеры, золотое сечение и природа — видео и стенограмма урока
Золотое сечение
Золотое сечение , представленное греческой буквой фи, приблизительно равно 1.618. Золотое сечение, как и Пи, — это иррациональное число, которое продолжает существовать. Фактическое значение выглядит так: 1.618033988764989. . .
Вам может быть интересно, как последовательность Фибоначчи соотносится с этим числом. Покажи нам.
Начнем с деления пар чисел в последовательности Фибоначчи. Мы пропустим ноль и начнем с пары единиц. 1/1 = 1. Следующая пара — это один и два. 2/1 = 2. В каждой паре мы делим большее на меньшее число. Давайте продолжим и посмотрим, куда это нас приведет:
| Пара Фибоначчи | Результат |
|---|---|
| 2 и 3 | 3/2 = 1.5 |
| 3 и 5 | 5/3 = 1,6666. . . |
| 5 и 8 | 8/5 = 1,6 |
| 8 и 13 | 13/8 = 1,625 |
| 13 и 21 | 21/13 = 1,6154. . . |
| 21 и 34 | 34/21 = 1,619. . . |
| 34 и 55 | 55/34 = 1,618. . . |
| 55 и 89 | 89/55 = 1.618.. . |
| 89 и 144 | 144/89 = 1,618. . . |
По мере того, как числа становятся больше, начинают происходить интересные вещи. Результат деления пар чисел дает приблизительное значение золотого сечения 1,618. . .
С математической точки зрения последовательность Фибоначчи сходится к по золотому сечению. Это означает, что по мере роста последовательности Фибоначчи, когда вы делите пару чисел из последовательности, результат будет становиться все ближе и ближе к фактическому значению золотого сечения.Посмотрев на таблицу, вы можете увидеть, что, начиная с пары 34 и 55, результат имеет точность до трех знаков после запятой. По мере того, как пары становятся больше, результат будет более точным до десятичной дроби.
Природа
Последовательность Фибоначчи приближается к золотому сечению, которое можно найти в мире природы. Вы можете увидеть это на собственном теле, в том, как растут ракушки, и в количестве лепестков в цветках. Давайте посмотрим на эти примеры из реальной жизни.
Взгляните на свои пальцы.Обратите внимание, что каждый палец состоит из трех частей. Если вы измерите каждую секцию и разделите пары секций, вы получите приблизительное значение золотого сечения. Если наименьшая часть вашего пальца измеряет одну единицу, то нижняя часть будет иметь размер примерно две единицы, а третья часть будет иметь размер примерно три единицы. Обратите внимание, как каждое измерение соответствует числу Фибоначчи.
Ракушки растут по последовательности Фибоначчи.Если вы выложите квадраты с размерами, соответствующими последовательности Фибоначчи (1, 1, 2, 3, 5 и т. Д.), И начертите спираль, которая соединяется с каждым внешним краем, вы увидите, как формируется морская ракушка.
Вы также увидите числа Фибоначчи в том, как цветы растут на своих лепестках. У орхидеи, например, несколько слоев лепестков, и каждый слой соответствует числу Фибоначчи. Посмотрите на изображение орхидеи, и вы увидите слой из двух лепестков, затем слой из трех лепестков, за которым следует внешний слой из пяти лепестков.
Резюме урока
Подводя итог, последовательность Фибоначчи начинается с 0 и 1, и каждое последующее число является суммой двух предыдущих чисел. По мере роста последовательности Фибоначчи, если вы разделите пары чисел в последовательности (большее на меньшее), вы получите приблизительное значение золотого сечения, которое составляет примерно 1,618.
Результаты обучения
Когда вы закончите, вы сможете:
- Описывать и идентифицировать последовательность Фибоначчи
- Объясните взаимосвязь между последовательностью Фибоначчи и золотым сечением
- Вспомните некоторые примеры последовательности Фибоначчи в природе
чисел Фибоначчи — узнайте, как использовать числа Фибоначчи для инвестирования
Что такое числа Фибоначчи?
Числа Фибоначчи — это числа, входящие в целочисленную последовательность, называемую последовательностью Фибоначчи.Последовательность — это последовательность чисел, характеризующаяся тем, что каждое число представляет собой сумму двух предшествующих ему чисел. Первыми двумя числами в последовательности являются либо 1 и 1, либо 0 и 1, и каждое последующее число представляет собой сумму двух предыдущих, как показано ниже:
1, 1, 2, 3, 5, 8, 13, 21 , 34, 55, 89, 144, ……… .. или 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …….
Последовательность Фибоначчи выражается следующим образом:
Числа Фибоначчи названы в честь итальянского математика Леонардо Фибоначчи, также известного как Леонардо Пизано.В своей книге 1202 года, Liber Abaci, Фибоначчи представил последовательность европейским математикам, хотя последовательность уже была известна индийским математикам. Поскольку отец Фибоначчи был торговцем, он много путешествовал, что позволило ему выучить индуистско-арабскую арифметическую систему, когда он рос в Северной Африке.
В Liber Abaci, математик отметил числовую последовательность, когда думает о разведении кроликов. Он задал следующий вопрос: «Если предположить, что новорожденная пара кроликов, самец и самка, будут помещены в поле, сколько пар будет там через год?» Он сделал предположения, что:
- Кролики не умирают.
- Кролики достигают половой зрелости за один месяц.
- Срок беременности у кроликов — один месяц.
- После достижения половой зрелости самки кроликов рожают ежемесячно.
- Кролик рождает одного кролика и одну девочку.
Идея разведения кроликов представлена на диаграмме ниже:
В течение первого месяца новорожденная пара кроликов еще не достигла половой зрелости и, следовательно, не может спариваться.Во втором месяце кролики спариваются и в конце того же месяца рожают одну пару кроликов, в результате чего получается две пары кроликов. На третьем месяце первая самка кролика спаривается и рождает вторую пару, в результате чего в поле получается три пары.
В конце четвертого месяца исходная самка производит еще одну пару кроликов, а самка, родившаяся во втором месяце, также дает первую пару, что составляет пять пар кроликов. Схема продолжается до 12 -го месяца.В n-м месяце общее количество кроликов будет равно количеству новых пар (n-1) плюс количество пар, живущих в предыдущем месяце (n-1).
Восстановление Фибоначчи
Восстановление Фибоначчи — популярный инструмент, используемый техническими трейдерами. Механизмы торговли. Механизмы торговли относятся к различным методам торговли активами. Двумя основными типами торговых механизмов являются механизмы торговли на основе котировок и заявок, которые основаны на числах, определенных итальянским математиком.Инструмент использует математические отношения между числами в последовательностях Фибоначчи больше, чем сами числа.
Требуются крайние точки на графике акций Инвестиции в акции: руководство по инвестированию в рост Инвесторы могут воспользоваться преимуществами новых стратегий инвестирования в рост, чтобы более точно отточить акции или другие инвестиции, предлагающие потенциал роста выше среднего, например, минимальный и высокие ценовые уровни долгосрочного тренда, и делит вертикальное расстояние между ними на коэффициент Фибоначчи, равный 23.6%, 38,2%, 50%, 61,8% и 100%. После определения уровней соотношений на графике рисуются горизонтальные линии, представляющие уровни соотношений, указывающие на возможные уровни поддержки (цена перестает снижаться) и сопротивления (цена перестает идти выше).
В последовательности чисел Фибоначчи каждое число примерно в 1,618 раза больше предыдущего. Например, 21/13 = 1,615, а 55/34 = 1,618.
В ключевых соотношениях Фибоначчи соотношение 61,8% получается делением одного числа в ряду на число, которое следует за ним.Например, 8/13 = 0,615 (61,5%), а 21/34 = 0,618 (61,8%).
Коэффициент 38,2% получается путем деления одного числа в ряду на число, расположенное двумя позициями вправо. Например, 5/13 = 0,385 (38,5%) и 55/144 = 0,3818 (38,2%).
23,6% рассчитывается путем деления одного числа в последовательности на число, которое находится на три знака вправо. Например, 13/55 = 0,236 (23,6%), а 2/8 = 0,23076 (23,1%).
0% — это начало отката, а 100% — полный разворот исходной части движения.
Трейдеры используют уровни коррекции Фибоначчи для определения стратегических мест для торговли, стоп-лоссов, стоп-лосс, стоп-лосс, стоп-лосс, это инструмент, используемый трейдерами и инвесторами для ограничения потерь и снижения подверженности риску. Узнайте больше об ордерах стоп-лосс в этой статье, или целевых ценах. Цена удара. Цена исполнения — это цена, по которой держатель опциона может исполнить опцион на покупку или продажу базовой ценной бумаги в зависимости от того, чтобы получить выгодную цену. Во время восходящего тренда уровни коррекции Фибоначчи могут использоваться в качестве потенциальных точек покупки при откатах, в то время как при нисходящем тренде уровни цен могут использоваться как потенциальные точки входа для коротких продаж, ожидая, что восстановление цены вверх обратится к нижней стороне от уровня восстановления Фибоначчи.
Когда ценовой уровень Фибоначчи перекрывается с ценовыми уровнями другого технического индикатора, он становится укрепленным ценовым уровнем с еще более сильной поддержкой или сопротивлением. В отличие от скользящих средних, уровни коррекции Фибоначчи статичны, что позволяет трейдерам реагировать при тестировании определенных ценовых уровней. Концепция коррекции используется в различных индикаторах, таких как теория волн Эллиота, уровни Тирона и паттерны Гартли.
Расширения Фибоначчи
Расширения Фибоначчи — это расширения, производные от отношения, которые превышают стандартный уровень 100% восстановления.Они обычно используются трейдерами для определения уровней поддержки и сопротивления, которые могут сформироваться в будущем, и которые могут использоваться для определения потенциальных целей фиксации прибыли. Наиболее практично вычислять расширения Фибоначчи, когда акции находятся на новых максимумах или минимумах и когда на графике нет четких уровней поддержки и сопротивления выше нового максимума или ниже нового минимума.
Однако трейдеры не должны полагаться только на расширения Фибоначчи при принятии решения о покупке или продаже. Им следует следить за другими техническими индикаторами, такими как свечные модели, чтобы подтвердить потенциальные развороты рынка.
Другие ресурсы
CFI предлагает страницу программы коммерческого банковского и кредитного аналитика (CBCA) ™ — сертификат CBCAGet CFI CBCA ™ и возможность стать коммерческим банковским и кредитным аналитиком. Зарегистрируйтесь и продвигайтесь по карьерной лестнице с помощью наших программ и курсов сертификации. программа сертификации для тех, кто хочет вывести свою карьеру на новый уровень. Чтобы продолжить обучение и продвигаться по карьерной лестнице, вам будут полезны следующие ресурсы:
- Технический анализ — Руководство для новичков Технический анализ — Руководство для новичков Технический анализ — это форма оценки инвестиций, которая анализирует прошлые цены для прогнозирования будущих ценовых действий.Технические аналитики считают, что коллективные действия всех участников рынка точно отражают всю соответствующую информацию и, следовательно, постоянно определяют справедливую рыночную стоимость ценных бумаг.
- Линии скорости — Технический анализ Линии скорости — Технический анализ Линии скорости — это инструмент анализа, используемый для определения уровней поддержки и сопротивления. Они не предназначены для использования в качестве отдельного технического индикатора.
- Инвестирование в акции — руководство по стоимостному инвестированию Фондовые инвестиции: руководство по стоимостному инвестированию После публикации Бена Грэхема «Интеллектуального инвестора» так называемое «стоимостное инвестирование» стало одним из наиболее уважаемых и широко используемых комплектации.
- Стратегии инвестирования в акцииСтратегии инвестирования в акцииСтратегии инвестирования в акции относятся к различным типам инвестирования в акции. Эти стратегии включают в себя вложение стоимости, роста и индексного инвестирования.
 Как открыть хостел | HowToHostel Как открыть хостел …
Как открыть хостел | HowToHostel Как открыть хостел … 

 Фроста и Р. Пректер «Волновой принцип Эллиотта» — там хорошо описаны принципы классической волновой теории Эллиота в ее изначальном виде..
Фроста и Р. Пректер «Волновой принцип Эллиотта» — там хорошо описаны принципы классической волновой теории Эллиота в ее изначальном виде..