Число Фибоначчи. Почему оно так популярно в природе?
Таинственное число Фибоначчи, равное 1,618, будоражит умы ученых уже на протяжении нескольких тысячелетий. Кто-то считает это число строителем мироздания, кто-то называет его числом Бога, а кто-то, не мудрствуя лукаво, просто применяет его на практике и получает невероятные архитектурные, художественные и математические творения. Число Фибоначчи было обнаружено даже в пропорциях знаменитого «Витрувианского человека» Леонардо Да Винчи, который утверждал, что знаменитое число, пришедшее из математики, руководит всей Вселенной.
«Витрувианский человек» Леонардо да Винчи обладает идеальными пропорциями, основанными на знании свойств числа Фибоначчи
Кто такой Фибоначчи?
Леонардо Пизанский считается самым первым крупным математиком в истории средневековой Европы. Несмотря на это, свое знаменитое прозвище «Фибоначчи» ученый получил далеко не из-за своих экстраординарных математических способностей, но из-за своего везения, так как «боначчи» по-итальянски означает «удачливый». Перед тем как стать одним из самых известных математиков раннего Средневековья, Леонардо Пизанский изучал точные науки у самых продвинутых учителей своего времени, которыми считались арабы. Именно благодаря этой деятельности Фибоначчи, в Европе появились десятичная система счисления и арабские цифры, которыми мы пользуемся до сих пор.
Перед тем как стать одним из самых известных математиков раннего Средневековья, Леонардо Пизанский изучал точные науки у самых продвинутых учителей своего времени, которыми считались арабы. Именно благодаря этой деятельности Фибоначчи, в Европе появились десятичная система счисления и арабские цифры, которыми мы пользуемся до сих пор.
В одном из своих самых известных трудов под названием «Liber abaci», Леонардо Пизанский приводит уникальную закономерность чисел, которые при постановке в ряд образуют линию цифр, каждая из которых является суммой двух предыдущих чисел.
Последовательность Фибоначчи
Иными словами, последовательность Фибоначчи выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 и так далее.
Каждое число из ряда Фибоначчи, разделенное на последующее, имеет значение, стремящееся к уникальному показателю, которое составляет 1,618. Первые числа ряда Фибоначчи не дают настолько точное значение, однако по мере нарастания, соотношение постепенно выравнивается и становится все более точным.
Леонардо Пизанский — тот самый создатель числа Фибоначчи
Читайте также: Найдено самое длинное простое число Мерсенна, состоящее из 22 миллионов цифр
Где используется число Фибоначчи
Из-за своего повсеместного применения в природе, золотое сечение (именно так число Фибоначчи иногда называют в искусстве и математике) считается одним из самых гармонизирующих законов мироздания, который упорядочивает структуру окружающего нас мира и направляет жизнь на развитие. Так, правило золотого сечения применяется природой для образования траекторий движения вихревых потоков в ураганах, при образовании эллиптических галактик, к которым относится и наш Млечный Путь, при «строительстве» раковины улитки или ушной раковины человека, направляет движение косяка рыб и показывает траекторию движения испуганной стаи оленей, врассыпную убегающую от хищника.
Проявление золотого сечения в природе
Эстетичность такой гармонизации мироздания воспринимается человеком, который всегда стремился улучшить окружающую его действительность, в качестве стабилизирующего природу закона. Находя золотое сечение в лице того или иного человека, мы инстинктивно воспринимаем собеседника в качестве гармоничной личности, чье развитие происходит без сбоев и нарушений. Этим можно объяснить то, почему иногда нам по непонятным причинам больше нравится одно лицо, чем другое. Оказывается, о наших возможных симпатиях позаботилась природа!
Находя золотое сечение в лице того или иного человека, мы инстинктивно воспринимаем собеседника в качестве гармоничной личности, чье развитие происходит без сбоев и нарушений. Этим можно объяснить то, почему иногда нам по непонятным причинам больше нравится одно лицо, чем другое. Оказывается, о наших возможных симпатиях позаботилась природа!
Как вы считаете, является ли повсеместное применение числа Фибоначчи в природе совпадением или свидетельством наличия некоего вселенского разума? Давайте попробуем обсудить этот вопрос в нашем Telegram-чате.
Наиболее распространенное определение золотого сечения гласит, что меньшая часть так относится к большей, как большая часть относится ко всему целому. Уникальное правило встречается во всех областях природы, науки и искусства, позволив некоторым именитым исследователям Средних Веков сделать предположение, что три основные части золотого сечения олицетворяют собой христианских Отца, Сына и Святого Духа.
Правилу золотого сечения следуют даже галактики.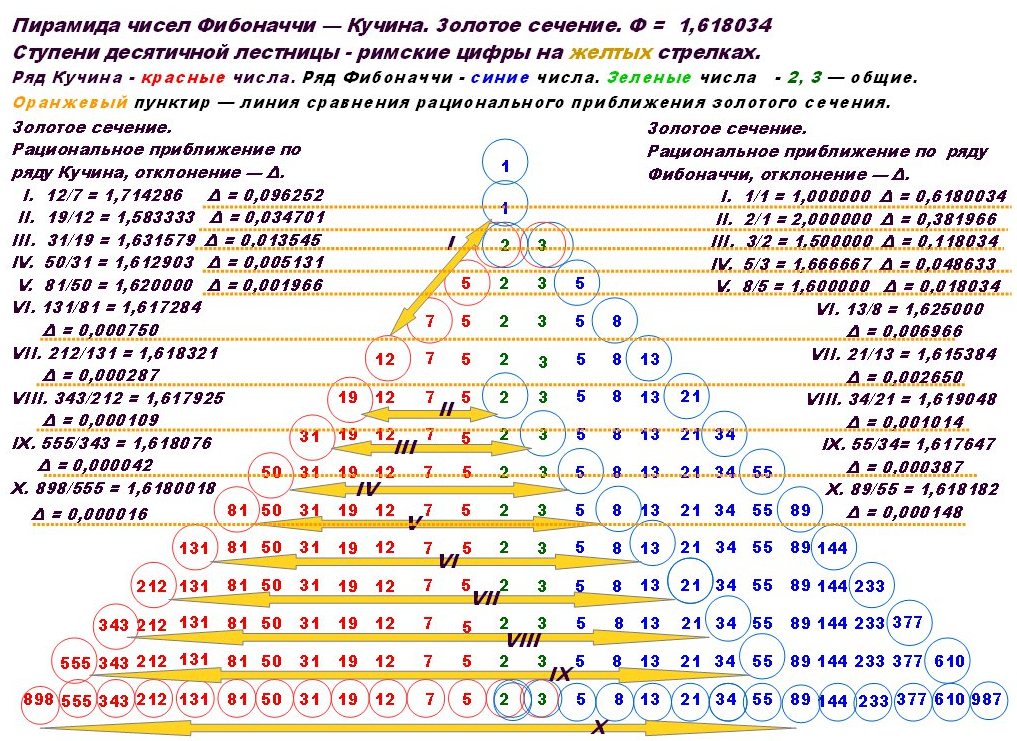 Наш Млечный Путь в этом плане не является исключением
Наш Млечный Путь в этом плане не является исключением
Что такое золотое сечение
С точки зрения математики, золотое сечение представляет собой некую идеальную пропорцию, к которой каким-то образом стремится все живое и неживое в природе.
Так выглядит «золотое сечение»
Используя основные принципы ряда Фибоначчи, растут семечки в центре подсолнуха, движется спираль ДНК, был построен Парфенон и написана самая знаменитая картина в мире — «Джоконда» Леонардо Да Винчи.
Даже коты неосознанно (хотя, кто знает?) следуют принципу золотого сечения, становясь любимцами большей части населения планеты
Есть ли в природе гармония? Несомненно, есть. А ее доказательством служит число Фибоначчи, происхождение которого нам еще только предстоит отыскать.
Что такое числа Фибоначчи, золотое сечение? ⋆ FutureNow
Последовательность Фибоначчи – одна из самых известных формул математики. Так, что такое числа Фибоначчи, золотое сечение и какая их интересная стория?
Что такое числа Фибоначчи?Каждое число в последовательности Фибоначчи – это сумма двух чисел, предшествующих ему.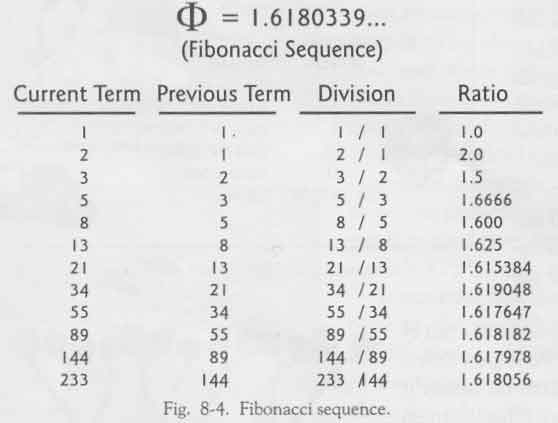
Итак, последовательность выглядит так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и т. Математическое уравнение, описывающее число Фибоначчи: Xn + 2 = Xn + 1 + Xn
Фибоначчи числа иногда называют “секретным кодом природы” и “общем правилом природы”. Говорят, что данная последовательность руководит размерами всего сущего, в том числе обьясняет Великую пирамиду в Гизе, так и многие вещи, с которыми мы сталкиваемся каждый день.
Числа Фибоначчи: богатая историяПоэтому какова реальная история стоит за этой знаменитой последовательностью?
Многие источники утверждают, что ее впервые обнаружил или “изобрел” Леонардо Фибоначчи.
Итальянский математик, родился около 1170 года нашей эры и первоначально был известен как Леонардо из Пизы. Лишь в 19 веке историки придумали прозвище Фибоначчи, чтобы отличить математика от другого известного Пизарського Леонардо.
Но Леонардо из Пизы на самом деле не изобрел последовательность. Ее впервые упоминают древние санскритские тексты, в которых использовалась индуистско-арабская система числения, еще много веков до Леонардо Пизы.
Ее впервые упоминают древние санскритские тексты, в которых использовалась индуистско-арабская система числения, еще много веков до Леонардо Пизы.
Однако в 1202 Леонардо из Пизы опубликовал большой том “Liber Abaci,” книгу по математике “о том, как производить вычисления”. “Liber Abaci”, написанная для торговцев, где изложена индуистско-арабский арифметика, которая является полезной для отслеживания прибыли, убытков, остатков по кредитам и тому подобное.
ЧТО ТАКОЕ ШАРОВАЯ МОЛНИЯ: СУЩЕСТВУЕТ ЛИ ОНА?
В книге Леонардо из Пизы вводит последовательность с задачей о кроликах. Проблема заключается в следующем: начнем с самца и самки кролика. Через месяц они созревают и дают помет в результате которого мы имеем еще самца и самку кролика. Через месяц эти кролики размножаются и получается – вы догадались – еще один самец и самка, которые также могут спариваться через месяц. Через год сколько бы у вас было кроликов? Ответ, 144, спрятан в формуле, которая сейчас известна как последовательность Фибоначчи.
“Liber Abaci” впервые представила эту последовательность западному миру. Но после нескольких скудных абзацев о разведении кроликов Леонардо из Пизы больше никогда не вспоминал ее.
На самом деле эти числа Фибоначчи были забыты до 19 века, когда математики подробнее изучили математические свойства последовательности. В 1877 году французский математик Эдуард Лукас официально назвал задачу о кроликах “последовательностью Фибоначчи”.
Мы узнали что такое числа Фибоначчи, но какое же значение имеет последовательность Фибоначчи?
Кроме как учебный инструмент, она проявляется во многих случаях в природе. Однако, это не какой-то секретный код, который руководит архитектурой Вселенной.
Это правда, что последовательность Фибоначчи тесно связана с тем, что сейчас известно как “золотое сечение”. Проще говоря, отношение чисел в последовательности, поскольку последовательность идет к бесконечности, приближается к золотому сечению, который составляет +1,6180339887498948482 … Оттуда математики могут вычислить то, что называется золотой спиралью, или логарифмической спирали, коэффициент роста которой равен золотому сечению.
Золотое сечение объясняет рост некоторых растений. Например, спиральное расположение листьев или лепестков на некоторых растениях соответствует золотому сечению. Но есть также растения, которые не соблюдают этого правила.
Мистификации и выдумкиКогда люди начинают связывать человеческое тело, искусство и архитектуру, много вымышленных теорий и мистификаций ссылаются на последовательность Фибоначчи.
“Понадобится большая книга, чтобы задокументировать всю дезинформацию о золотом сечении, многие из которой – это просто повторение одних и тех же фантазий разных авторов”, – написал Джордж Марковский, математик из университета Мэн в 1992 году.
Значительная часть этой дезинформации может быть отнесена к книге 1855 года немецкого психолога Адольфа Зейзинга. Он утверждал, что пропорции человеческого тела основана на золотом сечении.
Золотое соотношение проросло в “золотые прямоугольники”, “золотые треугольники” и всевозможные теории об этих знаковых размерах.
С тех пор люди говорят, что золотое соотношение или золотое сечение можно найти в размерах Пирамиды в Гизе, Парфеноне, “Витрувийським человеке” Леонардо да Винчи и ренессансных сооружениях.
Под сомнение можно поставить и беспрекословное утверждение о том, что золотое сечение является “однозначно приятным” для человеческого глаза – на чем часто настаивают фотографы.
Часто все эти утверждения, когда их проверяют, являются ошибочными. Люди часто выдают желаемое за действительное.
Источник: www.livescience.com/
Числа Фибоначчи — что это и для чего они нужны?
Содержание статьи
КУРС ШКОЛА ИНВЕСТИЦИЙ
Леонардо Пизано, по прозвищу Фибоначчи, — итальянский математик — родился в Пизе в 1170 году. Его отец работал в торговом порту на северо-востоке Алжира и часто путешествовал.
Фибоначчи изучал математику и во время обширных путешествий познакомился с индийско-арабской системой счисления. Оттуда математик и узнал о числовой последовательности, которую в древней Индии использовали в стихосложении.
Названа последовательность в честь итальянца, потому что именно он представил ее европейскому обществу в труде «Книга абака».
Что такое числа Фибоначчи?
Числа Фибоначчи — это ряд, состоящий из целых чисел. Их особенность заключается в том, что каждый элемент представляет собой сумму двух предыдущих чисел.
Последовательность Фибоначчи начинается с 0 и 1. Продолжить ряд легко: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и так до бесконечности.
Математик обратил внимание на числовую последовательность, когда думал о разведении кроликов.
Задача была поставлена следующим образом: «Если новорожденную пару кроликов, самца и самку, поместить в поле, то сколько пар кроликов будет через год?». Но как известно, ни одну практическую задачу невозможно решить без некоторых ограничений и предположений. Поэтому, к условию задачи добавились следующие допущения:
Поэтому, к условию задачи добавились следующие допущения:
- Кролики не умирают;
- Кролики достигают половой зрелости за один месяц;
- Срок беременности у кроликов – один месяц;
- Достигнув половой зрелости, кролики-самки рожают ежемесячно кролика-самца и кролика-самку.
Схема разведения кроликов выглядит следующим образом:
Так как по условию задачи в поле поместили новорожденных кроликов, то спариваться они не могут, так как не достигли половой зрелости. Через месяц кролики начинают спариваться и еще через один – рождается первая пара потомков. «Родители» продолжают наращивать потомство, а дети месяц ждут своего взросления, чтобы тоже стать родителями. В итоге, через 3 месяца по полю будут бегать три пары кроликов. Через 4 месяца уже 5 пар, а через 5 месяцев – 8.
Уже прослеживается закономерность. В конце каждого месяца количество пар кроликов будет больше, чем в предыдущем месяце ровно на столько, сколько пар было два месяца назад.
С точки зрения математики — это красивая последовательность. Но больший интерес для исследователей представляет не сам ряд, а частное соседних чисел, равное, примерно 1,618 для всех элементов ряда. Эта пропорция больше известна как золотое сечение.
Но больший интерес для исследователей представляет не сам ряд, а частное соседних чисел, равное, примерно 1,618 для всех элементов ряда. Эта пропорция больше известна как золотое сечение.
Это соотношение можно найти во предметах, которые нас отгружают: гармония в гранях снежинок, в расположении лепестков цветов, ячеек ананаса, завитки раковин у улитки — все подчиняется правилу золотого сечения. Даже строение нашего тела гармонично: если измерить наш рост и разделить на расстояние от пояса до ступней или длину руки на расстояние от локтя до кончиков пальцев, получится известное нам соотношение 1,618.
КУРС ШКОЛА ИНВЕСТИЦИЙ
Если мы видим человека и его внешность кажется красивой, то скорее всего пропорции его лица соотносятся с соотношением чисел Фибоначчи.
Природа полагается на эту врожденную пропорцию для поддержания баланса.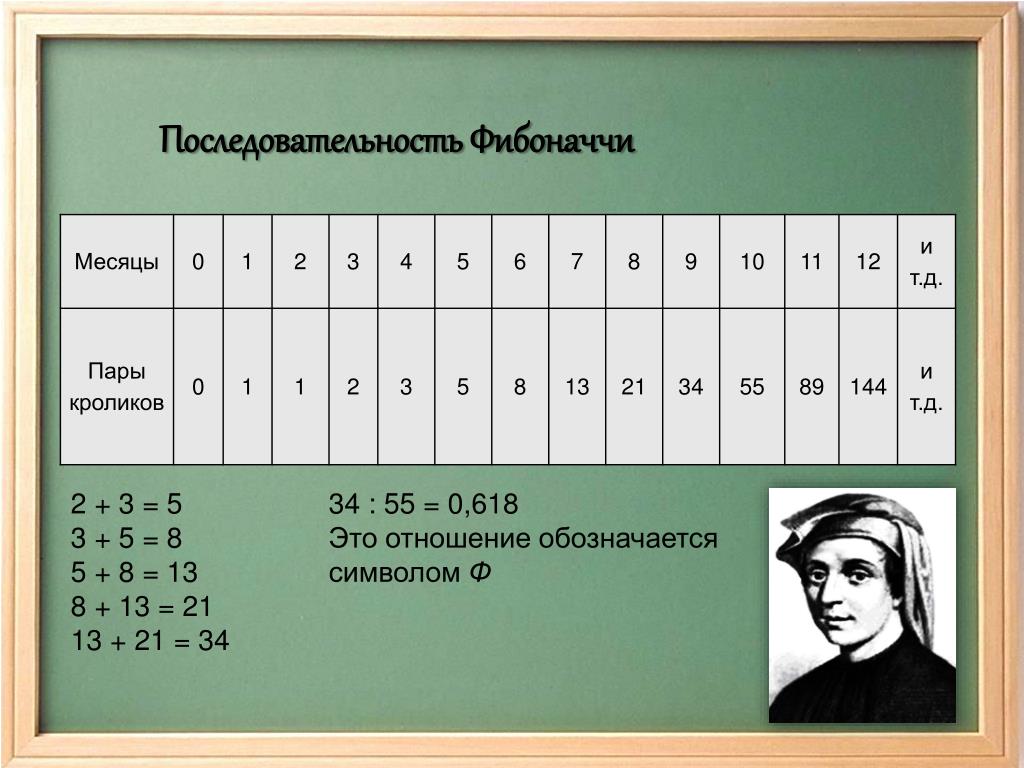
Финансовые рынки имеют ту же математическую основу, что и перечисленные природные явления. Давайте рассмотрим некоторые способы применения золотого сечения к финансам и покажем несколько диаграмм в качестве доказательства.
Числа Фибоначчи в трейдингеВпервые изучением графиков биржевых котировок и поиском взаимосвязей занялся Ральф Hельсон Эллиотт, американский финансист. Ему удалось обнаружить в поведении фондового рынка особую гармонию. Как вы уже догадались – гармонию золотого сечения.
Мы рассмотрим четыре инструмента технического анализа, использующих последовательность Фибоначчи, активно применяемые трейдерами – это уровни, дуги, веер и временные зоны Фибоначчи.
Сначала поговорим об уровнях коррекции.
1. Коррекции ФибоначчиКоррекция Фибоначчи — популярный инструмент, используемый трейдерами. Еще больше об инструментах, которые используют трейдеры, можно узнать на открытом курсе «Трейдинг и личные инвестиции».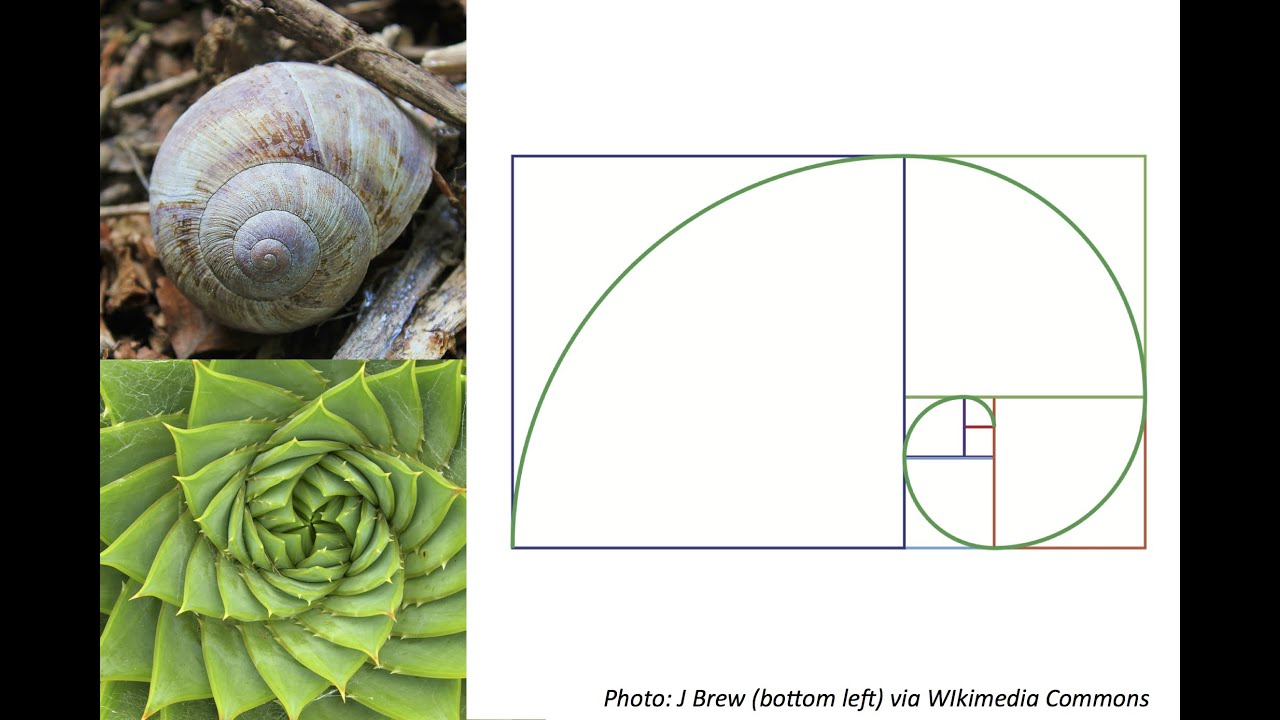
Как это работает: берутся экстремальные точки на графике акций: нижний и верхний уровни цены долгосрочного тренда, и вертикальное расстояние между ними делится на коэффициенты Фибоначчи: 23,6%, 38,2%, 50%, 61,8% и 100%. После определения уровней соотношений на графике рисуются горизонтальные линии, представляющие уровни, указывающие на возможные уровни поддержки (цена перестает идти ниже) и сопротивления (цена перестает идти выше).
Откуда берутся эти значения процентов?
- Как мы уже сказали, в последовательности чисел Фибоначчи каждое число примерно в 1,618 раза больше предыдущего. Например, 21/13 = 1,615, а 55/34 = 1,618.
- Соотношение 61,8% получается делением одного числа в ряду на число, которое следует за ним. Например, 8/13 = 0,615 (61,5%), а 21/34 = 0,618 (61,8%).
- Соотношение 38,2% получается путем деления одного числа в ряду на число, расположенное двумя позициями позже. Например, 5/13 = 0,385 (38,5%), а 55/144 = 0,3818 (38,2%).
- 23,6% рассчитывается путем деления одного числа в последовательности на число на три позиции выше.
 Например, 13/55 = 0,236 (23,6%), а 2/8 = 0,23076 (23,1%).
Например, 13/55 = 0,236 (23,6%), а 2/8 = 0,23076 (23,1%). - 0% — это начало отката, а 100% — полный разворот исходной части движения.
Трейдеры используют уровни коррекции Фибоначчи для определения стратегических моментов для получения выгодной цены. Если тренд возрастает, то уровни коррекции Фибоначчи используются как потенциальные точки покупки при откатах, если тренд убывающий, то как точки входа для коротких продаж.
2. Дуги ФибоначчиДуги Фибоначчи учитывают как время, так и цену, также указывая на потенциальные области поддержки и сопротивления.
Поиск максимума и минимума графика — это первый шаг к построению дуг Фибоначчи. Затем рисуются три изогнутые линии, похожие на полукруги, на расстоянии 38,2%, 50% и 61,8% от желаемой точки. Полукруглые дуги показывают, где цена находит поддержку или сопротивление в будущем.
После роста цены дуги показывают до чего цена может откатиться, прежде чем снова начнет расти. После снижения цены дуги показывают, куда цена может подняться, прежде чем снова начнет падать.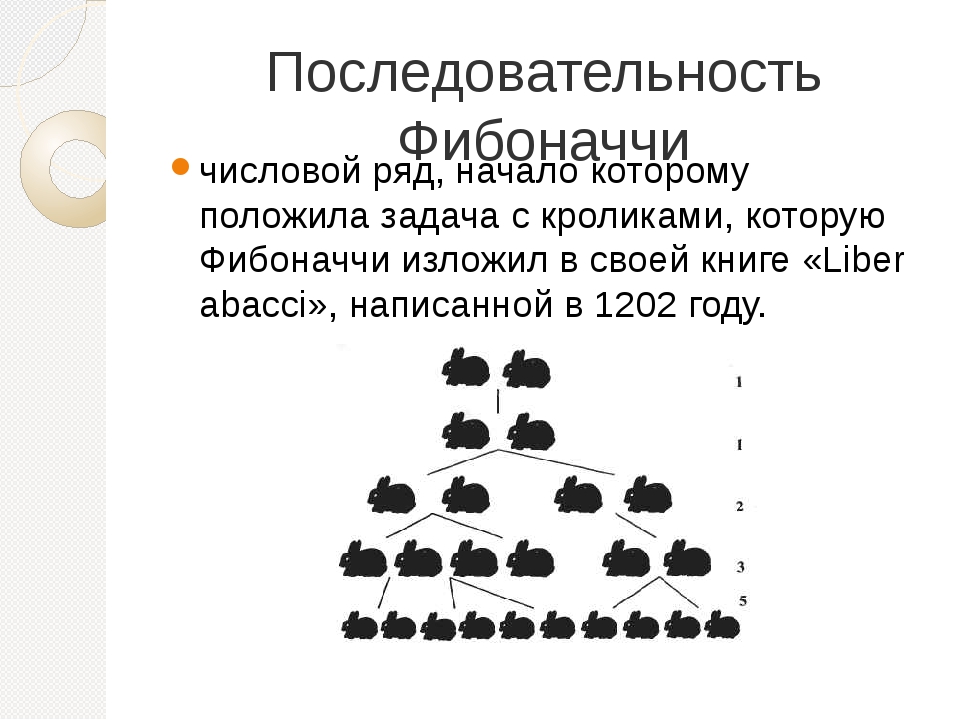
Веера Фибоначчи — это диагональные линии, образующие веер. Как и в предыдущих методах, сначала находятся максимум и минимум тренда. Если траектория возрастающая, то через точку максимума, если убывающие – через точку минимума условно проводится вертикальная линия.
Затем на линии отмечаются уровни: 38,2%, 50% и 61,8%. Дальше соединяются точки первого экстремума и точки, условно отмеченные на невидимой прямой. Получившиеся диагональные линии также указывают на области поддержки и сопротивления.
4. Временные зоны ФибоначчиВременные зоны — это серия линий, параллельных оси ОУ, отстоящих друг от друга на расстоянии, пропорциональном элементам последовательности Фибоначчи (1, 1, 2, 3, 5, 8, 13 и т. д.).
Трейдер отмечает на графике очевидный ценовой тренд (его минимум и максимум). Расстояние между этими точками будет задавать единичный отрезок. Дальше рисуются прямые линии соответственно последовательности Фибоначчи: представьте, что вы строите график на координатной плоскости OXY. Ось OX разбита на длины единичного отрезка от 0 до бесконечности: 0, 1, 2, 3, 4, 5, 6, 7, 8…. и так далее.
Ось OX разбита на длины единичного отрезка от 0 до бесконечности: 0, 1, 2, 3, 4, 5, 6, 7, 8…. и так далее.
Теперь вспомним, как выглядит ряд Фибоначчи: 0, 1, 2, 3, 5, 8…. Теперь именно в этих точках на оси OX и будут строиться вертикальные линии, соответствующие временным зонам. Каждая линия указывает время, в которое можно ожидать резкий скачок или спад цены.
Описанные инструменты далеко не единственные методы анализа графиков, использующих золоте сечение и числа Фибоначчи. Возможно, вы слышали и о таких инструментах, как клин, канал, спираль, также названных в честь Фибоначчи. Они отличаются способами построения и внешним видом, но смысл остается один — оценить области поддержки и сопротивления цены. Часто используют несколько методов одновременно для улучшения качества прогнозирования. Подробнее об инструментах, которые используются в трейдинге, можно узнать в бесплатной демо-версии книги по трейдингу.
Надеемся, вы тоже найдете собственное «нишевое» применение исследованиям Фибоначчи и добавите эти методы в свой набор инвестиционных инструментов.
Автор: Алексанян Андрон, эксперт SF Education
КУРС ШКОЛА ИНВЕСТИЦИЙ
ПОСЛЕДОВАТЕЛЬНОСТЬ ФИБОНАЧЧИ — это… Что такое ПОСЛЕДОВАТЕЛЬНОСТЬ ФИБОНАЧЧИ?
Последовательность Фибоначчи — Числа Фибоначчи элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух предыдущих чисел. Название по… … Википедия
ФИБОНАЧЧИ — (Fibonacci) Леонардо (ок. 1170 ок. 1240), итальянский математик. Автор «Liber Abaci» (ок. 1200), первого западноевропейского труда, в котором предлагалось принять арабскую (индийскую) систему написания цифр. Разработал математическую… … Научно-технический энциклопедический словарь
Фибоначчи — (Fibonacci) Фибоначчи первый крупный математик средневековой Европы Десятичная система счисления, арабские цифры, числа, последовательность, уровни, ряд, линии и спираль Фибоначчи Содержание >>>>>>>>> … Энциклопедия инвестора
Фибоначчи числа — Числа Фибоначчи элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух предыдущих чисел. Название по… … Википедия
Название по… … Википедия
Последовательность Падована
Фибоначчи — Леонардо Пизанский Leonardo Pisano Дата рождения: ок. 1170 года … Википедия
Фибоначчи числа — элементы числовой возвратной последовательности (См. Возвратная последовательность) 1, 1, 2, 3, 5, 8,… (ряда Фибоначчи), в которых каждый последующий член равен сумме двух предыдущих. Название по имени средневекового математика Леонардо … Большая советская энциклопедия
ФИБОНАЧЧИ МЕТОД — разновидность одномерного поиска экстремума функции путем последовательного сужения интервала неопределенности. Единственное ограничение, налагаемое на исследуемую функцию требование строгой унимодальности на заданном интервале.
Последовательность Люка — Не следует путать с числами Люка. В математике, последовательностями Люка называют семейство пар линейных рекуррентных последовательностей второго порядка, впервые рассмотренных Эдуардом Люка. Последовательности Люка представляют собой пары… … Википедия
Последовательность — одно из основных понятий математики. П. образуется из элементов любой природы, занумерованных натуральными числами 1, 2,…, n,…, и записывается в виде x1, x2, …, xn, … или коротко, {xn}. Элементы, из которых составляется П., называются … Большая советская энциклопедия
«Что такое числа Фибоначчи и почему их выделили в отдельную группу чисел?» – Яндекс.Кью
Числа Фибоначчи в Европе популяризовал Леонардо Пизанский (по прозвищу Фибоначчи – сын Боначчи), в задаче о кроликах:
Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый день января.
Эта пара кроликов производит новую пару кроликов (самку и самца) в первый день февраля и затем в первый день каждого следующего месяца. Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов. Возникает вопрос: сколько пар кроликов будет в огороженном месте через год, то есть через 12 месяцев с начала размножения.
Оказывается, число кроликов по месяцам описывается последовательностью
1, 2, 3, 5, 8, 13,…
В ней каждое число равно сумме двух предыдущих. Условия задачи все равно нереалистичны, так что можно не стесняться: предположить, что кролики бессмертны, и продолжить последовательность до бесконечности:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, ….
Есть свидетельства, что последовательность задолго до Леонардо была известна в Индии, и что в честь Фибоначчи ее назвал Эдуард Люка.
Про экспоненциальный рост
Как мы видим, последовательность очень быстро растет (экспоненциально, как последовательность степеней). Примерно как 1, 2, 4, 8, 16, 32, … или 1, 10, 100, 1000, … (тоже экспоненциальный рост.) Экспоненциальный рост вообще встречается в природе и в приложениях: так растут популяции, капиталы в банке, число радиоактивных атомов и число зерен на шахматной доске (Вы же помните легенду про жадного султана и бедного изобретателя шахмат ;))
В природе экспоненциальный рост имеет место лишь приблизительно и только в некоторых пределах.
Красивые фотографии
Последовательности в природе, напоминающие Фибоначчи, тоже похожи на Фибоначчи только приблизительно и в некоторых пределах. Широко известны примеры из мира растений: семена подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса. Видимо, здесь задействован один механизм (я скопировала первую попавшуюся картинку из интернета):
Отчасти популярность чисел Фибоначчи связана с такими красивыми картинками. В интернете их полным-полно.
В интернете их полным-полно.
А вот скажем, закон радиоактивного распада не менее поразителен, история его открытия драматична, человечество поставило его себе на службу… но он не так популярен в СМИ. Нет для него таких красивых картинок, да и описывается он дифференциальным уравнением, а любителей дифференциальных уравнений меньше, чем любителей красивых картинок.
В математике
В математике бывают объекты, которые задаются очень просто, но показывают удивительно сложные и многогранные связи между своими компонентами. Например: треугольник в планиметрии, конические сечения, треугольник Паскаля, простые числа, … Они завораживают нас как картинки в калейдоскопе. Чуть повернешь – и открываются новые узоры, новые свойства. Числа Фибоначчи –один из таких объектов. Каждый математик на пути в науку их обязательно встречал.
Чтобы перечислить все их удивительные свойства, нужна отдельная книга (и кстати, выходит журнал с таким названием, посвященный одним только числам Фибоначчи). Скажу только, что отношение каждого числа Фибоначчи к предыдущему приближает золотое сечение, и чем числа больше, тем приближение лучше.
Скажу только, что отношение каждого числа Фибоначчи к предыдущему приближает золотое сечение, и чем числа больше, тем приближение лучше.
Почему же математики выделили числа Фибоначчи в отдельную группу чисел
Потому что любят все классифицировать и раскладывать по полочкам. Раз есть объект – надо дать ему название. На сайте https://oeis.org/A000045 , где собраны большинство последовательностей чисел, встречающихся в математике, последовательность Фибоначчи идет под номером 45. Она вовсе не такая уж исключительная, кроме неё на этом сайте собрано около трети миллиона последовательностей. Каждая из них тоже представляет собой «отдельную группу чисел».
Специалист по теории чисел Леопольд Кронекер считал, что только одна из них создана Богом (и это вовсе не последовательность Фибоначчи, а другая, на сайте ее номер 27), а остальные – дело рук человеческих.
В целом журналисты несколько преувеличивают значимость чисел Фибоначчи: они, безусловно, прекрасны, но стоят в одном ряду с многими другими не менее прекрасными и полезными математическими объектами.
Фибоначчи повсюду!. Числа Фибоначчи названы в честь… | by Сергей Базанов | Paradox Review
Числа Фибоначчи и золотое сечение
Как известно, последовательность Фибоначчи начинается с 1 и 1, после чего каждое новое число является результатом сложения двух предыдущих чисел:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Если разделить два последовательных числа в этом ряду, например 144/89, в конечном итоге получится число 1,618, которое называется «Золотое число» или «Золотое сечение».
Последовательное приближение соотношения двух соседних чисел ряда Фибоначчи к Золотому сечению.Пропорция золотого сечения считается эстетически приятной и из-за этого многие художники и архитекторы, в том числе Сальвадор Дали и Ле Корбюзье использовали её в своих работах.
Последовательность Фибоначчи и Золотое сечение тесно взаимосвязаны. Отношение последовательных чисел Фибоначчи сходится и приближается к золотому сечению, а выражение замкнутой формулы для последовательности Фибоначчи включает Золотое сечение.
Золотой прямоугольник (розовый) с длинной стороной a и короткой стороной b, и находящийся рядом с ним квадрат со стороной длиной a , создадут подобный золотой прямоугольник с длинной стороной а + b и короткой стороной a. Это изобажение иллюстрирует взаимосвязь отношений (a+b)/a = a/b.Спираль Фибоначчи или золотая спираль — это последовательность соединенных четвертей окружностей, вписанных внутри массивов квадратов со сторонами равными числам Фибоначчи. Квадраты идеально подходят друг к другу из-за природы последовательности Фибоначчи, в которой следующее число равно сумме двух перед ним (см.предыдущий рисунок). Любые два последовательных числа Фибоначчи имеют отношение, очень близкое к золотому сечению, которое составляет примерно 1.618034. Чем больше пара чисел Фибоначчи, тем ближе это приближение. Спираль и результирующий прямоугольник называются золотым прямоугольником.8 или 21 -ИЗ), результат действия выразится в отношении, которое колеблется вокруг иррационального числа 1,61803398875, чуть больше или чуть меньше соседних отношений ряда. Отношение никогда, до бесконечности, не будет точным до последней цифры (даже при использовании самых мощных компьютеров, созданных в наше время). Ради краткости, будем использовать в качестве отношения Фибоначчи число 1,618 и просим читателей не забывать об этой погрешности.
Числа Фибоначчи имеют важное значение и во время выполнения анализа Алгоритм Евклида для определения наибольшего общего делителя двух чисел. Числа Фибоначчи происходят в формулу о диагонали треугольником Паскаля (биномиальных коэффициентов).
Числа Фибоначчи оказались связанными с « золотым сечением».
О золотом сечении знали еще в древнем Египте и Вавилоне, в Индии и Китае. Что же такое « золотое сечение»? Ответ неизвестен до сих пор. Числа Фибоначчи действительно актуальны для теории практики в наше время. Подъем значимости произошел в 20 веке и продолжается до сих пор. Использование чисел Фибоначчи в экономике и информатике и привлекло массы людей к их изучению.
Методика моего исследования заключалась в изучении специализированной литературы и обобщении полученной информации, а так же проведении собственных исследований и выявлений свойств чисел и сферы их использования.
В ходе научных исследования определила само понятия чисел Фибоначчи, их свойства. Так же я выяснила интересные закономерности в живой природе, непосредственно в строении семян подсолнуха.
На подсолнухе семечки выстраиваются в спирали, причем количества спиралей, идущих в другую сторону, различны — они являются последовательными числами Фибоначчи.
На этом подсолнухе 34 и 55.
То же наблюдается и на плодах ананаса, где спиралей бывает 8 и 14. С уникальным свойством чисел Фибоначчи связаны листьев кукурузы.
Дроби вида a/b, соответствующие винтообразному расположению листьев ног стебелька растения, часто являются отношениями последовательных чисел Фибоначчи. Для орешника это отношение равно 2/3, для дуба-3/5, для тополя 5/8, для ивы 8/13 и т. д.
Рассматривая расположения листьев на стебле растений можно заметить, что между каждыми парами листьев (А и С) третья расположено в месте золотого сечения(В)
Ещё интересное свойство числа Фибоначчи является, что произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
В результате исследования я пришла к следующим выводам: числа Фибоначчи — уникальная арифметическая прогрессия, появившаяся в 13 веке нашей эры. Данное прогрессия не теряет своей актуальности, что и подтвердилось в ходе моих исследований. Число Фибоначчи встречаются не то и в программировании и экономических прогнозах, в живописи, архитектуре и музыке. Картины таких известных художников, как Леонардо да Винчи, Микеланджело, Рафаэля и Боттичелли скрывают в себе магию золотого сечения. Даже И. И. Шишкин использовал золотое сечение в своей картине «Сосновая роща».
В это сложно поверить, но золотое сечение встречается и в музыкальных произведениях таких великих композиторов, как Моцарт, Бетховен, Шопен и т. д.
Числа Фибоначчи встречается и в архитектуре. Например, золотое сечение использовалось при строительстве Парфенона и собора Парижской Богоматери
Я обнаружила, что Числа Фибоначчи используются и в наших краях. Например, наличники домов, фронтоны.
Что такое последовательность Фибоначчи? И как это применимо к гибкой разработке
Что такое последовательность Фибоначчи?
Последовательность Фибоначчи — это последовательность чисел, в которой число представляет собой сложение двух последних чисел, начиная с 0 и 1.
Последовательность Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…
Обычно пишется выражение:
X n = X n-1 + X n-2
Руководство по гибкой разработке
Это руководство представляет собой основу для перехода вашей команды к гибкой разработке.
Спираль Фибоначчи и золотое сечение
Последовательность Фибоначчи часто визуализируется в виде графика, такого как тот, что в заголовке этой статьи. Каждый из квадратов показывает площадь следующего числа в последовательности. Затем спираль Фибоначчи рисуется внутри квадратов, соединяя углы прямоугольников.
Квадраты идеально подходят друг к другу, потому что соотношение между числами в последовательности Фибоначчи очень близко к золотому сечению [1], которое приблизительно равно 1.618034. Чем больше числа в последовательности Фибоначчи, тем ближе отношение к золотому сечению.
Спираль и результирующий прямоугольник также известны как золотой прямоугольник [2].
Истоки последовательности Фибоначчи
Фиббоначи (Леанардо Пизано Боголло [3], его прозвище Фибоначчи) впервые представил серию чисел, известную как последовательность Фибоначчи, в своей книге Liver Abaci [4] в 1202 году. Фибоначчи был членом влиятельной итальянской торговой семьи. 12 и 13 века.Будучи частью торговой семьи, математика была неотъемлемой частью бизнеса. Фибоначчи путешествовал по Ближнему Востоку и Индии и был очарован математическими идеями из своих путешествий. Его книга, Liver Abaci , была беседой о математических методах торговли, которые Фибоначчи наблюдал во время своих путешествий.
Фибоначчи известен двумя важными вкладами в западную математику:
- Он помог распространить использование индуистских систем записи чисел в Европе (0,1,2,3,4,5 вместо римских цифр).
- На первый взгляд незначительный ряд чисел позже назвал в его честь Последовательность Фибоначчи.
Фибоначчи открыл последовательность, задав следующий вопрос:
Если пару кроликов поместить в закрытое пространство, сколько кроликов родится там, если мы предположим, что каждый месяц пара кроликов производит еще пары и что кролики начинают рожать детенышей через два месяца после их рождения?
- Начало: На старте кролики не рождаются, так как первая пара еще не успела забеременеть и родилась (0) .
- Первый месяц: рождается одна пара кроликов (1) .
- Второй месяц: снова рождается одна пара кроликов, поскольку новые кролики еще не созрели, чтобы вынашивать детенышей (1) .
- Третий месяц: две пары кроликов размножаются, а одна пара не готова, поэтому рождаются две пары кроликов (2) .
- Четвертый месяц: три пары кроликов размножаются, а две пары кроликов не готовы, поэтому рождаются три пары кроликов (3) .
- Пятый месяц: пять пар кроликов производят, а три еще не готовы, поэтому рождается пять пар кроликов (5) .
- И так далее.
Хотя вопрос Фибоначчи о кроликах — нереалистичный сценарий, последовательность можно наблюдать в природе, например, в массиве семян подсолнечника и других растений, а также в форме галактик и ураганов.
Семена подсолнечника — это яркая демонстрация последовательности Фибоначчи в природе.
Важность последовательности Фибоначчи
Хотя эта серия чисел из этой простой головоломки может показаться несущественной, она была заново открыта в удивительном разнообразии форм, от разделов продвинутой математики [5] до приложений в компьютерных науках [6], статистике [7], природе [ 8] и гибкой разработки.
Как последовательность Фибоначчи используется в гибкой разработке
Теперь вы можете сказать себе: « Это хорошо, но какое отношение это имеет к гибкой разработке? », и это отличный вопрос. Какое отношение имеет последовательность Фибоначчи к гибкой разработке? Интересно, что последовательность Фибоначчи — полезный инструмент для оценки времени выполнения задач.
Оценка задач в Agile
Большая часть управления Agile-командой — это оценка времени, которое потребуется для выполнения задач.Система баллов часто используется, чтобы дать общую оценку масштаба или размера конкретной задачи. Чем больше и сложнее, тем больше очков, а меньше — меньше. Затем менеджеры могут просматривать и расставлять приоритеты задач в соответствии с назначенной шкалой.
Использование последовательности Фибоначчи с вашей командой
Чтобы использовать последовательность Фибоначчи, проинструктируйте свою команду оценивать задачи из последовательности Фибоначчи до 21.
1, 2, 3, 5, 8, 13, 21
Одна из самых маленьких простых задач и двадцать один из больших проектов.Что касается того, почему вы должны использовать последовательность Фибоначчи вместо, скажем, размеров футболки, проверьте мою следующую статью о . 5 причин, по которым использование последовательности Фибоначчи сделает вас лучше при оценке задач в гибкой разработке .
А чтобы узнать больше о руководстве командой Agile eLearning Development, ознакомьтесь с нашим приятным электронным руководством The Agile Guide to Agile Development.
Статьи по теме:
1. 5 причин, по которым использование последовательности Фибоначчи делает вас лучше в гибкой разработке
2.8 компонентов и использование диаграмм выгорания в гибкой разработке
3. Электронная книга: Agile Guide to Agile Development
Список литературы- Золотое сечение
- Золотой прямоугольник
- Леонардо Пизано Фибоначчи
- Liber Abaci Фибоначчи: Перевод на современный английский язык Книги расчетов Леонардо Пизано (Источники и исследования по истории математики и физических наук)
- Последовательность Фибоначчи
- Почему числа Фибоначчи важны в информатике?
- Числа Фибоначчи, статистическая сходимость и приложения
- Фибоначчи в природе
Что такое последовательность Фибоначчи?
Последовательность Фибоначчи — одна из самых известных формул в математике.
Каждое число в последовательности представляет собой сумму двух предшествующих ему чисел. Итак, последовательность такова: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Математическое уравнение, описывающее его: Xn + 2 = Xn + 1 + Xn
Опора средней школы и студентов, его называют «секретным кодом природы» и «универсальным правилом природы». Говорят, что он определяет размеры всего, от Великой пирамиды в Гизе до культовой морской ракушки, которая, вероятно, украшала обложку вашего школьного учебника математики.
И, скорее всего, почти все, что вы знаете об этом, неверно.
Разрозненная история
Итак, что же на самом деле стоит за этой знаменитой сценой?
Многие источники утверждают, что он был впервые обнаружен или «изобретен» Леонардо Фибоначчи. Итальянский математик, родившийся около 1170 года нашей эры, первоначально был известен как Леонардо Пизанский, сказал Кейт Девлин, математик из Стэнфордского университета. По словам Девлина, только в 19 веке историки придумали прозвище Фибоначчи (что примерно означает «сын клана Боначчи»), чтобы отличить математика от другого известного Леонардо Пизанского.[Большие числа, определяющие Вселенную]
Но Леонардо из Пизы на самом деле не обнаружил последовательность, — сказал Девлин, который также является автором книги «В поисках Фибоначчи: поиски заново забытого математического гения, изменившего мир» (Принстон University Press, 2017). Древние санскритские тексты, в которых использовалась индуистско-арабская система счисления, впервые упоминают об этом, и те, которые предшествуют Леонардо Пизанскому на века.
«Это было всегда», — сказал Девлин Live Science.
Однако в 1202 году Леонардо Пизанский опубликовал огромный фолиант «Liber Abaci», математическую «поваренную книгу» о том, как проводить вычисления », — сказал Девлин.«Liber Abaci», написанная для торговцев, излагает индуистско-арабскую арифметику, полезную для отслеживания прибылей, убытков, остатков ссуд и т. Д., Сказал Девлин.
В одном месте книги Леонардо Пизанский вводит последовательность с задачей с участием кроликов. Задача состоит в следующем: начните с кролика-самца и кролика-самки. Через месяц они созревают и производят помет с еще одним кроликом и самкой. Через месяц эти кролики размножаются и выходят, как вы уже догадались, еще один самец и самка, которые также могут спариваться через месяц.(Игнорируйте здесь невероятно невероятную биологию.) Сколько кроликов у вас будет через год? Оказывается, ответ — 144, и формула, использованная для получения этого ответа, теперь известна как последовательность Фибоначчи. [11 самых красивых математических уравнений]
«Liber Abaci» впервые представила последовательность в западном мире. Но после нескольких скудных абзацев о разведении кроликов Леонардо из Пизы никогда больше не упоминал последовательность. Фактически, об этом почти забыли до 19 века, когда математики больше узнали о математических свойствах последовательности.В 1877 году французский математик Эдуард Лукас официально назвал задачу о кролике «последовательностью Фибоначчи», — сказал Девлин.
Последовательность Фибоначчи и золотое сечение — красноречивые уравнения, но не такие волшебные, как могут показаться. (Изображение предоставлено Shutterstock)Воображаемое значение
Но каково именно значение последовательности Фибоначчи? Помимо того, что это изящный инструмент обучения, он обнаруживается в нескольких местах на природе. Однако, по словам Девлина, архитектурой вселенной управляет не какой-то секретный код.
Это правда, что последовательность Фибоначчи тесно связана с тем, что сейчас известно как золотое сечение (которое даже не является истинным соотношением, потому что это иррациональное число). Проще говоря, соотношение чисел в последовательности, когда последовательность стремится к бесконечности, приближается к золотому сечению, которое составляет 1,6180339887498948482 … Отсюда математики могут вычислить так называемую золотую спираль или логарифмическую спираль, коэффициент роста которой равен золотое сечение. [9 самых значительных чисел в мире]
«Золотое сечение», кажется, действительно учитывает некоторые типы роста растений, — сказал Девлин.Например, спиральное расположение листьев или лепестков на некоторых растениях соответствует золотому сечению. Сосновые шишки имеют золотую спираль, как и семена подсолнечника, согласно «Филлотаксису: системное исследование морфогенеза растений» (Cambridge University Press, 1994). Но столько же растений не соблюдают это правило.
«Это не« единственное Божье правило »для выращивания растений, скажем так, — сказал Девлин.
И, возможно, самый известный пример из всех, морская ракушка, известная как наутилус, на самом деле не выращивает новые клетки в соответствии с последовательностью Фибоначчи, сказал он.
Когда люди начинают рисовать связи с человеческим телом, искусством и архитектурой, связи с последовательностью Фибоначчи переходят от призрачных к совершенно вымышленным.
«Требуется большая книга, чтобы задокументировать всю дезинформацию о золотом сечении, большая часть которой является просто повторением одних и тех же ошибок разными авторами», — писал Джордж Марковски, математик, работавший в то время в Университете штата Мэн. в статье 1992 года в College Mathematics Journal.
Большая часть этой дезинформации может быть отнесена к книге 1855 года немецкого психолога Адольфа Цейзинга.Цейзинг утверждал, что пропорции человеческого тела основаны на золотом сечении. Золотое сечение породило «золотые прямоугольники», «золотые треугольники» и всевозможные теории о том, где возникают эти знаковые измерения. С тех пор люди говорят, что золотое сечение можно найти в размерах пирамиды в Гизе, Парфенона, «Витрувианского человека» Леонардо да Винчи и ряда зданий эпохи Возрождения. По словам Девлина, общие утверждения о том, что это соотношение «исключительно приятно» для человеческого глаза, были сформулированы некритически.
Все эти утверждения, когда они проверяются, оказываются в значительной степени ложными, сказал Девлин.
«Мы хорошие распознаватели образов. Мы можем видеть закономерности независимо от того, есть они или нет», — сказал Девлин. «Это все просто принятие желаемого за действительное».
Определение линий чисел Фибоначчии их использование
Что такое числа и линии Фибоначчи?
Числа Фибоначчи используются для создания технических индикаторов с использованием математической последовательности, разработанной итальянским математиком, обычно называемым «Фибоначчи», в 13 веке.Последовательность чисел, начинающаяся с нуля и единицы, создается путем сложения двух предыдущих чисел. Например, ранняя часть последовательности — 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 и т. Д.
Затем эту последовательность можно разбить на коэффициенты, которые, по мнению некоторых, позволяют понять, куда будет двигаться данный финансовый рынок.
Последовательность Фибоначчи важна из-за так называемого золотого сечения 1,618 или его обратной величины 0,618. В последовательности Фибоначчи любое данное число приблизительно равно 1.618 раз больше предыдущего числа, игнорируя первые несколько чисел. Каждое число также составляет 0,618 числа справа от него, опять же без учета первых нескольких чисел в последовательности. Золотое сечение широко распространено в природе, где оно описывает все, от количества жилок на листе до магнитного резонанса спинов в кристаллах ниобата кобальта.
Изображение Сабрины Цзян © Investopedia 2021
Ключевые выводы
- Числа и линии Фибоначчи созданы с помощью соотношений, найденных в последовательности Фибоначчи.
- Общие числа Фибоначчи на финансовых рынках: 0,236, 0,382, 0,618, 1,618, 2,618, 4,236. Эти соотношения или проценты можно найти, разделив определенные числа в последовательности на другие числа.
- Хотя официально это не числа Фибоначчи, многие трейдеры также используют 0,5, 1,0 и 2,0.
- Цифры отражают, как далеко цена может зайти после очередного ценового движения. Например, если акция движется с 1 до 2 долларов, к этому могут быть применены числа Фибоначчи. Снижение до 1,76 доллара — 23.6% откат от ценового движения в 1 доллар (округлено).
- Два общих инструмента Фибоначчи — это откаты и расширения. Уровни коррекции Фибоначчи измеряют, насколько далеко может зайти откат. Расширения Фибоначчи измеряют, насколько далеко может зайти импульсная волна.
Формулы для чисел и уровней Фибоначчи
У чисел Фибоначчи нет конкретной формулы, это скорее числовая последовательность, в которой числа имеют определенные отношения друг с другом.
Как рассчитать уровни коррекции Фибоначчи
Числовую последовательность Фибоначчи можно использовать по-разному для получения уровней восстановления Фибоначчи или уровней расширения Фибоначчи.Вот как их найти. Как их использовать, обсуждается в следующем разделе.
Для коррекции Фибоначчи на графике необходимо выбрать две ценовые точки, обычно максимум и минимум колебания. Как только эти две точки выбраны, числа / линии Фибоначчи рисуются в процентах от этого движения.
Если акция вырастет с 15 до 20 долларов, то уровень 23,6% составит 18,82 доллара, или 20 долларов — (5 долларов x 0,236) = 18,82 доллара. Уровень 50% составляет 17,50 долларов, или 15 долларов — (5 долларов x 0,5) = 17,50 долларов.
Уровни расширения Фибоначчи также выводятся из числовой последовательности.По мере продвижения последовательности разделите одно число на предыдущее, чтобы получить коэффициент 1,618. Разделите число на два разряда слева, и получится 2,618. Разделите число на три слева, и получится 4,236.
Расширение Фибоначчи требует трех ценовых точек. Начало движения, конец движения, а затем точка где-то посередине (откат).
Если цена вырастет с 30 до 40 долларов, и эти два ценовых уровня являются точками один и два, то уровень 161,8% будет равен 16 долларам.18 (1,618 x 10 долларов США) выше цены, выбранной для третьего пункта. Если третий пункт равен 35 долларам, уровень расширения 161,8% составляет 51,18 доллара (35 долларов + 16,18 доллара).
Уровни 100% и 200% не являются официальными числами Фибоначчи, но они полезны, поскольку проецируют движение, аналогичное (или кратному) тому, что только что произошло на ценовом графике.
Что вам говорят числа и линии Фибоначчи?
Некоторые трейдеры считают, что числа Фибоначчи играют важную роль в финансах. Как обсуждалось выше, последовательность чисел Фибоначчи может использоваться для создания соотношений или процентов, которые используют трейдеры.
К ним относятся: 23,6%, 38,2%, 50%, 61,8%, 78,6%, 100%, 161,8%, 261,8%, 423,6%.
Эти проценты применяются с использованием множества различных методов:
- Коррекции Фибоначчи. Это горизонтальные линии на графике, обозначающие области поддержки и сопротивления.
- Расширения Фибоначчи. Это горизонтальные линии на графике, указывающие, где может достигнуть сильная ценовая волна.
- Дуги Фибоначчи. Это подобные компасу движения, исходящие от максимума или минимума, которые представляют области поддержки и сопротивления.
- Веера Фибоначчи. Это диагональные линии, построенные с использованием максимума и минимума, которые представляют области поддержки и сопротивления.
- Часовые пояса Фибоначчи. Это вертикальные линии в будущее, предназначенные для прогнозирования основных движений цен.
Уровни коррекции Фибоначчи — наиболее распространенная форма технического анализа, основанного на последовательности Фибоначчи. Во время тренда можно использовать откаты Фибоначчи, чтобы определить, насколько глубоким может быть откат.Импульсные волны — это более крупные волны в направлении тренда, а откаты — это более мелкие волны между ними. Поскольку это волны меньшего размера, они будут составлять процент от большей волны. В это время трейдеры будут следить за соотношением Фибоначчи от 23,6% до 78,6%. Если цена останавливается около одного из уровней Фибоначчи, а затем начинает двигаться обратно в трендовом направлении, трейдер может открыть сделку в трендовом направлении.
Уровни Фибоначчи используются в качестве ориентиров, возможных областей, в которых может развиться торговля.Цена должна подтвердить, прежде чем действовать на уровне Фибоначчи. Заранее трейдеры не знают, какой уровень будет значительным, поэтому им нужно подождать и посмотреть, какой уровень соответствует цене, прежде чем открывать сделку.
Дуги, вееры, расширения и часовые пояса — это схожие концепции, но они по-разному применяются к диаграммам. Каждая из них показывает потенциальные области поддержки или сопротивления, основанные на числах Фибоначчи, примененных к предыдущим ценовым движениям. Эти уровни поддержки или сопротивления могут использоваться для прогнозирования того, где цена может прекратить падение или рост в будущем.
Разница между числами Фибоначчи и числами Ганна
У.Д. Ганн был известным трейдером, который разработал несколько подходов к торговле, основанных на числах. Индикаторы, основанные на его работе, включают веер Ганна и квадрат Ганна. В веере Ганна, например, используются углы в 45 градусов, которые Ганн считал особенно важными. Работа Ганна в основном вращалась вокруг циклов и углов. С другой стороны, числа Фибоначчи в основном связаны с отношениями, полученными из последовательности чисел Фибоначчи.Ганн был трейдером, поэтому его методы были созданы для финансовых рынков. Методы Фибоначчи не создавались для торговли, а были адаптированы к рынкам трейдерами и аналитиками.
Ограничения использования чисел и уровней Фибоначчи
Использование исследований Фибоначчи является субъективным, поскольку трейдер должен использовать максимумы и минимумы по своему выбору. Выбор максимума и минимума повлияет на результаты, которые получит трейдер.
Еще один аргумент против методов торговли числами Фибоначчи состоит в том, что этих уровней так много, что рынок обязательно отскочит или изменит направление около одного из них, что делает индикатор значимым в ретроспективе.Проблема в том, что трудно понять, какое число или уровень будут важны в реальном времени или в будущем.
Сколько раз вы видели Фибоначчи в природе? Вот 7 примеров для вас … — Stemettes Zine
Последовательность Фибоначчи находится путем сложения двух предыдущих чисел последовательности. Вы заметили это в природе?
Фибоначчи (настоящее имя Леонардо Боначчи) был математиком, который разработал последовательность Фибоначчи. Последовательность находится путем сложения двух предыдущих чисел последовательности.Выглядит это так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34… И так далее. Этот шаблон также можно увидеть как:
Последовательность Фибоначчи также встречается повсюду в природе. Это естественный образец. Вот несколько примеров Фибоначчи в природе…
Дерево ФилиалыХотя мы все обычно видим деревья повсюду в повседневной жизни, как часто вы искали в них закономерности? У деревьев Фибоначчи начинается с роста ствола, а затем по спирали направляется наружу по мере того, как дерево становится больше и выше.
Мы также видим золотое сечение в их ветвях, поскольку они начинают с одного ствола, который разделяется на 2, затем одна из новых ветвей разветвляется на 2, и этот образец продолжается.
БуряВаше око бури похоже на 0 или 1 в последовательности Фибоначчи, когда вы продолжаете движение по спирали против часовой стрелки, вы обнаруживаете, что она увеличивается в соответствии с закономерностью. Этот паттерн очень похож на золотое сечение. Но является ли ураган спиралью Фибоначчи?
Вам также стоит прочитать «Знакомьтесь, Челси Такер»
РакушкиПри разрезании раковины наутилуса образуют логарифмическую спираль, состоящую из секций с камерами, называемых камерами.Каждая новая камера равна размеру двух камер перед ней, что создает логарифмическую спираль. Этот пропорциональный рост происходит потому, что наутилус растет с постоянной скоростью на протяжении всей жизни, пока не достигнет своего полного размера.
Лепестки цветовЛепестки цветка растут по Фибоначчи. Из наиболее заметных последовательностей Фибоначчи в растениях лилии с тремя лепестками и лютики с пятью лепестками являются одними из наиболее легко узнаваемых.
Галактики
Золотую спираль можно найти в форме «рукавов» галактик, если присмотреться. Нельзя сказать, следуют ли галактики по идеальной спирали, потому что мы не можем точно измерить галактику, но на бумаге мы можем измерить ее и увидеть размер. Узнайте больше о фибоначчи в галактиках здесь.
Цветочные головкиВ большинстве случаев семена выходят из центра цветочной головки и мигрируют наружу. Прекрасный тому пример — подсолнухи с их спиралевидным узором.Иногда их семенные головки забиваются настолько, что их количество может быть чрезвычайно большим, иногда до 144 и более. При анализе этих спиралей почти всегда число Фибоначчи.
ВЫ!Вы — пример красоты последовательности Фибоначчи. Человеческое тело имеет различные представления пропорций последовательности Фибоначчи, от вашего лица до ушей и рук. Доказано, что вы великолепны с математической точки зрения.
Узнайте больше о Фибоначчи на Odyssey.
Знаете ли вы о каких-либо других примерах Фибоначчи, которые мы упустили? Дайте нам знать в Stemette Society ниже.
Сейчас читаю:
Познакомьтесь с женщинами, занимающимися математикой
Абстрактная математика
Каковы ваши главные советы для начала математической карьеры?
Связанные
Последовательность Фибоначчи влияет на фондовый рынок | Наука
В пятницу, 20 марта, когда фондовый рынок США завершил свою худшую неделю с 2008 года из-за беспорядков, связанных с коронавирусом (прежде чем на следующей неделе несколько восстановились), перед инвесторами встал вопиющий вопрос: все ли идет под откос? В условиях такой экономической нестабильности некоторые исследователи рынка обращаются к знакомому мощному набору чисел для предсказания будущего.
«Коррекция Фибоначчи» — это инструмент, который технические аналитики используют для определения своих взглядов на поведение покупателей и продавцов на рынках. Этот метод назван в честь известной последовательности Фибоначчи, набора чисел, свойства которой связаны со многими природными явлениями. Хотя использование этих чисел для прогнозирования рыночных движений гораздо менее надежно, чем их использование для расчета структуры семян подсолнечника, появление последовательности в области финансов является еще одним свидетельством ее способности захватывать человеческое воображение.
Что такое последовательность Фибоначчи?
Последовательность Фибоначчи — это известная группа чисел, начинающаяся с 0 и 1, в которой каждое число является суммой двух перед ним. Он начинается с 0, 1, 1, 2, 3, 5, 8, 13, 21 и продолжается бесконечно. Паттерн скрывает мощный секрет: если вы разделите каждое число в последовательности на его предшественник (кроме 1, деленного на 0), то по мере продвижения к более высоким числам результат сходится к константе phi , или приблизительно 1.61803, иначе известное как золотое сечение.
Последовательность имеет долгую историю. В Европе это было решение проблемы разведения кроликов, описанной в книге Liber Abaci итальянского математика Леонардо Пизанского в 1202 году нашей эры.Но этот образец был известен в Индии гораздо раньше, возможно, даже в седьмом веке. Название последовательности происходит от прозвища Фибоначчи, что означает «сын Боначчи», данного Леонардо в 19 веке, согласно книге Кейта Девлина В поисках Фибоначчи: В поисках нового забытого математического гения, изменившего мир .Затем математик Эдуоард Лукас в 1870-х годах дал название «последовательность Фибоначчи» последовательности, полученной из сценария с кроликом. (Это также проявилось при подсчете количества пчел в последовательных поколениях).
Между тем, золотое сечение можно записать как половину суммы 1 плюс квадратный корень из 5. И хотя фи не дает такого праздника, как пи, такая константа появляется в природных явлениях. Число спиралей в шишках — это числа Фибоначчи, как и количество лепестков в каждом слое определенных цветов.У спиралевидных растений каждый лист растет под углом по сравнению с его предшественником, равным 360 / phi 2 , и семена подсолнечника упакованы в спиралевидное образование в центре своего цветка, геометрия которого также регулируется золотым сечением.
«Привлекательность золотого сечения проистекает в первую очередь из того факта, что оно имеет почти сверхъестественный способ появиться там, где его меньше всего ожидают», — пишет Марио Ливио в книге «» Золотое сечение: история самого удивительного числа в мире «Фи». .
Но почему эта последовательность так повсеместна? «Многие вещи в математике и, вероятно, в реальном мире регулируются простыми рекурсивными правилами, где каждое вхождение регулируется простой формулой с точки зрения предыдущего вхождения», — сказал Кен Рибет, профессор математики Калифорнийского университета. Беркли. «А у числа Фибоначчи есть простейшая из возможных формул, просто сумма двух предыдущих».
Фибоначчи выходит на рынок
Люди запрограммированы на идентификацию закономерностей, и когда дело доходит до чисел Фибоначчи, мы не ограничиваемся поиском и восприятием последовательности в природе.Фибоначчи и фи можно найти в некоторых произведениях искусства, архитектуры и музыки (хотя это миф, что пирамиды Египта имеют к этому какое-то отношение). И хотя поведение покупателей и продавцов в значительной степени непредсказуемо, некоторые финансовые аналитики клянутся, что они тоже могут увидеть эти цифры в игре, в том числе в нынешнем экономическом кризисе.
Крупный план подсолнечника (Wiki Commons / Alex M3rcer)Инвестиционные исследователи, которых называют «техническими аналитиками», изучают исторические формы графиков, чтобы определить, будет ли текущая тенденция покупки или продажи продолжаться или измениться.Некоторые делают свои прогнозы, используя «уровни восстановления Фибоначчи», полученные из известной последовательности.
Технические аналитики могут смотреть на целый набор чисел, соответствующих соотношениям чисел в последовательности Фибоначчи, но некоторые важные из них — 61,8% и 38,2%. Любое данное число Фибоначчи, деленное на его преемник, составляет приблизительно 1 / фи, или 0,618. Число Фибоначчи, деленное на число на два разряда выше в последовательности, приблизительно равно 0.382.
Например, рассмотрим S&P 500. В разгар рецессии 2008 года индекс достиг своей самой низкой точки в 2009 году — 666 пунктов. С тех пор он, как правило, находится на длительном подъеме, достигнув пика в 3393 человека до резкого падения, вызванного коронавирусом в последние недели.
Чтобы понять тенденции нынешнего спада, Кэти Стоктон, основатель и управляющий партнер фирмы технического анализа Fairlead Strategies, LLC в Стэмфорде, штат Коннектикут, изучает, пробиваются ли ключевые индексы и акции через различные уровни.Если вы возьмете минимум 2009 года в 666 за нижнюю (0 процентов) и максимум 2020 года в 3393 как за верхнюю (100 процентов), Стоктон будет следить за тем, закрывается ли S&P 500 две пятницы подряд ниже того, что она определяет как « уровень поддержки »38,2 процента. Этот уровень соответствует максимуму 3393 минус 1042 (38,2 процента разницы между максимумом и минимумом), что составляет 2351.
Пока что во время кризиса цены не падали так низко две пятницы подряд, хотя 20 марта индекс закрылся на мрачном уровне 2304.92. Если 27 марта цена закроется ниже этого уровня Фибоначчи 2351, это будет второй страйк подряд. Для таких аналитиков, как Стоктон, это будет означать, что S&P рискует упасть ниже уровня 61,8%, или около 1708 года, что, согласно этой точке зрения, делает сейчас менее оптимальным временем для покупок.
Самореализующееся пророчество?
Рибет, математик, отвергает идею поиска паттернов, связанных с последовательностью Фибоначчи, для прогнозирования рынков.Но даже если это неправда, что числа Фибоначчи связаны с фундаментальными рыночными силами, рынки по своей природе реагируют на убеждения своих игроков. Поэтому, если инвесторы массово покупают из-за анализа Фибоначчи, они в любом случае создают восходящий тренд; аналогично для продажи.
Стоктон признает, что это, по крайней мере, частично объясняет движение золота в прошлом году, когда инвесторы внимательно отслеживали, поднимется ли цена унции выше определенного уровня Фибоначчи. Цены на золото значительно упали с 2012 по 2015 год, затем колебались в пределах от 1200 до 1400 долларов за унцию в течение четырех лет до июня 2019 года, когда, похоже, цена снова начала расти.
«Это был большой прорыв Фибоначчи, за которым наблюдали многие люди, даже до такой степени, что он стал настолько широко отслеживаемым уровнем, что, я думаю, он становится неким самореализующимся свойством», — сказал Стоктон.
Идея о том, что числа Фибоначчи управляют торговлей акциями людей, может быть волшебной мыслью, но достаточное количество людей с таким же магическим мышлением может двигать рынки. Готовясь к еще большему хаосу, мы, по крайней мере, можем успокоиться, зная, что сами числа Фибоначчи вечны.
Fabulous Fibonacci
Введение
Числа Фибоначчи — интересная математическая идея. Хотя обычно они не преподаются в школьной программе, особенно в младших классах, преобладание их внешнего вида в природе и легкость их понимания делают их отличным принципом для обучения детей младшего возраста.
Цели обучения
После завершения уроков этого раздела учащиеся смогут:
- Объясните числа Фибоначчи и их происхождение.
- Определите числа Фибоначчи в природе и искусстве.
- Сгенерировать следующие числа в последовательности Фибоначчи.
- Создайте исходную номерную серию.
- Создайте прямоугольник и спираль Фибоначчи.
- Напишите стихотворение акростиха Фибоначчи.
Препарат
- Внимательно прочтите уроки.
- Соберите материалы.
- Распечатайте уроки на цветном принтере.
Урок 1: Введение в числа Фибоначчи
Вы когда-нибудь отрывали лепестки от ромашки? Если вы внимательно посмотрите на центр ромашки, вы обнаружите, что желтый центр не сплошной.Он состоит из наборов спиралей, выходящих из центра. Это не только ромашки! Природа — это математика.
Посмотрите фотографии сосновой шишки. У него такие же спирали. Они не ходят по кругу — они гаснут, как фейерверк. Посмотрите на изображения ниже, чтобы увидеть, как это выглядит. Сколько спиралей идет по часовой стрелке (зеленые линии)? Сколько спиралей идет против часовой стрелки (желтые линии)? Разве это не странно? Разве вы не ожидали, что они будут такими же?
Чтобы понять спирали в сосновых шишках, ананасах, маргаритках и многих других вещах в природе, нам нужно встретиться с математиком по имени Леонардо де Пиза.Большинство людей называют его Фибоначчи (произносится как фиб-о-науч-и). Около 800 лет назад он написал книгу, в которую включил математическую задачу следующего вида:
«Некий человек посадил пару кроликов на место, обнесенное стеной. Сколько пар кроликов можно произвести от этой пары за год, если предполагается, что каждый месяц каждая пара порождает новую пару, от которой второй месяц становится продуктивным? »
(Liber abbaci, стр. 283-284)
(Разве не странно, что 800 лет назад у них были проблемы со словами?) Работа Фибоначчи над этой проблемой привела его к следующей последовательности чисел:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
Можете ли вы определить, какое будет следующее число в последовательности?
Мы называем это последовательностью Фибоначчи, а числа — числами Фибоначчи.Чтобы получить следующее число в последовательности, вы складываете два предыдущих числа вместе. Теперь вернитесь и посмотрите на эти спирали из шишек. Что вы заметили в количестве спиралей в каждом направлении, теперь, когда вы знаете о числах Фибоначчи?
Урок 2: Нахождение Фибоначчи
Теперь, когда вы знаете, что такое числа Фибоначчи, вы готовы к охоте на Фибоначчи.
Цветы
Посмотрите на этот цветок (это лилейник Blizzard Bay, изображение любезно предоставлено Barossa Daylilies).Сколько у него лепестков? Вы видите шесть? Вы думаете, что шесть — это не число Фибоначчи? Посмотри внимательнее. Вы видите, что на самом деле есть два набора по три лепестка? Внешние лепестки с прямыми краями на самом деле не являются лепестками. Их называют чашелистиками. Так сколько же настоящих лепестков?
Не все цветы имеют по три лепестка. У некоторых есть намного больше. Некоторых сложно сосчитать, потому что лепестков слишком много или они расположены рядами. И есть несколько цветов, для лепестков которых нет чисел Фибоначчи.Посмотрите, сможете ли вы найти рисунок ромашки. Являются ли лепестки числом Фибоначчи?
Семенные головки
Семенные головки цветов расположены в виде спиралей последовательности Фибоначчи, как вы видели в сосновых шишках. Посмотрите на семенную головку этого подсолнуха. Вы видите, как упакованы семена? Но ни один из них не разбит. Спиральный узор позволяет цветку поместиться в большинство семенных головок на минимальном пространстве.
Как вы думаете, вы могли бы использовать эту информацию в своей жизни? Как вы думаете, сработает ли попытка упаковать такой чемодан? Почему или почему нет?
Еда
Посмотрите на это изображение фиолетовой цветной капусты.Если вы посмотрите внимательно, вы можете увидеть его центр, где начинаются маленькие цветочки (соцветия).
Вы видите спираль?
Природа полна чисел Фибоначчи и последовательностей Фибоначчи. Посмотрите на плакат Лесной службы с изображением полевых цветов. Сколько примеров чисел Фибоначчи вы можете найти на плакате? (Не беспокойтесь, что слова расплывчаты; просто посмотрите на изображения цветов.)
Урок 3: Работа с Фибоначчи
Материалы
- Большой лист бумаги
- Миллиметровая бумага (Если вам нужна миллиметровая бумага, распечатайте ее на enchantedlearning.com / math / graphs / graphpaper)
- Линейка
- Компас
- Карандаши цветные
Прямоугольники Фибоначчи
Давайте нарисуем несколько прямоугольников, используя числа Фибоначчи. Это перенесет нас в удивительное место. Завершите последовательность Фибоначчи ниже (попробуйте сделать это без посторонней помощи!):
0, 1, 1, 2, 3, 5, __, __, __, __,
Отлично! Вы готовы начать. Во-первых, мы собираемся сделать простую задачу на миллиметровой бумаге.
Интересная особенность создания таких прямоугольников заключается в том, что соотношение (число, показывающее, как стороны соотносятся друг с другом) остается неизменным, независимо от того, насколько большим становится прямоугольник.Это соотношение дает нам прямоугольники, которые мы называем «Золотым прямоугольником», потому что они считаются самыми красивыми прямоугольниками для его внешнего вида. Это соотношение называется золотым сечением. Вы можете найти его, разделив длинную сторону на короткую. Итак, если у вас есть прямоугольник 3 × 5, вы должны разделить 5 на 3. Это даст нам число примерно 1,61. (Узнайте больше о золотом сечении.)
Сможете ли вы найти вокруг себя золотые прямоугольники? Как насчет этой бумажки?
Теперь вы создадите золотой прямоугольник самостоятельно (на большом листе бумаги, а не на миллиметровой бумаге) и увидите что-то действительно удивительное!
- Сначала нарисуйте два квадрата рядом.С помощью линейки сделайте из них квадрат 0,5 см.
- Теперь создайте квадрат 2 × 2 поверх первого квадрата. Итак, если бы первый квадрат был 0,5 см, квадрат 2 × 2 был бы квадратом 1 см, верно?
- Продолжайте эту модель, делая каждый квадрат следующего размера в последовательности Фибоначчи. Итак, после квадрата 2 × 2 вы должны сделать квадрат 3 × 3 (1,5 см × 1,5 см), затем квадрат 5 × 5 (2,5 см × 2,5 см) и так далее. Это похоже на то, что вы делали с миллиметровой бумагой, только с помощью линейки. Продолжайте идти, пока не получите квадрат 21 × 21 (10.5 см × 10,5 см).
- У каждого квадрата будет край, который представляет собой сумму двух квадратов перед ним, как и в последовательности Фибоначчи.
- См. Схему ниже, чтобы узнать, как это должно выглядеть. Последний еще не готов. Вы видите, куда он пойдет?
Теперь с помощью циркуля нарисуйте дугу в квадратах с радиусом, равным размеру края квадрата. Не волнуйтесь из-за этих громких слов; они просто означают, что дуга будет составлять четверть круга.Дуги в первых квадратах будут действительно очень маленькими. Но посмотрите, как они растут!
Посмотрите на это изображение раковины наутилуса. Что ты заметил?
Art Connection
А теперь посмотрите на эту картину Мондриана:
Какие связи вы обнаруживаете между тем, что вы рисовали, и тем, что рисовал Мондриан? Все ли его прямоугольники выглядят для вас как прямоугольники, основанные на Фибоначчи?
Добавочный номер
Оценка
Числа природы: последовательность Фибоначчи
Числа природы: последовательность Фибоначчи
Последовательность Фибоначчи всегда привлекала внимание людей, поскольку, помимо особых математических свойств, другие числа, столь широко распространенные, как числа Фибоначчи, не существуют больше нигде в математике: они появляются в геометрии, алгебре, теории чисел и во многих других областях. области математики и даже в природе! Давайте вместе узнаем, что это такое…
Жизнь Фибоначчи
Леонардо Пизано по имени Фибоначчи (Фибоначчи означает filius Bonacii ) родился в Пизе около 1170 года.Его отец, Гульельмо деи Боначчи, богатый пизанский купец и представитель купцов Пизанской республики в районе Буджи в Кабилии (в современном северо-восточном Алжире), после 1192 года забрал с собой сына, потому что хотел, чтобы Леонардо был стать купцом.
Источник: Википедия
Таким образом, он заставил Леонардо учиться под руководством мусульманского учителя, который руководил им в изучении методов вычисления, особенно тех, которые касались индо-арабских чисел, которые еще не были введены в Европе.Обучение Фибоначчи началось в Беджая и продолжилось также в Египте, Сирии и Греции, местах, которые он посетил со своим отцом на торговых путях, прежде чем окончательно вернуться в Пизу примерно с 1200 года. В течение следующих 25 лет Фибоначчи посвятил себя написанию математических рукописей: из них Liber Abaci (1202), благодаря которым Европа узнала индо-арабские числа, сегодня нам известны Practica Geometriae (1220), Flos (1225) и Liber Quadratorum (1225). .
Репутация Леонардо как математика стала настолько велика, что император Федерико II попросил аудиенции в Пизе в 1225 году. После 1228 года о жизни Леонардо мало что известно, за исключением того, что он получил титул « Discretus et sapiens magister» Леонардо Биголло »В знак признания большого прогресса, которого он добился в математике. Фибоначчи умер где-то после 1240 года, предположительно в Пизе.
Кролики Фибоначчи и знаменитая последовательность
Liber Abaci , помимо ссылки на индо-арабские числа, которые впоследствии заменили римские цифры, также включали в себя большой набор задач, адресованных торговцам, относительно цен на продукты, расчет прибыли от бизнеса, конвертация валюты в различные монеты, используемые в странах Средиземноморья, а также другие проблемы китайского происхождения.Наряду с этими коммерческими проблемами были и другие, гораздо более известные, которые также оказали большое влияние на более поздних авторов. Среди них наиболее известным, источником вдохновения для многих математиков более поздних веков является следующее: «Сколько пар кроликов родится за год, начиная с одной пары, если каждый месяц каждая пара рождает нового? пара, которая становится репродуктивной со второго месяца? ». Решением этой проблемы является знаменитая «последовательность Фибоначчи»: 0, 1, 1, 2, 3, 5, 8, 13, 21,34,55,89… последовательность чисел, в которой каждый член является суммой предыдущие два.
Источник: Oilproject
Важной характеристикой последовательности является тот факт, что отношение между любым числом и предыдущим в серии стремится к четко определенному значению: 1,618… Это золотое сечение или золотое сечение φ (Phi), которое часто встречается в природе (чтобы узнать больше: Совершенство улитки).
Когда Фибоначчи проиллюстрировал эту последовательность как решение проблемы «развлекательной математики», он не придал ей особого значения.Только в 1877 году математик Эдуард Лукас опубликовал ряд важных исследований этой последовательности, которые, как он утверждал, обнаружил в Liber Abaci и которые в честь автора он назвал «последовательностью Фибоначчи». Впоследствии количество исследований увеличилось, и были обнаружены многочисленные и неожиданные свойства этой последовательности, так что с 1963 года издается журнал, посвященный исключительно ей, «Ежеквартальный отчет Фибоначчи».
Последовательность Фибоначчи в природе
Наблюдая за геометрией растений, цветов или фруктов, легко распознать наличие повторяющихся структур и форм.Последовательность Фибоначчи, например, играет жизненно важную роль в филлотаксисе, который изучает расположение листьев, ветвей, цветов или семян у растений с основной целью выявить существование регулярных паттернов. Различное расположение природных элементов следует удивительным математическим закономерностям: Д’арси Томпсон заметил, что царство растений имеет любопытное предпочтение определенным числам и определенной спиральной геометрии, и что эти числа и геометрии тесно связаны.
Мы можем легко найти номера последовательности Фибоначчи в спиралях, образованных отдельными цветками в составных соцветиях маргариток, подсолнечника, цветной капусты и брокколи.
У подсолнечника отдельные цветки расположены по изогнутым линиям, которые вращаются по и против часовой стрелки. Источники: Последовательность Фибоначчи в филлотаксисе — Лаура Реста (диссертация по биоматематике)
Кеплер заметил, что на многих типах деревьев листья выровнены по образцу, который включает два числа Фибоначчи. Начиная с любого листа, после одного, двух, трех или пяти витков спирали всегда есть лист, выровненный с первым, и, в зависимости от вида, это будет второй, третий, пятый, восьмой или тринадцатый. лист.
Расположение листьев на стебле. Источники: Последовательность Фибоначчи в филлотаксисе — Лаура Реста (диссертация по биоматематике)
Другой простой пример, в котором можно найти последовательность Фибоначчи в природе, дается количеством лепестков цветов. У большинства их три (например, лилии и ирисы), пять (парнасия, плоды шиповника) или восемь (космея), 13 (некоторые маргаритки), 21 (цикорий), 34, 55 или 89 (сложноцветные).
 Как открыть хостел | HowToHostel Как открыть хостел …
Как открыть хостел | HowToHostel Как открыть хостел … 
 Например, 13/55 = 0,236 (23,6%), а 2/8 = 0,23076 (23,1%).
Например, 13/55 = 0,236 (23,6%), а 2/8 = 0,23076 (23,1%). Эта пара кроликов производит новую пару кроликов (самку и самца) в первый день февраля и затем в первый день каждого следующего месяца. Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов. Возникает вопрос: сколько пар кроликов будет в огороженном месте через год, то есть через 12 месяцев с начала размножения.
Эта пара кроликов производит новую пару кроликов (самку и самца) в первый день февраля и затем в первый день каждого следующего месяца. Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов. Возникает вопрос: сколько пар кроликов будет в огороженном месте через год, то есть через 12 месяцев с начала размножения.