Определить реальную доходность инвестиций используя формулу фишера – . . , —

ФОРМУЛА ФИШЕРА. Перевод номинальной ставки в реальную и наоборот. — КиберПедия

В процессе оценки необходимо учитывать, что номинальные и реальные (то есть, включающие и не включающие инфляционный компонент) безрисковые ставки.

Номинальная ставка процента— это рыночная процентная ставка без учета инфляции, отражающая текущую оценку денежных активов.

Реальная ставка процента — это рыночная процентная ставка с учетом инфляции

При пересчете номинальной ставки в реальную и наоборот, целесообразно использовать формулу американского экономиста Фишера, выведенную им еще в 30-е годы:

Rн = Rр + Jинф + Rр * Jинф

Rр = (Rн – Jинф) / (1+ Jинф)

где: Rн — номинальная ставка;

Rр — реальная ставка;

Jинф — годовые темпы прироста инфляции.

Важно отметить, что при использовании номинальных потоков доходов коэффициент капитализации (и ее составные части) должны быть рассчитаны в номинальном выражении, а при реальных потоках доходов — реальном. Для преобразования номинальных потоков доходов в реальные нужно номинальную величину разделить на соответствующий индекс цен, то есть выраженное в процентах отношение уровня цен за тот год, в котором возникнут денежные потоки к уровню цен базового периода.

Например:

Объект недвижимости, сданный на условиях чистой аренды, будет приносить по 1000 долл. ежегодно в течение 2-х лет. Индекс цен в текущем периоде равен 140% и ожидается, что в следующем году он составит 156,7%, а через год 178,5%. Для преобразования номинальных величин в реальные, их необходимо выразить в ценах базисного года. Построим базисный индекс цен для каждого из трех лет. Индексы цен текущего года равны 140/140 = 1, для прогнозного периода: первый год — 156,7/140 = 1,119; второй год — 178,5/140 = 1,275.

Таким образом, реальная величина номинальной 1000 долл., которая будет получена в первом прогнозном году, равна 1000 долл./1,119 = 893,65 долл., во 2-м году (1000 долл./1,275) = 784,31 долл.).

Таким образом, в результате инфляционной корректировки происходит приведение ретроспективной информации, используемой в оценке, к сопоставимому виду, а также учет инфляционного роста цен при составлении прогнозов денежных потоков.

Общая идея – между ожидаемой инфляцией и процентной ставкой (доходностью долгосрочных облигаций) существует долгосрочная связь.

Содержание – повышение ожидаемой инфляции вызывает примерно такое же повышение процентной ставки и наоборот.

Уравнение Фишера – формула для количественной оценки связи между ожидаемой инфляцией и процентной ставкой.

 

Упрощенное уравнение.

Если номинальная процентная ставка N равна 10, ожидаемая инфляция I равна 6, R – реальная ставка процента, то реальная ставка процента равна 4, поскольку R = N – I или N = R + I.

 

Точное уравнение.

Реальная процентная ставка будет во столько раз отличаться от номинальной, во сколько раз изменяться цены. 1 + R = (1 + N)/(1 + I). Если раскрыть скобки, то в полученном уравнении значение NI при N и I меньше 10% можно считать стремящимся к нулю. В итоге мы и получим упрощенную формулу.

 

Расчет по точному уравнению при N равном 10 и I равном 6 даст следующее значение R.

1 + R = (1 + N)/(1 + I), 1 + R = (1 + 0,1)/(1 + 0,06), R = 3,77%.

 

В упрощенном уравнении мы получили 4 процента. Очевидно что граница применение упрощенного уравнение — значение инфляции и номинальной ставки менее 10%.

 

Билет 4

1.Связь между уровнем рентабельности и авансированным капиталом. Дисконтированный срок окупаемости проекта (на примере).

Доходность и рентабельность – показатели эффективности деятельности организации.

Рентабельность

характеризует отношение (уровень) прибыли к авансированному капиталу или его элементам; источникам средств или их элементам; общей величине текущих расходов или их элементам. Показатели рентабельности отражают сумму прибыли, полученную организацией на каждый рубль капитала, активов, доходов, расходов и т.д.

Авансированный капитал – финансы, вложенные в производство для извлечения прибыли, причем не разовой, а регулярной. На эти средства приобретаются материалы, оборудование, здания и многое другое, что необходимо для производственного процесса. Следовательно, это показатель важен для увеличения рентабельности предприятия. Ведь предприниматель, инвестируя финансы, планирует получить больше прибыли и в значительно короткие сроки.

Рентабельность – показатель, который определяет количество прибыли, полученной с каждой единицы вложенных средств. Если предприятие конкурентоспособно и эффективно функционирует, значит, показатель будет расти.

На процесс роста компании оказывает большое влияние оборот авансированного капитала. Увеличение скорости приводит к сокращению производственного цикла и ускорению получения прибыли.

Увеличение скорости оборота авансированного капитала приводит к сокращению производственного цикла и ускорению получения прибыли.

Чтобы ускорить оборот, необходимо выполнить следующие процессы:

· Закупать сырье только высокого качества.

· Оптимизировать работу логистического отдела.

· Регулярно стимулировать реализацию товара различными способами.

· Внедрять в производство инновации, направленные на сокращение производственного процесса.

Теперь от теории перейдем к практике и посмотрим, как рассчитать рентабельность авансированного капитала.

Как рассчитать рентабельность

Для расчетов применятся следующая формула рентабельности авансированного капитала:

Р ав. к. = (Пр/ав. к.) х 100%, где:

Р ав. к. – рентабельность авансируемого капитала;

Пр – чистая прибыль фирмы;

ав. к. – авансированный капитал.

Данный показатель рассчитывается как для определения общего финансового состояния предприятия, так и для инвестора для создания пакета информации, на основании которой он принимает решение о сотрудничестве.

Дисконтированный период окупаемости (Discounted payback period, DPP) является одним из наиболее распространенных и понятных показателей оценки эффективности инвестиционного проекта.

Дисконтирование, по сути, характеризует изменение покупательной способности денег, то есть их стоимости, с течением времени. На его основе производят сопоставление текущих цен и цен будущих лет.

Рассматривая механизм формирования показателя периода окупаемости, следует обратить внимание на ряд его особенностей, снижающих потенциал его использования в системе оценки эффективности инвестиционных проектов.

Дисконтированный срок окупаемости инвестиции (Discounted Payback Period, DPP или DPВP) — это момент времени, когда современная ценность доходов, получаемых при реализации проекта, сравняется с объемом инвестиционных затрат.

Для расчета данного показателя используется формула:

Где,

СFt-годовые доходы

-сумма всех инвестиций

−срок завершения инвестирования

При использовании критерия DPP (и PP) при оценке инвестиционных проектов решения могут приниматься исходя из следующих условий:

— проект принимается, если окупаемость имеет место;

— проект принимается только в том случае, если срок окупаемости не превышает установленного для конкретной компании предельного срока.

Преимущества DPP:

– учет стоимости денег во времени;

— учет факта неравноценности денежных потоков, возникающих в различные моменты времени.

Недостатки DPP::

— в отличие от показателя NPV, он не обладает свойством аддитивности.

— не учитывает последующих притоков денежных средств, а потому может служить неверным критерием привлекательности проекта.

В общем случае определение периода окупаемости носит вспомогательный характер относительно чистой текущей стоимости проекта или внутренней нормы рентабельности.

 

Коэффициент дисконтирования или барьерная ставка это показатель, используемый для приведения величины денежного потока в n-периоде оценки эффективности инвестиционного проекта, другими словами ставка дисконтирования это процентная ставка, используемая для перерасчета будущих потоков доходов в единую величину текущей стоимости.

Рассматривая механизм формирования показателя периода окупаемости, следует обратить внимание на ряд его особенностей, снижающих потенциал его использования в системе оценки эффективности инвестиционных проектов.

Первой особенностью показателя периода окупаемости является то, что он не учитывает те суммы чистого денежного потока, которые формируются после периода окупаемости инвестиционных затрат:

График формирования чистого денежного потока по реальному инвестиционному проекту в течение его полного жизненного цикла

Так, по инвестиционным проектам с длительным сроком эксплуатации после периода их окупаемости может быть получена гораздо большая сумма чистого денежного потока, чем по инвестиционным проектам с коротким сроком эксплуатации (при аналогичном и даже более быстром периоде окупаемости последних).

Второй особенностью показателя периода окупаемости, снижающей его оценочный потенциал, является то, что на его формирование существенно влияет (при прочих равных условиях) период времени между началом проектного цикла и началом фазы эксплуатации проекта. Чем большим является этот период, тем соответственно выше и размер показателя периода окупаемости проекта.

Третьей особенностью периода окупаемости, определяющей механизм его формирования, является значительный диапазон его колебания под влиянием изменения уровня принимаемой дисконтной ставки. Чем выше уровень дисконтной ставки, принятый в расчете настоящей стоимости исходных показателей периода окупаемости. тем в большей степени возрастает его значение и наоборот. Он может быть использован как один из вспомогательных показателей на стадии отбора инвестиционных проектов в инвестиционную программу предприятия (в этом случае инвестиционные проекты с более высоким периодом окупаемости при равенстве других показателей оценки будут предприятием отвергаться).

Дисконтированный срок окупаемости разумно понимать как тот срок, в расчете на который вложение средств в рассматриваемый проект даст ту же сумму денежных потоков, приведенных по фактору времени (дисконтированных) к настоящему моменту, которую за этот же срок можно было бы получить с альтернативного доступного для покупки инвестиционного актива.

Для инвестиционного планирования и выбора антикризисных инвестиционных проектов показатель дисконтированного срока окупаемости проекта практически важен в первую очередь тем, что он указывает на тот горизонт времени в бизнес-плане инвестиционного проекта, в пределах которого план-прогноз денежных потоков по проекту должен быть особенно надежным.

cyberpedia.su

Формула Фишера: инфляция и связь с доходностью инвестиций

Ирвинг Фишер американский экономист, представитель неоклассического направления в экономической науке. Родился 27 февраля 1867 года в Согертис, шт. Нью-Йорк. Он внес большой вклад в создание теории денег, а так же вывел уравнение Фишера и уравнение обмена.

Его труды были взяты за основу современных методик для расчета уровня инфляции. Кроме того, они во многом помогли понять закономерности явления инфляции и ценообразования.

Полная и упрощенная формула Фишера

В упрощенном виде формула будет выглядит так:

i = r + π

Где:

• i номинальная процентная ставка,
• r реальная процентная ставка,
• π темп инфляции.

Данная запись является приближенной. Чем меньше значения r и π, тем точнее выполняется это уравнение.

Более точной будет является такая запись:

r = (1 + i)/(1 + π) 1 = (i π)/(1 + π)

Количественная теория денег

Количественная теория денег это экономическая теория, которая изучает воздействие денег на экономическую систему.

В соответствии с моделью, выдвинутой Ирвингом Фишером, государство должно регулировать объем денежных масс в экономике, чтобы избежать их недостатка или чрезмерного количества.

Согласно этой теории, явление инфляции возникает по причине несоблюдении этих принципов.

Недостаточное или чрезмерное количество денежной массы в обороте влечет за собой рост темпа инфляции.

В свою очередь рост инфляции предполагает рост номинальной процентной ставки.

• Номинальная процентная ставка отражает только текущую прибыль от вкладов без учета инфляции.
• Реальная процентная ставка это номинальная ставка процента за вычетом ожидаемого уровня инфляции.

Уравнение Фишера описывает соотношения возникающие между этими двумя показателями и уровнем инфляции.

Видео

Советуем посмотреть данное видео, чтобы лучше разобраться в теории:

Как применять для расчета доходности инвестиции

Предположим, что вы делаете вклад в размере 10 000, номинальная процентная ставка составляет 10%, а уровень инфляции 5% в год. В таком случае реальная процентная ставка составит 10% 5% = 5%. Таким образом, реальная процентная ставка тем меньше, чем выше уровень инфляции.

Именно эту ставку стоит учитывать, чтобы рассчитать количество денег, которое данный вклад принесет вам в будущем.

Типы начисления процентов

Как правило, начисления процентов прибыли происходит в соответствии с формулой сложного процента.

Сложный процент это метод начисления процентов прибыли, при котором они прибавляются к основной сумме и в дальнейшем сами участвуют в создании новой прибыли.

Краткая запись формулы сложных процентов выглядит так:

K = X * (1 + %)n

Где:

• K итоговая сумма,
• X начальная сумма,
• % процентное значение выплат,
• n количество периодов.

Интересно: Баррель нефти как перевести в литры, килограммы или галлоны

При этом, реальный процент, который вы получите сделав вклад под сложные проценты, будет тем меньше, чем выше уровень инфляции.

При этом для любого вида инвестиций имеет смысл рассчитывать эффективную (реальную) процентную ставку: по своей сути это процент от начального вклада, который инвестор получит в конце срока инвестирования. Проще говоря, это отношение полученной суммы к первоначально инвестированной сумме.

r(ef) = (Pn P)/P

Где:

• ref эффективный процент,
• Pn итоговая сумма,
• P начальный вклад.

Используя формулу сложных процентов получим:

ref = (1 + r/m) m 1

Где m количество начислений за период.

Международный эффект Фишера

Международный эффект Фишера это теория обменного курса, выдвинутая Ирвингом Фишером. Суть этой модели заключается в расчете настоящих и будущих номинальных процентных ставок для того, чтобы определять динамику изменений курса обмена валют. Данная теория работает в чистом виде в том случае, если капитал свободно движется между государствами, валюты которых могут быть соотнесены друг с другом по стоимости.

Анализируя прецеденты роста инфляции в разных странах, Фишер заметил закономерность в том, что реальные процентные ставки, несмотря на рост количества денег не увеличиваются. Данное явление объясняется тем, что оба параметра со временем уравновешиваются посредством рыночного арбитража. Этот баланс соблюдается по той причине, что процентная ставка устанавливается с учетом риска инфляции и рыночных прогнозах по валютной паре. Это явление получило название эффект Фишера.

Экстраполировав эту теории на международные экономические отношения, Ирвинг Фишер сделал вывод, что изменение номинальных процентных ставок оказывает непосредственное влияние на подорожание или удешевление валюты.

Данная модель так и не была протестирована в реальных условиях. Основным её недостатком принято считать необходимость выполнения паритета покупательной способности (одинаковая стоимость аналогичных товаров в разных странах) для точного прогнозирования. И, к тому же, неизвестно, можно ли использовать международный эффект Фишера в современных условиях, с учетом колеблющихся курсов валют.

Прогнозирование инфляции

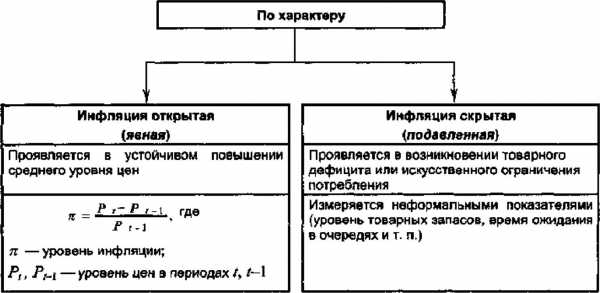
Явление инфляции заключается чрезмерном количестве, обращающихся в стране денег, что ведет к их обесцениванию.

Классификация инфляции происходит по признакам:

Равномерности зависимости темпа инфляции от времени.

Однородности распространения влияния на все товары и ресурсы.

Прогнозирование инфляции рассчитывается с помощью индекса инфляции и скрытой инфляции.

Основными факторами при прогнозировании инфляции являются:

• изменение курса валют,
• увеличение количества денег,
• изменение процентных ставок,

Также распространенным метод является расчет уровня инфляции на основе дефлятора ВВП. Для прогнозирования в этой методике фиксируют такие изменения в экономике:

• изменение прибыли,
• изменение выплат потребителям,
• изменение импортных и экспортных цен,
• изменение ставок.

Расчет доходности инвестиций с учетом уровня инфляции и без него

Доходностью инвестиций принято считать процентное отношение полученной прибыли к сумме начального взноса.

Формула доходности без учета инфляции будет выглядеть следующим образом:

X = ((Pn P) / P )*100%

Где:

• X доходность,
• Pn итоговая сумма,
• P начальный взнос,

В этом виде итоговая доходность рассчитывается без учета потраченного времени.

Для того, чтобы рассчитать доходность в процентах годовых, необходимо воспользоваться следующей формулой:

Xt = ((Pn P) / P ) * (365 / T) * 100%

Где T количество дней владения активом.

Оба способа не учитывают влияния инфляции на доходность.

Доходность с учетом инфляции (реальную доходность) следует рассчитывать по формуле:

Интересно: Ликвидность: что это такое простыми словами

R = (1 + X) / (1 + i) 1

• R реальная доходность,
• X номинальная ставка доходности,
• i инфляция.

Исходя из модели Фишера, можно сделать один главный вывод: инфляция не приносит доходов.

Повышение номинальной ставки вследствие инфляции никогда не будет больше, чем количество денег вложенных, которое обесценилось. Кроме того, высокий темп роста инфляции предполагает значительные риски для банков, и компенсация этих рисков лежит на плечах вкладчиков.

Применение формулы Фишера в международных инвестициях

Как можно заметить, в приведенных выше формулах и примерах, уровень высокий инфляции всегда снижает доходность инвестиций, при неизменной номинальной ставке.

Таким образом, основным критерием надежности инвестиции является не объем выплат в процентном выражении, а целевой уровень инфляции.

Подтверждением тому служит рейтинг стран, в которые поступает больше всего инвестиций. Первые места в нем занимают Китай и США. Рост инфляция в этих странах за последние 5 лет не превышал отметку в 3%.

Описание Российского инвестиционного рынка посредством формулы Фишера

Приведенная выше модель четко прослеживается на примере инвестиционного рынка РФ.

Падение инфляции в 2011-2013 году с 8.78% до 6.5% привело к повышению иностранных инвестиций: в 2008-2009 году они не превышали 43 млдр. долларов в год, а к 2013 достигли отметки в 70 млдр. долларов.

Резкое же повышение инфляции 2014-2015 привело к снижению иностранных инвестиций до исторического минимума. За эти два года сумма вложений в экономику России составила всего 29 млдр. долларов.

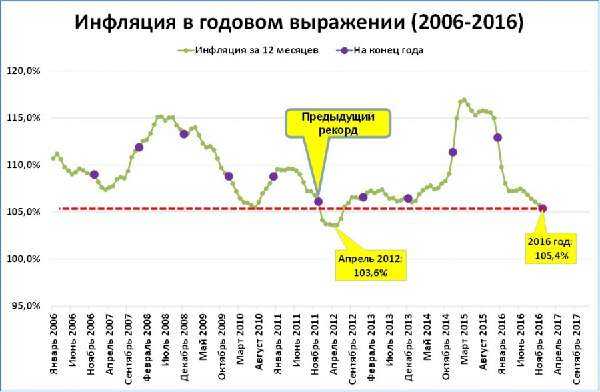
На данный момент, инфляция в России упала до 2.09%, что уже привело к притоку новых вложений от инвесторов.

В данном примере можно заметить, что в вопросах международного инвестирования основным параметром является именно реальная процентная ставка, расчет которой происходит по формуле Фишера.

Как рассчитывается индекс инфляции товаров и услуг

Индекс инфляции или индекс потребительских цен это показатель, который отражает изменение цен товаров и услуг, покупаемых населением.

Численно индекс инфляции представляет собой отношение цен на товары в отчетный период к ценам на аналогичные товары базисного периода.

ip = p1 / p

Где:

• ip индекс инфляции,
• p1 цены на товары в отчетный период,
• p2 цены на товары в базисный период.

Проще говоря, индекс инфляции указывает на то, во сколько раз изменились цены за определенный промежуток времени.

Зная индекс инфляции, можно сделать вывод о динамике инфляции. Если индекс инфляции принимает значения больше единицы, то цены растут, а значит растет и инфляция. Индекс инфляции меньше единицы инфляция принимает отрицательные значения.

Для прогнозирования изменений индекса инфляции используют следующие способы:

Формула Ласпейреса:

IL = ( ∑p1 * q ) / ( ∑p0 * q0 )

• IL индекс Ласпейреса,
• Числитель суммарная стоимость товаров проданных в предыдущем периоде по ценам отчетного периода,
• Знаменатель реальная стоимость товаров в предыдущем периоде.

Инфляции, при повышении цен, дается высокая оценка, а при их падении заниженная.

Индекс Пааше:

Ip = ( ∑p1 * q ) / ( ∑p0 * q1 )

Числитель фактическая стоимость продукции отчетного периода,

Знаменатель фактическая стоимость продукции отчетного периода.

Интересно: CAGR: что это за показатель и как его рассчитать

Идеальный индекс цен Фишера:

Ip = √ ( ∑p1 * q ) / ( ∑p0 * q1 ) * ( ∑p1 * q ) / ( ∑p0 * q0 )

Учет инфляции при расчете инвестиционного проекта

Учёт инфляции в таких инвестициях играет ключевую роль. Инфляции может повлиять на реализацию проекта в двух аспектах:

• В натуральном выражении то есть, повлечь за собой изменение плана реализации проекта.
• В денежном выражении то есть, повлиять на итоговою доходность проекта.

Способы влияния на инвестиционный проект в случае повышения инфляции:

1. Изменение валютных потоков в зависимости от инфляции,
2. Учет инфляционной премии в ставке дисконтирования.

Анализ уровня инфляции и её возможного влияния на инвестиционный проект требуют следующих мер:

• учет потребительского индекса,
• прогнозирование изменения индекса инфляции,
• прогнозирование изменения дохода населения ,
• прогнозирование объема денежных сборов.

Формула Фишера для расчета зависимости стоимости товаров от количества денег

В общем виде формула Фишера для расчета зависимости стоимости товаров от количества денег имеет следующую запись:

MV = PQ

Где:

• М — объем денежных масс в обороте,
• V — частота, с которой деньги используются,
• Р — уровень стоимости товаров,
• Q — количеств товаров в обороте.

Преобразовав эту запись, можно выразить уровень цен: P=MV/Q.

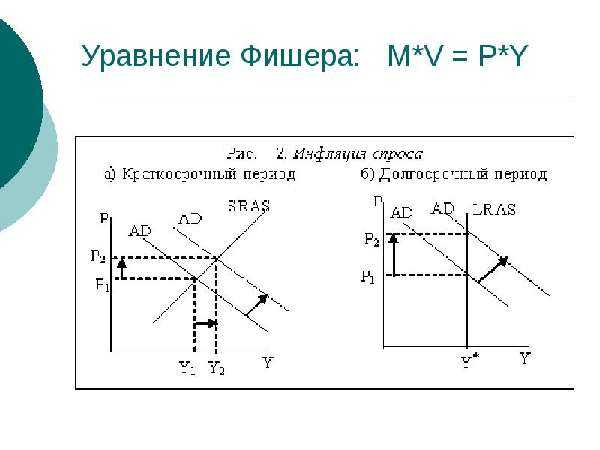
Главным выводом из данной формулы является обратная пропорциональность между стоимостью денег и их количеством. Таким образом, для нормального товарообращения в пределах государства, требуется контроль количества денег, находящихся в обороте. Повышения количества товаров и цен на них требует увеличения количества денег, а, в случае уменьшения этих показателей, следует уменьшать денежную массу. Такого рода регулирование объема денег в обращении возлагается на государственный аппарат.

Формула Фишера в применении к монопольному и конкурентному ценообразованию

Чистая монополия прежде всего предполагает, что один производитель полностью контролирует рынок и совершенной информированностью о его состоянии. Основной целью монополии является максимальная прибыль при минимальных расходах. Монополия всегда устанавливает цену выше значения предельных затрат, а объем выпуска ниже, чем в условиях совершенной конкуренции.

Присутствие на рынке производителя-монополиста как правило имеет серьезные экономические последствия: потребитель тратит больше денег, чем в условиях жесткой конкуренции, при этом рост цен происходит вместе с ростом индекса инфляции.

Если изменение этих параметров учесть в формуле Фишера, то мы получим увеличение денежной массы и постоянное уменьшение количества обращающихся товаров. Такое положение приводит экономику к порочному циклу, в котором увеличение уровня инфляции ведет к увеличению только к увеличению цен, что в конце концов ещё больше стимулирует темп роста инфляции.

Конкурентный же рынок, в свою очередь, реагирует на повышение индекса инфляции совершенно другим образом. Рыночный арбитраж приводит к соответствию цен конъюктуре. Таким образом, конкуренция препятствует чрезмерному увеличению денежной массы в обороте.

Пример связи изменения процентных ставок с уровнем инфляции для России

На примере России, можно заметить прямую зависимость процентных ставок по вкладам от инфляции

Год	Процентная ставка, %	Инфляция, %
2017	9.75-7.75	2.09
2016	10.5-10.0	5.38
2015	15.0-11.0	12.91
2014	7.0-17.0	11.36

Таким образом видно, что нестабильность внешних условий и увеличение волатильности на финансовых рынках заставляет Центральный Банк снижать ставки, при повышении инфляции.

Загрузка…

my-cshost.ru

Эффект Фишера | Азбука трейдера

Начнём сразу с формулировки гипотезы Фишера (эффекта Фишера), которая гласит, что номинальная процентная ставка зависит от двух величин: от реальной процентной ставки и от темпа инфляции. Зависимость эта имеет следующий вид:

i=r+π, где

i – номинальная процентная ставка;

r – реальная процентная ставка;

π – уровень инфляции в стране.

Данная формула получила своё название по имени американского экономиста Ирвинга Фишера внёсшего значительный вклад в теорию денег.

Таким образом, согласно формуле Фишера, номинальная процентная ставка (являющаяся по своей сути ни чем иным как ценой на кредит) также как и цена на любой потребительский товар или услугу, подлежит коррекции через уровень инфляции.

Формула Фишера позволяет оценить реальную прибыльность инвестиций. Так, например, инвестор, вкладывающий деньги в банк под 12% годовых имеет разный реальный доход при различных значениях уровней инфляции. Если инфляция в течение года будет составлять 6%, то реальный процент полученный инвестором будет:

r=i-π=0.12-0.06=6%

Если же предположить, что уровень инфляции за год достигнет значения в 12%, то эффективность инвестиций при данной номинальной процентной ставке сведётся к нулю:

r=i-π=0.12-0.12=0

Полная формула Фишера

Выше приведена формула в упрощённом её виде. Полный её вариант имеет следующий вид:

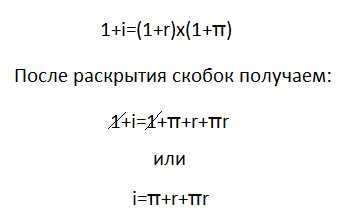
Как видите, полная формула отличается от приближенной наличием произведения rπ. Простая математика показывает нам, что при уменьшении значений r и π, их сумма уменьшается не так стремительно как их произведение. Следовательно, при π и r стремящихся к нулю, произведением rπ можно пренебречь.

Смотрите сами, при значениях π и r равных 10% их сумма составит 0,1+0,1=0,2=20%, а их произведение: 0,1х0,1=0,01=10%. А при значениях π и r равных 1%, их сумма будет равна 0,01+0,01=0,02=2%, а произведение всего: 0,01х0,01=0,0001=0,01%. То есть, чем меньше значения π и r, тем более точные результаты даёт приближенная формула Фишера.

www.azbukatreydera.ru

Всё про доходность инвестиций: как рассчитать, формулы

Для того, чтобы выбрать среди огромного количества вариантов инвестиций в Интернете самые перспективные, инвесторам нужны универсальные критерии оценки. Самый очевидный — это доходность, мера увеличения или уменьшения суммы инвестиций за определенное время.

Доходность измеряется в процентах и показывает отношение прибыли от реальных или финансовых инвестиций к количеству вложенных денег. Она показывает не сколько конкретно инвестор заработал, а эффективность вложений. Инвесторы при анализе вариантов инвестиций смотрят на доходность в первую очередь, нередко забывая о возможных инвестиционных рисках.

Я бы не писал большую статью, если бы для всех случаев работала одна формула — подводных камней при расчёте доходности в разных случаях хватает. В принципе, можно не заморачиваться и использовать для этих целей мой бесплатный инструмент, но все же желательно разобраться в сути вопроса.

В статье рассказывается о часто встречающихся ситуациях, связанных с доходностью инвестиций. Будет много математики класса эдак 8-го, так что готовьтесь 😉 Приятного прочтения! Содержание:

Что такое доходность? Формулы расчёта доходности инвестиций

Базовая формула доходности инвестиций выглядит так:

Сумма вложений — это первоначальная сумма инвестиций плюс дополнительные вложения («доливки»). Инвестиционная прибыль может состоять из разницы между ценой покупки и продажи актива или чистой прибыли инвестиционного проекта. Также сюда могут быть включены регулярные выплаты по источникам пассивного дохода (например, дивиденды акций).

Если неизвестна прибыль, но вы знаете начальную сумму вложений и текущий баланс (суммы покупки и продажи актива тоже подойдут) — пользуйтесь такой формулой:

Доходность инвестиций измеряется в процентах и может служить надежным ориентиром для сравнения двух инвестиционных проектов. Очень показательным выглядит такой пример:

Проект А — 1000$ прибыли за год при начальных инвестициях 5000$. Доходность — 1000$/5000$ = 20%

Проект Б — 1000$ прибыли за год при начальных инвестициях 2000$. Доходность — 1000$/2000$ = 50%

Очевидно, проект Б выгоднее, так как дает более высокую отдачу на вложения, несмотря на то, что чистая прибыль инвестора одна и та же — 1000$. Если увеличить сумму инвестиций в проект Б до 5000$, при доходности 50% за год инвестор заработает уже 2500$.

То есть доходность четко показывает, в каком проекте при прочих равных инвестор заработает больше. Поэтому инвестор с ограниченным размером инвестиционного портфеля старается подобрать активы с более высокой доходностью.

↑ К СОДЕРЖАНИЮ ↑

Расчёт доходности за несколько периодов инвестирования

На практике часто встречаются ситуации, когда инвестиции работают много периодов подряд — начинают работать простые (прибыль снимается после каждого периода) или сложные проценты (прибыль реинвестируется).

Формулы сложных процентов рассчитаны на то, что ставка доходности всегда остаётся постоянной. Но так бывает, пожалуй, только в банках — намного чаще доходность за каждый новый временной период будет отличаться. Как вычислить доходность инвестиций в таком случае?

Если в конце каждого инвестиционного периода прибыль снимается, то все просто — складываем доходности:

Например, если проект принес 5% в первый год и 10% во второй — то таки да, доходность за 2 года составит 15%. Но только при условии вывода прибыли или покрытия убытков. Чаще инвесторы не заморачиваются этим и реинвестируют полученный доход. Для таких ситуаций формула расчёта доходности меняется — мы теперь не складываем, а перемножаем:

Покажу на примере, чтобы было понятнее:

Инвестиционный проект принес 15% за один год, 10% за второй и 20% за третий. Прибыль реинвестируется (работают сложные проценты). Какова итоговая доходность проекта?

Доходность = ((15% + 1)*(10%+1)*(20%+1) — 1) * 100% = (1.15*1.10*1.20 — 1)*100% = (1.518-1)*100% = 0.518*100% = 51.8%

По предыдущей формуле мы получили бы 15%+10%+20% = 45% доходности. Разница в 6.8% достигнута за счёт реинвестирования прибыли — и если её не учитывать, можно получить весьма неточные показатели доходности.

↑ К СОДЕРЖАНИЮ ↑

Расчёт доходности инвестиций с учётом вводов и выводов

Задачка, которая актуальна больше для активных вебинвесторов — они могут перетасовывать свой инвестиционный портфель даже чаще чем раз в неделю.

Для начала, что такое вводы и выводы? Это любое изменение начального инвестиционного капитала, которое не связано с получением прибыли или убытка. Самый простой пример — ежемесячные пополнения инвестиционного счёта из зарплаты.

Каждый раз при вводе или выводе средств меняется знаменатель нашей формулы доходности — сумма вложений. Чтобы вычислить точную доходность вложений, необходимо узнать средневзвешенный размер вложений, рассчитать прибыль от инвестиций с учётом вводов/выводов и вычислить таким образом доходность. Начнем с прибыли, формула будет такой:

Все операции по инвестиционным счетам обычно записываются в специальном разделе вроде «История платежей» или «История переводов».

Как узнать средневзвешенный размер вложений? Вам нужно разбить весь период инвестирования на части, разделенные операциями ввода и вывода. И воспользоваться формулой:

Ворд не очень хочет слушаться и формула получилась корявой на вид. Объясню её на пальцах — мы считаем «рабочую» сумму вложений в каждый из периодов между операциями ввода и вывода и умножаем её на длину периода (в днях/неделях/месяцах), который эта сумма проработала. После всё складываем и делим на полную длину периода, который вас интересует.

Давайте теперь на примере посмотрим как это работает:

Инвестор вложил 1000$ в инвестиционный инструмент. Через 4 месяца инвестор решил добавить еще 300$. Еще через 6 месяцев инвестору понадобились деньги, он снял 200$. В конце года инвестиционный счёт достиг размера 1500$. Какова доходность инвестиционного инструмента?

Шаг 1 — рассчитываем полученную инвестиционную прибыль:

Прибыль = (1500$ + 200$) — (1000$ + 300$) = 400$

Шаг 2 — считаем средневзвешенный размер вложений:

Сумма вложений = (4*1000$ + 6*(1000$+300$) + 2*(1000$+300$-200$))/12 = (4000$+7800$+2200$)/12 = 1166.67$

Шаг 3 — считаем доходность:

Доходность = (400$/1166.67$) * 100% = 0.3429 * 100% = 34.29%

И никак не 50%, если бы мы проигнорировали вводы и выводы — (1500$-1000$)/1000$ * 100% = 50%.

↑ К СОДЕРЖАНИЮ ↑

Расчёт средней доходности инвестиций

Поскольку доходность многих инвестиционных инструментов постоянно меняется, удобно использовать некоторый усредненный показатель. Средняя доходность позволяет привести колебания доходности к одному небольшому числу, которое удобно использовать для дальнейшего анализа и сравнения с другими вариантами инвестиций.

Есть два способа рассчитать среднюю доходность. Первый — по формуле сложных процентов, где у нас есть сумма первоначальных инвестиций, полученная за это время прибыль, а также мы знаем количество периодов инвестирования:

Начальная сумма инвестиций — 5000$. Доходность за 12 месяцев составила 30% (сразу в уме переводим 5000$*30% = 1500$). Какова средняя месячная доходность проекта?

Подставляем в формулу:

Средняя доходность = (((6500/5000)^1/12) — 1) * 100% = ((1.3^1/12) — 1) * 100% = (1.0221 — 1) * 100% = 0.0221 * 100% = 2.21%

Второй способ ближе к реальности — есть доходности за несколько одинаковых периодов, надо посчитать среднюю. Формула:

Проект в первый квартал принес 10% доходности, во второй 20%, в третий -5%, в четвертый 15%. Узнать среднюю доходность за квартал.

Подставляем:

Средняя доходность = (((10%+1)*(20%+1)*(-5%+1)*(15%+1))^(1/4) — 1) * 100% = ((1.1*1.2*0.95*1.15)^(1/4) — 1) * 100% = (1.0958 — 1) * 100% = 0.0958 * 100% = 9.58%

Один из частных случаев вычисления средней доходности — определение процентов годовых, с которыми мы сталкиваемся на каждом шагу в виде рекламы банковских депозитов. Зная доходность инвестиций за определенный период, мы можем рассчитать годовую доходность по такой формуле:

Инвестор вложил 20000$ и за 5 месяцев (округлим до 150 дней) заработал 2700$ прибыли. Сколько это в процентах годовых? Подставляем:

Доходность = (2700$/20000$ * 365/150) * 100% = (0.135 * 2.4333) * 100% = 0.3285 * 100% = 32.85% годовых

↑ К СОДЕРЖАНИЮ ↑

Взаимосвязь доходности и риска инвестиций

Чем больше доходность — тем лучше, вроде бы очевидно. Это правило хорошо работало бы среди безрисковых активов, но таких просто не существует. Всегда есть вероятность потерять часть или всю сумму инвестиций — такова их природа.

Более высокая доходность намного чаще достигается за счет дополнительного увеличения рисков, чем за счёт более высокого качества самого инструмента. Это подтверждается реальными данными — когда я проводил исследование 3000 ПАММ-счетов компании Alpari, обнаружил сильную взаимосвязь между показателем риска СКО (среднеквадратическое отклонение) и доходностью за год:

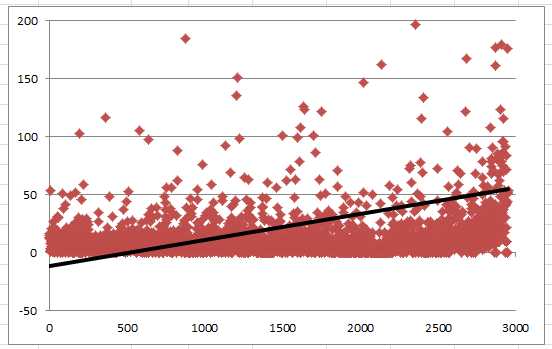
Ось X — доходность за год, ось Y — СКО. Линия тренда показывает, что чем выше годовая доходность, тем выше риски ПАММ-счёта в виде показателя СКО.

Такая взаимосвязь простыми словами — это корреляция, причем достаточно сильная. В исследовании 3000 ПАММ-счетов я рассчитывал корреляцию показателя СКО и доходности и получил значение 0.44, что на такой большой выборке означает крепкую зависимость. Другими словами, взаимосвязь доходности и рисков подтверждается математически.

Задача инвестора — найти собственный баланс между доходностью и риском, точнее определить свою склонность к рискованным вложениям. Для веб-инвестиций минимальная допустимая доходность — на уровне банковской, умноженная на два (большой банк сам по себе надежнее форекс-брокера). Дальше уже зависит от инвестора — сконцентрироваться на минимизации рисков и получать x2-x3 от банковской доходности или пытаться взять на себя дополнительные риски чтобы заработать больше.

Все приведенные выше формулы позволяют рассчитать конечную доходность инвестиций — мы вложили, прошло время, деньги получили. Если говорить о таких инвестиционных инструментах, как ПАММ-счета, торговые роботы, копирование сделок — этого мало, существуют торговые риски и множество других подводных камней, которые могут привести к ненужным потерям.

Инвестор должен знать, что будет происходить с его деньгами в процессе, по этой причине эти инструменты всегда сопровождаются графиками доходности.

↑ К СОДЕРЖАНИЮ ↑

Графики доходности

График доходности — незаменимый инструмент для анализа вариантов инвестирования. Он позволяет посмотреть не просто на общий результат вложений, но и оценить происходящее в промежутке между событиями «вложение денег» и «вывод прибыли».

Существует несколько видов графиков доходности. Чаще всего встречается накопительный график доходности — он показывает, насколько вырос бы в % первоначальный депозит, на основе доходностей за несколько временных промежутков или по результатам отдельных сделок.

Примерно вот так выглядит накопительный график доходности:

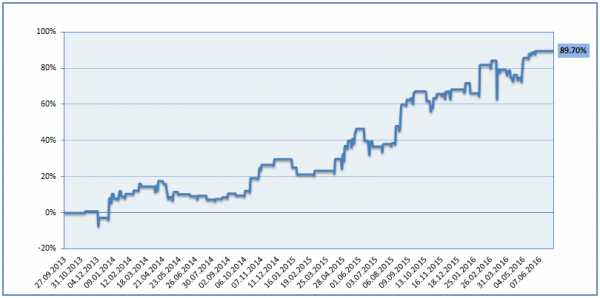
График чистой доходности инвестора ПАММ-счёта Solandr

По нему можно понять несколько важных вещей — например, равномерно ли растёт прибыль (чем более гладкий график, тем лучше), насколько большие просадки (то есть незафиксированные потери в процессе инвестирования) могут ожидать инвестора и т.д.

Очень подробно об анализе графиков доходности я писал в статье о том, как выбрать ПАММ-счёт для инвестирования.

Также часто используются графики доходности по неделям или месяцам:

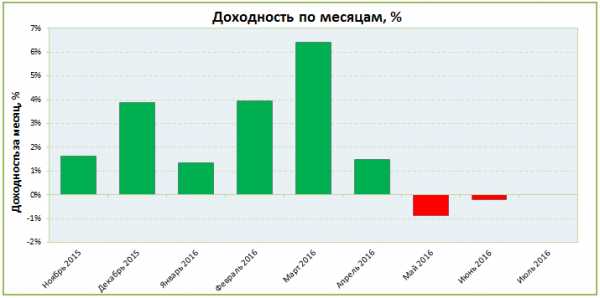
График чистой доходности инвестора ПАММ-счёта Stability Dual Turbo по месяцам

Столбцы говорят сами за себя — март был удачным, а вот за последние три месяца прибыли вообще не было. Если смотреть только на этот график и не брать в расчёт более старые счета Stability, то можно сделать такой вывод — торговая система дала сбой и перестала приносить прибыль. Грамотной стратегией в таком случае будет вывести деньги и ждать пока ситуация вернется в нормальное состояние.

Вообще, графики доходности и ПАММ-счета — это отдельная интересная история.

↑ К СОДЕРЖАНИЮ ↑

Особенности расчёта доходности инвестиций в ПАММ-счета

Начнем с самого очевидного — графики доходности ПАММ-счетов у всех брокеров не соответствуют реальной доходности инвестора! То что мы видим — доходность именно ПАММ-счёта, то есть всей суммы инвестиций, включая и деньги управляющего, и комиссию за управление.

Когда мы видим такие цифры:

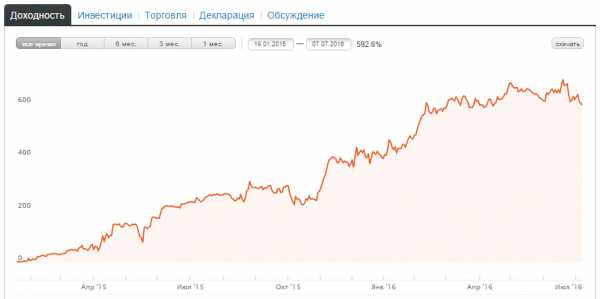
600% за полтора года, рука сразу же тянется к кнопке «Инвестировать», золотая жила же! Однако если мы учтем 29% комиссии управляющего, то реальная доходность окажется такой:

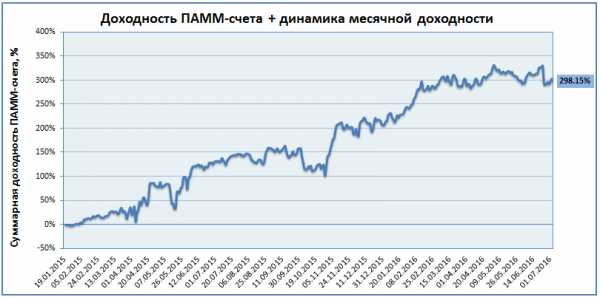
В 2 раза меньше! Я не спорю, 300% за полтора года тоже смотрятся отлично, но это далеко не 600%.

Ну а если углубиться в суть, то доходность ПАММ-счёта считается так:

• Общая доходность считается по формуле доходности за несколько периодов с реинвестированием.
• Положительный результат уменьшается на процент комиссии управляющего, кроме случаев в п.4 и 5.
• Отрицательный результат всегда остается как есть.
• Если положительный результат получен после убытка, он не уменьшается из-за комиссии, пока общая доходность не обновит максимум.
• Если после положительного результата превышен максимум общей доходности — комиссия снимается только с той части, которая превысила максимум.

В итоге получаем весьма замороченную формулу, которая необходима для высокой точности расчётов. Что делать, если вам нужно посчитать чистую доходность инвестора ПАММ-счёта? Предлагаю использовать такой алгоритм:

1. Общая доходность считается по формуле доходности за несколько периодов с реинвестированием.
2. Положительный результат уменьшается на процент комиссии управляющего.
3. Отрицательный результат уменьшается на процент комиссии управляющего.

Все что нужно — умножить официальные цифры доходности ПАММ-счёта на единицу минус комиссия управляющего. Причем не итоговый результат, а данные с графика ПАММ-счёта (в Альпари их можно скачать в удобном виде) и посчитать по формуле доходности за несколько периодов.

Для наглядности посмотрите на один и тот же график доходности, посчитанный тремя способами:

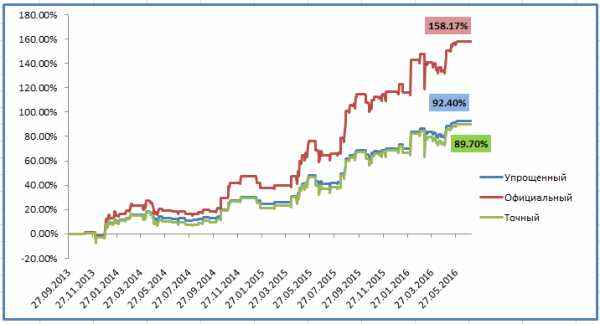
Разница с учётом и без учёта комиссии управляющего — почти в 2 раза! По упрощенному алгоритму мы получили результат 92%, по точному — 89%. Разница не существенная, но для тысяч процентов она станет вполне заметной:

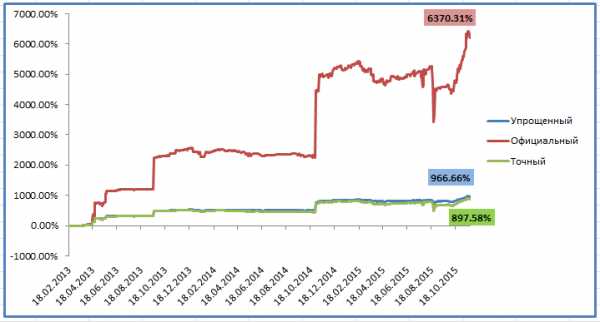
Реальная доходность инвестора ниже в 6 раз, а разница между точным и упрощенным алгоритмом 70% — на больших цифрах всё заметнее.

Кстати, вы хотите знать, откуда вообще берется эта разница? Кроме того, что упрощенный способ подсчета доходности уменьшает размер просадок, есть еще одна фишка — регулярные выплаты вознаграждения управляющего уменьшают вашу долю в ПАММ-счёте.

Вы все поймете, взглянув на эту картинку:

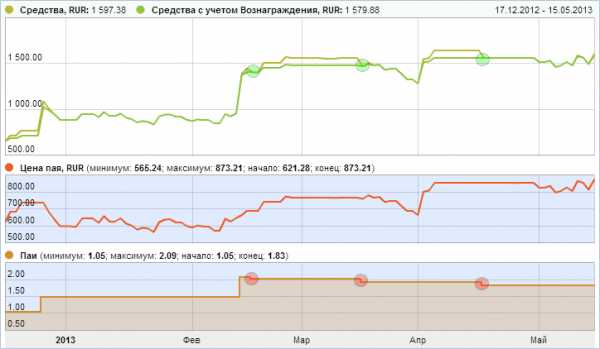
Зелеными кружками показаны моменты выплаты вознаграждения управляющего, красными — уменьшение ваших паёв в ПАММ-счёте. Что такое пай? Это ваша доля в ПАММ-счёте, ваш кусочек общего пирога прибыли.

Для понимания подойдет такое сравнение — паи это определенное количество акций ПАММ-счёта. По этим акциям вы получаете дивиденды — процент от прибыли компании. Количество акций уменьшается — снижаются дивиденды, соответственно и доходность вложений.

Почему же паи уменьшаются? Дело в том, что изначально вы получаете прибыль на всю сумму своих инвестиций — как и должны. Наступает момент выплаты комиссии управляющего — и она берется из вашей суммы, вашего «кусочка пирога». Кусочек стал меньше со всеми вытекающими.

То, что я вам показал — это не плохо, это как есть. Так работают ПАММ-счета, а вкладывать деньги или нет — выбор всегда за вами.

↑ К СОДЕРЖАНИЮ ↑

Друзья, я понимаю что статья довольно сложная, поэтому если есть какие-либо вопросы — задавайте их в комментариях, я постараюсь ответить. И не забывайте делиться статьёй в соцсетях, это лучшая благодарность автору:

Ну и пожелание напоследок: инвестируйте в действительно доходные проекты!

Автор: Александр Дюбченко (добавляйтесь в друзья Вконтакте и на Facebook). С 2016 года веду блог об инвестировании в Интернете, изучаю инвестиции в ПАММ-счета, акции, криптовалюты, драгоценные металлы, валютный рынок. Также разрабатываю вспомогательные инструменты для инвесторов на основе MS Excel. Всегда готов ответить на любые ваши вопросы.

webinvestor.pro

Доходность капитала банка (Реальная процентная ставка), а также Уровень инфляции, Номинальный процент и Формула Фишера

Известно, что индекс потребительских цен в стране в предыдущем периоде равнялся 112%, а в текущем периоде данный индекс равен 120%. Некий коммерческий банк желает предоставить кредит. Процент по кредиту составит 14%. Еще нам известно, что банк предполагает, что темп инфляции в запланированном периоде не изменится и останется на прежнем уровне.

Необходимо определить, чему будет равна доходность капитала анализируемого коммерческого банка, если указано, что темп инфляции за предыдущий период был равен 6%.

 

Решение:

 

1. Мы с вами приступаем к решению данной задачи и, прежде всего, нам нужно рассчитать уровень инфляции в текущем (отчетном) периоде:
Уровень инфляции = (Индекс потребительских цен _{текущий период} – Индекс потребительских цен _{предыдущий период} — 1) / (Индекс потребительских цен _{предыдущий период} — 1)

отсюда:

Уровень инфляции = (120 — 112) / 112 = 0,071 или 7,1%

 

2. Теперь, зная, чему равен уровень инфляции, мы можем определить номинальный процент, используя знаменитую и всем известную формулу Фишера:
Номинальная ставка = (Процент по кредиту _{коэффициент} + Уровень инфляции _{коэффициент}) × 100 / (1 + Уровень инфляции _{коэффициент})

следовательно, получаем:

Номинальная ставка = (0,14 + 0,071) × 100 / (1 + 0,071) = 21,1 / 1,071 = 19,7% или 0,197

 

3. Из условия задачи нам известно, что в предыдущем периоде темп инфляции был равен 6% и не изменился в отчетном периоде. Следовательно, опять-таки, используя формулу Фишера, давайте найдем реальную ставку процента (доходность капитала) – наш последний показатель:

Доходность капитала = Номинальная ставка × (1 + Темп инфляции _{предыдущий период}) — Темп инфляции _{предыдущий период}

подставляем цифры и получаем:

Реальная процентная ставка = 0,197 × (1 + 0,06) — 0,06 = 0,197 × 1,06 – 0,06 = 0,149 или 14,9%

stud-time.ru

Как рассчитать доходность инвестиций | SPRINTinvest.RU

Сегодня мы разберем очень простой и предельно корректный способ расчета доходности инвестиций, применимый для случаев, когда в течение некоторого периода осуществляется ввод/вывод (приток/отток) средств в пределах инвестиционного портфеля.

Мы воспользуемся элегантной формулой расчета доходности инвестиций, которая применима как для оценки доходности портфельных инвестиций в целом, так и отдельных входящих в его состав активов (акций, депозитов и т.п.).

Статья имеет ощутимую ПРАКТИЧЕСКУЮ ценность, поэтому постарайтесь быть повнимательней.

Потраченные усилия с лихвой окупятся, когда вы столкнетесь с необходимостью ТОЧНО и БЫСТРО, а главное — ПРАВИЛЬНО оценить доходность ваших капиталовложений.

Простейшая формула доходности инвестиций

Расчет доходности инвестиций в случаях, когда «тело» инвестиционного портфеля (или отдельного финансового инструмента) пребывает, так сказать, в покое, обычно особых затруднений не вызывает.

Достаточно подставить соответствующие значение в простую и понятную формулу:

N = [∆S/S_нач] *365/T * 100%, где

N – доходность инвестиций, выраженная в процентах,

прибыль, полученная в конце периода,

S_нач – размер первоначальных инвестиций,

T – период инвестирования, выраженный в днях.

К примеру, если, вложившись в какой-нибудь ПАММ-счет в сумме 1000 долл., вы спустя месяц (30 дней) смогли вывести 1100 долл., то доходность ваших инвестиций, выраженная в процентах ГОДОВЫХ, будет составлять 121,67%:

N = [100 долл./1000 долл.] *365 дней/30 дней * 100% = 121,67 % (!).

На практике, однако, бывают ситуации, когда в течение инвестиционного периода вы захотите пополнить свой портфель дополнительными вливаниями или, наоборот, часть средств изъять из инвестиционного портфеля по тем или иным соображениям.

В таком случае корректно рассчитать доходность инвестиционного портфеля будет гораздо сложнее.

Приведенная выше формула в представленном виде окажется бесполезной.

Корректный расчет доходности инвестиций

Итак, рассмотрим способ, с помощью которого можно корректно рассчитать доходность инвестиций для случаев, когда в рамках инвестиционного периода случаются притоки (вводы) или оттоки (выводы) средств.

Примеры ВВОДА средств: пополнение банковского депозита, приобретение дополнительного пакета акций или облигаций, привлечение в инвестиционный портфель новых активов и т.п.

Примерами ВЫВОДА средств являются случаи погашения инвестиционных паев, снятия денег с банковских вкладов, продажи акций, иных ценных бумаг и т.п.

Каждый факт ввода/вывода средств влияет на общую стоимость инвестиционного портфеля.

На конечный результат (размер доходности) влияют и периоды, в течение которых производились эти вводы/выводы.

Чтобы не ходить вокруг да около, рассмотрим формулу доходности инвестиций, которая применяется для решения нашей задачи:

N = [∆S/P] *365/T * 100%, где

∆S = (S_кон + ∑S_вывод) – (S_нач + ∑S_ввод),

P = (T₁ * S_нач + … + T_n * (S_нач + ∑S_ввод — ∑S_вывод))/∑T.

В приведенных формулах приняты следующие обозначения:

N – доходность инвестиций, выраженная в процентах,

∆S – прибыль, полученная в конце периода,

S_кон – итоговая стоимость в конце периода,

∑S_вывод – размер всех выводов средств,

S_нач – размер первоначальных инвестиций (или первоначальная стоимость инвестиционного портфеля),

∑S_ввод – размер всех вводов средств,

P – средневзвешенная сумма инвестиций,

T₁, T₂, T_n – периоды инвестирования, выраженные в днях,

∑T – весь инвестиционный период (дней).

Несмотря на некоторую громоздкость нашей формулы, она в действительности очень проста в применении. Чтобы понять это, рассмотрим конкретный пример.

Применение формулы расчета доходности

ЗАДАЧА. Пусть стоимость нашего инвестиционного портфеля (или размер первоначальной инвестиции) на начало периода составляет 1000 долл.

В процессе инвестиционного периода, равного 1 году (365 дней), производились следующие вводы/выводы средств:

1. Через 160 дней инвестор докупил облигаций на сумму 400 долл.

2. Еще через 80 дней снял с депозита 300 долл.

3. Спустя еще 40 дней приобрел дополнительно акций на сумму 500 долл.

4. На конец инвестиционного периода стоимость портфеля составила 1750 долл.

Как посчитать доходность инвестиций при заданных условиях на конец года?

РЕШЕНИЕ. Для наглядности изобразим наши вводы/выводы на графике:

Теперь последовательно рассчитаем значения ∆S и P:

∆S = (S_кон + ∑S_вывод) – (S_нач + ∑S_ввод) = (1750 + 300) – (1000 + 900) = 150 долл.

P = (T₁ * S_нач + … + T_n * (S_нач + ∑S_ввод — ∑S_вывод))/∑T =[(160 * 1000 + 80 * (1000 + 500) + 40 * (1000 + 500 – 300) + 85 * (1000 + 500 – 300 + 400)] / 365 = 1271,23 долл.

Отсюда искомая доходность инвестиций составит 11,8% годовых:

N = [∆S/P] *365/T * 100% = [150/1271,23] * 365/365 * 100% = 11,8%.

Заключение

Предлагаемая публикация продолжает цикл статей, посвященных методам расчета доходности инвестиций.

Ранее мы уже вели речь о вычислении доходности за период владения активом (HPR) и формуле расчета приблизительной доходности инвестиций при однократном или многократном поступлении дохода.

Формула доходности инвестиций, рассмотренная нами сегодня, является уникальным способом вычисления доходности инвестиций в случаях, когда имеют место вводы (притоки) и (или) выводы (оттоки) средств в процессе формирования одного инвестиционного портфеля.

Оценка доходности инвестиций, получаемая с помощью нашей формулы, отличается точностью и сравнительной простотой. Удачных инвестиций!

sprintinvest.ru