Как правильно решить: «Как правильно решить пример по действиям 3 класс 27:3*5+26-18* 4 =?» – Яндекс.Кью

Как правильно решить пример 10-10×10+10

А = 181738 972965 837181 569279 181569 837229 a) Найдите размерность линейной оболочки строк матрицы A. b) Найдите размерность линейной оболочки столб … цов матрицы A.

1. Какую цифру нужно приписать к числу 2022, чтобы оно делилось на 12? 0 2 4 6 8 нет верного ответа 2. Сейчас отцу 36 лет, сыну 13, дочери 3. Через ск … олько лет сыну и дочери вместе будет столько же лет, сколько и отцу? 13 16 20 30 18 15 3. Турист полетел в Москву на самолёте со скоростью 500 км/ч, обратно возвращался поездом со скоростью 80 км/ч. Какая средняя скорость была на всем пути? Путь туда и обратно считаем одинаковым. Ответ округлить до целых. 290 км/ч 150 км/ч 138 км/ч 235 км/ч 215 км/ч 420 км/ч 4. В записи числа 78*4* замените звездочки на цифры так, чтобы полученное число делилось на 36. Что это за число? 78441 78148 78040 78444 78041 78042 5. Какое свойство из перечисленных является общим для чисел: 2, 4, 6, 10? Куб числа делится на 6 Квадрат числа делится на 3 Куб числа делится на 8 Модуль числа меньше 10 Квадрат числа делится на 6 Модуль противоположных чисел меньше 10 6.

Какое из чисел делится на 9 без остатка? 101333 333112 123003 112202 202002 333133 7. На плане изображён бассейн со сторонами 2 см и 3 см. Какую площадь он займёт на участке земли, если масштаб 1:250? 60 м2 37,5 м2 375 м2 37500 м2 375 см2 3750 см2 8. Известно, что C=7•D, D – натуральное число, не равное 1. Чему равно НОК (C,D) 1 7 D C+D C C•D 9. Оле нужно разрезать лист бумаги размером 91 см на 143 см на одинаковые квадраты наибольшего размера, чтобы от листа не осталось обрезков. Какое количество квадратов должно получится? 132 13 77 7 21 76 10. Таня нашла на чердаке последний отрывок бумажной книги (на каждом листе находятся по 2 страницы, страницы идут подряд). На первой странице стоит номер 325, а последняя записывается теми же цифрами, но в другом порядке. Сколько листов в отрывке книге, если общее число листов в книге более 200? 182 96 98 192 106 104 11. Плата работнику за 30 дней – 20 динаров и 2 платья. Он работал 3 дня и заработал 2 платья. Сколько динаров стоит 1 платье? 1 6 2 и 2/9 3 1 и 1/9 2 12. Сколько положительных корней имеет уравнение? (X2 + 1)•(|X| – 3)•(|X| + 3) = 0 2 4 5 1 3 6 13. У учительницы есть 14 одинаковых апельсинов. Ей нужно разделить их на 24 ученика поровну и раздать. Как это сделать, если каждый апельсин нельзя резать больше, чем на 4 части? 3 разрезать на 4 части, 11 разрезать на 4 части 6 разрезать на 4 части, 8 разрезать на 3 части 14 разрезать на 4 части 5 разрезать на 3 части, 9 разрезать на 4 части 7 разрезать на 2 части, 7 разрезать на 4 части 7 разрезать на 4 части, 7 разрезать на 3 части 14. Числитель и знаменатель дроби в сумме дают 108. Какая есть подобная дробь с наибольшим числителем, если известно, что она меньше 1/5 ? 18/90 20/88 24/84 17/91 30/78 15/90 15. Число a составляет 80% числа b, число с составляет 140% числа b. Чему равны числа a, b, c, если известно, что c больше а на 72? a=96, b=120, c=168 a=80, b=112, c=152 a=60, b=84, c=132 a=100, b=140, c =172 a=120, b=150, c=192 a=20, b=28, c=92

математика пятый класс страница 181 упражнение 535​

3 если AB= 6 2 4 2. Точки А, В и С лежат на одной прямой. Определите как расположены эти точки, 1 АС= 2 , ВС=9 — 4 A) точка В лежит между АиС В) точка … С лежит между А и В C) точка А лежит между ВиС D) точки совпадают E) нет такой точкидам 10 балов пжжж​

Пусть система векторов a1, a2, a3 линейно независима. Докажите, что тогда и система 2a1 − 2a2 − a3, 2a1 + 3a2 − 2a3, −2a1 + 3a2 + 2a3 линейно независи … ма.

1. Какое утверждение неверно? А) вертикальные углы равны B) из трех точек на прямой одна и только Одна лежит между двумя другими C) смежный угол тупог … о угла есть острый угол D) на любой полупрямой от ее начальной точки можно отложить сколько угодно отрезков заданной длины E) сумма смежных углов 180°помогите пжжжждд​

помогите решить задания по математике, очень нужно ​

Урок 40 • Письменное МАТЕМАТИРА В ЖИЗНИ 7 Сколько квадратных метров линолеума потребуется, чтобы покрыть пол, Длина которого 5 м, а ширина Какой длины … кусок нужно отрезать От рулона линолеума шириной 2 м? ТВОРЧЕСКАЯ РАБОТАМне нужно только условия и всё!!!!!!!​

Из-за внедрения нового оборудования количество деталей для грузовых автомобилей выпускаемых на заводе каждый месяц стала увеличивать вдвое Сколько дет … алей было изготовлено в мае? в февраль 102 штук 2 раза больше? в март 2 раза больше ? В апрель 2 раза больше? в май 2 раза больше?

x:107-3003=2107 как решить?

Порядок действий в Математике

Основные операции в математике

Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление.

Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).

Операции действия:

• сложение (+)
• вычитание (-)
• умножение (*)
• деление (:)

Операции отношения:

• равно (=)
• больше (>)
• меньше (<)
• больше или равно (≥)
• меньше или равно (≤)
• не равно (≠)

Сложение — операция, которая позволяет объединить два слагаемых.

• Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.

Вычитание — действие, обратное сложению.

• Запись вычитания: 10 — 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.

Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 — 1 = 9.

Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.

• Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.
• 3 * 4 = 3 + 3 + 3 + 3

В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 * 2 = 5 + 5 = 10.

Поэтому и множитель, и множимое называют сомножителями.

Деление — арифметическое действие обратное умножению.

• Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.

В этом случае произведение делителя 6 и частного 5, в качестве проверки, дает делимое 30.

Если в результате операции деления, частное является не целым числом, то его можно представить в виде дроби.

Возведение степень — операция умножения числа на самого себя несколько раз.

Основание степени — число, которое повторяется сомножителем определённое количество раз.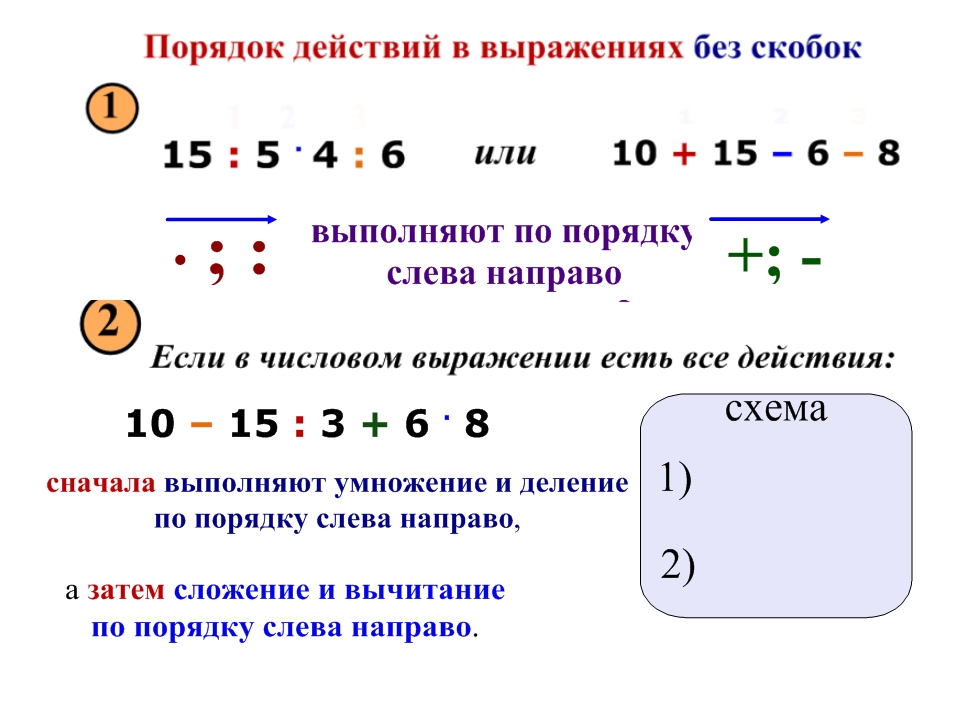 4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).

2√16 = 4 — корень второй степени называется — квадратным.

При знаке квадратного корня показатель корня принято опускать: √16 = 4.

3√8 = 2 — корень третьей степени называется — кубическим.

Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно представляют обратные друг другу действия. Далее узнаем порядок выполнения арифметических действий.

 

Порядок вычисления простых выражений

Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:

• действия выполняются по порядку слева направо
• сначала выполняется умножение и деление, а затем — сложение и вычитание.

Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.

Что первое, умножение или деление? — По порядку слева направо. Сначала умножение или сложение? — Умножаем, потом складываем.

Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Рассмотрим порядок арифметических действий в примерах.

Пример 1. Выполнить вычисление: 11- 2 + 5.

Как решаем:

В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.

Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.

Ответ: 14.

Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?

Как рассуждаем:

Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.

Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.

Ответ: 7.

Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.

Например, в такой последовательности можно решить пример по действиям:

Действия первой и второй ступени

В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.

• Действиями первой ступени называют сложение и вычитание, а умножение и деление — действиями второй ступени.

С этими терминами правило определения порядка выполнения действий звучит так:

Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).

Порядок вычислений в выражениях со скобками

Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:

Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.

Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.

Рассмотрим порядок выполнения действий на примерах со скобками.

Пример 1. Вычислить: 10 + (8 — 2 * 3) * (12 — 4) : 2.

Как правильно решить пример:

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.

Начнем с первого 8 — 2 * 3. Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание. Получается так:

8 — 2 * 3 = 8 — 6 = 2.

Переходим ко второму выражению в скобках 12 — 4. Здесь только одно действие – вычитание, выполняем: 12 — 4 = 8.

Подставляем полученные значения в исходное выражение:

10 + (8 — 2 * 3) * (12 — 4) : 2 = 10 + 2 * 8 : 2.

Порядок действий: умножение, деление, и только потом — сложение. Получится:

10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.

На этом все действия выполнены.

Ответ: 10 + (8 — 2 * 3) * (12 — 4) : 2 = 18.

Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.

Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).

Как решаем:

Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:

2 + 3 = 5.

Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:

5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.

Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.

Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.

 

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.

Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.

И, как всегда, рассмотрим, как это работает на примере.

Пример 1. Вычислить (4 + 1) * 3 + 62 : 3 — 7.

Как решаем:

В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.

Подставляем полученное значение в исходное выражение:

(4 + 1) * 3 + 36 : 3 — 7.

Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:

(4 + 1) * 3 + 36 : 3 — 7 = 3 * 3 + 36 : 3 — 7 = 9 + 12 — 7 = 14.

Ответ: (3 + 1) * 2 + 62 : 3 — 7 = 14.

У нас есть статья «знаки больше, меньше или равно», она может быть полезной для тебя!

Как правильно решать семейные конфликты: советы психолога

Уметь правильно разрешать споры — очень важный навык, особенно в семейной жизни, ведь нет идеальных людей и ситуаций. Как этому научиться, рассказала психолог сектора ранней профилактики семейного центра «Диалог» Юлия Грачева.

Одними из наиболее распространенных конфликтов считаются споры между супругами. Основные причины таких ситуаций — невозможность выразить свои чувства, отсутствие связи, проявления гнева, нечеткие границы личной территории.

Основные стратегии конфликтов:

1. Стратегия избегания (ухода). В таком случае конфликт не решается, а происходит замалчивание интересов сторон и замораживание их общего развития.
2. Доминирование. Заранее обречено на неуспех. В таком случае игнорирование интересов и потребностей одного партнера в пользу другого еще больше усугубит ситуацию.
3. Уступчивость. Приведет к фрустрированному состоянию (чувству невозможности удовлетворения собственных потребностей) одного из членов семьи, дисбалансу в отношениях (права, власть, обязанности). Так же, как в стратегии доминирования, происходит игнорирование потребностей одного из членов семьи.
4. Компромисс. В таком случае внешне конфликт кажется разрешенным, однако взаимные уступки могут быть непростыми для каждой из сторон, так как не учтена совместимость и общность интересов.
5. Сотрудничество. Это наиболее оптимальный вариант решения конфликта. Конфликтующие стороны вступают в диалог и находят выход, который помогает каждой из них максимально реализовать свои интересы и сохранить долгосрочные отношения.

Правила мирного спора

1. Не опускайтесь до оскорблений. Это важное и обязательное правило для любого конфликта.
2. Сохраняйте спокойствие. Если чувствуете, что сейчас не сможете сдержать эмоций, переключите внимание — например, досчитайте до 10, попробуйте сесть на стул или диван, в такой позе выражать гнев сложнее.
3. Не всегда ситуация разрешима мгновенно, иногда нужно побыть друг без друга несколько часов, чтобы найти более рациональное решение.
4. Слушайте друг друга: например, можно ставить таймер по 2 минуты на каждого оратора.
5. Если градус ссоры велик — скажите заранее оговоренное слово-стоп, после которого воцаряется минутная пауза. Часто этого хватает, чтобы обе стороны успели стабилизировать свое эмоциональное состояние.
6. После каждой ссоры анализируйте причину, почему она возникла. Если вы неправы, признайте это.
7. В диалоге используйте технику, которая помогает говорить в конфликте так, чтобы вас услышали: «я-сообщения», когда предложения строятся в формате транслирования своих чувств и желаний, без оценки другого. Формула «я-сообщения»: факт + чувства + потребности + ожидаемый результат. Нужно говорить только о себе:

• Когда я вижу, что происходит … (описывайте факт без привязки к другому человеку)
• Я чувствую … (как можно точнее называйте свои эмоции: растерянность, обиду, злость)
• Потому что мне важно … (наиболее подробно конкретизируйте и описывайте то, что вам важно)
• Я бы хотел(а), чтобы ситуация развивалась . .. (описывайте свои ожидания. Старайтесь избегать местоимения «ты»!)

Например, муж не вынес мусор: «Когда я увидела, что мусор остался в корзине, я расстроилась. Потому что мне важно, чтобы наши договоренности соблюдались. Я хотела бы, чтобы в следующий раз мусор был вынесен вовремя». Как и любую технику, чтобы она работала, нужно отрабатывать, поэтому сейчас вспомните пару-тройку конфликтных ситуаций и сформулируйте свою мысль с помощью этих техник.

«Помните, что применение в конфликтной ситуации сотрудничества, уважения и выражения свои эмоций через „я-сообщение“ позволит прийти к конструктивному диалогу. И если вы оказались в ситуации, когда ссоры и непонимание стали неотъемлемой частью жизни, когда говорить с каждым днем становится все сложнее и сложнее, лучше обратитесь к специалисту, который поможет вам с этим справиться лично» — советует Юлия.

Если вы зашли в тупик в своих отношениях и не знаете, что с этим делать и как поступить, обращайтесь к специалистам столичных семейных центров.

Источник

Пресс-служба Департамента труда и социальной защиты населения города Москвы

Как решать задачи правильно и с чего начать решение задачи

В этой статье Вы узнаете как решать задачи по математике, если не знаете с чего начать.

Часто при решении задач школьники «входят в ступор» — в голове туман, мысли куда-то разбежались, и кажется, что собрать их уже не возможно.

Я хочу на примере решения задачи из Открытого банка заданий показать, какие простые действия нужно сделать, чтобы собраться с мыслями и как решать задачи правильно.

 

 

Как решать задачи. Задание B13 (№ 26582)

Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 98 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 7 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.

1. Внимательно читаем задачу. Возможно, несколько раз.

2. Определяем, о каком процессе идет речь в задаче,  и какие формулы описывают этот процесс. Выписываем эти формулы. В данном случае это задача на движение, и формула, которая описывает этот процесс S=vt.

3. Выписываем размерность каждой переменной, которая входит в состав уравнения:

• S — расстояние  — км
• v — скорость —  км/ч
• t — время — ч

Знание размерности поможет нам при проверке получившихся формул.

4. Выписываем  все  числа, которые встречаются в условии задачи, пишем,  что они обозначают и их размерность:

98 км — расстояние между городами,

7 км/ч  — на столько скорость велосипедиста на обратном пути больше, чем скорость на пути из  города А в город В,

7 часов — время остановки велосипедиста (это время он не ехал)

5. Ещё раз читаем вопрос задачи.

6. Решаем, какую величину мы примем  за неизвестное. Удобно принимать за неизвестное ту величину, которую надо узнать в задаче. В данном случае это скорость велосипедиста на пути из А в В.

Итак: пусть  скорость велосипедиста на пути из А в В равна х. Тогда, поскольку скорость велосипедиста на обратном пути на 7 км/ч больше, чем скорость на пути из  города А в город В, то она равна x+7.

7. Составляем уравнение. Для этого  выразим третью величину уравнения движения (время) через первые две. Тогда:

• время, которое затратил велосипедист на дорогу из А в В равно  98/x,

• а на дорогу из В в А — 98/(x+7)+7 — вспомним, что на пути обратно велосипедист сделал остановку на 7 часов, то есть его время в пути складывается из времени  движение и времени стоянки.

Уравнение составляем для времени. Ещё раз читаем в условии задачи, что в нем говорится о времени: В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. То есть время  «туда » равно времени «обратно». Приравниваем время «туда» и время «обратно» Получим уравнение:

98/x=98/(x+7)+7.

Ещё раза проверяем размерность величин, которые входят в уравнение — нужно следить за тем, чтобы, например, не прибавлять к километрам часы.

8. Решаем уравнение. Теперь нужно сосредоточиться на решении уравнения. Для этого определим, какого типа это уравнение. Поскольку неизвестное находится в знаменателе дробей, это рациональное уравнение. Чтобы его решить, нужно перенести все слагаемые влево и привести дроби к общему знаменателю. Заметим, что числа 98 и 7 кратны 7.

Чтобы упростить решение, разделим обе части уравнения на 7. Получим уравнение: 14/x=14/(x+7)+1

После этого переносим все слагаемые влево, приводим к общему знаменателю, и приравниваем числитель к нулю.

Получаем в числителе: 14(x+7)-14x-x(x+7)=0 Раскроем скобки, приведем подобные слагаемые и решим квадратное уравнение.

Его корни: -14 и 7.

Число -14 не подходит по условию задачи: скорость должна быть положительной.

Ещё раз читаем вопрос задачи и соотносим его с величиной, которую мы нашли: за неизвестное мы приняли скорость велосипедиста на пути из А в В, и эту же величину требуется найти.

Ответ: 7 км/ч.

Как решать задачи. Итог

Заметим, что весь путь решения задачи мы разбили на маленькие кусочки, и на каждом участке сосредотачивались именно на обдумывании конкретного действия. И только после  того, как это действие выполнялось, делали следующий шаг.

Когда не ясно что делать, нужно решить, какой маленький шаг  можно сделать прямо сейчас, сделать его, а потом уже думать о следующем.

Нереалистичные обещания онлайн-школ по подготовке к ЕГЭ

Ольга Абашкина

учитель обществознания

Профиль автора

Заниматься в онлайн-школах выгоднее, чем с репетиторами: разница в цене между ними — минимум полтора раза.

Но не все онлайн-школы одинаково хороши: иногда они заманивают клиентов нереалистичными обещаниями, а в итоге абитуриент проваливается на экзаменах. В этой статье я расскажу, каким популярным рекламным фразам не стоит верить и как на самом деле помочь ребенку сдать ЕГЭ с хорошим результатом.

«Мы гарантируем 80, 90, 100 баллов на экзамене»

Почему не стоит верить. Балл на экзамене зависит не только от знаний, но еще и от везения и способности ученика сохранять хладнокровие. Занятия в школе или с репетитором могут повлиять только на первую составляющую. Все, что можно обещать: ученик окончит обучение, зная больше, чем раньше — и то при условии ответственного отношения к занятиям.

Центр обещает вернуть деньги, если ученик получит меньше 80 баллов на экзамене

Как быть. Чтобы понять, насколько качественно учит школа, я рекомендую перед началом занятий самостоятельно проверить свой уровень знаний. Для этого можно пройти очное или онлайн-тестирование в Московском центре качества образования, Московском государственном центре диагностики успеваемости, дистанционную диагностику в РГПУ им. Герцена или решить пробный вариант ЕГЭ на сайте онлайн-школы «Фоксфорд».

Такая диагностика часто платная: прохождение тестов стоит 1500—3000 Р за предмет

Бесплатные тесты на сайтах вроде «Решу ЕГЭ» или «Яндекс-репетитор» не заменяют такую проверку полностью: система не позволяет оценить выполнение заданий с развернутым ответом, например историческое эссе или сложный план в ЕГЭ по обществознанию.

Тестирование позволит родителям и ребенку понять стартовый уровень. Затем раз в два-три месяца стоит повторять проверки и отслеживать прогресс. Если за несколько месяцев в онлайн-школе общий балл не вырос, значит, конкретная школа некачественно учит или ребенку не подходит формат обучения. Возможно, ему не хватает обратной связи от преподавателя или школа тратит мало времени на объяснение сложных нюансов решения заданий. Не исключено, что школа просто дает не те знания, которые реально нужны на экзамене.

«Мы вернем деньги, если ребенок не поступит в университет»

Почему не стоит верить. Обычно школы, которые дают такое обещание, страхуют себя от будущих судебных исков и прописывают дополнительные условия, необходимые для возврата денег. Например, в условиях программы «Гарантированное поступление в вуз мечты» одной известной онлайн-школы можно найти такие требования:

1. Просмотреть 100% занятий по всем курсам выбранной программы.
2. Выполнить 100% домашних заданий и контрольно-проверочных работ по всем курсам выбранной программы с задержкой не более 2 недель.
3. Решить верно не менее 50% заданий всех курсов.
4. Правильно заполнить документы для поступления в вуз.

Требования, касающиеся посещения занятий и выполнения домашних заданий, в целом посильны и требуют лишь дисциплинированности и крепкого здоровья, чтобы не пропускать занятия по болезни. Но требование к верности выполнения предполагает, что у школьника в ходе обучения не должно возникать проблем. Это нереалистично: в онлайн-школы приходят именно для того, чтобы подтянуть сложные предметы.

Если не смотреть в условия программы, кажется, что ученик надежно защищен

Аналогичное обещание дают и другие школы. Обычно требуется посетить 95% занятий, просмотреть 100% материалов, выполнить 100% заданий, при этом не подглядывая в ответы.

Бывает, что деньги обещают вернуть только тем абитуриентам, которые подадут документы в максимальное количество мест по закону и не поступят ни в один университет — а не только туда, куда действительно хотели попасть.

Иногда онлайн-школы требуют, чтобы ученик занимался на курсах всеми предметами, которые будет сдавать на ЕГЭ, иначе условия для возврата считаются невыполненными. Выходит, придется посещать занятия даже по той дисциплине, с которой ребенок не испытывает затруднений. Если для поступления нужны английский, русский и математика, а сложности только с последним предметом, первыми двумя тоже придется заниматься на курсах, иначе в случае непоступления деньги не вернут.

Как быть. Внимательно читать договор, чтобы точно знать условия. Но лучше не рассматривать обещание вернуть деньги как значимый критерий при выборе школы: возврат получить сложно, и он не примирит с неудачным результатом.

«У нас вы будете учиться в легкой игровой форме, весело и без напряжения»

Почему не стоит верить. Онлайн-школы нередко стремятся предельно упростить материал. Якобы подростки не готовы читать тексты длиннее двух предложений, предложения длиннее пяти слов и вообще предпочитают картинки, а не слова.

Психолог Никита Логинов о клиповом мышлении

В результате во время занятий выпускников зачастую не тренируют формулировать мысли развернуто и обоснованно, тогда как на экзамене этого не избежать. Формат «короткие подписи к ярким картинкам» не позволяет дать подробное объяснение того или иного явления, не учит понимать запутанные условия заданий.

Для ЕГЭ важно уметь классифицировать объекты, а классификация в этом материале может сбить с толку. Почему проблема «использования Мирового океана» выделяется как самостоятельная, а не относится к экологическим или сырьевым? Еще одна проблема конспектов — попытка написать коротко, но при этом книжно. Формулировки вроде «духовный аристократизм» большинство учеников не воспроизведут самостоятельно, а кто-то, к сожалению, просто не поймет Пример задания из ЕГЭ по обществознанию. Как видно, составители просят дать развернутый ответ. Но в примерах конспектов, которые я привела выше, нет полных мыслей, лишь краткие тезисы

Как быть. Сама по себе идея о том, что материал должен доноситься просто, не плоха. Но в целом изложение учебного материала должно соответствовать академическим стандартам. Иначе у школьника в памяти не сохранится ничего, кроме картинок, а на экзамене этого может оказаться недостаточно. Чтобы убедиться, что материал курсов соответствует требованиям экзамена, на сайте ФИПИ можно скачать кодификаторы по всем предметам — подробные перечни тем, которые надо знать выпускнику, — и сравнить программу онлайн-школы с этими требованиями.

Чтобы выпускник мог аргументированно изложить позицию, ответить на вопросы по тексту, привести развернутые примеры, ему стоит почитать хорошие научные или научно-популярные тексты. Если самостоятельно оценить источники сложно, воспользуйтесь, к примеру, лонг-листом премии «Просветитель».

Попробуйте купить ребенку хорошую учебную литературу. Неплохой вариант — вузовские учебники для первокурсников по непрофильным дисциплинам. Например, учебник по российскому праву Кашаниных подойдет для подготовки к экзамену по обществознанию, а для изучения русского языка подойдет проверенный временем «Справочник по правописанию и стилистике» Д.  Э. Розенталя.

Также лучше выбирать школы, которые работают в режиме лекций или онлайн-семинаров, а не те, где предлагают заранее записанные вебинары. Так ребенок сможет уточнить что-то напрямую у преподавателя, если столкнется с противоречием в конспекте или чего-то не поймет.

«Мы замотивируем ребенка на учебу»

Почему не стоит верить. За мотивацию в онлайн-школах обычно отвечают кураторы или наставники. Как правило, это бывшие выпускники школы или студенты-первокурсники, которые получают за свой труд небольшие деньги. Например, «сотрудник чата поддержки» в одной из онлайн-школ получает 100 Р в час, а «координатор обучения» с гораздо большим количеством обязанностей — в среднем 20 000 Р в месяц.

Это люди без специального образования, которые не владеют необходимыми навыками для успешной мотивации учеников: вся «мотивация», которую обещают школы, часто сводится к напоминанию о времени урока и о домашних заданиях.

Задачи куратора в одной из онлайн-школ

Как быть. Если ребенка действительно нужно мотивировать к занятиям, я рекомендую выбрать школу, которая предусматривает систему «штрафов» для учащихся, а не родителей и не предлагает услуги куратора. На мой взгляд, пример ниже — хорошая мотивация и по сути, и по форме.

У ученика есть жизни, как в компьютерной игре. После потери всех жизней ученика отчислят с курса

Окно с жизнями — не сухое уведомление о расторжении договора в случае невыполнения требований школы, а предложение почувствовать себя хорошим игроком, который сумел успешно пройти миссию.

Геймификация, хоть и кажется несерьезным способом мотивации, на самом деле работает, в том числе и на взрослых людях. Например, приложение для изучения иностранных языков «Лингвалео» предлагает учащимся зарабатывать за выполнение заданий виртуальные фрикадельки, которыми можно кормить льва. Приложение популярно среди взрослых, несмотря на «детскую» мотивацию.

Но важно, чтобы учеба все же не воспринималась как игра, особенно во время подготовки к экзамену.

«Наши онлайн-курсы будут требовать всего 60 свободных минут в неделю»

Почему не стоит верить. Если школьнику действительно достаточно часового занятия раз в неделю, ему не нужен репетитор. Подобные уроки — скорее психотерапия, нежели учеба: возможность еще раз убедиться, что все понятно и не вызывает вопросов. Ради этого не стоит тратить деньги весь год, проще походить к преподавателю в индивидуальном формате пару недель перед экзаменом. В остальных случаях старшеклассник не успеет пройти программу за час в неделю.

Описание годового курса по русскому языку. За 25 часовых занятий ученику, «нацеленному на 100 баллов», предлагают освоить всю программу, необходимую для сдачи ЕГЭ Другая школа предлагает подготовиться к экзамену по обществознанию за 26 занятий общей продолжительностью 30 часов. На изучение экономики — одного из разделов курса, по которому на ЕГЭ примерно 20% заданий, — школа отводит два занятия

Как быть. Сравните, сколько часов на изучение предмета отводится в госстандарте. На обществознание за 10—11 классы в сумме должно быть запланировано 140 часов — ЕГЭ проверяет материал, который проходят как раз за эти два года.

Поэтому выбирайте курсы, программа которых предполагает занятия два-три раза в неделю и обязательное домашнее задание, необходимое для допуска к следующему занятию или хотя бы к следующему блоку курса. Еще лучше, если в самой школе есть промежуточная аттестация.

Число занятий в неделю, на мой взгляд, важнее общего количества часов: два часовых занятия в неделю лучше одного двухчасового. Мой опыт подготовки ребят к ЕГЭ показывает, что для сдачи экзамена по русскому на 80—90 баллов обычному школьнику — не двоечнику и не медалисту — нужно заниматься не менее полутора часов в неделю с сентября по май. Это около 35 недель с учетом зимних каникул, больше 50 часов за год. Обществознанием, историей, биологией, литературой — предметами с большим объемом теории — нужно заниматься в два раза больше. Мои ученики обычно занимаются дважды в неделю по 90 минут — за год получается больше 100 часов.

Этого мнения придерживается и Бенедикт Кэри — автор книги How We Learn. Он использует отличное сравнение: «Можно поливать лужайку раз в неделю полтора часа или три раза в неделю по полчаса. Если делать это трижды в неделю, газон будет зеленее».

Если школьник уделит изучению материала час в неделю, информация будет быстро улетучиваться: другие уроки ее вытеснят. На занятии ему придется сначала долго вспоминать, о чем идет речь, и систематизировать знания будет трудно. К тому же формат групповых занятий не позволяет преподавателю убедиться, что каждый слушатель помнит предыдущие темы, так что пробелы в знаниях будут накапливаться.

Как правильно включать печку? | Практические советы | Авто

Несмотря на то, что климатические установки имеют автоматический режим работы, они во многом зависят от действий человека. Если правила эксплуатации нарушаются, то печка зимой может превратиться из помощника во врага автомобиля. Ситуация усугубляется на машинах, у которых нет блока автоматического управления заслонками и температурой. Водителю приходится самому настраивать температуру и потоки воздуха. Как же правильно пользоваться системой отопления салона?

Борьба с наледью

В холода важно быстро решить несколько проблем. В первую очередь важно справиться с замерзанием стекол, а затем решить трудности с их запотеванием при околонулевых температурах. В современных машинах для размораживания применяется специальная функция, которая выведена на отдельную кнопку. При ее нажатии обороты вентилятора печки поднимаются до максимальных значений, а весь поток направляется в верхние дефлекторы у основания лобового стекла. При этом радиатор отопления набирает тепло из системы охлаждения постепенно и повышает температуру воздуха поэтапно.

При этом для усиления эффективности обдува рекомендуется опустить противосолнечные козырьки вниз, чтобы теплый воздух из дефлекторов врезался в них и создавал подушку, которая поможет предотвратить рассеивание потока. Таким образом, нагревание лобового стекла будет проходить равномерно.

Если действовать иначе и дать печке нагреваться без оттока тепла в салон, то при включении вентиляторов теплый воздух может привести к нежелательным температурным расширениям материалов обивки. При резком нагреве пластиковые детали может «повести». Под температурный удар попадает и ветровое стекло. Если сразу обдать его горячей струей, то разница температур у основания и у верхней части стекла будет составлять 20-30 градусов, отчего стекло начнет коробить. Мелкие повреждения, сколы и незаметные раковины начнут давать «усики», которые будут расползаться по стеклу. В итоге появится «стрелка», которая со временем при вибрациях и тряске во время движения разрастется в крупную трещину через все стекло. В этом случае придется менять его целиком.

Сушка ковров

После лобового стекла необходимо просушить коврики и обогреть нижнюю часть салона. Делать это лучше в движении, потому что двигатель лучше отдает энергию под нагрузкой. Достаточно нескольких плавных разгонов, чтобы силовой агрегат уже через несколько минут достиг рабочей температуры и начал выдавать горячий поток воздуха. Его необходимо направить в ноги.

Дело в том, что на ковриках скапливается вода с обуви или мокрый снег, превращающийся в лужи. Вода испаряется и может повлиять на запотевание боковых стекол, которые не имеют хорошего обдува. Обдув помогает избавиться от влаги и позволяет водителю создать комфортную атмосферу. Теплый воздух начинает подниматься от пола вверх и нагревает тело.

Когда лужи высохли, можно поменять потоки обдува и направить их не только на ноги, но и на стекло, чтобы предотвратить его обмораживание во время движения на высоких скоростях. Затем самое время включить кондиционер, если, конечно, он есть в автомобиле.

Сушка воздуха

Кондиционер пригодится для сушки воздуха в салоне. Если идет сильный снег или несколько пассажиров уселись в машину в промокшей обуви, то стекла быстро запотевают. Кондиционер перегоняет воздух и удаляет влагу, создавая комфортную среду.

Кондицинер активируется, только когда температура поступающего в него воздуха выше нуля градусов. В морозы при промороженном салоне он не включится, так как электроника не позволит. Блок управления деактивирует муфту, чтобы не повредить компрессор, при этом кнопка А/С может быть нажатой.

Запускать сушку воздуха важно и с целью технической профилактики. Кондиционер — это сложный технический узел, и его исправность зависит от условий эксплуатации. Если любую технику оставить без движения на полгода, то в механизмах произойдут необратимые изменения. Резинки рассыхаются, патрубки трескаются от перемены температур, а хладагент улетучивается. Смазка компрессора циркулирует нормально только во время работы устройства, поэтому кондиционер осенью и зимой следует включать ежедневно как минимум для обеспечения работоспособности, а также чтобы не закисла прижимная металлическая пластина муфты.

Как правильно спорить с начальником и выжить

Руководители, конечно, бывают разные, но, согласитесь, при устройстве на работу чаще начальник выбирает сотрудника под себя, а не наоборот. Это люди с множеством забот, только представьте, сколько вопросов им приходиться решать, а еще вы тут. Бывают руководители, готовые слушать мнения своих подчиненных, а бывают тираны, которые считают, что их решения единственно правильные. Что делать, если ваш шеф ошибается, ну или вы так считаете? Вот нехитрые правила, которые могут спасти вашу карьеру, а могут ее еще и укрепить.

Уверенность

Если во время рабочего процесса вы осознали, что ваш руководитель не прав, то не спешите ему об этом заявлять. Проверьте несколько раз свою теорию. Вы точно должны разбираться в сути вопроса, если не лучше, то, во всяком случае, не хуже руководства. Проконсультируйтесь с коллегами, если такая возможность есть, вдруг они вам помогут понять, что не правы как раз вы. Только не вздумайте говорить о шефе в негативном ключе при обсуждении с коллегами, просто выскажите сомнение. При споре с руководителем вы всегда в более проигрышном положении. Лучше рассмотреть вопрос с разных сторон и убедиться в своей правоте. Заручитесь уверенностью.

www.globallookpress.com

Эмоции

Мир несправедлив, а начальник неправ. Хочется всем доказать, что так поступать неправильно или ваш офисный корабль движется неверным курсом. Не спешите бежать в кабинет шефа и тыкать ему этим в лицо. Даже если вы сто раз правы, это не дает вам никаких особых полномочий показывать свои эмоции и срываться на жесткую критику начальника. Остыньте, соберитесь с мыслями и возьмите себя в руки. Спокойный, конструктивный разговор по волнующему вас вопросу куда эффективней эмоций и случайных фраз.

Место спора

Для столь серьезного разговора, как работа над ошибками руководства, не стоит выбирать пространство, которое будет на виду у всех коллег. Помните, что ваш начальник, скорее всего, хочет быть авторитетным человеком для подчиненных. Если вы заведете спор при других сотрудниках, то это уже минус десяток баллов с вашего счета. Вряд ли он захочет показать другим, что не прав, а вы тут такой молодец и все поняли. Обсудите вопрос в переговорной или в личном кабинете руководителя. Не нужно стремиться показать всем свое превосходство в данный момент. Ни при каких обстоятельствах нельзя подрывать авторитет начальника в глазах коллег. Он это запомнит и в будущем у вас могут быть неприятности. Да и вообще, это не красиво. Вы можете нарваться на отпор, и любые ваши доводы будут разбиты.

www.globallookpress.com

Разговор

Если вы с чем-то не согласны, это еще не повод лезть в бутылку. В любом случае будет так, как скажет руководитель. Главное, проявляйте уважение к вашему шефу, он прекрасно почувствует, если вы будете ни во что его не ставить. Не начинайте разговор с фразы типа «Вы не правы», «Я не буду делать это, потому что полный бред», «Что за фигня, так нельзя». Старайтесь высказывать ваше сомнение в нейтральной форме. Например, начните разговор так: «Я не совсем согласен», «Я не уверен, но может быть лучше будет сделать так». Высказав свои взгляды на проблему, внимательно и не перебивая, выслушайте доводы своего руководителя. Если он с вами не согласен, то не стоит включать эмоции. Он может говорить четко и уверено, аргументировано доказывая, что вы ошибаетесь. Не покупайтесь на это, у начальника работа такая: излагать свои решения в правильном ключе. В вашу задачу не должно входить желание переспорить и настоять на своем, вы должны совместно выработать правильно решение. У начальника свое мнение и вам нужно понять его аргументы. Попробуйте скорректировать свое понимание проблемы и предложить более подходящее на ваш взгляд решение, скрестив ваши аргументы с тем, что хочет видеть он. Будет идеально, если вы сделаете так, что ваша идея станет частью предложения начальника, словно это он сам и придумал.

Денис Балин

Какова правильная установка для решения математических задач ?: Написание арифметических выражений — видео и стенограмма урока

Надевание математических меток

Первый шаг в правильной постановке нашей задачи с математическими словами — это пометить важные части задачи. Под важными я имею в виду те части проблемы, которые нам нужно использовать для решения проблемы. Как мы узнаем, что это такое? Мы начинаем с поиска ответа, который хочет решить проблема. В нашей задаче проблема заключается в том, чтобы узнать общую сумму, заработанную в конце недели.Я продолжаю и выделяю фразу, которая гласит: сколько денег он должен потратить в конце одной недели. Затем я думаю о том, что мне нужно, чтобы вычислить этот ответ. Что ж, мне нужно знать, сколько он работал и сколько зарабатывает. Проблема подсказывает мне, что он зарабатывает 12,50 долларов в час. Я могу выделить эту часть. Проблема также говорит мне, что он работает 5 часов в субботу и 3 часа в пятницу. Я продолжаю и выделяю эту информацию. Мне нужно что-то еще решить? Нет, поэтому я могу игнорировать другие слова в задаче.

Теперь я могу обозначить эти части проблемы. Я собираюсь пометить то, что я ищу, свой ответ, x . Я пишу это x рядом с выделенной частью проблемы, которая говорит мне, что нужно решать. Я могу сократить до «S», чтобы обозначить заработок за субботу, и «F», чтобы обозначить доход за пятницу.

Написание математического выражения

Я закончил разметку, и теперь мне нужно написать математическое выражение, которое позволит мне легко решить задачу. Эта часть требует некоторого размышления, но оно того стоит!

Я начинаю писать математическое выражение, записывая x = так как я знаю, что мой ответ что-то равен.Я поставил x для своей части ответа, которую я пометил, и поставил знак равенства, чтобы сообщить мне, что мне нужно что-то решить, чтобы найти свой ответ. Что идет после знака равенства? Что ж, проблема хочет знать, сколько Джеймс зарабатывает за неделю. Если Джеймс работает только по пятницам и субботам, то общая сумма заработка за неделю будет равна его заработку за пятницу плюс его заработок за субботу. Я уже обозначил эти части проблемы, так что я собираюсь записать эти ярлыки. Я могу написать «пятничный доход» или «F», и я могу написать «субботний доход» или «S». Я поставил знак плюса между этими двумя частями, чтобы сообщить мне, что мне нужно сложить их вместе. Итак, теперь мое математическое выражение выглядит так: x = F + S. Но что такое F и S? Если Джеймсу платят 12,50 долларов в час, то сумма, которую он зарабатывает каждый день, зависит от того, сколько часов он работает. Мне нужно умножить его заработок на количество часов, которые он работает. Для пятницы это будет 12,50 долларов * 3, а для субботы — 12,50 долларов * 5. Итак, я могу заменить букву F на 12,50 долларов * 3, а букву S на 12,50 долларов * 5. Теперь у меня есть математическая задача x = 12 долларов.50 * 3 + 12,50 долларов * 5.

Решение проблемы

Кажется, эту проблему легко решить, не так ли? Все, что мне нужно сделать, это произвести умножение и сложить результаты. Это совсем не плохо. Позвольте мне пойти дальше и посмотреть, какой я получу ответ. Умножение 12,50 доллара на 3 дает мне 37,50 доллара, а умножение 12,50 доллара на 5 дает мне 62,50 доллара. Теперь мне нужно сложить их, чтобы получить 100 долларов. И угадай что? Я решил свою проблему. Джеймс зарабатывает 100 долларов в конце недели, и именно столько денег он должен потратить в конце недели.

Сводка урока

Вы можете увидеть, как правильная постановка задачи по математике упрощает решение конечного ответа. Самое сложное — это написать математическое выражение, но, немного подумав, это можно сделать. Как только это будет сделано, остальное легко!

Мы узнали, что правильный способ постановки задачи по математике состоит в выполнении определенных шагов.

1. Пометьте важные детали. Сначала вам нужно выяснить, в чем проблема, а затем подумать над информацией, которая вам нужна, чтобы найти ответ.Вы выделяете эти части проблемы. Затем вы наклеиваете на них ярлыки, чтобы упорядочить их и не позволить запутать вас. Используйте описательные фразы или буквы. Я обычно обозначаю ответ как x , чтобы отделить его от всех остальных ярлыков.

2. Напишите математическое выражение, которое нужно решить. После того, как вы все пометили, пришло время написать математическое выражение. Вы начинаете с x =, а затем записываете другие метки, используя правильную математическую операцию, чтобы найти свой ответ.Эта часть требует некоторого размышления, чтобы знать, как расположить метки и какую математическую операцию поставить. Подумайте о своем базовом сложении, вычитании, умножении и делении. Вы знаете, что делают эти операции, поэтому не задумывайтесь над проблемой. Для этикеток запишите для них важные числа, как мы это сделали с нашей проблемой.

3. Решите математическое выражение. Когда вы закончите писать математическое выражение, вашим следующим и последним шагом будет его решение. Следуйте своему порядку действий, чтобы решить и получить ответ.

Результаты обучения

После просмотра этого видеоурока вы должны уметь делать следующее:

• Обозначьте различные части математической задачи со словами
• Решите математические задачи со словами, выполнив серию шагов

стратегий решения проблем со словами

Простое добавление этих слов увеличивает сложность (а иногда и математическую тревогу) примерно на 100!

Как вы можете помочь своим ученикам научиться уверенно решать словесные задачи? Обучая своих учеников решать текстовые задачи поэтапно и организованно, вы дадите им инструменты, необходимые для более эффективного решения текстовых задач.

Вот семь стратегий, которые я использую, чтобы помочь студентам решать задачи со словами.

1. Прочитать все слово Задача

Прежде чем учащиеся будут искать ключевые слова и пытаться понять, что им делать, им нужно немного замедлиться и прочитать всю текстовую задачу один раз (а еще лучше, дважды). Это помогает детям получить более широкую картину, чтобы понять ее немного лучше.

2. Подумайте о проблеме со словами

Студенты должны задавать себе три вопроса каждый раз, когда они сталкиваются с проблемой со словами.Эти вопросы помогут им составить план решения проблемы.

Вот вопросы:

A. В чем именно заключается вопрос?

В чем проблема? Часто составители учебных программ включают в задачу дополнительную информацию без видимых на то веских причин, за исключением, может быть, для того, чтобы научить детей игнорировать эту постороннюю информацию (грррр!). Студенты должны быть в состоянии оставаться сосредоточенными, игнорировать эти лишние детали и выяснять, в чем реальный вопрос конкретной проблемы.

B. Что мне нужно, чтобы найти ответ?

Студентам необходимо сузить круг вопросов, даже больше, чтобы выяснить, что необходимо для решения задачи, будь то сложение, вычитание, умножение, деление или их комбинация. Им потребуется общее представление о том, какая информация будет использоваться (или не использоваться) и что они будут делать.

Здесь очень помогают ключевые слова. Когда учащиеся учатся распознавать, что одни слова означают сложение (например, всего вместе, вместе ), в то время как другие означают вычитание, умножение или деление, это помогает им решить, как поступить немного лучше

Вот таблица ключевых слов, которую я люблю использовать при обучении задачам со словами.Раздаточный материал можно было скопировать в меньшем размере и вклеить в интерактивные тетради по математике. Его можно поместить в математические папки или в подшивки под математическим разделом, если ваши ученики используют подшивки.

Однажды я сделал огромные математические знаки (символы сложения, вычитания, умножения и деления) и написал ключевые слова вокруг символов. Они служили постоянным напоминанием о ключевых словах для словесных задач в классе.

Если вы хотите загрузить БЕСПЛАТНЫЙ раздаточный материал по ключевым словам, нажмите здесь:

С.Какая информация у меня уже есть?

Здесь учащиеся сосредоточатся на числах, которые будут использоваться для решения задачи.

3. Напишите в Word Задача

Этот шаг укрепляет мышление, имевшее место на втором шаге. Студенты используют карандаш или цветные карандаши, чтобы записывать информацию на рабочих листах (конечно, не в книгах, если они не расходные материалы). Есть много способов сделать это, но вот что мне нравится делать:

• Обведите любые числа, которые вы хотите использовать.

• Слегка зачеркните любую ненужную информацию.

• Подчеркните фразу или предложение, в котором точно указано, что вам нужно найти.

4.

Нарисуйте простую картинку и подпишите ее

Рисование картинок с использованием простых форм, таких как квадраты, круги и прямоугольники, помогает учащимся визуализировать проблемы. Также помогает добавление номеров или имен в качестве меток.

Например, если в словарной задаче говорится, что было пять коробок и в каждой коробке было по 4 яблока, дети могут нарисовать пять квадратов с числом четыре в каждом квадрате.Мгновенно дети могут увидеть ответ намного легче!

5. Оцените ответ, прежде чем решать

Имея общее представление о приблизительном ответе на проблему, учащиеся узнают, является ли их реальный ответ разумным или нет. Эта быстрая приблизительная оценка — хорошая математическая привычка. Это помогает учащимся по-настоящему задуматься о точности своего ответа, когда проблема, наконец, будет решена.

6. Проверьте свою работу, когда закончите

Эта стратегия соответствует пятой стратегии. Одна из фраз, которые я постоянно использую во время математических занятий, это: Разумный ли ваш ответ ? Я хочу, чтобы ученики делали больше, чем просто вычисляли числа, но на самом деле думали о том, что означают эти числа.

Кроме того, когда учащиеся приобретают привычку проверять работу, они более склонны замечать неосторожные ошибки, которые часто являются причиной неправильных ответов.

7. Часто повторяйте проблемы со словами

Точно так же, как требуется практика, чтобы научиться играть на кларнете, вести мяч в футболе и реалистично рисовать, чтобы стать мастером решения словесных задач, требуется практика.

Когда студенты решают задачи со словами, часто происходит несколько вещей. Проблемы со словами становятся менее страшными (нет, правда).

Они начинают замечать сходство типов проблем и могут быстрее понять, как их решать. Они обретут уверенность, даже когда будут иметь дело с новыми типами задач со словами, зная, что в прошлом они успешно решали многие задачи со словами.

Если вы ищете карточки с задачами со словами, у меня их довольно много для учащихся 3-5 классов.

В этом наборе карточек с заданиями по математике для 3-го класса есть задачи со словами почти в каждом из 30 наборов карточек с заданиями.

Существуют также специальные наборы, посвященные задачам со словами и двухэтапным задачам со словами. Мне это нравится, потому что для каждого стандарта есть карточки с заданиями.

НАЖМИТЕ ЗДЕСЬ, чтобы ознакомиться с 3-м классом:

В этом наборе карточек с заданиями по математике для 4-х классов также есть множество задач со словами почти в каждом из 30 наборов карточек с заданиями.Эти карты идеально подходят для центров, всего класса и для один на один.

НАЖМИТЕ ЗДЕСЬ, чтобы увидеть 4-й класс:

Этот комплект карточек с заданиями по математике для 5-х классов также содержит задачи со словами, чтобы ваши ученики могли целенаправленно практиковаться.

НАЖМИТЕ ЗДЕСЬ, чтобы посмотреть 5 класс:

Хотите попробовать БЕСПЛАТНЫЙ набор карточек с заданиями по математике, чтобы узнать, что вы думаете?

3-й класс: округление целых чисел в карточках

4-й класс: преобразование дробей и десятичных карточек задач

5-й класс: карточки задач «Чтение, запись и сравнение десятичных знаков»

Спасибо, что заглянули!

Решение вопросов Word

МНОГО примеров!

В алгебре мы часто задаем вопросы, например:

Пример: Сэм и Алекс играют в теннис.

В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр.

Сколько игр сыграл Алекс?

Как мы их решаем?

Уловка состоит в том, чтобы разбить решение на две части:

Превратите английский в алгебру.

Затем решите с помощью алгебры.

Превращение английского в алгебру

Превратить английский в алгебру помогает:

• Прочтите сначала все
• Сделайте эскиз , если возможно
• Назначьте букв для значений
• Найдите или разработайте формул

Вам также следует записать , что на самом деле требуется для , чтобы вы знали, куда вы собираетесь и когда вы прибыли!

Также ищите ключевые слова:

Когда вы видите		Думай
сложить, итого, сумма, увеличить, больше, вместе, вместе, плюс, более		+
минус, меньше, разница, меньше, уменьшено, уменьшено		–
умноженное на умножение на произведение, множитель		×
разделенное, частное, на, из, соотношение, соотношение, процент, ставка		÷
развернуть или свернуть		геометрия формулы
Скорость, скорость		расстояние формулы
Сколько дней, часов, минут, секунд		раз

Ясное мышление

Некоторые формулировки могут быть хитрыми, из-за чего трудно думать «правильно», например:

$

Пример: У Сэма на 2 доллара меньше, чем у Алекса.Как это записать в виде уравнения?

• Пусть S = долларов у Сэма
• Пусть A = долларов у Алекса

Теперь … вот что: S — 2 = A

или должно быть: S = A — 2

или должно быть: S = 2 — A

Правильный ответ: S = A — 2

( S — 2 = — распространенная ошибка, так как в вопросе написано «Сэм … на 2 меньше … Алекс»)

Пример: на нашей улице собак вдвое больше, чем кошек.Как это записать в виде уравнения?

• Пусть D = количество собак
• Пусть C = количество кошек

Теперь … это что: 2D = C

или должно быть: D = 2C

Подумайте внимательно!

Правильный ответ: D = 2C

( 2D = C — распространенная ошибка, так как в вопросе написано «дважды … собаки … кошки»)

Примеры

Давайте начнем с очень простого примера , чтобы увидеть, как это делается:

Пример: прямоугольный сад размером 12 на 5 м, какова его площадь?

Превратите английский в алгебру:

Эскиз:

.

Письма:

• Используйте w для ширины прямоугольника: w = 12 м
• Используйте h для высоты прямоугольника: h = 5m

Формула для площади прямоугольника: A = w × h

Нас спрашивают о Районе.

Решить:

A = ш × в = 12 × 5 = 60 м ²

Площадь кв.м. 60 кв.м. .

Теперь давайте попробуем пример сверху страницы:

Пример: Сэм и Алекс играют в теннис. В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр. Сколько игр сыграл Алекс?

Превратите английский в алгебру:

Письма:

• Используйте S , чтобы узнать, сколько игр Сэм сыграл
• Используйте A , чтобы узнать, сколько игр сыграл Алекс

Мы знаем, что Сэм сыграл на 4 игры больше, чем Алекс, поэтому: S = A + 4

И мы знаем, что вместе они сыграли 12 игр: S + A = 12

Нас спрашивают, сколько игр сыграл Алекс: A

Решить:

Начать с: S + A = 12

S = A + 4 , поэтому мы можем
заменить «A + 4» на S: (A + 4) + A = 12

Упростить: 2A + 4 = 12

Вычтем 4 с обеих сторон: 2A = 12-4

Упростить: 2A = 8

Разделите обе части на 2: A = 4

Это означает, что Алекс сыграл 4 игры в теннис.

Проверка: Сэм сыграл на 4 игры больше, чем Алекс, поэтому Сэм сыграл 8 игр. Вместе они сыграли 8 + 4 = 12 игр. Да!

Немного более сложный пример:

Пример: Алекс и Сэм также создают таблицы.

Вместе они делают 10 столов за 12 дней.

Алекс, работая в одиночку, может заработать 10 за 30 дней.

Сколько времени потребуется Сэму, работая в одиночку, чтобы сделать 10 столов?

Превратите английский в алгебру:

Письма:

• Используйте a для скорости работы Алекса
• Используйте с для скорости работы Сэма

12 дней Алекса и Сэма — это 10 столов, поэтому: 12a + 12s = 10

30 дней одного Алекса — это тоже 10 столов: 30a = 10

Нас спрашивают, сколько времени потребуется Сэму, чтобы сделать 10 столов.

Решить:

30a = 10 , поэтому ставка Алекса (столов в день) составляет: a = 10/30 = 1/3

Начать с: 12a + 12s = 10

Положите «1/3» для a: 12 (1/3) + 12s = 10

Упростить: 4 + 12s = 10

Вычтем 4 с обеих сторон: 12s = 6

Разделите обе стороны на 12: s = 6/12

Упростить: с = 1/2

Это означает, что ставка Сэма составляет половину стола в день (быстрее, чем у Алекса!).

Итак, 10 столов займет у Сэма всего 20 дней.

Интересно, стоит ли Сэму платить больше?

И еще пример «подстановки»:

Пример: Дженна усиленно тренируется, чтобы пройти квалификацию к Национальным играм.

У нее обычный еженедельный распорядок дня: в одни дни она тренируется по пять часов в день, а в другие — по 3 часа в день.

В общей сложности она тренируется 27 часов в семидневную неделю. Сколько дней она тренируется по пять часов?

Письма:

• Количество «5 часовых» дней: d
• Количество «3-х часовых» дней: e

Мы знаем, что в неделе семь дней, поэтому: d + e = 7

И она тренируется 27 часов в неделю, из них d 5 часов в день и e 3 часа в день: 5d + 3e = 27

Нас спрашивают, сколько дней она тренируется по 5 часов: d

Решить:

д + е = 7

Итак: e = 7 — d

Положим, что в 5d + 3e = 27 5d + 3 (7 − d) = 27

Упростить: 5d + 21 — 3d = 27

Вычтем 21 с обеих сторон: 5d — 3d = 6

Упростить: 2d = 6

Разделим обе части на 2: d = 3

Количество «5 часовых» дней — 3

Проверка : Она тренируется по 5 часов 3 дня в неделю, поэтому она должна тренироваться по 3 часа в день в остальные 4 дня недели.

3 × 5 часов = 15 часов, плюс 4 × 3 часа = 12 часов дает в сумме 27 часов

Некоторые примеры из Geometry:

Пример: круг имеет площадь 12 мм

² , каков его радиус?

Письма:

• Используйте A для Area: A = 12 мм ²
• Используйте r для радиуса

И формула для площади: A = π r ²

У нас спрашивают радиус.

Решить:

Нам нужно переставить формулу, чтобы найти площадь

Начать с: A = π r ²

Поменять местами стороны: π r ² = A

Разделим обе части на π : r ² = A / π

Извлечь квадратный корень из обеих частей: r = √ (A / π)

Теперь мы можем использовать формулу: r = √ (12/ π)

И получаем: r = 1.954 (до 3-х мест)

Пример: куб имеет объем 125 мм

³ , какова его площадь поверхности?

Сделайте быстрый набросок:

Письма:

• Используйте V для Volume
• Используйте A для Area
• Используйте s для длины стороны куба

Формулы:

• Объем куба: В = с ³
• Площадь куба: A = 6s ²

У нас спрашивают площадь.

Решить:

Первая отработка s по формуле объема:

Начать с: В = с ³

Поменять местами стороны: s ³ = V

Извлечь кубический корень с обеих сторон: s = ∛ (V )

И получаем: s = ∛ (125 ) = 5

Теперь мы можем посчитать площадь поверхности:

Начать с: A = 6s ²

И получаем: А = 6 (5) ²

A = 6 × 25 = 150 мм ²

Пример о деньгах:

Пример: Джоэл работает в местной пиццерии.Когда он работает сверхурочно, он зарабатывает в 1¼ раза больше обычного.

Одна неделя Джоэл проработал 40 часов с обычной оплатой, а также 12 часов сверхурочно. Если Джоэл заработал за эту неделю 660 долларов, какова его нормальная ставка заработной платы?

Письма:

• Обычная ставка оплаты труда Джоэла: N $ в час

Формулы:

• Джоэл работает 40 часов по цене N $ в час = 40N
• Когда Джоэл работает сверхурочно, он зарабатывает в 1¼ раза больше обычной ставки = 1 доллар.25N в час
• Джоэл работает 12 часов по цене 1,25 доллара США в час = (12 × 1 доллар США) = 15 долларов США
доллара США
• А вместе он заработал 660 долларов, итак:

$ 40N + $ (12 × 1¼N) = 660 $

У нас спрашивают нормальную ставку зарплаты Джоэла в $ N.

Решить:

Начните с $ 40N + $ (12 × 1¼N) = 660 $

Упростить: 40N + 15N = 660 $

Еще более упростите: $ 55N = 660 $

Разделим обе стороны на 55: $ N = 12 $

Итак, нормальная ставка оплаты труда Джоэла составляет 12 долларов в час.

Чек

Обычная ставка оплаты труда Джоэла составляет 12 долларов в час, поэтому его сверхурочная работа составляет 1¼ × 12 долларов в час = 15 долларов в час.Таким образом, его обычная зарплата 40 × 12 = 480 долларов плюс сверхурочная работа 12 × 15 = 180 долларов дает нам в общей сложности 660

долларов.

Подробнее о деньгах с этими двумя примерами, включающими сложный процент

Пример: Алекс вкладывает 2000 долларов в банк под 11% годовых. Сколько это будет стоить через 3 года?

Это формула сложных процентов:

Итак, мы будем использовать эти буквы:

• Текущая стоимость PV = 2000 долларов США
• Процентная ставка (десятичная дробь): r = 0.11
• Количество периодов: n = 3
• Будущее значение (значение, которое мы хотим): FV

Нас спрашивают о будущей стоимости: FV

Решить:

Начать с: FV = PV × (1 + r) ⁿ

Добавьте то, что мы знаем: FV = $ 2000 × (1 + 0,11) ³

Вычислить: FV = $ 2000 × 1,367631

Вычислим: FV = 2735 долларов.26 (с точностью до цента)

Пример: Роджер положил 1000 долларов на сберегательный счет. На заработанные деньги ежегодно начислялись проценты по той же ставке. Через девять лет депозит Роджера вырос до 1 551,33 доллара США

Какова была годовая процентная ставка по сберегательному счету?

Формула сложных процентов:

с:

• Текущая стоимость PV = 1000 долларов США
• Процентная ставка (желаемое значение):
р.
• Количество периодов: n = 9
• Будущая стоимость: FV = 1551 доллар.33

Нас спрашивают о процентной ставке:

р.

Решить:

Начать с: FV = PV × (1 + r) ⁿ

Добавьте то, что мы знаем: 1551,33 доллара = 1000 долларов × (1 + r) ⁹

Поменять стороны: 1000 $ × (1 + r) ⁹ = 1551,33 $

Разделите обе стороны на 1000: (1 + r) ⁹ = 1551,33 доллара США / 1000 долларов США

Упростить: (1 + r) ⁹ = 1.55133

корень 9-й степени: 1 + r = 1,55133 ^(1/9)

Вычислить: 1 + r = 1.05

Вычислить: r = 0,05 = 5%

Таким образом, годовая процентная ставка составляет 5%

Чек : 1000 долларов × (1,05) ⁹ = 1000 долларов × 1,55133 = 1551,33 доллара

И пример вопроса о соотношении:

Пример: В начале года соотношение мальчиков и девочек в классе было 2: 1

Но теперь, полгода спустя, четыре мальчика покинули класс и появились две новые девочки.Соотношение мальчиков и девочек сейчас составляет 4: 3

Сколько всего студентов сейчас?

Письма:

• Кол-во мальчиков сейчас: б
• Количество девочек сейчас: г

Коэффициент текущей ликвидности 4: 3

b г = 4 3

, который можно переставить на 3b = 4g

На начало года было (b + 4) мальчиков и (g — 2) девочек, и соотношение было 2: 1

б + 4 г — 2 = 2 1

, который можно переставить на b + 4 = 2 (g — 2)

Нас спрашивают, сколько всего студентов сейчас: b + g

Решить:

Начать с: b + 4 = 2 (г — 2)

Упростить: b + 4 = 2g — 4

Вычтем 4 с обеих сторон: b = 2g — 8

Умножаем обе стороны на 3 (получаем 3b): 3b = 6g — 24

Помните 3b = 4g : 4g = 6g — 24

Вычтем 6g с обеих сторон : −2g = -24

Разделим обе части на −2: г = 12

Есть 12 девушек !

И 3b = 4g , поэтому b = 4g / 3 = 4 × 12/3 = 16 , так что есть 16 мальчиков

Таким образом, сейчас в классе 12 девочек и 16 мальчиков, всего учеников — 28 человек.

Чек

Сейчас 16 мальчиков и 12 девочек, поэтому соотношение мальчиков и девочек составляет 16: 12 = 4: 3
В начале года было 20 мальчиков и 10 девочек, поэтому соотношение было 20: 10 = 2: 1

А теперь для некоторых квадратных уравнений:

Пример: Произведение двух последовательных четных целых чисел равно 168. Что такое целые числа?

Последовательные означают один за другим. И их , даже , так что они могут быть 2 и 4, или 4 и 6 и т. Д.

Мы назовем меньшее целое число n , поэтому большее целое число должно быть n + 2

И нам говорят, что произведение (то, что мы получаем после умножения) равно 168, поэтому мы знаем:

п (п + 2) = 168

Нас спрашивают целые числа

Решить:

Начать с: n (n + 2) = 168

Развернуть: n ² + 2n = 168

Вычтем 168 с обеих сторон: n ² + 2n — 168 = 0

Это квадратное уравнение, и есть много способов его решить.Используя решение квадратного уравнения, мы получаем −14 и 12.

Проверка −14: −14 (−14 + 2) = (−14) × (−12) = 168 ДА

Проверка 12: 12 (12 + 2) = 12 × 14 = 168 ДА

Итак, есть два решения: -14 и -12 — одно, 12 и 14 — другое.

Примечание: мы также могли попробовать «угадать и проверить»:

• Мы могли бы попробовать, скажем, n = 10: 10 (12) = 120 NO (слишком мало)
• Затем мы могли бы попробовать n = 12: 12 (14) = 168 ДА

Но если мы не вспомним, что умножение двух отрицаний дает положительный результат, мы можем пропустить другое решение (−14) × (−12).

А:

Пример: вы архитектор. Вашему клиенту нужна комната вдвое больше ширины. Им также нужна веранда шириной 3 метра по длинной стороне.

У вашего клиента 56 квадратных метров красивой мраморной плитки для покрытия всей площади.

Какой должна быть длина комнаты?

Давайте сначала сделаем набросок, чтобы все было правильно !:

Письма:

• Длина помещения: L
• Ширина помещения: Вт
• Общая площадь с верандой: А,

Мы знаем:

• ширина комнаты составляет половину ее длины: W = ½L
• общая площадь равна (ширина комнаты + 3), умноженная на длину: A = (W + 3) × L = 56

Нас спрашивают о длине комнаты: L

Решить:

Начать с: (Ш + 3) × Д = 56

Заменитель W = ½L : (½L + 3) × L = 56

Упростить: ½L ² + 3L = 56

Умножьте все члены на 2: L ² + 6L = 112

Вычесть 112 с обеих сторон : L ² + 6L — 112 = 0

Это квадратное уравнение , есть много способов его решить, на этот раз воспользуемся факторингом:

Начать с: L ² + 6L — 112 = 0

Два числа, которые умножаются и дают ac = −112,
и сложить, чтобы получить b = 6, 14 и −8: L ² + 14L — 8L — 112 = 0

Группа: L (L +14) — 8 (L + 14) = 0

Группа: (L — 8) (L + 14) = 0

Итак, L = 8 или -14

Есть два решения квадратного уравнения, но только одно из них возможно, так как длина комнаты не может быть отрицательной!

Так длина помещения 8 м

Чек

L = 8, поэтому W = ½L = 4

Итак, площадь прямоугольника = (W + 3) × L = 7 × 8 = 56

Вот и мы…

… Я надеюсь, что эти примеры помогут вам понять, как отвечать на словесные вопросы. А как насчет практики?

GRE Стратегии решения проблем (для тестируемых)

вопросов в мере количественного мышления Общего теста GRE® просят вас смоделировать и решить проблемы, используя количественные или математические методы. Как правило, решение математической задачи состоит из трех основных шагов:

• Шаг 1. Разберитесь в проблеме
• Шаг 2: Реализуйте стратегию решения проблемы
• Шаг 3. Проверьте свой ответ

Вот описание трех шагов, за которым следует список полезных стратегий для решения математических задач.

Шаг 1. Понять проблему

Первый шаг — внимательно прочитать формулировку проблемы, чтобы убедиться, что вы понимаете предоставленную информацию и проблему, которую вас просят решить.

Некоторая информация может описывать определенные количества. Количественная информация может быть дана словами или математическими выражениями, или их комбинацией. Кроме того, в некоторых задачах вам может потребоваться прочитать и понять количественную информацию в представлениях данных, геометрических фигурах или системах координат.Другая информация может принимать форму формул, определений или условий, которым должны удовлетворять количества. Например, условия могут быть уравнениями или неравенствами или могут быть словами, которые можно перевести в уравнения или неравенства.

Помимо понимания информации, которую вам дают, важно понимать, что вам нужно сделать, чтобы решить проблему. Например, какие неизвестные количества необходимо найти? В какой форме они должны быть выражены?

Шаг 2: Реализация стратегии решения проблемы

Решение математической задачи требует большего, чем понимание описания проблемы, то есть больше, чем понимание величин, данных, условий, неизвестных и всех других математических фактов, связанных с проблемой.Требуется определить, какие математические факты использовать, когда и как использовать эти факты для разработки решения проблемы. Это требует стратегии.

Математические задачи решаются с использованием самых разных стратегий. Также могут быть разные способы решения данной проблемы. Следовательно, вам следует разработать репертуар стратегий решения проблем, а также представление о том, какие стратегии могут лучше всего работать при решении конкретных проблем. Попытка решить проблему без стратегии может привести к большому объему работы без получения правильного решения.

После того, как вы определились со стратегией, вы должны ее реализовать. Если вы застряли, проверьте свою работу, чтобы увидеть, не допустили ли вы ошибки в своем решении. Важно иметь гибкий и непредвзятый настрой. Если вы проверяете свое решение и не можете найти ошибку или ваша стратегия решения просто не работает, поищите другую стратегию.

Шаг 3. Проверьте свой ответ

Когда вы получите ответ, вы должны проверить его разумность и правильность вычислений.

• Вы ответили на заданный вопрос?
• Является ли ваш ответ разумным в контексте вопроса? Проверить разумность ответа можно так же просто, как вспомнить основной математический факт и проверить, соответствует ли ваш ответ этому факту.Например, вероятность события должна быть от 0 до 1 включительно, а площадь геометрической фигуры должна быть положительной. В других случаях вы можете использовать оценку, чтобы убедиться, что ваш ответ обоснован. Например, если ваше решение включает сложение трех чисел, каждое из которых находится в диапазоне от 100 до 200, оценка суммы говорит вам, что сумма должна быть между 300 и 600.
• Вы допустили вычислительную ошибку при получении ответа? Ошибка ввода ключа с помощью калькулятора? Вы можете проверять наличие ошибок на каждом этапе вашего решения.Или вы можете напрямую проверить правильность вашего решения. Например, если вы решили уравнение для x и получили ответ, вы можете проверить свой ответ, подставив его в уравнение, чтобы увидеть это.

Стратегии

Нет установленных правил — применимых ко всем математическим задачам — для определения наилучшей стратегии. Способность определять стратегию, которая будет работать, растет по мере того, как вы решаете все больше и больше проблем. Ниже приводится краткое описание полезных стратегий.Вместе с каждой стратегией дается один или два типовых вопроса, на которые вы можете ответить с помощью стратегии. Эти стратегии не составляют полный список, и, кроме объединения первых четырех стратегий вместе, они не представлены в каком-либо определенном порядке.

Первые четыре стратегии — это стратегии трансляции, когда одно представление математической задачи переводится в другое.

Как быстрее решать математические задачи: 15 техник, которые нужно показать студентам

«Тестовое время.Никаких калькуляторов ».

Вы напугаете многих учеников, сказав это, но обучение методам решения математических задач с легкостью и скоростью может сделать это менее пугающим.

Это также может сделать математику более полезной. Вместо того, чтобы полагаться на калькуляторы, учащиеся изучают стратегии, которые могут улучшить их концентрацию и навыки оценки, одновременно развивая чувство числа. И хотя есть преподаватели, которые выступают против математических «уловок» по уважительным причинам, сторонники указывают на преимущества, такие как повышенная уверенность в решении сложных задач.

Вот 15 техник, которые можно показать учащимся, помогающие им быстрее решать математические задачи:

Сложение и вычитание

Многим учащимся сложно научиться складывать целые числа из трех или более вместе, но изменение шагов процесса может сделать так проще.

Первый шаг — добавить то, что легко. Второй шаг — добавить остальные.

Допустим, учащиеся должны найти сумму 393 и 89. Они быстро поймут, что прибавление 7 к 393 даст 400 — с этим числом легче работать.Чтобы сбалансировать уравнение, они могут затем вычесть 7 из 89.

В разбивке:

• 393 + 89
• (393 + 7) + (89-7)
• 400 + 82
• 482

С этой быстрой техникой большие числа теперь не будут выглядеть так страшно.

2. Двухэтапное вычитание

Существует аналогичный метод вычитания.

Удалите то, что легко. Затем удалите то, что осталось.

Предположим, учащиеся должны найти разницу 567 и 153.Большинство сочтет, что 500 — это более простое число, чем 567. Таким образом, им просто нужно отнять 67 от уменьшаемого — 567 — и вычитаемого — 153 — перед решением уравнения.

Вот процесс:

• 567 — 153
• (567 — 67) — (153 — 67)
• 500 — 86
• 414

Вместо двух комплексных чисел студентам придется решать один.

Зарегистрируйтесь сейчас

3. Вычитание из 1 000

Вы можете дать учащимся уверенность в том, что они могут обрабатывать четырехзначные целые числа с помощью этой быстрой техники.

Чтобы вычесть число из 1000, вычтите первые две цифры этого числа из 9. Затем вычтите последнюю цифру из 10.

Допустим, ученики должны решить 1000 — 438. Вот шаги:

• 9 — 4 = 5
• 9 — 3 = 6
• 10-8 = 2
• 562

Это также относится к 10 000, 100 000 и другим целым числам, которые следуют этому шаблону.

Умножение и деление

Когда учащимся нужно умножить два целых числа, они могут ускорить процесс, если одно — четное число.Им просто нужно уменьшить вдвое четное число и удвоить другое число.

Учащиеся могут остановить процесс, когда они больше не могут уменьшить вдвое четное число или когда уравнение станет управляемым.

Используя в качестве примера 33 x 48, вот процесс:

• 66 x 24
• 132 x 12
• 264 x 6
• 528 x 3
• 1,584

Единственным предварительным условием является понимание 2 таблица умножения.

5. Умножение на 2

Эта тактика представляет собой быстрый вариант удвоения и уменьшения вдвое.

Это упрощает умножение, если число в уравнении является степенью двойки, что означает, что оно работает для 2, 4, 8, 16 и так далее.

Вот что нужно сделать: Для каждой степени двойки, составляющей это число, удвойте другое число.

Например, 9 x 16 — это то же самое, что 9 x (2 x 2 x 2 x 2) или 9 x 24. Таким образом, учащиеся могут удвоить 9 четыре раза, чтобы получить ответ:

• 9 x 24
• 18 x 23
• 36 x 22
• 72 x 2
• 144

В отличие от удвоения и деления пополам, этот метод требует понимания экспонент наряду с сильным владением таблицей умножения на 2.

6. Умножение на 9

Для большинства студентов умножение на 9 — или 99, 999 и любое число, которое следует этому шаблону — сложно по сравнению с умножением на степень 10.

Но есть простая тактика, чтобы решить эту проблему. выпуск, а состоит из двух частей.

Сначала ученики округляют 9 до 10. Во-вторых, после решения нового уравнения они вычитают из ответа число, которое они только что умножили на 10.

Например, 67 x 9 даст тот же ответ, что и 67 x 10 — 67.Следуя порядку операций, вы получите результат 603. Аналогично, 67 x 99 это то же самое, что 67 x 100 — 67.

Несмотря на большее количество шагов, изменение уравнения таким образом обычно происходит быстрее.

Есть более простой способ умножить двузначные целые числа на 11.

Допустим, учащиеся должны найти произведение 11 x 34.

Идея состоит в том, чтобы поставить пробел между цифрами, чтобы получилось 3_4. Затем сложите две цифры и укажите сумму в поле.

Ответ 374.

Что произойдет, если сумма будет двухзначной? Студенты помещали вторую цифру в пробел и добавляли 1 к цифре слева от пробела. Например:

• 11 x 77
• 7_ (7 + 7) _7
• 7_ (14) _7
• (7 + 1) _4_7
• 847

Это умножение без умножения.

8. Умножение четных чисел на 5

Эта техника требует только базовых навыков деления.

Есть две ступеньки, и 5 x 6 служат для примера.Сначала разделите число, умноженное на 5, что составляет 6, пополам. Во-вторых, добавьте 0 справа от числа.

Результат — 30, что является правильным ответом.

Это идеальный и простой метод для студентов, осваивающих таблицу умножения на 5.

9. Умножение нечетных чисел на 5

Это еще одна тактика экономии времени, которая хорошо работает при обучении студентов 5-кратной таблице.

У этого есть три ступени, что 5 x 7 примером.

Сначала вычтите 1 из числа, умноженного на 5, и получится четное число.Во-вторых, сократите это число вдвое — в данном случае с 6 до 3. В-третьих, добавьте 5 справа от числа.

Ответ — 35.

Кому нужен калькулятор?

10. Возведение в квадрат двузначного числа, оканчивающегося на 1

Возведение в квадрат двухзначного числа старшего размера может быть утомительным, но есть ярлык, если 1 — вторая цифра.

Для этого ярлыка есть четыре шага, , пример 812:

• Вычтите 1 из целого числа: 81 — 1 = 80
• Возведите в квадрат целое число, которое теперь является более простым числом: 80 x 80 = 6400
• Сложите целое число с полученным квадратом дважды: 6,400 + 80 + 80 = 6,560
• Сложите 1: 6,560 + 1 = 6,561

Этот обходной путь устраняет трудности, связанные со второй цифрой, позволяя учащимся работать с числами, кратными 10.

11. Возведение в квадрат двухзначных чисел, оканчивающихся на 5

Возведение в квадрат чисел, заканчивающихся на 5, проще, поскольку состоит только из двух частей.

Во-первых, учащиеся всегда составляют 25 последних цифр продукта.

Во-вторых, чтобы определить первые цифры продукта, учащиеся должны умножить первую цифру числа, например 9, на целое число, которое на единицу больше, в данном случае 10.

Итак, учащиеся решали бы 952, обозначив 25 в качестве последних двух цифр.Затем они умножили бы 9 x 10, чтобы получить 90. Если сложить эти числа, получится , то получится 9 025.

Именно так сложная задача для многих студентов превращается в легкое умножение.

12. Расчет процентов

Перекрестное умножение — важный навык, который нужно развивать, но есть более простой способ расчета процентов.

Например, если учащиеся хотят знать, что составляет 65% от 175, они могут перемножить числа и переместить десятичный разряд на две цифры влево.

Результат 113,75, что действительно является правильным ответом.

Этот ярлык помогает сэкономить время на тестах и ​​викторинах.

13. Уравновешивание средних значений

Чтобы определить среднее среди набора чисел, учащиеся могут уравновесить их вместо использования сложной формулы.

Предположим, студент хочет работать волонтером в среднем 10 часов в неделю в течение четырех недель. В первые три недели студент работал по 10, 12 и 14 часов.

Чтобы определить количество часов, необходимых на четвертой неделе, ученик должен добавить, насколько он или она превзошли или пропустили целевой средний показатель в другие недели:

• 14 часов — 10 часов = 4 часа
• 12 — 10 = 2
• 10 — 10 = 0
• 4 часа + 2 часа + 0 часов = 6 часов

Чтобы узнать количество часов на последней неделе, ученик должен вычесть сумму из целевого среднего:

• 10 часов — 6 часов = 4 часа

На практике этот метод может даже не потребовать карандаша и бумаги.Вот как это просто.

Проблемы со словами

14. Выявление модных словечек

Учащимся, которым сложно преобразовать словесные задачи в уравнения, будет полезно научиться определять модные слова — фразы, указывающие на конкретные действия.

Это не уловка. Это тактика.

Научите учащихся искать эти модные слова, и какие умения они используют в большинстве случаев:

Не забудьте включить модные слова, которые обычно появляются в их учебниках (или других учебниках по математике), а также те, которые вы используете в тесты и задания.

В результате им будет легче обрабатывать текстовые задачи.

15. Создание подвопросов

Для сложных задач со словами покажите студентам, как анализировать вопрос, отвечая на три конкретных подвопроса.

Каждый студент должен спросить себя:

• Что я ищу? — Студенты должны перечитывать вопрос снова и снова, ища модные словечки и выделяя важные детали.
• Какая информация мне нужна? — Студенты должны определить, какие факты, цифры и переменные им нужны для решения вопроса.Например, если они решают, что вопрос основан на вычитании, им нужно уменьшить и вычесть.
• Какая у меня информация? — Учащиеся должны уметь составить основное уравнение, используя информацию в словесной задаче, после определения того, какие детали важны.

Эти подвопросы помогают учащимся избежать перегрузки.

Вместо того, чтобы писать и анализировать каждую деталь вопроса, они смогут определить ключевую информацию. Если вы определите учащихся, которые борются с этим, вы можете использовать взаимное обучение по мере необходимости.

Для более свежих подходов к обучению математике в классе рассмотрите возможность побаловать своих учеников различными увлекательными математическими упражнениями.

Заключительные мысли об этих способах более быстрого решения математических задач

Демонстрация этих 15 методов учащимся может дать им уверенность в решении сложных вопросов.

Это также упражнения по математике, помогающие им развить навыки, связанные с сосредоточением внимания, логикой и критическим мышлением.

Хороший класс равен интересному классу.Это уравнение легко запомнить.

> Создайте или войдите в свою учетную запись учителя на Prodigy — бесплатной адаптивной математической игре, которая корректирует контент с учетом проблемных участков игрока и скорости обучения. Он адаптирован к учебным программам США и Канады, его любят более 500 000 учителей и 15 миллионов студентов.

ПОДПИСАТЬСЯ / ВОЙТИ

Промежуточная алгебра Урок 8: Введение в решение проблем WTAMU > Виртуальная математическая лаборатория> Алгебра среднего уровня Цели обучения По завершении этого руководства вы сможете: Используйте четырехэтапный процесс Polya для решения словесных задач, связанных с числами, проценты, прямоугольники, дополнительные углы, дополнительные углы, последовательный целые числа и безубыточность. Введение Нравится вам это или нет, собираетесь ли вы мать, отец, учитель, программист, ученый, исследователь, владелец бизнеса, тренер, математик, менеджер, врач, юрист, банкир (список можно продолжать и на), решение проблем везде.Некоторые люди считать что ты либо можешь это сделать, либо нет. Вопреки этому убеждению, это может быть выученная профессия. Даже лучшие спортсмены и музыканты было немного наставничества и много практики. Вот что это также требует, чтобы уметь решать проблемы. Георгий Поля , г. известен как отец современного решения проблем, провел обширные исследования а также написал множество математических статей и три книги по проблеме решение. Я собираюсь показать вам его метод решения проблем, чтобы помочь вам через эти проблемы. Учебник Как упоминалось выше, я использую четыре шага Полии для решения проблемы решение для показать студентам, как решать задачи со словами. Просто Примечание что ваш учитель математики или учебник по математике могут назвать это немного иначе, но вы увидите, что все это в основном означает одно и то же. Если вы выполните эти шаги, это поможет вам стать более успешный в мир решения проблем. Поля создал свой знаменитый четырехэтапный процесс для решение проблем, , который используется повсюду, чтобы помочь людям в решении проблем: Шаг 1. Разберитесь в проблеме. Иногда проблема заключается в понимании проблема . Если вам неясно, что нужно решить, то, вероятно, вы будет получать неправильные результаты. Чтобы показать понимание проблемы, вы, конечно, должны прочитать проблему осторожно. Звучит достаточно просто, но некоторые люди прыгают с ума и пытаются начать решение проблема до того, как они прочитают всю проблему. Однажды проблема читается, вам нужно перечислить все компоненты и данные, которые вовлеченный. Здесь вы будете назначать свою переменную. Шаг 2: Разработайте план (переведите). Когда вы разрабатываете план (переводите) , вы придумать способ решать проблему. Составление уравнения, построение диаграммы и создание диаграммы — это все способы, которыми вы можете решить свою проблема. В этом уроке мы будем настраивать уравнения для каждого проблема. Вы переведете их так же, как мы это делали в Tutorial. 2: Учебник по алгебраическим выражениям и 5: Свойства действительных чисел. Шаг 3: Выполните план (решите). Следующий шаг, выполнить план (решить) , большой.Это где вы решаете уравнение, которое придумали, когда «разрабатываете план» шаг. Все уравнения в этом руководстве будут линейными. Если ты обязательно нужна помощь в их решении, вернитесь к Tutorial 7: Линейные уравнения в одной переменной и просмотрите эту концепцию. Шаг 4. Оглянитесь назад (проверьте и интерпретировать). Возможно, вам знакомо выражение «не оглядываться’. В решение проблем хорошо оглянуться назад (проверить и интерпретировать). . По сути, проверьте, использовали ли вы всю свою информацию и что отвечать имеет смысл. Если ваш ответ подтвердился, убедитесь, что вы записывать ваш окончательный ответ с правильной маркировкой. Пример 1 : двойная разница числа, и 1 больше на 4 чем этот номер. Найдите номер. Убедитесь, что вы внимательно прочитали вопрос. раз. Так как ищем номер, то введем x = число * Удалить () с помощью dist.опора * Получить все условия x на одной стороне * Инв. суб. 2 прибавить 2 Если вы возьмете двойную разницу 6 и 1, то есть так же, как 4 больше 6, так что это проверка. ОКОНЧАТЕЛЬНЫЙ ОТВЕТ: Число 6. Пример 2 : Одно число на 3 меньше другого. Если сумма двух чисел равна 177, найдите каждое число. Убедитесь, что вы внимательно прочитали вопрос. раз. Ищем два числа, и так как мы можем написать одно число по другому номеру допустим x = другое число Число ne на 3 меньше другого числа: x — 3 = одно число * Объединить похожие термины * Инв.из под 3 добавляется 3 * Инв. из мульт. 2 — это div. 2 Если мы сложим 90 и 87 (число 3 меньше 90), мы получим 177. ОКОНЧАТЕЛЬНЫЙ ОТВЕТ: Одно число — 90. Другой номер — 87. Всякий раз, когда вы работаете с проблемой процента, вы нужно убедиться вы пишете свой процент в десятичной форме. Вы делаете это, перемещая десятичный знак процента два слева. Например, 32% в десятичная форма: 0,32 Если вы хотите найти процент некоторых номер, запомнить что ‘of’ представляет собой умножение — так что вы умножите процентов (в десятичной форме) умноженное на число, от которого вы берете процент. Пример 3 : Найдите 45% от 125. Убедитесь, что вы внимательно прочитали вопрос. раз. Мы ищем число, которое составляет 45% от 125, мы позволит x = значение, которое мы есть ищу * Умножить 56.25 — это 45% от 125. ОКОНЧАТЕЛЬНЫЙ ОТВЕТ: Номер 56,25. Пример 4 : В математическом классе 30 учеников. Примерно 70% сдал последний тест по математике. Сколько студентов сдали последний математика тестовое задание? Убедитесь, что вы внимательно прочитали вопрос. раз. Смотрим, сколько учеников сдали последний тест по математике, сдадим x = количество студенты * Умножить 21 составляет 70% от 30. ИТОГОВЫЙ ОТВЕТ: 21 ученик сдали последний тест по математике. Пример 5 : Я купил новый телевизор в местном магазине электроники для 541,25 доллара США, включая налоги. Если ставка налога составляет 8,25%, найдите цена телевизора до того, как они добавили налог. Убедитесь, что вы внимательно прочитали вопрос. раз. Ищем цену на телевизор до того, как добавили налог, сдадим x = цена телевизора до того, как был добавлен налог. * Объединить похожие термины * Инв. В мульт. 1.0825 — это div. к 1.0825 Если добавить 8.25% налога до 500, вы получите 541,25. ОКОНЧАТЕЛЬНЫЙ ОТВЕТ: Первоначальная цена — 500 долларов США. Следующая формула пригодится для решения пример 6: Периметр прямоугольника = 2 (длина) + 2 (ширина) Пример 6 : На чертеже прямоугольной комнаты длина равна На 1 дюйм больше, чем в 3 раза ширины.Найдите размеры, если периметр должно быть 26 дюймов. Убедитесь, что вы внимательно прочитали вопрос. раз. Ищем длину и ширину прямоугольник. С длину можно записать через ширину, допустим w = ширина длина на 1 дюйм больше ширины более чем в 3 раза: 1 + 3 w = длина * Удалить () с помощью dist.опора * Объединить похожие термины * Инв. доп. 2 является суб. 2 * Инв. из мульт. на 8 дел. по 8 Если ширина равна 3, то длина, которая на 1 дюйм больше, чем 3 раз больше ширины должно быть 10.Периметр прямоугольника шириной 3 дюймов, а длина 10 дюймов получается 26. ОКОНЧАТЕЛЬНЫЙ ОТВЕТ: Ширина 3 дюйма. Длина 10 дюймов. Дополнительные и дополнительные уголки Сумма дополнительных углов составляет 180 градусов. Сумма дополнительных углов составляет 90 градусов. Пример 7: Найдите размер каждого угла на рисунке. ниже. Обратите внимание: поскольку углы составляют прямую линию, они равны дополнительный друг другу. Убедитесь, что вы внимательно прочитали вопрос. раз. На рисунке уже дано, что x = один угол 5 x = другой угол * Объединить похожие термины * Инв.из мульт. на 6 дел. по 6 Если x равно 30, то 5 x = 5 (30) = 150. 150 и 30 делают сложить, чтобы быть 180, так что это дополнительные углы. ОКОНЧАТЕЛЬНЫЙ ОТВЕТ: Два угла: 30 градусов и 150 градусов. Целые числа, идущие подряд — целые числа, следующие за друг друга в порядок. Например, 5, 6 и 7 — три последовательные целые числа. Если мы позволим x представить первое целое число, как бы мы представили второе подряд целое число в виде x ? Что ж, если мы посмотрим на 5, 6 и 7 — обратите внимание, что 6 — это один больше 5, первое целое число. В общем, можно было бы обозначить вторым последовательное целое число на x + 1 . А как насчет третьего целого числа подряд. Ну заметьте, как 7 на 2 больше 5. В в общем, мы могли бы представить третье последовательное целое число как x + 2. Последовательные ЧЕТНЫЕ целые числа — четные целые числа, следовать друг за другом чтобы. Например, 4, 6 и 8 — три последовательных даже целые числа. Если мы позволим x представить первое ЧЕТНОЕ целое число, как бы мы представили второе подряд четное целое число в виде x ? Обратите внимание, что 6 на два больше, чем 4, первое четное число. В общем, можно было бы обозначить вторым последовательное ЧЕТНОЕ целое число по x + 2 . А как же третий подряд четный целое число? Хорошо подмечено как 8 на 4 больше, чем 4. В общем, мы могли бы представить в третьих последовательное ЧЕТНОЕ целое число как x + 4. Последовательные целые нечетные числа — нечетные целые числа, следовать друг за другом чтобы. Например, 5, 7 и 9 — три последовательных нечетные целые числа. Если мы позволим x представить первое целое нечетное число, как бы мы представили второе подряд нечетное целое число x ? Обратите внимание, что 7 на два больше, чем 5, первое нечетное целое число. В общем, можно было бы обозначить вторым последовательное нечетное целое число по x + 2. А как насчет третьего подряд нечетного целое число? Ну заметьте как 9 на 4 больше, чем 5. В общем, можно было бы представить третьим последовательный Целое число ODD как x + 4. Обратите внимание, что распространенное заблуждение состоит в том, что, поскольку мы хотим нечетное число что мы не должны складывать 2, которое является четным числом. Держать в помните, что x представляет ODD число и что следующее нечетное число находится на расстоянии 2, точно так же, как 7 находится на расстоянии 2 от 5, поэтому мы нужно прибавить 2 к первому нечетному числу, чтобы перейти ко второму подряд нечетное число. Пример 8: Сумма трех последовательных целых чисел равна 258. Находить целые числа. Убедитесь, что вы внимательно прочитали вопрос. раз. Ищем 3 последовательных целых числа, допустим x = 1-е целое число подряд x + 1 = 2-е целое число подряд x + 2 = 3-е последовательное целое число * Объединить похожие термины * Инв.добавления 3 является подпунктом. 3 * Инв. из мульт. на 3 — div. по 3 Сумма 85, 86 и 87 действительно равна 258. ОКОНЧАТЕЛЬНЫЙ ОТВЕТ: Три последовательных целых числа: 85, 86 и 87. Пример 9: Возраст трех сестер равен 3 года подряд. целые числа. Если сумма удвоенного 1-го четного целого числа, 3-кратного 2-го четного целого числа, и третье четное целое число 34, найдите каждый возраст. Убедитесь, что вы внимательно прочитали вопрос. раз. Ищем 3 ЧЕТЫЕ последовательных целых числа, будем пусть x = 1-е последовательное четное целое число x + 2 = 2-е подряд четное целое число x + 4 = 3-е последовательное четное целое число * Удалить () с помощью dist.опора * Объединить похожие термины * Инв. доп. 10 является суб. 10 * Инв. из мульт. на 6 дел. по 6 Если мы возьмем сумму двух умноженных на 4, трех умноженных на 6 и 8, мы получаем 34 ОКОНЧАТЕЛЬНЫЙ ОТВЕТ: Возраст трех сестер — 4, 6 и 8 лет. Business Problem: Breaking (Бизнес-проблема: ломка) Даже В задаче, связанной с бизнесом, уравнение затрат C — это стоимость производства продукта. В уравнении дохода R — это сумма денег, которые производитель зарабатывает на продукте. Если производитель хочет знать, сколько предметов необходимо быть проданным, чтобы сломать даже то, что можно найти, установив стоимость равной выручке. Пример 10: Стоимость C до произвести x количество компакт-дисков C = 50 + 5 x . Компакт-диски продаются оптом по 15 долларов за штуку, поэтому доход рэнд равен рэнд = 15 x . Узнайте, сколько компакт-дисков нужно изготовить и продать, чтобы их сломать. даже. Убедитесь, что вы внимательно прочитали вопрос. раз. Мы ищем количество проданных компакт-дисков безубыточность, сдадим x = количество cd’s * Получить все условия x с одной стороны * Инв.из мульт. на 10 — дел. к 10 Когда x равно 5, стоимость и доход как равно 75. ОКОНЧАТЕЛЬНЫЙ ОТВЕТ: 5 компакт-дисков. Практические задачи Это практические задачи, которые помогут вам следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти типы проблем. Math работает так же, как что-нибудь иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться Это. Даже лучшим спортсменам и музыкантам помогали на протяжении всего пути. практиковаться, практиковаться, практиковаться, чтобы стать лучше в своем виде спорта или инструменте. На самом деле не бывает слишком много практики. Чтобы получить максимальную отдачу от них, вы должны работать проблема на свой собственный, а затем проверьте свой ответ, щелкнув ссылку для ответ / обсуждение для этой проблемы . По ссылке вы найдете ответ а также любые шаги, которые позволили найти этот ответ. Практика Задачи 1a — 1g: Решите проблему со словом. 1с. В местном мебельном магазине потрясающий продажа. Они снижают каждую цену на 45%. Если кушетка у вас есть на глаз стоит 440 долларов после уценки, какой был оригинал цена? Сколько бы вы сэкономили, если бы купили его на этой распродаже? (ответ / обсуждение к 1c) 1г.Прямоугольный сад имеет ширину 8 футов меньше чем вдвое длиннее. Найдите размеры, если периметр 20 ноги. (ответ / обсуждение к 1d) 1д. Сумма дополнительных углов составляет 90 градусов. Находить размер каждого угла на рисунке ниже. Обратите внимание, что поскольку в углы составляют прямой угол, они дополняют друг друга. (ответ / обсуждение к 1e) 1г. Стоимость C к произвести x номеров видеомагнитофонов C = 1000 + 100 x . Видеомагнитофоны продаются оптом по 150 долларов за штуку, поэтому выручка рассчитывается по формуле R = 150 x .Узнайте, сколько видеомагнитофонов производитель необходимо производить и продавать, чтобы достичь безубыточности. (ответ / обсуждение до 1 г) Нужна дополнительная помощь по этим темам? Последний раз редактировал Ким Сьюард 1 июля 2011 г. Авторские права на все содержимое (C) 2002 — 2011, WTAMU и Kim Seward. Все права защищены.

Почему я обучаю студентов нескольким стратегиям решения математических задач

Я большой сторонник обучения студентов нескольким стратегиям решения задач и позволяю студентам выбирать лучшую стратегию, которая им подходит. Мне нравится, когда ученики могут взять на себя ответственность за определенный способ решения проблемы и достижения успеха. Они действительно понимают, почему это работает, и затем могут применить его к множеству других проблем.

Опытные математики-мыслители имеют в своем арсенале различные стратегии решения проблем и могут получить к ним быстрый и эффективный доступ. Они понимают, что одна и та же стратегия не работает для всех проблем, и могут применять лучшую, наиболее эффективную стратегию для каждой решаемой проблемы почти без усилий или даже не задумываясь об этом.

Я хочу, чтобы все мои ученики стали квалифицированными математиками , которые считают, что они хороши в математике .

Когда я учился в школе, я помню, как учительница писала, как решить задачу на накладных расходах, и мы записали, как она это сделала, в свои тетради.Мы должны были скопировать точно , как она решила задачу, и применить его ко всем задачам на странице в наших учебниках по математике. Вы помните, как вас так учили? Как правило, был только один правильный способ для решения проблемы. Интересно, как многого мне не хватало из-за того, что меня учили только одному способу. Я хорошо учился по математике, но мне это никогда не нравилось. Это было скучно, обыденно, и мы делали одно и то же каждый день.

Перенесемся в мои первые несколько лет преподавания. Я участвовал в некотором профессиональном развитии, который научил меня различным способам решения задач сложения и вычитания многозначных чисел, а также работы с дробями.

Мои глаза открылись на совершенно новый мир. Я обнаружил, что хорошо разбираюсь в математике. Благодаря обучению нескольким ключевым фундаментальным идеям я обнаружил, что могу подойти к сложной проблеме и рассуждать через нее, выясняя свой собственный способ ее решения. Я любил математику. Этого я хочу для своих учеников.

Каждый раз, когда я публикую эту фотографию в Facebook, она всегда привлекает к себе массу внимания, как положительного, так и отрицательного. Я получаю «почему бы вам просто не научить их добавлять» комментариев, «какая классная идея» комментариев и все, что между ними.

Мне нравится использовать его, чтобы начать разговор об обучении нескольким стратегиям решения проблем. Это такой наглядный пример того, как использовать 10 для решения фактов сложения.

Вы видите, что обучение студентов тому, как решать задачи с использованием различных стратегий, — не новая идея. Помните новую математику в 80-х и начале 90-х годов? Это было. Это повторилось и в начале 2000-х годов. Учителя давно обучают стратегиям решения математических задач.

Однако Common Core и многие государственные стандарты сделали его более явным и фактически поощряют использование нескольких стратегий до обучения традиционному алгоритму.Благодаря новым стандартам и профессиональному развитию идея обучения нескольким стратегиям снова вышла на первый план.

Следует ли обучать традиционному алгоритму? да. Но перед тем, как дать его студентам, они должны понять, почему сокращенный путь традиционных алгоритмов работает и что делать, если он не работает (например, выяснить их ошибку!).

Все дело в математике в уме. Большинство из нас делают это автоматически в продуктовом магазине, когда выясняют, сколько мы хотим потратить.Хотя мы можем вытащить свой iPhone, часто это быстрее делается в голове. В следующий раз, когда вы решите проблему сложения в голове, подумайте, как вы решите задачу . Делаете ли вы десять или округление до следующего дружественного числа? Вы оцениваете? Вы удваиваете или уменьшаете число вдвое? Как решить проблему?

Готов поспорить, вы используете какую-то стратегию, которую либо изобрели, либо которую кто-то вас научил. Вы, вероятно, не думаете о традиционном алгоритме (хотя, возможно, и думаете, если это все, чему вас учили).

Я хочу, чтобы все мои ученики стали опытными математическими мыслителями, которые считают, что они хороши в математике. Click To Tweet

Обучение студентов различным стратегиям помогает им переходить от бумажных и карандашных вычислений к мысленным вычислениям. Большинство математических задач могут быть решены в нашей голове, даже самые сложные, если мы сможем удержать там все числа. Студенты найдут стратегии, которые им подходят. Нам просто нужно обучить нескольким стратегиям, чтобы учащиеся могли найти те, которые им подходят.

Это приводит меня к. . .

В идеале мы хотим, чтобы учащиеся обладали гибким математическим мышлением. Мы хотим, чтобы они хорошо разбирались в математике и были уверены в своей способности «делать» . Для этого я учу студентов различным способам решения задач в надежде, что один из способов найдет отклик у каждого студента.

Студенты находятся в разных местах своего математического пути. Один из лучших инструментов, которые я видел, чтобы объяснить это путешествие, — это контексты для обучения.Пейзаж для обучения описывает пути, по которым учащиеся могут понять сложение и вычитание и умножение и деление. Каждый путь индивидуален, но есть тенденции.

Пейзажи можно найти в следующих документах: Сложение и вычитание и Умножение и деление. Их стоит скачать и изучить.

В этих документах много слов, которые вам, возможно, придется поискать, но я хочу подчеркнуть, что студенты постоянно находят новые способы решения задач.Их математическое мышление не застойно, а плавно перемещается по разным уровням по мере того, как они сталкиваются со все большим и большим количеством проблем. Обучение студентов различным стратегиям решения проблем помогает им увидеть новые, более эффективные стратегии, которые могут им найти отклик.

Мы хотим, чтобы ученики правильно и эффективно решали задачи. Обучение различным стратегиям поможет им увидеть разные способы решения проблем, и ученики будут стремиться к тому пути, который лучше всего подходит для того, где они находятся. Наша задача — подтолкнуть их немного дальше и стать более эффективными математическими мыслителями.

Это похоже на предыдущую идею в том, что я хочу, чтобы студенты нашли стратегии, которые работают для них, но я также хочу подтолкнуть студентов к экспериментам и поиску новых стратегий, которые могут оказаться вне их досягаемости.

В моем блоге все сообщения о различных моделях и стратегиях сложения и вычитания двузначных чисел, я более подробно рассказываю о различных стратегиях сложения двузначных чисел. Эти стратегии создают основу для обучения студентов, чтобы они могли перейти от сложения однозначных чисел к сложению многозначных и глубоко изучить, что происходит с разрядами при сложении и вычитании.

Теперь есть тонкая грань между обучением строительных лесов и предоставлением костыля. Ключ всегда заключается в том, чтобы побуждать учеников пробовать то, что находится за пределами их уровня комфорта, что называется зоной ближайшего развития. Мы всегда хотим подтолкнуть наших учеников сделать еще один шаг вперед, не слишком усердно, но достаточно, чтобы побудить их учиться больше.

Есть ли у вас ученики, которые просто не любят математику? Тем, кто не думает, что они хороши в математике? Это был я в детстве.

У меня не было мотивации заниматься математикой, потому что это было скучно. Тем не менее, я обнаружил, что, обучая студентов различным способам решения проблем, а затем немного отступая, мои ученики погрузятся в проблемы и начнут исследовать. У них гораздо больше мотивации работать во время математики, чем когда-либо в детстве. Я дал студентам точки входа в проблему и позволил им подойти к ней на своем уровне, решая ее с помощью базовых навыков, которые они знают и понимают.

Я дал ученикам возможность заниматься математикой, потому что научил их различным стратегиям, которые можно добавить в их инструментарий.

Я обучаю нескольким стратегиям решения математических задач, потому что:

• ясно показывает, что происходит в наших головах
• помогает студентам выбрать наиболее эффективную стратегию
• обеспечивает основу, чтобы студенты могли найти место для участия в процессе решения задач
• мотивирует студентов учиться больше.

А ты? Обучаете ли вы студентов нескольким стратегиям решения математических задач? Я хотел бы услышать ваше мнение по этой теме в комментариях ниже.