Линии чисел Фибоначчи и их использование – Финансовая энциклопедия
Что такое Линии чисел Фибоначчи и их использование?
Числа Фибоначчи используются для создания технических индикаторов с использованием математической последовательности, разработанной итальянским математиком, обычно называемым «Фибоначчи», в 13 веке.Последовательность чисел, начинающаяся с нуля и единицы, создается путем сложения двух предыдущих чисел.Например, ранняя часть последовательности – 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 и так далее.1
Затем эту последовательность можно разбить на коэффициенты, которые, по мнению некоторых, дают представление о том, куда пойдет данный финансовый рынок.
Последовательность Фибоначчи важна из-за так называемого золотого сечения 1,618 или его обратной величины 0,618. В последовательности Фибоначчи любое данное число примерно в 1,618 раз больше предыдущего, без учета первых нескольких чисел. Каждое число также составляет 0,618 от числа справа от него, опять же без учета первых нескольких чисел в последовательности.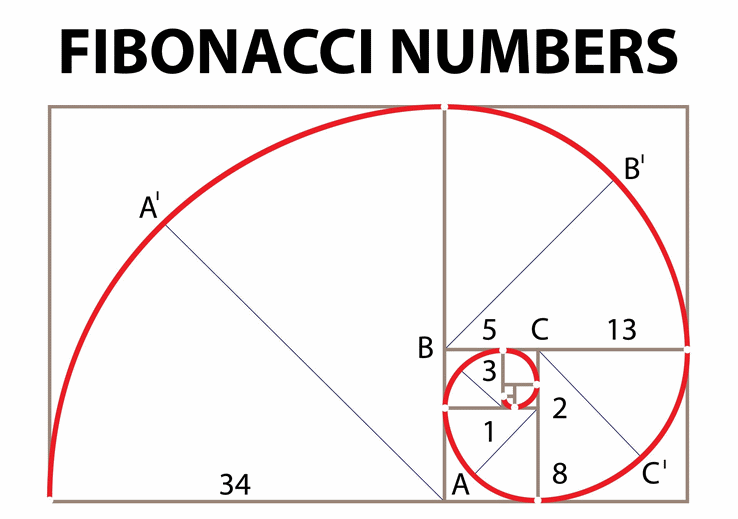
Ключевые моменты
- Числа и линии Фибоначчи создаются соотношениями, найденными в последовательности Фибоначчи.
- Общие числа Фибоначчи на финансовых рынках: 0,236, 0,382, 0,618, 1,618, 2,618, 4,236. Эти соотношения или проценты можно найти, разделив определенные числа в последовательности на другие числа.
- Хотя это официально не числа Фибоначчи, трейдеры могут также использовать 0,5, 1,0 и 2,0.
- Цифры отражают, как далеко цена может зайти после очередного ценового движения. Например, если акция движется с 1 доллара до 2 долларов, к этому могут быть применены числа Фибоначчи. Падение до 1,76 доллара представляет собой откат на 23,6% от движения цены в 1 доллар (округлено).
- Два распространенных инструмента Фибоначчи – это коррекция и расширение. Уровни коррекции Фибоначчи измеряют, насколько далеко может зайти откат .
 Расширения Фибоначчи измеряют, насколько далеко может зайти импульсная волна .
Расширения Фибоначчи измеряют, насколько далеко может зайти импульсная волна .
Формулы для чисел и уровней Фибоначчи
У чисел Фибоначчи нет конкретной формулы, это скорее числовая последовательность, в которой числа имеют определенные отношения друг с другом.
Как рассчитать уровни восстановления Фибоначчи
Последовательность чисел Фибоначчи может использоваться по-разному для получения уровней восстановления Фибоначчи или уровней расширения Фибоначчи . Вот как их найти. Как их использовать, обсуждается в следующем разделе.
Для коррекции Фибоначчи на графике необходимо выбрать две ценовые точки, обычно максимум и минимум колебания . После того, как эти две точки выбраны, числа / линии Фибоначчи рисуются в процентах от этого движения.
Если акция вырастет с 15 до 20 долларов, то уровень 23,6% составит 18,82 доллара, или 20 долларов – (5 долларов x 0,236) = 18,82 доллара. Уровень 50% составляет 17,50 долларов, или 15 долларов – (5 долларов х 0,5) = 17,50 долларов.
Уровни расширения Фибоначчи также выводятся из числовой последовательности. По мере развития последовательности разделите одно число на предыдущее, чтобы получить коэффициент 1,618. Разделите число на два разряда слева, и получится 2,618. Разделите число на три слева, и получится 4,236.
Расширение Фибоначчи требует трех ценовых точек. Начало движения, конец движения, а затем точка где-то посередине (откат).
Если цена вырастет с 30 до 40 долларов, и эти два ценовых уровня являются точками один и два, то уровень 161,8% будет на 16,18 долларов (1,618 x 10 долларов) выше цены, выбранной для точки три. Если третий пункт равен 35 долларам, уровень расширения 161,8% составляет 51,18 доллара (35 долларов + 16,18 доллара).
Уровни 100% и 200% не являются официальными числами Фибоначчи, но они полезны, поскольку проецируют движение, аналогичное (или кратному) тому, что только что произошло на ценовом графике.
Что вам говорят числа и линии Фибоначчи?
Некоторые трейдеры считают, что числа Фибоначчи играют важную роль в финансах . Как обсуждалось выше, последовательность чисел Фибоначчи может использоваться для создания соотношений или процентов, которые используют трейдеры.
Как обсуждалось выше, последовательность чисел Фибоначчи может использоваться для создания соотношений или процентов, которые используют трейдеры.
К ним относятся: 23,6%, 38,2%, 50%, 61,8%, 78,6%, 100%, 161,8%, 261,8%, 423,6%.
Эти проценты применяются с использованием множества различных методов:
- Коррекции Фибоначчи. Это горизонтальные линии на графике, обозначающие области поддержки и сопротивления .
- Расширения Фибоначчи. Это горизонтальные линии на графике, указывающие, где может достигнуть сильная ценовая волна.
- Дуги Фибоначчи .
- Веера Фибоначчи . Это диагональные линии, построенные с использованием максимума и минимума, которые представляют области поддержки и сопротивления.
- Часовые пояса Фибоначчи . Это вертикальные линии в будущее, предназначенные для предсказания основных движений цен.

Уровни коррекции Фибоначчи являются наиболее распространенной формой технического анализа, основанного на последовательности Фибоначчи. Во время тренда можно использовать откаты Фибоначчи, чтобы определить, насколько глубоким может быть откат. Импульсные волны – это более крупные волны в направлении тренда, а откаты – это более мелкие волны между ними. Поскольку это меньшие волны, они будут составлять процент от большей волны. В это время трейдеры будут следить за соотношением Фибоначчи от 23,6% до 78,6%. Если цена останавливается около одного из уровней Фибоначчи, а затем начинает двигаться обратно в трендовом направлении, трейдер может открыть сделку в трендовом направлении.
Уровни Фибоначчи используются как ориентиры, возможные области, в которых может развиваться торговля. Цена должна подтвердить, прежде чем действовать на уровне Фибоначчи. Заранее трейдеры не знают, какой уровень будет значительным, поэтому им нужно подождать и посмотреть, какой уровень соответствует цене, прежде чем открывать сделку.
Дуги, вееры, расширения и часовые пояса – это схожие концепции, но они по-разному применяются к диаграммам. Каждый из них показывает потенциальные области поддержки или сопротивления на основе чисел Фибоначчи, примененных к предыдущим ценовым движениям. Эти уровни поддержки или сопротивления можно использовать для прогнозирования того, где цена
Разница между числами Фибоначчи и числами Ганна
веер Ганна и квадрат Ганна. В веере Ганна, например, используются углы в 45 градусов, что Ганн считал особенно важными. Работа Ганна в основном вращалась вокруг циклов и углов. С другой стороны, числа Фибоначчи в основном связаны с отношениями, полученными из последовательности чисел Фибоначчи. Ганн был трейдером, поэтому его методы были созданы для финансовых рынков. Методы Фибоначчи не были созданы для торговли, но были адаптированы к рынкам трейдерами и аналитиками.
Ограничения использования чисел и уровней Фибоначчи
Использование исследований Фибоначчи является субъективным, поскольку трейдер должен использовать максимумы и минимумы по своему выбору. Выбранные максимумы и минимумы повлияют на результаты, которые получит трейдер.
Выбранные максимумы и минимумы повлияют на результаты, которые получит трейдер.
Еще один аргумент против методов торговли числами Фибоначчи состоит в том, что этих уровней так много, что рынок обязательно отскочит или изменит направление около одного из них, что делает индикатор значимым в ретроспективе. Проблема в том, что трудно понять, какое число или уровень будут важны в реальном времени или в будущем.
#ЛЧисла Фибоначчи — Справочник химика 21
Рассмотрим теперь алгоритм поиска, использующий числа Фибоначчи. Порядок его выполнения при поиске минимума складывается из следующих этапов [c.509]Двадцатое число Фибоначчи уже больше 10 000 (см. табл. [c.435]
Начав с листа О , видим, что лист 8 окажется в затененной ориентации по отношению к нему. Чтобы добраться до листа 8 , начиная с нулевого, нужно трижды обогнуть стебель. Отношеие двух чисел, а именно 3/8, показывает, что любой новый лист встречается через каждые 3/8 части стебля. Отношение 3/8 характерно для филлотаксиса (расположение листьев на стебле растения), так же как и значения 1/2, 1/3, 2/5 и даже 5/13. Почти ничего неизвестно об истоках филлотаксиса. Давно было замечено, что числа встречающиеся в этих характеристических соотношениях, таковы I, 1, 2, 3, 5, 8, 13,. .., а это не что иное, как числа ряда Фибоначчи, в котором каждый последующий член является суммой двух предыдущих. Числа Фибоначчи можно также найти, рассматривая снизу спиралевидное построение сосновых шишек. На рис. 8-16 можно видеть сосновую шишку в двух аспектах. Вид снизу показывает существование 13 левых и 8 правых спиралей из чешуек. Такие спирали с точными числами Фибоначчи обнаружены и в других растениях. Семечки подсолнечника можно рассматривать как спрессованное множество, расположенное вокруг стебля. На рис. 8-17 дано несколько примеров. Вероятно, больше всего поражает то, что продолжение характеристических соотношений в расположении листьев окончательно приводит к чрезвычайно важному иррациональному числу 0,381966.
Отношение 3/8 характерно для филлотаксиса (расположение листьев на стебле растения), так же как и значения 1/2, 1/3, 2/5 и даже 5/13. Почти ничего неизвестно об истоках филлотаксиса. Давно было замечено, что числа встречающиеся в этих характеристических соотношениях, таковы I, 1, 2, 3, 5, 8, 13,. .., а это не что иное, как числа ряда Фибоначчи, в котором каждый последующий член является суммой двух предыдущих. Числа Фибоначчи можно также найти, рассматривая снизу спиралевидное построение сосновых шишек. На рис. 8-16 можно видеть сосновую шишку в двух аспектах. Вид снизу показывает существование 13 левых и 8 правых спиралей из чешуек. Такие спирали с точными числами Фибоначчи обнаружены и в других растениях. Семечки подсолнечника можно рассматривать как спрессованное множество, расположенное вокруг стебля. На рис. 8-17 дано несколько примеров. Вероятно, больше всего поражает то, что продолжение характеристических соотношений в расположении листьев окончательно приводит к чрезвычайно важному иррациональному числу 0,381966.
За кажущейся простотой операции деления в крайнем и среднем отношении скрыто множество удивительных математических свойств и множество форм выражения золотого сечения [66]. Золотое сечение тесно связано с числами Фибоначчи. [c.60]
Как известно, два первых числа Фибоначчи определены как 1. а последующие есть сумма двух предыдущих. Результат задан как вектор-строка чисел Фибоначчи. [c.74]
Другим примером служит вычисление чисел Фибоначчи, которые играют важную роль при решении проблем оптимизации. Числа Фибоначчи рассчитывают по следующим формулам [c.142]
Для полученного значення N находится такое число Фибоначчи чтобы выполнялось неравенство [c.509]
Числами Фибоначчи называются члены численной последовательности, каждый из которых, начиная с третьего, равен сумме двух предыдущих, причем за начало такого ряда можно принять любые два числа, например, О и 1, 1 и 3 или ] и 4 и т.
Числа Фибоначчи являются членами геометрической прогрессии вида [c.61]
ТАБЛИЦА 14 Числа Фибоначчи [c.505]
Указанный процесс продолжается до тех пор, пока не будут исчерпаны все числа Фибоначчи в убывающей последовательности [c.507]
Более совершенную процедуру поиска экстремума унимодальной функции одного переменного дает метод Кифера — Джонсона [7]. Ими было показано, что, выполнив п опытов (или вычислений), можно локализовать оптимум в Рп части первоначального интервала, где Рп — я-е число Фибоначчи. Первые два числа Фибоначчи равны Ро = Р = , а последующие определяются рекуррентным соотношением [c.435]
В последнее время в теории распознавания введено понятие кластер и кластерный анализ . Под термином кластер понимается множество точек в пространстве признаков, не пересекающееся с другим множеством, поэтому в нашем случае этот термин является синонимом класс . Однако между кластерным анализом и классификацией имеется некоторая разница. Классификацию можно вести по разным параметрам, например классифицировать катализаторы по активности, селективности или механической прочности. Кластерный же анализ определяет границы между естественными группами реализаций, не пересекающимися, как указывалось, во всем пространстве рассматриваемых признаков. При такой терминологии определение естественной границы классов по алгоритмам без учителя есть кластерный анализ. Методам кластерного анализа посвящен ряд работ [12—14]. Простейшим, возможно не самым экономичным, алгоритмом кластерного анализа при дихотомии является построенный на процедуре поиска экстремума унимодальной функции Кифера — Джонсона [15], использующий числа Фибоначчи [c.110]
Однако между кластерным анализом и классификацией имеется некоторая разница. Классификацию можно вести по разным параметрам, например классифицировать катализаторы по активности, селективности или механической прочности. Кластерный же анализ определяет границы между естественными группами реализаций, не пересекающимися, как указывалось, во всем пространстве рассматриваемых признаков. При такой терминологии определение естественной границы классов по алгоритмам без учителя есть кластерный анализ. Методам кластерного анализа посвящен ряд работ [12—14]. Простейшим, возможно не самым экономичным, алгоритмом кластерного анализа при дихотомии является построенный на процедуре поиска экстремума унимодальной функции Кифера — Джонсона [15], использующий числа Фибоначчи [c.110]
ОТОЯ в ток ке направлении, что и предыдущий, но е последовательным уменьшением числе Фибоначчи нахахдои шаге по рис. 5.15 пер- вый шаг окезалоя удачным и выполнен переход в. точку [c.64]
Природа дает множество примеров расположения однородных элементов, описываемых числами Фибоначчи [67], в областях биологии, астрономии, пропорций человеческого тела, искусства, архитектуры и др, Наличие закона золотой пропорции находится в наиболее фундаментальных областях естествознания. Известно, что ядра атомов состоят из протонов и нейтронов. Чем больше в ядре атома протонов, тем больше в нем и нейтронов. Но с возрастанием номера элемента количество нейтронов превосходит количество протонов. Их число возрастает в таблиие элементов и у урана в ядре содержится 92 протона и 146 нейтронов, число [c.61]
Известно, что ядра атомов состоят из протонов и нейтронов. Чем больше в ядре атома протонов, тем больше в нем и нейтронов. Но с возрастанием номера элемента количество нейтронов превосходит количество протонов. Их число возрастает в таблиие элементов и у урана в ядре содержится 92 протона и 146 нейтронов, число [c.61]
Многое написано о симметрии, например, в музыке Белы Бартока [1]. Однако пока неизвестно и, возможно, мы не узнаем об этом никогда, сознательно ли он применял требования симметрии, или же он чисто интуитивно приходил к числам Фибоначчи и золотому сечению, которые так часто встречаются в его музыке. Другой вопрос, остающийся без ответа, состоит в том, как эта симметричность способствует привлекательности музыки Бартока и насколько большая часть этой привлекательности обязана нашему врожденному стремлению к симметрии. Сам Барток всегда отказывался обсуждать техническую сторону процесса сочинения музыки и лишь любил повторять В нашем творчестве мы следуем за природой .
 [c.11]
[c.11]Фибоначчи числа — Энциклопедия по машиностроению XXL
Природа дает множество примеров расположения однородных элементов, описываемых числами Фибоначчи. В структ ре многих растений можно обнаружить два семейства спиралей. В одном из этих семейств спирали завиваются по часовой стрелке, а в другом — против. Числа спиралей того и другого типов обычно являются числами Фибоначчи. Числа Фибоначчи проявляются в морфологии различных организмов Например, морские звезды. Число лучей у них отвечает ряду чисел Фибоначчи и равно 5, 8, 13, 21, 34, 55. У хорошо знакомого комара — три пары ног, брюшко делится на восемь сегментов, на голове пять усиков — антенн. Личинка комара членится на 12 сегментов. Число позвонков у многих домашних животных равно 55 [59]. Но проявление чисел Фибоначчи и золотой пропорции не останавливается на живой природе, они применимы практически во всех областях знания, начиная с архитектуры и кончая планетными расстояниями. [c.76]
[c.76]
При применении метода чисел Фибоначчи должно быть зафиксировано число точек N, в которых производится вычисление критерия оптимальности. [c.289]
Золотое сечение и числа Фибоначчи. [c.144]
Члены прогрессии an-a -q», где п 1, 2, 3, 4, 5, 6… являются числами Фибоначчи an=an,2+an-i, если q будет корнем квадратного уравнения q =l+q. Это [c.146]
Природа дает нам многочисленные примеры структур, описываемых золотой пропорцией и числами Фибоначчи, рассмотренных далее. [c.147]
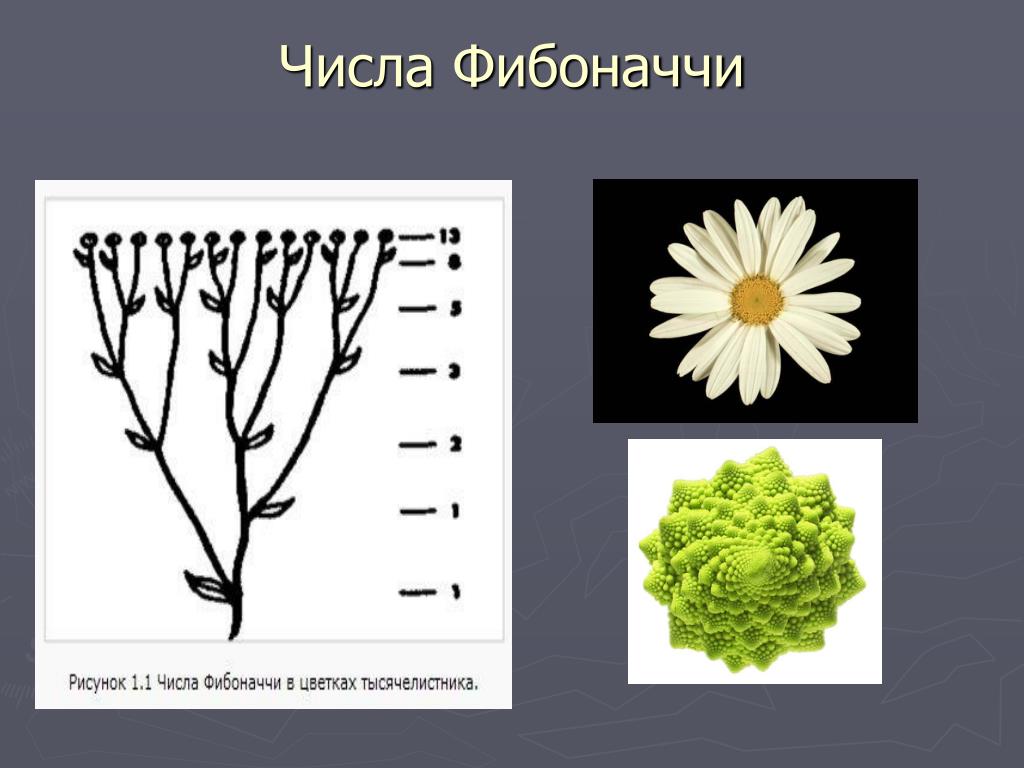
В разнообразных спиралевидных расположениях мелких частей растений обычно можно усмотреть два семейства спиралей. В одном из этих семейств спирали завиваются по часовой стрелке, а в другом — против. Числа спиралей того и другого типов часто оказываются соседними числами Фибоначчи. Так, взяв молодую сосновую веточку, легко заметить, что хвоинки образуют две спирали, идущие справа снизу налево вверх.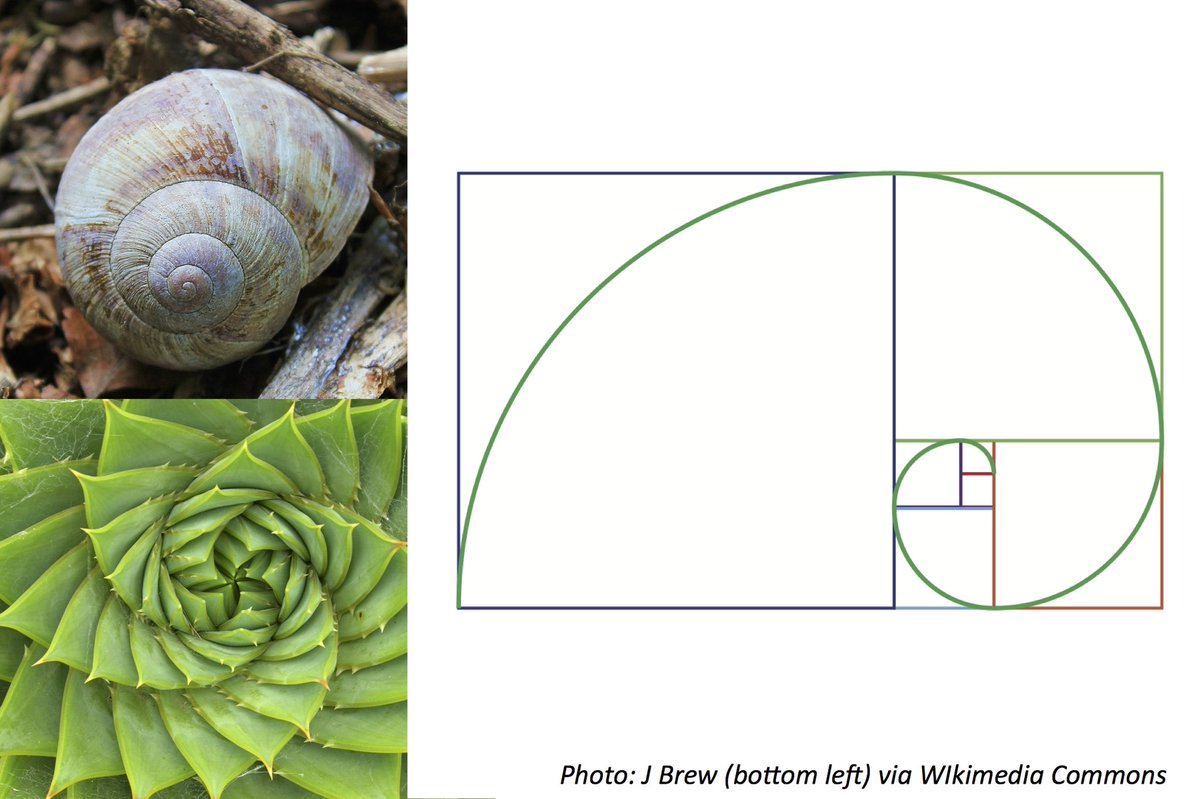 Вместе с тем они же составляют три спирали, идущие слева снизу направо вверх. Хорошо заметны такие спирали и на ананасе обычно их бывает 8 и 13.
[c.147]
Вместе с тем они же составляют три спирали, идущие слева снизу направо вверх. Хорошо заметны такие спирали и на ананасе обычно их бывает 8 и 13.
[c.147]
Проявляется вполне закономерная тенденция в творческой манере поэта он явно предпочитает стихотворения, размер которых близок к числам Фибоначчи. Следует учесть, что законы стихосложения требуют, как правило четного числа строк в стихотворении, так как строки попарно рифмуются. Неудивительно поэтому, что стихотворения с числом 12 и 14 встречаются значительно чаще, чем с числом строк 13. Эго же справедливо и для интервала 20 — 22 строки [5]. [c.162]
Содержание в различных почвах фосфора, калия и азота, а также продуктивность растительности образуют зеркально-симметричный ряд, который также подчиняется золотой пропорции. Даже по отражательной способности света почвы делятся на ряд, характеризуемый числами Фибоначчи [5]. [c.163]
Известно, что геологическая эволюция Земли носила циклический характер. В истории развития планеты выделено несколько геологических эр и периодов, отвечающих 70, 225, 600, 950, 1700, 2600, 3500 и 4500 миллионов лет [5]. Эти переломные моменты характеризуют переход в качественно новое состояние. Указанные числа близки числам Фибоначчи 1, 3, 8, 13, 21, 34, 55, 89, развернутым из настоящего в прошлое [5]. Они отражают основную фундаментальную закономерность эволюции нашей планеты, гармонию ее самоорганизации.
[c.164]
В истории развития планеты выделено несколько геологических эр и периодов, отвечающих 70, 225, 600, 950, 1700, 2600, 3500 и 4500 миллионов лет [5]. Эти переломные моменты характеризуют переход в качественно новое состояние. Указанные числа близки числам Фибоначчи 1, 3, 8, 13, 21, 34, 55, 89, развернутым из настоящего в прошлое [5]. Они отражают основную фундаментальную закономерность эволюции нашей планеты, гармонию ее самоорганизации.
[c.164]
Далее В.Д. Цветков обнаружил, что систолическое давление крови в аорте равно 0,382, а диастолическое 0,618 от среднего давления крови в аорте. Кроме того, работа сердца в отношении объемов желудочков оптимизирована по правилу золотого сечения. По мнению В.Д. Цветкова, организация сердечного цикла в соответствии с золотой пропорцией и числами Фибоначчи является результатом длительной эволюции млекопитающих, в которой организм стремился обеспечить себя при минимальной затрате энерг ии. [c.167]
Числами Фибоначчи называются члены численной последовательности, каждый из которых, начиная с третьего, равен сумме двух предыдущих, причем за начало такого ряда можно принять любые два числа, например, 0 и 1, 1 и 3 или 1 и 4 и Т. П.
[c.75]
П.
[c.75]
Числа Фибоначчи являются членами геометриче-А Со В ской прогрессии вида Оп= [c.75]
Числа Фибоначчи являются членами геометрической прогрессии вида а = где и=1. 2, 3,. .., если q будет корнем квадратного уравнения [c.254]
Несколько эффективней метода дихотомии так называемый метод Фибоначчи, в основу которого положена особая числовая последовательность, применявшаяся математиком XII века Фибоначчи. Этот метод сравнительно недавно разработан американским математиком Кифером [26]. Как и метод дихотомии, метод Фибоначчи выражается правилом деления каждого очередного интервала неопределенности, но не на две, а на три части, и не приращением А/ (х), а результатом одного вычисления в отличие от метода дихотомии, но так же, как при способе направленного перебора, число вычислений в каждом конкретном случае применения метода Фибоначчи колеблется в зависимости от непредвиденных сочетаний обсчитываемых точек и точки минимума х на каждом шаге поиска. Поэтому в отношении метода Фибоначчи применим только минимаксный принцип оптимальности, что обязательно надо иметь в виду, рассматривая изложенное ниже обоснование метода.
[c.158]
Поэтому в отношении метода Фибоначчи применим только минимаксный принцип оптимальности, что обязательно надо иметь в виду, рассматривая изложенное ниже обоснование метода.
[c.158]
Заметим, что поиск методом Фибоначчи, таким образом, можно начать, задавшись длиной остаточного интервала неопределенности или числом вычислений. Если это затруднительно, можно воспользоваться методом золотого сечения, который характеризуется примерно такой же эффективностью (см. [26]). [c.161]
Величину с откладываем от точки В на линии АВ. Число с=0,618 а получается из следующего ряда дробей (ряд Фибоначчи) [c.30]
К бесконечной десятичной дроби Ф можно прийти различными путями. Так, если брать число Ф с различной Точностью в виде отношения двух простых чисел, как это и принято на практике, то окажется, что все эти числа составят ряд, известный под названием ряда Фибоначчи (Ламэ) О, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,
[c. 69]
69]
Развиваются двоичные системы, веса разрядов к-рых находятся не в естественном (2), а в более сложном соотношении, образуя, напр., ряд Фибоначчи (или золотую пропорцию ) [1]. Число N в коде Фибоначчи представляется соотношением [c.397]
Согласно методу чисел Фибоначчи, используют числа Фибоначчи последовательность которых образуется по правилу при Rg = R =l, т. е. ряд чисел Фибоначчи имеет вид 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144. .. Метод аналогичен методу золотого сечения с тем отличием, что коэффициент а равен отношению R.JR., начальное значение i определяется из условия, что / .должно быть наименьшим числом Фибоначчи, превышающим величину В -А) Е, где Е — заданная допустимая погрешность определения экстремума. Так, если (В-А)/Е = 100, то начальное значение i = 12, поскольку R= 144, и а = 55/144 = 0,3819, на следующем шаге будет а = 34/89 = 0,3820 и т. д. [c.160]
Самоподобие эволюционных процессов и числа Фибоначчи
[c. 152]
152]
Следует отметить аналогию между золотым отношением, универсальным законом Фейгенбаума и последовательностью чисел Фибоначчи. Напомним, что числами Фибоначчи называются члены численной последовательности, каждый из которых, начиная с третьего, равен сумме двух предыдущих, например [c.153]
Метод Фибоначчи — это оптимальный последовательный метод, т.е. метод, обеспечивающий максимальное гарантированное сокращение отрезка локализации при заданном числе N вычислений функции. Он основан на использовании чисел Фибоначчи F , задаваемых рекуррентной формулой Fjj = I + 9 для n > 2 и начальными значениями Fq = 1, F, = 1. [c.139]
Особенностью этого ряда является то, что каждое последующее число Фибоначчи равно сумме двух предыдущих (N 2) [c.207]
Метод золотого сечения свободен от недостатка, присущего методу Фибоначчи, связанного с необходимостью назначения числа испытаний N. Но по эффективности метод золотого сечения в 1,17 раза хуже метода Фибоначчи. Метод золотого сечения отличается от метода Фибоначчи также процедурой проведения первых двух испытаний
[c.208]
Метод золотого сечения отличается от метода Фибоначчи также процедурой проведения первых двух испытаний
[c.208]
Другим уникальным свойством чисел Фибоначчи является то, что с ростом их номеров отнощения последующего к предыдущему, например, а(о / ад = 55/34 = 1,6176…., аи / = 89/55 = 1,6182. .. стремятся к золотому числу, то есть lim а,/ a +i = Ф = 1,618034… [c.27]
Природа дает множестпо примеров распололсепия однородных элементов, описываемых числами Фибоначчи. В структуре многих растений можно обнаружить два семейства спиралей. В одно.м из этих семейств спирали завиваются по часовой стрелке, з в другом — против. Числа спиралей того и другого типов обычно являются числами Фибоначчи. Числа Фибоначчи проявляются в морфологии различных организмов. Например, морские [c.254]
За кажупдейся простотой деления отрезка на части по указанному алгоритму скрыто множество математических свойств и многообразия выражения пропорции золотого сечения ( золотой пропорции ).
 Прежде всего следует отметить аналогию между золотой пропорцией и последовательностью чисел Фибоначчи. Напомним, что числами Фибоначчи называются члены численной последовательности, каждый из которых, начиная с третьего, равен сумме двух предыдущих. За начало такого ряда можно принять любые два числа, например, О и 1, 1 и 3 и т.п.
[c.145]
Прежде всего следует отметить аналогию между золотой пропорцией и последовательностью чисел Фибоначчи. Напомним, что числами Фибоначчи называются члены численной последовательности, каждый из которых, начиная с третьего, равен сумме двух предыдущих. За начало такого ряда можно принять любые два числа, например, О и 1, 1 и 3 и т.п.
[c.145]| Рисунок 3.3 — Рост дерева в соответствии с правилом Фибоначчи [2J Пусть некоторое дерево растет так, что каждая новая ветвь в первый год только тянется вверх или в сторону, а затем, начиная со второго года дает по одному боковому побегу (см. рисунок 3.3), Легко заметить, что у двухлетнего дерева имеегся (олько одна ветвь, у трехлетнего — две, у четырехлегнего число ветвей увеличивается до трех, у пятилетнего — до пяти, у шестилетно о — до восьми и т.д. в соответствии с последовательностью Фибоначчи, поскольку число ветвей равно сумме ветвей, которые были год назад, и вновь появившихся побегов. |
 Некоторые стихи построены по схеме 5 8, 5 3, 3 8, 5 8, 8 8. У А.С. Пушкина есть стихотворения с числом строк 13 и 21, то есть с нечетным числом строк, что явно не соответствует распространенным канонам стихосложения. Числа Фибоначчи определяют во мнотих случаях и внутреннюю композицию стихотворений число стихов и число строк в них.
[c.162]
Некоторые стихи построены по схеме 5 8, 5 3, 3 8, 5 8, 8 8. У А.С. Пушкина есть стихотворения с числом строк 13 и 21, то есть с нечетным числом строк, что явно не соответствует распространенным канонам стихосложения. Числа Фибоначчи определяют во мнотих случаях и внутреннюю композицию стихотворений число стихов и число строк в них.
[c.162]Указанные соотношения обеспечивают резонанс планет Солнечной системы, ее устойчивость [5]. К. Бутусов установил также, что ряд параметров планет (масса, объем, орбитальный момент, ускорение силы тяжести) пропорциональны числам Фибоначчи или производным им числам Люка. [c.165]
При применении метода Фибоначчи для отыскания точки А,, при которой 5оп(Х ) достигает минимума, прежде всего зададимся длиной остаточного интервала неопределенности S (т ) пусть 2 ост ( i ) = 0,04. Для того чтобы определить число вычислений, при So T ( г ) = 0,04 и при S (1) = 5,0, в соответствии с (8.10), [c.165]
Л = а 1ф (и — 1)-1-а ,ф (л —2)+. . . +Яоф (0), (4) где ф(га) — числа Фибоначчи, связанные соотиощекием ф п) = ф л —1)+ф(п —2), ф(0) 1, ф(1) = 2. Разложение (4) числа N неоднозначно. Для любого N существует код, в к-ром не встречается двух следуй щи.х подряд нулей, а также код, в к-ром по соседствуют единицы. Эти, а также др. структурные особенности кодов Фибоначчи и золотых кодов делают их удобными для построения самокорректирующихся преобразователей, запоминающих и вычислит, устройств, сервоприводов с цифровым управлеписм и т. п.
[c.397]
. . +Яоф (0), (4) где ф(га) — числа Фибоначчи, связанные соотиощекием ф п) = ф л —1)+ф(п —2), ф(0) 1, ф(1) = 2. Разложение (4) числа N неоднозначно. Для любого N существует код, в к-ром не встречается двух следуй щи.х подряд нулей, а также код, в к-ром по соседствуют единицы. Эти, а также др. структурные особенности кодов Фибоначчи и золотых кодов делают их удобными для построения самокорректирующихся преобразователей, запоминающих и вычислит, устройств, сервоприводов с цифровым управлеписм и т. п.
[c.397]
Методы Фибоначчи и золотого сечения позволяют достичь наилучшей точности при ограниченном числе вычислений значений функций ц>(х) благодаря сокращению числа вы-, числений до одного на каждом шаге после вы-. бора начального отрезка foo, йо1г содержащего точку X, Методы имеют единую схему - [c.131]
Известно множество примеров своеобразной упорядоченности структур как живой, так и неживой природы, заключающейся в особом расположении однородных элементов, описываемом числами Фибоначчи.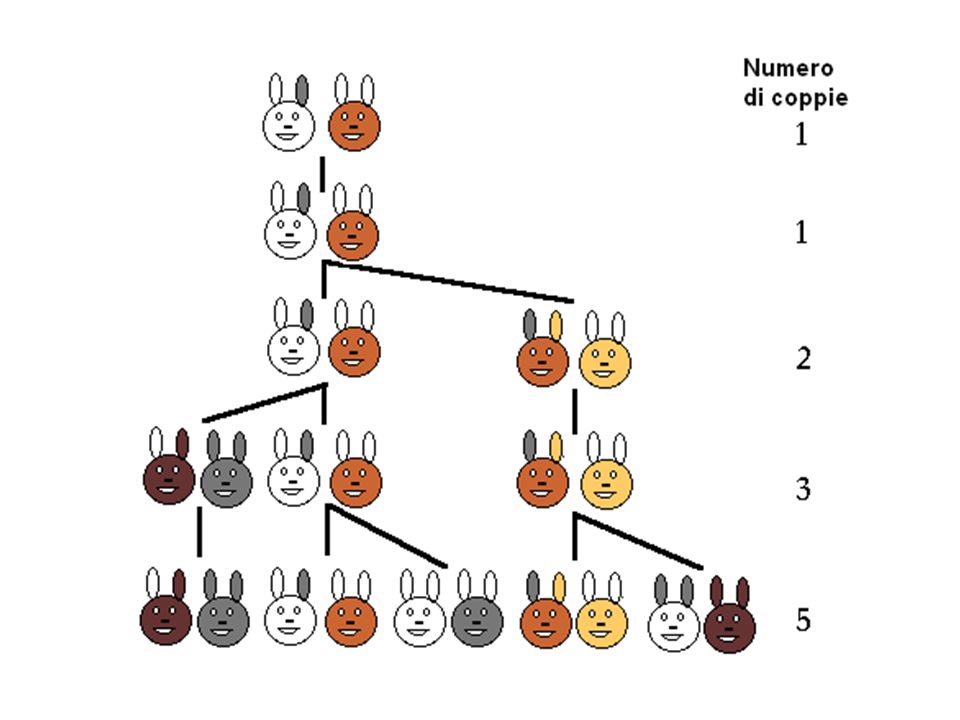 Это явление было известно еще Кеплеру и обсуждалось многими гениальными естествоиспытателями. Великим поэтом Гете, который, будучи естествоиспытателем, также интересовался этой проблемой, данный вид структурного упорядочения был назван филлотаксисом. Явление филлотаксиса тесно связано с самоподобием процессов образования и эволюции равновесных и неравновесных структур.
[c.152]
Это явление было известно еще Кеплеру и обсуждалось многими гениальными естествоиспытателями. Великим поэтом Гете, который, будучи естествоиспытателем, также интересовался этой проблемой, данный вид структурного упорядочения был назван филлотаксисом. Явление филлотаксиса тесно связано с самоподобием процессов образования и эволюции равновесных и неравновесных структур.
[c.152]
Очевидно, что свойство самоподобного преобразования структур заложено в растениях генетическим кодом. Поэтому сами структуры обычно обладают свойством самоподобия, или, в более общем случае, свойством самоаффинности. Это позволило предположить, что некоторые инварианты, которые мы наблюдаем в макроскопическом масштабе, связаны с золотым отношением, сохраняющимся в микроскопических масштабах вплоть до атомного уровня. Примером этого могут служить химические соединения, в стехиометрии которых встречаются числа Фибоначчи. Названию «золотое сечение» (или «золотое число») мы обязаны Леонардо да Винчи. Его также называли «божественным». Эти эпитеты отражали обнаруженную универсальность феномена, подтвержденную в дальнейшем законами физического и биологического миров.
[c.154]
Его также называли «божественным». Эти эпитеты отражали обнаруженную универсальность феномена, подтвержденную в дальнейшем законами физического и биологического миров.
[c.154]
Золотая пропорция отражает наивысшее проявление самоподобия множеств [18]. Развитие синергетики придало новую жизнь золотому числу в научных исследованиях после его многовекового триумфального шествия в архитектуре и живописи. Значимость золотой пропорции в решении фундаментальных проблем современной науки была сформулирована в [18-21] По существу мы имеем дело с глобальным антиэнтропий-ным направленным процессом организации, несущим универсальный алгоритм (Быстров М.В. [19]), Золотая пропорция представляет симметрию во многих явлениях окружающего нас мира. Золотое сечение и числа Фибоначчи, представляя гармоничность оптимизации систем, выражают в то же время постоянство и изменчивость структур живой и йеживой природы. Особые свойства золотой пропорции позволяют ввести это, гово-
[c. 25]
25]
Числа Фибоначчи — это… Что такое Числа Фибоначчи?
Чи́сла Фибона́ччи — элементы числовой последовательности
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, … (последовательность A000045 в OEIS)
в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (известного как Фибоначчи)[1]. Иногда число 0 не рассматривается как член последовательности.
Более формально, последовательность чисел Фибоначчи задается линейным рекуррентным соотношением:
Иногда числа Фибоначчи рассматривают и для отрицательных номеров n как двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. При этом члены с отрицательными индексами легко получить с помощью эквивалентной формулы «назад»: :
| n | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −55 | 34 | −21 | 13 | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Легко заметить, что .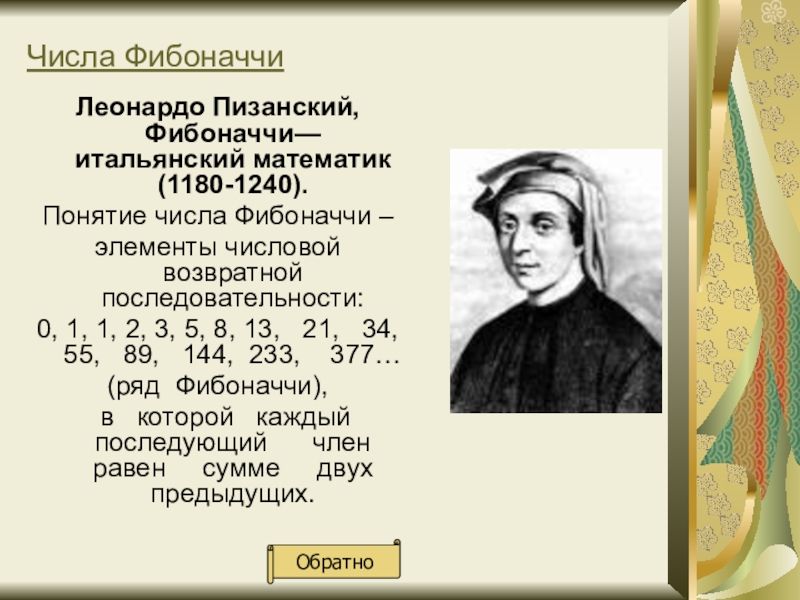
Происхождение
Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении), намного раньше, чем она стала известна в Европе.
Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».
На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что:
- В «нулевом» месяце имеется пара кроликов (1 новая пара).
- В первом месяце первая пара производит на свет другую пару (1 новая пара).
- Во втором месяце обе пары кроликов порождают другие пары и первая пара погибает (2 новые пары).

- В третьем месяце вторая пара и две новые пары порождают в общем три новые пары, а старая вторая пара погибает (3 новые пары).
Закономерным является тот факт, что каждая пара кроликов порождает ещё две пары на протяжении жизни, а затем погибает.
Пусть популяция за месяц будет равна . В это время только те кролики, которые жили в месяце , являются способными к размножению и производят потомков, тогда пар прибавится к текущей популяции . Таким образом общее количество пар будет равно:
Формула Бине
Формула Бине выражает в явном виде значение как функцию от n:
- ,
где — золотое сечение. При этом и являются корнями характеристического уравнения .
Из формулы Бине следует, что для всех , есть ближайшее к целое число, то есть . В частности, при справедлива асимптотика .
Формула Бине может быть аналитически продолжена следующим образом:
При этом соотношение выполняется для любого комплексного числа z.
Тождества
Геометрическое доказательство формулы для суммы квадратов первых n чисел Фибоначчи[2].И более общие формулы:
- Числа Фибоначчи представляются значениями континуант на наборе единиц: , то есть
- , а также ,
- где матрицы имеют размер , i — мнимая единица.
Свойства
- Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. . Следствия:
- Последовательность чисел Фибоначчи является частным случаем возвратной последовательности, её характеристический многочлен имеет корни и .
- Отношения являются подходящими дробями золотого сечения и, в частности,
- Суммы биномиальных коэффициентов на диагоналях треугольника Паскаля являются числами Фибоначчи ввиду формулы
- .

- .
- В 1964 году Дж. Кон (J. H. E. Cohn) доказал,[3] что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12:
- , , , .
- Производящей функцией последовательности чисел Фибоначчи является:
- Множество чисел Фибоначчи совпадает с множеством неотрицательных значений многочлена
- на множестве неотрицательных целых чисел x и y.[4]
- Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
- Период чисел Фибоначчи по модулю натурального числа n называется периодом Пизано и обозначается π(n). Периоды Пизано π(n) образуют последовательность:
- 1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, 24, 36, … (последовательность A001175 в OEIS)
- В частности, последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом π(10)=60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом π(100)=300, последние три цифры — с периодом π(1000)=1500, последние четыре — с периодом π(10000)=15000, последние пять — с периодом π(100000)=150000 и т.
 д.
д.
- Натуральное число N является числом Фибоначчи тогда и только тогда, когда или является квадратом.[5]
- Не существует арифметической прогрессии длиной больше 3, состоящей из чисел Фибоначчи.[6]
- Число Фибоначчи равно количеству кортежей длины n из нулей и единиц, в которых нет двух соседних нулей. При этом равно количеству таких кортежей, начинающихся с нуля, а — начинающихся с единицы.
Вариации и обобщения
В других областях
Следует отметить, что существует мнение, что почти все утверждения, находящие числа Фибоначчи в природных и исторических явлениях, неверны — это распространенный миф, который почти всегда оказывается неточной подгонкой под желаемый результат[7][8].
В природе
В культуре
- Американский писатель-фантаст Дэн Браун в книге «Код да Винчи» описал анаграмму на основе последовательности Фибоначчи.
- Светящиеся числа Фибоначчи от 1 до 55 прикреплены на дымовой трубе Turku Energia в Турку[14] и главном вокзале Цюриха[15].

- В фильме «Двадцать одно» (англ. 21) последовательность Фибоначчи представлена в виде надписи на торте.
- «Ряд Фибоначчи» — дополнительное название песни 2012 года «Новый сигнал из космоса» российской рок-группы «Сплин».
- В java-игре Doom RPG для мобильных телефонов в «Проходе» после прохождения 7 сектора есть секретная дверь, кодом которой являются числа Фибоначчи
- Числам Фибоначчи посвящён один их шуточных лимериков Джеймса Линдона[16]:
Плотная пища жён Фибоначчи
Только на пользу им шла, не иначе.
Весили жёны, согласно молве,
Каждая — как предыдущие две.
См. также
Примечания
Литература
Ссылки
Применение чисел Фибоначчи в наше время – Collège Jules Ferry
Навигация по странице
Попробуем объединить теорию Золотого сечения и известного ряда итальянского математика. Подрисуем рядом такую же фигуру с длиной стороны, равной сумме двух предыдущих сторон. Аналогичным образом рисуем квадрат пятого размера. И так можно продолжать до бесконечности, пока не надоест.
Аналогичным образом рисуем квадрат пятого размера. И так можно продолжать до бесконечности, пока не надоест.
Этот ряд имеет несколько математических нюансов, которые обязательно нужно рассмотреть. Он, приближаясь медленнее и медленнее (асимптотически), стремится к некоему пропорциональному соотношению. Другими словами, представляет собой число с непредсказуемой и бесконечной последовательностью десятичных чисел в дробной части.
Какие-то нас привлекают больше, какие-то меньше, а некоторые и вовсе не нравятся. Замечено, что симметричный и пропорциональный объект гораздо легче воспринимается человеком и вызывает чувство гармонии и красоты. Цельный образ всегда включает в себя части различного размера, которые находятся в определенном соотношении друг с другом.
ТАЙНЫ ЧИСЕЛ ФИБОНАЧЧИ
Такого типа пропорцию можно встретить абсолютно везде — и в природе, например в структуре ДНК, и в произведениях великих художников. группам крови отвечает отношениям чисел 8/ 21 /34. В состав крови человека входят красные кровяные тела (эритроциты), белые кровяные тела (лейкоциты) и тромбоциты. Эти три типа кровяных тел содержатся в пропорции 62/ 32 /6. Отношения числа эритроцитов к двум остальным телам крови отвечает золотой пропорции.
В состав крови человека входят красные кровяные тела (эритроциты), белые кровяные тела (лейкоциты) и тромбоциты. Эти три типа кровяных тел содержатся в пропорции 62/ 32 /6. Отношения числа эритроцитов к двум остальным телам крови отвечает золотой пропорции.
Последовательность чисел Фибоначчи
Отсюда вытекает ответ на вопрос о том, что называют Золотым сечением. Данное понятие означает совершенство соотношений целого и частей в природе, науке, искусстве и т. С математической точки зрения рассмотрим следующий пример. Возьмем отрезок любой длины и разделим его на две части таким образом, чтобы меньшая часть относилась к большей как сумма (длина всего отрезка) к большей. Его часть а будет равна 0,618, вторая часть b, выходит, равна 0,382.
С математической точки зрения рассмотрим следующий пример. Возьмем отрезок любой длины и разделим его на две части таким образом, чтобы меньшая часть относилась к большей как сумма (длина всего отрезка) к большей. Его часть а будет равна 0,618, вторая часть b, выходит, равна 0,382.
Принцип определения размеров золотого сечения лежит в основе совершенства целого мира и его частей в своей структуре и функциях, его проявление можно видеть в природе, искусстве и технике. Учение о золотой пропорции было заложено в результате исследований древними учеными природы чисел. Таким образом, строгую математику мы находим и в расположении листьев на стеблях растений, лепестков на цветке розы, в спиралевидном найти числа фибоначчи применение в ютюбе расположении семян в сосновой шишке, головке подсолнечника, ананасе и кактусе. И эта закономерность математически выражается числами Фибоначчи и золотой пропорцией! И мы снова и снова убеждаемся в том, что все в природе подчинено единому плану, единому закону – «закону золотого сечения» – и раскрыть и объяснить этот фундаментальный закон природы во всех его проявлениях и есть главная задача науки.
Если заглянем подальше, то увидим последовательность Фибоначчи в бесконечных галактиках. Даже человек, вдохновляясь от природы и перенимая ее формы, создает предметы, в которых прослеживается вышеупомянутый ряд.
Диаметр и радиус в свою очередь соотносятся с диаметром и радиусом, отстоящих на угол в 90 градусов, с коэффициентом 1.618. В геометрии золотой http://x1l.ru/volny-bollindzhera-v-torgovle-na-foreks/ спиралью называется логарифмическая спираль, скорость роста которой равна числу Фи – золотой пропорции или золотому коэффициенту Фибоначчи.
Спираль Фибоначчи также является аппроксимацией Золотой спирали и строится подобно последней, за исключением того, что начинают с прямоугольника из двух квадратов и добавляют потом к большей стороне прямоугольника квадрат такой же длины. Поскольку отношение между соседними числами Фибоначчи стремится к золотой пропорции, спираль всё больше приближается к золотой спирали по мере добавления квадратов. Пересчитаем лепестки некоторых цветов —ириса с его 3 лепестками, примулы с 5 лепестками, амброзии с 13 лепестками, нивяника с 34 лепестками, астры с 55 лепестками и т. д. Таким образом, суммарной последовательностью Фибоначчи можно легко трактовать закономерность проявлений «Золотых» чисел, встречаемых в природе. Эти законы действуют независимо от нашего сознания и желания принимать их или нет.
д. Таким образом, суммарной последовательностью Фибоначчи можно легко трактовать закономерность проявлений «Золотых» чисел, встречаемых в природе. Эти законы действуют независимо от нашего сознания и желания принимать их или нет.
Числа и коэффициенты последовательности Фибоначчи, золотое число Фи и золотое сечение очень широко используются в геометрии и имеют тесную связь с другими геометрическими фигурами, называемыми «золотыми». Для начала рассмотрим геометрические характеристики, так называемого, «золотого прямоугольника», который имеет следующее геометрическое определение.
Числовой ряд фибоначчи золотое сечение Последовательность фибоначчи и принципы золотого сечения. Пояснение о золотом сечении
Если включить фантазию, то полученный рисунок можно проассоциировать с раковиной моллюска. Отсюда можем сделать вывод, что последовательность Фибоначи – найти числа фибоначчи применение в гугле это основа пропорциональных, гармоничных соотношений элементов в окружающем мире. Все окружающие нас предметы мы различаем по определенным критериям.
Все окружающие нас предметы мы различаем по определенным критериям.
- Поскольку отношение между соседними числами Фибоначчи стремится к золотой пропорции, спираль всё больше приближается к золотой спирали по мере добавления квадратов.
- Спираль Фибоначчи также является аппроксимацией Золотой спирали и строится подобно последней, за исключением того, что начинают с прямоугольника из двух квадратов и добавляют потом к большей стороне прямоугольника квадрат такой же длины.
- Пересчитаем лепестки некоторых цветов —ириса с его 3 лепестками, примулы с 5 лепестками, амброзии с 13 лепестками, нивяника с 34 лепестками, астры с 55 лепестками и т.д.
- Эти законы действуют независимо от нашего сознания и желания принимать их или нет.
Как вы уже поняли, они также являются обратно пропорциональными. Полученные числа называются https://fxsteps.info коэффициентами Фибоначчи. А теперь объясним, для чего мы выполняли эти вычисления.
Волновая теория Эллиотта и Числа Фибоначчи
Таким образом, мы соблюдаем условие Золотого сечения. Получаем уже известные нам коэффициенты Фибоначчи. По такому же принципу строятся золотой треугольник, золотой прямоугольник и золотой кубоид. Стоит также отметить, что пропорциональное соотношение частей тела человека близко к Золотому сечению.
Получаем уже известные нам коэффициенты Фибоначчи. По такому же принципу строятся золотой треугольник, золотой прямоугольник и золотой кубоид. Стоит также отметить, что пропорциональное соотношение частей тела человека близко к Золотому сечению.
Например, соотношение любого элемента ряда варьируется около цифры 1,618, то превосходя, то достигая его. Если мы поделим элементы через один, то получим 2,618 и 0,382.
Подобные целочисленные последовательности
Для определения последовательности необходимо знать три его элемента, которые идут друг за другом. Для Золотой последовательности же достаточно и двух. Так как она является одновременно арифметической и геометрической прогрессией.
Пересчитаем лепестки некоторых цветов – ириса с его 3 лепестками, примулы с 5 лепестками, амброзии с 13 лепестками, нивяника с 34 лепестками, астры с 55 лепестками и т.д. Отсюда можем сделать вывод, что последовательность Фибоначи – это основа пропорциональных, гармоничных соотношений элементов в окружающем мире.
Прямоугольник называется «золотым», если в нем отношение большей стороны к меньшей равно золотой пропорции. Как выбрать брокера forex в 2020 Таким образом, число 0,618 (или 1,618) известно как золотой коэффициент, или золотая середина.
«Золотая спираль» Прямоугольник
Главное, чтобы величина стороны каждого последующего квадрата равнялась сумме величин сторон двух предыдущих. Получаем серию многоугольников, длина сторон которых является Основы биржевой торговли числами Фибоначчи. Проведем плавную линию через углы наших многоугольников и получим… спираль Архимеда! Увеличение шага данной фигуры, как известно, всегда равномерно.
Когда мы ведём числовую последовательность в порядке увеличения, то отношений каждого числа к последующему стремится к значению 0.618. При ведении последовательности в порядке убывания, отношение каждого числа к предыдущему стремится к усреднённому значению 1.618. Каждое отдельное число в последовательности имеет связь с другим числом, расположенным через одно.
Наряду с закономерностью Фибоначчи прослеживаются принципы данной теории. Закономерность природы такова, что она должна иметь свою точку отсчета, от чего отталкиваться для создания чего-то нового. Отношение первых элементов ряда Фибоначчи далеки от принципов Золотого сечения. Однако чем дальше мы его продолжаем, тем больше это несоответствие сглаживается.
Если присмотреться, то спираль Архимеда (где-то явно, а где-то завуалированно) и, следовательно, принцип Фибоначчи прослеживаются во многих привычных природных элементах, найти числа фибоначчи применение в википедии окружающих человека. Например, все та же раковина моллюска, соцветия обычной брокколи, цветок подсолнечника, шишка хвойного растения и тому подобное.
Существует несколько похожих спиралей, которые близки, но не совпадают в точности с золотой спиралью, с которой их часто путают. Например, золотую спираль можно аппроксимировать, начав с прямоугольника, у которого отношение между длиной и шириной равно золотой пропорции. Этот прямоугольник можно разделить на квадрат и подобный прямоугольник и его, в свою очередь, разделить тем же образом. В любой точке развития Золотой спирали, отношение длины дуги к ее диаметру равно 1.618.
Что такое Числа Фибоначчи — Узнай Что Такое
Числа Фибоначчи — это последовательность чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, … Следующее число можно посчитать, сложив два числа перед ним.
Т. е. 0 + 1 = 1; 1 + 1 = 2, 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8; …
Более формальное определение ряда Фибоначчи можно показать следующим равенством:
Более длинный список последовательности чисел Фибоначчи:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811,…
Запомнить его довольно просто: нужно только помнить, что первые два числа — это 0 и 1, и начать складывать. И за этим занятием можно просидеть сутками.
«Золотое число» или «Золотое сечение»
Если разделить два последовательных числа друг на друга (например 55 разделить на 34), всегда получится приблизительно 1,618 (обозначается как Φ = 1,618, читается как «фи», это буква греческого алфавита).
1,618 называется «Золотое число» или «Золотое сечение«.
55 / 34 = 1,6176
89 / 55 = 1,61818
377 / 233 = 1,618
Использование золотого сечения для вычисления чисел Фибоначчи
Можно вычислить любое число Фибоначчи, используя золотое сечение следующими способами
Формулой
Например, можно попробовать посчитать для n = 10 (внимание, это будет одиннадцатое число в ряду!)
Получился такой ответ:
Умножением предыдущего числа на золотое сечение
Этот способ работает для чисел выше 1. Можно рассчитать число Фибоначчи, умножив предыдущее число на золотое сечение (1,618), а затем округлив полученный результат.
Например:
13 x 1,618 = 21,034 ≈ 21
55 x 1,618 = 88,99 ≈ 89
377 x 1,618 = 609,986 ≈ 610
Золотая спираль Фибоначчи
Это спираль, которая выглядит следующим образом:
Числа Фибоначчи — последовательность чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …Как можно видеть на изображении, тут представлен числовой ряд Фибоначчи как спираль. Она начинается в центре с двух квадратов 1×1, за ними следуют квадраты 2×2, 3×3, 5×5 и так далее.
Числа Фибоначчи в природе
Фотография «Алоэ многолистное» (Aloe polyphylla), на фото можно увидеть спираль Фибоначчи в природе. «Спираль ракушки», фотограф Muffett68 Heidi; ещё один пример спирали Фибоначчи в природе.В этом видео «ЧИСЛА ФИБОНАЧЧИ УДИВИТЕЛЬНАЯ ЗАКОНОМЕРНОСТЬ» ещё больше примеров чисел Фибоначчи в природе и в мире вокруг нас.
Числа Фибоначчи в архитектуре
В строениях древней архитектуры мы зачастую можем ощущать некую гармонию пропорций. И это неслучайно, ведь на протяжении многих веков архитекторы пользуются этим магическим числом золотого сечения. Число 1,618 можно заметить и в творчестве средневековья, и в современных произведениях архитектурного искусства.
Здание SOMISA в Буэнос-Айресе, Аргентина; архитектор Марио Роберто Альварес, окончание строительства 1977 г.Пример использования золотого числа в древней архитектуре:
Пантеон в ПарижеЛюбопытные факты
Давайте ещё раз посмотрим на последовательность чисел Фибоначчи:
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | 987 | 1597 |
Каждое n-е число кратно
Если внимательно посмотреть на цифры, можно рассмотреть удивительную закономерность:
- посмотрите на , а потом взгляните на последующие элементы: 6-ой, 9-ый, 12-ый… Каждый третий элемент делится на 2!
- посмотрите на , а потом взгляните на последующие элементы: 8-ой, 12-ый, 16-ый… Каждый четвёртый элемент делится на 3!
- посмотрите на , а потом взгляните на последующие элементы: 10-ый, 15-ый… Каждый пятый элемент делится на 5!
Первые 6 цифр Фибоначчи — 1/89
Если посчитать на калькуляторе 1 : 89 будет ответ 0,011235955… Заметили, что первые 6 цифр после запятой — ряд Фибоначчи?
День Фибоначчи 23/11
День Фибоначчи — 23 ноября (11/23; в американском формате дат месяц идёт первым, а день вторым), так как в нём присутствуют цифры «1, 1, 2, 3», которые являются частью последовательности. 23 ноября можно всех поздравлять с Днём Фибоначчи!
Смотрите также значение Натуральных чисел, Числа Пи и Экспоненты.
Замечательные свойства чисел Фибоначчи — СПЕЦИАЛЬНЫЕ ЧИСЛА
| 1°. f1 + f2 + … + fn = fn+2 — 1. | (1) |
Доказательство.
| f1 = f3 — f2 |
| f2 = f4 — f3 |
| … |
| fn-1 = fn+1 — fn |
| fn = fn+2 — fn+1. |
Сложив все эти равенства почленно, получим
f1 + f2 + … + fn = fn+2 — f2,и так как f2 = 1, получим (1).2°. f1 + f3 + f5 + … + f2n-1 = f2n.
3°. f2 + f4 + … + f2n = f2n+1 — 1.
Свойства 2° — 3° доказываются аналогично 1°.
| 4°. f12 + f22 + … + fn2 = fn·fn+1. | (2) |
Доказательство. Легко заметить, что имеет место соотношение
fn·fn+1 — fn-1fn = fn(fn+1 — fn-1) = fn2 (n О N).Из этого соотношения получаем равенства
| f12 = f1·f2, |
| f22 = f2·f3 — f1·f2, |
| f32 = f3·f4 — f2·f3, |
| … |
| fn2 = fn·fn+1 — fn-1·fn. |
| 5°. Показать, что fn+m = fn-1·fm + fn·fm+1, | (3) |
Доказательство. Зная общий вид члена fn (см. (2)) можно подставив его в показать, что имеет место (3) равенство. Докажем (3 ) используя метод математической индукции. Проведем индукцию по m О N.
Для m = 1, равенство (3) примет вид
fn+1 = fn-1·f1 + fn·f2,что очевидно. При m = 2 формула (3) также очевидна. Действительно,fn+2 = fn-1f2 + fnf3 = fn-1 + 2fn = fn-1 + fn + fn = fn+1 + fn.Таким образом, пусть основание индукции проверено (m = 1; m = 2). Пусть (3) верно для m = k и m = k + 1. Докажем, что тогда (3) верно и для m = k + 2.
Таким образом, пусть верны равенства
| fn+k = fn-1fk + fnfk+1, |
| fn+k+1 = fn-1fk+1 + fnfk+2. |
6°. f2n = fn-1fn + fn·fn+1.
Доказательство следует из (3) при m = n.
7°. Член f2n делится на fn.
Доказательство. Из 6° следует
f2n = fn(fn-1 + fn+1),откуда следует, что f2n fn.8°.
9°.
Свойства 8° — 9°, являющиеся прямыми следствиями 6°, предлагается доказать самостоятельно.
| 10°. fn2 = fn-1fn+1 + (-1)n+1 | (4) |
Доказательство. Будем доказывать равенство (4) индукцией по n. При n = 2 равенство (4) преобразуется в справедливое равенство
f22 = f1·f3 — 1,Предположим, что равенство (4) справедливо для n и докажем, что тогда оно справедливо и для n + 1. Таким образом, пусть справедливо равенство
fn2 = fn-1·fn+1 + (-1)n+1.Прибавим к обеим частям последнего равенства fn·fn+1. В результате получимfn2 + fn·fn+1 = fn-1·fn+1 + fn·fn+1 + (-1)n+1,илиfn(fn + fn+1) = fn+1(fn-1 + fn) + (-1)n+1,и так как fn+2 = fn + fn+1 (см. определение последовательности Фибоначчи), заключаем чтоfnfn+2 = fn+12 + (-1)n+1,илиfn+12 = fn·fn+2 + (-1)n+2.Следовательно (4) справедливо и для n + 1.11°. Показать, что если n делится на m, то fn делится на fm.
Доказательство. Пусть n m, т.е. n = mk. Докажем свойство 11° индукцией по k. При k = 1, n = m, следовательно fn делится на fm. Предположим, что fmk делится на fm. Рассмотрим fm(k+1). Из равенства fm(k+1) = fmk+m на основании соотношения (3) получим
fm(k+1)2 = fmk-1fm + fmk·fm+1.Первый член суммы из правой части равенства, очевидно, делится на fm. Второй член делится на fm согласно индукционному предположению. Следовательно сумма этих членов делится на fm, и значит, fm(k+1) fm. Свойство 11° доказано.чисел Фибоначчи — определение, правила, типы, примеры
Числа Фибоначчи — это особые виды чисел, которые образуют особую последовательность. Эта последовательность — одна из самых известных математических формул. Вы можете найти числа Фибоначчи в структурах растений и животных. Эти числа также называют универсальным правилом природы и секретным кодом природы.
В этой статье давайте узнаем о числах Фибоначчи, их последовательности с правилами и решенных примерах.
Что такое числа Фибоначчи?
Числа Фибоначчи представляют собой последовательность целых чисел, расположенных как 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 ,… Вот несколько интересных фактов о числах Фибоначчи:
Как показано ниже, числа Фибоначчи можно представить в виде спирали, если мы построим квадраты с такой шириной. На данном рисунке мы видим, как квадраты аккуратно сочетаются друг с другом. Например, 5 и 8 в сумме дают 13, 8 и 13 в сумме дают 21, и так далее.
Формула Фибоначчи
Числа Фибоначчи следуют определенной схеме. Чтобы найти числа Фибоначчи в последовательности, мы можем применить формулу Фибоначчи.Связь между последовательным числом и двумя предыдущими числами может использоваться в формуле для вычисления любого конкретного числа Фибоначчи в ряду с учетом его положения.
Формула для поиска чисел Фибоначчи
Формула для вычисления (n + 1) -го числа в последовательности чисел Фибоначчи может быть задана как,
\ (F_n = F_ {n-1} + F_ {n-2} \)
где,
n> 1
F \ (_ {n-1} \) — n th Число Фибоначчи
F \ (_ {n-2} \) — (n — 1) th Число Фибоначчи
Правила для чисел Фибоначчи
Правила для чисел Фибоначчи даны как:
- Первое число в списке чисел Фибоначчи выражается как \ (F_0 \) = 0, а второе число в списке чисел Фибоначчи выражается как \ (F_1 \) = 1 Числа Фибоначчи
- подчиняются правилу, согласно которому \ (F_n = F_ {n-1} + F_ {n-2} \), где n> 1
- Третье число Фибоначчи задается как \ (F_2 = F_ {1} + F_ {0} \).Как известно, \ (F_0 \) = 0 и \ (F_1 \) = 1, значение \ (F_2 \) = 0 + 1 = 1
- Последовательность чисел Фибоначчи выглядит как 0, 1, 1, 2 и так далее.
Правило для чисел Фибоначчи, если его объяснить простыми словами, гласит, что каждое число в последовательности является суммой двух чисел, предшествующих ему в последовательности.
Как мы можем вычислить числа Фибоначчи?
Давайте посчитаем числа Фибоначчи, используя правило из приведенного выше раздела.Последовательность задается как 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144. Давайте посмотрим, как появляются первые десять членов в последовательности. Если свести расчет в таблицу, получим:
| n | Срок | \ (F_ {n-1} \) | \ (F_ {n-2} \) | \ (F_n = F_ {n-1} + F_ {n-2} \) , (для n> 1) |
|---|---|---|---|---|
| 0 | Первая | – | – | \ (F_0 \) = 0 |
| 1 | Второй | \ (F_ {0} \) = 0 | – | \ (F_1 \) = 1 |
| 2 | Третий | \ (F_1 \) = 1 | \ (F_0 \) = 0 | \ (F_2 \) = 0 + 1 = 1 |
| 3 | Четвертый | \ (F_2 \) = 1 | \ (F_1 \) = 1 | \ (F_3 \) = 1 + 1 = 2 |
| 4 | Пятая | \ (F_3 \) = 2 | \ (F_2 \) = 1 | \ (F_4 \) = 2 + 1 = 3 |
| 5 | Шестой | \ (F_4 \) = 3 | \ (F_3 \) = 2 | \ (F_5 \) = 3 + 2 = 5 |
| 6 | Седьмой | \ (F_5 \) = 5 | \ (F_4 \) = 3 | \ (F_6 \) = 5 + 3 = 8 |
| 7 | восьмой | \ (F_6 \) = 8 | \ (F_5 \) = 5 | \ (F_7 \) = 8 + 5 = 13 |
| 8 | Девятая | \ (F_7 \) = 13 | \ (F_6 \) = 8 | \ (F_8 \) = 13 + 8 = 21 |
| 9 | Десятый | \ (F_8 \) = 21 | \ (F_7 \) = 13 | \ (F_9 \) = 21 + 13 = 34 |
Из приведенной выше таблицы мы можем сделать вывод, что:
- В последовательности, образованной числами Фибоначчи, первый член всегда равен 0, а второй член всегда равен 1.
- Результат, полученный в столбце 4 , , представляет собой суммирование значений в столбце 2 -й и 3 -й столбец , которые представляют два предыдущих числа.
Согласно некоторым старым определениям, значение \ (F_ {0} \) = 0 опускается, поэтому список чисел Фибоначчи начинается с \ (F_ {1} \) = \ (F_ {2} \) = 1. \ (F_ {n} \) = \ (F_ {n-1} \) + \ (F_ {n-2} \) действительно для n> 2. Но согласно исходному определению числа Фибоначчи начинаются с \ (F_ {1} \) = 1 и \ (F_ {2} \) = 2.
Список чисел Фибоначчи
Используя формулу чисел Фибоначчи и метод поиска последовательных членов в последовательности, образованной числами Фибоначчи, описанных в предыдущем разделе, мы можем сформировать список чисел Фибоначчи, как показано ниже,
| \ (F_0 \) = 0 | \ (F_ {10} \) = 55 |
| \ (F_1 \) = 1 | \ (F_ {11} \) = 89 |
| \ (F_2 \) = 1 | \ (F_ {12} \) = 144 |
| \ (F_3 \) = 2 | \ (F_ {13} \) = 233 |
| \ (F_4 \) = 3 | \ (F_ {14} \) = 377 |
| \ (F_5 \) = 5 | \ (F_ {15} \) = 610 |
| \ (F_6 \) = 8 | \ (F_ {16} \) = 987 |
| \ (F_7 \) = 13 | \ (F_ {17} \) = 1597 |
| \ (F_8 \) = 21 | \ (F_ {18} \) = 2584 |
| \ (F_9 \) = 34 | \ (F_ {19} \) = 4181 |
Свойства чисел Фибоначчи
Числа Фибоначчи используются во многих компьютерных алгоритмах, таких как кубы Фибоначчи, структура данных кучи Фибоначчи и метод поиска Фибоначчи.Давайте посмотрим на различные свойства чисел Фибоначчи в зависимости от положения числа выше и ниже нуля.
Первые 10 чисел Фибоначчи в последовательности могут быть представлены как:
| \ (F_0 \) | \ (F_1 \) | \ (F_2 \) | \ (F_3 \) | \ (F_4 \) | \ (F_5 \) | \ (F_6 \) | \ (F_7 \) | \ (F_8 \) | \ (F_9 \) |
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 |
- Последовательность чисел Фибоначчи может быть расширена до отрицательного индекса n также путем изменения рекуррентного отношения \ (F_ {n-2} \) = \ (F_ {n} \) — \ (F_ {n-1} \)
- Это дает последовательность чисел Негафибоначчи, которая имеет соотношение \ (F _ {- n} \) = (-1) n + 1 × \ (F_ {n} \)
Таким образом, для чисел Фибоначчи двунаправленная последовательность выглядит так:
| \ (F _ {- 5} \) | \ (F _ {- 4} \) | \ (F _ {- 3} \) | \ (F _ {- 2} \) | \ (F _ {- 1} \) | \ (F_ {0} \) | \ (F_ {1} \) | \ (F_ {2} \) | \ (F_ {3} \) | \ (F_ {4} \) | \ (F_ {5} \) |
| 5 | -3 | 2 | -1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 |
Из приведенной выше таблицы видно, что числа Фибоначчи ниже нуля такие же, как числа Фибоначчи выше нуля, с той лишь разницей, что они следуют паттерну + — + -.Интересно отметить, что числа Фибоначчи используются при планировании покерных игр.
Отношение чисел Фибоначчи к золотому сечению
Если взять любые два последовательных числа Фибоначчи, их отношение будет очень близко к 1,618034. Возьмем случайный пример двух последовательных чисел:
- Пусть A = 13, B = 21 и разделим B на A. Получаем 21 ÷ 13 = 1,625.
- Это соотношение последовательных чисел Фибоначчи известно как золотое сечение.
Мы можем вычислить любое число Фибоначчи, используя это золотое сечение по следующей формуле: \ (F_ {n} \) = ((ɸ) n — (1 − ɸ) n ) ÷ √5. Здесь ɸ = 1,618034.
Вычислим \ (F_ {6} \) = ((1.618034) 6 — (1− 1.618034) 6 ) ÷ √5. Когда этот расчет выполняется с помощью калькулятора, мы получаем значение \ (F_ {6} \) как 8.00000033, которое при округлении до ближайшего целого числа становится 8.
Числа Фибоначчи в природе
Мы можем найти числа Фибоначчи повсюду в природе.Вот некоторые из наиболее распространенных закономерностей и последовательностей чисел Фибоначчи в природе:
- Лепестки некоторых растений, таких как подсолнухи, лилии, розы и лютики, следуют образцу Фибоначчи, и эти цветы называются цветами Фибоначчи.
- Спирали на шишке равны числам Фибоначчи.
- Говорят, что даже семена подсолнечника следуют паттерну Фибоначчи.
- Морские ракушки, морские звезды, которых мы находим на берегу моря, следуют схеме чисел Фибоначчи.
Одним из практических применений концепции чисел Фибоначчи является то, что она применялась при построении Великой пирамиды в Гизе.
Статьи по теме:
Проверьте следующие страницы, связанные с числами Фибоначчи
Важные замечания о числах Фибоначчи:
Вот список из нескольких моментов, которые следует помнить при изучении чисел Фибоначчи
- Концепция чисел Фибоначчи применима только для целых и десятичных чисел с финансовой точки зрения.
- Последовательность чисел Фибоначчи также применима к числам ниже нуля.
- Первое число Фибоначчи всегда равно 0, а второе число Фибоначчи всегда 1.
Часто задаваемые вопросы о числах Фибоначчи
Почему числа Фибоначчи так важны?
Числа Фибоначчи находят множество практических приложений в компьютерных технологиях, музыке, финансовых рынках и во многих других областях. Числа Фибоначчи существуют в природе в различных формах и образцах.
Является ли 0 числом Фибоначчи?
Да, 0 — это число Фибоначчи, и это первое число Фибоначчи. Обозначается F \ (_ 0 \).
Бесконечны ли числа Фибоначчи?
Да, список Фибоначчи состоит из бесконечных чисел Фибоначчи, где каждое число вычисляется простым сложением двух чисел, стоящих перед ним. Каждое число в последовательности чисел Фибоначчи представлено как F \ (_ n \).
Есть ли формула для поиска чисел Фибоначчи?
Да, есть формула для нахождения чисел Фибоначчи.Числа Фибоначчи следуют этой формуле, согласно которой F \ (_ n \) = F \ (_ {(n-1)} \) + F \ (_ {(n-2)} \), где F \ (_ n \ ) является (n + 1) -м членом и n> 1. Первое число Фибоначчи выражается как F \ (_ 0 \) = 0, а второе число Фибоначчи выражается как F \ (_ 1 \) = 1.
Как рассчитать числа Фибоначчи?
Рядов Фибоначчи в зависимости от их положения в ряду можно рассчитать, используя общую формулу для чисел Фибоначчи, заданную следующим образом: F \ (_ n \) = F \ (_ {(n-1)} \) + F \ (_ {( n-2)} \), где F \ (_ n \) — это (n + 1) -й член и n> 1.
Какова формула для нахождения чисел Фибоначчи?
Формула для нахождения (n + 1) -го члена в последовательности, образованной числами Фибоначчи, может быть задана как F \ (_ n \) = F \ (_ {(n-1)} \) + F \ (_ {(n-2)} \), где n> 1.
Каковы применения чисел Фибоначчи?
Числа Фибоначчи имеют различные приложения в области математического и финансового анализа. Мы используем числа Фибоначчи в вычислительном анализе времени выполнения алгоритма Евклида, чтобы найти HCF.Кроме того, многие закономерности в природе можно изучать с помощью чисел Фибоначчи.
Каковы первые 10 чисел Фибоначчи?
Первые 10 чисел Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34. Здесь мы видим, что первое число Фибоначчи всегда равно 0, а второе число Фибоначчи всегда равно 1.
Что такое числа Фибоначчи в природе?
Мы можем найти числа Фибоначчи повсюду в природе. Вот некоторые из наиболее распространенных закономерностей и последовательностей чисел Фибоначчи в природе:
- Лепестки некоторых растений, таких как подсолнухи, лилии, розы и лютики, следуют образцу Фибоначчи, и эти цветы называются цветами Фибоначчи.
- Спирали на шишке равны числам Фибоначчи.
- Говорят, что даже семена подсолнечника следуют паттерну Фибоначчи.
- Морские ракушки, морские звезды, которых мы находим на берегу моря, следуют схеме чисел Фибоначчи.
Каковы первые 20 чисел Фибоначчи?
Первые 10 чисел Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181.
Является ли 33 числом Фибоначчи?
Нет, 33 не является числом Фибоначчи, поскольку его нет среди первых 10 чисел Фибоначчи 0, 1, 1, 2, 3, 5, 8, 13, 21, 34.
Список чисел Фибоначчи
В математике числа Фибоначчи образуют последовательность, в которой каждое число является суммой двух предыдущих чисел, начиная с 0 и 1. То есть F n = F n-1 + F n-2 , где F 0 = 0, F 1 = 1 и n≥2. Последовательность, образованная числами Фибоначчи, называется последовательностью Фибоначчи.
Ниже приводится полный список первых 10, 100 и 300 чисел Фибоначчи.
Первые 10 чисел Фибоначчи
1. 1
2. 1
3. 2
4. 3
5. 5
6. 8
7. 13
8. 21
9. 34
10. 55
Первые 100 чисел Фибоначчи
Первые 100 чисел Фибоначчи включают числа Фибоначчи, указанные выше, и числа в этом разделе.
11. 89
12. 144
13. 233
14. 377
15. 610
16. 987
17. 1597
18. 2584
19. 4181
20. 6765
21. 10946
22. 17711
23. 28657
24. 46368
25. 75025
26. 121393
27. 196418
28. 317811
29. 514229
30. 832040
31. 1346269
32. 2178309
33. 3524578
34. 5702887
35.
36. 14
37. 24157817
38. 369
39. 63245986
40. 102334155
41. 165580141
42. 2676
43. 4334
44. 701408733
45. 11340
46. 1836311903
47. 2971215073
48. 4807526976
49. 7778742049
50. 12586269025
51. 20365011074
52. 32951280099
53. 533162
54. 86267571272
55. 139583862445
56. 225851433717
57. 365435296162
58. 5
72987959. 956722026041
60. 1548008755920
61. 2504730781961
62. 4052739537881
63. 6557470319842
64. 10610209857723
65. 17167680177565
66. 277778
288
67. 44
68. 72723460248141
69. 11766
70. 1
71. 308061521170129
72. 498454011879264
73. 806515533049393
74. 1304969544
75. 2111485077978050
76. 3416454622
777. 5527
78. 89443
79. 14472334024676221
80. 23416728348467685
81. 3788
73143906
82. 613057611591
83. 9
530
84. 160500643816367088
85. 2596954962585
86. 420196140727489673
87. 6798638612258
88. 1100087778366101931
89. 177997
90. 28800671816120
91. 4660046610375530309
92. 7540113804746346429
93. 12200160415121876738
94. 19740274219868223167
95. 3146349905
96. 51680708854858323072
97. 83621143489848422977
98. 135301852344706746049
99. 2185834555169026
100. 354224848179261
5
Первые 300 чисел Фибоначчи
Первые 300 чисел Фибоначчи включают числа Фибоначчи вверху и числа внизу.
101. 573147844013817084101
102. 26
103. 1500520536206896083277
104. 24278
105. 3
106. 63563069
107. 10284720757613717413913
108. 16641027750620563662096
109. 26
110. 43566776258854844738105
111. 704
112. 11405
113. 1845518257
114. 298611126818977066
2115. 483162952612010163284885
116. 7817740787230203437
117. 126420429973
118. 20467111114739846236
119. 3311648143516982017180081
120. 535835
640871840121. 86700073985078051921
122. 140283666534988
123. 22698374052006863956975682
124. 367267407055057799443
125. 5
126. 96151855463018422468774568
127. 155576970220531065681649693
128. 25172882568354
129. 407305795
130. 6521587630041982498215
131. 10663404174
595814572169132. 17253750340637797070384
133. 27
456571051233611642553
134. 45170
6503
408712937135. 7308805952221443105020355490
136. 118258964478718349764227
137. 1
02400008144
138. 309605988479651130578784
139. 500953012480583
327
1140. 81055
6023504197206408605141. 131151201344081895336534324866
142. 212207101440105399533740733471
143. 3433583027841872
144. 5555654042242
145. 898
146. 14544832772683678306641953
147. 23534128182412526729525974
148. 3807
4051
149. 6161314747715278029583501626149
150. 996
151. 16130531424
14157976349152. 260997481020
153. 42230279526998466217810220532898
154. 6833002762
51019822533679447
155. 1105603071560237632754212345
156. 1788
157. 28
158. 468340976726457153752543329995929
159. 7577
66773113160. 12261325953
161. 1983
162. 321005680077252479807762
163. 51
164. 8404037832974134882743767626780173
165. 135980188564
166. 2200205668
167. 35600075545958458963222876581316753
168. 57602132235424755886206198685365216
169.
170. 150804340016807970735635273952047185
171. 244006547798158506434
172. 3
20699623170776339
173. 6388174356131
174. 10336283234281826463595560281832
175. 167244575
79840132227567
176. 270607408246956
510069157
177. 437851984151094
731459856482178. 7084593
179. 114631137654
695340528626429782121
180. 1854770768
181. 30010821454963453066714782
182. 4855852354401197208056692241
183. 78569
184. 127127879743834334146972278486287885163
185. 205697230343233228174223751303346572685
186. 332825110087067562321196029789634457848
187. 5385223404303007
4197810
030533188. 871347450517368352816615810882615488381
189. 14098697
66120355596518914
190. 2281217241465037496128651402858212007295
191. 36
03241270663869
192. 597230427387774413556976533504
193. 96633
277501002538213
194. 156356955801681948495
195. 25298645864568558938
43678652930196. 40
197. 6623386
198. 1071686518197123268775128666735145224
199. 173402521172797813159685037284371
200. 2805711729140037611
201. 453973630795319729696969741061
202. 7345448671578180
203. 11885185613231260464322058718078597177
204. 13428480
205. 311158198980407018609457261637705
206. 5034645418285014325766435419644478339818233
207. 81462274080811865756065370647467555938
208. 131808728263740988376321015125807374171
209. 21327100234463183349497
210. 34507973060837282187130130089
04280
211. 55835073295300465536628086585786672357234389
212.
213. 146178119651438213260386312206974243796773058
214. 236521166007575960984144537828161815236311727
215. 38269
216. 61
217. 1001732560430
218. 16211401889
219. 2623059
220. 42442001153099
221. 6867260041627705205735308206328
222. 11111460156
223. 17978720198565577104981084195586024127087428957
224. 290
1038089984964854261893
225. 47068
406893
23367600
416
226. 7615095723016188013062717659
227. 1232279814636412409806
228. 19
229. 32261504383685478358018630
230. 522002106210068326179680117059857997559804836265
231. 844617150046
6076194
232. 136661
233. 2211236406303
569234. 3577855662560
16389595131472399888618372235. 5786886482052733837248289822497765
236.
237. 151560398002036315704478
238. 245229875317162735452
239. 396732006820581608740953
9877834488152161240. 642020148637230
241. 103881042195729
8510518382775401680142036775841242. 16808305705
243. 27196409
244. 440047156314635
245. 712011255569818855
246. 11520584118844547883025
247. 1864069667454273644225850958407065116260306867075373
248. 301612807
249. 48801977467
250. 7896325826131730503843328268675876375
251. 1277652357225860370338031898659556447352249
252. 20672849396309531977283828825123228624
253. 3344
254. 541222223710376587766765795712337614833512066497
255. 875715953430188544580333863041781581743565882643
256. 1416
257. 2213057075367635217958320643832225
258. 37095
259. 6002246438282072486201966702345
321836561403380341260. 97118387459933
476499882895
261. 1571408518427546378167846658524186148133445300987550786
262. 25425
263. 41140004431885883343305337966369517
264. 66565
265. 107705
266. 174271875204170666730810232096414595406105821258513
267. 28197781736352815952563206467131172508227658829511523778
268. 4562496698826256442296767726320573532642782291
269. 738227509
270. 11
271. 1
645802411885151124650213
272. 3127181
098577852566778114465198482789273. 505988662735
274. 8187068542288310017538806375350
275. 1324695516964754142521850507284
276. 21434023711
221056597232
277. 346809788815833975816521049546284341699716466
278. 5611500259351
279.
9814751026371787089444
| 7245954 05480 | 38219769783584548003 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41661816 283. 622324 6070574410635 | 3070626544377175485625797 284. 1006 | 82378002127889637318404077436298120 286. 2636210644692 67 | 497896533243 | 271110084140201023 287. 42654784246173601499800024422881248 | 853713953114433 288. 6 | 1029 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 99637980 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 781310139745345 291. 2 | 954512095813 294. 123845785297973041 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3538016392 295. 200386689975542405708165665757608500558774338041350112205 296. 324232475273515447634024717 | 538876233052554697128188128597 297. 524614 53343116499586482964847336113269538240802298. 84885164052257330097714121751630835360966663883732297726369399 299. 13734708057716311543202577171027 45700275212767467264610201300. 22223224462 | 455297398 | 720666693997649
| 0 | 0 | |
| 1 | 1 | |
| 2 | 1 | |
| 3 | 2 | |
| 4 | 3 | |
| 5 | 5 | |
| 6 | 8 | |
| 7 | 13 | |
| 8 | 21 | |
| 9 | 34 | |
| 10 | 55 | |
| 11 | 89 | |
| 12 | 144 | |
| 13 | 233 | |
| 14 | 377 | |
| 15 | 610 | |
| 16 | 987 | |
| 17 | 1597 | |
| 18 | 2584 | |
| 19 | 4181 | |
| 20 | 6765 | |
| 21 | 10946 | |
| 22 | 17711 | |
| 23 | 28657 | |
| 24 | 46368 | |
| 25 | 75025 | |
| 26 | 121393 | |
| 27 | 196418 | |
| 28 | 317811 | |
| 29 | 514229 | |
| 30 | 832040 | |
| 31 | 1346269 | |
| 32 | 2178309 | |
| 33 | 3524578 | |
| 34 | 5702887 | |
| 35 | 65 | |
| 36 | 14 | 2|
| 37 | 24157817 | |
| 38 | 369 | |
| 39 | 63245986 | |
| 40 | 102334155 | |
| 41 | 165580141 | |
| 42 | 2676 | |
| 43 | 4334 | |
| 44 | 701408733 | |
| 45 | 1134 | 0|
| 46 | 1836311903 | |
| 47 | 2971215073 | |
| 48 | 4807526976 | |
| 49 | 7778742049 | |
| 50 | 12586269025 | |
| 51 | 20365011074 | |
| 52 | 32951280099 | |
| 53 | 533162 | |
| 54 | 86267571272 | |
| 55 | 139583862445 | |
| 56 | 225851433717 | |
| 57 | 365435296162 | |
| 58 | 5729879 | |
| 59 | 956722026041 | |
| 60 | 1548008755920 | |
| 61 | 2504730781961 | |
| 62 | 4052739537881 | |
| 63 | 6557470319842 | |
| 64 | 10610209857723 | |
| 65 | 17167680177565 | |
| 66 | 277778 288 | |
| 67 | 44 | |
| 68 | 72723460248141 | |
| 69 | 11766 | 60994 |
| 70 | 1 | 4135 |
| 71 | 308061521170129 | |
| 72 | 498454011879264 | |
| 73 | 806515533049393 | |
| 74 | 1304969544 | |
| 75 | 2111485077978050 | |
| 76 | 34164546227 | |
| 77 | 5527 | 0884757 |
| 78 | 89443 | |
| 79 | 14472334024676221 | |
| 80 | 23416728348467685 | |
| 81 | 3788 73143906 | |
| 82 | 613057611591 | |
| 83 | 9 530 | |
| 84 | 160500643816367088 | |
| 85 | 2596954962585 | |
| 86 | 420196140727489673 | |
| 87 | 6798638612258 | |
| 88 | 1100087778366101931 | |
| 89 | 177997 | |
| 90 | 28800671 | |
| 91 | 4660046610375530309 | |
| 92 | 7540113804746346429 | |
| 93 | 12200160415121876738 | |
| 94 | 19740274219868223167 | |
| 95 | 31 | 46349905|
| 96 | 51680708854858323072 | |
| 97 | 83621143489848422977 | |
| 98 | 135301852344706746049 | |
| 99 | 218 | 5834555169026|
| 100 | 354224848179261 5 | |
| 101 | 573147844013817084101 | |
| 102 | 26 | |
| 103 | 1500520536206896083277 | |
| 104 | 24278 | 399975082453 |
| 105 | 3 | |
| 106 | 63563069 | 846248183 |
| 107 | 10284720757613717413913 | |
| 108 | 16641027750620563662096 | |
| 109 | 26 | 8508234281076009 |
| 110 | 43566776258854844738105 | |
| 111 | 704 | 7670814114 |
| 112 | 11405 | 25 | 0552219
| 113 | 1845518257 | |
| 114 | 2986111268189770662 | |
| 115 | 483162952612010163284885 | |
| 116 | 78177407 | 87230203437|
| 117 | 1264 | 20429973|
| 118 | 20467111114739846236 | |
| 119 | 3311648143516982017180081 | |
| 120 | 535835 | 640871840|
| 121 | 8670007398507 | 8051921|
| 122 | 140283666534988 | 1 |
| 123 | 22698374052006863956975682 | |
| 124 | 3672674070550577 | |
| 125 | 5 | |
| 126 | 96151855463018422468774568 | |
| 127 | 155576970220531065681649693 | |
| 128 | 25172882568354 | |
| 129 | 407305795 | |
| 130 | 65 |
456571051233611642553
6503
408712937024000
327
14051
51019822533679447
20699623170776339
79840132227567
510069157
695340528626429782121
4197810
66120355596518914
03241270663
13
04280
1038089984964854261893
406893
23367600
416
6076194
476499882895
645802411885151124650213
221056597232
9814751026371787089444
| 280 | 146406862188148 | 7245954 05480 | 382197697835|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 281 | 237706965543724518668151016 | 84548003 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 282 | 384617 | 2346400157540||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41661816 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 283 | 622324 6070574410635 | 3070626544377175485625797 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 284 | 1006 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 285 | 162 | 7982378002127889637318404077436298120 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 286 | 2636210644692 67 | 497896533243 | 271110084140201023 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 287 | 42654784246173 | 853713953114433 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 288 | 6 | 1029 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 99637980 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 289 | 11167167493 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 290 | 180688565632379 | 38||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 781310139745345 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 291 | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 292 | 47304880620403678140774067804 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 293 | 76540756 | 84158845383489763407680649954512095813 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 294 | 123845785297973041 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3538016392 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 295 | 200386689975542405708165665757608500558774338041350112205 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 296 | 324232475273515447634024717 | 538876233052554697128188128597 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 297 | 52461453343116499586482964847336113269538240802 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 298 | 84885164052257330097714121751630835360966663883732297726369399 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 299 | 1373470805771631154320257717102745700275212767467264610201 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 300 | 22223224462 | 455297398 | 720666693997649|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 301 | 35957 | 06583560961765665172189096721430 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 302 | 5818115698360040064558634095 | 53405766997246569401||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 303 | 9413 04258756745327122380628816531140136771503422 | 59202||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 304 | 15232024648785 | 6782440387231570435521120801226748728603||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 305 | 24645 | 98048006246675396881836888835835456250887805||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 306 | 3987795824799770715342824788687062628452272409956636682999616408 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 307 | 645238 20 | 674087279480253341013 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 308 | 104401850095207205720836975836208006537863817087422250120621 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 309 | 168 | 1 | 67042882457037855453867|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 310 | 27332756237962175339332 27162783750745455 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 311 | 44225333398004061429732838340729878012027363723832270745251370289 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 312 | 715580 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 313 | 115783425999770513860373 | 3635095356961600163955231274253486033 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 314 | 1873415186015369662 050 | 03127018958366040781255601777 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 315 | 303124 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 316 | 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 317 | 7935 804151 | 371268819610710140145037958273777397 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 318 | 128405787100699637303619708866360684958036398351225665283 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 319 | 207764 | 111482996299 | 4016312244381 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 320 | 336170714981814467266618721 | 04827980338677164658343636350711365||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 321 | 543 | 2862 | 72296177350244602806380313370817060034433662955746|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 322 | 8801063578447437644962364569698707634360652047981718378070013667111 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 323 | 14240420007076730617258541 3310440740965418798778412503676622857 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 324 | 23041483585524168262220964201807510161746678049676 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 325 | 37281
|
 Как открыть хостел | HowToHostel Как открыть хостел …
Как открыть хостел | HowToHostel Как открыть хостел … 
 Расширения Фибоначчи измеряют, насколько далеко может зайти импульсная волна .
Расширения Фибоначчи измеряют, насколько далеко может зайти импульсная волна .
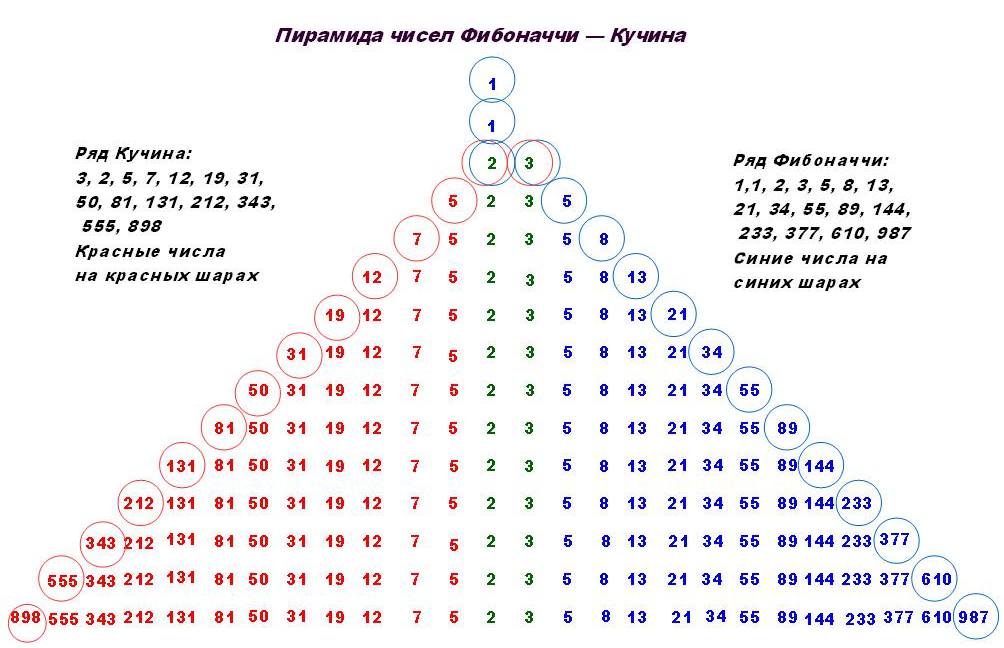
 д.
д.