Квантовая суперпозиция — это… Что такое Квантовая суперпозиция?
Ква́нтовая суперпози́ция (когерентная суперпозиция) — это суперпозиция состояний, которые не могут быть реализованы одновременно с классической точки зрения, это суперпозиция альтернативных (взаимоисключающих) состояний. Принцип существования суперпозиций состояний обычно называется в контексте квантовой механики просто принципом суперпозиции.
Если функции и являются допустимыми волновыми функциями, описывающими состояние квантовой системы, то их линейная суперпозиция, , также описывает какое-то состояние данной системы. Если измерение какой-либо физической величины в состоянии приводит к определённому результату , а в состоянии — к результату , то измерение в состоянии приведёт к результату или с вероятностями и соответственно.
Из принципа суперпозиции также следует, что все уравнения на волновые функции (например, уравнение Шрёдингера) в квантовой механике должны быть линейными.
Любая наблюдаемая величина (например, положение, импульс или энергия частицы) является собственным значением эрмитова линейного оператора, соответствующим конкретному собственному состоянию этого оператора, то есть определённой волновой функции, действие оператора на которую сводится к умножению на число — собственное значение. Линейная комбинация двух волновых функций — собственных состояний оператора также будет описывать реально существующее физическое состояние системы. Однако для такой системы наблюдаемая величина уже не будет иметь конкретного значения, и в результате измерения будет получено одно из двух значений с вероятностями, определяемыми квадратами коэффициентов (амплитуд), с которыми базисные функции входят в линейную комбинацию. (Разумеется, волновая функция системы может быть линейной комбинацией и более чем двух базисных состояний, вплоть до бесконечного их количества).
Важными следствиями квантовой суперпозиции являются различные интерференционные эффекты (см.
Популярный пример парадоксального поведения квантовомеханических объектов с точки зрения макроскопического наблюдателя — кот Шрёдингера, который может представлять собой квантовую суперпозицию живого и мёртвого кота. Впрочем, достоверно ничего не известно о применимости принципа суперпозиции (как и квантовой механики вообще) к макроскопическим системам.
Отличия от других суперпозиций
Квантовую суперпозицию (суперпозицию «волновых функций»), несмотря на сходство математической формулировки, не следует путать с принципом суперпозиции для обычных волновых явлений (поля). Возможность складывать квантовые состояния не обуславливает линейность каких-то физических систем. Суперпозиция поля для, скажем, электромагнитного случая, означает например то, что из двух разных состояний фотона можно сделать состояние электромагнитного поля с двумя фотонами, чего суперпозиция
 А полевой суперпозицией состояния вакуума (нулевого состояния) и некой волны будет всё та же волна, в отличие от квантовых суперпозиций 0- и 1-фотонного состояний, являющихся новыми состояниями. Квантовая суперпозиция может быть применима к подобным системам независимо от того, описываются они уравнениями линейными или нелинейными (то есть, справедлив или нет полевой принцип суперпозиции). См. Статистика Бозе — Эйнштейна по поводу связи между квантовой и полевой суперпозициями для случая бозонов.
А полевой суперпозицией состояния вакуума (нулевого состояния) и некой волны будет всё та же волна, в отличие от квантовых суперпозиций 0- и 1-фотонного состояний, являющихся новыми состояниями. Квантовая суперпозиция может быть применима к подобным системам независимо от того, описываются они уравнениями линейными или нелинейными (то есть, справедлив или нет полевой принцип суперпозиции). См. Статистика Бозе — Эйнштейна по поводу связи между квантовой и полевой суперпозициями для случая бозонов.Также, квантовую (когерентную) суперпозицию не следует путать с так называемыми смешанными состояниями (см. матрица плотности) — «некогерентной суперпозицией». Это тоже разные вещи.
См. также
Что такое квантовая суперпозиция простыми словами. Трёхщелевой эксперимент: теория
Основания квантовой теории
Квантовая теория, безусловно, самое странное описание реальности, когда-либо созданное физиками. Но они верят в нее потому, что, несмотря на десятилетия строгих проверок, ни один эксперимент не опроверг ее. Кроме того, квантовая теория привела к многочисленным практическим применениям — бытовым устройствам, которые бы просто не работали, если бы странные квантовые явления не происходили на атомном уровне. Например, то, что эта страница перед вами на экране компьютера, во многом происходит благодаря квантовым эффектам. Законы, управляющие транзисторами, на которых работает ваш компьютер, а также магнитные эффекты, используемые для хранения этой страницы на жестком диске, лежат в области квантовой теории.
Кроме того, квантовая теория привела к многочисленным практическим применениям — бытовым устройствам, которые бы просто не работали, если бы странные квантовые явления не происходили на атомном уровне. Например, то, что эта страница перед вами на экране компьютера, во многом происходит благодаря квантовым эффектам. Законы, управляющие транзисторами, на которых работает ваш компьютер, а также магнитные эффекты, используемые для хранения этой страницы на жестком диске, лежат в области квантовой теории.
Несмотря на успехи теории, она настолько остро оскорбляет наш общепринятый здравомыслящий взгляд на мир, что, даже если мы используем теорию для точного описания результатов того или иного эксперимента, мы вряд ли признаем, что действительно понимаем квантовую теорию. Вот что говорили о квантовой теории два Нобелевских лауреата: «Тот, кто не шокирован квантовой теорией, не понял ее» (Нильс Бор) и «Я думаю, могу с уверенностью сказать, что никто не понимает квантовую механику» (Ричард Фейнман).
Квантовая странность
Сердце квантовой странности заключается в том, что известно как принцип суперпозиции. Предположим, у нас есть один мяч, который спрятан в одной из двух коробок. Даже если мы не знаем, в какой коробке находится мяч, мы склонны полагать, что на самом деле он лежит в одной из двух коробок, в то время как в другой коробке нет ничего. Однако если вместо мяча мы возьмем микроскопический объект вроде атома, то в общем случае было бы неправильно предположить, что атом находится только в одной из двух коробок. В квантовой теории атом может вести себя так, что он, в некотором смысле, находится в обоих коробках сразу – в суперпозиции, казалось бы, взаимоисключающих альтернатив. Это странное поведение необходимо для работы природы на микроскопических масштабах и оно плотно вплетено в саму ткань реальности.
Что мы имеем в виду, когда говорим: атом может вести себя так, как будто он находится в двух местах одновременно? Рассмотрим классический эксперимент с двумя щелями, в котором поток одинаковых частиц (с одинаковой скоростью и направлением) направлен на перегородку с двумя щелями. Частицы могут быть электронами, атомами или даже большими молекулами — это не имеет никакого значения. Некоторые частицы будут заблокированы перегородкой, в то время как другие пройдут ее и столкнуться со вторым регистрирующим экраном. Предположим, что интенсивность потока очень низка, так что за один раз из аппарата вылетает только одна частица. Это гарантирует, что все странное наблюдаемое поведение связано с отдельными частицами, в отличие от двух или более частиц, имеющих какое-то влияние друг на друга. Экспериментальные результаты могут быть обобщены следующим образом:
· Частицы, прибывающие по одной, ударяются о регистрирующий экран в случайных местах. Даже если все они имеют одно и то же «состояние», место ударения не может быть предсказано заранее. В природе существует истинная случайность, более глубокая, чем случайность в бросаемом кубике.
В природе существует истинная случайность, более глубокая, чем случайность в бросаемом кубике.
· По мере роста числа частиц на регистрирующем экране возникает четкая картина ударов – частицы стремятся ударять в одних местах чаще, чем в других. Этот узор говорит нам о вероятности того, что данная частица попадет в данное место.
Оказывается, что этот вероятностный узор может быть рассчитан очень точно несколькими математически эквивалентными способами, например:
a) Один из способов состоит в том, чтобы забыть о частицах и рассмотреть вместо них мнимые волны, проходящие через перегородку. Такой волновой фронт будет проходить через обе щели одновременно, две волны появятся с другой стороны, по одной из каждой щели. Они будут распространяться по направлению к регистрирующему экрану, перекрывать и интерферировать друг с другом — как волны воды на озере. В результате интерференционной картины в некоторых местах на экране волны будут более интенсивными, чем в других местах.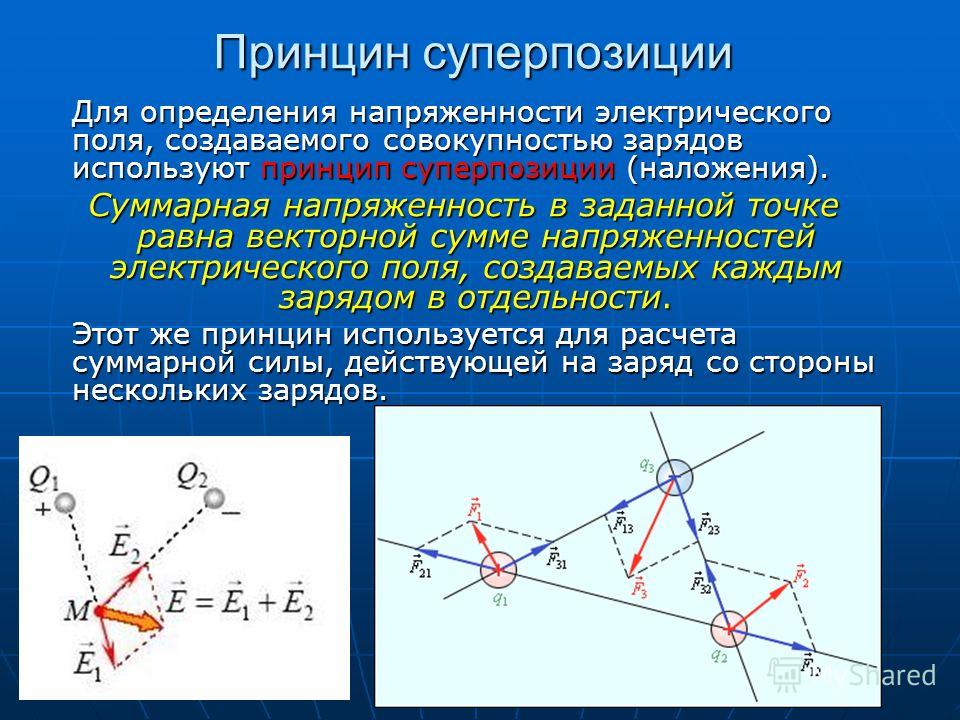 При правильном выборе расстояния между гребнями волн (длина волны), эта интерференционная картина может точно соответствовать нашему узору вероятности для частиц.
При правильном выборе расстояния между гребнями волн (длина волны), эта интерференционная картина может точно соответствовать нашему узору вероятности для частиц.
б) Другой способ заключается в попытке понять эксперимент строго в терминах частиц, проходящих через устройство. В конце концов, частицы испускаются источником и частицы появляются на регистрирующем экране. В этом случае математика говорит нам о том, что для получения любой заданной точки на регистрирующем экране, каждая отдельная частица существует на двух путях сразу, один проходит через левую щель, другой проходит через правую. Вероятность, с которой частица действительно попадет в регистрируемую точку, может быть рассчитана на основе определенных чисел, связанных с двумя путями, и мы снова приходим к тому же узору вероятностей частиц.
Математический аппарат, применяемый здесь, довольно простой, но все интерпретации того, что он предполагает о природе Вселенной, связаны с той или иной формой принципиально странных представлений.
Чтобы убедиться в этом более ясно, заметим, что при обеих открытых щелях на регистрирующем экране есть места, куда частицы никогда не попадают. Тем не менее, дальнейшие эксперименты показывают, что для частиц нет никаких проблем попасть в эти места, когда они вынуждены проходить только через одну щель (когда другую щель временно заблокировали). Иными словами, на экране есть места, куда частицы могут попасть, когда открыта только левая щель или только правая щель, но никогда не попадут, если открыты обе щели. Если предположить, что любая данная частица в действительности проходит только через одну щель (правую или левую), как она может «знать», что другая щель (левая или правая) открыта или нет, и поэтому «знает» куда «разрешено» попадать, а куда нет? Каким-то образом частица ведет себя так, как будто она может быть в двух местах одновременно, в левой и правой щелях.
То же самое можно сказать иначе. Главный вопрос в обычной (не квантовой) физике можно сформулировать так: зная начальное положение и скорость (величину и направление) мяча, какова его последующая траектория? В квантовой физике, тип вопроса совсем иной: зная, что я видел частицу здесь и сейчас, какова вероятность того, что я увижу ее там и тогда? Более того, вычисления этой вероятности предполагают странные идеи. Например: при переходе отсюда туда, частица существует одновременно во всех возможных путях, в том числе с остановкой на Луне! В последние десятилетия ученые начали применять эти квантовые странности для развития новых и мощных технологий, таких как квантовая криптография и квантовые вычисления – см. квантовая информация.
Запутанность
Если у нас есть более чем одна частица, квантовая суперпозиция может привести к еще более странному явлению, называемому квантовая запутанность. Две частицы, скажем электроны, в «запутанном состоянии» демонстрируют очень таинственный вид связи, или «корреляции». Если один каким-либо образом возмущается, это мгновенно влияет на другой, даже если они разнесены в пространстве очень далеко (например, один электрон на Земле, а другой на Марсе). Значение слова «влияет», которое здесь используется, довольно тонкое. Запутанность не является достаточно сильной, чтобы позволить нам мгновенно отправлять информацию, т.е. быстрее, чем скорость света (и, следовательно, не существует никаких нарушений теории относительности Эйнштейна). Но запутанность достаточно сильна, чтобы иметь некоторые интересные измеримые последствия (то, что раздражало Эйнштейна и называлось им «ужасное действие на расстоянии»). Здесь проявляется глубокое и увлекательное взаимодействие между теорией относительности и квантовой теорией. Например, можно задать такие вопросы: «Если одна из запутанной пары частиц падает в черную дыру, а другая вылетает наружу, где мы можем ее обнаружить, можно ли вторую частицу (или множество таких частиц) использовать для извлечения информации о том, что уже упало в черную дыру, или даже, как черная дыра была сформирована?»
Например, можно задать такие вопросы: «Если одна из запутанной пары частиц падает в черную дыру, а другая вылетает наружу, где мы можем ее обнаружить, можно ли вторую частицу (или множество таких частиц) использовать для извлечения информации о том, что уже упало в черную дыру, или даже, как черная дыра была сформирована?»
Чтобы по достоинству оценить странность квантовой запутанности, рассмотрим простой мысленный эксперимент. Предположим, что мы подбросили монетку и, не глядя на нее, разрезали пополам (так, чтобы отделить две грани монеты), затем спрятали каждую половину в запечатанной коробке, отдали одну коробку Алисе, а другую коробку Бобу, и отправили Алису на Венеру, а Боба на Марс. Когда Алиса откроет свой ящик, она найдет половину монеты или с орлом, или с решкой, а Боб найдет другую половину. В этом нет ничего удивительного.
Но теперь вместо монеты с двумя сторонами, предположим, что у нас есть два электрона. Легко приготовить два электрона в двух противоположных состояниях, один со спином вверх и другой со спином вниз (по аналогии с орлом и решкой), и снова провести подобный эксперимент. Разница в том, что в квантовом мире, два случая (А) спин вверх в коробке Алисы и спин вниз в коробке Боба, и (B) спин вниз в коробке Алисы и спин вверх в коробке Боба — могут существовать одновременно. Вместо обычного А или В, мы можем иметь А и B, что соответствует интерпретации квантовой теории, которую мы обсуждали выше. Пока Алиса не заглянет внутрь, ее коробка содержит электрон, который определенно не обладает ни спином вверх, ни спином вниз. Это неопределенное состояние может быть описано только путем рассмотрения электронов в двух коробках как частей единой системы, они не могут быть описаны отдельно. Аналогичная ситуация складывается и для электрона в коробке Боба.
Разница в том, что в квантовом мире, два случая (А) спин вверх в коробке Алисы и спин вниз в коробке Боба, и (B) спин вниз в коробке Алисы и спин вверх в коробке Боба — могут существовать одновременно. Вместо обычного А или В, мы можем иметь А и B, что соответствует интерпретации квантовой теории, которую мы обсуждали выше. Пока Алиса не заглянет внутрь, ее коробка содержит электрон, который определенно не обладает ни спином вверх, ни спином вниз. Это неопределенное состояние может быть описано только путем рассмотрения электронов в двух коробках как частей единой системы, они не могут быть описаны отдельно. Аналогичная ситуация складывается и для электрона в коробке Боба.
Если Алиса теперь заглянет в свою коробку, она заставит природу выбрать то или иное определенное состояние, А или В, причем природа выберет его случайным образом. Пусть природа выбирает состояние А (спин вверх для Алисы, спин вниз для Боба). Примечательно, что этот выбор влияет одновременно на обе коробки, независимо от того, как далеко они находятся друг от друга. В момент, когда Алиса заглянет в свою коробку, она повлияет не только на свой электрон, чтобы он приобрел определенный спин вверх, но и на электрон Боба (в его пока запечатанной коробке), чтобы он приобрел определенный спин вниз. Взгляд Алисы на ее электрон мгновенно влияет на электрон Боба, независимо от расстояния между ними. Казалось бы, это ведет к нарушению принципа Эйнштейна для скорости света! Но поскольку Алиса не имеет никакого контроля над тем, какое из двух определенных состояний примет ее электрон (природа выбирает случайным образом), процесс не может быть использован для мгновенной передачи информации, поэтому, строго говоря, нет никакого нарушения предела скорости света. Тем не менее, все это, безусловно, странно!
В момент, когда Алиса заглянет в свою коробку, она повлияет не только на свой электрон, чтобы он приобрел определенный спин вверх, но и на электрон Боба (в его пока запечатанной коробке), чтобы он приобрел определенный спин вниз. Взгляд Алисы на ее электрон мгновенно влияет на электрон Боба, независимо от расстояния между ними. Казалось бы, это ведет к нарушению принципа Эйнштейна для скорости света! Но поскольку Алиса не имеет никакого контроля над тем, какое из двух определенных состояний примет ее электрон (природа выбирает случайным образом), процесс не может быть использован для мгновенной передачи информации, поэтому, строго говоря, нет никакого нарушения предела скорости света. Тем не менее, все это, безусловно, странно!
Помимо постановки глубоких и увлекательных вопросов о природе реальности, квантовая запутанность имеет важные приложения в квантовой криптографии. Она делает возможным перенос очень деликатной квантовой информации (например, квантового состояния электронов в атоме) из одного места в другое в процессе, называемом «квантовая телепортация», с важными приложениями в квантовой вычислительной технике.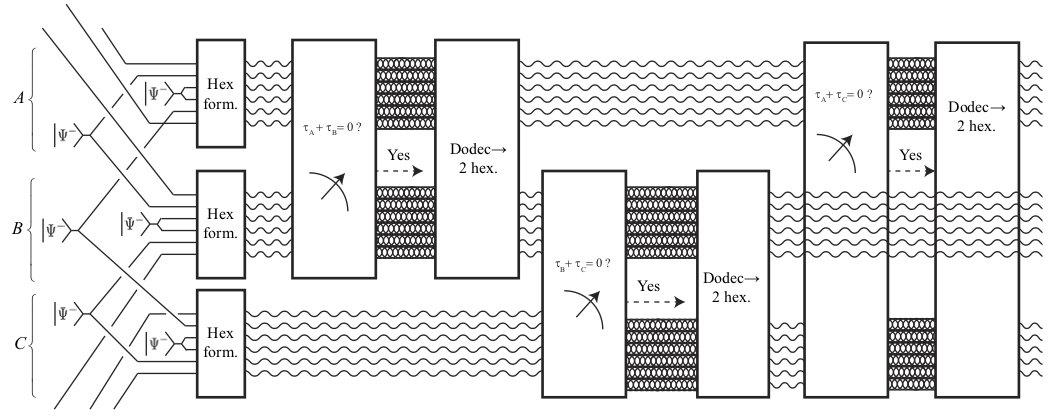 Оба этих приложения обсуждаются в разделе о квантовой информации.
Оба этих приложения обсуждаются в разделе о квантовой информации.
Интерпретация квантового мира
Что же нам делать с этим странным квантовым миром? Как мы уже упомянули, в то время как математика квантовой теории хорошо понятна, эти странности привели к различным интерпретациям природы «реальности».
Вернемся к нашему атому, существующему в виде суперпозиции в коробке 1 и в коробке 2. Когда мы «смотрим» в коробки (например, направив свет внутрь и обнаружив свет, рассеянный атомом), мы всегда найдем один атом в коробке 1 или в коробке 2, но никогда в обоих, так как существует только один атом. Но что на самом деле представляет собой такое измерение? Существуют ли некоторые физические взаимодействия, с помощью которых измерительное устройство заставляет квантовую систему получать определенный результат (сильная версия того, что называется «Копенгагенская интерпретация», и интерпретация, лежащая в основе дискуссии в этой статье)? Или определенность — это иллюзия, а прибор и квантовая частица – лишь части большой квантовой системы, в которой реализуются все возможные результаты измерений? То есть, для каждого полученного результата в «параллельных реальностях» есть мириады копий измерительных приборов, получающих все возможные результаты («Многомировая интерпретация»)? Или сама непредсказуемость — это иллюзия, и квантовая теория может быть построена на каком-то скрытом основании, которое само по себе следует предсказуемой эволюции («Бомовская механика»)?
Ответы на эти вопросы об основах квантовой теории стали очень важными в контексте ряда фундаментальных проблем, имеющих многочисленные последствия. Например, поскольку очень ранняя Вселенная должна описываться как квантовая система, вопросы о основаниях квантовой теории становятся важными для понимании происхождения нашей Вселенной, то есть, для квантовой космологии. Более глубокое понимание оснований квантовой теории может помочь нам в решении одной из великих нерешенных проблем квантовой теории: Как включить в нее гравитацию и получить теорию квантовой гравитации?
Например, поскольку очень ранняя Вселенная должна описываться как квантовая система, вопросы о основаниях квантовой теории становятся важными для понимании происхождения нашей Вселенной, то есть, для квантовой космологии. Более глубокое понимание оснований квантовой теории может помочь нам в решении одной из великих нерешенных проблем квантовой теории: Как включить в нее гравитацию и получить теорию квантовой гравитации?
Ква́нтовая суперпози́ция (когерентная суперпозиция) — суперпозиция состояний , которые не могут быть реализованы одновременно с классической точки зрения, это суперпозиция альтернативных (взаимоисключающих) состояний. Принцип существования суперпозиций состояний обычно называется в контексте квантовой механики просто принципом суперпозиции .
Из принципа суперпозиции также следует, что все уравнения на волновые функции (например, уравнение Шрёдингера) в квантовой механике должны быть линейными.
Любая наблюдаемая величина (например, положение, импульс или энергия частицы) является собственным значением эрмитова линейного оператора , соответствующим конкретному собственному состоянию этого оператора, то есть определённой волновой функции, действие оператора на которую сводится к умножению на число — собственное значение. Линейная комбинация двух волновых функций — собственных состояний оператора также будет описывать реально существующее физическое состояние системы. Однако для такой системы наблюдаемая величина уже не будет иметь конкретного значения, и в результате измерения будет получено одно из двух значений с вероятностями, определяемыми квадратами коэффициентов (амплитуд), с которыми базисные функции входят в линейную комбинацию. (Разумеется, волновая функция системы может быть линейной комбинацией и более чем двух базисных состояний, вплоть до бесконечного их количества).
Линейная комбинация двух волновых функций — собственных состояний оператора также будет описывать реально существующее физическое состояние системы. Однако для такой системы наблюдаемая величина уже не будет иметь конкретного значения, и в результате измерения будет получено одно из двух значений с вероятностями, определяемыми квадратами коэффициентов (амплитуд), с которыми базисные функции входят в линейную комбинацию. (Разумеется, волновая функция системы может быть линейной комбинацией и более чем двух базисных состояний, вплоть до бесконечного их количества).
Важными следствиями квантовой суперпозиции являются различные интерференционные эффекты (см. опыт Юнга , дифракционные методы), а для составных систем — зацепленные состояния .
Популярный пример парадоксального поведения квантовомеханических объектов с точки зрения макроскопического наблюдателя — кот Шрёдингера , который может представлять собой квантовую суперпозицию живого и мёртвого кота. Впрочем, достоверно ничего не известно о применимости принципа суперпозиции (как и квантовой механики вообще) к макроскопическим системам.
Квантовую суперпозицию (суперпозицию «волновых функций »), несмотря на сходство математической формулировки, не следует путать с принципом суперпозиции для обычных волновых явлений (поля). Возможность складывать квантовые состояния не обуславливает линейность каких-то физических систем. Суперпозиция поля для, скажем, электромагнитного случая, означает например то, что из двух разных состояний фотона можно сделать состояние электромагнитного поля с двумя фотонами, чего суперпозиция квантовая сделать не может. А полевой суперпозицией состояния вакуума (нулевого состояния) и некой волны будет всё та же волна, в отличие от квантовых суперпозиций 0- и 1-фотонного состояний, являющихся новыми состояниями. Квантовая суперпозиция может быть применима к подобным системам независимо от того, описываются они уравнениями линейными или нелинейными (то есть, справедлив или нет полевой принцип суперпозиции). См. Статистика Бозе — Эйнштейна по поводу связи между квантовой и полевой суперпозициями для случая бозонов.
Также, квантовую (когерентную) суперпозицию не следует путать с так называемыми смешанными состояниями (см. матрица плотности) — «некогерентной суперпозицией». Это тоже разные вещи.
Квантовый принцип суперпозиции является центральным принципом квантовой физики. Применительно к описанию состояний фотона его можно пояснить так. Если фотон может попасть в состояние несколькими способами, результирующая амплитуда попадания в данное состояние равна векторной сумме амплитуд попадания каждым из способов. Надо иметь в виду, что амплитуды складываются только в том случае, когда принципиально невозможно различить, каким из способов произошло попадание в данное состояние . Если же при проведении эксперимента использовать какое либо устройство, позволяющее определить, каким из способов произошло попадание в конечное состояние, то амплитуды не складываются – складываются вероятности осуществления всех способов. В этом случае квантовой интерференции амплитуд вероятности нет.
Пример квантовой интерференции. Пучок фотонов одной и той же энергии направим на две параллельные друг другу плоскопараллельные пластинки (интерферометр Фабри-Перо). Будем регистрировать отраженные от системы фотоны.
Описание опыта на классическом языке выглядит так. Электромагнитная волна частично проходит и частично отражается от первой пластинки. С прошедшей частью происходит то же самое. Отраженная волна представляет собой суперпозицию двух волн — отраженной от первой и отраженной от второй пластинки. Если разность хода отраженных волн равна целому числу волн, то будет наблюдаться усиление отраженного света. Если же разность хода отраженных волн равна нечетному числу полуволн, то будет наблюдаться ослабление отраженного света. Поэтому при плавном изменении расстояния между пластинками должно наблюдаться попеременное усиление и ослабление отраженного света. Это предсказание согласуется с опытными данными.
Оказывается, все предсказания на основе классической волновой теории, подтверждаемые экспериментально, следуют и из квантовой теории. Проведем квантовые рассуждения. Падающий на первую пластинку фотон имеет амплитуду отразиться, обозначим ее через a1 , и имеет амплитуду пройти, обозначим ее через b1 . Очевидно, a1 и b1 должны удовлетворять условию ça1 ç2+ çb1 ç2=1 . Амплитуда вероятности Y2 фотону, отраженному от второй пластинки, выйти из первой пластинки имеет фазу, большую фазы амплитуды вероятности отражения от первой пластинки Y1=a1 на Dj=2kb (для простоты не учитываем показатель преломления пластинок, то есть считаем пластинки бесконечно тонкими), потому что точка выхода фотона, отраженного от второй пластинки, отстоит от точки отражения от первой пластинки вдоль траектории фотона на двойное расстояние между пластинками. Детектор фотонов, установленный перед пластинками, принципиально не может отличить, от первой или второй пластинки отразился фотон. Поэтому, результирующая амплитуда вероятности того, что фотон отразится от системы пластинок, равна векторной сумме амплитуд Y1 и Y2 . Из рисунка видно, что при разности фаз амплитуд вероятности, равной целому числу 2p , сумма амплитуд равна сумме длин стрелок, а при разности фаз, равной нечетному числу p , сумма амплитуд равна разности длин стрелок. В первом случае вероятность прохождения равна квадрату суммы длин стрелок, а во втором — квадрату разности длин стрелок. В общем случае вероятность отражения P вычислится по теореме косинусов
P= |Y1 |2+ |Y2 |2+2 |Y1 |× |Y2 |cos2kb (3)
Точно так же, как и классическая, квантовая теория предсказывает чередующиеся усиления и ослабления частоты срабатывания детектора при плавном изменении расстояния между пластинками. Если обеспечить выполнение условия çY1 ç= çY2 ç, то при определенных расстояниях b вероятность отражения может равняться нулю, хотя амплитуды отражения и от первой и от второй пластинок не равны нулю.
Следующая задача является центром занятия.
Задача 4. Через две щели, ширина каждой из которых меньше длины волны амплитуды вероятности l , пропускают пучок электронов. Электроны попадают на экран, расположенный на расстоянии L от щелей. Амплитуды попадания электрона в верхнюю и в нижнюю щели одинаковы. Рассмотрите ситуацию L>>l, b, x .
а) Полагая, что модули амплитуд вероятности электрону и из верхней и из нижней щелей попасть на экран в начало координат одинаковы и равны Y , определите частоту срабатывания детектора I , закрепленного на экране на расстоянии x от начала координат. Считайте, что частота срабатывания детектора, установленного в начале координат, равна I0 . Полагайте также, что Y не зависит от x .
б) Получите приближенное выражение расстояния между центральным и первым максимумом интенсивности попадания электронов.
в) Дайте качественное предсказание изменения дифракционной картины в случае, когда модули амплитуд попадания электрона на экран из щелей не равны и обратно пропорциональны расстоянию от щели до места попадания.
г) Как изменится дифракционная картина, если фаза амплитуды вероятности попадания электрона в верхнюю щель меньше фазы амплитуды вероятности попадания электрона в нижнюю щель на p/6 ?
Решение. а) Поскольку принципиально невозможно определить, из какой щели прилетает электрон в точку x , постольку результирующая амплитуда попадания равна сумме амплитуд. Амплитуды попадания электрона из верхней и нижней щелей имеют разность фаз , где D l- разность хода в точку x из верхней и из нижней щелей. Она равна
(4)
Соответствующая разность фаз при этом
(5)
Далее складываем амплитуды по теореме косинусов, и определяем вероятность попадания электрона в точку x , как это было сделано в примере
(6)
Центральный максимум находится в точке x=0 . Так как интенсивность срабатывания детектора в центральном максимуме равнаI0 , то , и интенсивность срабатывания в точке x запишется в виде
(7)
б) Расстояние между центральным и первым максимумами определится из условия
(8)
Откуда
(9)
в) По мере удаления от центрального максимума при перемещении вдоль экрана будет наблюдаться различие в длинах стрелок амплитуды вероятности. В отличие от ситуации, описываемой формулой (13), которая в точках минимума дает нулевую интенсивность срабатывания детектора, вычитание волн амплитуд вероятности попадания из разных щелей не будет давать нуль. На дифракционную картину будет налагаться монотонная “подсветка”.
г) К разности фаз амплитуд вероятности, задаваемой формулой (5), добавится p/6 , поэтому новая разность фаз будет равна
(10)
Соответственно формула (17) преобразуется к виду
(11)
Формула (11) говорит, что вся дифракционная картина смещается вниз на расстояние .
Подведем итоги решения задачи 4. При рассеянии пучка электронов на двух щелях волны амплитуды вероятности, прошедшие через верхнюю и через нижнюю щель, налагаются друг на друга (интерферируют) и возникает дифракционная картина подобная картине дифракции света на двух щелях. Замечательно, что если по очереди прикрывать ту или иную щель, то картина рассеяния не будет иметь минимумов или максимумов (так как щели очень тонкие). Максимумы и минимумы возникают только в том случае, когда открыты обе щели. Складываются амплитуды вероятности двух возможностей. Нельзя утверждать, что электрон попадает в детектор, прилетев из верхней щели или из нижней щели. Он прилетает сразу из двух щелей. Не смотря на то, что электрон является неделимой частицей, каким-то образом он пролетает сразу через две щели.
Возможность интерференции состояний является главной чертой квантовой физики. Это ее главная суть.
Точки зрения, это суперпозиция альтернативных (взаимоисключающих) состояний. Принцип существования суперпозиций состояний обычно называется в контексте квантовой механики просто принципом суперпозиции .
Если функции Ψ 1 {\displaystyle \Psi _{1}\ } и Ψ 2 {\displaystyle \Psi _{2}\ } являются допустимыми волновыми функциями, описывающими состояние квантовой системы, то их линейная суперпозиция, Ψ 3 = c 1 Ψ 1 + c 2 Ψ 2 {\displaystyle \Psi _{3}=c_{1}\Psi _{1}+c_{2}\Psi _{2}\ } , также описывает какое-то состояние данной системы.{2}\ } соответственно.
Из принципа суперпозиции также следует, что все уравнения на волновые функции (например, уравнение Шрёдингера) в квантовой механике должны быть линейными.
Любая наблюдаемая величина (например, положение, импульс или энергия частицы) является собственным значением эрмитова линейного оператора , соответствующим конкретному собственному состоянию этого оператора, то есть определённой волновой функции, действие оператора на которую сводится к умножению на число — собственное значение. Линейная комбинация двух волновых функций — собственных состояний оператора также будет описывать реально существующее физическое состояние системы. Однако для такой системы наблюдаемая величина уже не будет иметь конкретного значения, и в результате измерения будет получено одно из двух значений с вероятностями, определяемыми квадратами коэффициентов (амплитуд), с которыми базисные функции входят в линейную комбинацию. (Разумеется, волновая функция системы может быть линейной комбинацией и более чем двух базисных состояний, вплоть до бесконечного их количества).
Важными следствиями квантовой суперпозиции являются различные интерференционные эффекты (см. опыт Юнга , дифракционные методы), а для составных систем — зацепленные состояния .
Популярный пример парадоксального поведения квантовомеханических объектов с точки зрения макроскопического наблюдателя — кот Шрёдингера , который может представлять собой квантовую суперпозицию живого и мёртвого кота. Впрочем, достоверно ничего не известно о применимости принципа суперпозиции (как и квантовой механики вообще) к макроскопическим системам.
Отличия от других суперпозиций
Квантовую суперпозицию (суперпозицию «волновых функций »), несмотря на сходство математической формулировки, не следует путать с
Ква́нтовая суперпози́ция (когерентная суперпозиция) — это суперпозиция состояний , которые не могут быть реализованы одновременно с классической точки зрения, это суперпозиция альтернативных (взаимоисключающих) состояний. Принцип существования суперпозиций состояний обычно называется в контексте квантовой механики просто принципом суперпозиции .{2}\ } соответственно.
Простыми словами формула Ψ n + 1 = c 1 Ψ 1 + c 2 Ψ 2 . . . + c n Ψ n {\displaystyle \Psi _{n+1}=c_{1}\Psi _{1}+c_{2}\Psi _{2}\ …+c_{n}\Psi _{n}\ } является функцией суммы -ых произведений функций на их вероятности, а следовательно суммой вероятных состояний всех функций | Ψ ⟩ {\displaystyle |\Psi \rangle } .
Из принципа суперпозиции также следует, что все уравнения на волновые функции (например, уравнение Шрёдингера) в квантовой механике должны быть линейными.
Любая наблюдаемая величина (например, положение, импульс или энергия частицы) является собственным значением эрмитова линейного оператора , соответствующим конкретному собственному состоянию этого оператора, то есть определённой волновой функции, действие оператора на которую сводится к умножению на число — собственное значение. Линейная комбинация двух волновых функций — собственных состояний оператора также будет описывать реально существующее физическое состояние системы. Однако для такой системы наблюдаемая величина уже не будет иметь конкретного значения, и в результате измерения будет получено одно из двух значений с вероятностями, определяемыми квадратами коэффициентов (амплитуд), с которыми базисные функции входят в линейную комбинацию. (Разумеется, волновая функция системы может быть линейной комбинацией и более чем двух базисных состояний, вплоть до бесконечного их количества).
Важными следствиями квантовой суперпозиции являются различные интерференционные эффекты (см. опыт Юнга , дифракционные методы), а для составных систем — зацепленные состояния .
Популярный пример парадоксального поведения квантовомеханических объектов с точки зрения макроскопического наблюдателя — кот Шрёдингера , который может представлять собой квантовую суперпозицию живого и мёртвого кота. Впрочем, достоверно ничего не известно о применимости принципа суперпозиции (как и квантовой механики вообще) к макроскопическим системам.
Энциклопедичный YouTube
1 / 5
Просмотров:
Квантовый принцип суперпозиции. Кот шредингера простыми словами
Квантовый принцип суперпозиции. Кот шредингера простыми словами
Ква́нтовая суперпози́ция (когерентная суперпозиция) — суперпозиция состояний , которые не могут быть реализованы одновременно с классической точки зрения, это суперпозиция альтернативных (взаимоисключающих) состояний. Принцип существования суперпозиций состояний обычно называется в контексте квантовой механики просто принципом суперпозиции .
Из принципа суперпозиции также следует, что все уравнения на волновые функции (например, уравнение Шрёдингера) в квантовой механике должны быть линейными.
Любая наблюдаемая величина (например, положение, импульс или энергия частицы) является собственным значением эрмитова линейного оператора , соответствующим конкретному собственному состоянию этого оператора, то есть определённой волновой функции, действие оператора на которую сводится к умножению на число — собственное значение. Линейная комбинация двух волновых функций — собственных состояний оператора также будет описывать реально существующее физическое состояние системы. Однако для такой системы наблюдаемая величина уже не будет иметь конкретного значения, и в результате измерения будет получено одно из двух значений с вероятностями, определяемыми квадратами коэффициентов (амплитуд), с которыми базисные функции входят в линейную комбинацию. (Разумеется, волновая функция системы может быть линейной комбинацией и более чем двух базисных состояний, вплоть до бесконечного их количества).
Важными следствиями квантовой суперпозиции являются различные интерференционные эффекты (см. опыт Юнга , дифракционные методы), а для составных систем — зацепленные состояния .
Популярный пример парадоксального поведения квантовомеханических объектов с точки зрения макроскопического наблюдателя — кот Шрёдингера , который может представлять собой квантовую суперпозицию живого и мёртвого кота. Впрочем, достоверно ничего не известно о применимости принципа суперпозиции (как и квантовой механики вообще) к макроскопическим системам.
Квантовую суперпозицию (суперпозицию «волновых функций »), несмотря на сходство математической формулировки, не следует путать с принципом суперпозиции для обычных волновых явлений (поля). Возможность складывать квантовые состояния не обуславливает линейность каких-то физических систем. Суперпозиция поля для, скажем, электромагнитного случая, означает например то, что из двух разных состояний фотона можно сделать состояние электромагнитного поля с двумя фотонами, чего суперпозиция квантовая сделать не может. А полевой суперпозицией состояния вакуума (нулевого состояния) и некой волны будет всё та же волна, в отличие от квантовых суперпозиций 0- и 1-фотонного состояний, являющихся новыми состояниями. Квантовая суперпозиция может быть применима к подобным системам независимо от того, описываются они уравнениями линейными или нелинейными (то есть, справедлив или нет полевой принцип суперпозиции). См. Статистика Бозе — Эйнштейна по поводу связи между квантовой и полевой суперпозициями для случая бозонов.
Также, квантовую (когерентную) суперпозицию не следует путать с так называемыми смешанными состояниями (см. матрица плотности) — «некогерентной суперпозицией». Это тоже разные вещи.
Квантовая суперпозиция — суперпозиция взаимоисключающих состояний. Теоретическим примером такой суперпозиции является мысленный эксперимент «кот Шредингера». Согласно его условиям, кот, помещенный в закрытую коробку с радиоактивным веществом, вероятность распада которого неизвестна, и синильной кислотой, может являться для макроскопического наблюдателя одновременно и живым, и мертвым. На практике квантовая суперпозиция реализуется, например, в кубитах — элементах хранения данных в квантовых компьютерах.
В новом исследовании ученые зафиксировали квантовую суперпозицию двухатомных молекул газообразного йода с помощью рентгеновского лазера на свободных электронах LCLS. Находясь в свободном движении, молекулы вещества расщеплялись на возбужденные и нейтральные атомы за счет поглощения энергии. Излучение LCLS удаляло последние друг от друга и рекомбинировало их в виде рентгенограммы с шагом в 30 фемтосекунд. Минимальным шагом движения молекул на разных снимках стали 0,3 ангстрем (0,03 нанометра) — меньше ширины атома.
Подчеркивается, что электронный удар лазерного импульса непосредственно касался лишь 4–5 процентов молекул, но, с точки зрения квантовой механики, возбуждал все молекулы вещества по аналогии с «котом Шредингера». Подтверждением факта квантовой суперпозиции стала фиксация LCLS отраженного излучения от обоих состояний молекул одновременно. На рентгенограмме это выглядело как серия концентрических колец, более ярких на этапе синхронизации межмолекулярных колебаний, и более темных на этапе рассинхронизации.
«Сперва молекула вибрирует, а ее атомы отклоняются в сторону и удаляются друг от друга. Затем связь между атомами нарушается, и они проваливаются в пустоту. При этом связь по-прежнему сохраняется. Некоторое время атомы остаются на расстоянии друг от друга, прежде чем перейти в первоначальное состояние. Постепенно вибрация молекулы нивелируется, и молекула возвращается в состояние покоя. Весь процесс длится не более триллионных долей секунды», — описал явление профессор Фил Баксбаум.
Он добавил, что при наличии разрыва межатомной связи регистрация квантовой суперпозиции оказалась бы невозможной. Команда стала первой, кто использовал интенсивные ультракороткие импульсы когерентного излучения в таких целях. Между тем описанная методика может применяться не только в будущих, но и прошлых исследованиях, отметили ученые. Они также выразили готовность продолжить съемку «молекулярного кино» в иных областях, например, в биологии — для изучения механизмов защиты ДНК от ультрафиолета.
«Молекулярное кино», снятое LCLS. Синие точки — возбужденные атомы, красные точки — нейтральные атомы, существующие одновременно. © J. M. Glownia et al
Основания квантовой теории
Квантовая теория, безусловно, самое странное описание реальности, когда-либо созданное физиками. Но они верят в нее потому, что, несмотря на десятилетия строгих проверок, ни один эксперимент не опроверг ее. Кроме того, квантовая теория привела к многочисленным практическим применениям — бытовым устройствам, которые бы просто не работали, если бы странные квантовые явления не происходили на атомном уровне. Например, то, что эта страница перед вами на экране компьютера, во многом происходит благодаря квантовым эффектам. Законы, управляющие транзисторами, на которых работает ваш компьютер, а также магнитные эффекты, используемые для хранения этой страницы на жестком диске, лежат в области квантовой теории.
Несмотря на успехи теории, она настолько остро оскорбляет наш общепринятый здравомыслящий взгляд на мир, что, даже если мы используем теорию для точного описания результатов того или иного эксперимента, мы вряд ли признаем, что действительно понимаем квантовую теорию. Вот что говорили о квантовой теории два Нобелевских лауреата: «Тот, кто не шокирован квантовой теорией, не понял ее» (Нильс Бор) и «Я думаю, могу с уверенностью сказать, что никто не понимает квантовую механику» (Ричард Фейнман). С тех пор как квантовая теория была разработана в 1920-х годах, вопрос о том, что действительно теория говорит о «ткани реальности», волновал многих величайших мыслителей в физике и философии. Глубокое погружение в исследование основ квантовой теории не ослабевает по сей день.
Квантовая странность
Сердце квантовой странности заключается в том, что известно как принцип суперпозиции. Предположим, у нас есть один мяч, который спрятан в одной из двух коробок. Даже если мы не знаем, в какой коробке находится мяч, мы склонны полагать, что на самом деле он лежит в одной из двух коробок, в то время как в другой коробке нет ничего. Однако если вместо мяча мы возьмем микроскопический объект вроде атома, то в общем случае было бы неправильно предположить, что атом находится только в одной из двух коробок. В квантовой теории атом может вести себя так, что он, в некотором смысле, находится в обоих коробках сразу – в суперпозиции, казалось бы, взаимоисключающих альтернатив. Это странное поведение необходимо для работы природы на микроскопических масштабах и оно плотно вплетено в саму ткань реальности.
Что мы имеем в виду, когда говорим: атом может вести себя так, как будто он находится в двух местах одновременно? Рассмотрим классический эксперимент с двумя щелями, в котором поток одинаковых частиц (с одинаковой скоростью и направлением) направлен на перегородку с двумя щелями. Частицы могут быть электронами, атомами или даже большими молекулами — это не имеет никакого значения. Некоторые частицы будут заблокированы перегородкой, в то время как другие пройдут ее и столкнуться со вторым регистрирующим экраном. Предположим, что интенсивность потока очень низка, так что за один раз из аппарата вылетает только одна частица. Это гарантирует, что все странное наблюдаемое поведение связано с отдельными частицами, в отличие от двух или более частиц, имеющих какое-то влияние друг на друга. Экспериментальные результаты могут быть обобщены следующим образом:
· Частицы, прибывающие по одной, ударяются о регистрирующий экран в случайных местах. Даже если все они имеют одно и то же «состояние», место ударения не может быть предсказано заранее. В природе существует истинная случайность, более глубокая, чем случайность в бросаемом кубике.
· По мере роста числа частиц на регистрирующем экране возникает четкая картина ударов – частицы стремятся ударять в одних местах чаще, чем в других. Этот узор говорит нам о вероятности того, что данная частица попадет в данное место.
Оказывается, что этот вероятностный узор может быть рассчитан очень точно несколькими математически эквивалентными способами, например:
a) Один из способов состоит в том, чтобы забыть о частицах и рассмотреть вместо них мнимые волны, проходящие через перегородку. Такой волновой фронт будет проходить через обе щели одновременно, две волны появятся с другой стороны, по одной из каждой щели. Они будут распространяться по направлению к регистрирующему экрану, перекрывать и интерферировать друг с другом — как волны воды на озере. В результате интерференционной картины в некоторых местах на экране волны будут более интенсивными, чем в других местах. При правильном выборе расстояния между гребнями волн (длина волны), эта интерференционная картина может точно соответствовать нашему узору вероятности для частиц.
б) Другой способ заключается в попытке понять эксперимент строго в терминах частиц, проходящих через устройство. В конце концов, частицы испускаются источником и частицы появляются на регистрирующем экране. В этом случае математика говорит нам о том, что для получения любой заданной точки на регистрирующем экране, каждая отдельная частица существует на двух путях сразу, один проходит через левую щель, другой проходит через правую. Вероятность, с которой частица действительно попадет в регистрируемую точку, может быть рассчитана на основе определенных чисел, связанных с двумя путями, и мы снова приходим к тому же узору вероятностей частиц.
Математический аппарат, применяемый здесь, довольно простой, но все интерпретации того, что он предполагает о природе Вселенной, связаны с той или иной формой принципиально странных представлений. В случаях (а) и (б), описанных выше, эта странность появляется в том, что каждая отдельная частица, проходя через устройство, каким-то образом знает об обеих щелях: представляем ли мы воображаемые волны, связанные с частицей, или саму частицу, проходящую через обе щели одновременно.
Чтобы убедиться в этом более ясно, заметим, что при обеих открытых щелях на регистрирующем экране есть места, куда частицы никогда не попадают. Тем не менее, дальнейшие эксперименты показывают, что для частиц нет никаких проблем попасть в эти места, когда они вынуждены проходить только через одну щель (когда другую щель временно заблокировали). Иными словами, на экране есть места, куда частицы могут попасть, когда открыта только левая щель или только правая щель, но никогда не попадут, если открыты обе щели. Если предположить, что любая данная частица в действительности проходит только через одну щель (правую или левую), как она может «знать», что другая щель (левая или правая) открыта или нет, и поэтому «знает» куда «разрешено» попадать, а куда нет? Каким-то образом частица ведет себя так, как будто она может быть в двух местах одновременно, в левой и правой щелях. Возвращаясь к атому и двум коробкам, мы имеем аналогичную ситуацию: в повседневной жизни можно было бы ожидать «атом в коробке 1» или «атом в коробке 2». В квантовом мире, однако, мы можем, и, как правило, имеем «атом в коробке 1» и «атом в коробке 2».
То же самое можно сказать иначе. Главный вопрос в обычной (не квантовой) физике можно сформулировать так: зная начальное положение и скорость (величину и направление) мяча, какова его последующая траектория? В квантовой физике, тип вопроса совсем иной: зная, что я видел частицу здесь и сейчас, какова вероятность того, что я увижу ее там и тогда? Более того, вычисления этой вероятности предполагают странные идеи. Например: при переходе отсюда туда, частица существует одновременно во всех возможных путях, в том числе с остановкой на Луне! В последние десятилетия ученые начали применять эти квантовые странности для развития новых и мощных технологий, таких как квантовая криптография и квантовые вычисления – см. квантовая информация.
Запутанность
Если у нас есть более чем одна частица, квантовая суперпозиция может привести к еще более странному явлению, называемому квантовая запутанность. Две частицы, скажем электроны, в «запутанном состоянии» демонстрируют очень таинственный вид связи, или «корреляции». Если один каким-либо образом возмущается, это мгновенно влияет на другой, даже если они разнесены в пространстве очень далеко (например, один электрон на Земле, а другой на Марсе). Значение слова «влияет», которое здесь используется, довольно тонкое. Запутанность не является достаточно сильной, чтобы позволить нам мгновенно отправлять информацию, т.е. быстрее, чем скорость света (и, следовательно, не существует никаких нарушений теории относительности Эйнштейна). Но запутанность достаточно сильна, чтобы иметь некоторые интересные измеримые последствия (то, что раздражало Эйнштейна и называлось им «ужасное действие на расстоянии»). Здесь проявляется глубокое и увлекательное взаимодействие между теорией относительности и квантовой теорией. Например, можно задать такие вопросы: «Если одна из запутанной пары частиц падает в черную дыру, а другая вылетает наружу, где мы можем ее обнаружить, можно ли вторую частицу (или множество таких частиц) использовать для извлечения информации о том, что уже упало в черную дыру, или даже, как черная дыра была сформирована?»
Чтобы по достоинству оценить странность квантовой запутанности, рассмотрим простой мысленный эксперимент. Предположим, что мы подбросили монетку и, не глядя на нее, разрезали пополам (так, чтобы отделить две грани монеты), затем спрятали каждую половину в запечатанной коробке, отдали одну коробку Алисе, а другую коробку Бобу, и отправили Алису на Венеру, а Боба на Марс. Когда Алиса откроет свой ящик, она найдет половину монеты или с орлом, или с решкой, а Боб найдет другую половину. В этом нет ничего удивительного.
Но теперь вместо монеты с двумя сторонами, предположим, что у нас есть два электрона. Легко приготовить два электрона в двух противоположных состояниях, один со спином вверх и другой со спином вниз (по аналогии с орлом и решкой), и снова провести подобный эксперимент. Разница в том, что в квантовом мире, два случая (А) спин вверх в коробке Алисы и спин вниз в коробке Боба, и (B) спин вниз в коробке Алисы и спин вверх в коробке Боба — могут существовать одновременно. Вместо обычного А или В, мы можем иметь А и B, что соответствует интерпретации квантовой теории, которую мы обсуждали выше. Пока Алиса не заглянет внутрь, ее коробка содержит электрон, который определенно не обладает ни спином вверх, ни спином вниз. Это неопределенное состояние может быть описано только путем рассмотрения электронов в двух коробках как частей единой системы, они не могут быть описаны отдельно. Аналогичная ситуация складывается и для электрона в коробке Боба.
Если Алиса теперь заглянет в свою коробку, она заставит природу выбрать то или иное определенное состояние, А или В, причем природа выберет его случайным образом. Пусть природа выбирает состояние А (спин вверх для Алисы, спин вниз для Боба). Примечательно, что этот выбор влияет одновременно на обе коробки, независимо от того, как далеко они находятся друг от друга. В момент, когда Алиса заглянет в свою коробку, она повлияет не только на свой электрон, чтобы он приобрел определенный спин вверх, но и на электрон Боба (в его пока запечатанной коробке), чтобы он приобрел определенный спин вниз. Взгляд Алисы на ее электрон мгновенно влияет на электрон Боба, независимо от расстояния между ними. Казалось бы, это ведет к нарушению принципа Эйнштейна для скорости света! Но поскольку Алиса не имеет никакого контроля над тем, какое из двух определенных состояний примет ее электрон (природа выбирает случайным образом), процесс не может быть использован для мгновенной передачи информации, поэтому, строго говоря, нет никакого нарушения предела скорости света. Тем не менее, все это, безусловно, странно!
Помимо постановки глубоких и увлекательных вопросов о природе реальности, квантовая запутанность имеет важные приложения в квантовой криптографии. Она делает возможным перенос очень деликатной квантовой информации (например, квантового состояния электронов в атоме) из одного места в другое в процессе, называемом «квантовая телепортация», с важными приложениями в квантовой вычислительной технике. Оба этих приложения обсуждаются в разделе о квантовой информации.
Интерпретация квантового мира
Что же нам делать с этим странным квантовым миром? Как мы уже упомянули, в то время как математика квантовой теории хорошо понятна, эти странности привели к различным интерпретациям природы «реальности».
Вернемся к нашему атому, существующему в виде суперпозиции в коробке 1 и в коробке 2. Когда мы «смотрим» в коробки (например, направив свет внутрь и обнаружив свет, рассеянный атомом), мы всегда найдем один атом в коробке 1 или в коробке 2, но никогда в обоих, так как существует только один атом. Но что на самом деле представляет собой такое измерение? Существуют ли некоторые физические взаимодействия, с помощью которых измерительное устройство заставляет квантовую систему получать определенный результат (сильная версия того, что называется «Копенгагенская интерпретация», и интерпретация, лежащая в основе дискуссии в этой статье)? Или определенность — это иллюзия, а прибор и квантовая частица – лишь части большой квантовой системы, в которой реализуются все возможные результаты измерений? То есть, для каждого полученного результата в «параллельных реальностях» есть мириады копий измерительных приборов, получающих все возможные результаты («Многомировая интерпретация»)? Или сама непредсказуемость — это иллюзия, и квантовая теория может быть построена на каком-то скрытом основании, которое само по себе следует предсказуемой эволюции («Бомовская механика»)?
Ответы на эти вопросы об основах квантовой теории стали очень важными в контексте ряда фундаментальных проблем, имеющих многочисленные последствия. Например, поскольку очень ранняя Вселенная должна описываться как квантовая система, вопросы о основаниях квантовой теории становятся важными для понимании происхождения нашей Вселенной, то есть, для квантовой космологии. Более глубокое понимание оснований квантовой теории может помочь нам в решении одной из великих нерешенных проблем квантовой теории: Как включить в нее гравитацию и получить теорию квантовой гравитации?
Физики создали квантовую механику, чтобы описать законы мира, в котором живут микрообъекты. Но эти законы оказались настолько загадочны и контринтуитивны, что с некоторыми их аспектами учёные разбираются до сих пор. О свежих работах, посвящённых изучению явления квантовой суперпозиции, рассказывает кандидат физико-математических наук, старший научный сотрудник Института прикладной физики РАН, автор научно-популярного блога physh.ru Артём Коржиманов.
Квантовая суперпозиция — основа квантовой механики
Квантовая механика, зародившаяся в начале XX века и окончательно сформировавшаяся в 1930-х годах, сейчас является хорошо проверенной и чрезвычайно успешной физической теорией. Наша цивилизация немыслима без технических достижений, обязанных своим появлением именно ей. Достаточно упомянуть, что компьютер, ноутбук или смартфон, с помощью которых вы читаете этот текст, никогда бы не были созданы, если бы не было квантовой механики.
Учёным, правда, пришлось заплатить большую цену за эти достижения, поскольку принципы, заложенные в основу квантовой теории, настолько сильно противоречат нашей интуиции, что даже самые сильные умы человечества выбрасывали белый флаг в попытках дать им какое-либо истолкование, которое отличалось бы от знаменитой фразы, приписываемой то Ричарду Фейнману, то Дэвиду Мермину: «Заткнись и считай!».
Одним из таких парадоксальных принципов является принцип квантовой суперпозиции. Вообще, с принципом суперпозиции все мы хорошо знакомы, хотя, возможно, и не называем его так в обыденной жизни. Обычно под суперпозицией понимают простое наблюдение: если одно действие приводит к одному результату, а второе действие — ко второму, то их совместное действие даст оба результата. Например, если вы купите яблоко, и ваш друг купит яблоко, то вместе вы купите два яблока. Принцип суперпозиции, конечно, выполняется не всегда: если в магазине в продаже осталось только одно яблоко, то двух яблок вы с другом никогда не купите, хотя по отдельности купить яблоко могли бы.
Квантовая суперпозиция, однако, существенно отличается от суперпозиции классической. Речь в квантовой теории идёт о суперпозиции не действий, а состояний. Например, если у вас есть две коробки, то электрон может находиться как в одной из них, так и в другой, но кроме того, оказывается, что он может находиться в суперпозиции этих двух состояниях — то есть в некотором смысле — в обоих коробках одновременно. Этот факт, противоречащий всему нашему житейскому опыту, был неоднократно подтверждён в различных экспериментах, причём не только с электронами, но и с более крупными объектами, вплоть до вполне себе макроскопических сверхпроводящих металлических колец, в которых ток одновременно течёт как по часовой, так и против часовой стрелки.
Двухщелевой эксперимент
Классическим примером, демонстрирующим явление квантовой суперпозиции, является опыт с двумя щелями. Этот эксперимент имеет настолько большое значение для понимания квантовой механики, что известный физик Ричард Фейнман в своих не менее известных «Фейнмановских лекциях по физике» называет его явлением, «которое невозможно, совершенно, абсолютно невозможно объяснить классическим образом. В этом явлении таится самая суть квантовой механики».
Суть опыта относительно проста. Пусть имеется источник частиц — это могут быть частицы света фотоны, электроны, атомы, а недавно опыт был проведён и для молекул, — и этот источник освещает непрозрачную для частиц пластинку. В пластинке проделаны две тонкие щели, а сзади неё поставлен экран, на котором прилетевшие частицы оставляют следы. Если мы закроем одну из щелей, то увидим на экране более или менее тонкую полосу напротив второй щели. Если мы закроем вторую щель и откроем первую, результат будет тот же, но полоса появится напротив первой щели. Вопрос в том, что будет, если открыть обе щели одновременно?
Обыденная интуиция подсказывает, что в этом случае на экране мы увидим просто две полосы. Или, если щели расположены достаточно близко друг к другу, одна более толстая полоска, получившаяся просто наложением полос от каждой из щелей. Однако Томас Юнг, который первым осуществил этот эксперимент ещё в начале XIX века, с удивлением наблюдал совсем другую картину. На экране явственно виднелось множество полосок, толщина которых была меньше толщины полос, получавшихся изначально. Сейчас мы называем это интерференционной картиной, а сам эффект — интерференцией на двух щелях.
.Томас Юнг, однако, работал не с отдельными частицами, а с большим их количеством — с ярким источником света. Поэтому хотя его наблюдения и доказали, что свет — это волна, но истинного переворота в мировоззрении не произвели. Учёные просто стали описывать свет как волны. А для волн явление интерференции является естественным. Бросьте в воду два камушка, и вы увидите, что расходящиеся от них круги, пересекаясь, образуют довольно сложный узор, который и будет интерференционной картиной.
Переворот случился в начале XX века. Сначала в теоретических работах Макса Планка и Альберта Эйнштейна была введена гипотеза, что свет состоит из частиц, а затем британскому физику Джефри Инграму Тейлору удалось повторить опыт Юнга, но с настолько слабым источником света, что на экране можно было засечь приход отдельных фотонов. При этом интерференционная картина, получавшаяся после прихода большого количества фотонов, оставалась такой же, как у Юнга. Таким образом, оказалось, что свет вроде бы состоит из частиц, но эти частицы ведут себя как волны.
Ещё сильнее усложнило ситуацию то, что аналогичный эффект был предсказан и для электронов — частиц, от которых уж точно ожидать волновых свойств и явления интерференции не приходилось. И хотя аналог опыта Юнга для электронов был осуществлён только в 1961 году немецким физиком Клаусом Йонссоном, наличие у них волновых свойств было доказано другими методами ещё в 1920-х годах.
.Чтобы разрешить создавшееся противоречие, которое получило название корпускулярно-волнового дуализма, учёным пришлось предположить, что каждой частице соответствует некая волна — она получила название волновой функции, — которая зависит от того, в каком состоянии находится частица. Например, если частица прошла через одну щель, то это одно состояние и у него одна волновая функция, а если частица прошла через другую щель, то она находится в другом состоянии и у него другая волновая функция. Принцип квантовой суперпозиции при этом утверждает, что при двух открытых щелях частица находится в состоянии суперпозиции первого и второго состояний, и соответственно её волновая функция — это сумма двух волновых функций. Эта сумма и приводит к возникновению интерференционной картины. В этом смысле говорят, что частица проходит сразу через обе щели, поскольку если бы она проходила только через одну из них, то интерференционной картины бы не было.
Удивительно, но, несмотря на то, какую роль в квантовой физике играет двухщелевой эксперимент, многие учёные понимают его не совсем правильно. Более того, это некорректное объяснение присутствует в большинстве учебников по квантовой механике. Дело в том, что обычно явление суперпозиции в этом опыте объясняют так: волновая функция состояния, в котором находится электрон, прошедший через две щели, является суммой волновых функций состояний, в которых он находился бы, если бы одна из щелей была бы закрыта. Это объяснение, однако, не учитывает, что открывая вторую щель, мы можем изменить то, как электрон проходит через первую. Возвращаясь к примеру с яблоками, представьте, что вы покупаете яблоко на деньги, которые взяли в долг у друга, тогда покупка двух яблок уже не пройдёт так же, гладко, как покупка одним из вас одного яблока, потому что суммарных денег вам может и не хватить.
Трёхщелевой эксперимент: теория
Суть того, что происходит, когда открыто более одной щели, проще объяснить на примере опыта, в котором добавлена ещё одна щель. Кроме того, удобно перейти к альтернативному описанию квантовой физики, придуманному тем же Ричардом Фейнманом. В конце 1940-х годов он показал, что все результаты уже хорошо развитой тогда квантовой механики можно получить, не вводя никаких волновых функций, но предположив, что частица движется из одной точки в другую сразу по всем возможным траекториям, но «вес» каждой траектории, то есть её вклад в окончательный результат, различен и определяется по особым правилам.
Наибольшим весом обладают такие траектории, которые близки к классическим. Например, в случае двух щелей такие траектории показаны на рисунке ниже зелёным цветом.
R. Sawant et al., PRL 113, 120406 (2014)Но вклад дают и многие другие траектории, и даже такие экзотические, на которых частица часть пути движется назад, а не вперёд. Среди них есть и такие, которые войдя в одну из щелей, затем проходят через другую и выходят через третью, как это показано фиолетовым на рисунке ниже.
Sawant et al., PRL 113, 120406 (2014)Именно наличие таких неклассических траекторий и приводит к тому, что состояние частицы после прохода трёх щелей не равняется простой сумме состояний её прохода через каждую из них в отдельности при закрытых двух других. Отличие, конечно, обычно невелико, но, во-первых, оно может быть существенным, если вас интересуют какие-то слабые эффекты, а во-вторых, его можно усилить, прибегнув к специальным ухищрениям.
Первым на некорректность обычного объяснения принципа суперпозиции для двухщелевого эксперимента указал, по всей видимости, японский физик Х. Ябуки ещё в 1986 году, но его работа долгое время оставалась незамеченной. Современный интерес к этой теме возродила работа 2012 года, опубликованная в авторитетном журнале Physical Review A. В ней авторы рассмотрели случай классической волновой интерференции на трёх щелях на примере электромагнитных волн. Путём прямого численного моделирования фундаментальных для этой области уравнений Максвелла, они показали, что отличие правильного ответа от того, который получается при неправильной интерпретации принципа суперпозиции, в реалистичных условиях составляет около 0,5 %. И хотя эта величина невелика, и измерить её экспериментально пока невозможно, сам эффект является неоспоримым.
Но всё же учёным хотелось бы проверить этот факт и экспериментально, поэтому в 2014 и 2015 годах одна и та же группа учёных, возглавляемая физиком-женщиной из Индии Урбаси Синха, опубликовала две статьи в Physical Review Letters и Scientific Reports, в которых подробно рассмотрела квантовую теорию прохождения частиц через три щели и показала, что эффект несовпадения правильного результата с предсказанием неправильной интерпретации может быть заметно усилен, если проводить измерения с электромагнитными волнами не оптического диапазона, то есть светом, а микроволнового диапазона — такие волны используются, например, в бытовых микроволновых печах для разогрева пищи.
Трёхщелевой эксперимент: практика
Урбаси Синха, комментируя статью 2014 года, утверждала, что её группа уже начала эксперимент с микроволнами, но их результаты до сих пор не опубликованы. Зато совсем недавно вышла статья ещё одной группы учёных, возглавляемых известным физиком Робертом Бойдом (он знаменит, например, тем, что первым осуществил эксперимент с «замедленным» светом). Статья была опубликована в Nature Communications и экспериментально продемонстрировала обсуждаемый эффект. Правда, идея этого эксперимента была другой.
Роберт Бойд и его коллеги предложили усилить «вес» неклассических траекторий вблизи пластинки со щелями за счёт использования так называемых плазмонов. Плазмоны — это что-то вроде «фотонов на привязи», которые могут бегать только вдоль поверхности металла от одной щели к другой. Для этого пластинку со щелями сделали из золота. Золото — отличный проводник, поэтому оно создаёт особо сильные плазмоны.
В эксперименте источник света облучал только одну из трёх щелей. При этом если две другие были закрыты, то наблюдалась типичная картина немного размытой полосы напротив открытой щели. Но когда две другие щели открывались, картина кардинально отличалась: возникала типичная интерференционная картинка со значительно более узкими полосками.
Сравнение изображений на экране в случае, когда две щели из трёх закрыты (слева) и когда открыты все три щели (справа). O. S. Magaña-Loaiza et al., Nat. Commun. 7, 13987 (2016)Зачем нужны все эти тонкости?
Могут ли эти исследования иметь какое-то практическое значение? Авторы упомянутых работ надеются, что да. Явление квантовой суперпозиции широко используется для так называемой квантовой коммуникации. На её основе, например, работает квантовая криптография. Именно явление суперпозиции даёт неоспоримые преимущества квантовым компьютерам по сравнению с компьютерами, основанными на традиционной электронике. Поэтому в этих направлениях точное понимание того, как работает квантовая суперпозиция, чрезвычайно важно. И именно поэтому можно надеяться, что исследования интерференции на трёх щелях помогут придумать новые, более эффективные протоколы для работы квантовых устройств.
- Hans De Raedt, Kristel Michielsen, and Karl Hess, «Analysis of multipath interference in three-slit experiments» // Phys. Rev. A 85, 012101 (2012)
- Rahul Sawant, Joseph Samuel, Aninda Sinha, Supurna Sinha, and Urbasi Sinha, «Nonclassical Paths in Quantum Interference Experiments» // Phys. Rev. Lett. 113, 120406 (2014)
- Michael Schirber, «Curvy Photon Trajectories Could Be Detectable» // Physics 7, 96 (2014)
- Stuart Mason Dambrot, «Superposition revisited: Proposed resolution of double-slit experiment paradox using Feynman path integral formalism» // phys.org (2014-10-02)
- Hamish Johnston, «Photons weave their way through a triple slit» // PhysicsWorld (2014-09-25)
- Aninda Sinha, Aravind H. Vijay & Urbasi Sinha, «On the superposition principle in interference experiments» // Scientific Reports 5, 10304 (2015)
- Omar S Magaña-Loaiza, Israel De Leon, Mohammad Mirhosseini, Robert Fickler, Akbar Safari, Uwe Mick, Brian McIntyre, Peter Banzer, Brandon Rodenburg, Gerd Leuchs & Robert W. Boyd, «Exotic looped trajectories of photons in three-slit interference» // Nature Communications 7, 13987 (2016)
- Lisa Zyga, «Physicists detect exotic looped trajectories of light in three-slit experiment» // phys.org
К своему стыду хочу признаться, что слышал это выражение, но не знал вообще что оно означает и хотя бы по какой теме употребляется. Давайте я вам расскажу, что вычитал в интернете про этого кота …-
«Кот Шредингера » – так называется знаменитый мысленный эксперимент знаменитого австрийского физика-теоретика Эрвина Шредингера, который также является лауреатом Нобелевской премии. С помощью этого вымышленного опыта ученый хотел показать неполноту квантовой механики при переходе от субатомных систем к макроскопическим системам.
Оригинальная статья Эрвина Шредингера вышла в свет 1935 году. В ней эксперимент был описан с использованием или даже олицетворение:
Можно построить и случаи, в которых довольно бурлеска. Пусть какой-нибудь кот заперт в стальной камере вместе со следующей дьявольской машиной (которая должна быть независимо от вмешательства кота): внутри счётчика Гейгера находится крохотное количество радиоактивного вещества, столь небольшое, что в течение часа может распасться только один атом, но с такой же вероятностью может и не распасться- если же это случится, считывающая трубка разряжается и срабатывает реле, спускающее молот, который разбивает колбочку с синильной кислотой.
Если на час предоставить всю эту систему самой себе, то можно сказать, что кот будет жив по истечении этого времени, коль скоро распада атома не произойдёт. Первый же распад атома отравил бы кота. Пси-функция системы в целом будет выражать это, смешивая в себе или размазывая живого и мёртвого кота (простите за выражение) в равных долях. Типичным в подобных случаях является то, что неопределённость, первоначально ограниченная атомным миром, преобразуется в макроскопическую неопределённость, которая может быть устранена путём прямого наблюдения. Это мешает нам наивно принять «модель размытия» как отражающую действительность. Само по себе это не означает ничего неясного или противоречивого. Есть разница между нечётким или расфокусированным фото и снимком облаков или тумана.
Другими словами:
- Есть ящик и кот. В ящике имеется механизм, содержащий радиоактивное атомное ядро и ёмкость с ядовитым газом. Параметры эксперимента подобраны так, что вероятность распада ядра за 1 час составляет 50%. Если ядро распадается, открывается ёмкость с газом и кот погибает. Если распада ядра не происходит — кот остается жив-здоров.
- Закрываем кота в ящик, ждём час и задаёмся вопросом: жив ли кот или мертв?
- Квантовая же механика как бы говорит нам, что атомное ядро (а следовательно и кот) находится во всех возможных состояниях одновременно (см. квантовая суперпозиция). До того как мы открыли ящик, система «кот-ядро» находится в состоянии «ядро распалось, кот мёртв» с вероятностью 50% и в состоянии «ядро не распалось, кот жив» с вероятностью 50%. Получается, что кот, сидящий в ящике, и жив, и мёртв одновременно.
- Согласно современной копенгагенской интерпретации, кот-таки жив/мёртв без всяких промежуточных состояний. А выбор состояния распада ядра происходит не в момент открытия ящика, а ещё когда ядро попадает в детектор. Потому что редукция волновой функции системы «кот-детектор-ядро» не связана с человеком-наблюдателем ящика, а связана с детектором-наблюдателем ядра.
Согласно квантовой механике, если над ядром атома не производится наблюдение, то его состояние описывается смешением двух состояний — распавшегося ядра и нераспавшегося ядра, следовательно, кот, сидящий в ящике и олицетворяющий ядро атома, и жив, и мёртв одновременно. Если же ящик открыть, то экспериментатор может увидеть только какое-нибудь одно конкретное состояние — «ядро распалось, кот мёртв» или «ядро не распалось, кот жив».
Суть человеческим языком: эксперимент Шредингера показал, что, с точки зрения квантовой механики, кот одновременно и жив, и мертв, чего быть не может. Следовательно, квантовая механика имеет существенные изъяны.
Вопрос стоит так: когда система перестаёт существовать как смешение двух состояний и выбирает одно конкретное? Цель эксперимента — показать, что квантовая механика неполна без некоторых правил, которые указывают, при каких условиях происходит коллапс волновой функции, и кот либо становится мёртвым, либо остаётся живым, но перестаёт быть смешением того и другого. Поскольку ясно, что кот обязательно должен быть либо живым, либо мёртвым (не существует состояния, промежуточного между жизнью и смертью), то это будет аналогично и для атомного ядра. Оно обязательно должно быть либо распавшимся, либо нераспавшимся ().
Еще одной наиболее свежей интерпретацией мысленного эксперимента Шредингера является рассказ Шелдона Купера, героя сериала «Теория большого взрыва» («Big Bang Theory»), который он произнес для менее образованной соседки Пенни. Суть рассказа Шелдона заключается в том, что концепция кота Шредингера может быть применена в отношениях между людьми. Для того чтобы понять, что происходит между мужчиной и женщиной, какие отношения между ними: хорошие или плохие, – нужно просто открыть ящик. А до этого отношения являются одновременно и хорошими, и плохими.
Ниже приведен видеофрагмент этого диалога «Теории большого взрыва» между Шелдоном и Пении.
Иллюстрация Шрёдингера является наилучшим примером для описания главного парадокса квантовой физики: согласно её законам, частицы, такие как электроны, фотоны и даже атомы существуют в двух состояниях одновременно («-живых»- и «-мёртвых»-, если вспоминать многострадального кота). Эти состояния называются .
Американский физик Арт Хобсон () из университета Арканзаса (Arkansas State University) предложил своё решение данного парадокса.
«-Измерения в квантовой физике базируются на работе неких макроскопических устройств, таких как счётчик Гейгера, при помощи которых определяется квантовое состояние микроскопических систем — атомов, фотонов и электронов. Квантовая теория подразумевает, что если вы подсоедините микроскопическую систему (частицу) к некому макроскопическому устройству, различающему два разных состояния системы, то прибор (счётчик Гейгера, например) перейдёт в состояние квантовой запутанности и тоже окажется одновременно в двух суперпозициях. Однако невозможно наблюдать это явление непосредственно, что делает его неприемлемым»-, — рассказывает физик.
Хобсон говорит, что в парадоксе Шрёдингера кот играет роль макроскопического прибора, счётчика Гейгера, подсоединённого к радиоактивному ядру, для определения состояния распада или «-нераспада»- этого ядра. В таком случае, живой кот будет индикатором «-нераспада»-, а мёртвый кот — показателем распада. Но согласно квантовой теории, кот, так же как и ядро, должен пребывать в двух суперпозициях жизни и смерти.
Вместо этого, по словам физика, квантовое состояние кота должно быть запутанным с состоянием атома, что означает что они пребывают в «-нелокальной связи»- друг с другом. То есть, если состояние одного из запутанных объектов внезапно сменится на противоположное, то состояние его пары точно также поменяется, на каком бы расстоянии друг от друга они ни находились. При этом Хобсон ссылается на этой квантовой теории.
«-Самое интересное в теории квантовой запутанности — это то, что смена состояния обеих частиц происходит мгновенно: никакой свет или электромагнитный сигнал не успел бы передать информацию от одной системы к другой. Таким образом, можно сказать, что это один объект, разделённый на две части пространством, и неважно, как велико расстояние между ними»-, — поясняет Хобсон.
Кот Шрёдингера больше не живой и мёртвый одновременно. Он мёртв, если произойдёт распад, и жив, если распад так и не случится.
Добавим, что похожие варианты решения этого парадокса были предложены ещё тремя группами учёных за последние тридцать лет, однако они не были восприняты всерьёз и так и остались незамеченными в широких научных кругах. Хобсон , что решение парадоксов квантовой механики, хотя бы теоретические, совершенно необходимы для её глубинного понимания.
Шредингер
А вот совсем недавно ТЕОРЕТИКИ ОБЪЯСНИЛИ, КАК ГРАВИТАЦИЯ УБИВАЕТ КОТА ШРЁДИНГЕРА, но это уже сложнее …-
Как правило, физики объясняют феномен того, что суперпозиция возможна в мире частиц, но невозможна с котами или другими макрообъектами, помехами от окружающей среды. Когда квантовый объект проходит сквозь поле или взаимодействует со случайными частицами, он тут же принимает всего одно состояние — как если бы его измерили. Именно так и разрушается суперпозиция, как полагали учёные.
Но даже если каким-либо образом стало возможным изолировать макрообъект, находящийся в состоянии суперпозиции, от взаимодействий с другими частицами и полями, то он всё равно рано или поздно принял бы одно-единственное состояние. По крайней мере, это верно для процессов, протекающих на поверхности Земли.
«-Где-то в межзвёздном пространстве, может быть, кот и имел бы шанс , но на Земле или вблизи любой планеты это крайне маловероятно. И причина тому — гравитация»-, — поясняет ведущий автор нового исследования Игорь Пиковский () из Гарвард-Смитсоновского центра астрофизики.
Пиковский и его коллеги из Венского университета утверждают, что гравитация оказывает разрушительное воздействие на квантовые суперпозиции макрообъектов, и потому мы не наблюдаем подобных явлений в макромире. Базовая концепция новой гипотезы, к слову, в художественном фильме «-Интерстеллар»-.
Эйнштейновская общая теория относительности гласит, что чрезвычайно массивный объект будет искривлять вблизи себя пространство-время. Рассматривая ситуацию на более мелком уровне, можно сказать, что для молекулы, помещённой у поверхности Земли, время будет идти несколько медленнее, чем для той, что находится на орбите нашей планеты.
Из-за влияния гравитации на пространство-время молекула, попавшая под это влияние, испытает отклонение в своём положении. А это, в свою очередь, должно повлиять и на её внутреннюю энергию — колебания частиц в молекуле, которые изменяются с течением времени. Если молекулу ввести в состояние квантовой суперпозиции двух локаций, то соотношение между положением и внутренней энергией вскоре заставило бы молекулу «-выбрать»- только одну из двух позиций в пространстве.
«-В большинстве случаев явление декогеренции связано с внешним влиянием, но в данном случае внутреннее колебание частиц взаимодействует с движением самой молекулы»-, — поясняет Пиковский.
Этот эффект пока что никто не наблюдал, поскольку другие источники декогеренции, такие как магнитные поля, тепловое излучение и вибрации, как правило, гораздо сильнее, и вызывают разрушение квантовых систем задолго до того, как это сделает гравитация. Но экспериментаторы стремятся проверить высказанную гипотезу.
Подобная установка также может быть использована для проверки способности гравитации разрушать квантовые системы. Для этого необходимо будет сравнить вертикальный и горизонтальный интерферометры: в первом суперпозиция должна будет вскоре исчезнуть из-за растяжения времени на разных «-высотах»- пути, тогда как во втором квантовая суперпозиция может и сохраниться.
источники
http://4brain.ru/blog/%D0%BA%D0%BE%D1%82-%D1%88%D1%80%D0%B5%D0%B4%D0%B8%D0%BD%D0%B3%D0%B5%D1%80%D0%B0-%D1%81%D1%83%D1%82%D1%8C-%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%8B%D0%BC%D0%B8-%D1%81%D0%BB%D0%BE%D0%B2%D0%B0%D0%BC%D0%B8/
http://www.vesti.ru/doc.html?id=2632838
Вот еще немного околонаучного: вот например , а вот . Если вы еще не в курсе, почитайте про и что такое . А и узнаем, что за
| Адроны | msimagelist>|
| Альфа-распад | msimagelist>|
| Альфа-частица | msimagelist>|
| Аннигиляция | msimagelist>|
| Антивещество | msimagelist>|
| Антинейтрон | msimagelist>|
| Антипротон | msimagelist>|
| Античастицы | msimagelist>|
| Атом | msimagelist>|
| Атомная единица массы | msimagelist>|
| Атомная электростанция | msimagelist>|
| Барионное число | msimagelist>|
| Барионы | msimagelist>|
| Бета-распад | msimagelist>|
| Бетатрон | msimagelist>|
| Бета-частицы | msimagelist>|
| Бозе – Эйнштейна статистика | msimagelist>|
| Бозоны | msimagelist>|
| Большой адронный коллайдер | msimagelist>|
| Большой Взрыв | msimagelist>|
| Боттом. Боттомоний | msimagelist>|
| Брейта-Вигнера формула | msimagelist>|
| Быстрота | msimagelist>|
| Векторная доминантность | msimagelist>|
| Великое объединение | msimagelist>|
| Взаимодействие частиц | msimagelist>|
| Вильсона камера | msimagelist>|
| Виртуальные частицы | msimagelist>|
| Водорода атом | msimagelist>|
| Возбуждённые состояния ядер | msimagelist>|
| Волновая функция | msimagelist>|
| Волновое уравнение | msimagelist>|
| Волны де Бройля | msimagelist>|
| Встречные пучки | msimagelist>|
| Гамильтониан | msimagelist>|
| Гамма-излучение | msimagelist>|
| Гамма-квант | msimagelist>|
| Гамма-спектрометр | msimagelist>|
| Гамма-спектроскопия | msimagelist>|
| Гаусса распределение | msimagelist>|
| Гейгера счётчик | msimagelist>|
| Гигантский дипольный резонанс | msimagelist>|
| Гиперядра | msimagelist>|
| Глюоны | msimagelist>|
| Годоскоп | msimagelist>|
| Гравитационное взаимодействие | msimagelist>|
| Дейтрон | msimagelist>|
| Деление атомных ядер | msimagelist>|
| Детекторы частиц | msimagelist>|
| Дирака уравнение | msimagelist>|
| Дифракция частиц | msimagelist>|
| Доза излучения | msimagelist>|
| Дозиметр | msimagelist>|
| Доплера эффект | msimagelist>|
| Единая теория поля | msimagelist>|
| Зарядовое сопряжение | msimagelist>|
| Зеркальные ядра | msimagelist>|
| Избыток массы (дефект массы) | msimagelist>|
| Изобары | msimagelist>|
| Изомерия ядерная | msimagelist>|
| Изоспин | msimagelist>|
| Изоспиновый мультиплет | msimagelist>|
| Изотопов разделение | msimagelist>|
| Изотопы | msimagelist>|
| Ионизирующее излучение | msimagelist>|
| Искровая камера | msimagelist>|
| Квантовая механика | msimagelist>|
| Квантовая теория поля | msimagelist>|
| Квантовые операторы | msimagelist>|
| Квантовые числа | msimagelist>|
| Квантовый переход | msimagelist>|
| Квант света | msimagelist>|
| Кварк-глюонная плазма | msimagelist>|
| Кварки | msimagelist>|
| Коллайдер | msimagelist>|
| Комбинированная инверсия | msimagelist>|
| Комптона эффект | msimagelist>|
| Комптоновская длина волны | msimagelist>|
| Конверсия внутренняя | msimagelist>|
| Константы связи | msimagelist>|
| Конфайнмент | msimagelist>|
| Корпускулярно волновой дуализм | msimagelist>|
| Космические лучи | msimagelist>|
| Критическая масса | msimagelist>|
| Лептоны | msimagelist>|
| Линейные ускорители | msimagelist>|
| Лоренца преобразования | msimagelist>|
| Лоренца сила | msimagelist>|
| Магические ядра | msimagelist>|
| Магнитный дипольный момент ядра | msimagelist>|
| Магнитный спектрометр | msimagelist>|
| Максвелла уравнения | msimagelist>|
| Масса частицы | msimagelist>|
| Масс-спектрометр | msimagelist>|
| Массовое число | msimagelist>|
| Масштабная инвариантность | msimagelist>|
| Мезоны | msimagelist>|
| Мессбауэра эффект | msimagelist>|
| Меченые атомы | msimagelist>|
| Микротрон | msimagelist>|
| Нейтрино | msimagelist>|
| Нейтрон | msimagelist>|
| Нейтронная звезда | msimagelist>|
| Нейтронная физика | msimagelist>|
| Неопределённостей соотношения | msimagelist>|
| Нормы радиационной безопасности | msimagelist>|
| Нуклеосинтез | msimagelist>|
| Нуклид | msimagelist>|
| Нуклон | msimagelist>|
| Обращение времени | msimagelist>|
| Орбитальный момент | msimagelist>|
| Осциллятор | msimagelist>|
| Отбора правила | msimagelist>|
| Пар образование | msimagelist>|
| Период полураспада | msimagelist>|
| Планка постоянная | msimagelist>|
| Планка формула | msimagelist>|
| Позитрон | msimagelist>|
| Поляризация | msimagelist>|
| Поляризация вакуума | msimagelist>|
| Потенциальная яма | msimagelist>|
| Потенциальный барьер | msimagelist>|
| Принцип Паули | msimagelist>|
| Принцип суперпозиции | msimagelist>|
| Промежуточные W-, Z-бозоны | msimagelist>|
| Пропагатор | msimagelist>|
| Пропорциональный счётчик | msimagelist>|
| Пространственная инверсия | msimagelist>|
| Пространственная четность | msimagelist>|
| Протон | msimagelist>|
| Пуассона распределение | msimagelist>|
| Пузырьковая камера | msimagelist>|
| Радиационный фон | msimagelist>|
| Радиоактивность | msimagelist>|
| Радиоактивные семейства | msimagelist>|
| Радиометрия | msimagelist>|
| Расходимости | msimagelist>|
| Резерфорда опыт | msimagelist>|
| Резонансы (резонансные частицы) | msimagelist>|
| Реликтовое микроволновое излучение | msimagelist>|
| Светимость ускорителя | msimagelist>|
| Сечение эффективное | msimagelist>|
| Сильное взаимодействие | msimagelist>|
| Синтеза реакции | msimagelist>|
| Синхротрон | msimagelist>|
| Синхрофазотрон | msimagelist>|
| Синхроциклотрон | msimagelist>|
| Система единиц измерений | msimagelist>|
| Слабое взаимодействие | msimagelist>|
| Солнечные нейтрино | msimagelist>|
| Сохранения законы | msimagelist>|
| Спаривания эффект | msimagelist>|
| Спин | msimagelist>|
| Спин-орбитальное взаимодействие | msimagelist>|
| Спиральность | msimagelist>|
| Стандартная модель | msimagelist>|
| Статистика | msimagelist>|
| Странные частицы | msimagelist>|
| Струи адронные | msimagelist>|
| Субатомные частицы | msimagelist>|
| Суперсимметрия | msimagelist>|
| Сферическая система координат | msimagelist>|
| Тёмная материя | msimagelist>|
| Термоядерные реакции | msimagelist>|
| Термоядерный реактор | msimagelist>|
| Тормозное излучение | msimagelist>|
| Трансурановые элементы | msimagelist>|
| Трек | msimagelist>|
| Туннельный эффект | msimagelist>|
| Ускорители заряженных частиц | msimagelist>|
| Фазотрон | msimagelist>|
| Фейнмана диаграммы | msimagelist>|
| Фермионы | msimagelist>|
| Формфактор | msimagelist>|
| Фотон | msimagelist>|
| Фотоэффект | msimagelist>|
| Фундаментальная длина | msimagelist>|
| Хиггса бозон | msimagelist>|
| Цвет | msimagelist>|
| Цепные ядерные реакции | msimagelist>|
| Цикл CNO | msimagelist>|
| Циклические ускорители | msimagelist>|
| Циклотрон | msimagelist>|
| Чарм. Чармоний | msimagelist>|
| Черенковский счётчик | msimagelist>|
| Черенковсое излучение | msimagelist>|
| Черные дыры | msimagelist>|
| Шредингера уравнение | msimagelist>|
| Электрический квадрупольный момент ядра | msimagelist>|
| Электромагнитное взаимодействие | msimagelist>|
| Электрон | msimagelist>|
| Электрослабое взаимодействие | msimagelist>|
| Элементарные частицы | msimagelist>|
| Ядерная физика | msimagelist>|
| Ядерная энергия | msimagelist>|
| Ядерные модели | msimagelist>|
| Ядерные реакции | msimagelist>|
| Ядерный взрыв | msimagelist>|
| Ядерный реактор | msimagelist>|
| Ядра энергия связи | msimagelist>|
| Ядро атомное | msimagelist>|
| Ядерный магнитный резонанс (ЯМР) | msimagelist>
Общие сведения о квантовых вычислениях — Azure Quantum
- Чтение занимает 4 мин
В этой статье
В квантовых вычислениях для обработки информации используются принципы квантовой механики. По этой причине для них требуется иной подход, чем для традиционных вычислений. Одним из примеров такого отличия является используемый в квантовых компьютерах процессор. Классические компьютеры используют знакомые нам кремниевые микросхемы, а квантовые компьютеры — квантовые системы на основе атомов, ионов, фотонов или электронов. Они используют их квантовые свойства для представления бит, которые могут иметь одно из состояний в квантовой суперпозиции: 1 или 0.
Эти квантовые материалы ведут себя в соответствии с законами квантовой механики. Их поведение описывают такие понятия, как вероятностные вычисления, суперпозиция и запутанность. Эти понятия, в свою очередь, являются основой квантовых алгоритмов, которые позволяют использовать возможности квантовых вычислений для решения сложных задач. В этой статье описываются некоторые основные понятия квантовой механики, лежащие в основе квантовых вычислений.
Общие сведения о квантовой механике
Квантовая механика (или квантовая теория) — это раздел физики, изучающий частицы на атомном и субатомном уровнях. При этом многие законы традиционной механики не применяются на квантовом уровне. В основе квантовых вычислений лежат три явления — суперпозиция, квантовое измерение и запутанность.
Суперпозиция и двоичные вычисления
Представьте, что вы тренируетесь у себя в комнате. Вы выполняете полный поворот налево, а затем полный поворот направо. Теперь попробуйте повернуться одновременно и налево, и направо. Вы не можете это сделать (по крайней мере таким образом, чтобы не разорваться на две части). Очевидно, что вы не можете находиться в обоих этих состояниях одновременно, то есть вы не можете смотреть налево и направо одновременно.
Но если бы вы были квантовой частицей, то у вас была бы определенная вероятность выполнить поворот налево И определенная вероятность выполнить поворот направо. Это возможно благодаря явлению, которое называется суперпозицией (или когерентностью).
Квантовая частица, в частности электрон, имеет собственные свойства поворота налево или направо, например спин, ориентированный вверх или вниз, или, оперируя более традиционными понятиями бинарных вычислений, значение 1 или 0. Когда квантовая частица находится в состоянии суперпозиции, это линейная комбинация бесконечного числа состояний между 1 до 0. Но вы не знаете, в каком именно состоянии она находится, пока не посмотрите на нее. здесь мы переходим к следующему явлению — квантовому измерению.
Квантовое измерение
Теперь представим, что к вам пришел друг, который хочет сфотографировать вас во время тренировки. Скорее всего, он получит ваше размытое изображение во время поворота — где-то между крайней левой и правой точками.
Но если бы вы были квантовой частицей, произошло бы нечто интересное. Независимо от вашего реального положения, на снимке вы будете изображены так, будто выполнили полный левый или правый поворот.
Так происходит потому, что процесс наблюдения или измерения квантовой частицы приводит к коллапсу состояния суперпозиции (происходит декогеренция), и частица переходит в классическое бинарное состояние: 1 или 0.
Это бинарное состояние удобно для нас, так как компьютеры могут выполнять множество операций со значениями 1 и 0. При этом когда квантовая частица измеряется и коллапсирует, она навсегда (как и вы на фотографии) остается в этом состоянии, определяемым значением 1 или 0. Тем не менее, как вы увидите позже, в квантовых вычислениях существуют операции, которые могут вернуть частицу обратно в состояние суперпозиции, чтобы ее можно было снова использовать для квантовых вычислений.
Запутанность
Возможно, наиболее интересным явлением квантовой механики является способность двух или более квантовых частиц запутываться друг с другом. Когда частицы запутываются, они образуют единую систему, и квантовое состояние любой из них не может быть описано независимо от квантового состояния других частиц. Это означает, что любая операция или процесс, который вы применяете к одной частице, влияет и на другие частицы.
Наряду с этой взаимозависимостью частицы могут поддерживать связь, даже будучи разделенными на невероятно большие расстояния (вплоть до таких, которые измеряются световыми годами). Эффекты квантового измерения также применимы к запутанным частицам, поэтому, когда одна частица измеряется и коллапсирует, другая тоже коллапсирует. Так как между запутанными кубитами существует корреляция, при измерении состояния одного кубита можно получить сведения о состоянии другого. Это свойство очень полезно в квантовых вычислениях.
Кубиты и вероятность
Обычные компьютеры хранят и обрабатывают информацию в битах, которые могут иметь состояние, определяемое значением 1 или 0, но не обеими значениями одновременно. Эквивалентом этому в квантовых вычислениях является кубит, который представляет состояние квантовой частицы. Из-за суперпозиции кубиты могут иметь значение 1 либо 0 или промежуточное значение. В зависимости от конфигурации, кубит имеет определенную вероятность сколлапсировать до 1 или 0. Эта вероятность коллапса в одно или другое состояние определяется квантовой интерференцией.
Помните друга, который вас фотографировал? Предположим, у него есть специальные фильтры на камере, называемые интерференционными. Если выбрать фильтр 70/30 и начать фотографировать, на 70 % снимков вы будете смотреть налево, а на 30 % — направо. Фильтр изменил обычное состояние камеры, чтобы повлиять на вероятность, определяющую ее поведение.
Аналогичным образом квантовая интерференция воздействует на состояние кубита, чтобы повлиять на вероятность получения определенного результата во время измерения. Этот вероятностный характер и делает квантовые вычисления такими мощными.
Например, мы можем взять два бита, лежащих в основе обычных вычислений. Каждый из них может принимать значение 1 или 0, следовательно, всего вы можете хранить четыре возможных значения: 00, 01, 10 и 11. При этом в определенный момент времени доступно только одно такое значение. Но при наличии двух кубитов в суперпозиции каждый из них может иметь значение 1, 0 или оба эти значения, поэтому вы можете получить те же самые четыре значения одновременно. С тремя кубитами вы получаете восемь значений, с четырьмя кубитами — 16 значений и т. д.
Сводка
Эти важные фундаментальные понятия описывают квантовую механику очень поверхностно. Но они лежат в основе квантовых вычислений.
- Суперпозиция — способность квантовых частиц представлять комбинацию всех возможных состояний.
- Квантовое измерение — процесс наблюдения за квантовыми частицами в суперпозиции, что приводит к переходу в одно из возможных состояний.
- Запутанность — взаимозависимость квантовых частиц, когда результаты измерения одних частиц влияют на состояние других.
- Кубит — базовая единица информации в квантовых вычислениях. Кубит — это квантовая частица, которая находится в суперпозиции всех возможных состояний.
- Интерференция — внутреннее поведение кубита, обусловленное суперпозицией, которое влияет на вероятность его коллапса в одно из состояний.
Next Steps
Квантовые компьютеры и квантовые симуляторы
Суперпозиция состояний (квантовая или когерентная суперпозиция) | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Тема: Квантовая механика
Вероятностный характер предсказаний квантовой механики заставил по-новому взглянуть на проблему детерминизма. Классическая физика исходила из представления о том, что состояние мира в настоящий момент определяет его состояние в следующий, так что будущее полностью детерминировано (предопределено). С таким детерминизмом связаны трудности философского порядка, он, в частности, противоречит представлениям о свободе воли человека. Это сложная проблема, и квантовая теория осветила ее с неожиданной стороны.
Волновые свойства присущи не только каким-то специальным частицам микромира. Это свойство всех частиц. Летящая пуля также обладает волновыми свойствами. Но соответствующая пуле длина волны настолько мала, что ее волновые свойства практически не проявляются (длины волн света также сравнительно малы, и волновые свойства света долго не обнаруживались).
Структура уравнения Шредингера, из которого находится волновая функция, такова, что, если две функции ψ1, ψ2удовлетворяют уравнению, их линейная суперпозиция, т. е. функция вида α1ψ1 + α2ψ2, где α 1, α 2 — константы, также удовлетворяет уравнению и представляет, таким образом, возможное состояние частицы. Это математический факт. Но его физическим следствием является одно из самых поразительных свойств квантовомеханических систем:
состояние системы может быть суперпозицией двух или вообще любого числа других состояний.
Что это означает физически?
Одно из решений уравнения Шредингера для свободной частицы — волновая функция в виде плоской волны с определенной частотой. В этом состоянии измерение импульса частицы с вероятностью, равной единице, даст величину p = h / λ. Материал с сайта http://worldofschool.ru
Состояние частицы в классической механике задается ее координатами и импульсом. Остальные характеристики частицы (момент импульса, кинетическая энергия) однозначно определяются координатами и импульсом и могут быть найдены. Второй закон Ньютона позволяет определить изменение состояния во времени при заданных условиях, и состояние частицы в каждый момент времени вполне определенно. В рамках классической механики суперпозиция состояний — лишенное смысла словосочетание. То, что в квантовой теории эти слова имеют смысл, связано с тем, что смысл понятия «состояние» в классической и квантовой теориях различный.
На этой странице материал по темам:Принцип суперпозиции квантовых состояний шпаргалка
Квантовая суперпозиция формула
Φuωkα: км
#φuωkα
Спин электрона — это векторная величина. Он характеризуется направлением, как, например, скорость. Как и скорость, его можно разложить на составляющие по некоторому базису (системе координат). Только в отличие от скорости длина вектора спина всегда равна одному и тому же значению, условной единице.
Например, если ракета летит под углом 45° к земле со скоростью 1 км/с, мы можем измерить её горизонтальную и вертикальную скорости, обе получатся равны 1/√2 км/с. В принципе, то же можно проделать и со спином. Например, пусть спин электрона направлен так же под углом 45°. Мы можем измерить его в горизонтальном направлении. Он получится равен 1/√2. Стоп, нет! Это невозможно, спин не может быть дробным.
Что же тогда мы получим при измерении? Оказывается, для разных электронов мы получим разный результат. Для одних измеренный спин будет направлен вправо (засчитаем его как +1), для других — влево (засчитаем его как -1). Но что интересно — если мы возьмём среднее арифметическое по результатам измерений многих электронов, мы как раз и получим примерно 1/√2.
То же самое будет для других направлений. Если ракета летит вертикально вверх, её горизонтальная скорость равна нулю. Если спин измеряемых электронов направлен вертикально вверх, то их измеренный горизонтальный спин в среднем будет тоже равен нулю, хотя для каждого отдельного электрона мы получим +1 или -1 с вероятностью 50%.
Возникает вопрос, «знает» ли электрон заранее свой спин по каждому направлению или он генерируется случайным образом в момент измерения? В первом случае результат измерения детерминирован неким внутренним состоянием электрона, которое нам неизвестно, но тем не менее присутствует внутри. Во втором случае никакого такого внутреннего состояния нет, а результат измерения истинно случаен.
В этом и заключался спор Эйнштейна и Бора. Эйнштейн выступал за первый вариант, Бор — за второй. И никто из них не надеялся, что спор можно будет разрешить экспериментально. В самом деле, как можно проверить, есть ли у электрона внутреннее ненаблюдаемое состояние? Но вот пришёл Белл и объяснил, что можно. К сожалению, ни Эйнштейн, ни Бор до этого не дожили.
Интересно, что для понимания неравенств Белла не требуется знания сложной математики. Достаточно элементарной теории множеств. Но почему-то в интернете почти нет доступных объяснений. Попробуем этот пробел исправить.
Сначала предположим, что прав Эйнштейн. Спин по каждому направлению уже заранее содержится внутри электрона. При измерении мы просто его узнаём.
Возьмём пачку электронов и измерим спин каждого из них по двум перпендикулярным направлениям A и C. Предсказания квантовой теории нам говорят, что измерения совпадут в 50% случаев. То есть из всех электронов, у которых внутри скрыт спин A+, половина внутри должны иметь спин C+, а вторая половина C-. И наоборот — из C+ электронов половина должна быть A+, а половина A-. Заметим, что это возможно, только когда количество A+ и C+ электронов одинаково.
Такую конфигурацию легко представить при помощи кругов Эйлера (на самом деле диаграмм Венна), Вот, например, для случая, когда A+ и C+ электронов по 8 штук:
Теперь изменим угол и будем измерять спин по направлениям A и B, под 45° друг к другу. Если у нас линейная зависимость вероятности от угла, то мы получим 75% совпадений. Заметим, что снова количество A+ и B+ электронов должно совпадать, чтобы процент работал в обе стороны.
Теперь возьмём направления B и C. Поскольку между ними у нас тоже 45°, то и по ним мы должны получить 75% совпадений. И количество B+ и C+ тоже должно совпадать. В кругах Эйлера это будет выглядеть так:
Теперь важный момент. Если вдруг зависимость от угла у нас нелинейная, то вместо 75% мы получим какой-нибудь другой процент. Но он не может превышать 75%. Это видно по картинке. Если пересечение A+ и C+ составляет половину от B+, то B+ может дополнительно содержать только ещё четверть от A+ и четверть от C+, никак не больше.
То есть 75% — это максимально допустимый процент совпадений под 45° в модели Эйнштейна, когда спин по всем направлениям задан заранее. Для большего процента вы не сможете подобрать скрытые параметры электронов в выборке так, чтобы выполнялись все указанные выше соотношения. Такого множества просто не существует.
Ну и что вы думаете? Квантовая механика требует, чтобы этот процент был больше 75%, а именно в районе 85%.
Это легко посчитать. Помните, мы говорили, что среднее арифметическое спина, измеренного под 45° к исходному, должно равняться 1/√2? Подставим это число в формулу матожидания и найдём вероятность p:
p * (+1) + (1 — p) * (-1) = 1/√2
2p — 1 = 1/√2
p = (1 + 1/√2) / 2 = 0.8535…
Зависимость от угла тут не линейная, а косинусная, т. к. 1/√2 в данном случае — это не что иное как cos 45°.
Так что вы не сможете подобрать такое множество электронов со скрытыми спинами, чтобы в нём A+ электроны пересекались с B+ на 85%, B+ с C+ — тоже на 85%, но при этом A+ с C+ — на 50%. У вас обязательно где-нибудь не сойдётся.
Что говорит о том, что теория скрытых параметров неверна, электрон не содержит внутри информацию о своих спинах по всем направлениям, а при измерении получается по-настоящему случайный результат. И прав был Бор, а не Эйнштейн.
Тут внимательный читатель наверное уже извёлся, доказывая мне, что так не работает. Ведь если мы измеряем один электрон по разным направлениям, то ведь каждое измерение влияет на состояние электрона и может изменять его скрытые параметры. А мы почему-то предполагаем, что они остаются неизменными. Так что наше доказательство — не доказательство.
Совершенно верно, в таком виде — не доказательство. Поэтому вместо последовательных измерений одного электрона производят параллельные измерения на паре спутанных электронов, спин которых всегда противоположен друг другу. Например, один электрон измеряют по направлению A, другой — по направлению B и т. д.
Для каждой пары спутанных электронов выбирают случайную пару направлений — AB, AC или BC, а затем усредняют цифры по каждой паре направлений. Электроны предварительно разносятся на приличное расстояние, а измерения делаются одновременно, чтобы убедиться, что один электрон не успел передать другому информацию со скоростью света.
Проведённые многочисленные эксперименты все подтвердили правильность предсказаний квантовой теории, поэтому либо электроны не содержат скрытых параметров, либо они общаются быстрее скорости света. Вторая опция (сверхсветовое влияние), кстати, тоже допустима, и в частности она используется в теории волны-пилота. Так что не надо забывать, что Белл отменил скрытые параметры не совсем, а только при отсутствии сверхсветового взаимодействия.
P. S. Идею объяснения теоремы Белла я взял из этого видео:
Только у них там всё объясняется на примере поляризации света, а я адаптировал для спина электронов.
Квантовая физика может быть даже страшнее, чем вы думаете
Это центральный вопрос квантовой механики, и никто не знает ответа: что на самом деле происходит в суперпозиции — в особых обстоятельствах, при которых частицы кажутся находящимися в двух или более местах или говорится сразу? В 2018 году группа исследователей из Израиля и Японии предложила эксперимент, который, наконец, позволил нам кое-что сказать наверняка о природе этого загадочного явления.
Их эксперимент был разработан, чтобы позволить ученым украдкой взглянуть на то, где объект — в данном случае частица света, называемая фотоном — на самом деле находится, когда он помещен в суперпозицию.И исследователи предсказывают, что ответ будет еще более странным и шокирующим, чем «два места одновременно».
Классический пример суперпозиции включает запуск фотонов в две параллельные щели в барьере. Одним из фундаментальных аспектов квантовой механики является то, что крошечные частицы могут вести себя как волны, так что частицы, проходящие через одну щель, «мешают» проходящим через другую, их волнистая рябь либо усиливает, либо нейтрализует друг друга, создавая характерный узор на экране детектора. .Однако странно то, что эта интерференция возникает, даже если одновременно выстреливается только одна частица. Кажется, что частица каким-то образом проходит через обе щели одновременно, мешая себе. Это суперпозиция.
И это становится еще более странным: измерение, через какую щель проходит такая частица, неизменно показывает, что она проходит только через одну, но тогда волнообразная интерференция («квантовость», если хотите) исчезает. Кажется, что сам акт измерения «разрушает» суперпозицию. «Мы знаем, что в суперпозиции происходит что-то подозрительное, — говорит физик Авшалом Элицур из Израильского института перспективных исследований.«Но вам не разрешено его измерять. Вот что делает квантовую механику такой дьявольской ».
На протяжении десятилетий исследователи зашли в этот очевидный тупик. Они не могут точно сказать, что такое суперпозиция, не глядя на нее, но если они попытаются взглянуть на нее, она исчезнет. Одно из возможных решений, разработанное бывшим наставником Элицура, израильским физиком Якиром Аароновым, ныне работающим в Университете Чепмена, и его сотрудниками — предлагает способ сделать какие-то выводы о квантовых частицах перед их измерением.Подход Ааронова называется формализмом двух векторов состояний (TSVF) квантовой механики и постулирует, что квантовые события в некотором смысле определяются квантовыми состояниями не только в прошлом, но и в будущем. То есть TSVF предполагает, что квантовая механика работает одинаково как вперед, так и назад во времени. С этой точки зрения может показаться, что причины распространяются назад во времени, возникая после их следствия: это явление называется ретропричинностью.
Но не стоит понимать это странное понятие буквально.Скорее в TSVF, можно получить ретроспективное знание того, что произошло в квантовой системе, выбрав результат: вместо простого измерения того, где оказывается частица, исследователь выбирает конкретное место, в котором будет ее искать. Это называется поствыбором, и он предоставляет больше информации, чем любой безусловный просмотр результатов. Это связано с тем, что состояние частицы в любой момент оценивается ретроспективно в свете всей ее истории, вплоть до измерения.Странность возникает потому, что кажется, что исследователь — просто выбирая поиск определенного результата, — затем вызывает этот результат. Но это немного похоже на вывод о том, что если вы включите телевизор, когда запланирована ваша любимая программа, ваше действие заставит эту программу транслироваться именно в этот момент. «Принято считать, что TSVF математически эквивалентен стандартной квантовой механике, — говорит Дэвид Уоллес, философ науки из Университета Южной Калифорнии, специализирующийся на интерпретации квантовой механики.«Но это действительно приводит к тому, что можно увидеть такие вещи, которые иначе невозможно было бы увидеть».
Возьмем, к примеру, версию эксперимента с двумя щелями, разработанную Аароновым и его коллегой Львом Вайдманом из Тель-Авивского университета в 2003 году, которую они интерпретировали с помощью TSVF. Пара описала (но не построила) оптическую систему, в которой одиночный фотон действует как «заслонка», закрывающая щель, заставляя другой «пробный» фотон, приближающийся к щели, отражаться обратно тем же путем, которым он пришел. Применяя постселекцию к измерениям зондирующего фотона, как показали Ааронов и Вайдман, можно было различить фотон затвора в суперпозиции, закрывающей обе (или даже произвольно много) щелей одновременно.Другими словами, этот мысленный эксперимент теоретически позволил бы с уверенностью сказать, что фотон затвора одновременно находится «здесь» и «там». Хотя эта ситуация кажется парадоксальной из нашего повседневного опыта, это один хорошо изученный аспект так называемых нелокальных свойств квантовых частиц, где исчезает само понятие четко определенного местоположения в пространстве.
В 2016 году физики Рио Окамото и Сигеки Такеучи из Киотского университета экспериментально подтвердили предсказания Ааронова и Вайдмана, используя световодную схему, в которой фотон затвора создается с помощью квантового маршрутизатора, устройства, которое позволяет одному фотону управлять маршрутом, пройденным другим.«Это был новаторский эксперимент, который позволил вывести одновременное положение частицы в двух местах», — говорит коллега Элитцура Элиаху Коэн из Оттавского университета в Онтарио.
Теперь Элицур и Коэн объединились с Окамото и Такеучи, чтобы придумать еще более ошеломляющий эксперимент. Они считают, что это позволит исследователям с уверенностью сказать что-то о местоположении частицы в суперпозиции в серии различных моментов времени — до того, как будет произведено какое-либо фактическое измерение.
На этот раз путь пробного фотона будет разделен на три части частичными зеркалами. На каждом из этих путей он может взаимодействовать с фотоном затвора в суперпозиции. Эти взаимодействия можно рассматривать как происходящие в прямоугольниках, обозначенных A, B и C, один из которых расположен вдоль каждого из трех возможных маршрутов фотона. Глядя на самоинтерференцию зондирующего фотона, можно ретроспективно заключить с уверенностью, что частица затвора находилась в заданном ящике в определенное время.
Эксперимент разработан таким образом, что зондирующий фотон может показывать интерференцию только в том случае, если он взаимодействует с фотоном затвора в определенной последовательности мест и времени, а именно, если фотон затвора в какой-то момент находился в обоих ящиках A и C ( t 1 ), затем в более позднее время ( t 2 ) только в C, а в еще более позднее время ( t 3 ) как в B, так и в C. Таким образом, интерференция в зондирующем фотоне будет Окончательный знак — фотон затвора создал эту причудливую, противоречащую логике последовательность разрозненных появлений между коробками в разное время — идею, которую Элицур, Коэн и Ааронов предложили в качестве возможной в 2017 году для единственной частицы, распределенной по трем коробкам.«Мне нравится, как в этой статье вопросы о том, что происходит, формулируются с точки зрения всей истории, а не мгновенных состояний», — говорит физик Кен Уортон из Государственного университета Сан-Хосе, который не участвует в новом проекте. «Разговор о« государствах »- это давнее повсеместное предубеждение, тогда как полные истории, как правило, гораздо более богаты и интересны».
Элитцур и его коллеги утверждают, что это богатство и есть то, к чему TSVF дает доступ. Очевидное исчезновение частиц в одном месте в одно время — и их повторное появление в другое время и в других местах — наводит на мысль о необычном видении процессов, лежащих в основе нелокального существования квантовых частиц.Через призму TSVF, говорит Элицур, это мерцающее, постоянно меняющееся существование можно понять как серию событий, в которых присутствие частицы в одном месте «отменяется» ее собственной «противоположной частицей» в том же месте. Он сравнивает это с идеей, предложенной британским физиком Полом Дираком в 1920-х годах, который утверждал, что частицы обладают античастицами, и, если их собрать вместе, частица и античастица могут аннигилировать друг друга. Сначала это понятие казалось просто способом выражения, но вскоре привело к открытию антивещества.Исчезновение квантовых частиц не является «аннигиляцией» в том же смысле, но в некотором смысле аналогично: эти предполагаемые двойники, утверждает Элицур, должны обладать отрицательной энергией и отрицательной массой, что позволяет им нейтрализовать свои аналоги.
Итак, хотя традиционный взгляд на суперпозицию «два места одновременно» может показаться достаточно странным, «вполне возможно, что суперпозиция — это совокупность состояний, которые еще более безумны», — говорит Элицур. «Квантовая механика просто сообщает вам их среднее значение.«Постселекция затем позволяет изолировать и исследовать только некоторые из этих состояний с большим разрешением», — предполагает он. Такая интерпретация квантового поведения была бы, по его словам, «революционной», поскольку повлекла бы за собой неизвестный до сих пор зверинец реальных (но очень странных) состояний, лежащих в основе противоречивых квантовых явлений.
Окамото и его коллеги в Киото уже провели предложенный эксперимент с использованием фотонов, но они все еще анализируют результаты. Тем не менее, говорит Коэн, «предварительные результаты хорошо согласуются с теорией.Он говорит, что японские исследователи сейчас вносят улучшения в установку, чтобы уменьшить погрешности.
А пока некоторые сторонние наблюдатели не ждут, затаив дыхание. «Эксперимент обязательно сработает», — говорит Уортон, но добавляет, что «никого ни в чем не убедит, поскольку результаты предсказываются стандартной квантовой механикой». Другими словами, не было бы веских причин интерпретировать результат с точки зрения TSVF, а не одного из многих других способов интерпретации исследователями квантового поведения.
Элицур соглашается, что их эксперимент можно было бы задумать с использованием общепринятого взгляда на квантовую механику, который преобладал несколько десятилетий назад, но этого никогда не было. «Разве это не хороший показатель надежности TSVF?» он спрашивает. И если кто-то думает, что может сформулировать иную картину того, «что на самом деле происходит» в этом эксперименте, используя стандартную квантовую механику, он добавляет: «Что ж, пусть идут вперед!»
Он уверен, что эта работа знаменует «не что иное, как революцию в квантовой механике.«Теперь, когда методы измерения стали достаточно точными, — говорит он, — вы можете быть уверены, что такие понятия, как ретропричинность, станут неотъемлемой частью квантовой реальности».
Новый рекорд квантовой суперпозиции — ScienceDaily
Принцип квантовой суперпозиции был протестирован в невиданных ранее масштабах в новом исследовании, проведенном учеными Венского университета в сотрудничестве с Базельским университетом. Горячие сложные молекулы, состоящие почти из двух тысяч атомов, были объединены в квантовую суперпозицию и были вынуждены интерферировать.Подтвердив это явление — «сердце квантовой механики», по словам Ричарда Фейнмана, — в новом масштабе масс, были наложены улучшенные ограничения на теории, альтернативные квантовой механике. Работа будет опубликована в журнале Nature Physics .
От квантового к классическому?
Принцип суперпозиции является отличительной чертой квантовой теории, которая вытекает из одного из самых фундаментальных уравнений квантовой механики — уравнения Шредингера. Он описывает частицы в рамках волновых функций, которые, как и волны воды на поверхности пруда, могут проявлять интерференционные эффекты.Но в отличие от волн на воде, которые представляют собой коллективное поведение многих взаимодействующих молекул воды, квантовые волны также могут быть связаны с отдельными отдельными частицами.
Возможно, наиболее элегантным примером волновой природы частиц является эксперимент с двумя щелями, в котором волновая функция частицы одновременно проходит через две щели и интерферирует. Этот эффект был продемонстрирован для фотонов, электронов, нейтронов, атомов и даже молекул, и это поднимает вопрос, над которым физики и философы боролись с самых первых дней квантовой механики: как эти странные квантовые эффекты переходят в классический мир, с которым мы все знакомы
Экспериментальный подход
Эксперименты Маркуса Арндта и его команды из Венского университета подходят к этому вопросу самым прямым из возможных способов, то есть путем демонстрации квантовой интерференции со все более массивными объектами.Молекулы в недавних экспериментах имеют массу более 25 000 атомных единиц массы, что в несколько раз больше, чем предыдущий рекорд. Одна из самых больших молекул, проходящих через интерферометр, C707h360F908N16S53Zn4, состоит из более чем 40 000 протонов, нейтронов и электронов с длиной волны де Бройля, которая в тысячу раз меньше диаметра даже одного атома водорода. Марсель Майор и его команда из Базельского университета использовали специальные методы для синтеза таких массивных молекул, которые были достаточно стабильными, чтобы сформировать молекулярный пучок в сверхвысоком вакууме.Для доказательства квантовой природы этих частиц также потребовался интерферометр материальных волн с двухметровой базой, специально построенный в Вене.
Альтернативные квантовые модели и макроскопичность
Один класс моделей, нацеленных на согласование очевидного перехода от квантового режима к классическому, предсказывает, что волновая функция частицы спонтанно коллапсирует со скоростью, пропорциональной квадрату ее массы. Экспериментально показывая, что суперпозиция сохраняется для тяжелой частицы в течение заданного промежутка времени, таким образом, напрямую накладывает ограничения на то, как часто и насколько локализованным может быть такой процесс коллапса.В этих экспериментах молекулы оставались в суперпозиции более 7 мс, достаточно долго, чтобы установить новые интерферометрические границы для альтернативных квантовых моделей.
Обобщенная мера, называемая макроскопичностью, используется для классификации того, насколько хорошо альтернативные модели исключаются такими экспериментами и экспериментами Фейна и др. . опубликованные в Nature Physics действительно демонстрируют увеличение макроскопичности на порядок. «Наши эксперименты показывают, что квантовая механика, при всей ее странности, также удивительно надежна, и я оптимистично настроен в отношении того, что будущие эксперименты проверит ее в еще более широком масштабе», — говорит Фейн.Граница между квантовой и классической все время стирается.
История Источник:
Материалы предоставлены Венским университетом . Примечание. Содержимое можно редактировать по стилю и длине.
квантовая суперпозиция и что это значит для квантовых вычислений | Аджай Нараянан
Квантовые вычисления — одна из самых многообещающих тем исследований этого поколения. Квантовая теория оставила мир в заблуждении как с точки зрения теоретических возможностей, которые уже были исследованы исследователями, так и с точки зрения практических приложений, к которым может привести эта новая технология.Для компьютерного ученого ускорение квантовых компьютеров заключается в способности таких компьютеров выполнять параллельную обработку данных, о чем раньше даже не догадывались. Квантовые компьютеры принципиально отличаются от своих классических аналогов. В основе квантовых вычислений лежит принцип квантовой суперпозиции, который, как и всю квантовую теорию, очень трудно визуализировать. Этот блог будет направлен на то, чтобы пролить свет на эту «жуткую» науку, как назвал ее сам Эйнштейн.
1.Десять тенденций в области искусственного интеллекта (ИИ) в 2019 году
2. Разрыв пузырей жаргона — глубокое обучение
3. Как мы можем улучшить качество наших данных?
4. Машинное обучение с использованием логистической регрессии в Python с кодом
Принцип квантовой суперпозиции
Честно говоря, концепция суперпозиции кажется невозможной в том смысле, что невозможно наблюдать это явление в мир, который мы физически наблюдаем каждый день.Это не похоже на гравитацию, что может быть доказано чем-то таким простым, как падающее яблоко. Вопрос о суперпозиции возникает только в мире субатомных частиц. В этой сфере существования законы классической физики, кажется, полностью перестают работать. Принцип квантовой суперпозиции просто утверждает, что квантовая частица может существовать в двух разных местах одновременно. Согласно этой теории, квантовая частица может существовать одновременно в нескольких состояниях, если не выполняется операция измерения.
Квантовая суперпозицияЧтобы понять, что такое квантовая суперпозиция, внимательно просмотрите короткое видео выше. Видео демонстрирует посредством анимации то, что известно как кубиты в квантовых вычислениях. Кубит — это основная единица квантовой информации, параллельная Биту как основной единице классической информации. Как показано на видео, кубит может быть равен 0 и 1 одновременно, пока он не будет соблюден. Это свойство кубита находиться в суперпозиции двух состояний одновременно — это то, что обеспечивает квантовым компьютерам экспоненциальное ускорение по сравнению с классическими компьютерами.
Суперпозиция в молекуле водыДавайте отступим от разговоров о кубитах и квантовых компьютерах. Квантовая суперпозиция — это то, что происходит в природе. Ученые считают, что естественные вычисления, такие как химические реакции и образование молекул, происходят так быстро из-за присущей им квантовой суперпозиции субатомных частиц. Чтобы прояснить этот момент, позвольте мне взять пример с водой, которая является наиболее известным элементом на Земле. Я надеюсь, что все читатели имеют четкое представление о том, как образуются молекулы воды.Кислород делит свои 2 электрона с каждой молекулой водорода и образует с ними связь. Согласно классической химии, это совместное использование означает, что общие электроны находятся в свободном пространстве между молекулами водорода и кислорода. По мнению ученых Quantum, это не совсем так. Общие электроны фактически существуют в суперпозиции между молекулами кислорода и водорода. Это означает, что общие электроны одновременно присутствуют как в молекулах кислорода, так и в молекулах водорода, и положение этих электронов не всегда должно быть между двумя.
Экспоненциальное ускорение вычислительной мощности
Одним из наиболее изученных приложений квантовой суперпозиции является возможное ускорение вычислений. Чтобы объяснить это, мы должны вернуться к Кубиту и его свойствам. Все компьютеры в мире, от самого большого суперкомпьютера до маленьких умных часов, работают на тех же принципах, что и машина Тьюринга, построенная во время Второй мировой войны.
Машина ТьюрингаЭта машина работает на основе наличия или отсутствия щелчков, вызванных вращением этих механических рычагов.Хотя мы перешли от механических рычагов к цифровым битам, эта же концепция по-прежнему управляет всеми нашими вычислительными усилиями. Концепцию кубита можно легко объяснить, сказав, что он может быть 0 и 1 одновременно. Но в механическом корпусе одновременный щелчок и отсутствие щелчка кажется абсурдным. Это причина того, почему даже исследователи, работающие над квантовыми технологиями, не могут полностью представить себе их мощь и возможности.
Однако давайте попробуем разобраться в ситуации.В любом случае вычислительная мощность напрямую зависит от количества вычислительных состояний, существующих одновременно. Возьмем, к примеру, навигацию по лабиринту.
Представьте, что квантовая частица проходит через этот лабиринт. Помните, что квантовая частица обладает уникальным свойством находиться в двух местах одновременно из-за принципа квантовой суперпозиции. Итак, когда квантовая частица встречает различные пути в лабиринте, она может решить пройти все эти пути одновременно, используя суперпозицию.Если задуматься, этот процесс очень напоминает парадигму параллельных вычислений. Благодаря квантовой суперпозиции квантовая частица может перемещаться по лабиринту за экспоненциально меньшее время, чем классический бит.
Классический бит, с другой стороны, не обладает этой волшебной способностью суперпозиции. Классический бит легче вообразить, поскольку мы можем просто представить себя идущим через лабиринт. За один раз мы можем исследовать только один из путей в лабиринте.Если путь, по которому проходит классическая частица, заходит в тупик, мы должны вернуться назад и начать заново, выбрав другой путь. Как видите, это трудоемкий процесс, и мы бы ужасно проиграли, если бы соревновались с квантовой частицей. Ученые считают, что именно это уникальное свойство квантовых частиц обуславливает высокую скорость вычислений на субатомном уровне.
Как классический компьютер решает лабиринтЗаключение — Мир становится все более странным
Мы никогда не можем себе представить, чего может достичь такая новая технология в следующие 10 лет.Исследователи работают над созданием полноценных квантовых компьютеров для решения задач, которые сегодня слишком сложны для классических компьютеров. Многие области, такие как криптография, машинное обучение, информационная безопасность, могут вскоре претерпеть радикальные изменения из-за появления возможностей квантовых вычислений. Мир науки и технологий с каждым днем становится все сложнее и сложнее объяснить. Мы даже представить себе не можем, как вся концепция вычислений может измениться в ближайшие годы, и это меня больше всего волнует!
Физики-теоретики описывают новый вид квантового временного порядка
Одним из фундаментальных принципов квантовой механики является квантовая суперпозиция, в которой частица существует в двух или более состояниях одновременно.В статье, опубликованной в журнале Nature Communications , физик из Университета Квинсленда Магдалена Зих и ее коллеги показывают, что частицы — не единственные объекты, которые могут существовать в состоянии суперпозиции, как и само время.
Zych и др. предоставляют первый прямой анализ квантовых причинно-следственных связей, возникающих в результате пространственной суперпозиции массивного объекта; они показывают, как временной порядок между подобными времени событиями может накладываться друг на друга или даже запутываться.Изображение предоставлено: Университет Квинсленда.
«Последовательность событий может стать квантово-механической», — сказал соавтор доктор Игорь Пиковски, физик из Технологического института Стивенса.
«Мы рассмотрели квантовый временной порядок, в котором нет различия между одним событием, вызывающим другое, и наоборот».
Работа команды является одной из первых, раскрывающих квантовые свойства времени, при которых течение времени не наблюдает прямую стрелку вперед, а указывает на то, что причина и следствие могут сосуществовать как в прямом, так и в обратном направлении.
В грядущую эру квантовых компьютеров эта работа имеет особые перспективы: квантовые компьютеры, которые используют квантовый порядок выполнения операций, могут превзойти устройства, которые работают с использованием только фиксированных последовательностей.
Чтобы продемонстрировать этот сценарий, физики объединили две, казалось бы, противоречивые теории — квантовую механику и общую теорию относительности — и провели мысленный эксперимент, способ использования воображения для исследования природы вещей.
«Это открытие явилось результатом эксперимента, который мы разработали, чтобы объединить элементы двух больших, но противоречащих друг другу физических теорий, разработанных в прошлом веке», — сказал д-р.Зыч объяснил.
«Наше предложение было направлено на открытие: что происходит, когда объект, достаточно массивный, чтобы влиять на течение времени, помещается в квантовое состояние?»
«Теория Эйнштейна описывает, как присутствие массивного объекта замедляет время», — добавила она.
«Представьте себе два космических корабля, которых попросили стрелять друг в друга в определенное время, уклоняясь от атаки».
«Если один сработает слишком рано, он уничтожит другой».
«Согласно теории Эйнштейна, могущественный противник мог бы использовать принципы общей теории относительности, поместив массивный объект — например, планету — ближе к одному кораблю, чтобы замедлить течение времени.”
«Из-за задержки во времени корабль, наиболее удаленный от массивного объекта, выстрелит раньше, уничтожив другой».
«Вторая теория, квантовая механика, утверждает, что любой объект может находиться в состоянии суперпозиции. Это означает, что его можно найти в разных состояниях — подумайте о коте Шредингера ».
«Используя теорию квантовой механики, если враг переводит планету в состояние квантовой суперпозиции, время также должно быть нарушено», — сказал доктор Зих.
«Будет новый способ разворачивания порядка событий, при котором ни одно из событий не будет первым или вторым — но в подлинном квантовом состоянии, когда оно будет одновременно первым и вторым.”
«Хотя« наложение планет », возможно, никогда не станет возможным, технологии позволили моделировать, как время работает в квантовом мире — без использования гравитации», — сказал соавтор доктор Фабио Коста из Университета Квинсленда.
«Даже если эксперимент невозможно провести, исследование актуально для технологий будущего».
«В настоящее время мы работаем над квантовыми компьютерами, которые, проще говоря, могли бы эффективно перемещаться во времени, чтобы выполнять свои операции намного эффективнее, чем устройства, работающие в фиксированной последовательности во времени, как мы знаем это в нашем« нормальном »мире.”
_____
Magdalena Zych и др. . 2019. Теорема Белла для временного порядка. Nature Communications 10, номер статьи: 3772; DOI: 10.1038 / s41467-019-11579-x
одинаковых атомов существуют в двух местах на расстоянии почти 2 футов одновременно
Getty Images
Квантовая механика может похвастаться множеством восхитительно странных функций. Дело в том, что две разделенные частицы могут мгновенно взаимодействовать, это явление называется квантовой запутанностью.(Эйнштейн осудил теорию, которую он назвал «жутким действием на расстоянии», но есть существенные доказательства, подтверждающие теорию квантовой запутанности.) И есть еще одно явление, называемое квантовой суперпозицией. Этот принцип квантовой механики предполагает, что частицы могут существовать одновременно в двух разных местах.
Физики из Стэнфордского университета продемонстрировали суперпозицию группы атомов на большем расстоянии, чем когда-либо прежде: 54 сантиметра, или около 1.77 футов. Самое большое расстояние, которое когда-либо было достигнуто до этого, было меньше сантиметра.
Квантовая суперпозиция еще больше сбивает с толку тот факт, что она может происходить только тогда, когда частицы не наблюдаются. Просто наблюдая за частицей в двух разных квантовых состояниях, вы вызываете то, что известно как коллапс волновой функции, и частица снова существует только в одном или другом состоянии (а в случае суперпозиции только в одном физическом местоположении). Поэтому измерение частицы в суперпозиции невероятно сложно.
Стэнфордские исследователи использовали облако из 10 000 атомов рубидия, охлажденное до почти абсолютной нулевой температуры, названное конденсатом Бозе-Эйнштейна (БЭК), чтобы продемонстрировать суперпозицию. Облако атомов размером несколько миллиметров было помещено в камеру высотой 33 фута. Лазеры использовались, чтобы подтолкнуть облако вверх по камере, процесс, который также разделил атомы на два квантовых состояния. Когда атомы упали обратно на дно камеры, они вернулись в одно квантовое состояние и, казалось, прибыли с двух разных высот на расстоянии 54 см друг от друга, подтверждая, что они находились в суперпозиции наверху камеры.BEC оставался в суперпозиции около секунды, что в четыре раза дольше, чем в предыдущих демонстрациях.
Именно эксперименты, подобные этому, могут помочь создать новый набор физических законов для атомного мира, принципов, которые могут привести к прорывам в таких областях, как квантовые вычисления, и революционизировать нашу способность обрабатывать огромные объемы данных. А пока мы можем просто наслаждаться невероятной странностью жутких частиц.
Источник: New Scientist
Джей Беннетт Заместитель редактора Джей Беннетт — заместитель редактора PopularMechanics.com.Этот контент создается и поддерживается третьей стороной и импортируется на эту страницу, чтобы помочь пользователям указать свои адреса электронной почты. Вы можете найти больше информации об этом и подобном контенте на сайте piano.io.
Есть ли у квантовых суперпозиций предел размера?
- Джордж К. Коли
- NTT Basic Research Laboratories, NTT Corporation, 3-1 Morinosato-Wakamiya, Atsugi, Kanagawa 243-0198, Japan
& bullet; Физика 8, 6
Блуждание атома в оптической решетке используется для проверки ключевого принципа квантовой физики.
Рисунок 1: В экспериментальном тесте, проведенном Robens et al. , большой атом (цезий) движется в одном из двух возможных оптических полей, обозначенных здесь красным и синим. Поля имеют периодический потенциал, подобный «яичной коробке». Авторы подготовили атом в суперпозиции двух атомных состояний, что было эквивалентно атому, одновременно находящемуся в красной оптической коробке и синей оптической коробке, и определили положение атома, обнаружив его флуоресценцию, когда две коробки раздвинулись.В экспериментальном тесте, проведенном Robens et al. , большой атом (цезий) движется в одном из двух возможных оптических полей, обозначенных здесь красным и синим. Поля имеют периодический потенциал, подобный «яичной коробке». Авторы подготовили атом в суперпозиции t … Показать еще Рисунок 1: В экспериментальном тесте Робенса и др. , большой атом (цезий) движется в одном из двух возможных оптических полей, обозначенных здесь красным и синим. Поля имеют периодический потенциал, подобный «яичной коробке».Авторы подготовили атом в суперпозиции двух атомных состояний, что было эквивалентно атому, одновременно находящемуся в красной оптической коробке и синей оптической коробке, и определили положение атома, обнаружив его флуоресценцию, когда две коробки раздвинулись. ×Повседневный опыт подсказывает нам, что большие объекты — яйца и люди — не существуют в суперпозиции состояний, подобных той, которая возможна для большего количества квантовых объектов, таких как электроны. Означает ли это, что квантовая физика принципиально неприменима к объектам сверх определенного размера? Новый эксперимент, который позволяет отслеживать движение большого атома в оптической решетке, может помочь в поисках ограничения по размеру.Используя эту установку, Карстен Робенс из Боннского университета, Германия, и его коллеги продемонстрировали, что атом цезия движется по-настоящему неклассическим образом, перемещаясь как квантовая суперпозиция состояний и, таким образом, занимая более одного определенного местоположения одновременно [1] . Было обнаружено, что более крупные объекты обладают такими по своей сути квантовыми свойствами, но наблюдение Робенса и др. основан на строгом тесте, который считается золотым стандартом для подтверждения существования суперпозиции.Таким образом, их эксперимент ограничивает теории физики, которые стремятся заменить квантовую механику. Их метод также можно использовать для проверки суперпозиций на еще более макроскопических масштабах, например, с более крупными атомами или молекулами.
Большинство экспериментов, направленных на проверку того, что частица находится в квантовой суперпозиции состояний, ищут доказательства интерференции. Классический эксперимент состоит в том, чтобы пропустить электрон через пару щелей: получающиеся полосы наводят на мысль о волнообразном поведении, которое квантовая теория приписывает фундаментальным частицам.Тем не менее, даже несмотря на то, что эти эксперименты согласуются с предсказаниями квантовой теории, они не являются надежными тестами, поскольку возможно классическое объяснение: можно представить, что электрон на самом деле проходит через одну или другую щель, а не через обе одновременно (как это сделала бы квантовая физика. есть.)
В теоретической статье 1985 года Энтони Леггетт и Анупам Гарг [2] подошли к проблеме совершенно иначе. Вместо того, чтобы пытаться проверить квантовую теорию, они предложили вместо этого попытаться исключить альтернативы, продемонстрировав, что что-либо иное, кроме квантового описания, приводит к противоречию с экспериментальным наблюдением.Они определили точку зрения, называемую макрореализмом, которая основана на двух предположениях, противоречащих квантовой теории: объект достаточно большого размера всегда находится в одном месте в каждый момент времени (макроскопические суперпозиции не могут существовать), и местоположение объекта может быть определено, не нарушая его. . Они показали, что если макрореализм был правдой, измерения, выполненные на объекте в разное время, могли быть статистически коррелированы только до определенной степени, и это соотношение они выразили математически через неравенство Леггетта-Гарга.Эксперименты, указывающие на обратное, т. Е. Нарушающие это неравенство, ясно показали бы, что макрореализм ложен. Их работа вдохновила на ряд экспериментов [3] с фотонами [4], ядерными спинами [5,6] и сверхпроводящими цепями [7].
По сравнению с этими более ранними экспериментами, атомы, исследованные в экспериментах Robens et al. являются крупнейшими квантовыми объектами, с которыми было проверено неравенство Леггетта-Гарга с использованием так называемого нулевого измерения — «неинвазивного» измерения, которое позволяет подтвердить неравенство наиболее убедительным из возможных способов.В эксперименте исследователей атом цезия движется в одной из двух стоячих оптических волн с противоположными поляризациями электрического поля, и положение атома измеряется в разное время. Две стоячие волны можно представить как крошечную пару перекрывающихся одномерных полосок яичного картона — одну красную, одну синюю (рис. 1). Эксперимент состоит в измерении корреляции между положением атома в разное время. Robens et al. сначала помещает атом в суперпозицию двух внутренних сверхтонких спиновых состояний; это соответствует нахождению в обеих картонных коробках одновременно.Затем команда скользнула двумя оптическими волнами мимо друг друга, что заставило атом размазаться на расстояние до 2 микрометров в движении, известном как квантовое блуждание. Наконец, авторы оптически возбудили атом, заставив его флуоресцировать и выявить его местоположение в одном месте. Знание того, где начинался атом, позволяет им в среднем вычислить, двигался ли атом влево или вправо от своего исходного положения. Повторяя этот эксперимент, они могут получить корреляции между положением атома в разное время, которые являются входными данными для неравенства Леггетта-Гарга.
Так вот, макрореалист утверждал бы, что атом никогда не начинался в суперпозиции; скорее, в любой момент он был только в корзине одной или другой коробки. Более того, она могла бы возразить, что измерение флуоресценции было инвазивным для последующих измерений. Следовательно, как первоначально предложили Леггетт и Гарг, Robens et al. использовали метод измерения «нулевого результата» в один из промежуточных периодов своего эксперимента. Проще говоря, нулевое измерение позволяет экспериментатору определить местоположение атома, не взаимодействуя с ним напрямую.Для этого авторы просто сдвигают одну из стоячих волн — картонные коробки — на большое расстояние. Допустим, они убирают красную коробку. Если атом не загорается, когда выполняется более позднее измерение флуоресценции, можно знать, что атом находился в красной коробке, с ним сильно взаимодействовали и он оказался далеко. Однако, повторяя этот эксперимент, иногда можно обнаружить, что атом загорается. Тогда можно быть уверенным, что атом находился в синей коробке до сдвига, когда измерение было активировано. Более того, известно, что синяя картонная коробка и, следовательно, атом цезия не были подделаны.
Если бы макрореализм описывал реальность, нулевое измерение не повлияло бы на результат окончательного измерения флуоресценции, и общая степень корреляции положения атома в различных случаях во времени была бы понятна без квантовой механики. Но это поражает самую суть того, что делает квантовую механику такой странной. Что особенно важно, когда атом размазан, а не имеет определенное положение, даже нулевые измерения имеют эффект. Это размытие приводит к более сильной общей корреляции, чем это возможно при макрореализме, факт, математически зафиксированный в нарушении неравенства Леггетта-Гарга.Это именно то, что Robens et al. находят, а это означает, что макрореализм неприменим к их атому цезия.
Спустя почти столетие после квантовой революции в науке, возможно, удивительно, что физики все еще пытаются доказать существование суперпозиций. Настоящая мотивация кроется в будущем теоретической физики. Новые теории макрореализма вполне могут стать основой для следующего поколения «апгрейда» квантовой теории, установив масштаб границы между квантами и классикой.Благодаря результатам этого эксперимента мы можем быть уверены, что граница не может лежать ниже масштаба, в котором атом цезия, как было показано, ведет себя как волна. Насколько высока эта шкала? Теоретическая мера макроскопичности [8] (см. Синопсис от 18 апреля 2013 г.) дает атому цезия скромный рейтинг 6,8, выше единственного другого объекта, протестированного с помощью нулевых измерений [5], но намного ниже того места, где находится наиболее подозрительная граница. (Кошка Шредингера — 57 лет). Фактически, эксперименты по интерферометрии с материальной волной уже показали интерференционные полосы с молекулами бакминстерфуллерена [9], получившие оценку до 12.На мой взгляд, однако, мы можем быть уверены в демонстрации квантовости атома цезия из-за того, что авторы исключили макрореализм с помощью измерений с нулевым результатом. Следующий шаг — провести эти эксперименты с атомами большей массы, наложенными друг на друга в более длительных масштабах времени и разделенными на большие расстояния. Это расширит границы макроскопичности и раскроет еще больше о природе отношений между квантом и макромиром.
Это исследование опубликовано в журнале « Physical Review X».
Ссылки
- Карстен Робенс, Вольфганг Альт, Дитер Мешеде, Клайв Эмари и Андреа Альберти, «Идеальные отрицательные измерения в квантовых прогулках опровергают теории, основанные на классических траекториях», Phys. Rev. X 5 , 011003 (2015)
- А. Дж. Леггетт и А. Гарг, «Квантовая механика против макроскопического реализма: существует ли поток, когда никто не смотрит?», Phys. Rev. Lett. 54 , 857 (1985)
- К. Эмари, Н. Ламберт и Ф. Нори, «Неравенства Леггетта-Гарга», Rep.Прог. Phys. 77 , 016001 (2014)
- М.Э. Гоггин, член парламента Алмейда, М. Барбьери, Б.П. Ланьон, Дж. Л. О’Брайен, А. Г. Уайт и Дж. Дж. Прайд, «Нарушение неравенства Леггетта-Гарга при слабых измерениях фотонов», Proc. Natl. Акад. Sci. 108 , 1256 (2011)
- G.C. Knee et al. , «Нарушение неравенства Леггетта-Гарга с идеальными неинвазивными измерениями», Nature Commun. 3 , 606 (2012)
- Г. Вальдхерр, П. Нойман, С. Ф.Huelga, F. Jelezko, J. Wrachtrup, “Нарушение неравенства временного колокола для одиночных спинов в алмазном дефектном центре”, Phys. Rev. Lett. 107 , 090401 (2011)
- А. Паласиос-Лалой, Ф. Маллет, Ф. Нгуен, П. Бертет, Д. Вион, Д. Эстев, А. Н. Коротков, «Экспериментальное нарушение неравенства Колокола во времени с Слабое измерение », Nature Phys. 6 , 442 (2010)
- С. Ниммрихтер и К. Хорнбергер, «Макроскопичность механических квантовых состояний суперпозиции», Phys.Rev. Lett. 110 , 160403 (2013)
- К. Хорнбергер, С. Герлих, Х. Ульбрихт, Л. Хаккермюллер, С. Ниммрихтер, И. В. Голдт, О. Болталина, М. Арндт, «Теория и экспериментальная проверка Капицы — Интерферометрия Дирака – Тальбота – Лау // New J. Phys. 11 , 043032 (2009)
Об авторе
Джордж Ни получил степень магистра наук. получил степень доктора философии в области теоретической физики в Имперском колледже Лондона в 2010 году. окончила Оксфордский университет в 2014 году, а сейчас работает научным сотрудником в лабораториях фундаментальных исследований NTT в Японии.Он изучает теорию квантовой информации и любит переводить абстрактную математику в экспериментальные предложения. Его основные интересы связаны с основами квантовой теории и различными квантовыми технологиями, включая датчики, симуляторы и компьютеры.
 Как открыть хостел | HowToHostel Как открыть хостел …
Как открыть хостел | HowToHostel Как открыть хостел … 
 В природе существует истинная случайность, более глубокая, чем случайность в бросаемом кубике.
В природе существует истинная случайность, более глубокая, чем случайность в бросаемом кубике.