Соотношения Фибоначчи — Форекс Википедия
Соотношения Фибоначчи — последовательность чисел, часто наблюдающаяся в природе. Была использована древними цивилизациями при постройке Пирамид и других архитектурных строений. Данная последовательность широко используется и на финансовых рынках в виде индикаторов и инструментов.
История
В начале 1200-х годов итальянский математик Леонардо Пизано Фибоначчи раскрыл тайну древней Египетской цивилизации, которая произвела переворот во всем математическом мире и в том числе на финансовых рынках.
При изучении пирамиды Хеопса в Египте Фибоначчи сделал потрясающее открытие и обнаружил уникальную математическую последовательность чисел, которая изменила несколько тригонометрических, алгебраических и геометрических теорий.
Он разработал знаменитую последовательность чисел Фибоначчи, которая гласит, что третье число является суммой двух предыдущих чисел:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и так далее.
Но реальное значение этого ряда заключается в том, что отношение любого числа к следующему за ним числу составляет примерно 0,618, а к предыдущему числу – 1,618.
- Ключевое соотношение Фибоначчи 61,8%, которое также называют «золотым отношением» или «золотой серединой», вычисляется делением одного числа из ряда на число, следующее за ним. Например: 8/13 = 0,6153, и 55/89 = 0,6179.
- Аналогично соотношение 38,2% вычисляется делением одного числа из ряда чисел на число, находящееся от него на два числа вправо. Например: 55/144 = 0,3819.
- Соотношение 23,6% определяется делением одного числа из ряда чисел на число, находящееся от него на три числа вправо. Например: 8/34 = 0,2352.
На самом деле, все эти соотношения, разработанные Фибоначчи, берут свои истоки тысячи лет назад, со времен Древнего Египта и Древней Греции. В дополнение к математике эти цивилизации также использовали «золотую середину» в архитектуре и музыке.
Связь с финансовыми рынками
Впоследствии эти соотношения стали основой многих эффективных торговых систем, но, правда, они редко используются должным образом. И по иронии судьбы, хотя они являются одним из наиболее эффективных инструментов технического анализа, они также являются самым неправильно истолкованным инструментом.
И по иронии судьбы, хотя они являются одним из наиболее эффективных инструментов технического анализа, они также являются самым неправильно истолкованным инструментом.
Соотношения Фибоначчи могут точно предвидеть, когда рынок делает главный разворот и определить ключевые точки разворота для вершин и оснований… только если вы знаете, как их правильно интерпретировать. Если вы можете научиться правильно их использовать, вы можете увеличить вероятность прибыльных сделок и минимизировать возможные потери.
Эти числа являются более эффективными на валютном рынке, поскольку FOREX в своей основе является трендовым рынком. Цены на нем постоянно колеблются, тем самым достаточно точно следуя соотношениям Фибоначчи.
Уровни Фибоначчи выступают в роли сильных показателей уровней сопротивления и поддержки, которые помогают более точно определить точки входа и выхода для каждой сделки. Одно из самых больших преимуществ торговли с числами Фибоначчи является то, что, руководствуясь ими, вы также можете установить тейк-профит и стоп-лосс.
Различные соотношения Фибоначчи являются краеугольным камнем структуры цен, и они сходятся один к одному с эффективными графическими моделями, подобно волнам Эллиота, графическим паттернам, дивергенции и т.д.
Соотношения Фибоначчи можно разделить на четыре основные группы:
Значимость соотношений Фибоначчи
Рис. 1 Роль соотношений Фибоначчи на форекс столь же значима как и в природеПо тем или иным причинам эти соотношения играют важную роль на финансовых рынках, возможно столь же значимую как и в природе, и могут быть использованы для определения критических точек, которые побуждают цену развернуть свое направление. Цена имеет поразительную закономерность – соблюдая достаточно точно и часто соотношения Фибоначчи. Следовательно, их можно использовать для расстановки правильных технических уровней.
Движение цены никогда не бывает случайным, и каждая волна и колебание оставляет информацию о последующем движении цены. Таким образом, используя предыдущее движение цены, можно предвидеть ее последующее движение.
Однако каждая торговая ситуация требует соответствующего соотношения Фибоначчи с различными значениями. Применение этих соотношений в надлежащем порядке дает трейдерам огромное преимущество над толпой, тогда как неверное интерпретирование этого инструмента ведет к гибели депозита.
Основные правила построения
Рис. 2 ПримерНе смотря на то, что эти соотношения широко используются, люди не соблюдают основные правила, а потому неоправданно рискуют своими средствами. Ко всем соотношениям Фибоначчи применяются следующие правила:
- Соотношения Фибоначчи всегда должны быть построены на графике слева направо.
- Соотношения должны всегда быть нанесены на опорные точки (максимумы/минимумы колебания). Следует визуально определить уровни, в пределах которых происходит изменение трендового движения цены. Короче говоря, определить волны ценового движения.
- Нельзя наносить линии на разворотные точки в середине волны.
- Соотношения должны быть нанесены на точки хай/лоу теней, а не на тела свечей.

- С другой стороны, если мы ищем уровни поддержки/сопротивления, в любом соотношении Фибоначчи мы должны рассмотреть закрытие реального тела свечи.
Пример: рассмотрим рис. 2, мы наносим соотношение уровни коррекции Фибоначчи и видим, что цена находит поддержку на 61,8%; если при этом фитиль свечи зашел ниже уровня Фибоначчи 61,8% и у нас отсутствует закрытие реального тела ниже этого уровня, данный уровень поддержки будет недействительным.
Интерпретация соотношений Фибоначчи
Следующие правила применяются ко всем соотношениям Фибоначчи – уровням коррекции, проекциям, веерам и расширениям.
Рис. 3 USDCAD D1Интерпретация №1
Если цена пробивает один уровень Фибоначчи, существует очень высокая вероятность ее перехода на следующий уровень.
Фактически это означает, что эти уровни могут дать нам карту для ценового движения. Идеальный способ – построить эти уровни на более высоком таймфрейме и торговать в направлении ожидаемого тренда на меньшем таймфрейме.
Пример:
Для оценки уровней поддержки Фибоначчи на примере нанесены уровни коррекции Фибоначчи на дневной график валютной пары USD/CAD. На рис. 3 показано, что цена закрылась ниже уровня Фибоначчи 23,6. Это означает, что цена с очень высокой вероятностью будет двигаться вниз к следующему уровню Фибоначчи 38,2. Таким образом, на меньшем (часовом) таймфрейме, см. рис. 4, появилась возможность открывать короткие позиции с ожидаемой целью на уровне поддержки 38,2.
Рис. 4 USDCAD h2
Рис. 5 Фибоначчи и дивергенцияИнтерпретация №2
Разворот тренда имеет более высокую вероятность, когда сильный свечной паттерн (например, доджи) или графический паттерн (например, дивергенция) формируется именно на уровне Фибоначчи… По факту чаще всего происходит именно так. Рассмотрите пример, рис.5 демонстрирует эффективность этой концепции.
Цена откатилась до уровня Фибоначчи 61,8, где нашла сильную поддержку. На рисунке видно, что большое количество свечей не cмогли закрыться ниже уровня 61,8.
Важные уровни Фибоначчи
Как упоминалось ранее, большинство торговых систем, как правило, используют стандартные соотношения Фибоначчи 38,2, 50,0 и 61,8.
- Отношение 38,2% находится делением одного числа в последовательности Фибоначчи на число, которое находится на два разряда вправо. Например: 55/144 = 0,3819.
- Отношение 50,0 не является числом Фибоначчи, но используется только в качестве оценки половины меры любой ценовой коррекции.
- Ключевое соотношение Фибоначчи 61,8% – также известно как «золотое сечение» или «золотая середина» – определяется делением одного числа в последовательности Фибоначчи на число, которое следует за ним. Например: 8/13 = 0,6153 и 55/89 = 0,6179.
Соотношение 0,786
Это соотношение не столь популярно как «золотое сечение» 61,8, но не менее важно.
Пример: На 4-часовом графике валютной пары USD/CAD отображены уровни коррекции Фибоначчи на нисходящей волне (слева направо – от максимума колебаний цены к минимуму).
Цена поднялась и четко пробила уровни сопротивления Фибоначчи 38,2, 50,0 и 61,8.
По правилам, стоит ожидать, что цена дойдет до следующего уровня Фибоначчи 78,6, где она первоначально встретила свое сопротивление.
Если бы цена отбилась от барьерного уровня вниз, стоило отнести это восходящее движение как откат, ожидая продолжение нисходящего тренда.
Вывод: Если мы ожидаем изменения тренда, то лучше дождаться, когда цена пробьет уровень 78,6, что даст более сильный признак для смещения импульса.
Как правильно пользоваться коррекцией по Фибоначчи
Одним из важных инструментов технического анализа являются технические уровни. Это определенное значение цены, которое при приближении к нему курса будет препятствием для дальнейшего продвижения. Графически это выглядит как область, куда цена подошла, а далее цена на графике откатила, потом подошла еще раз и снова не смогла преодолеть сопротивление. Таких возвратов может быть несколько, и чем их больше, тем сильнее уровень.
Различают уровни поддержки и сопротивления. Поддержка находится в нижней части ценового диапазона, она не дает курсу обвалиться дальше вниз, а сопротивление препятствует продвижению цены вверх. Для текущего значения всегда есть уровни поддержки и сопротивления. Главное правило – цена от уровня скорее оттолкнется, чем уровень будет пробит.
Для текущего значения всегда есть уровни поддержки и сопротивления. Главное правило – цена от уровня скорее оттолкнется, чем уровень будет пробит.
Пробитие уровня возможно, по-этому будьте осторожны: оно обычно происходит на каком-то сильном импульсе, например, выход важных новостей, и тогда цена вылетает за уровень на большое количество пунктов. На этом основаны техники на пробой, но они считаются достаточно агрессивными.
Уровни коррекции Фибоначчи при движении цены тоже оказывают сопротивление или поддержку, но это уже частично компьютерный индикатор. В его раскладку заложена определенная зависимость, которая была выведена еще задолго до появления Форекса.
История создания
Леонардо Фибоначчи (12-13 века) – итальянский математик, который открыл ряд натуральных чисел, находящихся между собой в определенной зависимости. Смысл зависимости Фибоначчи – каждое последующее число равно сумме двух предыдущих. Начинается ряд с нуля, и продолжать его можно до бесконечности: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 188…
Сам же Фибоначчи изначально разрабатывал свою зависимость для нахождения формулы размножения кроликов.
Также между собой числа Фибо связаны и «золотой пропорцией». Это коэффициент 0,618. Начиная с 4 члена, каждое предыдущее число меньше последующего в 0,618 раз. Если любой член ряда Фибо разделить не на следующее число, а на число через один, то получим соотношение, приближенное к 0,382. А если возьмем третий член ряда после исходного, то соотношение между ними будет приблизительно 0,236.
Математик не открыл эту пропорцию, он только напомнил ее человечеству, ведь эти зависимости знали и использовали еще древние греки при строительстве Парфенона, египтяне для своих знаменитых пирамид.
Именно приближенность ряда Фибоначчи к «золотому сечению» обусловила создание на его основе набора инструментов для анализа и прогнозирования динамики рынка: веерные линии, дуги, уровни коррекции и временные периоды Фибоначчи.
Чаще всего используют 5 уровней коррекции. Между ними тоже наблюдается «золотая пропорция». Если мы уровень 61,8 умножим на 0,618, то получим уровень 38,2. В сумме они дают 100%. Уровни 23,6 и 76,4 тоже в сумме составляют 100%. Но сам я пользуюсь уровнем 78.6, получается он извлечением корня из 0.618.
В сумме они дают 100%. Уровни 23,6 и 76,4 тоже в сумме составляют 100%. Но сам я пользуюсь уровнем 78.6, получается он извлечением корня из 0.618.
Ключевые уровни – 38,2%, 50%, 61,8%, они будут оказывать наибольшее сопротивление и поддержку при изменениях курса.
Значения коррекции Фибоначчи: определение и схемы
Уровни коррекции Фибоначчи были адаптированы для трейдинга на бирже в соответствии с трудами Леонардо Фибоначчи – это известный итальянский математик, который вывел уникальный ряд чисел, которые впоследствии стали носить его имя. Он написал три великих работы. Благодаря одной из этих книг Европа узнала о индо-арабской системе чисел, которая не вписывалась в принятые рамки. Фибоначчи стал толчком для многих математиков и физиков.
Числа Фибоначчи – это числовая последовательность, в которой следующее число равняется суме двух предыдущих.
Числа Фибоначчи:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 188 (далее до бесконечности).
Основной особенностью этих чисел является постоянная связь между элементами ряда. Любопытных взаимосвязей множество.
Так, основными свойствами этой последовательности являются:
- Любое число — сумма двух предыдущих.
- Соотношение следующего и предыдущего чисел в ряду стремится к 1,618.
- Соотношение предыдущего и последующего чисел стремится к 0,618 и т.д.
Числа Фибоначчи принято считать математическим обоснованием «золотого сечения»: если отрезок разделить с помощью коэффициента 0,618, то соотношения отрезков сохранятся.
На фондовых площадках принято считать, что коррекция в большинстве случаев останавливается на числах Фибоначчи. Поэтому они так популярны в техническом анализе.
Когда происходит коррекция, рынок или разворачивается на уровнях Фибоначчи или демонстрирует отскок. Уровни Фибоначчи при этом — 23,6, 38,2, 50, 61,8, 76,4. Последний практически никогда не используется.
Чтобы построить уровни коррекции Фибоначчи нужно от минимальной точки трендового движения до максимальной провести линию, на которой нужно отметить уровни Фибоначчи 23,6%, 38,2%, 50%, 61,8% и 76,4%. По теории это и есть уровни самых вероятных коррекций тенденции.
По теории это и есть уровни самых вероятных коррекций тенденции.
Некоторые трейдеры проводят через эти уровни дополнительные горизонтальные линии. В результате получается «веер Фибоначчи». Эти проведенные линии принято считать линиями поддержки и сопротивления.
Существует два основных способа применения:
Для определения глубины коррекции.
Для определения возможных ценовых уровней при продолжении движения, после завершения коррекции.
Все остальное, модификации и наработки, например как у меня. По глубине коррекции, с помощью дополнительных уровней, я определяю цели. При достижении целей, цена, как правило, откатывает.
Но обо всем по порядку
Основными уровнями в стандартной линейке являются уровни 23,6%, 38,2%, 50,0%, 61,8%. Но только три последних являются ключевыми уровнями и оказывают наибольшее сопротивление и поддержку при изменениях курса цены. Но с большей популяризацией дополнительныхуровней, таких как 76,4% или 78,6%, 86. 0%, я бы не стал называть выше указанные уровни ключевыми. Да, они по-прежнему оказывают наибольшее влияние, но и маркет-мейкеры тоже «хитрят» и стали играть на прорыв 3 основных уровней.
0%, я бы не стал называть выше указанные уровни ключевыми. Да, они по-прежнему оказывают наибольшее влияние, но и маркет-мейкеры тоже «хитрят» и стали играть на прорыв 3 основных уровней.
Если начинается коррекция, то откат может быть на треть тенденции (38,2%), может быть наполовину (50%), на две трети (61,8%) во многих источниках это указывается как максимальный размер коррекции. Но по моим наблюдениям максимальный размер – это уровень 86,0%. Если цена откатывает больше, чем на 86,0 % – это уже не коррекция, а разворот движения в другую сторону. Это из личных наблюдений, говорить о чистой математике здесь бесполезно.
Определить точку завершения коррекции, очень сложно, я бы сказал практически невозможно. Коррекция выполняет свою задачу (приводит рынок в относительное равновесие) либо за счет глубины, либо за счет продолжительности. Заранее определить каким способом, это будет происходить, не возможно, а ведь от этого зависит определение цели. Так что, если цена не остановилась на одном из уровней, то, вероятно, дойдет до следующего.
Поговорим, о том, как необходимо все же правильно использовать и строить линейку Фибоначчи.
Линейка раскладывается между двумя ключевыми точками, на рисунке точки (1) и (2).
Как правило, за ключевые точки берутся локальные экстремумы, т.е. high и low за какой то период, к примеру, внутри дня. Я для этого включил отображение разделителей периодов. Но, бывают моменты, когда один экстремум находится в прошлом периоде, а второй в действующем. Это допускается.
Если цена выходит за уровни 0% и 100%, то для Фибо нужно искать другие ключевые точки.
На рисунке, я пометил крестиком, что построение синей линейки Фибо, неверно. Строить лучше так, как построена оранжевая на рисунке. Будет надежнее
Ниже еще один пример:
Но будьте внимательны, очень часто при таких ситуациях, происходит смена направления движения.
Если нам необходимо измерить глубину коррекции к волне (А), то используем предыдущую тенденцию, потому что движение сейчас – это коррекция к тому, что было раньше.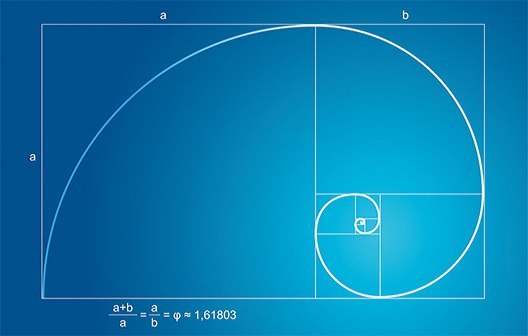 Т.е если сейчас курс идет вниз (В), то раскладывать фибо мы будем по предыдущему восходящему движению и наоборот. Всегда работаем от прошлого к будущему.
Т.е если сейчас курс идет вниз (В), то раскладывать фибо мы будем по предыдущему восходящему движению и наоборот. Всегда работаем от прошлого к будущему.
Раскладываем линейку так, чтобы уровень 0% находился в точке (2), точка завершения движения и начала коррекции, а уровень 100% в точке (1), точка начала движения, и тогда уровни будут располагаться по возрастающей. (Если Вы используете только три ключевых уровня 38,2; 50,0; 61,8, то принципиальной разницы не будет, как вы разложите линейку).
Строить можно на любых ТФ (таймфреймах, временных периодах). Все будет зависеть от того, какой ТФ у вас является рабочим. Например, для 15-ти минутных движений разложить уровни в таймфрейме 30 минут или 1 час. Если же Вы работаете с движениями, происходящими в часах, то фибо можно поставить на 4-х часах или днях, т.е. в периодах, которые по любому охватят нужное нам движение.
Использование Фибо в торговле
Техника на отбой
При движении курса может не сформироваться никакого четкого тренда, может не быть технических фигур, но уровни есть всегда.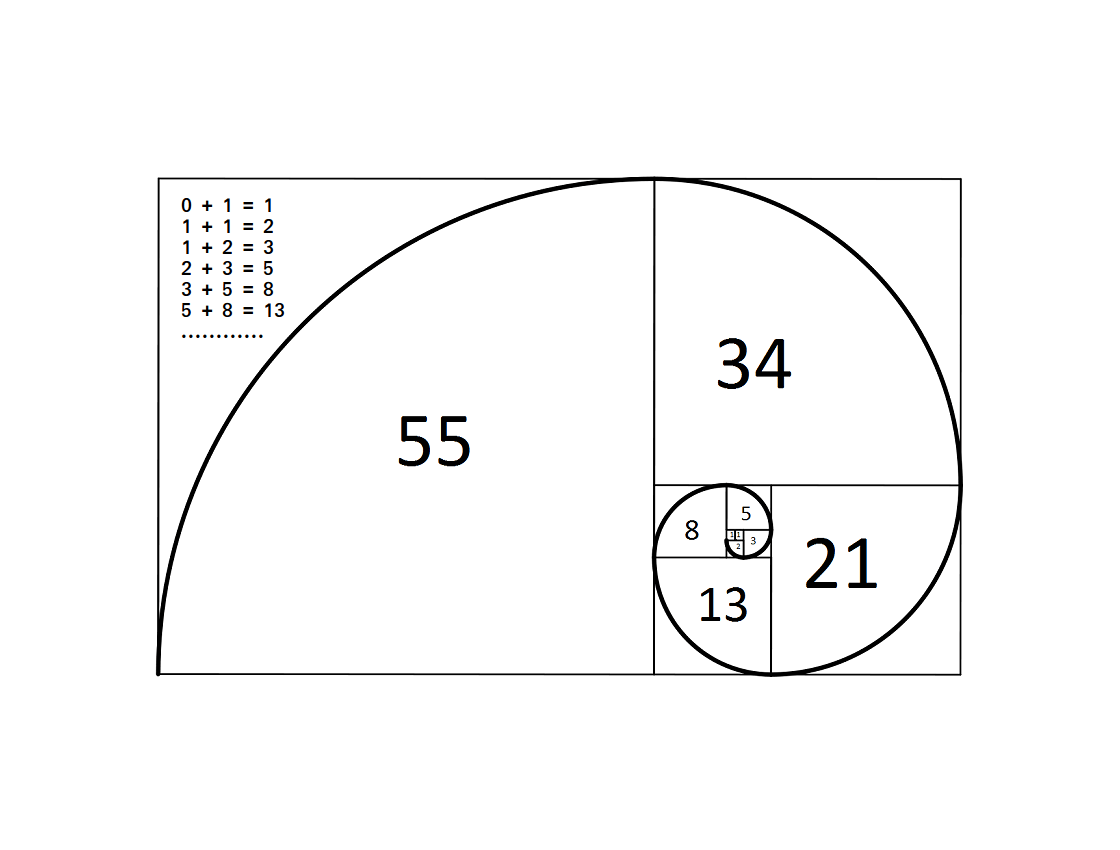 И Вы должны понимать где необходимо выйти из сделки.
И Вы должны понимать где необходимо выйти из сделки.
Уровни коррекции Фибо в этом смысле очень удобны в использовании. Во-первых, они показывают области сопротивления и поддержки, во-вторых, возможный размер коррекции. При этом на них распространяются все правила уровней.
Если вы видите, что цена подходит к уровню, то высока вероятность разворота, так как цене легче откатить, чем пытаться преодолеть какое-то препятствие. Соответственно, вы можете планировать уже следующую сделку после отскока курса от уровня. При этом в чем большем таймфрейме построена эта линейка, тем более сильное сопротивление уровни будут оказывать.
Предлагаю рассмотреть это на текущей (на момент написания статьи) ситуации по евродоллару. Для построения Фибо мы используем сильную восходящую тенденцию, которая образовалась в начале марта. Вторая ключевая точка стоит на историческом максимуме, за которым начался откат, что естественно после такого стремительного движения. Зная, что коррекция может быть больше, чем на треть движения, мы можем прогнозировать, что падение еще может продолжаться приблизительно до значения 1,3245, так как до этого движение цены ничего не сдерживает.
Далее, когда цена подойдет к уровню 38,2 (а это один из самых сильных), по классическим правилам теханализа с большей вероятностью курс оттолкнется и развернется вверх. Можно планировать сделку на покупку, и фиксировать прибыль перед уровнем 23,6, где-то в значении 1,3420-1,3430. Мы не закладываем в цель количество пунктов до самого уровня, потому что это все-таки исторический экстремум. Это общее правило для всех сделок – не рассчитывать в Тейк Профит тенденцию на все 100%, а брать на 70-80%, потому что рынок непредсказуем, и угадать его до пункта невозможно. Если мы поставим на покупку от уровня 38,2, то наша прибыль составит около 120-150 пунктов. То же самое и по поводу остальных уровней, но Вы должны понимать, что такая техника, с очень большим риском. Т.к. курс цены не всегда отбивается от каждого уровня, а при сильном импульсе проскакивает уровень до следующего.
Техника на пробой
Основное правило при работе с уровнями Фибо – работать в сторону пробоя. Хотя сам я работаю немного по-другому, я обычно вхожу в рынок после завершения коррекции, т.к. немного модифицированная мною линейка уже дает определять цели.
Хотя сам я работаю немного по-другому, я обычно вхожу в рынок после завершения коррекции, т.к. немного модифицированная мною линейка уже дает определять цели.
Итак, если уровень 38,2% будет пробит, и курс обвалится ниже, то, конечно, будем продавать. И тогда цель будет уже возле 50%, в значении 1,3100. Нужно учитывать и ситуацию «ложного» пробоя, т.е. когда цена вроде бы опускается ниже уровня, но потом идет возврат, и пробития как такового нет. Пробоем считается ситуация, когда новая свеча полностью открылась и закрылась за ключевым уровнем. Если за уровень вышел только шип, то здесь на пробой мы не работаем (смотрите свечу от 8 апреля).
Поэтому сделки мы открываем, если цена опускается ниже предыдущих шипов, в нашем примере это ниже 1,3157 (цена, которая находится за уровнем 38,2 и за шипом, который на этот уровень пробивался 9 апреля). В этом случае прибыль может составить порядка 50-60 пунктов. В данном примере сделку можно было начать и раньше,
Определение возможных ценовых уровней
Третий метод интереснее. Как я писал в начале, линейку фибо также применяют для определения возможных ценовых уровней при продолжении движения, после завершения коррекции. Как это работает?
Как я писал в начале, линейку фибо также применяют для определения возможных ценовых уровней при продолжении движения, после завершения коррекции. Как это работает?
В первую очередь, для этого линейку раскладывают наоборот. Т.е. уровень 0 не в точке завершения движения, а наоборот, в точке его начала.
И тогда в работу включаются дополнительные уровни 161,8%, 261,8%, 423,0% часто добавляют уровень 200,0%.
Эти уровни, дают возможные цели, если существующая тенденция сохранится. Вы видите, как на рисунке, курс цены, после того как завершил корректироваться, продолжил восходящее движение и достиг сначала уровня 161,8%, а затем и 200,0%. Но, увы, это бывает не всегда. Не зря, все таки, называют, возможные ценовые уровни.
Этот метод хорошо сочетать с техникой на отбой от уровней фибо. Но, Вы также должны понимать, что, пытаясь войти на каждом уровне на отбой, Вы также рискуете, если не знаете, на каком уровне завершится коррекция.
Как это можно использовать. Ждете подтверждения, что коррекция завершилась и входите либо на отбой на самом уровне, либо уже после того, как видно, что коррекция действительно закончилась, и по целевым уровням выставляете тейк-профит и ждете. Главное не забывайте перемещать стоп-лосс в безубыток.
Ждете подтверждения, что коррекция завершилась и входите либо на отбой на самом уровне, либо уже после того, как видно, что коррекция действительно закончилась, и по целевым уровням выставляете тейк-профит и ждете. Главное не забывайте перемещать стоп-лосс в безубыток.
Дополнительные уровни
Читая форумы, постоянно вижу, что большинство трейдеров использует лишь основные уровни – 38.2%, 50% и 61.8% линейки фибо. Поэтому хочу поделиться своими наблюдениями…. Я в торговле использую не только основные уровни, но и дополнительные, такие как 78.6%, 86% и 94.2%.
Что они дают?
Итак, дополнительные уровни, так же указывают на уровень завершения коррекции, и, как правило это далеко не самые слабые уровни, как считают многие, присваивая основным уровням силу по нарастанию.
Об этих мало используемых уровнях мало написано, но они упоминаются в работах Гартли и Пессавенто…. И довольно успешно работают…
Но, как говорят многие, и я в том числе, торговать необходимо по тренду, ловить коррекции дело неблагодарное. Большинство трейдеров видя, что цена пробила 62 уровень фибо, думают, что коррекция переросла в новое движение. И поэтому не входят в рынок, либо открываются по направлению пробоя. Но цена, дойдя до дополнительных уровней, начинает консолидироваться либо совершает обратный прыжок и уходит по направлению предыдущего движения. Это касаемо 78.6% и 86% уровней.
Большинство трейдеров видя, что цена пробила 62 уровень фибо, думают, что коррекция переросла в новое движение. И поэтому не входят в рынок, либо открываются по направлению пробоя. Но цена, дойдя до дополнительных уровней, начинает консолидироваться либо совершает обратный прыжок и уходит по направлению предыдущего движения. Это касаемо 78.6% и 86% уровней.
А 94.2% уровень я использую как уровень, который говорит, что уже точно не коррекция…Итак.
Все уровни фибо, можно использовать как точки входа. Можно входить от каждого уровня, но это не безопасно, увеличивается возможность получения убытка. Поэтому, используйте линейку фибо, как дополнение к своей торговой тактике, и если на каком либо уровне фибо есть еще и дополнительные индикаторы – средние скользящие, пивот поинты, то такие входы будут более безопасными. И определяйте цели по своей ТС.
ЧИСЛА ФИБОНАЧЧИ: МИФ ИЛИ РЕАЛЬНОСТЬ?!
ЧИСЛА ФИБОНАЧЧИ: МИФ ИЛИ РЕАЛЬНОСТЬ?!
Круглов Н. П. 1
П. 11Областное Государственное Бюджетное Профессиональное Образовательное Учреждение «Костромской торгово-экономический колледж»
Холинова О.А. 11Областное Государственное Бюджетное Профессиональное Образовательное Учреждение «Костромской торгово-экономический колледж»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
ВВЕДЕНИЕ
Математику называют «царицей всех наук». Древняя история богата выдающимися математиками. Многие достижения древней математической науки до сих пор вызывают восхищение остротой ума их авторов, а имена Евклида, Архимеда, Герона известны каждому образованному человеку. Иначе обстоит дело с математикой средневековья. Математика в эту эпоху развивалась чрезвычайно медленно, и крупных математиков тогда было очень мало. Тем больший интерес представляет для нас сочинение «Liber abacci» («Книга об абаке»), написанная знаменитым итальянским математиком Леонардо из Пизы (ок. 1170-после 1228), более известный под прозвищем Фибоначчи, который был, безусловно, самым значительным математиком средневековья. Роль его книг в развитии математики и распространении в Европе математических знаний трудно переоценить.
1170-после 1228), более известный под прозвищем Фибоначчи, который был, безусловно, самым значительным математиком средневековья. Роль его книг в развитии математики и распространении в Европе математических знаний трудно переоценить.
В исследовательской работе рассматриваются числа последовательности Фибоначчи, их свойства, а также, тесно связанный с этой темой, феномен золотого сечения, в котором большинство ученых видят одно из наиболее ярких, давно уже замеченных человеком проявлений гармонии природы. Феномен золотого сечения рассмотрен в работе в общей картине исторического становления архитектуры, на формах живой природы и за пределами предметного мира, в области гармонии и математических абстракций. Он рассмотрен и как объективная характеристика объектов искусства, экономики и т. д.
Общеизвестно, что золотое сечение – это закон пропорциональной связи целого и составляющих это целое частей. Классический пример золотого сечения – деление отрезка в среднепропорциональном отношении, когда целое так относится к большей своей части, как большая часть – к меньшей: (a+b)/b = b/a. Такая задача имеет решение в виде корней уравнения x2 – x – 1 = 0.За кажущейся простотой операции деления в крайнем и среднем отношении скрыто множество удивительных математических свойств и множество форм выражения пропорции золотого сечения.
Такая задача имеет решение в виде корней уравнения x2 – x – 1 = 0.За кажущейся простотой операции деления в крайнем и среднем отношении скрыто множество удивительных математических свойств и множество форм выражения пропорции золотого сечения.
Золотое сечение, как и загадочные свойства чисел Фибоначчи, владели мыслью и чувствами многих выдающихся мыслителей прошлого и продолжает волновать умы современников наших не ради самих математических свойств, а потому, что неотделимо от ценности объектов искусства и в то же время обнаруживает себя как признак структурного единства объектов природы. Скульптура, архитектура, музыка, астрономия, биология, психология, техника – вот те сферы, где так или иначе обнаруживает свою жизнь золотое сечение. Современные исследователи находят его при описании строения растений, пропорций тел животных, птиц, человека, в статистике популяций, в строении глаза и строении космоса и т. д.
Сегодня невозможно с абсолютной достоверностью определить, когда и как понятие золотого сечения было выделено в человеческом знании из интуитивной и опытной категорий.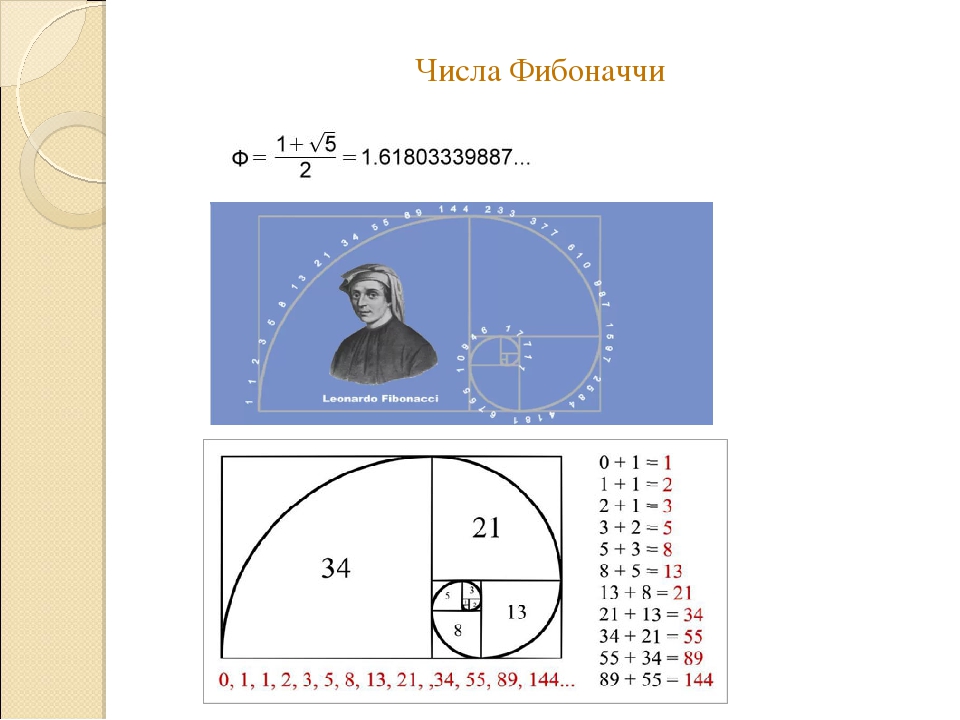 Но судить обоснованно, кто прав: те ли, кто относит открытие золотого сечения к цивилизациям древнего Востока (Египет. Индия), или те, кто, подобно Кеплеру, связывает открытие золотого сечения с именем Пифагора, можно, но для этого необходимо владеть базовыми историческими и математическими познаниями.
Но судить обоснованно, кто прав: те ли, кто относит открытие золотого сечения к цивилизациям древнего Востока (Египет. Индия), или те, кто, подобно Кеплеру, связывает открытие золотого сечения с именем Пифагора, можно, но для этого необходимо владеть базовыми историческими и математическими познаниями.
В эпоху Ренессанса среднепропорциональное отношение именовали Sectio divina – божественной пропорцией. Леонардо да Винчи дает ему имя Sectio aurea (золотое сечение), живое поныне, а много раньше, в 1202 г., открытием ряда Фибоначчи было обнажено фундаментальное свойство золотого сечения – единство аддитивности и мультипликативности.
Сегодня сущность гармонии невозможно выявить ни в биологии, ни в искусстве, ни в абстрактно-математических построениях, если рассматривать их раздельно, – здесь можно лишь наблюдать и осмысливать ее проявления. «Философия, – говорил Галилео Галилей, – написана в той величественной книге, которая постоянно открыта у нас перед глазами (я имею в виду Вселенную), но которую невозможно понять, если не научиться предварительно ее языку и не узнать те письмена, которыми она начертана». «Божественная пропорция – бесценное сокровище, одно из двух сокровищ геометрии», – развивает эту же мысль Кеплер. Действительно, гармония может быть расшифрована лишь на ее собственном языке, отображенном фундаментальными принципами естествознания.
«Божественная пропорция – бесценное сокровище, одно из двух сокровищ геометрии», – развивает эту же мысль Кеплер. Действительно, гармония может быть расшифрована лишь на ее собственном языке, отображенном фундаментальными принципами естествознания.
Существуют любопытные закономерности, которые могут быть описаны с помощью математики. Во вселенной еще много неразгаданных тайн, некоторые из которых ученые уже смогли определить и описать. Числа Фибоначчи и золотое сечение составляют основу разгадки окружающего мира, построения его формы и оптимального зрительного восприятия человеком, с помощью которых он может ощущать красоту и гармонию.
Актуальность данной работы заключается в необходимости исследования чисел Фибоначчи, так как они встречаются нам в различных творениях природы. Знания о них будут полезны во многих науках.
Цель: изучить практическую значимость чисел Фибоначчи
Задачи:
1. Познакомиться с числами Фибоначчи и историей их создания.
Познакомиться с числами Фибоначчи и историей их создания.
2. Рассмотреть рекурентную формулу ряда Фибоначчи.
3. Познакомиться с биографией итальянского математика Леонардо Пизанского (Фибоначчи).
4. Изучить свойства числового ряда Фибоначчи
5. Проверить на практике проявление чисел Фибоначчи в неживой природе, в строении человека и растений.
Предмет исследования — числа Фибоначчи.
Объект исследования — область применения чисел Фибоначчи; свойства чисел Фибоначчи.
Проблема, которую призвано разрешить наше исследование, заключается в том, что мы не знаем и не видим в окружающей нас жизни числовые закономерности, которые укладываются в ряд Фибоначчи.
Изучение этих чисел не предусмотрено уроками математики, поэтому чтобы познакомится с ними подробнее, необходимо использовать разнообразные источники информации: дополнительную литературу по предмету и интернет ресурсы.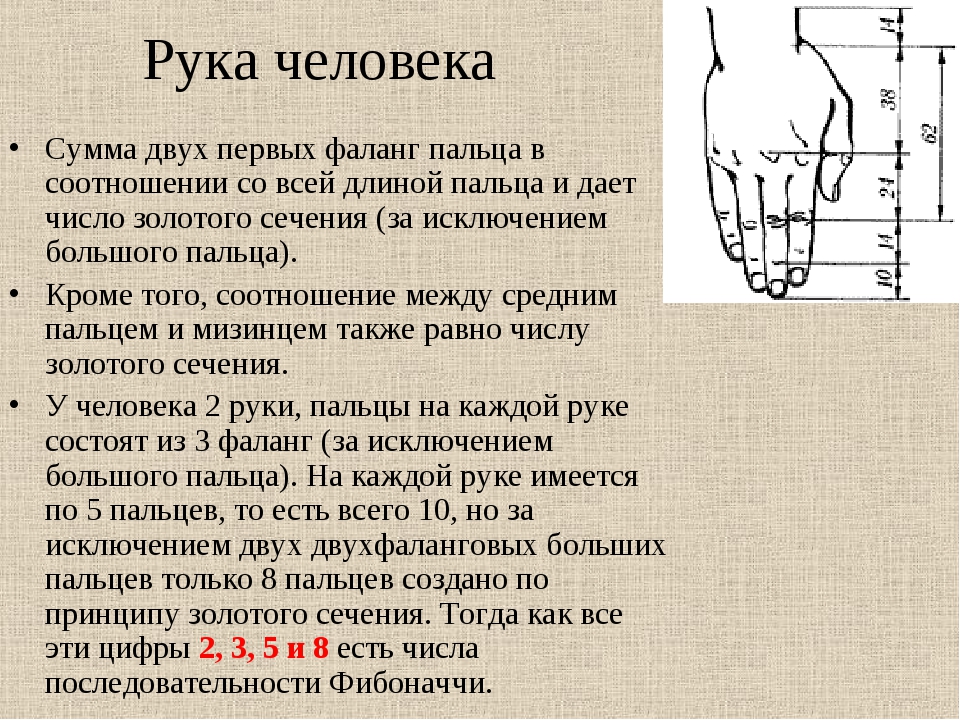
Методы исследования в работе:
теоретический (логическая ступень познания).
эмпирический (наблюдение, эксперимент, измерение).
сравнение.
классификация.
математическое моделирование
практический (расчеты числа фи)
Структура работы: исследовательская работа состоит из введения, двух глав, заключения, списка используемой литературы. Во введении определена актуальность темы, связанная с понятием последовательности ряда Фибоначчи и проявление чисел Фибоначчи в неживой природе, в строении человека и растений, цели, задачи, объекты и методы исследования. В первой главе описана историческая справка о Леонарде Пизанском, итальянском математике средневековья; последовательность ряда Фибоначчи и его свойства. Во второй главе рассмотрены проявления последовательности Фибоначчи в окружающем мире. Далее следует заключение. В нем определены выводы по проделанной работе. В списке используемых источников перечислена основная литература, которая использовалась в процессе работы.
Далее следует заключение. В нем определены выводы по проделанной работе. В списке используемых источников перечислена основная литература, которая использовалась в процессе работы.
В теоретической части исследования была изучена литература по данной теме, узнали, как образуется этот ряд, историю его возникновения, какими свойствами он обладает. Рассмотрели разные объекты природы где, обнаруживает себя ряд Фибоначчи. Оказывается, эти числа можно найти в подсолнухах и сосновых шишках, в крыльях стрекозы и морских звёздах, в ритмах человеческого сердца и в музыкальных ритмах, в строении человеческого тела и в строении раковин моллюсков, в океане, в космосе и т.д. В проверке этих фактов заключается практическая часть нашего исследования.
1 Числа Фибоначчи.
1.1.Биография Леонардо Пизанского
Удивительные числа были открыты итальянским математиком средневековья Леонардо Пизанским, более известным под именем Фибоначчи. Леонардо Пизанский (Фибоначчи)– это первый крупный математик средневековой Европы. Более известен под прозвищем Фибоначчи, что в переводе с итальянского означает «хороший сын родился».
Леонардо Пизанский (Фибоначчи)– это первый крупный математик средневековой Европы. Более известен под прозвищем Фибоначчи, что в переводе с итальянского означает «хороший сын родился».
Точная дата его рождения неизвестна. Предположительно Фибоначчи родился в 1170г. в городе Пиза, в Италии. Леонардо из Пизы, известный как Фибоначчи, был первым из великих математиков Европы позднего Средневековья. Будучи рожденным в Пизе в богатой купеческой семье, он пришел в математику благодаря сугубо практической потребности установить деловые контакты.
Его отец был купцом и государственным вельможей, представителем нового класса бизнесменов. Тогда Пиза была одним из крупнейших коммерческих центров, активно сотрудничавших с исламским Востоком, и отец Фибоначчи энергично торговал на северном побережье Африки, по торговым делам часто бывал в Алжире. Благодаря этому ему удалось «устроить» своего сына в одну из арабских школ, где он смог получить превосходное для того времени математическое образование.
Леонардо изучал труды математиков востока, по арабским переводам он ознакомился также с достижениями античных и индийских математиков.
Все эти знания он впитывал в себя как губка. А потом принес их в Европу, он «открыл» арабские цифры вместо римских и десятичную систему счисления для европейцев. Значительную часть усвоенных им знаний он изложил в своей выдающейся «Книге абака» (Libег аЬасi, 1202; до наших дней сохранилась только дополненная рукопись 1228 г.). Эта книга содержит почти все арифметические и алгебраические сведения того времени, изложенные с исключительной полнотой и глубиной и одно из величайших открытий всех времён и народов – десятичную систему счисления.
На протяжении нескольких столетий по труду Фибоначчи ученые знакомились с двумя важнейшими разделами математики – арифметикой и алгеброй и черпали из него задачи и оригинальные методы решения, благодаря чему уже в XV – XVI в. в. те разошлись по многочисленным итальянским, французским, немецким, английским, а позже и русским рукописям, печатным книгам и учебникам.
в. те разошлись по многочисленным итальянским, французским, немецким, английским, а позже и русским рукописям, печатным книгам и учебникам.
Когда Леонардо вернулся в Италию, там правил император Фридрих II. Он не признавал рыцарские турниры, вместо них он проводил гораздо менее кровавые математические соревнования, на которых противники обменивались не ударами, а задачами. На таких турнирах и заблистал талант Леонардо Фибоначчи.
Предположительно Фибоначчи умер во время одного из Крестовых походов в 1228 году, сопровождая императора Фридриха II.
1.2. Числа Фибоначчи и их свойства.
Древняя история богата выдающимися математиками. Многие достижения древней математической науки до сих пор вызывают восхищение остротой ума их авторов, а имена Евклида, Архимеда, Герона известны каждому образованному человеку.
Иначе обстоит дело с математикой средневековья. Кроме Виета, жившего в шестнадцатом столетии, и математиков более близких нам времен школьный курс математики не называет ни одного имени, относящегося к средним векам. Это, конечно, не случайно. Математика в эту эпоху развивалась чрезвычайно медленно, и крупных математиков тогда было очень мало. Тем больший интерес представляет сочинение «Liber abacci» («Книга об абаке»), написанная знаменитым итальянским математиком Леонардо из Пизы, который известен больше по своему прозвищу Фибоначчи (Fibonacci – сокращенное filius Bonacci, т. е. сын Боиаччи). Эта книга, написанная в 1202 г., дошла до нас во втором своем варианте, который относится к 1228 г.
Кроме Виета, жившего в шестнадцатом столетии, и математиков более близких нам времен школьный курс математики не называет ни одного имени, относящегося к средним векам. Это, конечно, не случайно. Математика в эту эпоху развивалась чрезвычайно медленно, и крупных математиков тогда было очень мало. Тем больший интерес представляет сочинение «Liber abacci» («Книга об абаке»), написанная знаменитым итальянским математиком Леонардо из Пизы, который известен больше по своему прозвищу Фибоначчи (Fibonacci – сокращенное filius Bonacci, т. е. сын Боиаччи). Эта книга, написанная в 1202 г., дошла до нас во втором своем варианте, который относится к 1228 г.
«Liber abacci» представляет собой объемистый труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший заметную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими («арабскими») цифрами.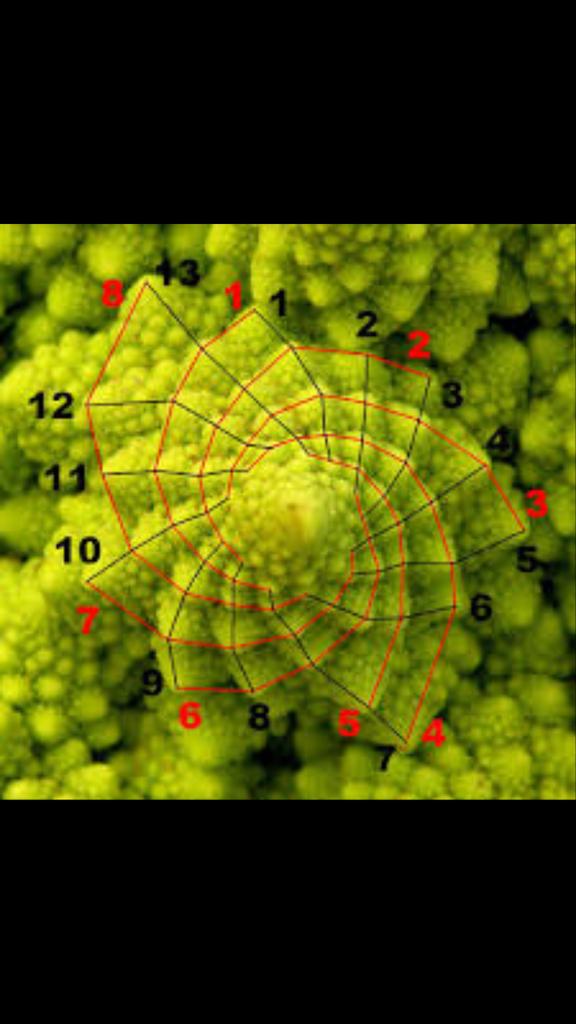 Сообщаемый в «Liber abacci» материал поясняется на большом числе задач, составляющих значительную часть этого трактата. Рассмотрим одну такую задачу, помещенную на стр. 123-124 рукописи 1228 г.
Сообщаемый в «Liber abacci» материал поясняется на большом числе задач, составляющих значительную часть этого трактата. Рассмотрим одну такую задачу, помещенную на стр. 123-124 рукописи 1228 г.
«Сколько пар кроликов в один год от одной пары рождается?»
«Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения. Так как первая пара в первом месяце дает потомство, удвой, и, рождает и в следующем месяце, так что во втором месяце оказывается 3 пары; из них в следующем месяце 2 пары будут давать потомство, так что в третьем месяце родятся еще 2 пары кроликов, и число пар кроликов в этом месяце достигнет 5; из них в этом же месяце будут давать потомство 3 пары, и число пар кроликов в четвертом месяце достигнет 8; из них 5 пар произведут другие 5 пар, которые, сложенные с 8 парами, дадут в пятом месяце 13 пар; из них 5 пар, рожденных в этом месяце, не дают в том же месяце потомства, а остальные 8 пар рождают, так что в шестом месяце оказывается 21 пара; сложенные с 13 парами, которые родятся в седьмом месяце, они дают 34 пары; сложенные с 21 парой, рожденной в восьмом месяце, они дают в этом месяце 55 пар; сложенные с 34 парами, рожденными в девятом месяце, они дают 89 пар; сложенные вновь с 55 парами, которые рождаются в десятом месяце, они дают в этом месяце 144 пары; снова сложенные с 89 парами, которые рождаются в одиннадцатом месяце, они дают в этом месяце 233 пары; сложенные вновь с 144 парами, рожденными в последнем месяце, они дают 377 пар; столько пар произвела первая пара в данном месте к концу одного года.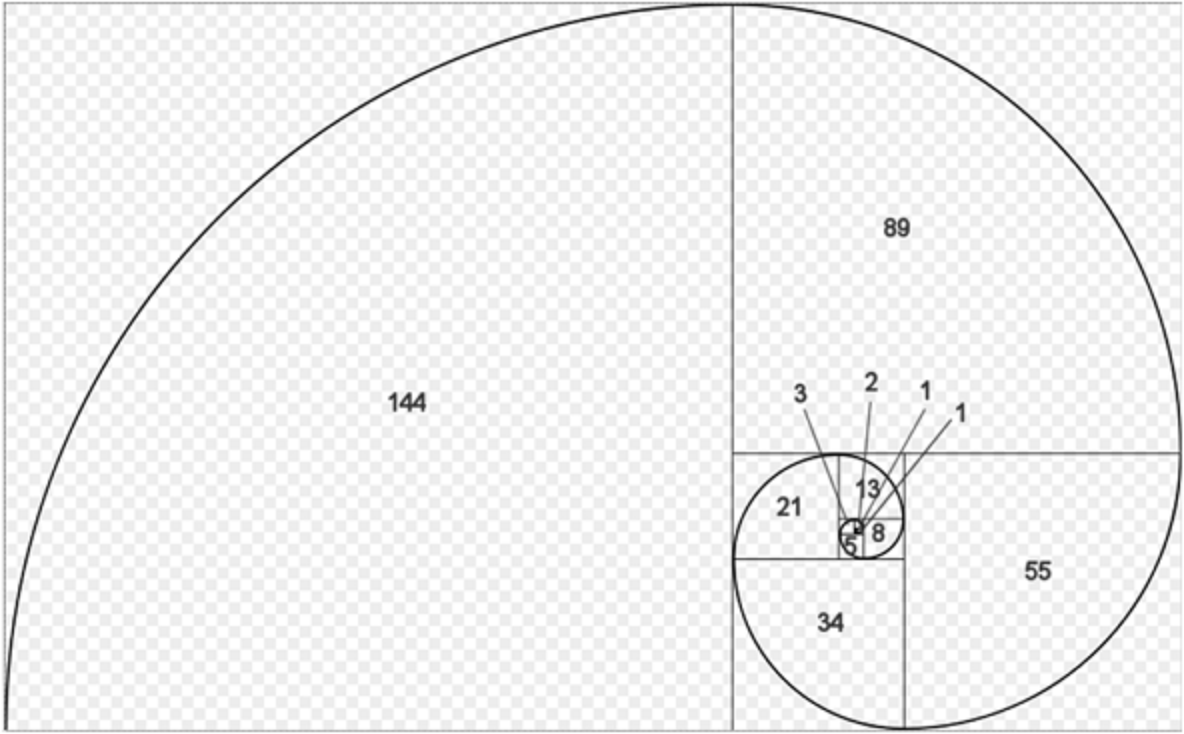
Действительно, на этих полях ты можешь увидеть, как мы это делаем; именно, мы складываем первое число со вторым, т. е. 1 и 2; и второе с третьим; и третье с. четвертым; и четвертое с пятым; и так одно за другим, пока не сложим десятое с одиннадцатым, т. е. 144 с 233; и мы получим общее число упомянутых кроликов, т. е. 377; и так можно делать по порядку до бесконечного числа месяцев».
Построим алгебраическую модель задачи о кроликах и рассмотрим следующую числовую последовательность: , в которой u1 = u2 = 1, а каждый член последовательности, начиная с третьего, равен сумме двух предыдущих членов, то есть при всяком n > 2 выполняется равенство: .
Такие последовательности, в которых каждый член определяется как некоторая функция предыдущих, часто встречаются в математике и называются рекуррентными или, по-русски, возвратными последовательностями. Сам процесс последовательного определения элементов таких последовательностей называется рекуррентным процессом, а равенство (2) – возвратным (рекуррентным) уравнением [2].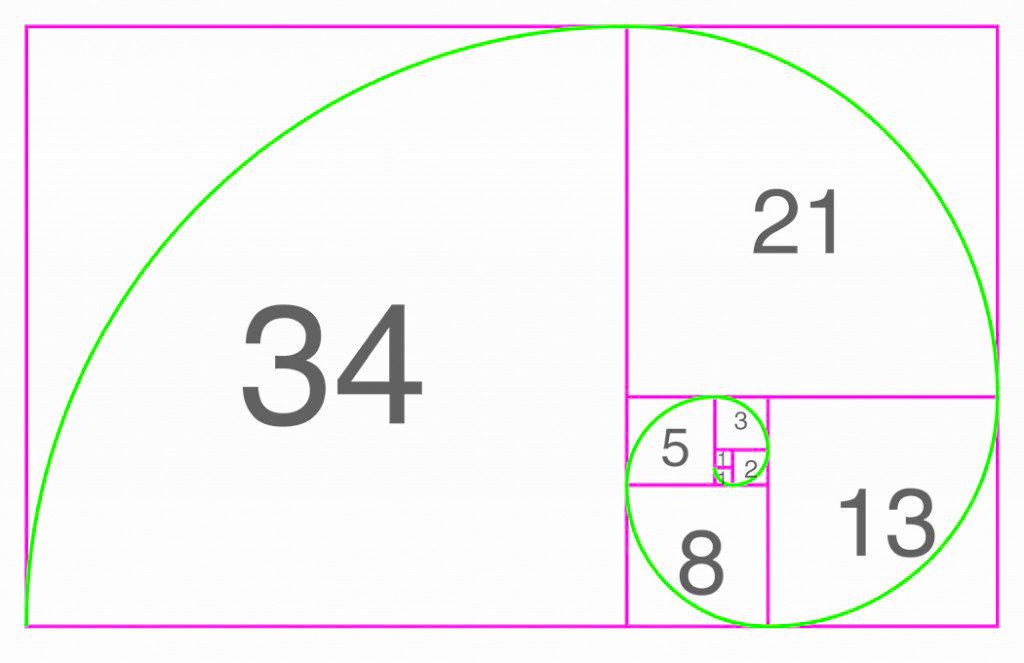
Возвратная последовательность, задаваемая условием u1 = u2 = 1 и формулой (2) называется последовательностью Фибоначчи, а её члены –
числами Фибоначчи.
Перечислим основные свойства последовательности Фибоначчи.
1) Каждое следующее число, начиная с третьего равно сумме двух предыдущих.
2) Отношение каждого числа к последующему при увеличении порядкого номера все более и более стремится к 0,618.
3) Отношение каждого числа ряда к предыдущему стремится к 1,618.
Последовательность Фибоначчм асимптотически (пpиближаясь все медленнее и медленнее) стремится к некотоpому постоянному соотношению. Однако, это соотношение иppационально, то есть пpедставляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифp в дpобной части. Его невозможно выразить точно.
Его невозможно выразить точно.
Если какой-либо член последовательности Фибоначчи pазделить на пpедшествующий ему pезультатом будет величина, колеблющаяся около иppационального значения 1.61803398875… и чеpез pаз то пpевосходящая, то не достигающая его. Hо даже затpатив на это Вечность, невозможно узнать сотношение точно, до последней десятичной цифpы. Kpаткости pади, мы будем пpиводить его в виде 1.618. Лука Пачиоли (сpедневековый математик) назвал его Божественной пpопоpцией. Cpеди его совpеменных названий есть такие, как Золотое сечение, Золотое сpеднее и oтношение веpтящихся квадpатов. Kеплеp назвал это соотношение одним из «сокpовищ геометpии». В алгебpе общепpинято его обозначение гpеческой буквой фи.
Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду, как арифметическому выражению закона золотого деления.
Учёные, анализируя дальнейшее применение этого числового ряда к природным феноменам и процессам, обнаружили, что эти числа содержатся буквально во всех объектах живой природы, в растениях, в животных и в человеке.
1.3 Спираль Фибоначчи
Спираль Фибоначчи – это некоторая кривая, которая огибает точку своего центра, приближаясь или удаляясь от неё, все зависит от направления, избранного вами. Эти фигуры могут быть как двухмерными, так и трехмерными, однако, если мы говорим о Фибоначчи, как о рыночной модели, то рассматривать можно только один вариант – двухмерный.
Когда строятся такие фигуры, то используется стартовая точка, построенная на плоскости, радиус выступает в роли непрерывной монотонной функции от угла.
Спираль Фибоначчи, отличается от Золотой пропорции и имеет точку начала. Беря начало в некоторой точке, такая фигура обычно разворачивается бесконечно долго.
У последовательности Леонардо есть интересные свойства. Ряд Фибоначчи отличается от Золотого Сечения, так как начинается с единицы или нуля и при этом стремится к Золотой пропорции.
Также он постоянно увеличивает точность. В некоторой точке (когда почти достигнута фи =1,618) уже невозможно найти разницу, которая прослеживалась между двумя спиралями. Понимание этого свойства Спирали Фибоначчи и определяет её удивительность.
Это поразительно, однако, строение спирали Фибоначчи можно наблюдать в большом количестве предметов и явлений.
2 Числа Фибоначчи в нашей жизни
2.1 Числа Фибоначчи в природе
С тех пор, как Фибоначчи открыл свою последовательность, были найдены много явлений природы, в которых его последовательность чисел прослеживается очень четко. Природа дает нам многочисленные примеры расположения предметов, описываемых числами Фибоначчи.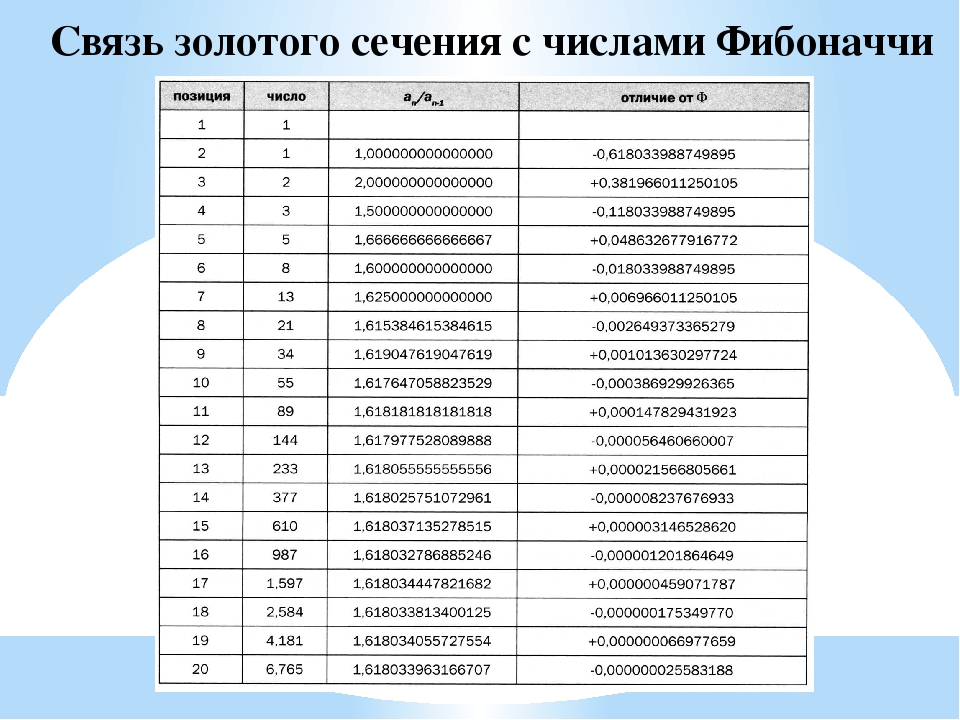 Спиралевидное расположение листьев на ветках деревьев подметили давно. Выяснилось, что в расположении листьев на ветке (филлотаксис — листорасположение), в числе оборотов на стебле, в числе листьев в цикле проявляет себя ряд чисел Фибоначчи.
Спиралевидное расположение листьев на ветках деревьев подметили давно. Выяснилось, что в расположении листьев на ветке (филлотаксис — листорасположение), в числе оборотов на стебле, в числе листьев в цикле проявляет себя ряд чисел Фибоначчи.
Чёткая, симметричная форма цветов также подчинена строгому закону.
У многих цветов количество лепесточков является числами из ряда Фибоначчи.
Встретить числовые закономерности в живой природе можно в различных спиральных формах, которыми так богат мир растений. Обычно можно усмотреть два вида спиралей. В одном спирали завиваются по часовой стрелке, а в другом против. Число «правых «и «левых» спиралей часто оказываются соседними числами Фибоначчи
Можно привести множество примеров.
Первый и очень яркий пример – это подсолнухи. Их семена расположены так, чтобы максимально использовать всю площадь соцветия, не теряя ни миллиметра. А расположены они в виде двух пересекающихся спиралей справа налево и наоборот. Пары этих спиралей встречаются разные, у меньших соцветий 13 и 21, 21 и 34, у больших 34 и 55, 55 и 89. И отклонений от этих пар быть не может.
А расположены они в виде двух пересекающихся спиралей справа налево и наоборот. Пары этих спиралей встречаются разные, у меньших соцветий 13 и 21, 21 и 34, у больших 34 и 55, 55 и 89. И отклонений от этих пар быть не может.
Нечто подобное происходит и с ячейками ананаса: у него 8 правосторонних спиралей, 13 левосторонних и 21 вертикальная. И снова последовательность Фибоначчи.
В сосновой шишке, если хорошо присмотреться, можно увидеть две спирали, закручены одна по часовой стрелкой, а другая против. Число этих спиралей 8 и 13.
Количество лепестков во многих соцветиях совпадает с числами из этой последовательности, например, ирис имеет 3 лепестка, у примулы их 5, у амброзии полыннолистной — 13, у астр бывает 55 или 89 лепестков.
Листья на деревьях и других растениях распределены в последовательности, основанной на золотом числе, таким способом, чтобы получать максимум света и не мешать друг другу.
У многих бабочек отношения размеров грудной и брюшной части тела очень близки к золотому числу.
Раковины моллюсков закручены по спирали, и если измерить ее завитки, то их отношение постоянно и равно 1.618.
Спиралеобразно паук плетет паутину. По спирали закручивается ураган. Стадо северных оленей по тревоге разбегается по спирали. По спирали закручиваются волны, которые разбиваются об берега океана. Молекулы ДНK живых организмов закручены двойной спиралью. Гете называл эту спираль «кривой жизни».
2.2. Числа Фибоначчи в строении животных
Кроме растений, числа Фибоначчи проявляются в строении различных живых организмов. Например, морские звезды. Число лучей у них отвечает ряду чисел Фибоначчи и равно 5, 8, 13.
У хорошо знакомого комара – три пары ног, брюшко делится на 8 сегментов на голове 5 усиков – антенн. И опять мы видим числа 3,5,8, числа последовательности Фибоначчи.
И опять мы видим числа 3,5,8, числа последовательности Фибоначчи.
2.3. Числа Фибоначчи в строении человека
Числа Фибоначчи отражают основную закономерность роста организмов, следовательно проявляются и в строении человеческого тела. Рассмотрим это поподробнее.
У человека одно туловище, одна голова, одно сердце и т. д. Многие части тела и органы парные, например, руки, ноги, глаза, почки. Из трех частей состоят ноги, руки, пальцы рук. На руках и ногах по пять пальцев, а рука вместе с пальцами состоит из восьми частей. Можно рассмотреть части тела и с другой стороны. У человека 2 руки, пальцы на каждой руке состоят из 3 фаланг (за исключением большого пальца). На каждой руке имеется по 5 пальцев, только 8 пальцев трехфаланговые. Все эти цифры 2, 3, 5 и 8 есть числа последовательности Фибоначчи. (Приложение 1, 2).
Позвоночник человека состоит из 34 позвонков. Как видно из приведенного перечисления частей человеческого тела, в его членении на части присутствуют все числа Фибоначчи от 1 до 34. Общее число костей скелета человека близко к 233, то есть отвечает еще одному числу Фибоначчи.
Как видно из приведенного перечисления частей человеческого тела, в его членении на части присутствуют все числа Фибоначчи от 1 до 34. Общее число костей скелета человека близко к 233, то есть отвечает еще одному числу Фибоначчи.
Числа Фибоначчи можно обнаружить и в «крови» у человека. Так распределение людей по трём группам крови отвечает отношениям чисел 8/ 21 /3.
Сердечная мышца сокращается до 0,618 от своей изначальной длины и нарушение этого числа при сокращении ведет к болезням сердца. А это число отражает одно из свойств чисел Фибоначчи. В результате математической обработки экспериментальных медицинских данных, появились отношения чисел, характеризующих сердечный цикл: 0,050; 0,081; 0,131; 0,210; 0,340. Мы видим, что они отражают последовательность ряда чисел Фибоначчи 5, 8, 13, 21, 34. В строении человеческого лица и кисти существуют и иные воплощения ряда Фибоначчи. (Приложение 1, 2).
Этот ряд получается, если провести измерения длин фаланг пальцев и расстояний между различными частями лица.
2.4. Числа Фибоначчи и золотой прямоугольник
Было отмечено, что числа Фибоначчи тесно связаны со спиралевидным строением многих представителей живой и неживой природы. Чтобы рассмотреть еще несколько таких примеров, необходимо познакомиться с так называемым «золотым прямоугольником». Золотой прямоугольник обладает многими необычными свойствами. Отрезав от золотого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, мы снова получим золотой прямоугольник меньших размеров.
Этот процесс можно продолжать до бесконечности. Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие золотые прямоугольники. Причем располагаться они будут по спирали, которая называется спираль Фибоначчи.
Эту спираль можно обнаружить в самых различных и неожиданных предметах и явлениях.
У большинства улиток, которые обладают раковинами, раковина растет в форме спирали. Раковины улиток подчиняются последовательности и спирали Фибоначчи.
Раковины улиток подчиняются последовательности и спирали Фибоначчи.
Паук плетет паутину спиралеобразно. Интересно, что спиралью закручиваются ураган, облака циклона и это хорошо видно из космоса.
Числа Фибоначчи оказались и в спирали, описывающей изгиб гребня набегающей волны в океане, и в спирали, убегающей воды в раковине умывальника. Да и живём мы тоже в спирали, ведь галактика – это спираль, соответствующая спирали Фибоначчи.
На рисунке показаны относительные размеры Земли и Луны в масштабе.
Нарисуем радиус Земли. Проведем отрезок от центральной точки Земли до центральной точки Луны. Нарисуем отрезок для соединения двух данных отрезков, чтобы сформировать треугольник. Получаем золотой треугольник.
Сатурн показывает золотую пропорцию в нескольких ее измерениях
Диаметр Сатурна очень близко находится в отношении золотой пропорции с диаметром колец, как показано зелеными линиями. Радиус внутренней части колец находится в отношении, очень близком к с внешним диаметром колец, как показано синей линией.
Радиус внутренней части колец находится в отношении, очень близком к с внешним диаметром колец, как показано синей линией.
Расстояние планет от Солнца также подчиняется золотой пропорции.
2.5 Числа Фибоначчи в архитектуре
В качестве примера ученые исследовали шедевры архитектуры, созданные по правилам «золотого сечения»: египетские пирамиды, Пантеон, Парфенон, Собор Нотр-Дам де Пари, храм Василия Блаженного и др.
Парфенон — одно из красивейших зданий в Древней Греции (5 в. до н.э.) — имеет 8 колонн и 17 по разным сторонам, отношение его высоты к длине сторон равно 0,618. Выступы на его фасадах сделаны по «золотому сечению» (фото ниже).
Одним из ученых, который придумал и успешно применял усовершенствование модульной системы пропорций для архитектурных объектов (так называемый «модулор»), — был французский архитектор Ле Корбюзье. В основу модулора положена измерительная система, связанная с условным делением на части человеческого тела.
В основу модулора положена измерительная система, связанная с условным делением на части человеческого тела.
Русский архитектор М. Казаков, построивший несколько жилых домов в Москве, а также здания сената в Кремле и Голицынской больницы (сейчас 1-я Клиническая им. Н. И. Пирогова), — был одним из архитекторов, которые использовали при проектировании и строительстве законы о золотом сечении.
2.6.Числа Фибоначчи в искусстве
В конце XIX – начале XX вв. появилось немало чисто формалистических теории о применении золотого сечения в произведениях искусства и архитектуры. С развитием дизайна и технической эстетики применение закона золотого сечения распространилось на конструирование машин, мебели и пр.
Пропорция, выражаемая числом Ф, по мнению многих исследований, является наиболее приятной для человеческого глаза.
Леонардо де Винчи считал, что идеальные пропорции человеческого тела должны быть связаны с числом Ф.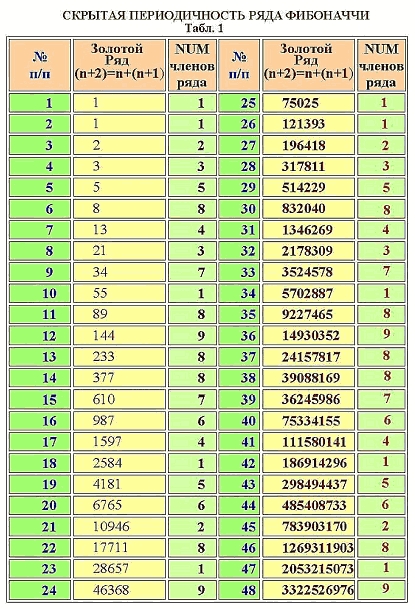 Деление отрезка в отношении Ф он назвал «золотым сечением». В эпоху возрождения «золотое сечение» было очень популярно среди художников, скульпторов и архитекторов. Размеры картины было принято брать такими, чтобы отношение ширины к высоте равнялось Ф. Этот термин сохранился до наших дней, и само «золотое сечение» по прежнему играет важную роль в искусстве. Им руководствовался, например, великий архитектор Ле Корбюзье.
Деление отрезка в отношении Ф он назвал «золотым сечением». В эпоху возрождения «золотое сечение» было очень популярно среди художников, скульпторов и архитекторов. Размеры картины было принято брать такими, чтобы отношение ширины к высоте равнялось Ф. Этот термин сохранился до наших дней, и само «золотое сечение» по прежнему играет важную роль в искусстве. Им руководствовался, например, великий архитектор Ле Корбюзье.
Прямоугольник с таким отношением сторон стали называть «золотым прямоугольником».
Форму «золотого сечения» придавали книгам, столам почтовым открыткам. В дальнейшем книгам и другим бумажным изделиям стали чаще придавать форму прямоугольника с отношением сторон корень из двух. Это связано с тем, что при перегибании такого прямоугольника по средней линии образуются два прямоугольника с тем же соотношением сторон.
Число золотого сечения Ф обладает какой-то странной неуловимостью. Оно появляется в различных проекциях, так и не давая ответа на вопрос, как это число связано с тем или иным явлением. Интерес к мистическому числу Ф достаточно периодичен. Он возникает с обнаружением нового проявления этого числа в каком-либо явлении природы.
Оно появляется в различных проекциях, так и не давая ответа на вопрос, как это число связано с тем или иным явлением. Интерес к мистическому числу Ф достаточно периодичен. Он возникает с обнаружением нового проявления этого числа в каком-либо явлении природы.
Проходит время, и интерес к нему спадает. Но ненадолго. Числу Ф находят всё новое и новое применение, но оно так и остается недоступным для ясного и полного понимания его свойств и степени его влияния на окружающий мир.
2.7. Числа Фибоначчи и фотография
Применительно к фотографическому искусству правило золотого сечения делит кадр двумя горизонтальными и двумя вертикальными линиями на 9 неравных прямоугольников. Чтобы облегчить себе задачу съемки сбалансированных изображений, фотографы немного упростили задачу и стали делить кадр на 9 равных прямоугольников в соответствии с числами Фибоначчи. Так правило золотого сечения трансформировалось в правило третей, которое относится к одному из принципов построения композиции.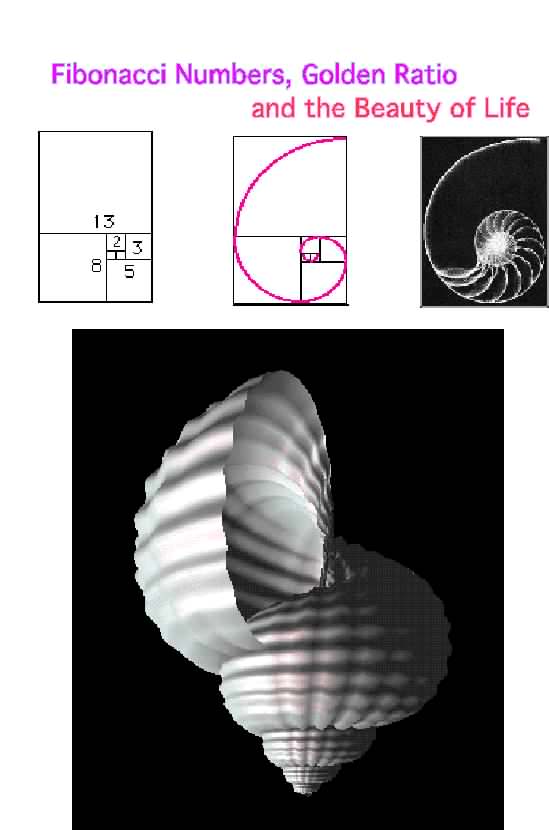
В видоискателях современных цифровых камер точки фокусировки расположены на позициях 2/8 или на воображаемых линиях, делящих кадр по правилу золотого сечения.
Наиболее удачным примером для демонстрации является пейзаж. Принцип композиции заключается в том, что небо и суша (либо водная гладь) должны иметь соотношение 1:2. Одну треть кадра следует отвести под небо, а две трети под сушу или наоборот.
Практическое исследование
Вторая часть нашего практического исследования заключается в конкретных подсчетах и измерениях.
Числа Фибоначчи в строении подсолнуха
Первым для изучения мы взяли подсолнух и сосчитали количество спиралей, идущих в одну сторону и количество спиралей в другую сторону. Правых спиралей, они закрашены красным, получилось 34, левых, они закрашены синим – 55. Эти числа 34 и 55 являются соседними в последовательности Фибоначчи.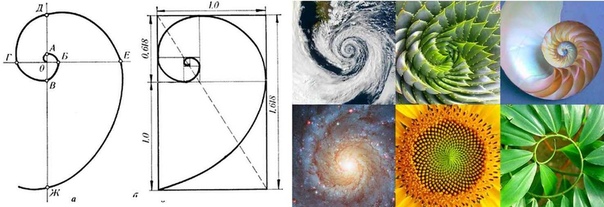
Числа Фибоначчи в строении еловой и сосновой шишек
Продолжая исследование, числа, входящие в ряд Фибоначчи мы увидели в сосновых и еловых шишках. Подсчет спиралей выявил следующие результаты. Замечаем две серии спиралей Фибоначчи: одна — по часовой стрелки, другая — против, их число 8 и 13.
Числа Фибоначчи в строении ананаса
На фотографиях показано как мы проводили подсчеты чешуек на кожуре ананаса. Нами получены числа: 8 и 13. Как мы снова можем убедиться, эти числа являются членами последовательности Фибоначчи.
Числа Фибоначчи в ветке дерева
Последовательность ответвлений, идущих по стволу растений, мы подсчитывали, рассматривая ветку дерева. Положив её на ватман, мы провели горизонтальные линии, соответствующие пазам выхода веток, и посчитали их количество. Получили следующие данные: 1,2,3,5,8… Полученный ряд является частью ряда Фибоначчи.
ЗАКЛЮЧЕНИЕ
Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве и архитектуре, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления.
Таким образом, суммарной последовательностью Фибоначчи легко можно трактовать закономерность проявлений Золотых чисел, встречаемых в природе. Эти законы действуют в независимости от нашего знания, от чьего-то желания принимать или не принимать их.
В своей работе, мы, конечно же, не можем до мельчайших подробностей изложить суть этого вопроса, но мы постарались отразить наиболее интересные и весомые аспекты. Мы рассказали о Леонардо Пизанском и дали понятное определение последовательности Фибоначчи; затем, на ярких примерах показали присутствие чисел Фибоначчи и Золотого сечения в разных сферах нашей жизни; выяснили что такое «Закон сохранения света», «Платоновы тела» и как они связаны с последовательностью.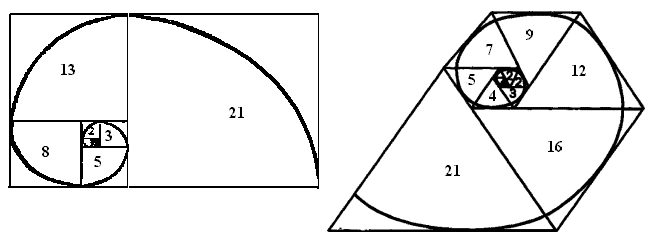
Золотое сечение и последовательность чисел Фибоначчи помогают учёным описывать строение галактик и планетарных систем, а некоторые социологи начинают их использовать для прогнозирования различных катаклизмов, обусловленных массовой истерией (войн, беспорядков, революций и т.д).
Одна и та же закономерность используется в совершенно разных областях, практически не связанных между собой, а это значит, что она является универсальной.
Экономика, как и другие общественные сферы жизни человека поддаются определенным законам, несмотря на свою определенную непредсказуемость и зависимость от многих факторов современные экономические системы (в теории волнового анализа) поддаются законам «уровней Фибоначчи» построенных на основе одноименной последовательности.
С появлением финансовых рынков математики и статисты попробовали при помощи золотых чисел Фибоначчи строить уровни поддержки и сопротивления.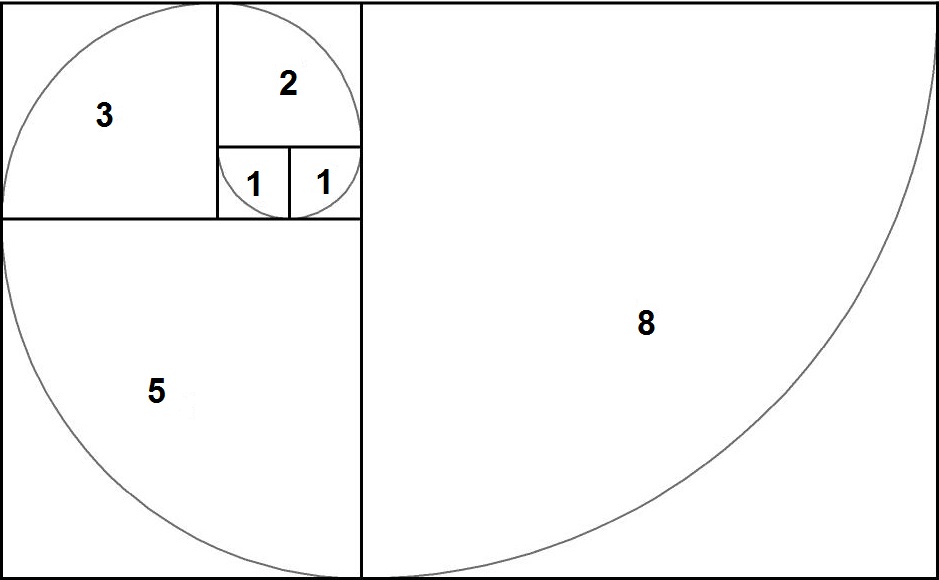 Логично, ведь если поведение социума подчиняется божественной пропорции, разумно предположить, что и в действиях участников рынка также будет прослеживаться данная закономерность.
Логично, ведь если поведение социума подчиняется божественной пропорции, разумно предположить, что и в действиях участников рынка также будет прослеживаться данная закономерность.
Как известно, эксперимент оказался удачным, и сегодня золотые числа Фибоначчи на Форекс используются для построения сеток, расширений, вееров, каналов и временных зон. В частности, при помощи первого инструмента можно найти сильные уровни, на которых следует ждать завершения коррекции, сформированной по отношению к последнему импульсу.
Мы убеждены, что данная тема будет актуальна еще долгое время, и будут открываться все новые и новые факты, подтверждающие присутствие и влияние суммационной последовательности Фибоначчи на нашу жизнь.
Список литературы
1. Маркушевич, А. И. Возвратные последовательности. / А. И. Маркушевич.М.: Наука, 1975.
2. Воробьёв, Н. Н. Числа Фибоначчи. / Н. Н. Воробьёв. М.: Наука, 1978.
Н. Числа Фибоначчи. / Н. Н. Воробьёв. М.: Наука, 1978.
3. Савин, А. П. Энциклопедический словарь юного математика. / А. П. Савин. М.: Педагогика, 1989.
4. Мохнаткина, К. В. Последовательности в школьном курсе. / К. В. Мохнаткина // Учитель – ученик: проблемы, поиски, находки: Сборник научных трудов: Выпуск 3. Саратов: Научная книга, 2005. С. 63-67.
5. Мохнаткина, К. В. Изучение последовательностей в старших классах. / К. В. Мохнаткина // Учитель – ученик: проблемы, поиски, находки: Сборник научных трудов: Выпуск 4. Саратов: Научная книга, 2005. С. 59-63.
1.http://fb.ru/article/323642/chisla-fibonachchi-i-zolotoe-sechenie-vzaimosvyaz
2.https://studwood.ru/1851811/matematika_himiya_fizika/biografiya_fibonachchi
3.https://multiurok.ru/files/issliedovatiel-skaia-rabota-po-matiematikie-chisla-fibonachchi.html
4.http://fibonachi. gimnaziayanaul.edusite.ru/p11aa1.html
gimnaziayanaul.edusite.ru/p11aa1.html
Приложение 1.
Золотые пропорции в частях тела человека.
Приложение 2
Просмотров работы: 1125
Числа Фибоначчи
Числа Фибоначчи – на Forex являются математической взаимосвязью и фундаментом для различных методов и стратегий технического анализа на Forex-e. Данные числа — это основа теории Эллиота, и во многих других стратегиях рынка Форекс.
В его же честь, уже чуть позже последовательности таких чисел назвали именем самого основателя — «ряд Фибоначчи».
Леонардо Фибоначчи опубликовал одну из своих величайших работ, которая называется «Liber Abaci».
С помощью этой книги европейцы познали индо-арабскую последовательность чисел, после чего были вытеснены из использования римские цифры в математике и геометрии. Все работы Леонардо Фибоначчи, принесли огромную пользу в сферу развития физики, математики, астрономии и технических предметов. Сама уникальная формула Фибоначчи, удивительно проста: 1, 2, 3, 5, 8 (и так дальше до бесконечности).
Сама уникальная формула Фибоначчи, удивительно проста: 1, 2, 3, 5, 8 (и так дальше до бесконечности).
Числовой ряд Фибоначчи имеет очень необычные особенности, а именно, каждое число во взаимосвязи с предыдущим. Итог сложенных двух соседних чисел Фибоначчи, дает в результате число, следующее за первыми двумя. В пример, можно привести следующее: 2 + 2 = 4. Соотношение любого числа к предыдущему числу имеет значение близкое к золотой середине 1, 618. К примеру: 13 : 8 = 1, 625; или же 21 : 13 = 1, 615; и так далее.
Также рассмотрим иной пример последовательного ряда Леонардо Фибоначчи:
Обратите внимание, как соотношение чисел колеблется вокруг значения 0,618!
На самом деле, сам Леонардо Фибоначчи не считается первым открывателем этого числового ряда. Поскольку следы этой математической связи были обнаружены в музыке, биологии и архитектуре. Даже расположение планет и вся солнечная система основана на этих правилах.
Числа Фибоначчи использовали в строительстве греки при возведении Парфенона, а египтяне при построении известной пирамиды в «Гизе». Уникальные свойства «числовой середины» также были известны величайшим ученым древности как Платону, Пифагору, Архимеду и Леонардо да Винчи.
Уникальные свойства «числовой середины» также были известны величайшим ученым древности как Платону, Пифагору, Архимеду и Леонардо да Винчи.
Удивительная числовая закономерность Фибоначчи
Коэффициент чисел Леонардо Фибоначчи и % отношения уровня коррекции.
Как мы уже говорили, многие методы анализа биржи Форекс, основаны на последовательном ряде уровней Фибоначчи.
Так как из 3-х волн удлиняется как правило одна, две другие остаются одинаковыми по размеру и времени завершения.
В том случае, когда удлиняется волна 5, первая и третья, в большинстве случаев остаются практически одинаковыми.
Если растягивается третья, приближенно равными остаются первая и пятая.
Наименьшим показателем пика третьей волны должна быть точка. Ее числовые координаты вычисляют следующим образом:
- умножают размер (длину) первой волны, на число из ряда Фибоначчи — 1, 618,
- потом суммируют произведение этих чисел к показателю начала второй, (т.
 е. к значению, аналогичному наименьшей ее точке).
е. к значению, аналогичному наименьшей ее точке).
Верхний пик пятой, будет установлен порядком произведения размера первой на 3, 236 (т. е. это 2 * 1, 618). Выведенный результат, необходимо сложить со значением наивысшей точки или с основанием первой волны. В итоге, у нас получится минимальный или максимальный порядковый ориентир.
После того как, первая и третья волны будут равны, а пятая станет более длинной, тогда наш ориентир цены, можно рассчитать так:
Для начала, необходимо замерить дистанцию от наименьшей точки первой волны, до пика третьей, полученный результат надо умножить на — 1, 618.
Данное произведение, следует суммировать со значением наименьшей точки четвертой волны.
Во время коррекции тренда, если происходит стандартная зигзагообразная коррекции вида 5, 3, 5, как правило, волна С вырастает до уровня длины А.
Предполагаемый размер С, можно рассчитать, произведением числа 0, 618 и размера волны А, в последующем вычтя рассчитанное число из минимального значения А.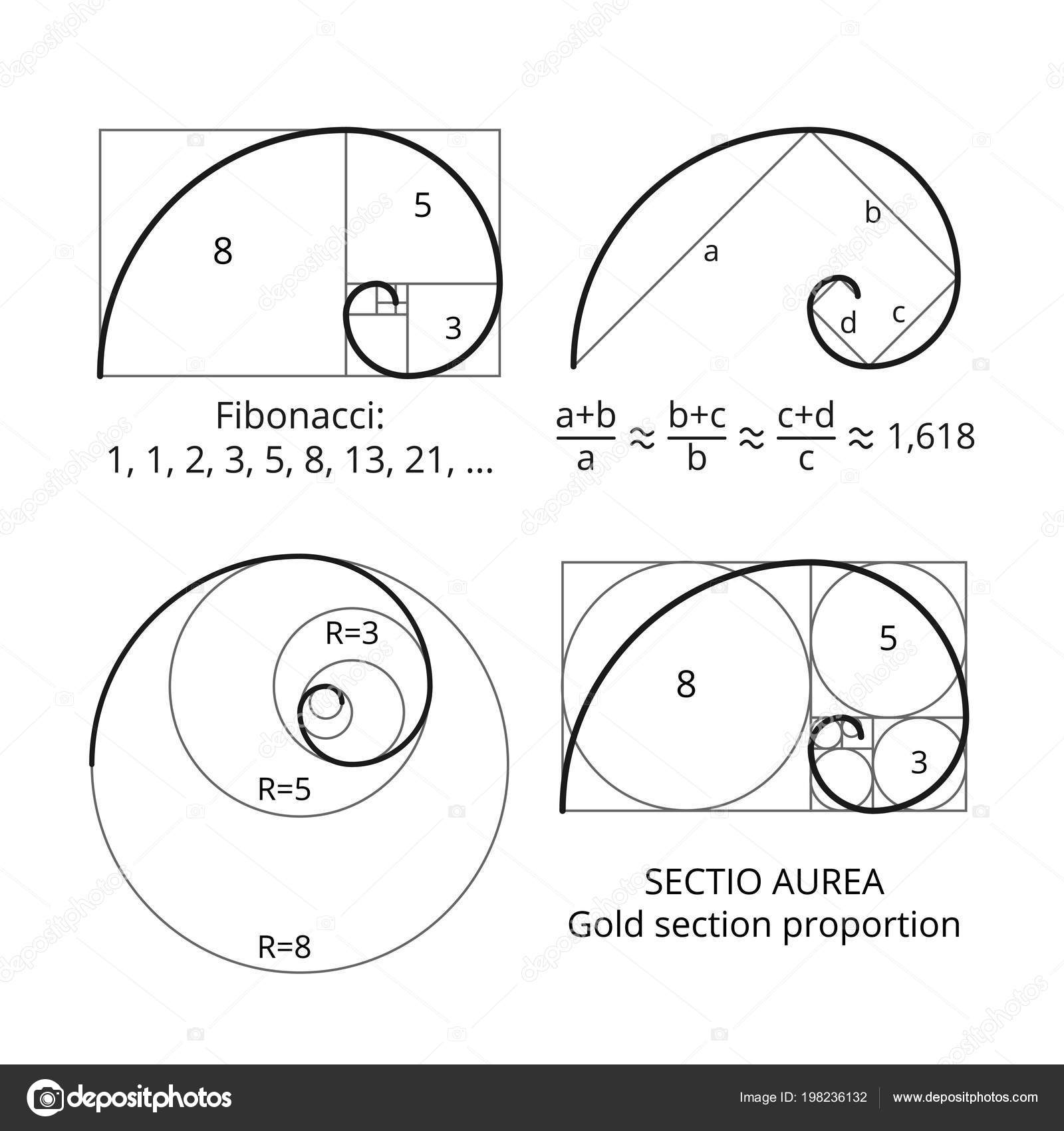
При горизонтальной коррекции вида 3, 3, 5, в то время когда В вырастает до уровня пика А, или возможно даже перекрывает его, С должна быть приблизительно равной такому значению — 1, 618 размера А. В соразмерном треугольнике каждая вновь идущая волна, относительно предшествующей, будет колебаться около этого значения — 0, 618.
Взаимосвязь числового ряда Фибоначчи и теории Эллиота.
Полный цикл повышающего рыночного движения содержит восемь волн. Из которых пять — это рост, вслед за которыми идут три — спад.
Тренд на рынке условно можно разделить на пять волн, в течение предстоящей в иерархии, наиболее долго длящейся тенденции рынка.
Как правило, коррекция постоянно состоит из 3 скачков…
Обычная коррекция подразделяется на 2 вида:
- это зигзаг 5, 3, 5,
- а также плоская волна 3, 3, 5.
На четвертой, обычно формируются треугольники, которые постоянно предшествуют последней образовавшейся волне. Эта формация также может быть корректирующей волной В.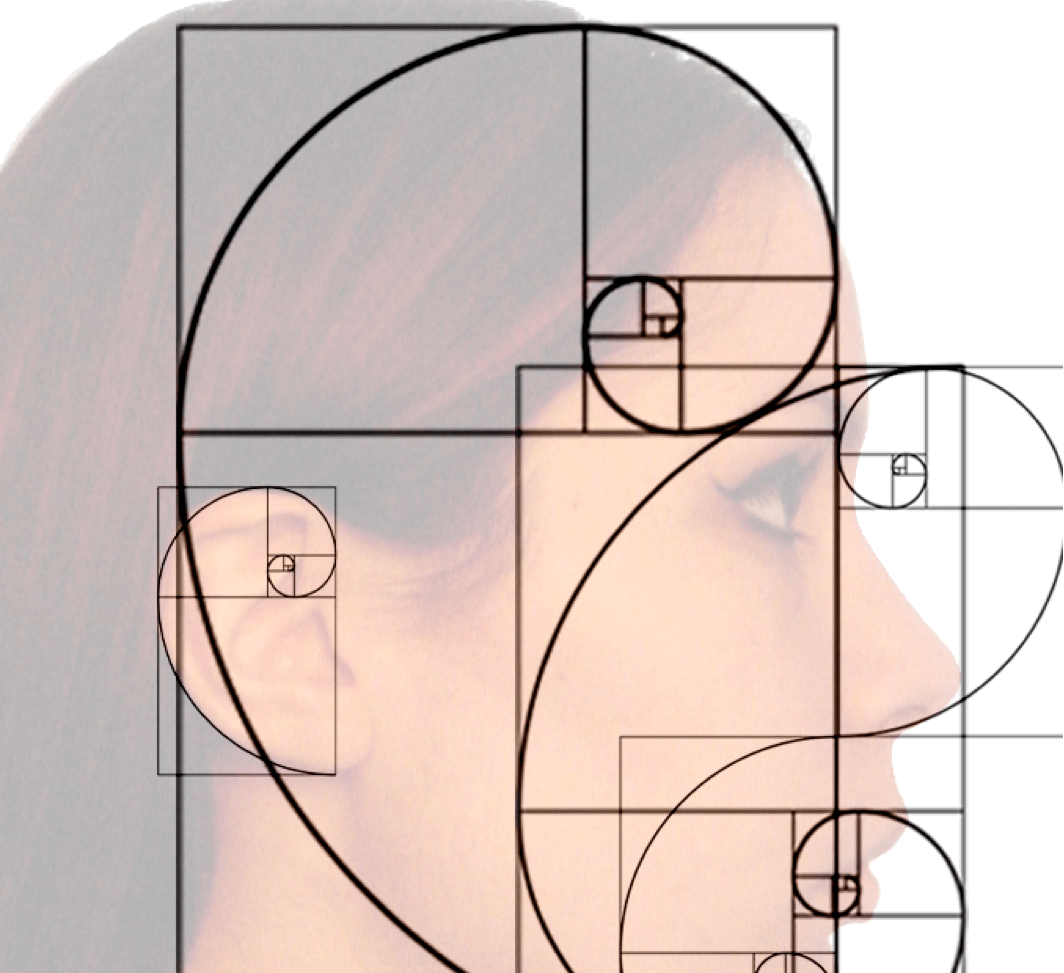
Всякая волна подразделяется на более маленькие и является составляющей более длинной.
Бывает так, что одна импульсная волна растягивается, а другие две как правило, должны быть одинаковыми по размеру и времени формирования.
Коэффициенты чисел Фибоначчи и отношения размеров коррекции, которые выведены с помощью этих чисел, применяются для нахождения ориентиров цены.
Взаимосвязь размера коррекции к предшествующему движению тренда, обычно равно: 62, 50, 38 процентам.
Метод чередования гласит: не следует дожидаться одного и того же проявления динамики цены 2 раза подряд.
Активный бычий рынок не может упасть ниже, чем начало предшествующей 4 волны.
Кроме того, 4 волна не должна пересекаться с первой.
Главными критериями теории Элиота выступают:
1) форма волны;
2) соотношение их длины;
3) период их развития.
Помимо этого, как мы уже упоминали, на последовательности выведенной Леонардо Фибоначчи, основывается еще много эффективных методов анализа на Форекс, которые обязательно будут затронуты в материалах этого сайта.
РЕКОМЕНДУЕМ ПОСМОТРЕТЬ:
Отношения Фибоначчи в геометрии
Стр 1 из 27Следующая ⇒Существование отношения Фибоначчи ФИ в геометрии очень хорошо известно. Однако подходящий для инвесторов способ применения этого отношения как геометрического инструмента к движению биржевых цен с использованием ФИ-спиралей и ФИ-эллип-сов до настоящего времени не публиковался. Чтобы применять ФИ-спирали и ФИ-эллипсы как аналитические инструменты, требуются квалификация программиста и сила компьютеров.
Поскольку компьютерные мощности сегодня легко доступны, препятствием является отсутствие не железа, а, скорее, некоторых знаний и соответствующего программного обеспечения.
Полностью готовый к работе пакет программ, прилагаемый к данной книге, позволяет каждому заинтересованному читателю/инвестору прослеживать приводимые примеры и генерировать подобные сигналы в торговле в режиме реального времени.
ФИ-спираль и ФИ-эллипс имеют необычные свойства, которые в соответствии с отношением Фибоначчи ФИ находятся в двух измерениях: цена и время. Весьма вероятно, что интегрирование ФИ-спирали и ФИ-эллипса намного повысит уровень интерпретации и использования отношения Фибоначчи. До сих пор отношение ФИ Фибоначчи в основном использовалось как инструмент для измерения коррекций и расширений ценовых колебаний. Прогнозы времени интегрировались редко, потому что они не представлялись столь же надежными, как анализ цен. Но с включением в геометрический анализ ФИ-спиралей и ФИ-эллипсов обе части — и ценовой, и временной анализ — могут комбинироваться правильно.
Чтобы лучше понять, как ФИ Фибоначчи геометрически встраивается в ФИ-спирали и ФИ-эллипсы, начнем с описания золотого сечения линии и прямоугольника и их соответствующих отношений к ФИ.
Греческий математик Евклид Мегарский (450—370 гг. до н. э.) — первый ученый, написавший о золотом сечении и, таким образом, сосредоточившийся на анализе прямой линии (рисунок 1.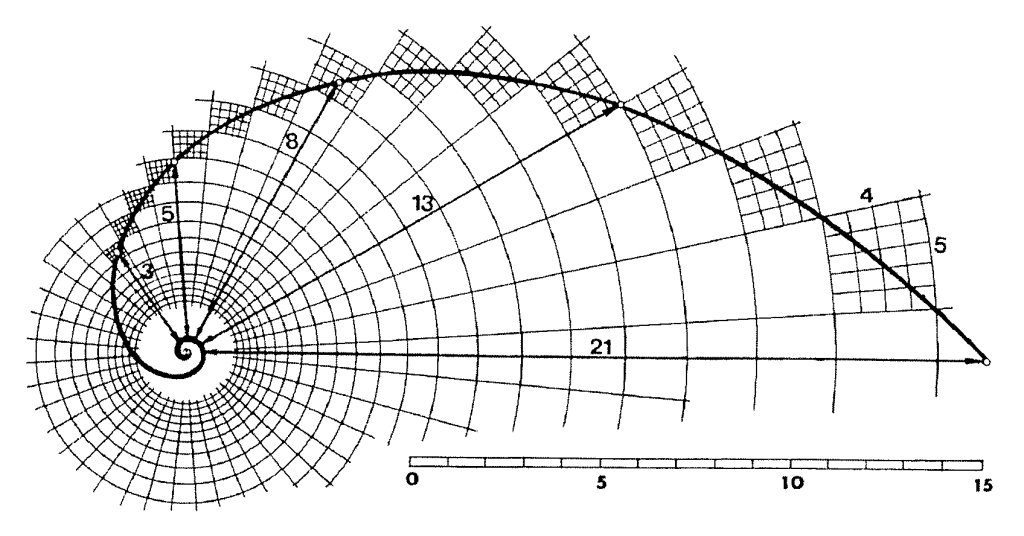 b называется золотым отношением.
b называется золотым отношением.
Рисунок 1.3 Золотое сечение линии. Источник: FAM Research, 2000.
Другими словами, точка С делит линию АВ на два отрезка таким образом, что отношения этих отрезков составляют 1,618 и 0,618; мы легко узнаем эти два числа по нашему анализу ряда суммирования Фибоначчи, как ФИ Фибоначчи и его обратное значение ФИ’.
Перемещаясь от одной колыбели науки к другой — из Древней Европы в Древнюю Африку или из Древней Греции в Древний Египет, мы узнаем, что в Великой Пирамиде Гизы прямоугольный этаж палаты фараона также иллюстрирует золотое сечение.
Золотое сечение прямоугольника лучше всего продемонстрировать, начертив квадрат, геометрическую конфигурацию, послужившую фундаментом Пирамиды Гизы. Этот квадрат можно затем преобразовать в золотой прямоугольник, как это схематично показано на рисунке 1.4.
Сторона АВ квадрата ABCD на рисунке 1. 4 делится пополам. Чертится дуга круга с центром в точке Е и радиусом ЕС, отсекающая продление АВ в точке F. Перпендикулярно AF чертится линия FG, пресекающая продление DC в точке G. AFGD — золотой прямоугольник. Согласно формальному определению, геометрическое представление золотого сечения в прямоугольнике означает, что длина прямоугольника этой формы в 1,618 раз больше, чем его ширина. И вновь появляется отношение Фибоначчи ФИ, на сей раз в пропорциях золотого прямоугольника.
4 делится пополам. Чертится дуга круга с центром в точке Е и радиусом ЕС, отсекающая продление АВ в точке F. Перпендикулярно AF чертится линия FG, пресекающая продление DC в точке G. AFGD — золотой прямоугольник. Согласно формальному определению, геометрическое представление золотого сечения в прямоугольнике означает, что длина прямоугольника этой формы в 1,618 раз больше, чем его ширина. И вновь появляется отношение Фибоначчи ФИ, на сей раз в пропорциях золотого прямоугольника.
Держа в уме представление отношения Фибоначчи ФИ в одномерной (линия) и двумерной (прямоугольник) геометрии, можно перейти к более сложным геометрическим объектам. Они подведут ближе к инструментам, которые мы хотим применять для анализа параметров времени и цены фондовых и фьючерсных рынков.
Рисунок 1.4 Золотое сечение прямоугольника. Источник: FAM Research, 2000.
Единственной математической кривой следующей модели естественного роста является спираль, выраженная в таких природных феноменах, как Spira mirabilis или раковина наутилуса. ФИ-спираль называют самой красивой математической кривой. Этот тип спирали часто встречается в природе. Ряд суммирования Фибоначчи и золотое сечение, представленное выше как его геометрический эквивалент, очень хорошо ассоциируются с этой замечательной кривой.
На рисунке 1.5 показана рентгенограмма раковины камерного наутилуса («кораблика»). Последовательные камеры наутилуса построены, следуя форме ФИ-спирали. По мере роста раковины размер камер увеличивается, но их форма остается неизменной.
Для демонстрации геометрии ФИ-спирали лучше всего использовать золотой прямоугольник как основание для геометрического анализа. Это показано схематично на рисунке 1.6.
Частное от деления длины на высоту прямоугольника ABCD на рисунке 1.6 можно вычислить. Как мы узнали ранее, оно составляет АВ-г-ВС = ФИ-Н = 1,618. Через точку Е, также называемую золотым сечением АВ, проводится линия EF, перпендикулярная АВ, отрезающая от прямоугольника квадрат AEFD. Остающийся прямоугольник EBCF — золотой прямоугольник. Если отделить квадрат EBGH, то остающаяся фигура HGCF также будет золотым прямоугольником. Этот процесс можно повторять неопределенно долго, пока конечный прямоугольник О не станет настолько маленьким, что будет неотличим от точки.
Конечная точка О называется полюсом равноугольной спирали, которая проходит через золотые сечения D, Е, G, J и так далее.
Рисунок 1.5 ФИ-спираль, представленная в раковине наутилуса.
Источник: The Divine Proportion, H. E. Huntley (New York: Dover, 1970), p. iv. Перепечатано с разрешения.
D F J С
Рисунок 1.6 Геометрия ФИ-спирали. Источник: FAM Research, 2000.
Стороны прямоугольника почти, но не полностью касательные кривой.
Отношение ФИ-спирали кряду Фибоначчи очевидно из рисунка 1.6, потому что ФИ-спираль проходит по диагонали через противоположные углы последовательных квадратов, например, DE, EG, GJ и так далее. Длины сторон этих квадратов формируют ряд Фибоначчи. Если самый маленький квадрат имеет сторону длиной d, смежный квадрат должен также иметь сторону длиной d. Следующий квадрат имеет сторону длиной 2d (вдвое длиннее d), следующий 3d (втрое длиннее d), формируя ряд Id, 2d, 3d, 5d, 8d, 13d… который является хорошо известной последовательностью Фибоначчи: 1—1—2—3—5—8—3— и так далее до бесконечности.
Спираль не имеет конечной точки. При бесконечном росте наружу (или внутрь) ее форма остается неизменной. Два сегмента спирали идентичны по форме, но отличаются по размеру точно на коэффициент ФИ. Все спирали, чьи темпы роста являются элементами ряда ФИ 0,618-1,000-1,618-2,618-4,236-6,854-11,090-и так далее, будут в контексте этой книги называться ФИ-спира-лями.
ФИ-спираль — связующее звено между рядом суммирования Фибоначчи, вытекающим из него отношением Фибоначчи ФИ, и волшебством природы, которое мы видим вокруг нас.
В дополнение к ФИ-спирали, в природе можно встретить и другие важные геометрические кривые. Из них наиболее существенные для цивилизации — горизонт океана, след метеора, парабола водопада, дуга перемещения солнца, полумесяц и, наконец, полет птицы. Многие из этих естественных кривых могут быть геометрически смоделированы с использованием эллипсов.
Эллипс — математическое выражение овала. Каждый эллипс можно точно описать с помощью всего лишь нескольких характеристик (рисунок 1.7).
S,S2 на рисунке 1.7 — длина большой оси эллипса. S3S4 — длина малой оси эллипса. Эллипс теперь определяется уравнением
Для нас представляет интерес (в контексте анализа Фибоначчи) отношение главной и малой оси эллипса, выраженное на математическом языке в следующей формуле
Рисунок 1.7 Геометрия ФИ-эллипса. Источник: FAM Research, 2000.
Эллипс превращается в ФИ-эллипс во всех тех случаях, где отношение большой оси к малой оси эллипса является элементным числом ряда ФИ 0,618-1,000-1,618-2,618-4,236-6,854- и так далее. Круг — специальный тип ФИ-эллипса, в котором а = Ь и отношение а-=-Ь= 1.
ФИ-эллипсы предпочтительнее всех других возможных эллипсов (с отношениями главных осей, деленных на малые оси, иными, чем числа ряда ФИ), поскольку эмпирические исследования показали, что люди находят приближения ФИ-эллипсов визуально значительно более удовлетворительными.
Когда участники исследовательского проекта сталкивались с различными формами эллипсов и их спрашивали об уровне комфорта, пробное эмпирическое исследование дало результаты, показанные в Таблице 1.1.
Три наблюдателя из четырех предпочли эллипсы, имеющие оси, чьи отношения равны отношению ФИ-эллипса (1,618) или так близко приближены к ФИ-эллипсу, чтобы были почти от него неотличимы.
После этого оптимистического обзора перейдем ко второй главной части нашего теоретического представления основных инструментов Фибоначчи.
К каким выводам можно прийти после того, что мы уже рассказали? И какие выводы сделал Эллиот, чтобы интегрировать ряд суммирования Фибоначчи и ФИ Фибоначчи с силами, которые двигают международные рынки?
| Таблица 1.1 Предпочтения ФИ-эллипсов Отношение Главная ось — малая ось a-b Процентная доля предпочтения | |
| 1,000 | 1,2 |
| 1,205 | 0,6 |
| 1,250 | 8,3 |
| 1,333 | 14,7 |
| 1,493 | 42,4 |
| 1,618 | 16,7 |
| 1,754 | 13,1 |
| 2,000 | 1,6 |
Источник: The Divine Proportion, H. E. Huntley (New York: Dover, 1970) p. 65. Перепечатано с разрешения.
ВОЛНОВОЙ ПРИНЦИП ЭЛЛИОТА
Ральф Нельсон Эллиот (1871—1948) начал свою карьеру инженером, а не профессиональным аналитиком рынка. Оправившись от тяжелой болезни в 30-х годах, он переключил свой интерес на анализ цен акций, сосредоточившись на Индексе Доу-Джонса.
После нескольких замечательно успешных прогнозов в 1939 году Эллиот опубликовал ряд крупных статей в журнале «Файнэншл уорлд» (Financial World), в которых впервые показал, что Индекс Доу-Джонса движется в определенном ритме.
Рыночная теория Эллиота основана на следующем факте: каждое явление на нашей планете движется по тому же принципу, что и приливы: за приливом следует отлив, за действием — противодействие. Время не влияет на эту схему, потому что структура рынка в своей полноте остается постоянной.
В этом разделе кратко рассмотрены и проанализированы концепции Эллиота. Однако важно обсудить его идеи, объясняющие фундаментальные концепции и использованные нами в анализе инструментов Фибоначчи. Не будем погружаться в особые детали; большинство фактов подробно описано в книге «Приложения и стратегии Фибоначчи для трейдеров».
Наше внимание будет сфокусировано на главных аспектах работы Эллиота, имеющих длительное значение. Даже если мы не соглашаемся с некоторыми открытиями Эллиота, его идеи достойны восхищения. Мы знаем, насколько трудно создавать новые концепции рыночного анализа без технической поддержки, доступной сегодня. Когда мы начали изучать работы Эллиота в 1977 году, было очень трудно достать все данные для глубокого анализа. Насколько же труднее это должно было быть для Эллиота в те годы, когда он начинал свою работу! Компьютерная технология, доступная сегодня, позволяет быстро тестировать и анализировать, но все же для того, чтобы начать, необходимо иметь в своем распоряжении идеи Эллиота.
Эллиот писал: «Закон природы охватывает наиболее важный изо всех элементов выбор времени. Закон природы не система или метод игры на рынке, а феномен, похоже, отмечающий прогресс всех видов человеческой деятельности. Его применение в прогнозировании революционно».*
Эллиот опирался в своем открытии на закон природы: «Этот закон, стоящий за рынком, можно увидеть только тогда, когда рынок рассматривается в надлежащем свете и затем анализируется с использованием этого подхода. Проще говоря, фондовый рынок создание человека, следовательно, он отражает характерные особенности человека» (с. 40).
Перспектива предсказывать движение цен с использованием принципов Эллиота побуждает легионы аналитиков трудиться день и ночь. Мы сосредоточимся на самой возможности предсказания и попробуем ответить на вопрос, возможно ли это.
Эллиот выразился очень определенно, когда представлял свою концепцию волн: «Любая человеческая деятельность имеет три отличительные особенности: модель (фигура), время и отношение, и все они подчиняются ряду суммирования Фибоначчи» (с. 48).
После того, как волны интерпретированы, это знание может применяться к любому движению, потому что одни и те же правила применяются к ценам акций, облигаций, зерновых и других фьючерсов.
Наиболее важный из трех этих упомянутых факторов — модель (ценовая фигура). Модель всегда развивается, формируясь вновь и вновь. Обычно, хотя и не всегда, можно заранее увидеть соответствующий тип модели. Эллиот описывает этот рыночный цикл как «…разделенный, прежде всего на ‘бычий рынок’ и ‘медвежий рынок'» (с. 48).
· The Complete Writings of R. N. Elliott with Practical Application from J. R. Hill, by J. R. Hill, Commodity Research Institute, NC, 1979 (последующих ссылки также сделаны на Эллиота), р. 84.
Бычий рынок может быть разделен на пять «главных волн», а медвежий рынок — на три главные волны. Главные волны 1, 3 и 5 бычьего рынка подразделены на пять «средних волн» каждая. Затем волны 1, 3 и 5 каждой средней волны подразделены на пять «малых волн»
Рисунок 1.8 «Идеальный» цикл фондового рынка по Эллиоту. Источник: Fibonacci Applications and Strategies for Traders, Robert Fischer (New York: Wiley, 1993), p. 13. Перепечатано с разрешения
Беда с этой общей рыночной концепцией в том, что в большинстве случаев регулярных (правильных) колебаний с 5 волнами не бывает. Регулярное колебание с 5 волнами лишь исключение из правила, которое Эллиот пытался довести до ума введением в концепцию сложных вариаций.
Эллиот представил ряд рыночных моделей (фигур), применимых почти к каждой ситуации рыночного развития. Если ритм рынка правильный, волна 2 не будет восстанавливаться (retrace) до начала волны 1, а волна 4 не будет корректироваться (correct) ниже вершины волны 1 (рисунок 1.9). В тех случаях, когда такое происходит, следует пересчитать волны.
Рисунок 1.9 Подсчет (а) ошибочен в восходящем движении с 3 волнами; (Ь) правилен в восходящем движении с 3 волнами; (с) ошибочен в восходящем движении с 5 волнами; (d) правилен в восходящем движении с 5 волнами. Источник: Fibonacci Applications and Strategies for Traders, Robert Fischer (New York: Wiley, 1993), p. 14. Перепечатано с разрешения.
Каждую из двух корректирующих волн 2 и 4 можно подразделить на три волны более низкой категории. Корректирующие волны 2 и 4 в фигуре чередуются. Эллиот назвал это правилом чередования. Если волна 2 простая, волна 4 будет сложная, и наоборот (рисунок 1.10). Сложность в этом смысле — еще один термин, не-обходимыый для описания того факта, что волна 2 (или волна 4) состоит из подволн и не идет прямолинейно, как это делают простые волны.
Простые и сложные волны (а) в волне 4; (Ь) в волне 2. Источник: Fibonacci Applications and Strategies for Traders, by Robert Fischer (New York: Wiley, 1993), p. 14. Перепечатано с разрешения.
Исходя из своего замечательного наблюдения о чередовании простых и сложных волн и формулирования этого факта как правила развития рынка, Эллиот привязал закон природы к человеческому поведению и, таким образом, к поведению инвесторов.
В природных феноменах, таких как подсолнечник, сосновая шишка и ананас, имеются спирали с чередующимся вращением — сначала по часовой стрелке, а затем против часовой стрелки. Это чередование рассматривается как эквивалент чередования простых и сложных совокупностей в корректирующих волнах 2 и 4.
В дополнение к коррекциям (как неотъемлемой части любого рыночного движения) Эллиот анализировал расширения как усиления трендов в ту или иную сторону рынка, будь то восходящие или нисходящие тренды. «Расширения могут появляться в любой из трех импульсных волн — волне 1, 3 или 5, но никогда не больше, чем в одной» (с. 55).
На рисунке 1.11 показаны комбинации импульсных волн и расширений в 1, 3 и 5 волне восходящего тренда рынка. Все эти три волновых расширения могут быть развернуты как импульсные волны и расширения нисходящих трендов.
На этом этапе воздержимся от рекомендаций читателям по всем возможным вариантам, приведенным в публикациях Эллиота. Вместо этого смоделируем принципиальную схему перемещений рынка, основанную на импульсных волнах, коррекциях и расширениях.
Цель этого беглого обзора — показать сущность идей Эллиота и проследить, как они все более усложняются. На наиболее сложных стадиях даже для очень опытных последователей Эллиота почти невозможно применять все правила волновых фигур Эллиота в торговле в режиме реального времени.
Рисунок 1.11 (а) Расширение первой волны в восходящем тренде; (Ь) расширение 3 волны в восходящем тренде; (с) расширение 5 волны в восходящем тренде.Источник:Fibonacci Applications and Strategies for Traders, by Robert Fischer (New York: Wiley, 1993), p. 17. Перепечатано с разрешения.
Эллиот и сам признавал: «Коррекции бычьих и медвежьих колебаний понять значительно труднее» (с. 48). Проблема в том, что сложная природа структуры волн не оставляет места для предварительных прогнозов будущих движений цен. Схемы и структуры выглядят совершенными лишь в ретроспективе. Множество описанных Эллиотом правил и ситуаций может использоваться для наложения на любую ценовую фигуру после ее появления. Но для торговли в режиме реального времени этого недостаточно.
Завершая комментарии по Эллиоту, резюмируем те сегменты открытий Эллиота, которые могут использоваться для построений концепций и инструментов торговли, легких в применении и имеющих отношение к тому, что мы говорили о ФИ Фибоначчи как константе естественного роста.
Принципы Эллиота, описывающие рынки, постоянно движущиеся в ритме волн, продуманы блестяще, прекрасно работают на равномерных рынках и дают ошеломляющие результаты при ретроспективном изучении графиков.
Наиболее значительная проблема их в том, что колебания рынка неравномерны. Отсюда трудности с конкретными ответами на вопросы типа:
• Является ли точка, в которой мы начинаем наш отсчет волн, частью импульсной волны или частью корректирующей волны?
• Будет ли пятая волна?
• Коррекция плоская или зигзагообразная?
• Будет ли расширение в волне 1, 3 или 5?
Эллиот по этому поводу специально писал: «Этот Принцип тщательно проверен и успешно использовался подписчиками для прогнозирования рыночных движений» (с. 107). И: «В дальнейшем письма будут публиковаться по завершении волны, не дожидаясь завершения всего цикла. В этой связи изучающие смогут понять, как составлять свои собственные прогнозы, причем совершенно бесплатно. Этот феномен и его практическое применение становятся все более и более интересными, потому что рынок непрерывно демонстрирует новые примеры, к которым могут применяться неизменные правила» (с. 137).
Наша собственная работа с концепциями Эллиота, осуществляемая под множеством различных углов на протяжении более 20 лет, не поддерживает утверждение, что структура волны обладает прогнозирующим потенциалом. Структура волны слишком сложна, особенно в корректирующих волнах. Правило чередования чрезвычайно полезно, но эта абстрактная схема не говорит нам, например, следует ли ожидать:
• коррекции трех волн,
• двойной боковой коррекции или
• тройного бокового движения.
Еще менее вероятна возможность прогнозирования ценовой фигуры с 5 волнами. Появление расширений в волне 1, волне 3 или волне 5 еще более усложняет проблему. Прелесть работы с концепцией Эллиота не в количестве волн. Мы можем только согласиться, когда Дж. Р. Хилл заявляет в своем практическом приложении: «Представленная концепция чрезвычайно полезна, но люди буквально «лезут на стену», когда пытаются подогнать фигуры графиков в точное соответствие с волной Эллиота» (с. 33).
Эллиот сосредоточивается на распознавании фигур. Вся его работа направлена на предсказание будущих движений цены на основе существующих фигур, но он, похоже, в этой области не преуспевает.
Эллиот и сам выражал неуверенность в нумерации волн, когда писал в различных информационных бюллетенях: «Боковое движение в течение этих пяти недель было лишено фигуры, чего никогда прежде не отмечалось» (с. 167).
В другом месте он писал: «Фигура движения через основание настолько редка, что даже не упоминается в Трактатах. Эти детали расстраивают любую нумерацию» (с. 165).
И вновь: «Элемент времени [имеется в виду ряд суммирования Фибоначчи] как независимый инструмент, однако, продолжает сбивать с толку, когда делаются попытки применить любое известное правило последовательности к продолжительности трен-да» (с. 180).
И наконец: «Элемент времени основан на ряде суммирования Фибоначчи, но имеет свои ограничения и может использоваться только как дополнение волнового принципа» (с. 186).
Эллиот не понимал, что важна не нумерация волн, а ФИ Фибоначчи. Отношение Фибоначчи — закон природы и человеческое поведение. При наблюдении колебаний рынка мы пытаемся измерить не больше и не меньше, чем ФИ Фибоначчи. В то время как ряд суммирования Фибоначчи и отношение Фибоначчи ФИ постоянны, нумерация волн вводит в заблуждение.
Эллиот пробовал предсказывать движение цены из пункта В в пункт С, основываясь на рыночных фигурах (рисунок 1.12). Мы считаем это невозможным, и сам Эллиот никогда не утверждал, что он способен делать это механически.
Изучая публикации Эллиота более тщательно, все же можно выделить некое правило, имеющее прогнозирующую силу. «Циклическая фигура, или мера массовой психологии — это пять волн вверх и три волны вниз, всего восемь волн. Эти фигуры имеют прогнозирующее значение: когда заканчиваются пять волн вверх,
Рисунок 1.12 Прогнозирование движения цены из точки В в точку С невозможно. Источник: Fibonacci Applications and Strategies for Traders, Robert Fischer (New York: Wiley, 1993), p. 23. Перепечатано с разрешения.
3 – 6420
последуют три волны вниз, и наоборот» (с. 112). С этим утверждением нельзя не согласиться. Рисунок 1.13 визуализирует эти последние выводы Эллиота.
Наиболее вероятно, Эллиот не понимал, что в его стратегии произошло полное изменение. Это последнее заявление Эллиота представляет собой стратегию, противоположную по сравнению с подходом на рисунке 1.12. Вместо попытки предсказать движение цены из точки В в точку С он ждет, согласно рисунку 1.13, до самого конца 5-волнового движения, потому что потом можно ожидать три волны в противоположном направлении.
Можно предсказать движение цены после конца 5-волнового цикла. Источник: Fibonacci Applications and Strategies for Traders, Robert Fischer (New York: Wiley, 1993), p. 23. Перепечатано с разрешения.
Мы полностью принимаем этот подход Эллиота и в последующих разделах укрепим его идею дополнительными правилами. Числа 5 и 3 члены ряда суммирования Фибоначчи, следовательно, они не могут вводить в заблуждение в нашем анализе.
Мы представим и другие инвестиционные стратегии, близко связанные с отношением Фибоначчи. Мы охватим коррекции и расширения, как это делал Эллиот, но сделаем это по-другому, всегда фокусируясь на отношении Фибоначчи ФИ и его представлении в инструментах, которые мы анализируем.
Эллиот никогда не работал с геометрическим подходом. Мы, однако, разработали компьютеризированные ФИ-спирали и ФИ-эллипсы, готовые к применению в анализе. Мы абсолютно уверены, что в этом решение проблемы объединения цены и времени в составном аналитическом подходе. Это идет гораздо дальше того,с чего мы начали в нашей первой книге приблизительно восемь лет назад.
Используя наши торговые инструменты Фибоначчи и компьютерную программу WINPHI, мы в последующих главах сконцентрируем наши исследования главным образом на дневных ценовых гистограммах.
Все представленные инструменты тщательно протестированы нами и готовы к применению на фьючерсных и фондовых рынках. Исследования показывают, что можно также использовать внут-ридневные данные, но при других параметрах. Требуется провести больше исторических испытаний на тиковых или внутридневных данных прежде, чем смогут быть установлены определенные правила применения геометрических инструментов, основанных на Фибоначчи, в режиме реального времени.
РЕЗЮМЕ: ГЕОМЕТРИЧЕСКИЕ ИНСТРУМЕНТЫ ФИБОНАЧЧИ
Изучение ряда суммирования Фибоначчи и анализа Эллиота движения рынков в условиях равномерных волн позволило создать шесть общих инструментов. Их можно применять почти без ограничений к рядам рыночных данных, будь то наличные валюты, фьючерсы, Индексы, акции или взаимные фонды.
Эти шесть инструментов: (1) сам ряд суммирования Фибоначчи, (2) временные цели Фибоначчи, (3) коррекции и расширения в связи с отношением Фибоначчи, (4) ФИ-каналы, (5) ФИ-спира-ли и (6) ФИ-эллипсы.
Эти торговые инструменты описаны в данном разделе, чтобы читатели получили общее представление о функционировании и функциональных возможностях геометрических инструментов применительно к любому детальному анализу и приложению инструментов к рыночным данным.
Ряд суммирования Фибоначчи
Сначала это может показаться удивительным, но ряд суммирования Фибоначчи можно легко превратить в инструмент рыночного анализа, работающий устойчиво и надежно.
Приведем ряд суммирования Фибоначчи следующим образом:
1-1-2-3-5-8-13-21-34-55-89-144-…
Частные от деления каждого числа ряда Фибоначчи на предшествующее число асимптотически приближаются к значению ФИ = 1,618 (мы называем его отношением Фибоначчи).
Если объединить выводы Фибоначчи с выводами Эллиота, можно исключить теоретические волны Эллиота — пять плюс три плюс пять плюс три плюс пять, всего 21 главную волну, что является числом ряда суммирования Фибоначчи.
Если каждое 5-волновое движение в восходящем тренде разбить на пять плюс три плюс пять плюс три плюс пять меньших или промежуточных волн (всего 21 волну) и если каждую из получившихся волн разбить на пять плюс три плюс пять (всего 13) малых волн, получим общее количество 89 волн, число, которое, как мы видим, опять-таки часть ряда суммирования Фибоначчи.
Если проделать ту же процедуру с тремя корректирующими волнами, получим 55 волн для корректирующего 3-волнового движения и общее количество 144 волны для завершения одного из рыночных циклов Эллиота.
Общее применение этого принципа показывает: движение в определенном направлении продолжается до точки, в которой завершается временная структура, являющаяся частью и совместимая с числами ряда суммирования Фибоначчи.
Движение, длящееся более трех дней, не должно разворачиваться, пока не достигнуты пять дней. Движение, превышающее пять дней, должно длиться минимум восемь дней. Тренд, продолжающийся девять дней, не должен закончиться прежде, чем пройдут 13 дней, и так далее.
Наши открытия относительно связи между рядом суммирования Фибоначчи и волновым принципом Эллиота показаны на рисунке 1.14.
Эту базовую структуру вычисления изменений тренда можно одинаково успешно применять к часовым, дневным, недельным или месячным данным. Но это лишь идеальный тип фигуры, и трейдеры никогда не должны ожидать, что биржевые товары, фьючерсы, Индексные фьючерсы или акции будут вести себя таким точным и предсказуемым образом.
Отклонения могут и будут происходить как во времени, так и амплитуде, потому что отдельные волны и ценовые фигуры не всегда будут развиваться обычным путем. Мы также должны иметь в виду, что простое приложение ряда суммирования Фибоначчи предназначено, чтобы предсказывать длину движений тренда, но число гистограмм на боковых рынках остается непредсказуемым.
Рисунок 1.14 Ряд суммирования Фибоначчи, схематично встроенный в полный рыночный цикл в соответствии с классификацией волн по Эллиоту. Источник: Fibonacci Applications and Strategies for Traders, Robert Fischer (New York: Wiley, 1993), p. 20. Перепечатано с разрешения.
Однако, как мы увидим позже, числа 8, 13, 21, 34 и 55 могут иметь важное практическое значение, когда применяются для работы в комбинации с другими инструментами Фибоначчи. Один простой пример: при определении длины стандартного ФИ-эллипса продукта, которым мы хотим торговать, самый легкий способ идентифицировать изменение главного тренда — сначала проверить движения длиной в числа Фибоначчи 8, 13, 21, 34 или 55. Это не означает, что изменения тренда всегда произойдут в предварительно рассчитанных точках после гистограмм 8, 13, 21, 34 или 55, но это случается слишком часто, чтобы игнорировать.
Эллиот и его последователи пробовали вычислять изменения главного тренда фондового рынка, применяя числа ряда суммирования Фибоначчи к недельным, месячным и годовым данным. Это имело смысл, несмотря на то, что базовые структуры времени становились очень длинными и поворотные точки в исторической перспективе на недельной, месячной или годовой основе часто не материализовались вообще. Что касается внутридневных данных, мы считаем, что здесь числа имеют очень небольшое значение, потому что (1) рынки перемещаются в боковом направлении и (2) гораздо более беспорядочный характер движений рынка в течение дня (по сравнению с ежедневными движениями) делает использЧз-вание внутридневных чисел Фибоначчи почти непригодным для серьезного анализа. В нашем анализе, следовательно, мы концентрируемся на дневных данных и числах 8, 13, 21, 34 и 55.
Читайте также:
|
Метод Фибоначчи на Форекс
Как рассчитать уровни восстановления и расширения Фибоначчи
Три наиболее часто используемых уровня восстановления Фибоначчи — 0.382 или 38,2%, 0,500 (50%) и 0,618 (61,8%).
Три наиболее часто используемых уровня расширения Фибоначчи — это 0,618, 1,000 и 1,618. Также можно применить расширение 1.382.
Давайте посмотрим на следующую картинку:
В приведенном выше примере мы находимся в восходящем тренде. Наименьшее колебание — точка А — 120,75;
наивысшее колебание — точка B — 121,44.
Для расчета уровней коррекции и входа в длинную позицию в некоторой точке C мы делаем следующее:
Расчеты для восходящего тренда и ордера на покупку:
B — A =?
121.44 — 120,75 = 0,69
0,382 (38,2%) откат = 121,44 — 0,69 x 0,382 = 121,18
0,500 (50,0%) откат = 121,44 — 0,69 x 0,500 = 121,09
0,618 (61,8%) откат = 121,44 — 0,69 x 0,618 = 121.01
Формула уровней коррекции Фибоначчи для восходящего тренда:
C = B — (B — A) x N%
Теперь нам нужно рассчитать уровни расширения:
0,618 (61,8%) расширение = 121,44 + 0,69 x 0,618 = 121,87
1.000 (100,0%) расширение = 121,44 + 0,69 x 1.000 = 122.13
1,382 (138,2%) расширение = 121,44 + 0,69 x 1,382 = 122,39
1,618 (161,8%) расширение = 121,44 + 0,69 x 1,618 = 122,56
Формула уровней расширения Фибоначчи для восходящего тренда:
D = B + (B — A) x N%
Наш следующий пример — нисходящий тренд.
Наибольшее колебание — точка А — 158,20; наименьшее колебание — точка B — 156,44.
Расчеты для нисходящего тренда и ордера на продажу:
A — B =?
158,20 — 156,44 = 1,76
Из-за нисходящего тренда нам нужно добавить к самой низкой точке B, чтобы найти коррекцию.
0,382 (38,2%) ретрейсмент = 156,44 + 1,76 x 0,382 = 157,53
0,500 (50,0%) ретрейсмент = 156,44 + 1,76 x 0,500 = 157,32
0,618 (61,8%) ретрейсмент = 156,44 + 1,76 x 0,618 = 157,11
Fibtracement Формула уровней для нисходящего тренда:
C = B + (A — B) x N%
Теперь давайте найдем уровни расширения Фибоначчи (нисходящий тренд):
0,618 (61,8%) расширение = 156,44 — 1,76 x 0,618 = 155,35
1.000 ( 100%) extension = 156,44 — 1,76 x 1.000 = 154,68
1.382 (138,2%) расширение = 156,44 — 1,76 x 1,382 = 154,01
1,618 (161,8%) расширение = 156,44 — 1,76 x 1,618 = 153,59
Формула уровней расширения Фибоначчи для нисходящего тренда:
D = B — (A — B) x N%
Чтобы помочь вычислить уровни Фибоначчи, мы также сделали бесплатный инструмент для трейдеров Форекс — Бесплатный калькулятор Фибоначчи — доступный для загрузки.
Прибыльных сделок!
FX Leader
Copyright © Forexfibonacci.com Все права защищены
Торговля Фибоначчи на Форекс — BabyPips.com
Мы будем часто использовать отношения Фибоначчи в нашей торговле, чтобы вам лучше изучить его и полюбить, как домашнюю еду вашей матери.
Фибоначчи — огромная тема, и существует множество различных исследований Фибоначчи со странно звучащими названиями, но мы собираемся придерживаться двух: ретрейсмент и расширение .
Давайте сначала познакомим вас с самим человеком Фибоначчи… Леонардо Фибоначчи.Нет, Леонардо Фибоначчи не какой-то известный шеф-повар.Фактически, он был известным итальянским математиком, также известным как супер-пупер-супер-компьютерщик.
У него было «Ага!» момент, когда он обнаружил простой ряд чисел, которые создали отношения, описывающие естественные пропорции вещей во Вселенной.
Коэффициенты возникают из следующего числового ряда: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
Эта серия чисел получается путем начала с 0, за которым следует 1, а затем прибавления 0 + 1, чтобы получить 1, третье число.
Затем складываем второе и третье числа (1 + 1), чтобы получить 2, четвертое число и так далее.
После нескольких первых чисел в последовательности, если вы измеряете отношение любого числа к последующему более высокому числу, вы получите .618 .Например, 34, разделенное на 55, равно 0,618.
Если измерить соотношение между альтернативными числами, получится ,382 .
Например, 34 разделить на 89 = 0,382.
Вы только что познакомились с последовательностью Фибоначчи!
Последовательность Фибоначчи
Последовательность Фибоначчи формируется путем взятия 2 чисел, любых 2 чисел, и их сложения вместе, чтобы получить третье число.
Затем второе и третье числа снова складываются, чтобы получить четвертое число.
И вы можете продолжать, пока это не перестанет быть интересным.
Отношение последнего числа к предпоследнему примерно равно 1,618 .
Это соотношение можно найти во многих природных объектах, поэтому это соотношение называется золотым сечением .
Он много раз появляется в геометрии, искусстве, архитектуре и даже в Sonic the Hedgehog.
Золотое сечение на самом деле является иррациональным числом, таким как пи, и часто обозначается греческой буквой фи ( φ ).
Ладно, хватит болтовни.
Со всеми этими числами вы могли бы усыпить слона. Мы просто перейдем к делу; это коэффициенты, которые вы ДОЛЖНЫ знать:
Уровни коррекции Фибоначчи
0,236, 0,382, 0,618, 0,764
Уровни расширения Фибоначчи
0, 0.382, 0,618, 1.000, 1.382, 1.618
Вам действительно не нужно знать, как все это рассчитывать. Ваша программа для построения графиков сделает всю работу за вас. Кроме того, у нас есть хороший калькулятор Фибоначчи, который может волшебным образом вычислить эти уровни за вас.
Однако всегда полезно знать основную теорию, лежащую в основе индикатора, чтобы у вас были знания, чтобы произвести впечатление на свидание.
Уровни коррекции Фибоначчи работают на основе теории, согласно которой после того, как большая цена двинется в одном направлении, цена вернется на уровень или частично вернется к предыдущему ценовому уровню, прежде чем возобновить движение в исходном направлении.
Трейдеры используют уровни коррекции Фибоначчи как потенциальные области поддержки и области сопротивления .
Поскольку так много трейдеров следят за этими уровнями и размещают на них ордера на покупку и продажу, чтобы войти в сделки или разместить стопы, уровни поддержки и сопротивления имеют тенденцию становиться самореализующимися пророчествами.
Трейдеры используют уровни расширения Фибоначчи как уровни фиксации прибыли .Опять же, поскольку так много трейдеров следят за этими уровнями, чтобы выставлять ордера на покупку и продажу для фиксации прибыли, этот инструмент чаще срабатывает из-за самореализующихся ожиданий.
Большинство программного обеспечения для построения графиков включает в себя как уровни коррекции Фибоначчи, так и инструменты уровней расширения.
Чтобы применить уровни Фибоначчи к вашим графикам, вам необходимо определить точки максимума и минимума колебания.
A Swing High — это свеча с минимум двумя нижними максимумами слева и справа от себя.
A Swing Low — это свеча с минимум двумя более высокими минимумами слева и справа от себя.
У тебя все это есть? Не волнуйтесь, в следующих уроках мы объясним ретрейсменты, расширения и, самое главное, как получить несколько пунктов с помощью инструмента Фибоначчи.
Программа серии Фибоначчи на Java с использованием циклов и рекурсии
- Home
Testing
- Back
- Agile Testing
- BugZilla
- Cucumber
- 9000 Testing 9000 J9000 Database Testing
- Назад
- JUnit
- LoadRunner
- Ручное тестирование
- Мобильное тестирование
- Mantis
- Почтальон
- QTP
- Назад
- 000 000
000
000
000000000000000000- SoapUI
- Управление тестированием
- TestLink
SAP
- Назад 9 0006 ABAP
- APO
- Начинающий
- Basis
- BODS
- BI
- BPC
- CO
- Назад
- CRM
- Crystal Reports
- Назад
- PI / PO
- PP
- SD
- SAPUI5
- Безопасность
- Менеджер решений
- Successfactors
- SAP Back Tutorials
 Как открыть хостел | HowToHostel Как открыть хостел …
Как открыть хостел | HowToHostel Как открыть хостел … 
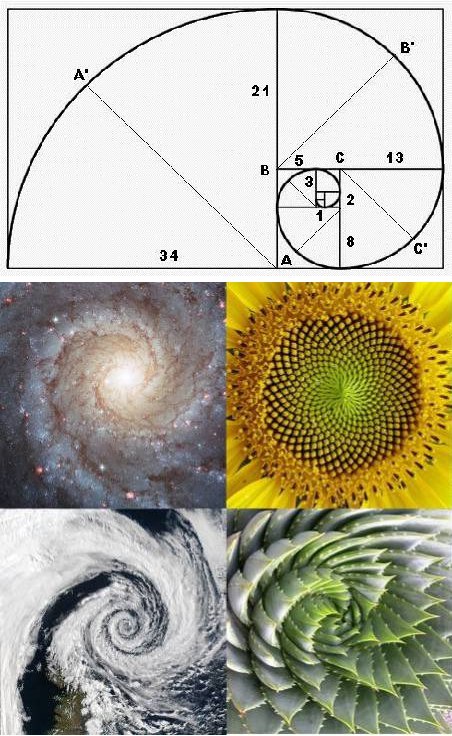
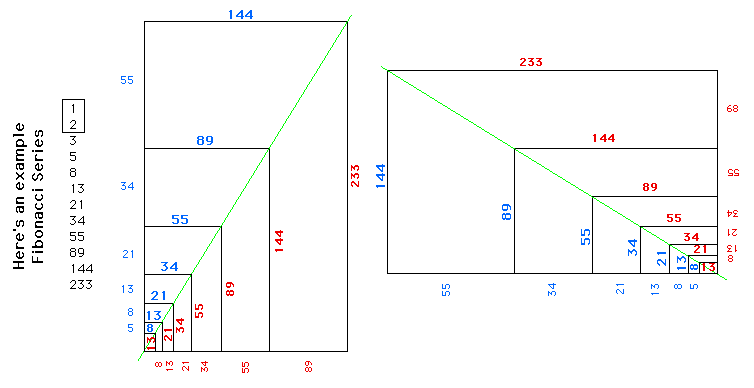 е. к значению, аналогичному наименьшей ее точке).
е. к значению, аналогичному наименьшей ее точке).