Расчет начислений: Калькулятор расчет зарплаты по окладу 2021

Взаиморасчеты – База знаний YCLIENTS

В разделе Расчет зарплат – Взаиморасчеты отображаются все операции по начислению и выплате зарплаты сотрудникам. Для просмотра этих данных по конкретному сотруднику выберите период и сотрудника, нажмите кнопку Показать.

Здесь отображаются даты и назначения начислений, суммы начислений (приход) и суммы выдачи (расход), а также остатки невыплаченной зарплаты (баланс).

Для начисления зарплаты перейдите в раздел Расчет зарплат – Взаиморасчеты и нажмите кнопку Создать расчетную ведомость.

При переходе на страницу создания ведомости выберите даты начала и окончания периода начисления, сотрудника, которому будет начислена зарплата, и комментарий.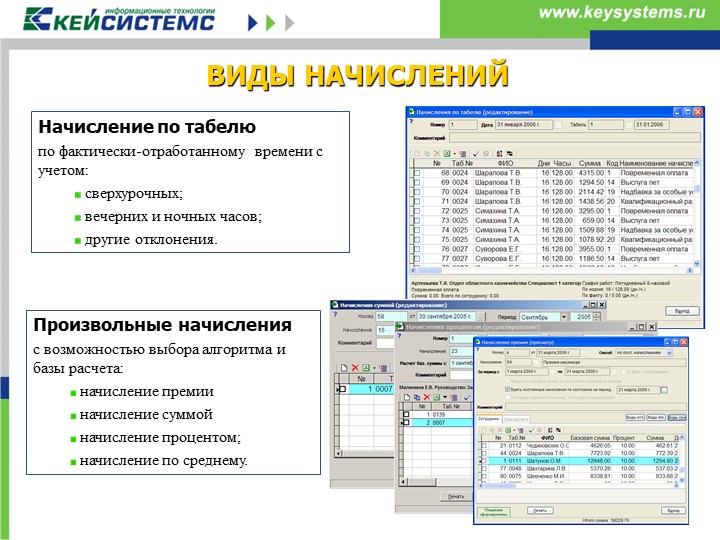

После этого нажмите кнопку Создать расчетную ведомость.

В открывшемся новом окне будет отображена детальная информация по всему начислению. Здесь же можно Добавить премию (1) и/или штраф (2). Подробнее о начислении премий и штрафов читайте здесь.

Также в разделе Расчет зарплат – Взаиморасчеты вы можете произвести Внеочередное начисление сотруднику. Более детально этот процесс описан в статье Внеочередные начисления.

После создания расчетной ведомости вы можете Сохранить и начислить зарплату сотруднику (3) или Сохранить как черновик созданную ведомость (4), черновик позволяет вам создать расчетную ведомость без начисления заработной платы. Также здесь вы можете 

Посмотреть взаиморасчеты с данным сотрудником (5) или Удалить расчетную ведомость (6).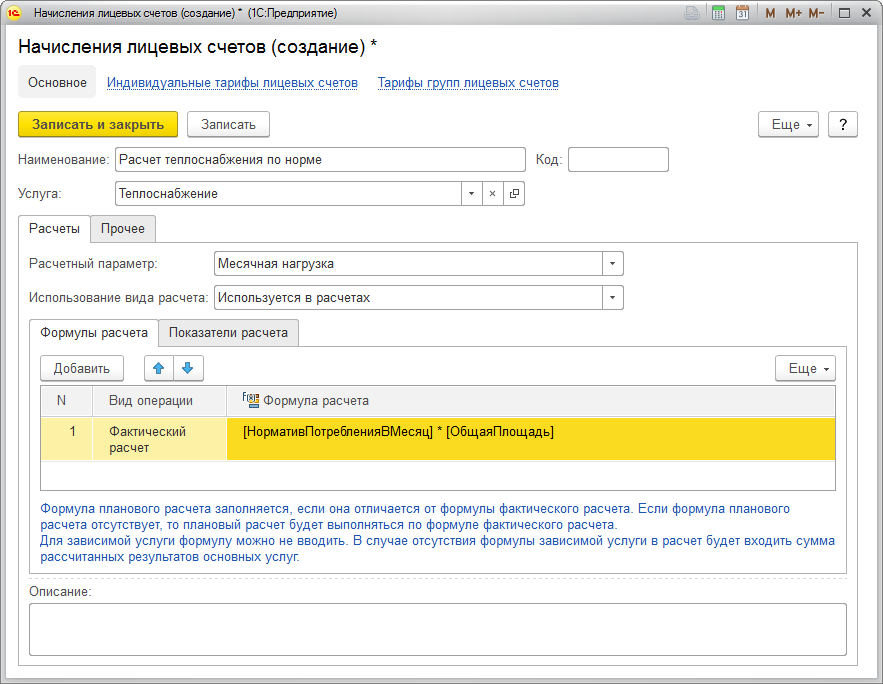

При переходе на детализацию ведомости со страницы взаиморасчетов у вас появится возможность Выгрузить ведомость в Excel (1), Выдать зарплату (2), Посмотреть взаиморасчеты (3) или Удалить ведомость(4).

 

В расчетной ведомости, может появится дополнительный цвет на некоторых позициях. 

• Красный цвет — означает, что позиция по которой была начислена зарплата, удалена и есть расхождение.
  
• Желтый цвет — означает, что после создания расчетной ведомости, вносились изменения в правило расчета зарплаты.  

В таких случаях, необходимо нажать кнопку Пересчитать и начислить для того, чтобы расчетная ведомость обновилась. 

Нажмите кнопку Выдать зарплату, после этого вы будете автоматически перенаправлены на страницу создания нового платежа в разделе Финансы – Финансовые операции (подробнее о создании платежей читайте здесь).

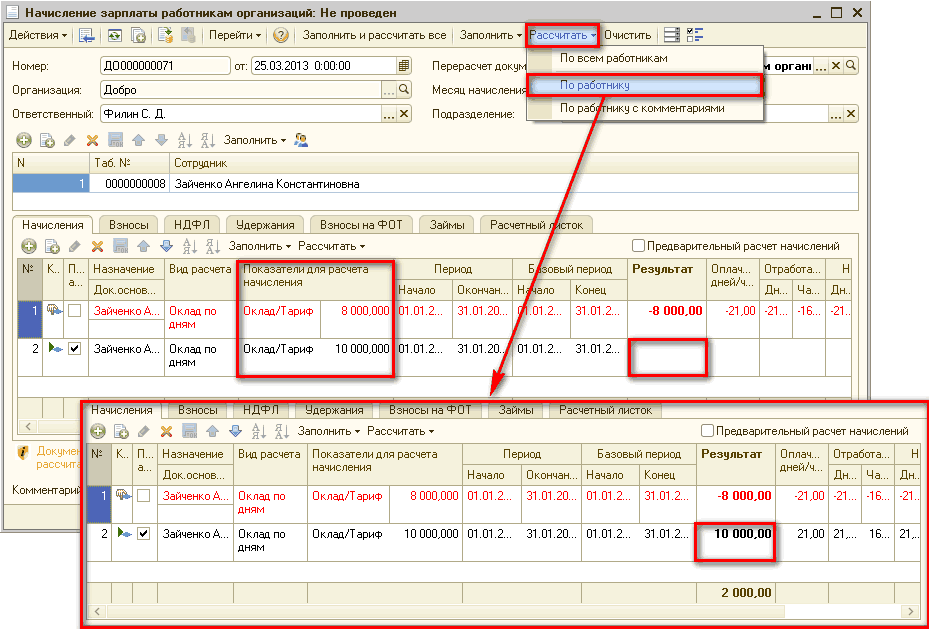
В открывшемся новом окне настройте дату и время платежа, выберите статью платежа (автоматически проставляется статья Зарплата персонала), выберите кассу, из которой будут списаны средства и сотрудника, которому выдается зарплата.

Сумма зарплаты проставляется автоматически в зависимости от того, в каком разделе вы нажали кнопку Выдать зарплату:

• если вы нажали кнопку в разделе Расчет зарплат – Взаиморасчеты, отобразится сумма из столбца Баланс;
• если вы нажали кнопку на странице расчетной ведомости, отобразится сумма начислений по этой ведомости.

Если вы хотите выдать другую сумму, измените ее. Добавьте комментарий и нажмите кнопку Сохранить.

Операция по выдаче зарплаты будет отображаться при переходе на страницу взаиморасчетов с сотрудником.

Порядок начислений и оплаты

В городе Томске большинство многоквартирных домов находятся на прямых расчетах с АО «ТомскРТС». При такой схеме взаимоотношений, в соответствии с «Правилами предоставления коммунальных услуг собственникам и пользователям помещений в многоквартирных домах и жилых домов», утвержденных постановлением Правительства РФ от 06.05.2011г. №354 (далее Правила), потребителями коммунальных услуг (контрагентами АО «ТомскРТС») являются наниматели жилого помещения по договорам социального найма, по договорам социального использования жилого помещения, по договорам найма жилого помещения государственного или муниципального жилого помещения, арендаторы жилого государственного или муниципального жилого помещения, члены жилищного кооператива, собственники жилого помещения и лица, принявшие от застройщика жилое помещение, введенного в эксплуатацию жилого дома.

Соответственно АО «ТомскРТС», на основании данных, предоставляемых ежемесячно управляющими компаниями, ЖСК или ТСЖ в соответствии с заключенными договорами энергоснабжения, (сведения об общей площади квартир, количестве зарегистрированных и временно проживающих человек, данные о собственниках или нанимателях,, показания индивидуальных (квартирных) и общедомовых приборов учёта), осуществляет расчет количества потребленной тепловой энергии и горячей воды, предъявляет потребителям на оплату платежные документы (квитанции) и осуществляет сбор денежных средств.

Управляющие многоквартирными домами организации, ЖСК и ТСЖ, жители которых находится на прямых расчетах с АО «ТомскРТС», не ведут начисления для таких потребителей (физических лиц), не производят сбор денежных средств. Основными функциями управляющих компаний в данном случае является обеспечение технического обслуживания жилых домов: подготовка системы теплопотребления к отопительному сезону, обеспечение качества и надежности работы систем теплопотребления, обслуживание и передача показаний общедомовых приборов учета и другой информации, необходимой для начисления оплаты.

Учет начислений и оплат ведется АО «ТомскРТС» в разрезе лицевых счетов, закрепленных за каждой квартирой. Расчеты с физическими лицами осуществляются в соответствии с «Правилами предоставления коммунальных услуг гражданам», утвержденные постановлением Правительства РФ от 23 мая 2006 г. № 307 и «Правилами предоставления коммунальных услуг собственникам и пользователям помещений в многоквартирных домах и жилых домов», утвержденные постановлением Правительства РФ от 6 мая 2011 г.

№ 354.

Порядок начислений

По услуге «Отопление»

По 1/12: При наличии в многоквартирном доме коллективных (общедомовых) приборов учета тепловой энергии, размер платы за отопление рассчитывается исходя из среднемесячных объемов потребления тепловой энергии за предыдущий год, а в случае отсутствия сведений об объемах потребления тепловой энергии за предыдущий год — исходя из нормативов потребления тепловой энергии и тарифа на тепловую энергию. При этом 1 раз в год производится корректировка платы за отопление рассчитанной по 1/12 до фактической.       

Одновременно расчёт производится «По факту», либо «По 1/9».

При наличии в многоквартирном доме коллективных (общедомовых) приборов учета тепловой энергии «По факту» — размер платы за отопление рассчитывается исходя из объемов фактического потребления тепловой энергии расчетного месяца.

В случае отсутствия коллективных (общедомовых) приборов учета тепловой энергии (По 1/9) — исходя из нормативов потребления тепловой энергии и тарифа на тепловую энергию

Нормативы утверждены Приказом ДЖКХ и Государственного Жилищного надзора     Томской области от 30.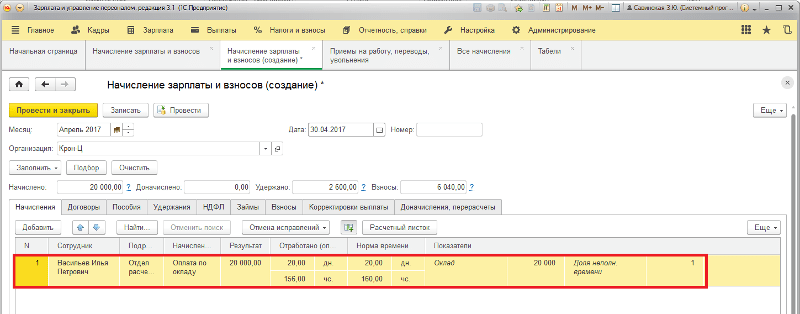 11.2012 № 47.

По услуге «Горячее водоснабжение»

При наличии индивидуального прибора учета (ИПУ) — по показаниям ИПУ, передаваемым потребителем путем заполнения счет-квитанции, через личный кабинет, по актам обследования и т.д.

При отсутствии индивидуального прибора учета (ИПУ) — на количество зарегистрированных в квартире человек по установленным нормативам потребления горячего водоснабжения.

В соответствии с Постановлением Правительства РФ от 06.05.2011 № 354, при отсутствии индивидуального или общего (квартирного) прибора учета горячей воды и в случае наличия обязанности установки такого прибора учета размер платы за коммунальную услугу горячему водоснабжению, предоставленную потребителю в жилом помещении, определяется исходя из норматива потребления коммунальной услуги по горячему водоснабжению с применением повышающего коэффициента, величина которого принимается равной 1,5.

Нормативы утверждены Приказом ДЖКХ и Государственного Жилищного надзора Томской области от 30. 11.2017 № 40

Порядок оплаты

Оплата за коммунальные услуги по отоплению и горячему водоснабжению должна производиться ежемесячно и в полном объеме.
Лица, несвоевременно и (или) не полностью внесшие плату за коммунальные услуги по отоплению и горячему водоснабжению, обязаны уплатить АО «ТомскРТС» пени в размере установленном п.14 ст. 155 Жилищного кодекса РФ.

Единый информационно-расчетный центр Ленинградской области

Выборгский район

Адрес
188800, Ленинградская область,
г. Выборг, ул. Железнодорожная, д. 2

Контактные телефоны
8 (813-78) 6-70-40

Режим приема граждан
Понедельник – среда с  08.00 до 17.15
Четверг с 8.00 до 19.00
Пятница с 08.00 до 13.00

Официальный сайт района

Приозерский район

Адрес
188760, Ленинградская область, г. Приозерск, ул. Калинина, 51

Контактные телефоны
8 (813-79) 5-90-00

Режим приема граждан
Понедельник – четверг с 09.00 до 18.00
Пятница с 09.00 до 17.00

Официальный сайт района

Всеволожский район

Адрес
188643, Ленинградская область, г. Всеволожск, Октябрьский проспект, 89 б

Контактные телефоны
8 (813-70) 9-70-12

Режим приема граждан
Понедельник – четверг с 09.00 до 18.00
Пятница с 09.00 до 16.45

Официальный сайт района

Кировский район

Адрес
187330, Ленинградская область, Кировский район, г. Отрадное, ул. Лесная, д. 1

Контактные телефоны
8 (813-62) 6-01-03

Режим приема граждан
Понедельник – четверг с 8:00 до 17:00
Пятница с 8:00 до 16:00

Официальный сайт района

Волховский район

Адрес
187403, Ленинградская область, г. Волхов, ул. Волгоградская, д.1а

Контактные телефоны
8 (813-63) 3-70-00

Режим приема граждан
Понедельник-четверг с 08.00 до 17.00
Пятница с 08.00 до 16.00

Официальный сайт района

Лодейнопольский район

Адрес
187700, Ленинградская область, г. Лодейное Поле, ул. Ульяновская, д. 15 корп. 1

Контактные телефоны
8 (813-64) 3-58-02

Режим приема граждан
Понедельник – четверг с 09.00 до 18.00
Пятница с 09.00 до 17.00

Подпорожский район

Адрес
187780, Ленинградская область, г. Подпорожье, ул. Комсомольская, д. 1А

Контактные телефоны
8 (813-65) 3-02-41

Режим приема граждан
Понедельник – четверг с 09.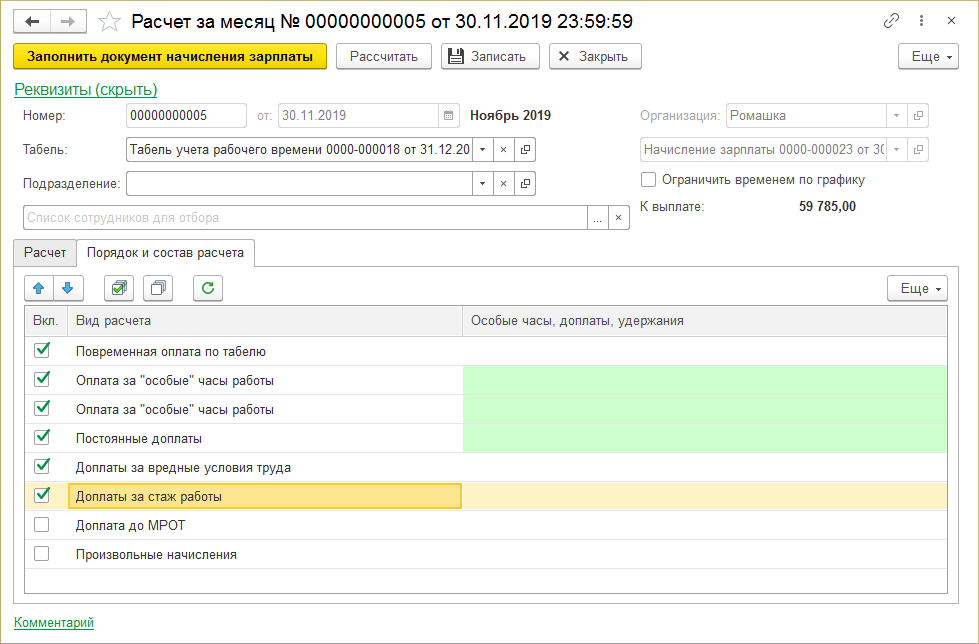 00 до 18.00
Пятница с 09.00 до 16.45

Официальный сайт района

Киришский район

Адрес
187110, Ленинградская область, г. Кириши, ул. Комсомольская, д. 3

Контактные телефоны
8 (813-68) 6-00-80

Режим приема граждан
Понедельник – четверг с 8:00 до 17:00
Пятница с 8:00 до 16:45

Официальный сайт района

Тихвинский район

Адрес
187553, Ленинградская область, г. Тихвин, 1-й микрорайон, д. 2 (3 этаж)

Контактные телефоны
8 (813-67) 3-41-00

Режим приема граждан:
Понедельник – четверг с 09.00 до 18.00
Пятница с 09.00 до 16.45

Официальный сайт района

Бокситогорский район

Адрес
187650, Ленинградская область, г. Бокситогорск, ул. Советская, д. 12

Контактные телефоны
8 (813-66) 2-00-20

Режим приема граждан
Понедельник – четверг с 08.45 до 18.00
Пятница с 09.00 до 17.00
Технологические перерывы с 13.00 до 14.00, с 15.00 до 15.30

Официальный сайт района

Сосновоборский ГО

Адрес
188540, Ленинградская область, г. Сосновый Бор, ул. Ленинградская, д. 26

Контактные телефоны
8 (813-69) 9-50-06

Режим приема граждан
Понедельник-четверг с 09.00 до 18.00
Пятница с 09.00 до 16.45

Официальный сайт района

Ломоносовский район

Адрес
198412, г. Санкт-Петербург, г. Ломоносов, Дворцовый пр-т, д. 22 а

Контактные телефоны
8 (813-76) 7-37-00

Режим приема граждан
Понедельник – пятница с 08. 30 до 17.30

Официальный сайт района

Гатчинский район

Адрес
188304, Ленинградская область, г. Гатчина, ул. Чехова, д. 23

Контактные телефоны
8 (813-71) 4-56-00

Режим приема граждан
Понедельник-пятница с 09.00 до 18.00
Пятница с 09.00 до 16.45

Официальный сайт района

Тосненский район

Адрес
187000, Ленинградская область, г. Тосно, пр-т Ленина, д. 19 (вход со двора между 1-м и 2-м подъездом со стороны Москвы)

Контактный телефон
8 (812) 630-20-10

Режим приема граждан
Понедельник-четверг с 09.00 до 18.00
Пятница с 09.00 до 16.45

Лужский район

Адрес
188230, Ленинградская область, г. Луга, ул. Тоси Петровой, д. 12 .

Контактные телефоны
8 (813-72) 2-01-57

Режим приема граждан
Понедельник – четверг с 08.00 до 17.00
Пятница с 08.00 до 16.00

Адрес
188560, Ленинградская обл., г.Сланцы, ул. Грибоедова, д.1.
Телефон: 8(813-74) 6-55-27

Режим приема граждан
Понедельник – четверг с 08.00 до 17.00
Пятница с 08.00 до 16.00

Официальный сайт района

Сланцевский район

Адрес
188560, Ленинградская обл., г. Сланцы, ул. Грибоедова, д.1.

Контактные телефоны
8 (813-74) 6-55-27

Режим приема граждан
Понедельник – четверг с 08.00 до 17.00
Пятница с 08.00 до 16.00

Официальный сайт района

Волосовский район

Адрес
188640, Ленинградская область, г. Волосово, Вингиссара пр-т, 35

Контактные телефоны
8 (813-73) 4-00-01

Режим приема граждан
Понедельник – четверг с 08.00 до 17.00
Пятница с 08.00 до 16.00

Кингисеппский район

Адрес
188480, Ленинградская область, г. Кингисепп, ул. Воровского, д. 3

Контактные телефон
8 (813-75) 5-50-02

Режим приема граждан
Понедельник – четверг с 08.00 до 17.00
Пятница с 08.00 до 16.00

 

Адрес
188490, Ленинградская область, г. Ивангород, ул. Гагарина, д. 45

Контактные телефоны
8 (813-75) 5-50-02

Режим приема граждан
Понедельник – среда, пятница с 08.00 до 12.00
Четверг – прием граждан не осуществляется

Официальный сайт района

Филиальная сеть “ЕИРЦ ЛО” представлена Территориальными управлениями в районах Ленобласти. Для получения подробной информации выберите на карте интересующих район.

1C Fresh

Зарегистрируйтесь и начните работу с программой:

Информационные письма о выпуске «1С:Расчет квартплаты и бухгалтерия ЖКХ»:

1С:Расчет квартплаты и бухгалтерия ЖКХ» – современный программный продукт, автоматизирующий расчет начислений по квартплате, коммунальным услугам, а также бухгалтерский и налоговый учет предприятиями жилищно-коммунальной отрасли.

«1С:Расчет квартплаты и бухгалтерия ЖКХ» – это решение, которое максимально отвечает типовым задачам различных организаций сферы ЖКХ:

• управляющих компаний;
• товариществ собственников жилья;
• расчетно-кассовых центров;
• жилищно-эксплуатационных управлений;
• абонентских отделов поставщиков услуг (тепловые, газовые и электросети, водоканалы и другие)

и сводит к минимуму возможные дополнительные затраты на внедрение, поддержку и доработку программы для расчета квартплаты, коммунальных услуг и ведения бухгалтерского учета в ЖКХ.

 

Важной особенностью решения является то, что оно разработано на базе наиболее популярной в России системы «1С:Бухгалтерия 8». Это позволяет пользователям работать со знакомыми инструментами и исключает трудности в освоении программного продукта. 
 

Автоматизация учетной и финансовой деятельности в ЖКХ на базе знакомых инструментов «1С:Бухгалтерия»

 

Отраслевое решение «1С:Расчет квартплаты и бухгалтерия ЖКХ» разработано на основе типовой конфигурации «1С:Предприятие 8. Бухгалтерия предприятия» редакции 3.0 и использует все преимущества технологической платформы «1С:Предприятие 8», обеспечивающей масштабируемость, открытость, простоту администрирования.

 

В решении реализованы специфические для ЖКХ бизнес-процессы, учтены актуальные требования нормативно-правовых актов и контролирующих органов. Расчет квартплаты и коммунальных услуг, формирование квитанций и отчетов, учет зданий и коммунальной инфраструктуры, подомовой учет, работа с должниками в ЖКХ, паспортный учет и множество других повседневных задач решается быстро и эффективно. Универсальность и гибкость настроек позволяет использовать эту программу расчета квартплаты, коммунальных услуг и ведения бухгалтерского учета в ЖКХ во всех регионах России.

 

Программный продукт содержит несколько базовых подсистем, тесно взаимосвязанных друг с другом и обеспечивающих автоматизацию основных направлений деятельности предприятий ЖКХ:

 

• Расчет, перерасчет начислений и учет оплаты предоставленных услуг ЖКХ – просто, удобно, прозрачно и в соответствии с требованиями законодательства
• Легкий доступ к необходимой для расчетов информации из карточки лицевого счета
• Полноценный паспортный учет и автоматизированное создание печатных форм
• Автоматизация работы юридической службы для эффективной работы с должниками
• Статистика и анализ рентабельности в подомовом учете
• Работа с поставщиками ресурсов
• Бухгалтерский учет и формирование регламентированной отчетности в соответствии с российским законодательством
• Отправка отчетности через Интернет

Эксперты объяснили, как проверить правильность начисления пенсии

+ A —

В будущем году проверить начисления можно будет на сайте Госуслуг

Эксперты предлагают россиянам самостоятельно проверить правильность начисления пенсии. Возможно, доказывать право на большую дотацию придется через суд. Это связано с изменением правил начисления компенсации.

Россиянам стоит самостоятельно проверить правильность начисления пенсии. Такое мнение высказала профессор кафедры финансов и цен РЭУ им. Г.В. Плеханова Юлия Финогенова. Она напомнила, что с 2022 года сделать это можно будет онлайн на сайте Госуслуг. Всем женщинам старше 40 лет и всем мужчинам старше 45 в личный кабинет раз в три года будут приходить сведения о состоянии пенсионного счета, накопленном стаже и предварительном размере пенсии по старости. Там же можно подать заявление, в случае если найдете ошибку.

Эксперт напомнила, что в нашей стране пенсия по старости состоит из двух частей — фиксированной выплаты и страховой. Первая часть практически у всех одинаковая. Она удваивается при достижении пенсионером возраста 80 лет и изменяется  раз в год при индексации. Также повышенная фиксированная часть пенсии есть у тех, кто отработал в районах Крайнего Севера.

А вот страховая часть зависит от стажа и уровня зарплаты. С 2002 года при расчете этой выплаты стали использовать размер страховых взносов. И именно из-за них возникает больше всего споров. Какие-то периоды работы специалисты Пенсионного фонда могут не учитывать. Например, если работодатель не оплачивал взносы, то и для государства этой организации как бы не существовало. Тогда трудовой стаж придется доказывать через суд.

Эксперт рекомендует изучить данные об учтенном стаже. Сделать это можно не только на сайте Госуслуг, но и на ресурсе Пенсионного фонда. А потом сравнить эти сведения с записями в трудовой. Если есть расхождение, то нужно обратиться с этой информацией в отделение фонда или МФЦ по месту жительства.

Заработная плата. Настройка. Начисление. Выдача – База знаний DIKIDI

Настройка и расчет заработной платы находится в разделе Сотрудники и призван автоматизировать расчет З/П персонала. Все расчеты производятся на основе данных из оформленных продаж в салоне и заранее настроенных схем расчета.  

Схемы расчета зарплаты в сервисе DIKIDI обеспечивают возможность настройки расчета для любой должности персонала в компании. Вы можете настроить схему зарплаты индивидуально под каждого сотрудника.

В разделе Сотрудники — расчет зарплаты вы сможете посмотреть размер заработной платы сотрудников по результатам расчета предварительно настроенными схемами, а и начислить необходимую сумму зарплаты к выдаче сотруднику. 

*Функционал рекомендовано подключать в составе комплексных пакетов вместе с Финансами, Продажами и Товарами в разделе Настройки — Платный функционал на сайте Beauty.dikidi.net/business

Функционал доступен в веб-версии сервиса на сайте beauty.dikidi.net/business с компьютера. Ведется разработка по добавлению данной функции и в мобильные приложения DIKIDI Business на iOS и Android 

Настройка схем зарплаты сотрудников

1. Процент от собственных продаж (услуг и товаров)
2. Процент от продаж салона (услуг и товаров)
3. Фиксированная оплата (ставка за рабочий день / повременная)

Настройка схемы зарплаты»>Процент от собственных продаж

Схема зарплаты Процент от собственных продаж чаще всего используется для мастеров. А также для администраторов, продающих продукцию в салоне. При расчете в данной схеме используется процент от продаж сотрудника, который является продавцом товаров или исполнителем услуг.

Процент может быть установлен единый для всех Услуг или для всех Товаров. А также существует гибкая настройка Процента для каждой отдельной услуги. В том числе в виде фиксированной суммы.

Для того чтобы настроить схему расчета зарплаты Процент от собственных продаж нажмите «Добавить схему» в разделе Зарплата-Схемы зарплаты. Настройка схем зарплаты производится только в Web-версии сервиса на сайте beauti.dikidi.net/business.

В открывшемся окне выберите Сотрудника, для которого будет действовать схема и дату, с которой будет рассчитываться з/п по данной схеме. Включите схему Процент с собственных продаж. Внесите размер процентной ставки за услуги и товары. 

 

Если с разных услуг сотрудник получает разный процент или установлена фиксированная ставка с продажи услуги для расчета зарплаты, нажмите «Указать детально» для настройки. 

В открывшемся окне внесите информацию по процентам и ставкам возле каждой услуги. 

 

Учитывать скидку клиента при расчете ЗП. Активация данного параметра включает в расчет конечные суммы продаж (с уже примененной скидкой) суммы продаж. Напротив, если галочка учета скидки НЕактивна, то расчет зарплаты будет осуществляться с полной стоимости услуги без учета скидки.    

Учитывать скидку, но не более чем. Данная настройка позволяет ограничить учитываемую скидку при расчете з/п сотрудника. Например клиенту выдали скидку 30% на услугу. При этом с мастером имеется договоренность, что максимальную скидку, которую он может предоставить = 10%. Таким образом, установив данное ограничение Учитывать скидку но не более чем 10% мастер недополучит лишь 10% выручки, а салон оставшиеся 20%. 

Учитывать себестоимость материалов. Если ваш мастер получает зарплату только со стоимости своей работы (за вычетом материалов, затраченных на оказание услуг), необходимо в схеме предусмотреть это, установив галочку Учитывать себестоимость материалов. Например: мастер парикмахер оказывает услуги по окрашиванию волос. Стоимость продажи этой услуги составила 3000. Из них 2000 — материалы и 1000 — работа. При поставленной галочке учета материалов, зарплата мастера будет рассчитываться именно, как % с 1000.   

 

Процент от продаж салона

Для некоторых видов должностей в салоне красоты действует схема расчета зарплаты, когда сотрудник получает процент от общей выручки салона. Для расчета зарплаты по такой схеме настройте ее в разделе Зарплата — Схемы зарплаты. 

Нажмите на кнопку Добавить схему! В открывшемся окне выберите сотрудника и дату начала действия его схемы расчета зарплаты. Включите в настройке схемы переключатель — Процент от продаж салона. Ниже вам будет предложено уточнить детали этой настройки и сами проценты по товарам и услугам. 

 

Не учитывать собственные продажи специалиста. Если в схеме зарплаты сотрудника включен процент от собственных продаж, и плюс к этому сотрудник получает процент от общей выручки салона, то необходимо понимать, что в таком случае, сотрудник может получить процент от выручки своих продаж дважды. Чтобы этого не происходило поставьте галочку возле настройки — Не учитывать собственные продажи специалиста. 

Учитывать только Продажи в рабочую смену сотрудника. Для того, чтобы сотрудник получал процент с Продаж салона, но только с оформленных в его смену, поставьте галку Учитывать только Продажи в рабочую смену сотрудника. 

После того, как ограничения расставлены перейдите к установке соответствующего процента за Продажи услуг и Товаров. При этом, как и в настройке Процента с собственных продаж вы можете указать разные проценты для разных услуг. 

Учитывать скидку но не более чем.  Данная настройка позволяет ограничить учитываемую скидку при расчете з/п сотрудника. Например клиенту выдали скидку 30% на услугу. При этом с сотрудником имеется договоренность, что максимальную скидку, которую он может предоставить = 10%. Таким образом, установив данное ограничение Учитывать скидку но не более чем 10% мастер недополучит лишь 10% выручки, а салон оставшиеся 20%. 

 

Фиксированная оплата (оклад)

Чаще всего применяется сотрудникам с повременной оплатой или же оплатой за выход. В данном случае учитывается время, задействования сотрудника. Настраивается такая схема также просто как и остальные, в разделе Зарплаты — Схемы зарплаты. 

Нажмите Добавить схему, выберите специалиста и дату начала расчета по данной схеме. 

Выберите вариант настройки — Фиксированная оплата

Если сотрудник получает зарплату за выход на рабочее место, поставьте галочку — Ставка за выход (за рабочий день) и впишите сумму выплачиваемую клиенту за выход.  

 

 

Если же у сотрудника фиксированная ставка не за весь рабочий день, а лишь за время, когда он непосредственно оказывал услуги, то выберите галочку Повременная. Выберите единицу измерения времени и ее стоимость. 

 

 

 

 

 

 

Сеть АЗС ПАО «Газпром нефть» и бонусная программа «Нам по пути»

Уважаемые клиенты!   Для Вас работает сервис «Единый центр поддержки клиентов», специалисты которого будут рады Вам помочь:   Проконсультируют Вас по вопросам, связанным с работой сети АЗС «Газпромнефть»:   Правила участия в Программе лояльности Схема начисления бонусов Условия блокировки или разблокировки бонусной карты Условия приобретения товаров АЗС в обмен на бонусы Условия восстановления бонусной карты в случае утери, кражи или поломки Доступ в личный кабинет Информация в чеке Баланс, статус бонусной карты История транзакций по бонусной карте Выполнят блокировку бонусной карты по звонку, разблокировку — при наличии письменного заявления   Сроки проведения Условия участия Список АЗС, на которых проходят акции Точки выдачи призов* Списки победителей*   Примут заявку в работу по вопросам: Начисления, списания бонусов по карте Программы лояльности «Нам по пути» Качества обслуживания на АЗС «Газпромнефть», в том числе Ваши предложения по улучшению работы и персонала АЗС Качества топлива Техническим неисправностям оборудования на АЗС     «Единый центр поддержки клиентов» принимает обращения клиентов по различным каналам связи: Звонок на номер 8-800-700-5151 Форма «Обратная связь» на сайте www.gpnbonus.ru Электронное письмо на адрес [email protected] Вопрос в чат онлайн-консультанту на сайте www.gpnbonus.ru   Мы стремимся к улучшению качества сервиса, поэтому для нас важно Ваше мнение. Мы ждем Ваших обращений и будем рады помочь Вам. С уважением, Сеть АЗС «Газпромнефть» *При проведении Федеральных рекламных акций сети АЗС «Газпромнефть»

Как рассчитать электрический заряд

Обновлено 17 сентября 2019 г.

Автор С. Хуссейн Атер

Будь то статическое электричество, исходящее от пушистой шерсти, или электричество, от которого питаются телевизоры, вы можете узнать больше об электрическом заряде, изучив лежащая в основе физика. Методы расчета заряда зависят от природы самого электричества, например, принципов распределения заряда по объектам. Эти принципы одинаковы, независимо от того, где вы находитесь во Вселенной, поэтому электрический заряд является фундаментальным свойством самой науки.

Формула электрического заряда

Существует множество способов вычисления электрического заряда для различных контекстов в физике и электротехнике.

Закон Кулона обычно используется при вычислении силы, создаваемой частицами, несущими электрический заряд, и является одним из наиболее распространенных уравнений электрического заряда, которые вы будете использовать. Электроны несут отдельные заряды -1,602 × 10 ^-19 кулонов (Кл), а протоны несут такое же количество, но в положительном направлении, 1.2}

, в котором k — постоянная k = 9,0 × 10 ⁹ Нм ² / C ² . Физики и инженеры иногда используют переменную e для обозначения заряда электрона.

Обратите внимание, что для зарядов противоположных знаков (плюс и минус) сила отрицательная и, следовательно, притягивающая между двумя зарядами. Для двух зарядов одного знака (плюс и плюс или минус и минус) сила отталкивающая. Чем больше заряды, тем сильнее сила притяжения или отталкивания между ними.

Электрический заряд и гравитация: сходства

Закон Кулона поразительно похож на закон Ньютона для гравитационной силы F _G = G м ₁ м ₂ / r ² для гравитационной силы F _G , масс м ₁ и _{м 2 и гравитационной постоянной G = 6,674 × 10 ⁻¹¹ м ³ / кг с ² .Оба они измеряют разные силы, изменяются с большей массой или зарядом и зависят от радиуса между обоими объектами во второй степени. Несмотря на сходство, важно помнить, что гравитационные силы всегда притягивают, в то время как электрические силы могут быть притягивающими или отталкивающими.}

Следует также отметить, что электрическая сила обычно намного сильнее гравитации, исходя из различий в экспоненциальной мощности констант законов. Сходство между этими двумя законами является еще большим свидетельством симметрии и закономерностей среди общих законов Вселенной.

Сохранение электрического заряда

Если система остается изолированной (т. Е. Без контакта с чем-либо еще вне ее), она будет сохранять заряд. Сохранение заряда означает, что общее количество электрического заряда (положительный заряд минус отрицательный заряд) остается неизменным для системы. Сохранение заряда позволяет физикам и инженерам вычислять, сколько заряда перемещается между системами и их окружением.

Этот принцип позволяет ученым и инженерам создавать клетки Фарадея, в которых используются металлические экраны или покрытия для предотвращения утечки заряда.Клетки Фарадея или щиты Фарадея используют тенденцию электрического поля к перераспределению зарядов внутри материала, чтобы нейтрализовать действие поля и предотвратить повреждение или проникновение зарядов внутрь. Они используются в медицинском оборудовании, таком как аппараты магнитно-резонансной томографии, для предотвращения искажения данных, а также в защитном снаряжении для электриков и монтажников, работающих в опасных средах.

Вы можете рассчитать чистый поток начислений для объема пространства, вычислив общую сумму вводимых затрат и вычитая общую сумму оставленных сборов.Благодаря электронам и протонам, несущим заряд, заряженные частицы могут создаваться или разрушаться, чтобы уравновесить себя в соответствии с законом сохранения заряда.

Число электронов в заряде

Зная, что заряд электрона равен -1,602 · 10 ⁻¹⁹ Кл, заряд −8 · 10 ⁻¹⁸ Кл будет состоять из 50 электронов. Вы можете найти это, разделив количество электрического заряда на величину заряда отдельного электрона.

Расчет электрического заряда в цепях

Если вам известен электрический ток , поток электрического заряда через объект, проходящий по цепи и продолжительность действия тока, вы можете рассчитать электрический заряд, используя уравнение для тока Q = Это , в котором Q — это общий заряд, измеренный в кулонах, I — ток в амперах, а t — время приложения тока в секундах.Вы также можете использовать закон Ома ( В = IR ) для расчета тока по напряжению и сопротивлению.

Для цепи с напряжением 3 В и сопротивлением 5 Ом, приложенной в течение 10 секунд, соответствующий ток будет равен I = В / R = 3 В / 5 Ом = 0,6 А, а общий заряд будет Q = It = 0,6 A × 10 с = 6 C.

Если вам известна разность потенциалов ( В, ) в вольтах, приложенная к цепи, и работа ( Вт, ) в джоулях, выполненная за период, за который он применяется, заряд в кулонах, Q = Вт / В .

Формула электрического поля

••• Syed Hussain Ather

Электрическое поле , электрическая сила на единицу заряда, распространяется радиально наружу от положительных зарядов к отрицательным зарядам и может быть рассчитана с помощью E = F _E / q , в котором F _E — электрическая сила, а q — заряд, создающий электрическое поле. Учитывая, насколько фундаментальными являются поле и сила для вычислений в электричестве и магнетизме, электрический заряд можно определить как свойство вещества, которое заставляет частицу иметь силу в присутствии электрического поля.

Даже если общий или общий заряд объекта равен нулю, электрические поля позволяют различным образом распределять заряды внутри объектов. Если внутри них есть распределения зарядов, которые приводят к ненулевому чистому заряду, эти объекты имеют поляризацию , а заряд, вызываемый этими поляризациями, известен как связанный заряд .

Чистый заряд Вселенной

Хотя ученые не все согласны с тем, каков общий заряд Вселенной, они сделали обоснованные предположения и проверили гипотезы с помощью различных методов.Вы можете заметить, что гравитация является доминирующей силой во Вселенной в космологическом масштабе, и, поскольку электромагнитная сила намного сильнее гравитационной силы, если бы у Вселенной был чистый заряд (положительный или отрицательный), вы бы были возможность видеть доказательства этого на таких огромных расстояниях. Отсутствие этих доказательств привело исследователей к мысли, что Вселенная заряжена нейтрально.

Всегда ли Вселенная была нейтральной по заряду или как заряд Вселенной изменился после Большого взрыва, также являются вопросами, которые вызывают споры.Если бы у Вселенной был чистый заряд, то ученые могли бы измерить их тенденции и влияние на все силовые линии электрического поля таким образом, чтобы вместо соединения положительных зарядов с отрицательными они никогда не закончились бы. Отсутствие этого наблюдения также указывает на аргумент, что у Вселенной нет чистого заряда.

Расчет электрического потока с зарядом

••• Сайед Хуссейн Атер

Электрический поток через планарную (т. Е.плоская) площадь A электрического поля E — поле, умноженное на составляющую площади, перпендикулярной полю. Чтобы получить этот перпендикулярный компонент, вы используете косинус угла между полем и интересующей плоскостью в формуле для потока, представленный как Φ = EA cos ( θ ) , где θ — угол между линией, перпендикулярной площади, и направлением электрического поля.

Это уравнение, известное как закон Гаусса , также говорит вам, что для поверхностей, подобных этим, которые вы называете гауссовскими поверхностями , любой чистый заряд будет находиться на ее поверхности плоскости, потому что было бы необходимо создать электрическое поле.

Поскольку это зависит от геометрии площади поверхности, используемой при расчете потока, она меняется в зависимости от формы. Для круглой области площадь потока A будет π_r_ ^{2 с r в качестве радиуса круга, или для криволинейной поверхности цилиндра площадь потока будет Ch , в которой C — это длина окружности круглой поверхности цилиндра, а h — высота цилиндра.}

Заряд и статическое электричество

Статическое электричество возникает, когда два объекта не находятся в электрическом равновесии (или электростатическом равновесии ), или когда существует чистый поток зарядов от одного объекта к другому.Когда материалы трутся друг о друга, они переносят заряды друг на друга. Эти виды электричества могут генерироваться при натирании носков о ковер или резинкой надутого воздушного шара о волосы. Шок переносит эти избыточные заряды обратно, чтобы восстановить состояние равновесия.

Электрические проводники

Для проводника (материала, передающего электричество), находящегося в электростатическом равновесии, электрическое поле внутри равно нулю, а общий заряд на его поверхности должен оставаться в электростатическом равновесии.Это связано с тем, что, если бы было поле, электроны в проводнике перераспределялись бы или перестраивались в ответ на поле. Таким образом, они аннулируют любое поле в момент его создания.

Алюминий и медная проволока являются общими проводящими материалами, используемыми для передачи токов, также часто используются ионные проводники, которые представляют собой решения, в которых используются свободно плавающие ионы, позволяющие легко проходить заряду. Полупроводники , такие как микросхемы, которые позволяют компьютерам функционировать, также используют свободно циркулирующие электроны, но не так много, как проводники.Полупроводники, такие как кремний и германий, также требуют больше энергии для циркуляции зарядов и обычно имеют низкую проводимость. Напротив, изоляторы , такие как дерево, не позволяют заряду легко проходить через них.

При отсутствии поля внутри для гауссовой поверхности, лежащей непосредственно внутри поверхности проводника, поле должно быть везде нулевым, чтобы поток был равен нулю. Это означает, что внутри проводника нет чистого электрического заряда. Из этого вы можете сделать вывод, что для симметричных геометрических структур, таких как сферы, заряд равномерно распределяется по поверхности гауссовой поверхности.

Закон Гаусса в других ситуациях

Поскольку чистый заряд на поверхности должен оставаться в электростатическом равновесии, любое электрическое поле должно быть перпендикулярно поверхности проводника, чтобы материал мог передавать заряды. Закон Гаусса позволяет вычислить величину этого электрического поля и магнитного потока для проводника. Электрическое поле внутри проводника должно быть нулевым, а снаружи оно должно быть перпендикулярно поверхности.

Это означает, что для цилиндрического проводника с полем, излучаемым от стенок под перпендикулярным углом, полный поток равен просто 2_E__πr_ ² для электрического поля E и радиус r круглой поверхности цилиндрического проводника.Вы также можете описать чистый заряд на поверхности, используя σ , плотность заряда на единицу площади, умноженную на площадь.

Как рассчитать кулоны | Sciencing

Обновлено 3 ноября 2020 г.

Клэр Гиллеспи

Электрический заряд, который проходит через что угодно, от батареи AA до молнии, измеряется в кулонах. Если вы знаете, какой ток в цепи и как долго он течет, вы можете рассчитать электрический заряд в кулонах.

Свойства кулонов

Электроны крошечные и имеют очень маленький заряд. В физике очень большое количество электронов определяется как 1 единица заряда, называемая кулоном. Один кулон эквивалентен 62 × 10 ¹⁸ электронов. Количество кулонов в секунду называется током (т. Е. Скоростью потока кулонов в цепи). Энергия кулона называется напряжением и измеряется в джоулях.

Как рассчитать электрический заряд

Чтобы определить величину электрического заряда, протекающего в цепи, вам необходимо знать, какой ток течет и как долго он протекает.Уравнение:

\ text {заряд в кулонах} = \ text {ток в амперах} \ times \ text {время в секундах}

Например, если ток 20 А течет в течение 40 с, расчет равен 20. × 40. Итак, электрический заряд равен 800 C.

Как рассчитать переданную энергию

Если вы знаете количество электрического заряда в кулонах и напряжение (также известное как разность потенциалов), вы можете вычислить, сколько энергии переносится. Уравнение:

\ text {энергия, преобразованная в джоулях} = \ text {разность потенциалов в вольтах} \ times \ text {заряд в кулонах}

Например, если разность потенциалов составляет 100 В, а заряд равен 3 Кл. , расчет 100 × 3.Таким образом передается 300 Дж энергии.

Использование закона Кулона

Произведение электрических зарядов в двух телах (т. Е. Притягиваются они или отталкиваются друг от друга) зависит от заряда каждого тела в кулонах, а также от расстояния между телами. Если полярности одинаковы (обе положительные или обе отрицательные), кулоновская сила отталкивается, но если полярности противоположны (отрицательная / положительная или положительная / отрицательная), кулоновская сила притягивается. Электрический заряд также обратно пропорционален квадрату расстояния между двумя телами.Это известно как закон Кулона, который сформулирован как:

В этом уравнении F — сила, приложенная к зарядам (q ₁ ) и (q ₂ ), k — постоянная Кулона и (r) — расстояние между (q ₁ ) и (q ₂ ). Значение k зависит от среды, в которую погружены заряженные объекты. Например, значение воздуха составляет приблизительно 9,0 × 10 ⁹ Нм ² / C ² . Закон Кулона можно использовать для решения многих физических задач, в которых известны все значения, кроме одного.

Калькулятор закона Кулона

Этот калькулятор электрической силы позволит вам определить силу отталкивания или притяжения между двумя статическими заряженными частицами. Продолжайте читать, чтобы лучше понять закон Кулона, условия его действия и физическую интерпретацию полученного результата.

Как использовать закон Кулона

Закон Кулона, также известный как закон обратных квадратов Кулона, описывает электростатическую силу, действующую между двумя зарядами.Сила действует по кратчайшей линии, соединяющей заряды. Отталкивает, если оба заряда имеют одинаковый знак, и притягивает, если они имеют противоположные знаки.

Закон Кулона формулируется следующим образом:

F = k e q₁q₂ / r²

где:

• F — электростатическая сила между зарядами (в Ньютонах),
• q₁ — величина первого заряда (в кулонах),
• q₂ — величина второго заряда (в кулонах),
• r — кратчайшее расстояние между зарядами (в м),
• k e — постоянная Кулона.Оно равно 8,98755 × 10⁹ Н · м² / К2 . Это значение уже заложено в калькулятор — запоминать его необязательно 🙂

Просто введите любые три значения в наш калькулятор электрической силы, чтобы в результате получить четвертое.

Зарядные устройства

Единицей электрического заряда является кулон (обозначение: C). Он определяется как заряд, переносимый постоянным током в 1 ампер в течение 1 секунды. Следовательно, 1 C = 1 A * 1 с , выраженное в единицах СИ.

Если вы не помните, что такое ампер, обратитесь к нашему калькулятору закона Ома.

Условия действия

Три основных условия должны быть выполнены для того, чтобы вычислитель электростатической силы возвращал действительные значения:

1. Заряды должны быть неподвижными — они не могут двигаться относительно друг друга.
2. Предполагаются точечные начисления. Это предположение также верно для любых сферических и симметричных зарядов. Например, заряженный металлический шар удовлетворяет этому условию, а заряженный металлический ящик — нет.
3. Заряды не могут перекрываться — они должны быть различимы и иметь хотя бы минимальное расстояние между ними.

Интерпретация результатов

Сила, полученная с помощью нашего калькулятора закона Кулона, может быть как положительной, так и отрицательной. Положительная сила подразумевает отталкивающее взаимодействие между зарядами. Отрицательная сила означает, что взаимодействие является привлекательным.

Вы заметили, что единица заряда по умолчанию в нашем калькуляторе закона Кулона — нанокулон (нКл)? Это потому, что типичный порядок величины электрического заряда составляет 10 -6 C или даже 10 -9 C .

Заинтересованы в электричестве? Также ознакомьтесь с нашим калькулятором стоимости электроэнергии!

Как рассчитать формальный платеж

Эй! Добро пожаловать на курс «Мастер органической химии», на случай, если вы впервые приехали.

В этом сообщении в блоге я объясняю, как рассчитать формальный заряд молекул. Тем не менее, вы можете найти мои видео, содержащие 10 решенных примеров формальных проблем с зарядкой, еще более полезными. Просто думал, что вы должны знать!

---

Нужно выяснить, является ли атом отрицательным, положительным или нейтральным? Вот формула для определения «формального заряда» атома:

Формальный заряд = [количество валентных электронов] — [электроны в неподеленных парах + 1/2 количества связывающих электронов]

В этой формуле явно указывается соотношение между количеством связывающих электронов и их отношением к тому, сколько из них формально «принадлежит» атому.

Например, применив это к BH ₄ (верхний левый угол на изображении ниже), мы получим:

• Число валентных электронов для бора равно 3 .
• Количество несвязанных электронов ноль .
• Общее количество связывающих электронов вокруг бора равно 8 (полный октет). Половина из них — 4 .

Итак, формальный платеж = 3 — (0 + 4) = 3 — 4 = –1

Однако есть более простой способ сделать это.

Так как химическая связь имеет два электрона, «количество связывающих электронов, деленное на 2» по определению равно как количеству связей , окружающих атом. Таким образом, мы можем вместо этого использовать эту сокращенную формулу :

Формальный заряд = [количество валентных электронов на атоме] — [несвязанные электроны + количество связей].

Применяем это снова к BH ₄ (верхний левый угол).

• Число валентных электронов для бора составляет 3 .
• Количество несвязанных электронов ноль .
• Число связей вокруг бора составляет 4 .

Итак, формальный заряд = 3 — (0 + 4) = 3-4 = –1

Формальный заряд B в BH ₄ отрицательный 1.

Применим его к : CH ₃ (один справа от ЧД ₄ )

• Число валентных электронов для углерода 4
• Число несвязанных электронов два (у него неподеленная пара)
• количество связей вокруг углерода — 3 .

Таким образом, формальный заряд = 4 — (2 +3) = 4-5 = –1

Формальный заряд C в: CH ₃ отрицательный 1.

Тот же формальный заряд, что и BH ₄ !

Рассмотрим последний пример. Давайте сделаем CH ₃ ⁺ (без неподеленных пар на углероде). Это оранжевый в нижнем ряду.

• Число валентных электронов углерода 4
• Число несвязанных электронов ноль
• Число связей вокруг углерода 3 .

Итак, формальный заряд = 4 — (0 +3) = 4 — 3 = +1

Вы можете применить эту формулу к любому атому, который хотите назвать.

Вот диаграмма для некоторых простых молекул в ряду B C N O. Я надеюсь, что бериллий и фтор не слишком обиделись, что я их пропустил, но они действительно не так интересны для целей этой таблицы.

Обратите внимание на интересный узор в геометрии (выделен цветом): BH ₄ (-), CH ₄ и NH ₄ (+) имеют одинаковую геометрию, как и CH ₃ (-), NH ₃ и OH ₃ (+).Карбокатион CH ₃ (+) имеет такую ​​же электронную конфигурацию (и геометрию), что и нейтральный боран, BH ₃ . Знакомую изогнутую структуру воды H ₂ O разделяет амид-анион NH ₂ (-). Эти общие геометрические формы являются одним из интересных следствий теории отталкивания электронных пар валентной оболочки (VSEPR — произносится как « vesper », так же как «Фавр» произносится как « Фарве» ).

Формальная формула заряда также работает для двойных и тройные облигации:

Вот вопрос.Алканы, алкены и алкины нейтральны, поскольку имеется четыре связи и нет несвязанных электронов: 4 — [4 + 0] = 0. Для каких других значений [связи + несвязанные электроны] вы также получите нулевое значение, и как могут выглядеть эти структуры? (Вы встретите некоторые из этих структур позже по ходу курса).

И последний вопрос — как вы думаете, почему это называется «формальным обвинением»?

Подумайте, какой будет формальная плата за BF ₄ . Отрицательный заряд на боре.Какой элемент здесь самый электроотрицательный? Фторид, конечно, с электроотрицательностью 4,0, с тактовой частотой бора 2,0. Как вы думаете, где на самом деле находится отрицательный заряд ?

Ну, дело не в боре. На самом деле он распространяется через более электроотрицательные фторид-ионы, которые становятся более богатыми электронами. Таким образом, хотя «формальный» адрес отрицательного заряда находится на боре, электронная плотность фактически распределена по фторидам. Другими словами, в данном случае формальное обвинение не имеет ничего общего с действительностью.

Еще одно напоминание — 10 видеороликов с решенными примерами формальных задач заряда, прямо здесь (см. Самый верх страницы)

Atomic Charge Calculator II: веб-инструмент для расчета частичных атомных зарядов | Исследование нуклеиновых кислот

Аннотация

Частичные атомные заряды служат простой моделью электростатического распределения молекулы, которая управляет ее взаимодействием с окружающей средой. Поскольку частичные атомные заряды часто используются в вычислительной химии, хемоинформатике и биоинформатике, было введено множество вычислительных подходов для их расчета.Наиболее применимыми являются быстрые и достаточно точные подходы к эмпирическому расчету заряда. Здесь мы представляем Atomic Charge Calculator II (ACC II), веб-приложение, которое позволяет рассчитывать частичные атомные заряды с помощью всех основных эмпирических подходов и для всех типов молекул. ACC II реализует 17 эмпирических методов расчета заряда, в том числе широко цитируемые (QEq, EEM), недавно опубликованные (EQeq, EQeq + C) и старые, но все еще часто используемые (PEOE). ACC II позволяет быстро рассчитывать заряды даже для больших макромолекулярных структур.Веб-сервер также предлагает визуализацию заряда благодаря мощной программе просмотра LiteMol. Настройка расчета ACC II очень проста и позволяет быстро рассчитать высококачественные частичные расходы. Приложение доступно по адресу https://acc2.ncbr.muni.cz.

ВВЕДЕНИЕ

Частичные заряды атомов — это действительные числа, которые моделируют распределение плотности заряда в молекуле. Таким образом, они дают ключ к разгадке химического поведения молекул, даже если они не являются физически наблюдаемыми объектами.Понятие частичных зарядов атомов впервые было использовано в химии для объяснения реакционной способности (1,2). Частичные атомные заряды также были приняты в вычислительной химии (например, приложения в молекулярной динамике, стыковке или конформационном поиске) (3–5), и они также стали популярными в хемоинформатике (например, дескрипторы для моделирования QSAR и QSPR или виртуальный скрининг) (6– 8) и биоинформатики (например, поиск сходства или изучение механизмов и эффектов, связанных с определенными химическими действиями) (9,10).Для их расчета было введено множество вычислительных подходов. Самый надежный метод расчета частичного заряда — это применение квантовой механики (КМ), как недавно было рассмотрено в Cho et al. (11). Поскольку методы QM обычно требуют времени, были разработаны более быстрые подходы к эмпирическому расчету заряда, отличные от QM. В частности, некоммерческие эмпирические методы не учитывают отдельные электроны (и / или базисные функции) в расчетах, но они работают на уровне атомов.Эти подходы можно разделить на конформационно-независимые, основанные на 2D-структуре (так называемые 2D-методы; например, PEOE Гастайгера и Марсили (12), MPEOE (13), KCM (14) или DENR (15)) и конформационно зависимые, которые вычисляются из трехмерной структуры (так называемые трехмерные методы; например, EEM (16), QEq (3) или EQeq (17)). Поскольку эмпирические методы, не относящиеся к QM, часто параметризуются в соответствии с методами QM, их точность сопоставима (см., Например, (18,19)), а из-за скорости вычислений они также применимы для биомакромолекул (10).По этой причине несколько эмпирических методов, не связанных с QM, часто используются и часто цитируются (например, PEOE> 3000 цитирований, EEM> 700 цитирований, QEq> 2000 цитирований), как было обнаружено при поиске литературы в базе данных Web of Science (https: //www.webofknowledge.com/, набор данных «Все базы данных»), который мы выполнили 31 марта 2020 года. Полные результаты поиска литературы показаны в дополнительной таблице S1.

Практическое использование подходов к расчету эмпирических сборов, не связанных с QM, сопряжено с тремя проблемами:

1. Большинство эмпирических подходов, не связанных с QM, описаны только в статье, и их реализация недоступна для сообщества.Лишь некоторые из эмпирических методов, не связанных с QM, доступны в виде программных инструментов для настольных ПК (OpenBabel (20), RDKit (https://www.rdkit.org/), VCharge (21), EEM-SOLVER (22) и ABEEM). -SOLVER (22)), и только один эмпирический метод, не связанный с QM (EEM), доступен как веб-приложение (AtomicChargeCalculator (ACC) (23)). Несмотря на ограниченную функциональность ACC, он стал часто использоваться (~ 2000 обращений в год).

2. В эмпирических подходах, не связанных с QM, используются параметры, взятые из физико-химических констант или зарядов QM.Эти параметры, однако, обычно оптимизируются только для определенных типов молекул и обычно не применяются. Поэтому было опубликовано много наборов параметров, и их ограничения не являются легкодоступной информацией.

3. Несмотря на то, что эмпирические подходы, не связанные с QM, намного быстрее, чем методы QM, временная сложность конформационно зависимых подходов часто составляет O (N ³ ), где N — количество атомов в молекуле, из-за решения система линейных уравнений.Для их применения в более крупных молекулярных системах (например, биомакромолекулах) необходимо интегрировать сложные алгоритмы снижения сложности (например, методы отсечения и покрытия (23)).

В этой статье мы решаем все эти проблемы, и мы предоставляем Atomic Charge Calculator II, обновление для ACC, которое включает следующие ключевые нововведения:

• Реализация 17 подходов к расчету заряда, включая высоко цитируемый (QEq , EEM), недавно опубликованный (EQeq, EQeq + C) и старый, но все еще часто используемый (PEOE).Там, где это применимо, подходы, включающие решение систем линейных уравнений, используют методы отсечения и покрытия (23) для быстрой обработки больших макромолекулярных структур. Если в подходах используются параметры, все опубликованные наборы параметров были собраны из литературы и интегрированы в ACC II. Список всех параметров, включенных в ACC II, доступен в дополнительной таблице S2.

• Для визуализации зарядов используется мощная программа просмотра LiteMol (24), которая предлагает несколько вариантов просмотра, а также управление результатами вычислений.

• Настройка расчета очень проста и позволяет быстро рассчитать высококачественные платежи.

ОПИСАНИЕ ВЕБ-СЕРВЕРА

ACC II — это интерактивное веб-приложение для расчета частичных атомных зарядов с помощью некоммерческих методов расчета эмпирических зарядов и для визуализации этих зарядов. ACC II состоит из внешнего и внутреннего интерфейса. Интерфейс — это современное веб-приложение, написанное на JavaScript с использованием библиотеки Bootstrap.Его первая функция — считывать вводимые пользователем данные, состоящие из молекулярных структур и параметров вычислений (например, один из методов расчета заряда, интегрированных в бэкэнд). Его вторая цель — представить результат, то есть рассчитанные расходы. Эти расходы доступны в виде загружаемых файлов данных, а также могут быть визуализированы с помощью программы просмотра LiteMol, которая является частью внешнего интерфейса ACC II. Бэкэнд — это приложение Python Flask. Все расчеты сборов выполняются основным приложением C ++, которое объединяет 17 подходов к эмпирическому расчету затрат, не связанных с QM.Он также включает реализацию методов обрезания и покрытия (23) для быстрого решения систем линейных уравнений. Все три части ACC II доступны на GitHub по лицензии MIT: интерфейс и бэкэнд доступны по адресу https://github.com/krab1k/AtomicChargeCalculator2, а ядро ​​доступно по адресу https://github.com/krab1k/. ChargeFW2.

Подходы к расчету эмпирических сборов без QM в ACC II

ACC II объединяет девять конформационно независимых (2D) методов (PEOE (12), DelRe (25), MPEOE (13), Charge2 (26), MGC (27,28), KCM (14), DENR (15), TSEF). (15) и VEEM (29)) и восемь конформационно-зависимых (3D) методов (EEM (16), ABEEM (30), SFKEEM (31), QEq (3), SMP / QEq (32), EQeq (17) , EQeq + C (33) и GDAC (34)).Обзор этих методов представлен на рисунке 1, где также показаны взаимосвязи между методами (т. Е. Если два метода соединены линией, верхний является преемником нижнего), их разделение на двухмерный и трехмерный подходы и год. их публикации.

Рисунок 1.

Обзор методов расчета эмпирических сборов, не связанных с QM, интегрированных в ACC II. Левая ось показывает год публикации метода. Методы делятся на 2D и 3D подходы.Когда два метода соединены линией, верхний был разработан на основе нижнего (например, ABEEM и SFKEEM являются преемниками EEM). Методы, выделенные жирным шрифтом, цитировались более 100 раз, а методы, выделенные зеленым шрифтом, цитировались более 20 раз. Цифры цитирования были получены в результате поиска литературы в базе данных Web of Science (https://www.webofknowledge.com/, набор данных «Все базы данных»), который мы провели 31 марта 2020 года. Подсчет цитирований для каждого метода, реализованного в ACC. II приведен в дополнительной таблице S1.

Рис. 1.

Обзор методов расчета эмпирических сборов, не связанных с QM, интегрированных в ACC II. Левая ось показывает год публикации метода. Методы делятся на 2D и 3D подходы. Когда два метода соединены линией, верхний был разработан на основе нижнего (например, ABEEM и SFKEEM являются преемниками EEM). Методы, выделенные жирным шрифтом, цитировались более 100 раз, а методы, выделенные зеленым шрифтом, цитировались более 20 раз. Номера цитирований были получены путем поиска литературы в базе данных Web of Science (https: // www.webofknowledge.com/, набор данных «Все базы данных»), который мы выполнили 31 марта 2020 года. Количество цитирований каждого метода, реализованного в ACC II, приведено в дополнительной таблице S1.

Принципы и теоретические основы всех этих методов (включая их критерии качества) описаны в Кратком описании методов в дополнительных данных.

Рабочий процесс ACC II

Процедура использования приложения ACC II включает шесть шагов: (i) загрузка структуры (структур), (ii) внутренняя проверка, (iii) выбор эмпирического метода, не связанного с QM, и его набора параметров, (iv) выполнение выбранного метод, (v) визуализация вычисленных сборов, (vi) загрузка вычисленных сборов.

(i) Загрузка структуры (ей) . Первый шаг — загрузить молекулярную структуру, для которой будут рассчитаны заряды. Структура может быть предоставлена ​​в файловых форматах SDF, MOL2, PDB или mmCIF. ACC II также может принимать более одной конструкции. В этом случае принятые форматы такие же, но входные файлы должны быть сжаты в один входной архив, который может быть в формате zip или tar.gz.

(ii) Внутренняя проверка . Затем входные файлы проверяются.В частности, ACC II проверяет, находятся ли файлы в одном из поддерживаемых форматов и содержат ли они необходимую информацию для описания молекулярной структуры (например, координаты атомов, определение связей в случае небольших молекул). Если входные файлы не проходят процедуру проверки, пользователь информируется об обнаруженных проблемах. Самый распространенный из них — входной файл не соответствует стандарту определенного формата файла.

(iii) Выбор эмпирического метода, отличного от QM, и его набора параметров .После считывания входной молекулы (ей) ACC II сначала обнаруживает эмпирические методы, не относящиеся к QM, которые могут быть выполнены с данными пользователя. В частности, каждый эмпирический подход, не связанный с QM, имеет один или несколько наборов параметров. В некоторых эмпирических подходах, не связанных с QM, в качестве параметров используются только табличные значения физико-химических констант. Но для большинства методов требуются более сложные наборы параметров, также содержащие параметры для отдельных элементов (например, если набор параметров ориентирован на белки, он содержит параметры для C, H, O, N и S, но может не иметь параметров для Cl. , Br, I, Si и др.). Такой метод может быть выполнен только для молекулы, состоящей из элементов, которые параметризованы по крайней мере в одном наборе параметров, принадлежащем методу. Обратите внимание, что методы, не требующие параметров для отдельных элементов, охватывают каждую молекулу. Если пользователь предоставляет набор молекул, он может использовать только те подходы, которые охватывают все входящие молекулы. Обратите внимание, что нет смысла использовать несколько наборов параметров для одного набора входных молекул, поскольку вычисленные заряды не будут сопоставимы.Методы, которые могут использоваться для конкретного набора входных данных, далее обозначаются как «применимые методы».

У пользователей есть два способа выбрать метод расчета эмпирических сборов, не связанный с QM, из применимых методов: они могут использовать автоматическую настройку с помощью кнопки «Вычислить сборы» или выбрать метод самостоятельно, нажав кнопку «Настроить расчет».

Если пользователи сами выбирают метод расчета, они могут не только выбрать метод, но и его набор параметров, где это применимо (например,г. если было опубликовано более одного набора параметров). На веб-странице «Настройки вычислений» каждый подход и каждый набор параметров дополняются ссылкой на публикацию, в которой он был описан.

Если пользователь предпочитает автоматическую настройку, ACC II выбирает подход, который был задокументирован как наиболее подходящий из доступных методов. Подробности о процессе выбора наиболее подходящего метода расчета сборов описаны в онлайн-документации ACC II (https: // acc2.ncbr.muni.cz/static/manual.pdf). Если подход имеет больше наборов параметров, выбирается тот, который наиболее подходит для конкретных входных молекул (например, набор параметров, специализированный на молекулах, подобных лекарству, используется для небольших органических молекул). Список наборов параметров, включенных в ACC II, доступен в дополнительной таблице S2.

(iv) Выполнение выбранного метода . Выбранный подход к расчету заряда выполняется на сервере для каждой входной молекулярной структуры.Каждое вычисление на бэкэнде имеет два входа: предоставленную пользователем молекулярную структуру и выбранный набор параметров. Если подход объединяет методы отсечения и покрытия для решения системы линейных уравнений, а молекулярная структура имеет> 20 000 атомов, но <80 000 атомов, используется метод отсечения. Если количество атомов равно или превышает 80 000, используется метод покрытия.

(v) Визуализация вычисленных зарядов . Рассчитанные расходы могут быть представлены пользователю через программу просмотра LiteMol, которая интегрирована в ACC II (в частности, на его веб-странице «Результаты вычислений»).Могут использоваться три модели визуализации: модель шаров и палочек, мультипликационная модель и модель поверхности. Все три модели визуализации можно раскрасить, используя значения вычисленных сборов. В модели шаров и палочек (см. Рисунок 2) шары окрашены непосредственно в соответствии со значениями парциальных зарядов атомов. В мультипликационной модели (см. Рис. 3) спирали, листы и трубки между ними разделены на области, которые представляют отдельные аминокислоты. Каждая область окрашена в соответствии с суммой атомных зарядов, принадлежащих определенной аминокислоте.В модели поверхности (см. Рис. 4B) поверхность разделена на части, принадлежащие отдельным поверхностным атомам. Затем каждая часть поверхности окрашивается в соответствии с частичным зарядом атома, который она представляет.

Рис. 2.

Частичные заряды атомов в пропофоле. Водород фенола отмечен синей стрелкой. Парциальные атомные заряды были рассчитаны с помощью EEM.

Рисунок 2.

Частичные атомные заряды в пропофоле. Водород фенола отмечен синей стрелкой.Парциальные атомные заряды были рассчитаны с помощью EEM.

Рисунок 3.

( A ) Неактивный BAX (PDB ID 1f16). ( B ) Активированный BAX (PDB ID 2k7w). Активатор помечен синим овалом , домен C отмечен зеленым овалом . C-домен активированного BAX деполяризован — он в основном белого или беловатого цвета. Эта деполяризация заставляет домен C высвобождаться и проникать через митохондриальную мембрану и инициировать апоптоз.Парциальные атомные заряды были рассчитаны с помощью EEM.

Рисунок 3.

( A ) Неактивный BAX (PDB ID 1f16). ( B ) Активированный BAX (PDB ID 2k7w). Активатор помечен синим овалом , домен C отмечен зеленым овалом . C-домен активированного BAX деполяризован — он в основном белого или беловатого цвета. Эта деполяризация заставляет домен C высвобождаться и проникать через митохондриальную мембрану и инициировать апоптоз. Парциальные атомные заряды были рассчитаны с помощью EEM.

Рисунок 4.

Структура никотинового ацетилхолинового рецептора (PDB ID 2bg9): ( A ) Схема, показывающая рецептор (серым цветом), проходящий через мембрану (красный). Рисунок взят из RCSB PDB. ( B ) Частичные атомные заряды (от ACC II), визуализированные на поверхности рецепторной структуры, демонстрирующие отдельные области: неполярная трансмембранная часть (в основном белая из-за заряда, близкого к нулю) и полярная поверхность внеклеточной и цитоплазматической частей (с мозаикой синих положительных и красных отрицательных зарядов).Парциальные атомные заряды были рассчитаны с помощью EEM.

Рисунок 4.

Структура никотинового ацетилхолинового рецептора (PDB ID 2bg9): ( A ) Схема, показывающая рецептор (серым цветом), проходящий через мембрану (красный). Рисунок взят из RCSB PDB. ( B ) Частичные атомные заряды (от ACC II), визуализированные на поверхности рецепторной структуры, демонстрирующие отдельные области: неполярная трансмембранная часть (в основном белая из-за заряда, близкого к нулю) и полярная поверхность внеклеточной и цитоплазматической частей (с мозаикой синих положительных и красных отрицательных зарядов).Парциальные атомные заряды были рассчитаны с помощью EEM.

Цветовая шкала простирается от синего через белый до красного. Отрицательные заряды имеют красный цвет (чем больше отрицательное значение заряда, тем ярче цвет), а положительные заряды — синий (чем больше положительное значение заряда, тем интенсивнее цвет). Чем ближе значение заряда к нулю, тем ближе его цвет к белому. Пользователь может выбрать относительную цветовую шкалу, которая простирается от наименьшего до наибольшего значения заряда в визуализированной структуре, или абсолютную цветовую шкалу, которая простирается от определенного пользователем значения до другого определяемого пользователем значения).

(vi) Загрузка рассчитанных сборов . Частичные атомные заряды, рассчитанные с помощью ACC II, можно загрузить в форматах файлов PQR, MOL2 и незашифрованного текста. ACC II предоставляет один ZIP-файл, содержащий заряды для всех входных молекул в соответствующих выходных форматах (PQR для белков, MOL2 для малых молекул, открытый текст для обоих).

Ограничения

ACC II в настоящее время имеет несколько ограничений: он включает только методы расчета эмпирических сборов, не относящиеся к QM (не QM), которые полностью автоматизированы (ручная настройка не требуется) и какая методология достаточно подробно описана в его публикации.Размер входного файла ограничен 10 МБ. Модель визуализации мультфильмов доступна только в том случае, если входной файл находится в формате PDB или mmCIF (т. Е. Форматах, содержащих информацию об аминокислотах и ​​других остатках). Эмпирические подходы, не связанные с QM, которые требуют параметров для отдельных атомов, могут обрабатывать только те молекулы, для которых хотя бы один из их наборов параметров охватывает эти молекулы. Методы отсечения и покрытия для быстрого решения систем линейных уравнений интегрированы в EEM, SFKEEM, QEq, SMP / QEq, EQeq, EQeq + C.Другие методы, которые включают системы линейных уравнений, используют другие схемы, для которых методы отсечения и покрытия не применимы напрямую. Из-за ограничений LiteMol результат вычислений не может быть визуализирован, если входная молекула была предоставлена ​​в файле mmCIF, в котором отсутствует запись «_atom_sites».

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Мы приводим три примера, демонстрирующих возможные варианты использования веб-приложения ACC II. Интерактивная форма этих примеров представлена ​​на веб-странице ACC II.Файлы со структурами из этих примеров доступны в дополнительных данных.

Пример I — диссоциация атомов водорода от фенолов

В первом примере мы показываем расчет стоимости семи фенольных лекарственных соединений (см. Таблицу 1), описанных в DrugBank. Мы получили их структуры из базы данных PubChem и рассчитали их парциальные атомные заряды с помощью ACC II (автоматическая установка). Результаты расчета доступны на веб-странице ACC II.В этом примере мы также хотели бы представить предварительный просмотр использования заряда — приложение в области исследования кислотной диссоциации. Кислотная диссоциация — это реакция, в которой молекула высвобождает атом водорода. Способность молекулы выделять водород описывается ее константой кислотной диссоциации ( K _a ) и ее отрицательным логарифмом (p K _a ). Связь между зарядом диссоциирующего водорода и p K _a хорошо известна и часто используется для предсказания p K _a (6,7,35).В нашем примере мы сосредоточились на этой связи. Диссоциирующий водород является частью фенольной группы ОН. Для каждого из наших семи соединений мы получили значение p K _a (из (7)) и заряд фенольного водорода и суммировали эти значения в таблице 1. Из таблицы 1 видно, что существует четкая зависимость между p K _a и зарядом на фенольном водороде. В частности, чем выше p K _a (диссоциация требует более высокого pH), тем ниже заряд водорода.Более подробную информацию о связи между p K _a и зарядами в фенолах и его применении можно найти здесь (7).

Таблица 1.

Сводная информация о фенольных лекарственных соединениях

8 0298

9028

Название соединения .	Идентификатор DrugBank .	PubChem CID .	p K a .	Заряд фенольного водорода .
2,4-Динитрофенол	DB04528	1493	4,09	0,467
4-Нитрофенол	DB04417	DB03110	7245	8,56	0,405
3-хлорфенол	DB01957	7933	9,12	0.393
м -Крезол	DB11143 *	342	10,10	0,379
o -Крезол	DB11143 *	9028 335 9028 9028 9028	DB00818	4943	11,10	0,350

8 0298

980

Название соединения .	Идентификатор DrugBank .	PubChem CID .	p K a .	Заряд фенольного водорода .
2,4-Динитрофенол	DB04528	1493	4,09	0,467
4-Нитрофенол	DB04417	DB03110	7245	8.56	0,405
3-хлорфенол	DB01957	7933	9,12	0,393
м -Крезол	DB11148 9028 9028 9028 o -Крезол	DB11143 *	335	10,30	0,376
Пропофол	DB00818	4943	11.10	0,350

Таблица 1.

Сводная информация о фенольных лекарственных соединениях

8 0298

980

Название соединения .	Идентификатор DrugBank .	PubChem CID .	p K a .	Заряд фенольного водорода .
2,4-динитрофенол	DB04528	1493	4.09	0,467
4-нитрофенол	DB04417	980	7,15	0,430
2-хлорфенол	DB03110 7245 908	DB01957	7933	9,12	0,393
м -Крезол	DB11143 *	342	10,10	0.379
o -Крезол	DB11143 *	335	10,30	0,376
Пропофол	DB00818	4943,10	9028 9016	соединение .	Идентификатор DrugBank .	PubChem CID .	p K a .	Заряд фенольного водорода .
2,4-Динитрофенол	DB04528	1493	4,09	0,467
4-Нитрофенол	DB04417	DB03110	7245	8,56	0,405
3-хлорфенол	DB01957	7933	9.12	0,393
м -Крезол	DB11143 *	342	10,10	0,379
o -Крезол	9028 9028 9028 9028 9028 9028 9028 9028 9028
Пропофол	DB00818	4943	11,10	0,350

Пример II — активация апоптотического белка

Во втором примере мы хотели бы показать применение зарядов в исследовании белков.В частности, мы фокусируемся на апоптотическом белке BAX в его неактивной и активированной формах. Мы получили структуры из Protein Data Bank (неактивная форма имеет PDB ID 1f16 и активный PDB ID 2k7w) и рассчитали их частичные атомные заряды с помощью ACC II (автоматическая настройка). В этом сравнении белок BAX инициирует апоптоз следующим образом: его C-домен (отмечен зеленым на рисунке 3) высвобождается и проникает через митохондриальную мембрану (10). Высвобождение активируется активатором (рис. 3B, синий овал), который вызывает перераспределение частичных атомных зарядов, деполяризацию домена C и разряд электростатических сил, связывающих домен (см. Рис. 3).Частичные атомные заряды дают нам ключ к пониманию механизма активации BAX. Этот механизм подробно описан в статье (10).

Пример III — трансмембранный белок

В третьем примере мы показываем расчет заряда для большого трансмембранного белка — никотинового рецептора ацетилхолина. Этот рецептор проходит через клеточную мембрану (см. Рис. 4A) и служит ионным каналом (36). Мы получили его структуру из банка данных белка (PDB ID: 2bg9), добавили недостающие атомы водорода с помощью WHAT IF (37)) и рассчитали частичные атомные заряды с помощью ACC II (автоматическая настройка).Визуализация частичных зарядов на поверхности (см. Рис. 4B) подчеркивает разницу между неполярной трансмембранной частью (в основном белой из-за заряда около нуля) и полярной поверхностью внеклеточной и цитоплазматической частей (с мозаикой из синего положительного и красного отрицательного обвинения). Сравнение показывает, что это распределение заряда согласуется с положением мембраны рецептора, описанным в литературе (36).

ЗАКЛЮЧЕНИЕ

В этой статье мы представили ACC II, новое веб-приложение для расчета частичных атомных зарядов с использованием всех основных эмпирических подходов, не связанных с QM, и для всех типов молекул, включая биомакромолекулы.ACC II также позволяет визуализировать заряды с помощью трех основных моделей визуализации заряда. Веб-приложение простое в использовании и не зависит от платформы. Просмотр результатов и манипуляции с ними полностью интерактивны. Все результаты ACC II можно загрузить в различных форматах (PQR, MOL2 и текстовый формат). Документация, объясняющая методологию и примеры, представлена ​​на веб-странице ACC II.

ACC II находится в свободном доступе по адресу https://acc2.ncbr.muni.cz и не требует входа в систему.

ДОПОЛНИТЕЛЬНЫЕ ДАННЫЕ

Дополнительные данные доступны в NAR Online.

ФИНАНСИРОВАНИЕ

Министерство образования, молодежи и спорта Чешской Республики: ELIXIR CZ [LM2018131]; Европейский фонд регионального развития — проект ELIXIR-CZ [CZ.02.1.01 / 0.0 / 0.0 / 16_013 / 0001777]. Финансирование платы за открытый доступ: Министерство образования, молодежи и спорта Чешской Республики в рамках проекта исследовательской инфраструктуры ELIXIR CZ, включая доступ к компьютерам и хранилищам [LM2018131]; Вычислительные ресурсы были предоставлены проектом «e-Infrastruktura CZ» (e-INFRA LM2018140) в рамках программы «Проекты крупных инфраструктур исследований, разработок и инноваций».

Заявление о конфликте интересов . Ничего не объявлено.

ССЫЛКИ

1.

Berzelius

J.

Erste fortsetzung des versuchs, die bestimmten und einfachen Verhältnisse aufzufinden, nach welchen die Bestandtheile der unorganischen Natur mit einander verbunden sind

.

Ann. Phys.

1811

;

38

:

161

—

226

.2.

Малликен

р.С.

Электронный анализ населения на молекулярных волновых функциях ЛКАО-МО. Я

.

J. Chem. Phys.

1955

;

23

:

1833

—

1840

.3.

Раппе

A.K.

,

Годдард

W.A.

Уравновешивание заряда для моделирования молекулярной динамики

.

J. Phys. Chem.

1991

;

95

:

3358

—

3363

.4.

Парк

H.

,

Lee

J.

,

Lee

S.

Критическая оценка автоматизированного AutoDock как нового стыковочного инструмента для виртуального скрининга

.

Proteins Struct. Funct. Биоинформа.

2006

;

65

:

549

—

554

. 5.

Вайнио

M.J.

,

Johnson

M.S.

Генерация конформерных ансамблей с использованием многокритериального генетического алгоритма

.

J. Chem. Инф. Модель.

2007

;

47

:

2462

—

2474

.6.

Брутто

K.C.

,

Сейболд

П.Г.

,

Хадад

C.M.

Сравнение различных схем атомных зарядов для прогнозирования вариаций pKa в замещенных анилинах и фенолах

.

Внутр. J. Quantum Chem.

2002

;

90

:

445

—

458

.7.

Svobodová Vařeková

R.

,

Geidl

S.

,

Ionescu

C.-M.

,

Skřehota

O.

,

Kudera

M.

,

Sehnal

D.

,

Bouchal

T.

,

Abagyan

R.

,

0003 Huber

,

Коча

J.

Прогнозирование значений pKa замещенных фенолов на основе атомных зарядов: сравнение различных квантово-механических методов и схем распределения заряда

.

J. Chem. Инф. Модель.

2011

;

51

:

1795

—

1806

.8.

Bissantz

C.

,

Folkers

G.

,

Rognan

D.

Виртуальный скрининг химических баз данных на основе белков. 1. Оценка различных комбинаций стыковки / подсчета очков

.

J. Med. Chem.

2000

;

43

:

4759

—

4767

,9.

Холлидей

Дж.S.

,

Jelfs

S.P.

,

Willett

P.

,

Gedeck

P.

Расчет межзамещенного сходства с использованием дескрипторов R-группы

.

J. Chem. Инф. Comput. Sci.

2003

;

43

:

406

—

411

.10.

Ионеску

C.-M.

,

Svobodová Vařeková

R.

,

Prehn

J.H.M.

,

Хубер

Х.J.

,

Koča

J.

Анализ профиля заряда показывает, что активация проапоптотических регуляторов bax и bak зависит от аллостерической регуляции

, опосредованной переносом заряда.

PLoS Comput. Биол.

2012

;

8

:

e1002565

.11.

Чо

М.

,

Сильвецкий

Н.

,

Эшафи

С.

,

Сантра

Г.

,

Ефременко

И.

,

Мартин

J.M.L.

Дендрарий атомных частичных зарядов: пытаемся увидеть лес за деревьями

.

ХимФисХим

.

2020

;

21

:

688

—

696

.12.

Gasteiger

J.

,

Marsili

M.

Новая модель для расчета атомных зарядов в молекулах

.

Tetrahedron Lett.

1978

;

34

:

3181

—

3184

.13.

№

К.Т.

,

Грант

J.A.

,

Scheraga

H.A.

Определение чистых атомных зарядов с использованием модифицированного метода частичного выравнивания орбитальной электроотрицательности. 1. Применение к нейтральным молекулам как моделям полипептидов

.

J. Phys. Chem.

1990

;

94

:

4732

—

4739

. 14.

Яковенко

О.

,

Олиференко

А.А.

,

Бджола

В.Г.

,

Палюлин

В.А.

,

Зефиров

Н.С.

Атомные заряды Кирхгофа, подогнанные к мультипольным моментам: реализация для системы виртуального экранирования

.

J. Comput. Chem.

2008

;

29

:

1332

—

1343

.15.

Шульга

Д.А.

,

Олиференко

А.А.

,

Писарев

С.А.

,

Палюлин

В.А.

,

Зефиров

Н.С.

Быстрые инструменты для расчета атомных зарядов, хорошо подходящие для разработки лекарств

.

SAR QSAR Environ. Res.

2008

;

19

:

153

—

165

.16.

Мортье

W.J.

,

Ghosh

S.K.

,

Шанкар

S.

Метод выравнивания электроотрицательности для расчета атомных зарядов в молекулах

.

J. Am. Chem. Soc.

1986

;

108

:

4315

—

4320

. 17.

Wilmer

C.E.

,

Kim

K.C.

,

Snurr

R.Q.

Расширенный метод уравновешивания заряда

.

J. Phys. Chem. Lett.

2012

;

3

:

2506

—

2511

. 18.

Geidl

S.

,

Bouchal

T.

,

Raček

T.

,

Svobodová Vařeková

R.

,

Hejret

V.

,

Křenek

A.

,

Abagyan

R.

,

Koča

9000-универсальный J. атомные заряды для приложений химиоинформатики

.

J. Cheminform.

2015

;

7

:

59

.19.

Raček

T.

,

Pazúriková

J.

,

Svobodová Vařeková

R.

,

Geidl

S.

,

Křenek

A.

,

Falginella

F.L.

,

Horský

V.

,

Hejret

V.

,

Koča

J.

NEEMP: программное обеспечение для проверки, точного расчета и быстрой параметризации затрат EEM

.

J. Cheminform.

2016

;

8

:

57

.20.

O’Boyle

N.M.

,

Banck

M.

,

Джеймс

C.A.

,

Morley

C.

,

Vandermeersch

T.

,

Hutchison

G.R.

Open Babel: открытый химический ящик с инструментами

.

J. Cheminform.

2011

;

3

:

33

. 21.

Гилсон

М.К.

,

Гилсон

H.S.R.

,

Potter

M.J.

Быстрое присвоение точных частичных атомных зарядов: метод выравнивания электроотрицательности, который учитывает альтернативные формы резонанса

.

J. Chem. Инф. Comput. Sci.

2003

;

43

:

1982

—

1997

.22.

Svobodová Vařeková

R.

,

Koča

J.

Оптимизированная и параллельная реализация метода выравнивания электроотрицательности и метода выравнивания электроотрицательности атомных связей

.

J. Comput. Chem.

2006

;

27

:

396

—

405

. 23.

Ионеску

К.-M.

,

Sehnal

D.

,

Falginella

F.L.

,

Pant

P.

,

Pravda

L.

,

Bouchal

T.

,

Svobodová Vařeková

R.

,

Geidl

S.

a

AtomicChargeCalculator: интерактивный сетевой расчет атомных зарядов в больших биомолекулярных комплексах и молекулах, подобных лекарствам

.

Дж.Химинформ.

2015

;

7

:

50

. 24.

Sehnal

D.

,

Deshpande

M.

,

Svobodová Vařeková

R.

,

Mir

S.

,

Berka

K.

ik, A.

Pravda

L.

,

Velankar

S.

,

Koča

J.

LiteMol Suite: интерактивная веб-визуализация крупномасштабных данных макромолекулярной структуры

.

Nat. Методы

.

2017

;

14

:

1121

—

1122

. 25.

Del Re

G.

Простой метод MO-LCAO для расчета распределений заряда в насыщенных органических молекулах

.

J. Chem. Soc.

1958

;

11

:

4031

—

4040

. 26.

Авраам

R.J.

,

Hudson

B.

Подходы к расчету заряда в молекулярной механике

.

J. Comput. Chem.

1982

;

3

:

407

—

416

. 27.

Олиференко

А.А.

,

Палюлин

В.А.

,

Нейман

А.В.

,

Зефиров

Н.С.

Новая топологическая модель для расчета частичных зарядов атомов

.

Докл. Chem.

2000

;

375

:

281

—

284

. 28.

Олиференко

А.А.

,

Палюлин

В.А.

,

Писарев

S.A.

,

Neiman

A.V.

,

Зефиров

Н.С.

Новые модели точечного заряда: надежные инструменты для молекулярной электростатики

.

J. Phys. Орг. Chem.

2001

;

14

:

355

—

369

. 29.

Wu

Y.-X.

,

Cao

C.-Z.

,

юаней

H.

Уравненная электроотрицательность на основе валентных электронов и ее применение

.

Китайский J. Chem. Phys.

2011

;

24

:

31

—

39

.30.

Ян

З.-З.

,

Ван

C.-S.

Метод выравнивания электроотрицательности атомных связей. 1. Расчет распределения заряда в больших молекулах

.

J. Phys. Chem. А

.

1997

;

101

:

6315

—

6321

.31.

Chaves

J.

,

Barroso

JM

,

Bultinck

P.

,

Carbó-Dorca

R.

На пути к альтернативной твердости EEM)

.

J. Chem. Инф. Модель.

2006

;

46

:

1657

—

1665

.32.

Zhang

M.

,

Fournier

R.

Метод самосогласованного уравновешивания заряда и его применение к Au ₁₃ Na _n (n = 1, 10) кластерам

.

J. Phys. Chem. А

.

2009

;

113

:

3162

—

3170

. 33.

Martin-Noble

G.C.

,

Reilley

D.

,

Rivas

L.M.

,

Smith

M.D.

,

Schrier

J.

EQeq + C: эмпирический метод облигации с поправкой на порядок заряда

J. Chem. Теория вычисл.

2015

;

11

:

3364

—

3374

.34.

Cho

K.H.

,

Канг

Ю.К.

,

№

К.Т.

,

Scheraga

H.A.

Быстрый метод расчета зависящих от геометрии чистых атомных зарядов для полипептидов

.

J. Phys. Chem. В

.

2001

;

105

:

3624

—

3634

.35.

Liptak

M.D.

,

Брутто

K.C.

,

Сейболд

П.G.

,

Feldgus

S.

,

Shields

G.C.

Определение абсолютного pKa замещенных фенолов

.

J. Am. Chem. Soc.

2002

;

124

:

6421

—

6427

.36.

Unwin

N.

Уточненная структура никотинового ацетилхолинового рецептора с разрешением 4 Å

.

J. Mol. Биол.

2005

;

346

:

967

—

989

.37.

Vriend

G.

ЧТО ЕСЛИ: программа молекулярного моделирования и дизайна лекарств

.

J. Mol. График.

1990

;

8

:

52

—

56

.

© Автор (ы) 2020. Опубликовано Oxford University Press от имени Nucleic Acids Research.

Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0 /), что разрешает неограниченное повторное использование, распространение и воспроизведение на любом носителе при условии правильного цитирования оригинальной работы.

AtomicChargeCalculator: интерактивный сетевой расчет атомных зарядов в больших биомолекулярных комплексах и молекулах, подобных лекарствам | Journal of Cheminformatics

1.

Giese B, Graber M, Cordes M (2008) Электронный перенос в пептидах и белках. Curr Opin Chem Biol 12 (6): 755–759. DOI: 10.1016 / j.cbpa.2008.08.026

2.

Grodick MA, Muren NB, Barton JK (2015) Транспорт заряда ДНК внутри клетки. Биохимия 54 (4): 962–973. DOI: 10.1021 / bi501520w

CAS Статья Google Scholar

3.

Li L, Wang L, Alexov E (2015) Об энергетических компонентах, определяющих молекулярное распознавание в рамках континуальных подходов. Front Mol Biosci. DOI: 10.3389 / fmolb.2015.00005

4.

Zheng G, Xiao M, Lu XH (2005) QSAR исследование аффинности связывания Ah-рецептора полигалогенированных дибензо-p-диоксинов с использованием сетевых дескрипторов атомного заряда и радиальной базовой нейронной сети.Anal Bioanal Chem. 383: 810–816. DOI: 10.1007 / s00216-005-0085-7

CAS Статья Google Scholar

5.

Карельсон М., Карельсон Г., Тямм Т., Тулп I, Янес Дж., Тямм К., Ломака А., Денисс С., Добчев Д. (2009) QSAR исследование фармакологической проницаемости. Arkivoc 2009 (2): 218–238

Статья Google Scholar

6.

Wood JS (1995) Рентгеновское определение электронного распределения в кристаллах гексапиридин-N-оксида перхлората кобальта (II) и электронной структуры иона Co2 +.Inorganica Chimica Acta 229 (1-2): 407-415. DOI: 10.1016 / 0020-1693 (94) 04272-W

CAS Статья Google Scholar

7.

Белоконева Е.Л., Губина Ю.К., Форсайт Дж. Б., Браун П. Дж. (2002) Распределение плотности заряда, его мультипольное уточнение и антиферромагнитная структура диоптазы, \ (Cu_ {6} [Si_ {6} O_ {18 }] \ cdot 6H_ {2} O \). Phys Chem Min 29 (6): 430–438. DOI: 10.1007 / s00269-002-0246-6

CAS Статья Google Scholar

8.

Шредингер Э. (1926) Волнообразная теория механики атомов и молекул. Phys Rev 28 (6): 1049

Статья Google Scholar

9.

Малликен Р.С. (1935) Электронные структуры молекул XI. Электроаффинность, молекулярные орбитали и дипольные моменты. J Chem Phys 3 (9): 573–585. DOI: 10.1063 / 1.1749731

CAS Статья Google Scholar

10.

Mulliken RS (1962) Критерии построения хороших самосогласованных полевых молекулярных орбитальных волновых функций и значимость популяционного анализа LCAO-MO. J. Chem Phys 36 (12): 3428. DOI: 10.1063 / 1.1732476

CAS Статья Google Scholar

11.

Löwdin P-O (1950) О проблеме неортогональности, связанной с использованием атомных волновых функций в теории молекул и кристаллов.J Chem Phys 18 (3): 365–375. DOI: 10.1063 / 1.1747632

Артикул Google Scholar

12.

Рид Э.А., Вайншток РБ, Вайнхольд Ф. (1985) Анализ естественного населения. J. Chem Phys 83 (2): 735–746. DOI: 10.1063 / 1.449486

CAS Статья Google Scholar

13.

Bader RFW, Larouche A, Gatti C, Carroll MT, MacDougall PJ, Wiberg KB (1987) Свойства атомов в молекулах: дипольные моменты и переносимость свойств.J. Chem Phys 87 (2): 1142–1152. DOI: 10.1063 / 1.453294

CAS Статья Google Scholar

14.

Hirshfeld FL (1977) Фрагменты связанных атомов для описания плотностей зарядов молекул. Теоретика Chimica Acta 44 (2): 129–138. DOI: 10.1007 / BF00549096

CAS Статья Google Scholar

15.

Bultinck P, Van Alsenoy C, Ayers PW, Carbó-Dorca R (2007) Критический анализ и расширение атомов Хиршфельда в молекулах.J. Cheml Phys. DOI: 10.1063 / 1.2715563

Google Scholar

16.

Бренеман CM, Wiberg KB (1990) Определение атомно-центрированных монополей на основе молекулярных электростатических потенциалов. Необходимость высокой плотности выборки при конформационном анализе формамида. J Comput Chem 11 (3): 361–373. DOI: 10.1002 / jcc.540110311

CAS Статья Google Scholar

17.

Besler BH, Merz KM, Kollman PA (1990) Атомные заряды, полученные с помощью полуэмпирических методов. J Comput Chem 11: 431–439. DOI: 10.1002 / jcc.540110404

CAS Статья Google Scholar

18.

Келли С.П., Крамер С.Дж., Трулар Д.Г. (2005 г.) Точные частичные атомные заряды для высокоэнергетических молекул с использованием моделей заряда IV класса с MIDI! базисный набор. Theor Chem Acc 113 (3): 133–151. DOI: 10.1007 / s00214-004-0624-x

19.

Манц Т.А., Шолль Д.С. (2010) Химически значимые атомные заряды, которые воспроизводят электростатический потенциал в периодических и непериодических материалах. J Chem Theory Comput 6 (8): 2455–2468. DOI: 10.1021 / ct100125x

CAS Статья Google Scholar

20.

Абрахам Р.Дж., Гриффитс Л., Лофтус П. (1982) Подходы к расчетам заряда в молекулярной механике. J. Comput Chem. 3 (3): 407–416. DOI: 10.1002 / jcc.540030316

CAS Статья Google Scholar

21.

Шульга Д.А., Олиференко А.А., Писарев С.А., Палюлин В.А., Зефиров Н.С. (2008) Параметризация эмпирических схем расчета частичного атомного заряда для воспроизведения электростатического потенциала молекул. Доклады химии 419 (1): 57–61. DOI: 10.1007 / s10631-008-3004-6

CAS Статья Google Scholar

22.

Мортье В.Дж., Гош С.К., Шанкар С. (1986) Метод выравнивания электроотрицательности для расчета атомных зарядов в молекулах.J Am Chem Soc 108 (15): 4315–4320. DOI: 10.1021 / ja00275a013

CAS Статья Google Scholar

23.

Раппе А.К., Годдард В.А. III (1991) Уравновешивание заряда для моделирования молекулярной динамики. J. Phys Chem. 95: 3358–3363. DOI: 10.1021 / j100161a070

Артикул Google Scholar

24.

Нистор Р.А., Полихронов Ю.Г., Мюзер М.Х. (2006) Обобщение метода уравновешивания заряда для неметаллических материалов.J Chem Phys. DOI: 10.1063 / 1.2346671

Google Scholar

25.

Гастайгер Дж., Марсили М. (1980) Итеративное частичное выравнивание орбитальной электроотрицательности — быстрый доступ к атомным зарядам. DOI: 10.1016 / 0040-4020 (80) 80168-2

26.

Cho K-H, Kang YK, No KT, Scheraga HA (2001) Быстрый метод расчета зависящих от геометрии чистых атомных зарядов для полипептидов. J. Phys Chem. 105 (17): 3624–3634.DOI: 10.1021 / jp0023213

CAS Статья Google Scholar

27.

Олиференко А.А., Писарев С.А., Палюлин В.А., Зефиров Н.С. (2006) Атомные заряды через уравнение электроотрицательности: обобщения и перспективы. DOI: 10.1016 / S0065-3276 (06) 51004-4

28.

Бэкеландт Б., Мортье В., Ливенс Дж. (1991) Исследование реакционной способности различных участков внутри молекулы или твердого тела путем прямого вычисления молекулярной чувствительности посредством расширения уравнивания электроотрицательности.J Am Chem Soc 113 (18): 6730–6734. DOI: 10.1021 / ja00018a003

CAS Статья Google Scholar

29.

York DM, Yang W (1996) Метод выравнивания химического потенциала для молекулярного моделирования. J. Chem Phys 104 (1): 159. DOI: 10.1063 / 1.470886

CAS Статья Google Scholar

30.

Yang Z-Z, Wang C-S (1997) Метод выравнивания электроотрицательности атомной связи.1. Расчет распределения заряда в больших молекулах. J. Phys Chem A 101 (35): 6315–6321. DOI: 10.1021 / jp9711048

CAS Статья Google Scholar

31.

Njo SL, Fan J, Van De Graaf B (1998) Расширение и упрощение метода выравнивания электроотрицательности. J Mol Catal A Chem 134: 79–88. DOI: 10.1016 / S1381-1169 (98) 00024-7

CAS Статья Google Scholar

32.

Диас Л.Г., Шимицу К., Фарах Дж.П.С., Хаимович Х. (2002) Простой метод быстрого расчета перераспределения заряда растворенных веществ в неявной модели растворителя. Chem Phys 282 (2): 237–243. DOI: 10.1016 / S0301-0104 (02) 00717-6

CAS Статья Google Scholar

33.

Чавес Дж., Баррозо Дж. М., Бултинк П., Карбо-Дорка Р. (2006) К альтернативной структуре матрицы ядра твердости в методе выравнивания электроотрицательности (EEM).J Chem Inform Model 46 (4): 1657–1665. DOI: 10.1021 / ci050505e

CAS Статья Google Scholar

34.

Ouyang Y, Ye F, Liang Y (2009) Модифицированный метод выравнивания электроотрицательности для быстрого и точного расчета атомных зарядов в больших биологических молекулах. Phys Chem Chem Phys PCCP 11 (29): 6082–6089. DOI: 10.1039 / b821696g

CAS Статья Google Scholar

35.

Verstraelen T, Van Speybroeck V, Waroquier M (2009) Метод уравнивания электроотрицательности и уравновешивание разделенного заряда, применяемые к органическим системам: параметризация, проверка и сравнение. J Chem Phys. DOI: 10.1063 / 1.3187034

Google Scholar

36.

Frisch M, Trucks G, Schlegel H, Scuseria G, Robb M, Cheeseman J, Scalmani G, Barone V, Mennucci B, Petersson G et al (2010) Gaussian 09 (редакция a.02), gaussian, inc., Wallingford ct (США). В: Naturforsch Z (ed) Vol. 10

37.

Hutter J, Iannuzzi M, Schiffmann F, Vandevondele J (2014) Cp2k: атомистическое моделирование систем конденсированного состояния. Wiley Interdiscip Rev Comput Mol Sci 4 (1): 15–25. DOI: 10.1002 / wcms.1159

CAS Статья Google Scholar

38.

Манц Т.А., Шолл Д.С. (2012) Улучшенный функционал распределения заряда между атомами и молекулами для одновременного воспроизведения электростатического потенциала и химических состояний в периодических и непериодических материалах.J Chem Theory Comput 8 (8): 2844–2867

CAS Статья Google Scholar

39.

Verstraelen T, Vandenbrande S, Chan M, Zadeh FH, González C, Limacher PA, Horton AM (2013). http://theochem.github.com/horton/

40.

Кейт Т.А. (2013) Aimall (версия 13.05.06). TK Gristmill Software, Overland Park

41.

Маренич А.В., Джером С.В., Крамер С.Дж., Трулар Д.Г. (2012) Модель заряда 5: расширение популяционного анализа Хиршфельда для точного описания молекулярных взаимодействий в газовой и конденсированной фазах.J Chem Theory Comput 8 (2): 527–541. DOI: 10.1021 / ct200866d

CAS Статья Google Scholar

42.

Malde AK, Zuo L, Breeze M, Stroet M, Poger D, Nair PC, Oostenbrink C, Mark AE (2011) Автоматическое построение топологии силового поля (ATB) и репозиторий: Версия 1.0. J Chem Theory Comput 7 (12): 4026–4037. DOI: 10,1021 / ct200196m

CAS Статья Google Scholar

43.

Medeiros DDJ, Cortopassi WA, Costa França TC, Pimentel AS (2013) ITP adjuster 1.0: новая служебная программа для корректировки расходов в файлах топологии, генерируемых сервером PRODRG. J Chem. DOI: 10.1155 / 2013/803151

Google Scholar

44.

Wang J, Wang W, Kollman PA, Case DA (2006) Автоматическое восприятие типа атома и типа связи в молекулярно-механических расчетах. Дж. Моль Graph Modeling 25 (2): 247–260. DOI: 10.1016 / j.jmgm.2005.12.005

Артикул Google Scholar

45.

Vanquelef E, Simon S, Marquant G, Garcia E, Klimerak G, Delepine JC, Cieplak P, Dupradeau FY (2011) R.E.D. Сервер: веб-сервис для получения зарядов RESP и ESP и создания библиотек силовых полей для новых молекул и молекулярных фрагментов. Nucl Acids Res. DOI: 10.1093 / nar / gkr288

Google Scholar

46.

Mukherjee G, Patra N, Barua P, Jayaram B (2011) Быстрая эмпирическая схема распределения частичного атомного заряда, совместимая с GAFF, для моделирования взаимодействий малых молекул с биомолекулярными мишенями. J. Comput Chem. 32 (5): 893–907. DOI: 10.1002 / jcc.21671

CAS Статья Google Scholar

47.

Вайнио М.Дж., Джонсон М.С. (2007) Создание конформерных ансамблей с использованием многоцелевого генетического алгоритма. J Chem Inform Modeling 47 (6): 2462–2474.DOI: 10.1021 / Ci6005646

CAS Статья Google Scholar

48.

Варжекова Р.С., Коча Я. (2006) Новости и обновления программного обеспечения Оптимизированная и распараллеленная реализация метода выравнивания электроотрицательности и метода выравнивания электроотрицательности атомных связей. J. Comput Chem. 27 (3): 396–405. DOI: 10.1002 / jcc.20344

Артикул Google Scholar

49.

Dolinsky TJ, Nielsen JE, McCammon JA, Baker NA (2004) PDB2PQR: автоматизированный конвейер для установки электростатических расчетов Пуассона-Больцмана. Nucl Acids Res. DOI: 10.1093 / nar / gkh481

Google Scholar

50.

О’Бойл Н.М., Бэнк М., Джеймс К.А., Морли С., Вандермерш Т., Хатчисон Г.Р. (2011) Open babel: открытый химический ящик с инструментами. J Cheminform. DOI: 10.1186 / 1758-2946-3-33

Google Scholar

51.

Cho AE, Guallar V, Berne BJ, Friesner R (2005) Важность точных зарядов в молекулярном стыковке: подход квантовой механики / молекулярной механики (QM / MM). J. Comput Chem. 26 (9): 915–931. DOI: 10.1002 / jcc.20222

CAS Статья Google Scholar

52.

Анисимов В.М. (2010) Квантово-механическая молекулярная динамика переноса заряда. Кинетика Динамика. DOI: 10.1007 / 978-90-481-3034-4_9

Google Scholar

53.

Nielsen JE, Gunner MR, García-Moreno EB (2011) The pK a Cooperative: совместная работа по продвижению структурных расчетов значений pK a и электростатических эффектов в белках. DOI: 10.1002 / prot.23194

54.

Baker CM (2015) Поляризуемые силовые поля для молекулярно-динамического моделирования биомолекул. Wiley Interdiscip Rev Comput Mol Sci 5 (2): 241–254. DOI: 10.1002 / wcms.1215

CAS Статья Google Scholar

55.

Heidler R, Janssens GOA, Mortier WJ, Schoonheydt RA (1996) Анализ чувствительности к заряду внутренней основности цеолитов типа фожазита с использованием метода выравнивания электроотрицательности (EEM). J. Phys Chem 100 (50): 19728–19734. DOI: 10.1021 / jp9615619

CAS Статья Google Scholar

56.

Haldoupis E, Nair S, Sholl DS (2012) Поиск MOF для высокоселективной адсорбции CO2 / N2 с использованием скрининга материалов на основе эффективного распределения атомных точечных зарядов.J Am Chem Soc 134 (9): 4313–4323. DOI: 10.1021 / ja2108239

CAS Статья Google Scholar

57.

Bultinck P, Langenaeker W, Carbó-Dorca R, Tollenaere JP (2003) Быстрый расчет квантово-химических молекулярных дескрипторов с помощью метода выравнивания электроотрицательности. J Chem Inform Comp Sci 43: 422–428. DOI: 10.1021 / ci0255883

CAS Статья Google Scholar

58.

Svobodová Vařeková R, Geidl S, Ionescu C-M, Skřehota O, Bouchal T, Sehnal D, Abagyan R, Koča J (2013) Прогнозирование значений p Ka на основе атомных зарядов EEM. Журнал Cheminform 5 (1): 18. DOI: 10.1186 / 1758-2946-5-18

Артикул Google Scholar

59.

Shimizu K, Chaimovich H, Farah JPS, Dias LG, Bostick DL (2004) Расчет дипольного момента для полипептидов с использованием обобщенного метода выравнивания прирожденной электроотрицательности: результаты в вакууме и континуальном диэлектрическом растворителе.J. Phys Chem B 108 (13): 4171–4177. DOI: 10.1021 / jp037315w

CAS Статья Google Scholar

60.

Chen S, Yang Z (2010) Моделирование молекулярной динамики \ (\ beta \) — шпильки фрагмента белка G с помощью метода выравнивания электроотрицательности атомных связей, интегрированного в молекулярную механику (ABEEM \ (\ delta \) \ (\ пи \) / ММ). Chin J Chem 28 (11): 2109–2118. DOI: 10.1002 / cjoc.2010

CAS Статья Google Scholar

61.

Ionescu CM, Svobodová Vařeková R, Prehn JHM, Huber HJ, Koča J (2012) Анализ профиля заряда показывает, что активация проапоптотических регуляторов bax и bak зависит от аллостерической регуляции, опосредованной переносом заряда. PLoS Comput Biol. DOI: 10.1371 / journal.pcbi.1002565

Google Scholar

62.

Chelli R, Procacci P, Righini R, Califano S (1999) Электрический отклик в схемах выравнивания химического потенциала.J. Chem Phys 111 (18): 8569. DOI: 10.1063 / 1.480198

CAS Статья Google Scholar

63.

Уоррен Ли Дж., Дэвис Дж. Э., Патель С. (2008) Происхождение и контроль масштабирования сверхлинейной поляризуемости в методах выравнивания химического потенциала. J. Chem Phy 128 (14): 144110. DOI: 10.1063 / 1.2872603

Артикул Google Scholar

64.

Verstraelen T, Pauwels E, De Proft F, Van Speybroeck V, Geerlings P, Waroquier M (2012) Оценка моделей атомного заряда для газофазных вычислений на полипептидах. J Chem Theory Comput 8 (2): 661–676. DOI: 10.1021 / ct200512e

CAS Статья Google Scholar

65.

van Duin ACT, Strachan A, Stewman S, Zhang Q, Xu X, Goddard WA (2003) реактивное силовое поле ReaxFF SiO для кремниевых и оксидных систем.J. Phys Chem. 107 (19): 3803–3811. DOI: 10.1021 / jp0276303

Артикул Google Scholar

66.

Пуранен Дж. С., Вайнио М. Дж., Джонсон М. С. (2009) Точные зависящие от конформации молекулярные электростатические потенциалы для открытия высокопроизводительных препаратов in silico. J. Comput Chem. DOI: 10.1002 / jcc.21460

Google Scholar

67.

Bultinck P, Langenaeker W, Lahorte P, De Proft F, Geerlings P, Van Alsenoy C, Tollenaere JP (2002) Метод выравнивания электроотрицательности II: применимость различных схем атомных зарядов.J. Phys Chem. A 106 (34): 7895–7901. DOI: 10.1021 / jp020547v

CAS Статья Google Scholar

68.

Bultinck P, Vanholme R, Popelier PLA, De Proft F, Geerlings P (2004) Высокоскоростной расчет зарядов AIM с помощью метода выравнивания электроотрицательности. J. Phys Chem A 108 (46): 10359-10366. DOI: 10.1021 / jp0469281

CAS Статья Google Scholar

69.

Варекова Р.С., Жироускова З., Ванек Дж., Сухомель С., Коджа Дж. (2007) Метод выравнивания электроотрицательности: параметризация и проверка для больших наборов органических, галогенорганических и металлоорганических молекул. Int J Mol Sci 8 (7): 572–582

CAS Статья Google Scholar

70.

Ionescu CM, Geidl S, Svobodová Vařeková R, Koča J (2013) Быстрый расчет точных атомных зарядов для белков с помощью метода выравнивания электроотрицательности.J Chem Inform Model 53 (10): 2548–2558. DOI: 10.1021 / ci400448n

CAS Статья Google Scholar

71.

Graham GG, Davies MJ, Day RO, Mohamudally A, Scott KF (2013) Современная фармакология парацетамола: терапевтические действия, механизм действия, метаболизм, токсичность и недавние фармакологические открытия. Инфламмофармакология 21 (3): 201–232. DOI: 10.1007 / s10787-013-0172-x

72.

Bertolini A, Ferrari A, Ottani A, Guerzoni S, Tacchi R, Leone S (2006) Парацетамол: новые перспективы старого препарата. CNS Drug Rev. 12 (3-4): 250-275. DOI: 10.1111 / j.1527-3458.2006.00250.x

73.

Svobodová Vařeková R, Geidl S, Ionescu CM, Skřehota O, Kudera M, Sehnal D, Bouchal T, Abagyan R, Huber HJ, Koča J (2011) Прогнозирование значений pKa замещенных фенолов на основе атомных зарядов: сравнение различных квантово-механических методов и схем распределения заряда.J Chem Inform Modeling 51 (8): 1795–1806. DOI: 10.1021 / ci200133w

Артикул Google Scholar

74.

Угур И., Марион А., Парант С., Дженсен Дж. Х., Монард Г. (2014) Рационализация значений pKa спиртов и тиолов с использованием дескрипторов атомного заряда и его применение для прогнозирования pKa аминокислот. J Chem Inform Modeling. DOI: 10.1021 / ci500079w

Google Scholar

75.

Dastmalchi S, Rashidi M, Rassi M (1995) Одновременное определение pka и коэффициента распределения октанол / вода (pm) ацетаминофена. J Sch Pharm Med Sci Univ Тегеран 4: 7–14

Google Scholar

76.

Соединения открытых баз данных NCI. Национальный институт рака. http://cactus.nci.nih.gov/. По состоянию на август 2015 г.

77.

Howard P, Meylan W (1999) База данных физических / химических свойств (PHYSPROP). Сиракузская исследовательская корпорация, Центр экологических наук, Северные Сиракузы

Google Scholar

78.

Geidl S, Svobodová Vařeková R, Bendová V, Petrusek L, Ionescu CM, Jurka Z, Abagyan R, Koča J (2015) Как методология подготовки трехмерной структуры влияет на качество прогноза p K a? J Chem Inform Modeling 55 (6): 1088–1097. DOI: 10.1021 / ci500758w

CAS Статья Google Scholar

79.

Bellm L, Lehrer RI, Ganz T (2000) Protegrins: новые антибиотики млекопитающего происхождения. Exp Opin Investigations Drugs 9 (8): 1731–1742.DOI: 10.1517 / 13543784.9.8.1731

CAS Статья Google Scholar

80.

Steinberg DA, Hurst MA, Fujii CA, Kung AHC, Ho JF, Cheng FC, Loury DJ, Fiddes JC (1997) Protegrin-1: быстро бактерицидный пептид широкого спектра действия с активностью in vivo. Противомикробные агенты Chemotherap 41 (8): 1738–1742

CAS Google Scholar

81.

Dong N, Zhu X, Chou S, Shan A, Li W, Jiang J (2014) Противомикробная активность и селективность упрощенных пептидов с симметричным концом.Биоматериалы 35 (27): 8028–8039. DOI: 10.1016 / j.biomaterials.2014.06.005

CAS Статья Google Scholar

82.

Mohanram H, Bhattacharjya S (2014) Протегрин-1 с удаленным цистеином (CDP-1): антибактериальная активность, разрушение внешней мембраны и селективность. Biochimica et Biophysica Acta (BBA) General Subjects 1840 (10): 3006–3016. DOI: 10.1016 / j.bbagen.2014.06.018

CAS Статья Google Scholar

83.

Остберг Н., Казнессис Ю. (2005) Взаимосвязи между структурой протегрина и активностью: использование моделей гомологии синтетических последовательностей для определения структурных характеристик, важных для активности. Пептиды 26 (2): 197–206. DOI: 10.1016 / j.peptides.2004.09.020

CAS Статья Google Scholar

84.

Фарнер Р.Л., Дикманн Т., Харвиг SSL, Лерер Р.И., Эйзенберг Д., Фейгон Дж. (1996) Структура раствора протегрина-1, антимикробного пептида широкого спектра действия из лейкоцитов свиней.Chem Biol 3 (7): 543–550. DOI: 10.1016 / S1074-5521 (96) -3

CAS Статья Google Scholar

85.

Bolintineanu DS, Langham AA, Davis HT, Kaznessis YN (2007) Моделирование молекулярной динамики трех антимикробных пептидов протегринового типа: взаимодействие между зарядами на концах, \ (\ beta \) - структура листа и амфифильные взаимодействия . DOI: 10.1080 / 08

0701393481

86.

Langham AA, Khandelia H, Schuster B, Waring AJ, Lehrer RI, Kaznessis YN (2008) Корреляция между смоделированными физико-химическими свойствами и гемоличностью протегриноподобных антимикробных пептидов: прогнозирование экспериментальной токсичности. Пептиды 29 (7): 1085–1093. DOI: 10.1016 / j.peptides.2008.03.018

CAS Статья Google Scholar

87.

Lai JR, Huck BR, Weisblum B, Gellman SH (2002) Дизайн нецистеинсодержащих антимикробных \ (\ beta \) - шпилек: исследования взаимосвязи структуры и активности с линейными аналогами протегрина-1.Биохимия 41 (42): 12835–12842. DOI: 10.1021 / bi026127d

CAS Статья Google Scholar

88.

Bedford L, Paine S, Sheppard PW, Mayer RJ, Roelofs J (2010) Сборка, структура и функция протеасомы 26S. DOI: 10.1016 / j.tcb.2010.03.007

89.

Gallastegui N, Groll M (2010) Протеасома 26S: сборка и функция деструктивной машины. DOI: 10.1016 / j.tibs.2010.05.005

90.

Unverdorben P, Beck F, Śledź P, Schweitzer A, Pfeifer G, Plitzko JM, Baumeister W, Förster F (2014) Глубокая классификация большого набора крио-ЭМ данных определяет конформационный ландшафт протеасомы 26S. Proc Natl Acad Sci USA 111 (15): 5544–5549. DOI: 10.1073 / pnas.1403409111

CAS Статья Google Scholar

91.

О’Хара А., Ховарт А., Варро А., Дималин Р. (2013) Роль бета-субъединиц протеасомы в опосредованной гастрином транскрипции ингибитора активатора плазминогена-2 и регенерирующего белка1.PLoS One. DOI: 10.1371 / journal.pone.0059913

Google Scholar

92.

Cron KR, Zhu K, Kushwaha DS, Hsieh G, Merzon D, Rameseder J, Chen CC, D'Andrea AD, Kozono D (2013) Ингибиторы протеасом блокируют репарацию ДНК и радиосенсибилизируют немелкоклеточный рак легких . PLoS One. DOI: 10.1371 / journal.pone.0073710

Google Scholar

1.5 Расчет электрических полей распределения зарядов - Введение в электричество, магнетизм и схемы

ЦЕЛИ ОБУЧЕНИЯ

---

К концу этого раздела вы сможете:

• Объясните, что такое непрерывное распределение заряда источника и как оно связано с концепцией квантования заряда
• Опишите линейные, поверхностные и объемные заряды
• Вычислить поле непрерывного распределения заряда источника любого знака

Распределение заряда, которое мы видели до сих пор, было дискретным: оно состояло из отдельных точечных частиц.Это контрастирует с непрерывным распределением заряда , которое имеет по крайней мере одно ненулевое измерение. Если распределение заряда является непрерывным, а не дискретным, мы можем обобщить определение электрического поля. Мы просто делим заряд на бесконечно малые части и рассматриваем каждую часть как точечный заряд.

Обратите внимание, что поскольку заряд квантуется, не существует такой вещи, как «действительно» непрерывное распределение заряда. Однако в большинстве практических случаев полный заряд, создающий поле, включает такое огромное количество дискретных зарядов, что мы можем спокойно игнорировать дискретную природу заряда и считать его непрерывным.Именно такое приближение мы делаем, когда имеем дело с ведром с водой как сплошной жидкостью, а не с набором молекул h3Oh3O.

Нашим первым шагом является определение плотности заряда для распределения заряда вдоль линии, по поверхности или в объеме, как показано на рисунке 1.5.1.

(рисунок 1.5.1)

Рисунок 1.5.1. Конфигурация элементов разности зарядов для (а) линейного заряда, (б) слоя заряда и (в) объема заряда.Также обратите внимание, что (d) некоторые компоненты полного электрического поля уравновешиваются, а оставшаяся часть приводит к чистому электрическому полю.

Определения плотности заряда:

Затем для линейного заряда, поверхностного заряда и объемного заряда сумма в уравнении 1.4.2 становится интегралом и заменяется на, или соответственно:

(1.5.1)

(1.5.2)

(1.5.3)

(1.5.4)

Интегралы являются обобщением выражения для поля точечного заряда.Они неявно включают и предполагают принцип суперпозиции. «Уловка» их использования почти всегда заключается в том, чтобы придумать правильные выражения для, или, в зависимости от обстоятельств, выразить в терминах, а также соответствующим образом выразить функцию плотности заряда. Может быть постоянным; это может зависеть от местоположения.

Внимательно обратите внимание на значение в этих уравнениях: это расстояние от элемента заряда до интересующего местоположения (точка в пространстве, где вы хотите определить поле).Однако не путайте это со значением; мы используем его и векторные обозначения для записи трех интегралов одновременно. То есть уравнение 1.5.2 на самом деле равно

.

ПРИМЕР 1.5.1

---

Электрическое поле линейного участка

Найдите электрическое поле на расстоянии выше середины отрезка прямой линии длиной, несущего однородную линейную плотность заряда.

Стратегия

Поскольку это непрерывное распределение заряда, мы концептуально разбиваем сегмент провода на отрезки разной длины, каждый из которых несет разную величину заряда.Затем мы вычисляем дифференциальное поле, создаваемое двумя симметрично расположенными отрезками провода, используя симметрию установки для упрощения расчета (рисунок 1.5.2). Наконец, мы интегрируем это выражение дифференциального поля по длине провода (фактически, по половине, как мы объясним ниже), чтобы получить полное выражение электрического поля.

(рисунок 1.5.2)

Рисунок 1.5.2 Равномерно заряженный отрезок провода. Электрическое поле в точке можно найти, применив принцип суперпозиции к симметрично расположенным элементам заряда и интегрировав.

Решение

Прежде чем мы перейдем к этому, как мы ожидаем, что поле «будет выглядеть» издалека? Поскольку это конечный отрезок линии, издалека он должен выглядеть как точечный заряд. Мы проверим полученное выражение, чтобы убедиться, что оно соответствует этому ожиданию.

Электрическое поле для линейного заряда дается общим выражением

Симметрия ситуации (наш выбор двух идентичных дифференциальных зарядов) подразумевает, что горизонтальные () -компоненты поля сокращаются, так что чистое поле указывает в -направлении.Проверим формально.

Общее поле - это векторная сумма полей каждого из двух элементов заряда (назовите их и, пока):

Потому что два элемента заряда идентичны и находятся на одинаковом расстоянии от точки, где мы хотим вычислить поле, поэтому эти компоненты отменяются. Остается

Эти компоненты также равны, поэтому имеем

, где в этом примере находится наш дифференциальный линейный элемент, поскольку мы интегрируем вдоль линии заряда, лежащей на оси -оси.(Пределы интегрирования заключаются в том, что мы построили чистое поле из двух дифференциальных частей заряда. Если мы проинтегрируем по всей длине, мы получим ошибочный множитель.)

В принципе на этом полно. Однако, чтобы фактически вычислить этот интеграл, нам нужно исключить все переменные, которые не указаны. В этом случае оба и меняются по мере того, как мы интегрируем наружу до конца линейного заряда, так что это переменные, от которых нужно избавиться. Мы можем сделать это так же, как и с двумя точечными зарядами: заметив, что

и

Подставляя, получаем

, что упрощается до

(1.5.5)

Значение

Еще раз обратите внимание на использование симметрии для упрощения задачи. Это очень распространенная стратегия расчета электрических полей. Поля несимметричного распределения заряда должны обрабатываться с помощью множественных интегралов, и может потребоваться численный расчет на компьютере.

ПРОВЕРЬТЕ ПОНИМАНИЕ 1.4

---

Как изменится использованная выше стратегия для расчета электрического поля в точке, находящейся на расстоянии выше одного конца конечного отрезка линии?

ПРИМЕР 1.5,2

---

Электрическое поле бесконечной линии заряда

Найдите электрическое поле на расстоянии выше середины бесконечной линии заряда, которая несет однородную линейную плотность заряда.

Стратегия

Это точно так же, как в предыдущем примере, за исключением того, что пределы интеграции будут равны.

Решение

Опять же, горизонтальные компоненты уравновешиваются, поэтому мы получаем

.

, где в этом примере находится наш дифференциальный линейный элемент, поскольку мы интегрируем вдоль линии заряда, лежащей на оси -оси.Опять же,

Подставляя, получаем

, что упрощается до

Значение

Наша стратегия работы с непрерывным распределением зарядов также дает полезные результаты для зарядов с бесконечной размерностью.

В случае конечной линии заряда обратите внимание, что для, доминирует в знаменателе, так что уравнение 1.5.5 упрощается до

Если вы помните, общий заряд на проводе, мы получили выражение для поля точечного заряда, как и ожидалось.

В пределе, с другой стороны, мы получаем поле бесконечного прямого провода , который представляет собой прямой провод, длина которого намного, намного больше любого из его других размеров, а также намного, намного больше расстояния в котором рассчитывается поле:

(1.5.6)

Интересным артефактом этого бесконечного предела является то, что мы утратили привычную зависимость. Это станет еще более интригующим в случае с бесконечной плоскостью.

ПРИМЕР 1.5.4

---

Поле диска

Найдите электрическое поле круглого тонкого диска радиуса и однородной плотности заряда на расстоянии выше центра диска (рисунок 1.5.4).

(рисунок 1.5.4)

Рисунок 1.5.4 Равномерно заряженный диск. Как и в примере линейного заряда, поле над центром этого диска можно рассчитать, воспользовавшись симметрией распределения заряда.

Стратегия

Электрическое поле для поверхностного заряда равно

.

Для решения задач поверхностного заряда мы разбиваем поверхность на симметричные дифференциальные «полосы», соответствующие форме поверхности; здесь мы будем использовать кольца, как показано на рисунке.Опять же, из-за симметрии горизонтальные компоненты сокращаются, и поле полностью находится в вертикальном направлении. Вертикальная составляющая электрического поля извлекается умножением на, так что

Как и раньше, нам нужно переписать неизвестные множители в подынтегральном выражении в терминах заданных величин. В данном случае

(Пожалуйста, обратите внимание на два разных «s» здесь; это расстояние от дифференциального кольца заряда до точки, где мы хотим определить поле, тогда как это расстояние от центра диска до дифференциального кольца заряда. .) Также мы уже выполнили интеграл по полярному углу в записи.

Решение

Подставив все это, получаем

или, проще говоря,

(1.5.7)

Значение

Опять же, можно показать (с помощью разложения Тейлора), что когда, это сокращается до

, что является выражением точечного заряда.

ПРОВЕРЬТЕ ПОНИМАНИЕ 1.5

---

Как изменится указанный выше предел при использовании равномерно заряженного прямоугольника вместо диска?

As, уравнение 1.5.7 сводится к полю бесконечной плоскости , которая представляет собой плоский лист, площадь которого намного, намного превышает его толщину, а также намного, намного превышает расстояние, на котором должно быть вычислено поле:

(1.5.8)

Обратите внимание, что это поле является постоянным. Этот удивительный результат, опять же, является артефактом нашего предела, хотя мы будем неоднократно использовать его в будущем. Чтобы понять, почему это происходит, представьте, что вас помещают над бесконечной плоскостью постоянного заряда.Изменится ли самолет, если вы измените высоту? Нет, вы все еще видите, как самолет уходит в бесконечность, независимо от того, как далеко вы от него. Важно отметить, что уравнение 1.5.8 вызвано тем, что мы находимся над плоскостью. Если бы мы были ниже, поле указывало бы в направлении -направлении.

ПРИМЕР 1.5.5

---

Поле двух бесконечных плоскостей

Найдите повсюду электрическое поле, возникающее из двух бесконечных плоскостей с равными, но противоположными плотностями заряда (Рисунок 1.5.5).

(рисунок 1.5.5)

Рисунок 1.5.5 Две заряженные бесконечные плоскости. Обратите внимание на направление электрического поля.

Стратегия

Мы уже знаем электрическое поле, возникающее из одной бесконечной плоскости, поэтому мы можем использовать принцип суперпозиции, чтобы найти поле из двух.

Решение

Электрическое поле направлено от положительно заряженной плоскости к отрицательно заряженной. Поскольку они равны и противоположны, это означает, что в области за пределами двух плоскостей электрические поля компенсируют друг друга до нуля.

Однако в области между плоскостями электрические поля складываются, и мы получаем

для электрического поля. Это потому, что на рисунке поле указывает в направлении.

Значение

Системы, которые можно представить как две бесконечные плоскости такого типа, предоставляют полезные средства для создания однородных электрических полей.

ПРОВЕРЬТЕ ПОНИМАНИЕ 1.6

---

Как могло бы выглядеть электрическое поле в системе с двумя параллельными положительно заряженными плоскостями с равными плотностями заряда?

Кандела Цитаты

Лицензионный контент CC, конкретная атрибуция

• Загрузите бесплатно по адресу http: // cnx.