Последовательность Фибоначчи — papanya77 — LiveJournal
Леона́рдо Пиза́нский (лат. Leonardus Pisanus, итал. Leonardo Pisano, около 1170 года, Пиза — около 1250 года, там же) — первый крупный математик средневековой Европы. Наиболее известен под прозвищем Фибона́ччи.Подробнее тут:http://ru.wikipedia.org/wiki/%D4%E8%E1%EE%ED%E0%F7%F7%E8
Последовательность Фибоначчи, известная всем по фильму «Код Да Винчи» — ряд цифр, описанный в виде загадки Итальянским математиком Леонардо Пизанским, более известным под прозвищем Фибоначчи, в XIII веке. Вкратце суть загадки:
Кто-то поместил пару кроликов в некоем замкнутом пространстве, чтобы узнать, сколько пар кроликов родится при этом в течении года, если природа кроликов такова, что каждый месяц пара кроликов производит на свет другую пару, а способность к производству потомства у них появляется по достижению двухмесячного возраста.

Последовательность Фибоначчи и Кролики
В итоге получается такой ряд цифр: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, где через запятую показано количество пар кроликов в каждом из двенадцати месяцев. Его можно продолжать бесконечно долго. Его суть в том, что каждое следующее число является суммой двух предыдущих.
У этого ряда есть несколько математических особенностей, которых обязательно нужно коснуться. Он асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.
Так отношение какого-либо члена ряда к предшествующему ему колеблется около числа 1,618, через pаз то превосходя, то не достигая его. Отношение к следующему аналогично приближается к числу 0,618, что обратно пропорционально 1,618. Если мы будем делить элементы через одно, то получим числа 2,618 и 0,382, которые так же являются обратно пропорциональными. Это так называемые коэффициенты Фибоначчи.
К чему всё это?
Так мы приближаемся к одному из самых загадочных явлений природы. Смекалистый Леонардо по сути не открыл ничего нового, он просто напомнил миру о таком явлении, как Золотое Сечение, которое не уступает по значимости теореме Пифагора.
Все окружающие нас предметы мы различаем в том числе и по форме. Какие-то нам нравятся больше, какие-то меньше, некоторые вовсе отталкивают взгляд. Иногда интерес может быть продиктован жизненной ситуацией, а порой красотой наблюдаемого объекта. Симметричная и пропорциональная форма, способствует наилучшему зрительному восприятию и вызывает ощущение красоты и гармонии. Целостный образ всегда состоит из частей разного размера, находящихся в определённом соотношении друг с другом и целым. Золотое сечение — высшее проявление совершенства целого и его частей в науке, искусстве и природе.
Если на простом примере, то Золотое Сечение — это деление отрезка на две части в таком соотношении, при котором большая часть относится к меньшей, как их сумма (весь отрезок) к большей.

Золотое Сечение — Отрезок
Если мы примем весь отрезок c за 1, то отрезок a будет равен 0,618, отрезок b — 0,382, только так будет соблюдено условие Золотого Сечения (0,618/0,382=1,618; 1/0,618=1,618). Отношение c к a равно 1,618, а с к b 2,618. Это всё те же, уже знакомые нам, коэффициенты Фибоначчи.
Разумеется есть золотой прямоугольник, золотой треугольник и даже золотой кубоид. Пропорции человеческого тела во многих соотношениях близки к Золотому Сечению.
Золотое сечение и Человеческое тело
Изображение: marcus-frings.de
Последовательность Фибоначчи — Анимация
Но самое интересное начинается, когда мы объединим полученные знания. На рисунке наглядно показана связь между последовательностью Фибоначчи и Золотым сечением. Мы начинаем с двух квадратов первого размера. Сверху добавляем квадрат второго размера. Подрисовываем рядом квадрат со стороной, равной сумме сторон двух предыдущих, третьего размера. По аналогии появляется квадрат пятого размера. И так далее пока не надоест, главное, чтобы длина стороны каждого следующего квадрата равнялась сумме длин сторон двух предыдущих. Мы видим серию прямоугольников, длины сторон, которых являются числами Фибоначчи, и, как не странно, они называются прямоугольниками Фибоначчи.
Если мы проведём плавную линий через углы наших квадратов, то получим ни что иное, как спираль Архимеда, увеличение шага которой всегда равномерно.
Спираль Фибоначчи
Ничего не напоминает?

Фото: ethanhein on Flickr
И не только в раковине моллюска можно найти спирали Архимеда, а во многих цветах и растениях, просто они не такие явные.
Алое многолистный:
Фото: brewbooks on Flickr
Броколи романеско:
Фото: beart.org.uk
Подсолнечник:
Фото: esdrascalderan on Flickr
Сосновая шишка:
Фото: mandj98 on Flickr
А если взглянуть чуть подальше, то можно разглядеть ряд Фибоначчи в недосягаемых галактиках.
И тут самое время вспомнить о Золотом Сечении! Ни одни ли из самых прекрасных и гармоничных творений природы изображены на этих фотографиях? И это далеко не все. Присмотревшись, можно найти похожие закономерности во многих формах.
Конечно заявление, что все эти явление построены на последовательности Фибоначчи звучит слишком громко, но тенденция на лицо. Да и к тому же сама она далека от совершенства, как и всё в этом мире.
Есть предположение, что ряд Фибоначчи — это попытка природы адаптироваться к более фундаментальной и совершенной золотосечённой логарифмической последовательности, которая практически такая же, только начинается из ниоткуда и уходит в никуда. Природе же обязательно нужно какое-то целое начало, от которого можно оттолкнуться, она не может создать что-то из ничего. Отношения первых членов последовательности Фибоначчи далеки от Золотого Сечения. Но чем дальше мы продвигаемся по ней, тем больше эти отклонения сглаживаются. Для определения любого ряда достаточно знать три его члена, идущие друг за другом. Но только не для золотой последовательности, ей достаточно двух, она является геометрической и арифметической прогрессией одновременно. Можно подумать, будто она основа для всех остальных последовательностей.
Каждый член золотой логарифмической последовательности является степенью Золотой Пропорции (z). Часть ряда выглядит примерно так: … z-5; z-4; z-3; z-2; z-1; z0; z1; z2; z3; z4; z5 … Если мы округлим значение Золотой пропорции до трёх знаков, то получим z=1,618, тогда ряд выглядит так: … 0,090 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854; 11,090 … Каждый следующий член может быть получен не только умножением предыдущего на 1,618, но и сложением двух предыдущих. Таким образом экспоненциальный рост обеспечивается путем простого сложения двух соседних элементов. Это ряд без начала и конца, и именно на него пытается быть похожей последовательность Фибоначчи. Имея вполне определённое начало, она стремится к идеалу, никогда его не достигая. Такова жизнь.
И всё-таки, в связи со всем увиденным и прочитанным, возникают вполне закономерные вопросы:
От куда взялись эти числа? Кто этот архитектор вселенной, попытавшийся сделать её идеальной? Было ли когда-то всё так, как он хотел? И если да, то почему сбилось? Мутации? Свободный выбор? Что же будет дальше? Спираль скручивается или раскручивается?
Найдя ответ на один вопрос, получишь следующий. Разгадаешь его, получишь два новых. Разберёшься с ними, появится ещё три. Решив и их, обзаведёшься пятью нерешёнными. Потом восьмью, потом тринадцатью, 21, 34, 55…
Источник:http://greenword.ru/2009/06/fibonacci-sequence.html
Подробнее о золотом сечение и ряде Фибоначчи тут:http://www.milogiya2007.ru/fibonachi.htm
И тут:
взято с сайта GreenWord
Последовательность Фибоначчи, известная всем по фильму «Код Да Винчи» — ряд цифр, описанный в виде загадки Итальянским математиком Леонардо Пизанским, более известным под прозвищем Фибоначчи, в XIII веке. Вкратце суть загадки:
![]() Кто-то поместил пару кроликов в некоем замкнутом пространстве, чтобы узнать, сколько пар кроликов родится при этом в течении года, если природа кроликов такова, что каждый месяц пара кроликов производит на свет другую пару, а способность к производству потомства у них появляется по достижению двухмесячного возраста.
Кто-то поместил пару кроликов в некоем замкнутом пространстве, чтобы узнать, сколько пар кроликов родится при этом в течении года, если природа кроликов такова, что каждый месяц пара кроликов производит на свет другую пару, а способность к производству потомства у них появляется по достижению двухмесячного возраста.
В итоге получается такая последовательность: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, где через запятую показано количество пар кроликов в каждом из двенадцати месяцев. Эту последовательность можно продолжать бесконечно долго. Её суть в том, что каждое следующее число является суммой двух предыдущих.
У этой последовательности есть ряд математических особенностей, которых обязательно нужно коснуться. Данная последовательность асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.
Так отношение какого-либо члена последовательности к предшествующему ему колеблется около числа 1,618, через pаз то превосходя, то не достигая его. Отношение к следующему аналогично приближается к числу 0,618, что обратно пропорционально 1,618. Если мы будем делить элементы последовательности через одно, то получим числа 2,618 и 0,382, которые так же являются обратно пропорциональными. Это так называемые коэффициенты Фибоначчи.
К чему всё это? Так мы приближаемся к одному из самых загадочных явлений природы. Фибоначчи по сути не открыл ничего нового, он просто напомнил миру о таком явлении, как Золотое Сечение, которое не уступает по значимости теореме Пифагора.
Все окружающие нас предметы мы различаем в том числе и по форме. Какие-то нам нравятся больше, какие-то меньше, некоторые вовсе отталкивают взгляд. Иногда интерес может быть продиктован жизненной ситуацией, а порой красотой наблюдаемого объекта. Симметричная и пропорциональная форма, способствует наилучшему зрительному восприятию и вызывает ощущение красоты и гармонии. Целостный образ всегда состоит из частей разного размера, находящихся в определённом соотношении друг с другом и целым.
Если на простом примере, то Золотое Сечение — это деление отрезка на две части в таком соотношении, при котором большая часть относится к меньшей, как их сумма (весь отрезок) к большей.
Если мы примем весь отрезок c за 1, то отрезок a будет равен 0,618, отрезок b — 0,382, только так будет соблюдено условие Золотого Сечения (0,618/0,382=1,618; 1/0,618=1,618). Отношение c к a равно 1,618, а с к b2,618. Это всё те же, уже знакомые нам, коэффициенты Фибоначчи.
Разумеется есть золотой прямоугольник, золотой треугольник и даже золотой кубоид. Пропорции человеческого тела во многих соотношениях близки к Золотому Сечению.
Изображение: marcus-frings.de
Но самое интересное начинается, когда мы объединим полученные знания. На рисунке наглядно показана связь между последовательностью Фибоначчи и Золотым сечением. Мы начинаем с двух квадратов первого размера. Сверху добавляем квадрат второго размера. Подрисовываем рядом квадрат со стороной, равной сумме сторон двух предыдущих, третьего размера. По аналогии появляется квадрат пятого размера. И так далее пока не надоест, главное, чтобы длина стороны каждого следующего квадрата равнялась сумме длин сторон двух предыдущих. Мы видим серию прямоугольников, длины сторон, которых являются числами Фибоначчи, и, как не странно, они называются прямоугольниками Фибоначчи.
Если мы проведём плавную линий через углы наших квадратов, то получим ни что иное, как спираль Архимеда, увеличение шага которой всегда равномерно.
Ничего не напоминает?
Фото: ethanhein on Flickr
И не только в раковине моллюска можно найти спирали Архимеда, а во многих цветах и растениях, просто они не такие явные.
Алое многолистный:
Фото: brewbooks on Flickr
Броколи романеско:
Фото: beart.org.uk
Подсолнечник:
Фото: esdrascalderan on Flickr
Сосновая шишка:
Фото: mandj98 on Flickr
А если взглянуть чуть подальше, то можно разглядеть последовательность Фибоначчи в недосягаемых галактиках.
И тут самое время вспомнить о Золотом Сечении! Ни одни ли из самых прекрасных и гармоничных творений природы изображены на этих фотографиях? И это далеко не все. Присмотревшись, можно найти похожие закономерности во многих формах.
Конечно заявление, что все эти явление построены на последовательности Фибоначчи звучит слишком громко, но тенденция на лицо. Да и к тому же сама последовательность далека от совершенства, как и всё в этом мире.
Есть предположение, что последовательность Фибоначчи — это попытка природы адаптироваться к более фундаментальной и совершенной золотосечённой логарифмической последовательности, которая практически такая же, только начинается из ниоткуда и уходит в никуда. Природе же обязательно нужно какое-то целое начало, от которого можно оттолкнуться, она не может создать что-то из ничего. Отношения первых членов последовательности Фибоначчи далеки от Золотого Сечения. Но чем дальше мы продвигаемся по ней, тем больше эти отклонения сглаживаются. Для определения любой последовательности достаточно знать три её члена, идущие друг за другом. Но только не для золотой последовательности, ей достаточно двух, она является геометрической и арифметической прогрессией одновременно. Можно подумать, будто она основа для всех остальных последовательностей.
Каждый член золотой логарифмической последовательности явлется степенью Золотой Пропорции (z). Часть ряда выглядит примерно так: … z-5; z-4; z-3; z-2; z-1; z0; z1; z2; z3; z4; z5 … Если мы округлим значение Золотой пропорции до трёх знаков, то получим z=1,618, тогда ряд выглядит так: … 0,090 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854; 11,090 … Каждый следующий член может быть получен не только умножением предыдущего на 1,618, но и сложением двух предыдущих. Таким образом экспоненциальный рост в последовательности обеспечивается путем простого сложения двух соседних элементов. Это ряд без начала и конца, и именно на него пытается быть похожей последовательность Фибоначчи. Имея вполне определённое начало, она стремится к идеалу, никогда его не достигая. Такова жизнь.
И всё-таки, в связи со всем увиденным и прочитанным, возникают вполне закономерные вопросы:
От куда взялись эти числа? Кто этот архитектор вселенной, попытавшийся сделать её идеальной? Было ли когда-то всё так, как он хотел? И если да, то почему сбилось? Мутации? Свободный выбор? Что же будет дальше? Спираль скручивается или раскручивается?
Найдя ответ на один вопрос, получишь следующий. Разгадаешь его, получишь два новых. Разберёшься с ними, появится ещё три. Решив и их, обзаведёшься пятью нерешёнными. Потом восьмью, потом тринадцатью, 21, 34, 5
Последовательность Фибоначчи
Источники: 1; 2; 3; 4
Оглавление. Жми для простмотра
Получаемые математиками закономерности и зависимости часто впоследствии обнаруживаются и в других окружающих явлениях. Таким образом подтверждается высокая степень соответствия математического аппарата для описания природных процессов. Один из примеров такой зависимости – числа Фибоначчи, в природе встречающиеся в самых различных масштабах.
Лучший брокер
Наблюдая за окружающим миром, нельзя не заметить, какое несметное количество листьев колышет ветер на растениях. При взгляде издалека может показаться, что последовательность их расположения совершенно хаотична, абсолютно произвольна. Но в действительности в каждом растении произрастание каждого листика и каждой ветки ясно угадывается та точность, какая может быть присуща только математике.
Появившись на свет, оно тут же начинает развиваться строго в соответствии с этим законом, согласно которому на нём не будет ни одного лишнего листка или цветка. Количество веток на новом дереве и где именно они отрастут, количество листьев на каждой из веток и порядок их расположения — всё это заранее записано в генетическом коде растения ещё на стадии его зарождения. Работая вместе, учёные из областей биологии и точных наук открыли миру невероятные законы развития природы — закономерность расположения листьев, известная как филлотаксис, число оборотов вокруг стебля и количество листков в нём происходит в соответствии с последовательностью Фибоначчи, то есть ясно угадывается закон золотого сечения.
Если искушённый исследователь желает найти подобные закономерности в биологическом мире, то пусть увидит, как часто они угадываются во всевозможных спиралевидных формах, широко распространённых в царстве растений. Листья обычно прикреплены к стеблю по спирали, идущей между двумя листками: 1/3 от оборота у орешника, например.
У подсолнуха семена располагаются по спирали, и численность описанных спиралей по каждому направлению равно числам Фибоначчи.

 Рисунок 1. В подсолнечнике семена образуют множество кривых рядов, хорошо описывающихся числами последовательности Фибоначчи.
Рисунок 1. В подсолнечнике семена образуют множество кривых рядов, хорошо описывающихся числами последовательности Фибоначчи.Ряд Фибоначчи также угадывается в законе симметричной формы цветов и количестве лепестков, как, например, у ириса (3 лепестка) или у златоцвета (8 лепестков).
Ряду Фибоначчи соответствует организация структуры широкого ряда систем из живого мира. Известно, что соседние цифры в последовательности Фибоначчи составляют отношение 1,618, а потому нельзя не поразиться факту, что в теле человека существует масса примеров числа фи. Неудивительно, что создано множество исследовательских работ по числу Фибоначчи в природе (например, эта).Число, примерно идентичное числу фи, можно обнаружить в соотношениях частей тела у людей. На этом основании облик человека являет собой идеал пропорций, отражаемый отношением: M/m=1,618.
Последовательность чисел Фибоначчи в живой природе и ее проявления в жизни
Рассматривая в качестве центра тела расположение его пупка, а длину от нее до ступни –за единичный отрезок, то пропорция человеческого роста составит примерно 1,618.
А если внимательно осмотреть свою кисть, а конкретно пальцы, то можно заметить отголоски последовательности Фибоначчи. Любой палец на руке составляют три фаланги, при том суммарная длина первых двух из относится к длине ладони как 1.62. Важно: к большому пальцу данное правило неприменимо. Также отношение длин среднего пальца и мизинца – золотое сечение.
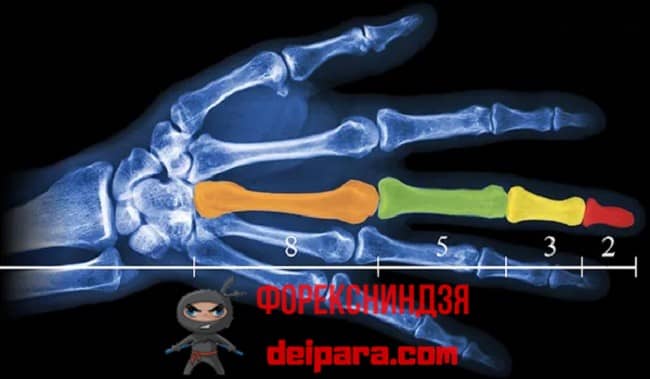
 Рисунок 2. Легко заметить проявление золотого сечения Фибоначчи в природе на фото скелета кисти руки.
Рисунок 2. Легко заметить проявление золотого сечения Фибоначчи в природе на фото скелета кисти руки.Человек обладает 2-мя руками и 10-ю пальцами на них, состоящих из 3-х фаланг (без учёта большого пальца). Если не принимать в расчёт пальцы с двумя фалангами, то под закон золотого сечения подпадают восемь пальцев. Так получается последовательность Фибоначчи: 2, 3, 5, 8.
Закон Фибоначчи в природе человеческих лёгких
В результате специального исследования, проведённого учёными Б.Д. Уэстом и А.Л. Гольдбергером, было обнаружено – общее устройство лёгких человека формируется по золотому сечению. Бронхи, являющиеся неотъемлемой частью человеческих лёгких, отличаются асимметричностью, и заключается это в том, что левый дыхательный путь длиньше, чем правый. Подобная асимметрия характерна и для их всевозможных продолжения, в каждом наиболее мягком дыхательном пути, но отношение длин коротких и длинных бронхов при этом составляет 1:1,618.
Многие люди творческих профессий, чья работа связана с изобразительным искусством, составляют свои предварительные зарисовки, применяя мерки с идеального по своей природе человеческого тела. Художники Возрождения творили свои шедевры, заранее взяв мерки геометрических отношений тела, полностью соответствующими золотому числу. Также эти соотношения применялись криминалистами и археологами с целью восстановления по фрагментам тела его полного облика.
Ряд Фибоначчи в природе молекулы ДНК
Она вмещает в себя все самые подробные данные о физиологическом строении живого существа. Это касается флоры и фауны. При этом ДНК в своём строении придерживается золотого сечения. Внешне она представляет конструкцию из двух переплетённых спиралей. Длина их равна 34 ангстремам, а ширина – 21.

 Рисунок 3. В структуре ДНК тоже проявляется ряд Фибоначчи в природе, разные исследовательские работы посвящены этому факту.
Рисунок 3. В структуре ДНК тоже проявляется ряд Фибоначчи в природе, разные исследовательские работы посвящены этому факту.Удивительно здесь то, что 21 и 24 идут подряд в Фибо-последовательности. Отношение размеров получающейся логарифмической спирали, которую представляет собой молекула ДНК, есть 1:1,618.
Живые организмы, независимо от своего ареала обитания — будь то суша, вода, воздух — принципами своего строения подчинены числу фи. Например, человеческая сердечная мышца способна сократиться до 0,618 от своего объёма. Пропорции улиточной раковины выстроены в соответствии с пропорцией Фибоначчи. При желании исследования природных объектов и процессов подобных примеров возможно отыскать очень много. Последовательности Фибоначчи проникли во все сферы и понятия природы, они поистине вездесущи, и изредка кажется, что только они и в состоянии объяснить строение Вселенной.
Спираль Фибоначчи – загадка природы (фото)
Математические науки не знают второй формы, способной сравниться своими свойствами со спиралью, получившей свои оригинальные свойства благодаря положенному в базис структуры Золотое сечение. Напомним, что формула имеет следующий вид: ( a + b )/ a = a / b.
Известный золотой прямоугольник приобрёл своё название именно в честь того, что он обладает как раз таким соотношением сторон — отношение его длинных сторон к меньшим равно 1,168:1.

 Рисунок 4. Спираль Фибоначчи проявляется в природе – это загадка последовательности чисел знаменитого ряда Фибоначчи.
Рисунок 4. Спираль Фибоначчи проявляется в природе – это загадка последовательности чисел знаменитого ряда Фибоначчи.Одним из необыкновенных свойств золотого прямоугольника является то, что если от такой фигуры отделить квадрат, с большей стороной равной длине малой стороны прямоугольника, в результате будет получен ещё один золотой прямоугольник, но меньший по площади.
Причём эту операцию можно повторять постоянно, и каждый раз её итогом будет получение золотого прямоугольника ещё меньшего размера. Интересно, что расположение этих прямоугольников будет соответствовать логарифмической спирали, играющей ключевую роль в математических моделях объектов, которые вполне реально обнаружить в природе.
Обычно спиральную структуру наблюдают в закономерности позиций семян подсолнечника, структуре лепестков некоторых видов цветов, в необычной геометрии ракушек.
У подавляющего большинства улиток раковина обладает именно спиралевидной формой. Поскольку эти существа не обладают разумом, они не могут владеть элементарными математическими знаниями, достаточными для создания собственной раковины подобной формы. Многие учёные не могут точно определить причину, по которой эти моллюски сумели выбрать такую необычную форму существования.
Ясно здесь только, что подобное развитие не может считаться случайным стечением обстоятельств, и сама по себе подобная гипотеза будет выглядеть глупо. Это явно осознанное творение.
Спирали легко обнаружить и в теле человека — к такому примеру можно отнести человеческое ухо, внутренне ухо которого так же включает в себя орган, известный как «Улитка», предназначенный для превращения звуковой вибрации в нейронные сигналы. Схожая с костью, эта структура внутри заполнена жидкостью и внешне напоминает улитку, традиционно соответствующую золотым пропорциям.
Спирали также можно найти на ладонях и пальцах человека, элементарно сняв отпечатки.
В животном мире встретить огромное количество спиралевидных форм можно буквально повсюду — закрученные рога и бивни некоторых видов животных, когти и клювы некоторых видов птиц.
Форму спирали принимает и ураган, и лучше всего это можно наблюдать на снимках, сделанных орбитальной космической станцией, глядя, как скручиваются облака циклона.
В волнах, закручивающихся на морской или океанской глади, ясно виден математический график золотого сечения Фибоначчи в природе со значениями 1, 1, 2, 3, 5, 8, 13, 21, 34 и 55. Не стоит так же забывать о водоворотах, или, по крайней мере, о воде, сливающейся в раковине в водосточную трубу.

 Рисунок 5. Загадки спирали Фибоначчи в природе до сих пор не разгаданы.
Рисунок 5. Загадки спирали Фибоначчи в природе до сих пор не разгаданы.К слову, золотое сечение угадывается даже в форме галактики.
Спираль заслуженно носит звание «Кривой жизни», ведь её причудливая форма имеет место и угадывается во многих областях. Это настоящий символ эволюции, ибо нет такого объекта, чьё развитие не двигалось бы по спирали.
И лишнее тому подтверждение — существование Золотого прямоугольника, что при разбиении на более мелкие прямоугольники в соответствии с последовательностью Фибоначчи с последующим разделением их в идентичной пропорции и далее, будет получена система под говорящим названием спираль Фибоначчи.
Что такое Числа Фибоначчи — Узнай Что Такое
Числа Фибоначчи — это последовательность чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, … Следующее число можно посчитать, сложив два числа перед ним.
Т. е. 0 + 1 = 1; 1 + 1 = 2, 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8; …
Более формальное определение ряда Фибоначчи можно показать следующим равенством:
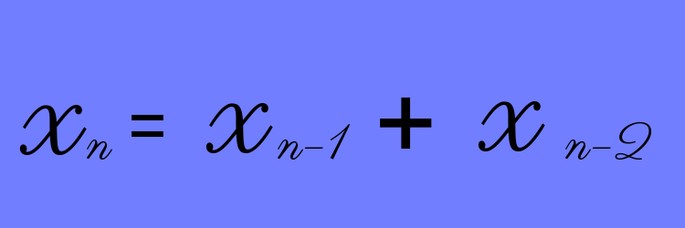
Более длинный список последовательности чисел Фибоначчи:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811,…
Запомнить его довольно просто: нужно только помнить, что первые два числа — это 0 и 1, и начать складывать. И за этим занятием можно просидеть сутками.
«Золотое число» или «Золотое сечение»
Если разделить два последовательных числа друг на друга (например 55 разделить на 34), всегда получится приблизительно 1,618 (обозначается как Φ = 1,618, читается как «фи», это буква греческого алфавита).
1,618 называется «Золотое число» или «Золотое сечение«.
55 / 34 = 1,6176
89 / 55 = 1,61818
377 / 233 = 1,618
Использование золотого сечения для вычисления чисел Фибоначчи
Можно вычислить любое число Фибоначчи, используя золотое сечение следующими способами
Формулой
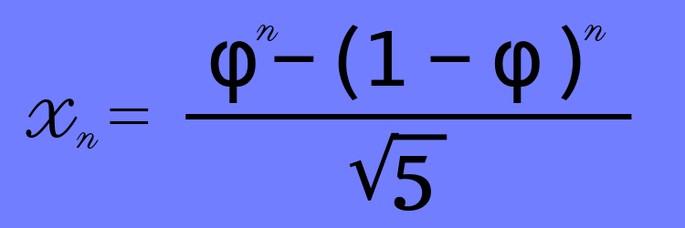
Например, можно попробовать посчитать для n = 10 (внимание, это будет одиннадцатое число в ряду!)
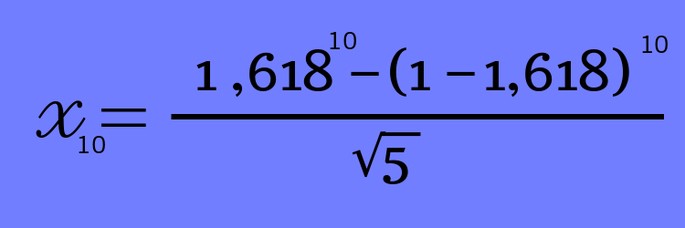
Получился такой ответ:

Умножением предыдущего числа на золотое сечение
Этот способ работает для чисел выше 1. Можно рассчитать число Фибоначчи, умножив предыдущее число на золотое сечение (1,618), а затем округлив полученный результат.
Например:
13 x 1,618 = 21,034 ≈ 21
55 x 1,618 = 88,99 ≈ 89
377 x 1,618 = 609,986 ≈ 610
Золотая спираль Фибоначчи
Это спираль, которая выглядит следующим образом:
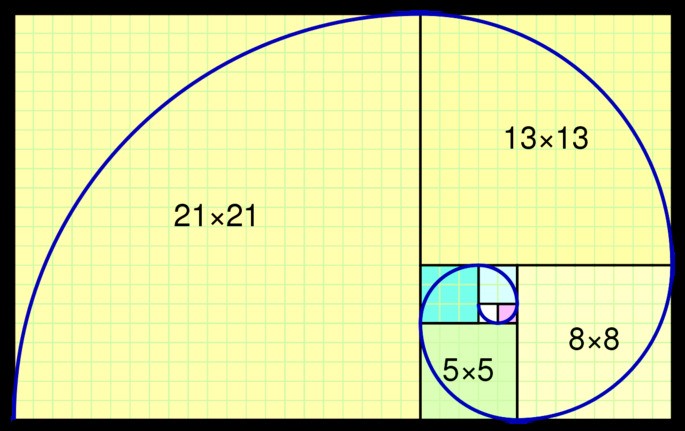 Числа Фибоначчи — последовательность чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
Числа Фибоначчи — последовательность чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …Как можно видеть на изображении, тут представлен числовой ряд Фибоначчи как спираль. Она начинается в центре с двух квадратов 1×1, за ними следуют квадраты 2×2, 3×3, 5×5 и так далее.
Числа Фибоначчи в природе
 Фотография «Алоэ многолистное» (Aloe polyphylla), на фото можно увидеть спираль Фибоначчи в природе.
Фотография «Алоэ многолистное» (Aloe polyphylla), на фото можно увидеть спираль Фибоначчи в природе.  «Спираль ракушки», фотограф Muffett68 Heidi; ещё один пример спирали Фибоначчи в природе.
«Спираль ракушки», фотограф Muffett68 Heidi; ещё один пример спирали Фибоначчи в природе.В этом видео «ЧИСЛА ФИБОНАЧЧИ УДИВИТЕЛЬНАЯ ЗАКОНОМЕРНОСТЬ» ещё больше примеров чисел Фибоначчи в природе и в мире вокруг нас.
Числа Фибоначчи в архитектуре
В строениях древней архитектуры мы зачастую можем ощущать некую гармонию пропорций. И это неслучайно, ведь на протяжении многих веков архитекторы пользуются этим магическим числом золотого сечения. Число 1,618 можно заметить и в творчестве средневековья, и в современных произведениях архитектурного искусства.
 Здание SOMISA в Буэнос-Айресе, Аргентина; архитектор Марио Роберто Альварес, окончание строительства 1977 г.
Здание SOMISA в Буэнос-Айресе, Аргентина; архитектор Марио Роберто Альварес, окончание строительства 1977 г.Пример использования золотого числа в древней архитектуре:
 Пантеон в Париже
Пантеон в ПарижеЛюбопытные факты
Давайте ещё раз посмотрим на последовательность чисел Фибоначчи:
n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
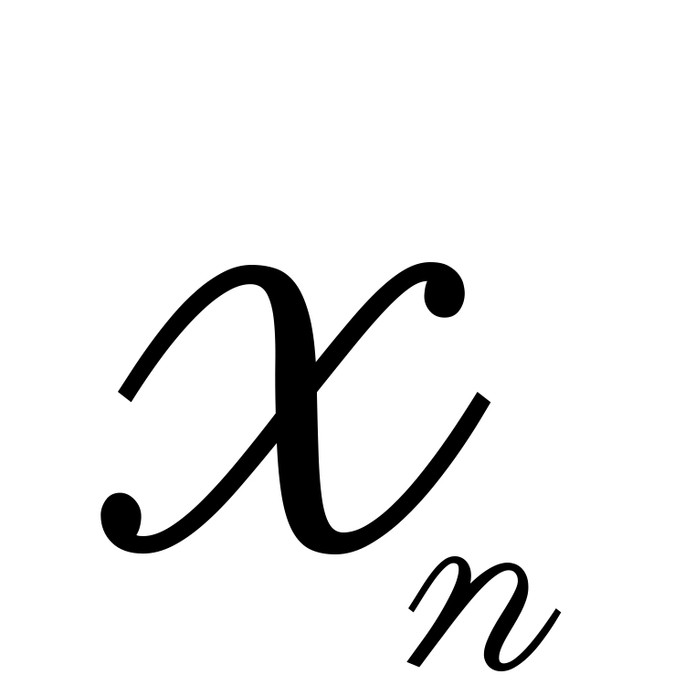 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | 987 | 1597 |
Каждое n-е число кратно 
Если внимательно посмотреть на цифры, можно рассмотреть удивительную закономерность:
- посмотрите на
 , а потом взгляните на последующие элементы: 6-ой, 9-ый, 12-ый… Каждый третий элемент делится на 2!
, а потом взгляните на последующие элементы: 6-ой, 9-ый, 12-ый… Каждый третий элемент делится на 2! - посмотрите на
 , а потом взгляните на последующие элементы: 8-ой, 12-ый, 16-ый… Каждый четвёртый элемент делится на 3!
, а потом взгляните на последующие элементы: 8-ой, 12-ый, 16-ый… Каждый четвёртый элемент делится на 3! - посмотрите на
 , а потом взгляните на последующие элементы: 10-ый, 15-ый… Каждый пятый элемент делится на 5!
, а потом взгляните на последующие элементы: 10-ый, 15-ый… Каждый пятый элемент делится на 5!
Первые 6 цифр Фибоначчи — 1/89
Если посчитать на калькуляторе 1 : 89 будет ответ 0,011235955… Заметили, что первые 6 цифр после запятой — ряд Фибоначчи?
День Фибоначчи 23/11
День Фибоначчи — 23 ноября (11/23; в американском формате дат месяц идёт первым, а день вторым), так как в нём присутствуют цифры «1, 1, 2, 3», которые являются частью последовательности. 23 ноября можно всех поздравлять с Днём Фибоначчи!
Смотрите также значения Числа Пи и Экспоненты.
Последовательность Фибоначчи — Числа Фибоначчи элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух предыдущих чисел. Название по… … Википедия
ФИБОНАЧЧИ — (Fibonacci) Леонардо (ок. 1170 ок. 1240), итальянский математик. Автор «Liber Abaci» (ок. 1200), первого западноевропейского труда, в котором предлагалось принять арабскую (индийскую) систему написания цифр. Разработал математическую… … Научно-технический энциклопедический словарь
Фибоначчи — (Fibonacci) Фибоначчи первый крупный математик средневековой Европы Десятичная система счисления, арабские цифры, числа, последовательность, уровни, ряд, линии и спираль Фибоначчи Содержание >>>>>>>>> … Энциклопедия инвестора
Фибоначчи числа — Числа Фибоначчи элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух предыдущих чисел. Название по… … Википедия
Последовательность Падована — Последовательность Падована это целочисленная последовательность P(n) с начальными значениями и линейным рекуррентным соотношением Первые значения P(n) таковы 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265 … Википедия
Фибоначчи — Леонардо Пизанский Leonardo Pisano Дата рождения: ок. 1170 года … Википедия
Фибоначчи числа — элементы числовой возвратной последовательности (См. Возвратная последовательность) 1, 1, 2, 3, 5, 8,… (ряда Фибоначчи), в которых каждый последующий член равен сумме двух предыдущих. Название по имени средневекового математика Леонардо … Большая советская энциклопедия
ФИБОНАЧЧИ МЕТОД — разновидность одномерного поиска экстремума функции путем последовательного сужения интервала неопределенности. Единственное ограничение, налагаемое на исследуемую функцию требование строгой унимодальности на заданном интервале. При… … Математическая энциклопедия
Последовательность Люка — Не следует путать с числами Люка. В математике, последовательностями Люка называют семейство пар линейных рекуррентных последовательностей второго порядка, впервые рассмотренных Эдуардом Люка. Последовательности Люка представляют собой пары… … Википедия
Последовательность — одно из основных понятий математики. П. образуется из элементов любой природы, занумерованных натуральными числами 1, 2,…, n,…, и записывается в виде x1, x2, …, xn, … или коротко, {xn}. Элементы, из которых составляется П., называются … Большая советская энциклопедия

Во многих классических учебниках по трейдингу часто упоминается постулат о неизменности рыночных колебаний, что позволяет нам и сегодня применять стратегии прошлого века. Подобное утверждение справедливо для долгосрочной и среднесрочной торговли. На уровне дейтрейдинга тренды с откатами все чаще заменяются стремительными импульсами.
Жизнь не стоит на месте: меняются люди, меняются технологии, меняются рынки. Трейдеры, пожалуй, больше представителей других профессий чувствуют и замечают эти изменения, причем одними из первых. И для прибыльной торговли на финансовых рынках должны всегда быть во всеоружии. Сегодня в нашем материале разберем вариацию на известный инструмент Фибоначчи в новых реалиях рынка, посмотрим, что это может дать нам, валютным спекулянтам.

Трансформация классических движений внутри дня происходит с первого дня развития электронной торговли. Каждое новое десятилетие XXI века приносит существенный прирост в скорости передачи данных и производительности процессоров.
На рынке форекс становится все больше скальперов, роботов, VPS-серверов; ордера выводятся и отменяются за миллисекунды. Миллиарды долларов ликвидности перемещаются между счетами участников рынка за считанные секунды.
Импульсные взлеты котировок валютных пар внутри дня – результат подобных быстрых перетоков ликвидности и робототорговли. Чтобы подстроиться под новую парадигму интрадея, приходится перестраивать инструменты теханализа, используя неоклассический подход.
Уровни Фибоначчи – наша первая попытка адаптации канонических теорий, обоснованная математически по тем же принципам, что и поиск первых линий коррекции.
Классическая теория Фибоначчи на рынке Форекс

На первой стадии обучения трейдингу при построении линий сопротивления и поддержки почти каждый из нас познакомился с уровнями Фибоначчи. Это одна из самых популярных тем на Форекс: только на нашем сайте можно найти более пяти статей и множество упоминаний, достаточно набрать в поисковике соответствующий тег.
Уровни Фибоначчи были обнаружены создателем волновой теории, финансистом Ральфом Нельсоном Эллиоттом, и использованы как константы коррекции тренда для обнаружения дна или вершины волн. Найденные коэффициенты оказались универсальны для определения продолжения тренда, каналов, кругов, кластеров и даже временных зон.
Эффективность уровней Фибоначчи доказана временем, они доступны в стандартном пакете любой торговой платформы. Аналитики используют этот ряд стандартных процентных значений для построения уровней поддержки и сопротивления, теоретики и практики трейдинга основывают на них стратегии и торговые системы.
Несмотря на множество вариантов применения (инверсии, зеркальные проекции и т. д.), десятки лет используется один и тот же ряд стандартных значений:
- 23,6 (этого уровня не было в классической теории Эллиотта)
- 38,2
- 50,0 (уровень придуман Эллиоттом)
- 61,8
- 76,4 (уровня не было в классической теории Эллиотта).
Вышеперечисленные уровни, кроме 50%, являются результатом математических вычислений, полученных путем деления чисел последовательности, найденной Фибоначчи в книгах математиков древней Индии еще в средние века. Обнаруженные коэффициенты – это константы пропорций многих геометрических и природных тел окружающего нас мира.
Этот факт объяснил использование основателем волновой теории результатов деления чисел в виде относительных процентных соотношений для определения дна или вершин волн. Уровни Фибоначчи можно считать следствием теории волнового движения, доказанной самой природой и математикой. Вершины и впадины волн делают эти уровни сопротивлениями и поддержками в трендовых движениях.
Как открыть новый уровень Фибоначчи?

Уникальное свойство чисел Фибоначчи состоит в том, что при делении друг на друга они дают постоянный одинаковый результат, поэтому найти новые уровни невозможно без математических преобразований.
В поиске новых значений обратимся к ряду Фарея, который открыл последовательность положительных несократимых дробей, где знаменатель всегда будет равен числу, на единицу большему, чем номер последовательности:

При последовательности n=8 знаменатель дроби никогда не будет превышать цифру 8, и т. д. Теорема и последовательность Фарея дает много интересных математических свойств, в частности, одним из них является наличие в ней чисел Фибоначчи.
Если в представленных рядах на картинке выше провести математическую операцию сложения, то можно свести их к следующему виду:

В результате получается ряд дробей бесконечной длины, где четко прослеживаются числа Фибоначчи:

В математике он получил название последовательности Фибоначчи — Фарея. Ее числа можно записать в другом виде:
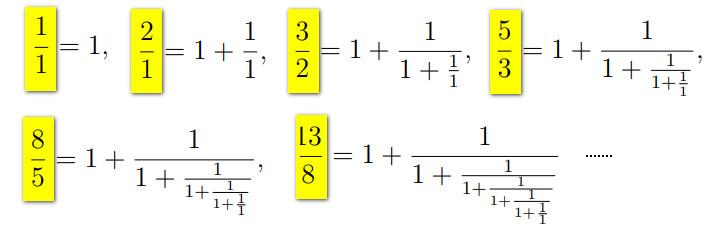
Математик Александр Вейц преобразовал этот ряд дробей в змеевидную форму последовательности Фибоначчи:

Перекрестное деление числителя предыдущей дроби на знаменатель последующей, исключая первый член, дает уровень 0,145. Во второй части убывающей змеевидной последовательности делением знаменателя предыдущей дроби на числитель следующей за ней дроби получаем уровень 68.
Уровни змеевидной последовательности Фибоначчи на рынке Форекс

Змеевидная последовательность Фибоначчи имеет всего два уровня, расположенных близко к минимумам/максимумам – 14,5% и более дальний 68%. С точки зрения технического анализа они наполнены почти тем же смыслом, что и пять стандартных линий:
- 14,5% – линия разворота или подтверждения продолжения тренда;
- 68% – линия завершения тренда.
Близкое расположение первой линии к экстремумам оправдано стремительным развитием валютных трендов, которые не успевают откатиться к старым уровням 23.6%, 38.2% и ниже. В большинстве случаев касание этих линий происходит при развороте или во флэте, заставляя трейдера пропускать большую часть направленного движения.
Кстати, самого близкого уровня 23,6% не существует в классической теории Эллиотта, он был добавлен позже по тем же соображениям, которые заставили нас искать неоклассическое толкование последовательности Фибоначчи.
Проблема отдаленности от максимума начинает проявляться негативным образом при продолжительном тренде. На рисунке ниже рассмотрен пример трехдневного роста котировок EURUSD. На часовом графике видно, что старая теория не дает войти трейдеру уже на третьем обновлении максимума, и он пропускает импульс на третий день.
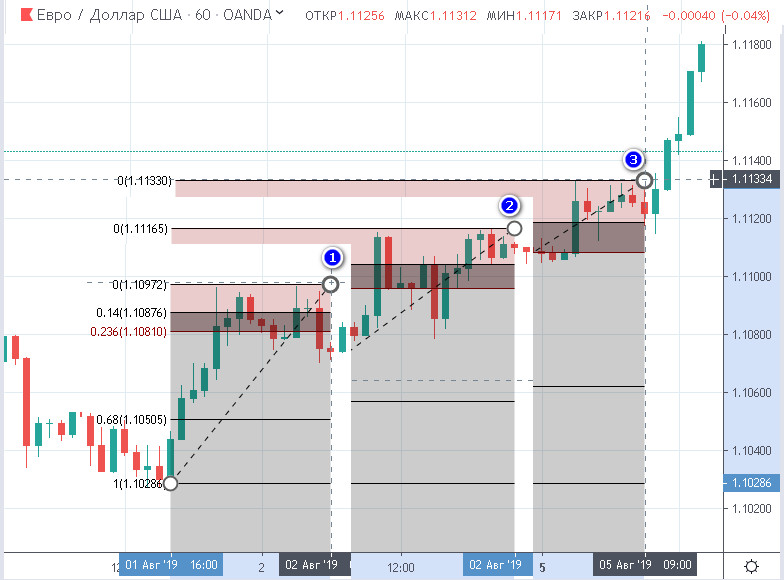
Один из подтверждающих сигналов продолжения тренда – это его переход из интрадея в среднесрочный вид, но именно в этот момент уровни перестают работать. Учитывая факт использования уровней 61,8 и 68 для размещения стоп-лосса, можно отметить, что дополнительные несколько процентов в этом случае спасают трейдера от лишних стопов благодаря использованию стратегии торговли по змеевидной последовательности Фибоначчи на Форекс, но только внутри дня.
Стратегия торговли по уровням змеевидной последовательности Фибоначчи на рынке Форекс

Уровни Фибоначчи обладают уникальным свойством подстраиваться под волатильность рынка, расширяясь или отдаляясь от текущей цены с увеличением диапазона колебаний. Внутридневная стратегия по неоклассическим линиям змеевидной последовательности берет за точку отсчета тренда начало дня, пропуская три первые свечи.
В это время открываются основные азиатские рынки, но волатильность на многих парах остается низкой, что позволяет совершить вход при минимальных затратах (стопах).
В 70% случаев азиатская сессия или следующий за ней европейский отрезок определяют общий тренд, самая высокая волатильность торгов приходится на конец дня. Это означает, что сигналы смены тренда – выбивание стопов на уровне 68% – будут выпадать на первую половину дня при минимальном расширении уровней, а значит, и убытка.
Характеристики стратегии
Платформа: MetaTrader 4
Валютные пары: любые, не содержащие AUD, NZD, JPY
Таймфрейм: h2
Время торговли: 3-00 – 21-00 МСК
Рекомендуемые брокеры: Alpari, RoboForex, AMarkets
Установка индикатора и настройка уровней змеевидной последовательности Фибоначчи
В торговой платформе Metatrader инструментам Фибоначчи отведен целый раздел, который открывается так: подменю «Вставка», опция «Линии».
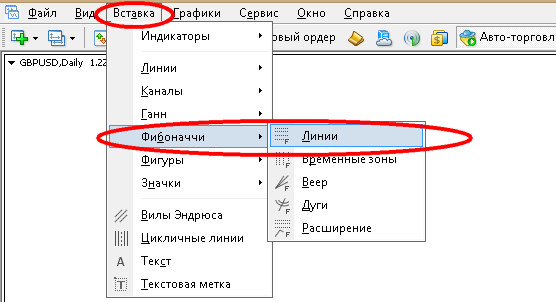
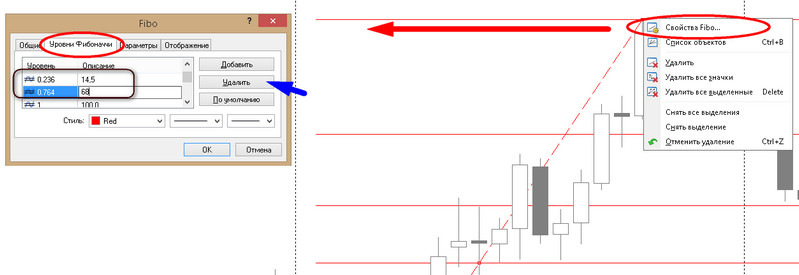
Чтобы изменить стандартные значения на пользовательские 14,5 и 68, надо растянуть уровни в любой точке графика, кликнув затем по ним правой клавишей мыши. Трейдеру откроется дополнительное меню, где через пункт «Свойства Fibo» можно вызвать окно настроек индикатора.
За отображение уровней отвечает вкладка с соответствующим названием, кликнув два раза в ячейках с цифрами, меняем их значения на 14,5 и 68, лишние убираем функцией «Удалить» (числа 23,6; 38,2; 50; 61,8; 76,4).
Что такое числа Фибоначчи и уровни Фибоначчи
olegas5 лет ago / 54 Views
Последовательность Фибоначчи это набор чисел (и проистекающих из них пропорций), который постоянно встречается в окружающей нас природе. Открытие этого явления приписывают математику 13-го века, Леонардо Фибоначчи.

В данной последовательности каждый член равен сумме двух предыдущих:
N(i)=N(i-1)+N(i-2)
Используя эту формулу, и предполагая, что первые две цифры ноль и единица, можно вычислить первые десять чисел последовательности следующим образом:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 2
2 + 1 = 3
3 + 2 = 5
5 + 3 = 8
8 + 5 = 13
13 + 8 = 21
21 + 13 = 34
Таким образом, первые десять чисел в последовательности Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34.
Количество лепестков на цветах часто совпадает с числами Фибоначчи, особенно 3, 5 и 8. Некоторые ромашки имеют 13 и 21 лепестков.
Коэффициенты Фибоначчи
Из последовательности Фибоначчи выводится ряд коэффициентов имеющих особое значение для трейдеров.
Наиболее важным коэффициентом является отношение очередного члена последовательности к следующему члену. Это соотношение практически одинаково для любых двух последовательно идущих членов и стремится к величине 0,618 или 61,8%. Это соотношение называют «золотой серединой» или «золотым сечением». Золотое сечение также имеет широкое распространение в природе, в частности пропорции человеческого тела, очень близки к нему. В трейдинге значение 61,8% является наиболее надежным уровнем прогнозирования отката. Например:
8 разделить на 13 = 0,615 = 61,5%
13 разделить на 21 = 0,619 = 61,9%
21 разделить на 34 = 0.617 = 61,7%
Два других коэффициента Фибоначчи часто используемые трейдерами это 38,2% и 23,6%. Эти два коэффициента считаются менее надежными, но также применяются в техническом анализе.
Отношение 38,2% получают путем деления любого члена последовательности на число стоящее через один разряд вправо. Например:
8 делится на 21 = 0,380 = 38,0%
144 делится на 377 = 0,381 = 38,1%
6765 делится на 17 716 = 0,381 = 38,1%
Аналогичным образом, отношение 23,6% получается делением любого члена последовательности на число через два разряда вправо:
5 делится на 21 = 0,238 = 23,8%
34 разделить на 144 = 0,236 = 23,6%
6765 делится на 28 667 = 0,235 = 23,5%
 |
| Кликните по рисунку для увеличения |
Практическое использование в трейдинге
Многие трейдеры уверены в том, что ценовое движение действительно подчиняется определённым ритмам и законам задаваемым последовательностью чисел и коэффициентов Фибоначчи, но есть и не мало противников данной теории.
Уверенность сторонников теории Фибонначи базируется на том, что рынок, являясь, по сути, одним из продуктов человеческой деятельности (а следовательно имеет прямую зависимость от природы человека), также подчиняется тем глобальным законам, которые характерны для природы в целом.
Считается, что первым кто обратил внимание на зависимость циклов ценовых движений от коэффициентов Фибоначчи, был американец Ральф Эллиот (создавший впоследствии на их основе теорию названную его именем). Он исследовал множество ценовых графиков за различные периоды времени и пришёл к выводу о том, что движение цены происходит волнообразно, при этом существуют волны большего и меньшего порядков отличающиеся друг от друга в пропорциях вытекающих из чисел последовательности Фибоначчи.
Заметьте, что Ральф Эллиот проводил свои исследования в 30-х годах прошлого века, когда не о каких компьютерах не было и речи. Каждый график требовалось отрисовывать и анализировать вручную. С развитием же современной компьютерной техники, возможность анализировать множество ценовых графиков на самых разных временных промежутках появилась у каждого трейдера имеющего в своём распоряжении мало-мальски приличный торговый терминал (например, тот же самый МТ4).
Числа, уровни и коэффициенты Фибоначчи на ценовых графиках
Давайте рассмотрим весь арсенал инструментов технического анализа основанных на применении чисел последовательности Фибоначчи. Ввиду большой популярности у трейдеров, все эти инструменты нашли своё отражение в современных торговых терминалах. Я покажу вам их на примере одного из самых распространённых терминалов — Мetatrader4 (МТ4).
Здесь их можно найти в меню «Insert» («Вставка») в разделе «Fibonacci»:

А кроме этого, здесь есть ещё и канальный индикатор на основе этих чисел. Его можно найти в разделе «Channels»:

Линии (Retracement)
Для построения на ценовом графике линий Фибоначчи вам нужно найти две базовые точки являющие собой два важных экстремума (в идеале — большой волны тренда). Соединив эти точки между собой вы получите шесть уровней от 0 до 100%.

Крайние из этих уровней (0% и 100%) будут соответствовать тем точкам, которые были выбраны в качестве базовых. А остальные четыре уровня: 23.6%, 38.2%, 50%, 61.8% будут показывать вероятные места разворотов и пределы откатов ценового движения.
Подробности построения и детали использования линий Фибоначчи изложены в материале: «Линии Фибоначчи. Построение, настройка и пример использования»
Временные зоны (Time Zones)
Точки разворота цены на графиках имеют две координаты. Одна из этих координат лежит на вертикальной оси (цены) и определяется горизонтальными уровнями на графике. Другая из координат находится на горизонтальной шкале времени. Временные зоны Фибоначчи как раз используются для того, чтобы определить эти самые вторые координаты важных разворотных точек на ценовом графике.
Для построения временных зон достаточно также выбрать два важных ценовых экстремума на графике.

Обратите внимание на то, как точно построенные временные зоны указывают на важные разворотные моменты графика. Более подробную информацию ищите здесь: «Временные зоны Фибоначчи. Как их установить и как правильно использовать»
Веер (Fan)
Также как и при построении вышеописанных инструментов, для того чтобы отобразить веер Фибоначчи на ценовом графике необходимо выбрать две базовые точки (например в виде экстремумов очередной волны тренда).

После этого на графике построится веер с вершиной в первой точке и тремя лучами соответствующими коэффициентам 38.2, 50.0, 60.8.
Как видите, последующие разворотные точки довольно точно накладываются на лучи построенного веера. Более подробно о веере вы можете прочитать здесь: «Веер Фибоначчи. Как установить, настроить и правильно использовать»
Дуги (Arcs)
Дуги также строятся на основе двух базовых точек, и таким же образом показывают наиболее вероятные границы на которых будут происходить развороты цены. Визуально они представляют собой три эллипса построенные по коэффициентам 38.2, 50.0, 60.8

О дугах читайте здесь: “Дуги Фибоначчи. Правильные настройка и использование“
Расширение (Expansion)
Для построения расширений Фибоначчи требуется уже не две, а три базовых точки. А в остальном они очень схожи с линиями Фибоначчи описанными выше. Базовые точки выбираются на экстремумах очередной волны тренда.

На восходящем тренде (как на рисунке выше) первая точка ставится на минимуме волны, вторая — на максимуме, а третья — на следующем минимуме (находящемся выше предыдущего). В случае нисходящего тренда первую точку ставим на максимуме волны, вторую – на следующем за ним минимуме и третью — на новом максимуме (который находится ниже предыдущего).
Как видно из представленного рисунка и здесь тоже развороты цены достаточно часто совпадают с уровнями заданными расширениями. Подробности по этому инструменту можно найти здесь: «Расширение Фибоначчи. Установка, настройка и использование»
Что такое последовательность Фибоначчи?
Давайте играть в игру! Мы покажем вам серию цифр, и мы хотим, чтобы вы увидели, можете ли вы найти шаблон. Готов? Вот и мы:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…
Вы видите шаблон? Каким будет следующий номер?
Если вы думаете, что следующий номер 89, вы правы! Вы только что решили модель под названием Последовательность Фибоначчи!
В чем прикол последовательности Фибоначчи? Чтобы найти следующий номер в последовательности, просто добавьте два предыдущих номера! Вот как это выглядит:
0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
… и так далее! Последовательность Фибоначчи никогда не заканчивается!
Название «Последовательность Фибоначчи» пришло от итальянского математика. Его звали Леонардо Фибоначчи, и он путешествовал по миру в начале тринадцатого века. Во время своих путешествий Фибоначчи узнал о том, как другие страны занимались математикой. Его очень интересовало, как люди делали математику в Индии и на Ближнем Востоке.
Когда он вернулся в Италию, Фибоначчи написал книгу под названием Liber Abaci . Эта книга была обо всей математике, которую Фибоначчи узнал во время своих путешествий! Liber Abaci — это место, где современные математики нашли последовательность Фибоначчи.Однако индийские математики знали о закономерностях за столетия до того, как Фибоначчи написал об этом в своей книге!
Вы, вероятно, задаетесь вопросом, почему последовательность Фибоначчи все еще имеет значение сегодня. Это может быть древним, но этот специальный образец все еще полезен! Иногда мы используем Последовательность Фибоначчи, чтобы делать предсказания. Люди, которые работают в торговле, используют его для прогнозирования изменений на фондовом рынке. Это помогает нам знать, чего ожидать в экономике! В природе мы можем использовать последовательность Фибоначчи, чтобы предсказать, сколько медоносных пчел живет в улье.Ботаники даже используют его, чтобы предсказать, сколько лепестков вырастет на цветке!
В следующий раз, когда вы будете на пляже, присмотритесь к раковине! Спиральные формы некоторых ракушек соответствуют последовательности Фибоначчи. Математики называют модель «Золотой спиралью» и повторяют ее, рисуя серию связанных квадратов, чьи области соответствуют числам из последовательности Фибоначчи. Ракушки — единственное место, где Золотая Спираль проявляется в природе. Вы можете также видеть это в образце семян на подсолнечнике, расположении семенных коробочек на сосновой шишке и даже в форме галактик.
Оглянись вокруг! Можете ли вы найти другие примеры последовательности Фибоначчи или Золотой спирали? Если вы посмотрите достаточно внимательно, вы можете просто открыть для себя новую модель.
,Что такое серия Фибоначчи? — Gifographic
Если вы читали книгу «Код Да Винчи», то вы уже знаете о последовательности Фибоначчи. Эта интригующая последовательность чисел является неотъемлемой частью так называемого «золотого сечения», которое называется отношением, в котором происходят многие природные явления. Будь то разветвление дерева или скопление звезд, золотое сечение можно наблюдать в большинстве естественных явлений. Итак, давайте узнаем еще немного об этой таинственной серии чисел.
Что такое последовательность Фибоначчи?
Последовательность Фибоначчи представляет собой последовательность чисел, начиная с 0, где каждое число является суммой двух предшествующих ему чисел. Таким образом, последовательность идет 0,1, 2, 3, 5, 8, 13, 21, 34 и так далее. Математическое уравнение, которое представляет эту последовательность: xn = xn-1 + xn-2.
Кто изобрел последовательность Фибоначчи?
Последовательность названа в честь Фибоначчи, итальянского математика, также известного как Леонардо Пизанский или Леонардо Пизано.Он был человеком, который много путешествовал и торговал. Поскольку знание математики было важно для трейдеров, его интерес культивируется в его юности. Числа Фибоначчи были впервые представлены Западному миру через его книгу «Liber Abaci» в 1202 году. Однако открытие этой последовательности предшествует Фибоначчи; это было обнаружено и описано как «Virahanka» в индийских математических священных писаниях.
Фибоначчи и проблема кроликов
Фибоначчи впервые заметил эту последовательность, когда размышлял над вопросом разведения кроликов.Он размышлял над вопросом: сколько пар кроликов может родиться за год? Сделав определенные предположения, он вывел определенную модель разведения кроликов. Паттерн следовал последовательности Фибоначчи. Если вам интересно, он пришел к выводу, что в конце года было 233 пары кроликов.
Почему Фибоначчи называют Кодексом Природы?
Последовательность Фибоначчи имеет большее значение, чем простой ответ на гипотетические вопросы о разведении кроликов.Эта таинственная последовательность появляется вокруг нас в природе. Лепестки цветка, семена фруктов, ряды семян на подсолнечнике или лепестки сосновых шишек и даже спирали на скорлупе развиваются или складываются в числа Фибоначчи.
Золотое сечение: Phi
Почему, спросите вы? Просто потому, что природа всегда следует за наиболее эффективным способом ведения дел. И именно поэтому числа Фибоначчи также называют кодом природы. Еще одна интересная вещь, которую стоит отметить, это то, что когда вы делите любое число Фибоначчи (скажем, 8), с его предыдущим числом (скажем, 5), результат очень близок к 1.618, который также называется «Фи». Идите вперед, выберите еще несколько чисел из последовательности и попробуйте! Учитывая все прекрасные чудеса природы, созданные в этом соотношении, оно считалось золотым сечением. Считается также, что «Фи» использовался в древней Греции для обозначения соотношения физического совершенства.
Красота природы ориентируется на математику. Разве это не делает математику чуть более интересной, если не много?
 Спираль Фибоначчи, созданная путем рисования линии через квадраты в тайле Фибоначчи; этот использует квадраты размеров 1, 1, 2, 3, 5, 8, 13, 21 и 34; увидеть золотую спираль
Спираль Фибоначчи, созданная путем рисования линии через квадраты в тайле Фибоначчи; этот использует квадраты размеров 1, 1, 2, 3, 5, 8, 13, 21 и 34; увидеть золотую спиральЧисла Фибоначчи представляют собой последовательность чисел в математике имени Леонардо Пизанского, известного как Фибоначчи. В 1202 году Фибоначчи написал книгу « Liber Abaci » («Книга вычислений»), которая ввела числовую модель в западноевропейскую математику, хотя математики в Индии уже знали об этом. [1] [2]
Первое число шаблона — 0, второе число — 1, и каждое число после этого равно суммированию двух чисел непосредственно перед ним. Например, 0 + 1 = 1 и 3 + 5 = 8. Эта последовательность продолжается вечно.
F 0 F 1 F 2 F 3 F 4 F 5 F 6 F 7 F 8 F 9 F 10 F 11 F 12 F 13 F 14 F 15 F 16 F 17 F 18 F 19 F 20 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765
Это можно записать как рекуррентное отношение,
- F N знак равно F N — 1 + F N — 2 {\ displaystyle F_ {n} = F_ {n-1} + F_ {n-2}}
Чтобы это имело смысл, нужно указать как минимум две исходные точки.Вот, F 0 знак равно 0 {\ displaystyle F_ {0} = 0} и F 1 знак равно 1 {\ displaystyle F_ {1} = 1} ,
 Головка подсолнуха с цветочками в спиралях 34 и 55 снаружи
Головка подсолнуха с цветочками в спиралях 34 и 55 снаружиЧисла Фибоначчи связаны с золотым отношением , которое проявляется во многих местах в зданиях и в природе. [3] Некоторыми примерами являются рисунок листьев на стебле, части ананаса, [4] цветение артишока, распускание папоротника и расположение сосновой шишки. [5] Числа Фибоначчи также встречаются в родословной медоносных пчел. [6] [7]
-е число Фибоначчи можно записать в терминах золотого сечения. Это позволяет избежать необходимости использовать рекурсию для вычисления чисел Фибоначчи, что может занять у компьютера много времени.
- F N знак равно φ N — ( 1 — φ ) N 5 {\ displaystyle F_ {n} = {\ frac {\ varphi ^ {n} — (1- \ varphi) ^ {n}} {\ sqrt {5}}}}
Где φ знак равно 1 + 5 2 {\ displaystyle \ varphi = {\ frac {1 + {\ sqrt {5}}} {2}}} Золотое сечение.
- ↑ Пармананд Сингх. «Ачарья Хемачандра и (так называемые) числа Фибоначчи». Математика Издание Siwan, 20 (1): 28-30, 1986. ISSN 0047-6269
- ↑ Пармананд Сингх, «Так называемые числа Фибоначчи в древней и средневековой Индии». Historia Mathematica 12 (3), 229–44, 1985.
- — S. Douady и Y. Couder (1996). «Филлотаксис как динамический самоорганизующийся процесс» (PDF). Журнал теоретической биологии . 178 (178): 255–274. DOI: 10.1006 / jtbi.1996.0026.
- 2 Джонс, Джуди; Уильям Уилсон (2006). «Наука». Неполное образование . Баллантин Книги. п. 544. ISBN 978-0-7394-7582-9 .
- — А. Брюссо (1969). «Статистика Фибоначчи в Хвойных». Фибоначчи Ежеквартально (7): 525–532.
- ↑ «Информатика для удовольствия — cs4fn: Знаки для кода да Винчи: B-». www.cs4fn.org .
- ↑ Скотт Т.С .; Marketos, P. (март 2014), О происхождении последовательности Фибоначчи (PDF), архив истории математики MacTutor, Университет Сент-Эндрюса
- Товары
- Клиенты
- Случаи использования
- Переполнение стека Публичные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимать технический талант
- реклама Связаться с разработчиками по всему миру
 Как открыть хостел | HowToHostel Как открыть хостел …
Как открыть хостел | HowToHostel Как открыть хостел … 
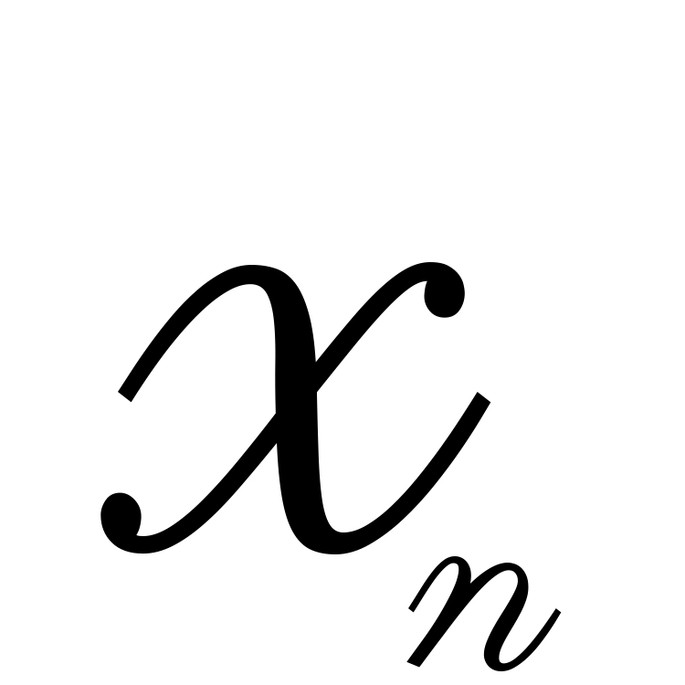
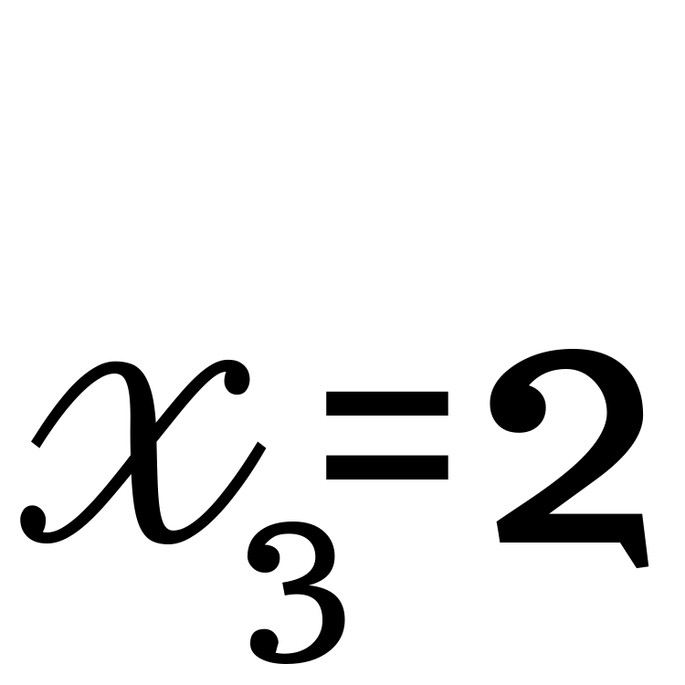 , а потом взгляните на последующие элементы: 6-ой, 9-ый, 12-ый… Каждый третий элемент делится на 2!
, а потом взгляните на последующие элементы: 6-ой, 9-ый, 12-ый… Каждый третий элемент делится на 2!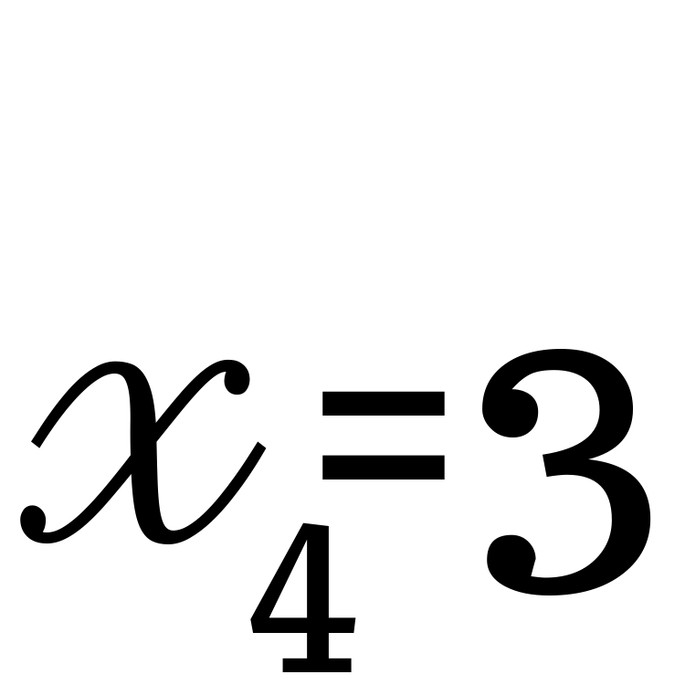 , а потом взгляните на последующие элементы: 8-ой, 12-ый, 16-ый… Каждый четвёртый элемент делится на 3!
, а потом взгляните на последующие элементы: 8-ой, 12-ый, 16-ый… Каждый четвёртый элемент делится на 3!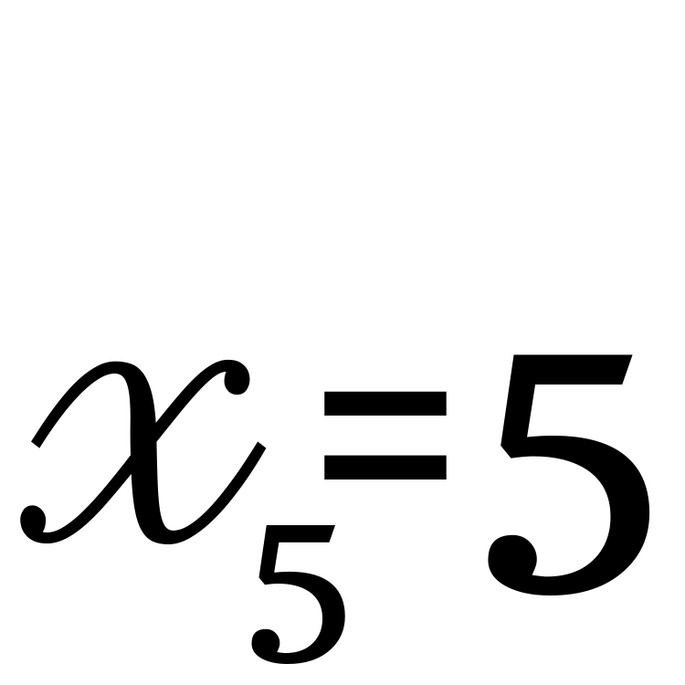 , а потом взгляните на последующие элементы: 10-ый, 15-ый… Каждый пятый элемент делится на 5!
, а потом взгляните на последующие элементы: 10-ый, 15-ый… Каждый пятый элемент делится на 5!