Последовательность фибоначчи что это – Число Бога, числа Фибоначчи, Золотое Сечение

Число Бога, числа Фибоначчи, Золотое Сечение

Первая тысяча знаков значения Φ

1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362

Числа Фибоначчи и золотое сечение составляют основу разгадки окружающего мира, построения его формы и оптимального зрительного восприятия человеком, с помощью которых он может ощущать красоту и гармонию.

Принцип определения размеров золотого сечения лежит в основе совершенства целого мира и его частей в своей структуре и функциях, его проявление можно видеть в природе, искусстве и технике. Учение о золотой пропорции было заложено в результате исследований древними учеными природы чисел.

Свидетельства использования древними мыслителями золотой пропорции приведены в книге Эвклида «Начала», написанной еще в 3 в. до н.э., который применял это правило для построения правильных 5-угольников. У пифагорейцев эта фигура считается священной, поскольку является одновременно симметричной и асимметричной. Пентаграмма символизировала жизнь и здоровье.

Числа Фибоначчи

Знаменитая книга Liber abaci математика из Италии Леонардо Пизанского, который в последующем стал известен, как Фибоначчи, увидела свет в 1202 г. В ней ученый впервые приводит закономерность чисел, в ряду которых каждое число является суммой 2-х предыдущих цифр. Последовательность чисел Фибоначчи заключается в следующем:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 и т.д.

Также ученый привел ряд закономерностей:

Любое число из ряда, разделенное на последующее, будет равно значению, которое стремится к 0,618. Причем первые числа Фибоначчи не дают такого числа, но по мере продвижения от начала последовательности это соотношение будет все более точным.

Если же поделить число из ряда на предыдущее, то результат устремится к 1,618.

Одно число, поделенное на следующее через одно, покажет значение, стремящееся к 0,382.

Применение связи и закономерностей золотого сечения, числа Фибоначчи (0,618) можно найти не только в математике, но и в природе, в истории, в архитектуре и строительстве и во многих других науках.

Для практических целей ограничиваются приблизительным значением Φ = 1,618 или Φ = 1,62. В процентном округлённом значении золотое сечение — это деление какой-либо величины в отношении 62 % и 38 %.

Исторически изначально золотым сечением именовалось деление отрезка АВ точкой С на две части (меньший отрезок АС и больший отрезок ВС), чтобы для длин отрезков было верно AC/BC = BC/AВ. Говоря простыми словами, золотым сечением отрезок рассечён на две неравные части так, что меньшая часть относится к большей, как большая ко всему отрезку. Позже это понятие было распространено на произвольные величины.

Число Φ называется также золотым числом.

Золотое сечение имеет множество замечательных свойств, но, кроме того, ему приписывают и многие вымышленные свойства.

Теперь подробности:

Определение ЗС — это деление отрезка на две части в таком соотношении, при котором большая часть относится к меньшей, как их сумма (весь отрезок) к большей.

То есть, если мы примем весь отрезок c за 1, то отрезок a будет равен 0,618, отрезок b — 0,382. Таким образом, если взять строение, например, храм, построенный по принципу ЗС, то при его высоте скажем 10 метров, высота барабана с куполом будут равны 3,82 см, а высота основания строения будет 6, 18 см. (понятно, что цифры взяты ровными для наглядности)

Далее можно рассчитать высоту двери, окон, креста. И везде будет просматриваться принцип ЗС.

А какова связь между ЗС и числами Фибоначчи?

Числа последовательности Фибоначчи это:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597…

Закономерность чисел в том, что каждое последующее число равно сумме двух предыдущих чисел.

0 + 1 = 1;
1 + 1 = 2;
2 + 3 = 5;
3 + 5 = 8;
5 + 8 = 13;
8 + 13 = 21 и т.д.,

а отношение смежных чисел приближается к отношению ЗС.
Так, 21 : 34 = 0,617, а 34 : 55 = 0,618.

То есть в основе ЗС лежат числа последовательности Фибоначчи.

Считается, что термин «Золотое сечение» ввел Леонардо Да Винчи, который говорил, «пусть никто, не будучи математиком, не дерзнет читать мои труды” и показывал пропорции человеческого тела на своём знаменитом рисунке «Витрувианский человек». “Если мы человеческую фигуру – самое совершенное творение Вселенной – перевяжем поясом и отмерим потом расстояние от пояса до ступней, то эта величина будет относиться к расстоянию от того же пояса до макушки, как весь рост человека к длине от пояса до ступней”.

Ряд чисел Фибоначчи наглядно моделируется (материализуется) в форме спирали.

А в природе спираль ЗС выглядит вот так:

При этом, спираль наблюдается повсеместно (в природе и не только):

— Семена в большинстве растений расположены по спирали
— Паук плетет паутину по спирали
— Спиралью закручивается ураган
— Испуганное стадо северных оленей разбегается по спирали.
— Молекула ДНK закручена двойной спиралью. Молекулу ДНК составляют две вертикально переплетенные спирали длиной 34 ангстрема и шириной 21 ангстрема. Числа 21 и 34 следуют друг за другом в последовательности Фибоначчи.
— Эмбрион развивается в форме спирали
— Спираль «улитки во внутреннем ухе»
— Вода уходит в слив по спирали
— Спиральная динамика показывает развитие личности человека и его ценностей по спирали.
— Ну и конечно, сама Галактика имеет форму спирали

Таким образом можно утверждать, что сама природа построена по принципу Золотого Сечения, оттого эта пропорция гармоничнее воспринимается человеческим глазом. Она не требует «исправления» или дополнения получаемой картинки мира.

Фильм. Число Бога. Неопровержимое доказательство Бога; The number of God. The incontrovertible proof of God.

Золотые пропорции в строении молекулы ДНК

 

Все сведения о физиологических особенностях живых существ хранятся в микроскопической молекуле ДНК, строение которой также содержит в себе закон золотой пропорции. Молекула ДНК состоит из двух вертикально переплетенных между собой спиралей. Длина каждой из этих спиралей составляет 34 ангстрема, ширина 21 ангстрема. (1 ангстрем — одна стомиллионная доля сантиметра).

21 и 34 — это цифры, следующие друг за другом в последовательности чисел Фибоначчи, то есть соотношение длины и ширины логарифмической спирали молекулы ДНК несет в себе формулу золотого сечения 1:1,618

Золотое сечение в строении микромиров

Геометрические фигуры не ограничиваются только лишь треугольником, квадратом, пяти- или шестиугольником. Если соединить эти фигуры различным образом между собой, то мы получим новые трехмерные геометрические фигуры. Примерами этому служат такие фигуры как куб или пирамида. Однако кроме них существуют также другие трехмерные фигуры, с которыми нам не приходилось встречаться в повседневной жизни, и названия которых мы слышим, возможно, впервые. Среди таких трехмерных фигур можно назвать тетраэдр (правильная четырехсторонняя фигура), октаэдр, додекаэдр, икосаэдр и т.п. Додекаэдр состоит из 13-ти пятиугольников, икосаэдр из 20-и треугольников. Математики отмечают, что эти фигуры математически очень легко трансформируются, и трансформация их происходит в соответствии с формулой логарифмической спирали золотого сечения.

В микромире трехмерные логарифмические формы, построенные по золотым пропорциям, распространены повсеместно. К примеру, многие вирусы имеют трехмерную геометрическую форму икосаэдра. Пожалуй, самый известный из таких вирусов — вирус Adeno. Белковая оболочка вируса Адено формируется из 252 единиц белковых клеток, расположенных в определенной последовательности. В каждом углу икосаэдра расположены по 12 единиц белковых клеток в форме пятиугольной призмы и из этих углов простираются шипообразные структуры.

Впервые золотое сечение в строении вирусов обнаружили в 1950-хх гг. ученые из Лондонского Биркбекского Колледжа А.Клуг и Д.Каспар. 13 Первым логарифмическую форму явил в себе вирус Polyo. Форма этого вируса оказалась аналогичной с формой вируса Rhino 14.

Возникает вопрос, каким образом вирусы образуют столь сложные трехмерные формы, устройство которых содержит в себе золотое сечение, которые даже нашим человеческим умом сконструировать довольно сложно? Первооткрыватель этих форм вирусов, вирусолог А.Клуг дает такой комментарий:

«Доктор Каспар и я показали, что для сферической оболочки вируса самой оптимальной формой является симметрия типа формы икосаэдра. Такой порядок сводит к минимуму число связующих элементов… Большая часть геодезических полусферических кубов Букминстера Фуллера построены по аналогичному геометрическому принципу. 14 Монтаж таких кубов требует чрезвычайно точной и подробной схемы-разъяснения. Тогда как бессознательные вирусы сами сооружают себе столь сложную оболочку из эластичных, гибких белковых клеточных единиц.»

Комментарий Клюга еще раз напоминает о предельно очевидной истине: в строении даже микроскопического организма, который ученые классифицируют как «самую примитивную форму жизни», в данном случае в вирусе, присутствует четкий замысел и осуществлен разумный проект 16. Этот проект несопоставим по своему совершенству и точности исполнения с самыми передовыми архитектурными проектами, созданными людьми. К примеру проектами, созданными гениальным архитектором Букминстером Фуллером.

Трехмерные модели додекаэдра и икосаэдра присутствуют также и в строении скелетов одноклеточных морских микроорганизмов радиолярий (лучевиков), скелет которых создан из кремнезёма.

Радиолярии формируют свое тело весьма изысканной, необычной красоты. Форма их составляет правильный додекаэдр. Причем из каждого его угла прорастает псевдоудлиннение-конечность и иные необычные формы-наросты.

В качестве примеров микроорганизмов, воплощающих в своем строении эти трехмерные геометрические фигуры, приведем Circigonia Icosahedra с икасаэдральным строе

www.o000o.ru

Последовательность Фибоначчи и принципы Золотого сечения :: SYL.ru

Последовательность Фибоначчи, ставшая известной большинству благодаря фильму и книге «Код да Винчи», это ряд чисел, выведенный итальянским математиком Пизанским Леонардо, более известным под псевдонимом Фибоначчи, в тринадцатом веке. Последователи ученого заметили, что формула, которой подчинен данный ряд цифр, находит свое отображение в окружающем нас мире и перекликается с другими математическими открытиями, тем самым открывая для нас дверь в тайны мироздания. В этой статье мы расскажем, что такое последовательность Фибоначчи, рассмотрим примеры отображения этой закономерности в природе, а также сравним с другими математическими теориями.

Формулировка и определение понятия

Ряд Фибоначчи – это математическая последовательность, каждый элемент которой равен сумме двух предыдущих. Обозначим некой член последовательности как х_n. Таким образом, получим формулу, справедливую для всего ряда: х_n+2=х_n+х_n+1. При этом порядок последовательности будет выглядеть так: 1, 1, 2, 3, 5, 8, 13, 21, 34. Следующим числом будет 55, так как сумма 21 и 34 равна 55. И так далее по такому же принципу.

Примеры в окружающей среде

Если мы посмотрим на растение, в частности, на крону из листьев, то заметим, что они распускаются по спирали. Между соседними листьями образуются углы, которые, в свою очередь, образуют правильную математическую последовательность Фибоначчи. Благодаря этой особенности каждый отдельно взятый листочек, который растет на дереве, получает максимальное количество солнечного света и тепла.

Математическая загадка Фибоначчи

Известный математик представил свою теорию в виде загадки. Звучит она следующим образом. Можно поместить пару кроликов в замкнутое пространство для того, чтобы узнать, какое количество пар кроликов родится в течении одного года. Учитывая природу этих животных, то, что каждый месяц пара способна производить на свет новую пару, а готовность к размножению у них появляется по достижении двух месяцев, в итоге он получил свой знаменитый ряд чисел: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 — где показано количество новых пар кроликов в каждом месяце.

Последовательность Фибоначчи и пропорциональное соотношение

Этот ряд имеет несколько математических нюансов, которые обязательно нужно рассмотреть. Он, приближаясь медленнее и медленнее (асимптотически), стремится к некоему пропорциональному соотношению. Но оно иррациональное. Другими словами, представляет собой число с непредсказуемой и бесконечной последовательностью десятичных чисел в дробной части. Например, соотношение любого элемента ряда варьируется около цифры 1,618, то превосходя, то достигая его. Следующее по аналогии приближается к 0,618. Что есть обратно пропорциональным к числу 1,618. Если мы поделим элементы через один, то получим 2,618 и 0,382. Как вы уже поняли, они также являются обратно пропорциональными. Полученные числа называются коэффициентами Фибоначчи. А теперь объясним, для чего мы выполняли эти вычисления.

Золотое сечение

Все окружающие нас предметы мы различаем по определенным критериям. Один из них – форма. Какие-то нас привлекают больше, какие-то меньше, а некоторые и вовсе не нравятся. Замечено, что симметричный и пропорциональный объект гораздо легче воспринимается человеком и вызывает чувство гармонии и красоты. Цельный образ всегда включает в себя части различного размера, которые находятся в определенном соотношении друг с другом. Отсюда вытекает ответ на вопрос о том, что называют Золотым сечением. Данное понятие означает совершенство соотношений целого и частей в природе, науке, искусстве и т. д. С математической точки зрения рассмотрим следующий пример. Возьмем отрезок любой длины и разделим его на две части таким образом, чтобы меньшая часть относилась к большей как сумма (длина всего отрезка) к большей. Итак, примем отрезок с за величину один. Его часть а будет равна 0,618, вторая часть b, выходит, равна 0,382. Таким образом, мы соблюдаем условие Золотого сечения. Отношение отрезка c к a равняется 1,618. А отношение частей c и b – 2,618. Получаем уже известные нам коэффициенты Фибоначчи. По такому же принципу строятся золотой треугольник, золотой прямоугольник и золотой кубоид. Стоит также отметить, что пропорциональное соотношение частей тела человека близко к Золотому сечению.

Последовательность Фибоначчи – основа всего?

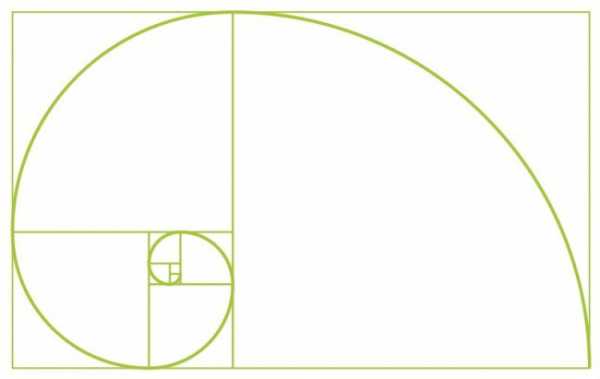
Попробуем объединить теорию Золотого сечения и известного ряда итальянского математика. Начнем с двух квадратов первого размера. Затем сверху добавим еще квадрат второго размера. Подрисуем рядом такую же фигуру с длиной стороны, равной сумме двух предыдущих сторон. Аналогичным образом рисуем квадрат пятого размера. И так можно продолжать до бесконечности, пока не надоест. Главное, чтобы величина стороны каждого последующего квадрата равнялась сумме величин сторон двух предыдущих. Получаем серию многоугольников, длина сторон которых является числами Фибоначчи. Эти фигуры называются прямоугольниками Фибоначчи. Проведем плавную линию через углы наших многоугольников и получим… спираль Архимеда! Увеличение шага данной фигуры, как известно, всегда равномерно. Если включить фантазию, то полученный рисунок можно проассоциировать с раковиной моллюска. Отсюда можем сделать вывод, что последовательность Фибоначи – это основа пропорциональных, гармоничных соотношений элементов в окружающем мире.

Математическая последовательность и мироздание

Если присмотреться, то спираль Архимеда (где-то явно, а где-то завуалированно) и, следовательно, принцип Фибоначчи прослеживаются во многих привычных природных элементах, окружающих человека. Например, все та же раковина моллюска, соцветия обычной брокколи, цветок подсолнечника, шишка хвойного растения и тому подобное. Если заглянем подальше, то увидим последовательность Фибоначчи в бесконечных галактиках. Даже человек, вдохновляясь от природы и перенимая ее формы, создает предметы, в которых прослеживается вышеупомянутый ряд. Тут самое время вспомнить и о Золотом сечении. Наряду с закономерностью Фибоначчи прослеживаются принципы данной теории. Существует версия, что последовательность Фибоначчи — это своего рода проба природы адаптироваться к более совершенной и фундаментальной логарифмической последовательности Золотого сечения, которая практически идентична, но не имеет своего начала и бесконечна. Закономерность природы такова, что она должна иметь свою точку отсчета, от чего отталкиваться для создания чего-то нового. Отношение первых элементов ряда Фибоначчи далеки от принципов Золотого сечения. Однако чем дальше мы его продолжаем, тем больше это несоответствие сглаживается. Для определения последовательности необходимо знать три его элемента, которые идут друг за другом. Для Золотой последовательности же достаточно и двух. Так как она является одновременно арифметической и геометрической прогрессией.

Заключение

Все-таки, исходя из вышесказанного, можно задать вполне логичные вопросы: «Откуда появились эти числа? Кто этот автор устройства всего мира, попытавшийся сделать его идеальным? Было ли всегда все так, как он хотел? Если да, то почему возник сбой? Что будет дальше?» Находя ответ на один вопрос, получаешь следующий. Разгадал его — появляются еще два. Решив их, получаешь еще три. Разобравшись с ними, получишь пять нерешенных. Затем восемь, далее тринадцать, двадцать один, тридцать четыре, пятьдесят пять…

www.syl.ru

ПОСЛЕДОВАТЕЛЬНОСТЬ ФИБОНАЧЧИ — это… Что такое ПОСЛЕДОВАТЕЛЬНОСТЬ ФИБОНАЧЧИ?

Последовательность Фибоначчи — Числа Фибоначчи  элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух предыдущих чисел. Название по… …   Википедия

ФИБОНАЧЧИ — (Fibonacci) Леонардо (ок. 1170 ок. 1240), итальянский математик. Автор «Liber Abaci» (ок. 1200), первого западноевропейского труда, в котором предлагалось принять арабскую (индийскую) систему написания цифр. Разработал математическую… …   Научно-технический энциклопедический словарь

Фибоначчи — (Fibonacci) Фибоначчи первый крупный математик средневековой Европы Десятичная система счисления, арабские цифры, числа, последовательность, уровни, ряд, линии и спираль Фибоначчи Содержание >>>>>>>>> …   Энциклопедия инвестора

Фибоначчи числа

— Числа Фибоначчи  элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS) в которой каждое последующее число равно сумме двух предыдущих чисел. Название по… …   Википедия

Последовательность Падована — Последовательность Падована  это целочисленная последовательность P(n) с начальными значениями и линейным рекуррентным соотношением Первые значения P(n) таковы 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265 …   Википедия

Фибоначчи — Леонардо Пизанский Leonardo Pisano Дата рождения: ок. 1170 года …   Википедия

Фибоначчи числа —         элементы числовой возвратной последовательности (См. Возвратная последовательность) 1, 1, 2, 3, 5, 8,… (ряда Фибоначчи), в которых каждый последующий член равен сумме двух предыдущих. Название по имени средневекового математика Леонардо …   Большая советская энциклопедия

ФИБОНАЧЧИ МЕТОД — разновидность одномерного поиска экстремума функции путем последовательного сужения интервала неопределенности. Единственное ограничение, налагаемое на исследуемую функцию требование строгой унимодальности на заданном интервале. При… …   Математическая энциклопедия

Последовательность Люка — Не следует путать с числами Люка. В математике, последовательностями Люка называют семейство пар линейных рекуррентных последовательностей второго порядка, впервые рассмотренных Эдуардом Люка. Последовательности Люка представляют собой пары… …   Википедия

Последовательность —         одно из основных понятий математики. П. образуется из элементов любой природы, занумерованных натуральными числами 1, 2,…, n,…, и записывается в виде x1, x2, …, xn, … или коротко, {xn}. Элементы, из которых составляется П., называются …   Большая советская энциклопедия

dic.academic.ru

Последовательность Фибоначчи — papanya77

Леона́рдо Пиза́нский (лат. Leonardus Pisanus, итал. Leonardo Pisano, около 1170 года, Пиза — около 1250 года, там же) — первый крупный математик средневековой Европы. Наиболее известен под прозвищем Фибона́ччи.
Подробнее тут:http://ru.wikipedia.org/wiki/%D4%E8%E1%EE%ED%E0%F7%F7%E8

Последовательность Фибоначчи, известная всем по фильму «Код Да Винчи» — ряд цифр, описанный в виде загадки Итальянским математиком Леонардо Пизанским, более известным под прозвищем Фибоначчи, в XIII веке. Вкратце суть загадки:

Кто-то поместил пару кроликов в некоем замкнутом пространстве, чтобы узнать, сколько пар кроликов родится при этом в течении года, если природа кроликов такова, что каждый месяц пара кроликов производит на свет другую пару, а способность к производству потомства у них появляется по достижению двухмесячного возраста.

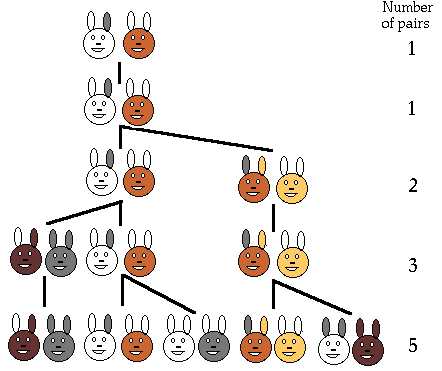
Последовательность Фибоначчи и Кролики
В итоге получается такой ряд цифр: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, где через запятую показано количество пар кроликов в каждом из двенадцати месяцев. Его можно продолжать бесконечно долго. Его суть в том, что каждое следующее число является суммой двух предыдущих.

У этого ряда есть несколько математических особенностей, которых обязательно нужно коснуться. Он асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.

Так отношение какого-либо члена ряда к предшествующему ему колеблется около числа 1,618, через pаз то превосходя, то не достигая его. Отношение к следующему аналогично приближается к числу 0,618, что обратно пропорционально 1,618. Если мы будем делить элементы через одно, то получим числа 2,618 и 0,382, которые так же являются обратно пропорциональными. Это так называемые коэффициенты Фибоначчи.

К чему всё это?

Так мы приближаемся к одному из самых загадочных явлений природы. Смекалистый Леонардо по сути не открыл ничего нового, он просто напомнил миру о таком явлении, как Золотое Сечение, которое не уступает по значимости теореме Пифагора.

Все окружающие нас предметы мы различаем в том числе и по форме. Какие-то нам нравятся больше, какие-то меньше, некоторые вовсе отталкивают взгляд. Иногда интерес может быть продиктован жизненной ситуацией, а порой красотой наблюдаемого объекта. Симметричная и пропорциональная форма, способствует наилучшему зрительному восприятию и вызывает ощущение красоты и гармонии. Целостный образ всегда состоит из частей разного размера, находящихся в определённом соотношении друг с другом и целым. Золотое сечение — высшее проявление совершенства целого и его частей в науке, искусстве и природе.

Если на простом примере, то Золотое Сечение — это деление отрезка на две части в таком соотношении, при котором большая часть относится к меньшей, как их сумма (весь отрезок) к большей.

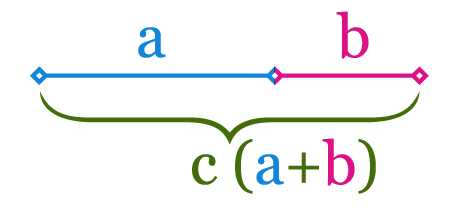
Золотое Сечение — Отрезок
Если мы примем весь отрезок c за 1, то отрезок a будет равен 0,618, отрезок b — 0,382, только так будет соблюдено условие Золотого Сечения (0,618/0,382=1,618; 1/0,618=1,618). Отношение c к a равно 1,618, а с к b 2,618. Это всё те же, уже знакомые нам, коэффициенты Фибоначчи.

Разумеется есть золотой прямоугольник, золотой треугольник и даже золотой кубоид. Пропорции человеческого тела во многих соотношениях близки к Золотому Сечению.

Золотое сечение и Человеческое тело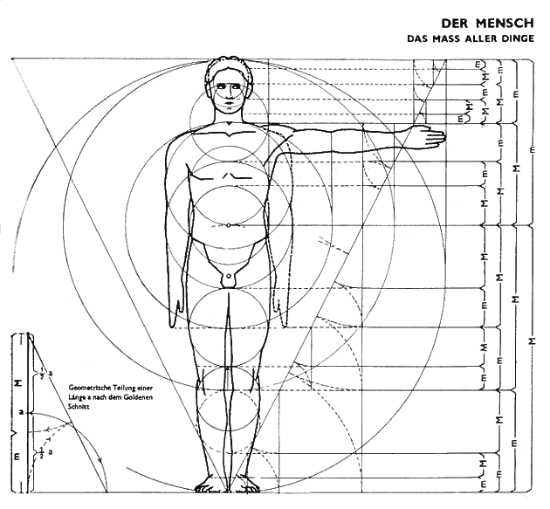

Изображение: marcus-frings.de

Последовательность Фибоначчи — Анимация

Но самое интересное начинается, когда мы объединим полученные знания. На рисунке наглядно показана связь между последовательностью Фибоначчи и Золотым сечением. Мы начинаем с двух квадратов первого размера. Сверху добавляем квадрат второго размера. Подрисовываем рядом квадрат со стороной, равной сумме сторон двух предыдущих, третьего размера. По аналогии появляется квадрат пятого размера. И так далее пока не надоест, главное, чтобы длина стороны каждого следующего квадрата равнялась сумме длин сторон двух предыдущих. Мы видим серию прямоугольников, длины сторон, которых являются числами Фибоначчи, и, как не странно, они называются прямоугольниками Фибоначчи.

Если мы проведём плавную линий через углы наших квадратов, то получим ни что иное, как спираль Архимеда, увеличение шага которой всегда равномерно.

Спираль Фибоначчи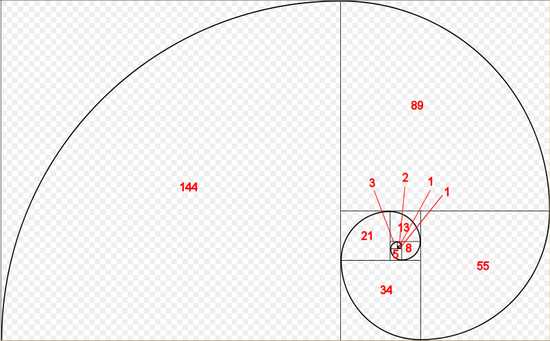

Ничего не напоминает?

Фото: ethanhein on Flickr

И не только в раковине моллюска можно найти спирали Архимеда, а во многих цветах и растениях, просто они не такие явные.

Алое многолистный:

Фото: brewbooks on Flickr

Броколи романеско:

Фото: beart.org.uk

Подсолнечник:

Фото: esdrascalderan on Flickr

Сосновая шишка:

Фото: mandj98 on Flickr

А если взглянуть чуть подальше, то можно разглядеть ряд Фибоначчи в недосягаемых галактиках.

И тут самое время вспомнить о Золотом Сечении! Ни одни ли из самых прекрасных и гармоничных творений природы изображены на этих фотографиях? И это далеко не все. Присмотревшись, можно найти похожие закономерности во многих формах.

Конечно заявление, что все эти явление построены на последовательности Фибоначчи звучит слишком громко, но тенденция на лицо. Да и к тому же сама она далека от совершенства, как и всё в этом мире.

Есть предположение, что ряд Фибоначчи — это попытка природы адаптироваться к более фундаментальной и совершенной золотосечённой логарифмической последовательности, которая практически такая же, только начинается из ниоткуда и уходит в никуда. Природе же обязательно нужно какое-то целое начало, от которого можно оттолкнуться, она не может создать что-то из ничего. Отношения первых членов последовательности Фибоначчи далеки от Золотого Сечения. Но чем дальше мы продвигаемся по ней, тем больше эти отклонения сглаживаются. Для определения любого ряда достаточно знать три его члена, идущие друг за другом. Но только не для золотой последовательности, ей достаточно двух, она является геометрической и арифметической прогрессией одновременно. Можно подумать, будто она основа для всех остальных последовательностей.

Каждый член золотой логарифмической последовательности является степенью Золотой Пропорции (z). Часть ряда выглядит примерно так: … z-5; z-4; z-3; z-2; z-1; z0; z1; z2; z3; z4; z5 … Если мы округлим значение Золотой пропорции до трёх знаков, то получим z=1,618, тогда ряд выглядит так: … 0,090 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854; 11,090 … Каждый следующий член может быть получен не только умножением предыдущего на 1,618, но и сложением двух предыдущих. Таким образом экспоненциальный рост обеспечивается путем простого сложения двух соседних элементов. Это ряд без начала и конца, и именно на него пытается быть похожей последовательность Фибоначчи. Имея вполне определённое начало, она стремится к идеалу, никогда его не достигая. Такова жизнь.

И всё-таки, в связи со всем увиденным и прочитанным, возникают вполне закономерные вопросы:
От куда взялись эти числа? Кто этот архитектор вселенной, попытавшийся сделать её идеальной? Было ли когда-то всё так, как он хотел? И если да, то почему сбилось? Мутации? Свободный выбор? Что же будет дальше? Спираль скручивается или раскручивается?

Найдя ответ на один вопрос, получишь следующий. Разгадаешь его, получишь два новых. Разберёшься с ними, появится ещё три. Решив и их, обзаведёшься пятью нерешёнными. Потом восьмью, потом тринадцатью, 21, 34, 55…

Источник:http://greenword.ru/2009/06/fibonacci-sequence.html

Подробнее о золотом сечение и ряде Фибоначчи тут:http://www.milogiya2007.ru/fibonachi.htm

И тут:

papanya77.livejournal.com

Числа Фибоначчи

по материалам книги Б. Биггса «вышел хеджер из тумана»

 

Числа Фибоначчи

Фибоначчи прожил долгую, особенно для своего времени, жизнь, которую посвятил решению ряда математических задач, сформулировав их в своем объемном труде «Книга о счетах» (начало 13 века). Его всегда интересовала мистика чисел — вероятно, он был не менее гениален, чем Архимед или Евклид. Задачи, связанные с квадратными уравнениями, ставились и частично решались и до Фибоначчи, например известным Омаром Хайямом — ученым и поэтом; однако Фибоначчи сформулировал задачу о размножении кроликов, выводы из которой и не позволили его имени затеряться в веках.

Вкратце задача заключается в следующем. В место, огороженное со всех сторон стеной, поместили пару кроликов, причем любая пара кроликов производит на свет другую пару каждый месяц, начиная со второго месяца своего существования. Размножение кроликов во времени при этом будет описываться последовательностью: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 и т.д. С математической точки зрения последовательность оказалась просто уникальной, поскольку обладала целым рядом выдающихся свойств:

• сумма двух любых последовательных чисел есть следующее число последовательности;

• отношение каждого числа последовательности, начиная с пятого, к предыдущему, равно 1.618;

• разница между квадратом любого числа и квадратом числа на две позиции левее, будет числом Фибоначчи;

• сумма квадратов стоящих рядом чисел будет числом Фибоначчи, которое стоит через две позиции после большего из возведенных в квадрат чисел

Из этих выводов наиболее интересен второй, поскольку в нем используется число 1.618, известное как «золотое сечение». Это число было известно еще древним грекам, которые использовали его при постройке Парфенона (кстати, по некоторым данным служившим грекам Центробанком). Не менее интересно и то, что число 1.618 можно обнаружить в природе как в микро-, так и макромасштабе — от витков спирали на панцире улитки до больших спиралей космических галактик.

Пирамиды в Гизе, созданные древними египтянами, при конструировании также содержали сразу несколько параметров ряда Фибоначчи. Прямоугольник, одна сторона которого больше другой в 1.618 раза, выглядит наиболее приятно для глаза — это соотношение использовал Леонардо да Винчи для своих картин, а в более житейском плане им пользовались при создании окон или дверных проемов. Даже волну, как на рисунке в начале статьи, можно представить в виде спирали Фибоначчи.

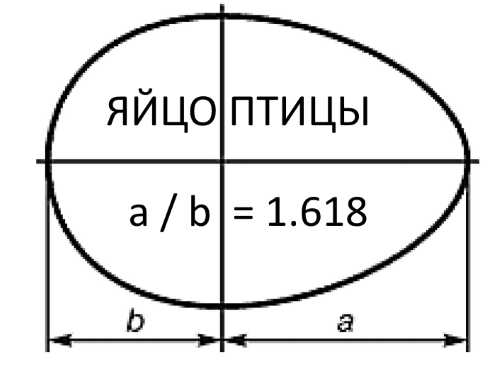
В живой природе последовательность Фибоначчи проявляется не менее часто — ее можно найти в когтях, зубах, подсолнухе, паутине и даже размножении бактерий. При желании последовательность обнаруживается практически во всем, включая человеческое лицо и тело. И тем не менее многие утверждения, находящие числа Фибоначчи в природных и исторических явлениях, явно неверны — это распространенный миф, который оказывается неточной подгонкой под желаемый результат.

 

Числа Фибоначчи на финансовых рынках

Одним из первых, кто наиболее плотно занимался приложением чисел Фибоначчи к финансовому рынку, был Р. Эллиот. Его труды не пропали даром в том смысле, что рыночные описания с применением теории Фибоначчи часто называются «волнами Эллиота». В основу развития рынков здесь была положена модель развития человечества из суперциклов с тремя шагами вперед и двумя назад.

То, что человечество развивается нелинейно, очевидно почти каждому — знания Древнего Египта и атомистическое учение Демокрита было полностью утрачено в Средневековье, т.е. спустя примерно 2000 лет. Однако даже если принять теорию шагов и их количество за истину, остается неясным размер каждого шага, что делает волны Эллиота сравнимыми с предсказательной силой орла и решки. Отправная точка и правильный расчет числа волн были и видимо будут главной слабостью теории.

Тем не менее локальные успехи у теории были. Боб Претчер, которого можно считать учеником Эллиота, правильно предсказал бычий рынок начала 80-х, а 1987 год — как поворотный. Это действительно случилось, после чего Боб очевидно чувствовал себя гением — по крайней мере, в глазах других он точно стал инвестиционным гуру.

Подписка на Elliott Wave Theorist Пречтера в тот год выросла до 20 000, однако уменьшилась в начале 1990-х годов, поскольку предсказываемые далее «гибель и мрак» американского рынка решили немного повременить. Однако для японского рынка это сработало, и ряд сторонников теории, «опоздавших» там на одну волну, потеряли либо свои капиталы, либо капиталы клиентов своих компаний. Равным образом и с теми же успехами теорию нередко пытаются применить к торговле на валютном рынке.

Волны Эллиота охватывают самые разные периоды торговли — от недельной, что роднит ее со стандартными стратегиями теханализа, до расчета на десятилетия, т.е. влезает на территорию фундаментальных предсказаний. Это возможно благодаря варьированию числа волн. Слабости теории, о которых говорилось выше, позволяют ее адептам говорить не о несостоятельности волн, а о собственных просчетах в их числе и неверном определении исходного положения. Это похоже на лабиринт — даже если у вас есть верная карта, то выйти по ней можно лишь при условии, что понимаешь, где именно находишься. Иначе пользы от карты нет. В случае же с волнами Эллиота есть все признаки сомневаться не только в правильности своего месторасположения, но и в верности карты как таковой.

 

Выводы

Волновое развитие человечества имеет под собой реальную основу — в средние века волны инфляции и дефляции чередовались между собой, когда войны сменяли относительно спокойную мирную жизнь. Наблюдение последовательности Фибоначчи в природе по крайней мере в отдельных случаях сомнения тоже не вызывает. Поэтому каждый на вопрос, кто есть Бог: математик или генератор случайных чисел — вправе давать собственный ответ. Лично мое мнение: хотя всю человеческую историю и рынки можно представить в волновой концепции, высоту и продолжительность каждой волны не дано предугадать никому.

Поделиться в соцсетях

Подписаться на статьи

Рекомендуемые статьи

investprofit.info

Последовательность Фибоначчи — это… Что такое Последовательность Фибоначчи?

Чи́сла Фибона́ччи — элементы числовой последовательности

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 … (последовательность A000045 в OEIS)

в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени средневекового математика Леонардо Пизанского (или Фибоначчи) ^[1].

Более формально, последовательность чисел Фибоначчи задается рекуррентным соотношением:

Иногда числа Фибоначчи рассматривают и для неположительных номеров n как двусторонне бесконечную последовательность, удовлетворяющую основному соотношению. Члены с такими номерами легко получить с помощью эквивалентной формулы «назад»: F_n = F_{n + 2} − F_{n + 1}:

n	−10	−9	−8	−7	−6	−5	−4	−3	−2	−1	0	1	2	3	4	5	6	7	8	9	10
Fn	−55	34	−21	13	−8	5	−3	2	−1	1	0	1	1	2	3	5	8	13	21	34	55

Легко видеть, что F _{− n} = ( − 1)^{n + 1}F_n. Для чисел Фибоначчи с отрицательными индексами остаются верными большинство нижеприведённых свойств.

Происхождение

Последовательность Фибоначчи была хорошо известна в древней Индии, где она применялась в метрических науках (просодии, другими словами — стихосложении), намного раньше, чем она стала известна в Европе.

Образец длиной n может быть построен путём добавления S к образцу длиной n-1, либо L к образцу длиной n-2; и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».

На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что:

• В «нулевом» месяце, имеется пара кроликов (0 новых пар).
• В первом месяце, первая пара производит на свет другую пару (1 новая пара).
• Во втором месяце, обе пары кроликов порождают другие пары и первая пара погибает (1 новая пара).
• В третьем месяце, вторая пара и две новые пары порождают в общем три новые пары, а старая вторая пара погибает (2 новые пары).

Закономерным является тот факт, что каждая пара кроликов порождает ещё две пары на протяжении жизни, а затем погибает.

Пусть популяция за месяц n будет равна F(n). В это время, только кролики которые жили в месяце n-2 являются способными к размножению и производят потомков, тогда F(n-2) пар прибавится к текущей популяции F(n-1). Таким образом общее количество пар будет равно F(n) = F(n — 1) + F(n — 2).

Формула Бине

Формула Бине выражает в явном виде значение F_n как функцию от n:

,

где  — золотое сечение. При этом и являются корнями квадратного уравнения .

Из формулы Бине следует, что для всех , F_n есть ближайшее к целое число, то есть . В частности, справедлива асимптотика .

Тождества

И более общие формулы:

• Числа Фибоначчи представляются значениями континуант на наборе единиц: , то есть

, а также ,

где матрицы имеют размер , i — мнимая единица.

Свойства

• Наибольший общий делитель двух чисел Фибоначчи равен числу Фибоначчи с индексом, равным наибольшему общему делителю индексов, т. е. (F_m,F_n) = F_(m,n). Следствия:
  • F_m делится на F_n тогда и только тогда, когда m делится на n (за исключением n = 2). В частности, F_m делится на F₃ = 2 (то есть является чётным) только для m = 3k; F_m делится на F₄ = 3 только для m = 4k; F_m делится на F₅ = 5 только для m = 5k и т. д.
  • F_m может быть простым только для простых m (с единственным исключением m = 4) (например, число 233 простое, и индекс его, равный 13, также прост). Обратное не верно, первый контрпример — . Неизвестно, бесконечно ли множество чисел Фибоначчи, являющихся простыми.

.

• В 1964 Дж. Кон (J. H. E. Cohn) доказал, что единственными точными квадратами среди чисел Фибоначчи являются числа Фибоначчи с индексами 0, 1, 2, 12: F₀ = 0² = 0, F₁ = 1² = 1, F₂ = 1² = 1, F₁₂ = 12² = 144. При этом для n=0,1,12 верно утверждение F_n = n².

• Множество чисел Фибоначчи совпадает с множеством положительных значений многочлена
      z(x,y) = 2xy⁴ + x²y³ − 2x³y² − y⁵ − x⁴y + 2y,
  на множестве неотрицательных целых чисел x и y ^[2].

• Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.

• Последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом 60, последняя пара цифр чисел Фибоначчи образует последовательность с периодом 300, последние три цифры — с периодом 1500, последние четыре — с периодом 15000, последние пять — с периодом 150000 и т. д.

Вариации и обобщения

В других областях

В природе

• Расстояния между листьями (или ветками) на стволе растения относятся примерно как числа Фибоначчи.

В культуре

См. также

Литература

Ссылки

Примечания

1. ↑ [1] БСЭ]
2. ↑ P. Ribenboim, The New Book of Prime Number Records, Springer, 1996, p. 193.

Wikimedia Foundation. 2010.

dic.academic.ru

Последовательность чисел Фибоначчи | Trading Academy «SViKK»

Последовательность чисел Фибоначчи. Вы впервые слышите об этом и даже не предполагаете, из какой это области знаний? Оказывается, закономерность явлений природы, строение и многообразие живых организмов на нашей планете, всё, что нас окружает, поражая воображение своей гармонией и упорядоченностью, законы мироздания, движение человеческой мысли и достижения науки – всё это объясняет суммационная последовательность Фибоначчи.

Извечное стремление человека познать себя и окружающий мир двигало науку вперёд.

Одним из наиболее значимых достижений в математике является введение арабских цифр вместо римских. Оно принадлежит одному из самых замечательных ученых двенадцатого столетия Фибоначчи (1175 г.). Его именем было названо ещё одно сделанное им открытие – суммационную последовательность: 1,1,2,3,5,8,13,21,34,55,89,144,… Это – так называемые числа Фибоначчи.

Эта закономерность в математике интересовала ещё одного ученого средневековья – Фому Аквинского. Движимый желанием «алгеброй гармонию измерить», учёный сделал вывод о прямой связи математики и красоты. Эстетические чувства, возникающие при созерцании гармоничных, пропорционально созданных природой объектов, Фома Аквинский объяснял тем же принципом суммационной последовательности.

Этот принцип поясняет, что начиная с 1,1, следующим числом будет сумма двух предыдущих чисел. Эта закономерность имеет большое значение.Это последовательность все медленнее и медленнее – асимптотически – приближается к некоему постоянному отношению. Однако отношение это является иррациональным, то есть имеет в дробной части бесконечную и непредсказуемую последовательность цифр. Точное его выражение невозможно. Разделив любой член последовательности Фибоначчи на член, предшествующий ему, мы получим величину, которая колеблется возле значения 1.61803398875… (иррациональное), которая будет то не достигать, то превосходить его всякий раз. Даже Вечности не хватит для того, чтобы точно определить это соотношение. Для краткости мы будем использовать его в виде 1.618.

Средневековый математик Лука Пачиоли назвал это соотношение Божественной пропорцией. Кеплеpом  суммационная последовательность названа “одним из сокровищ геометрии”. В современной науке суммационная последовательность Фибоначчи имеет несколько названий, не менее поэтичных: Отношение вертящихся квадратов, Золотое среднее, Золотое сечение. В математике его обозначают греческой буквой фи (Ф=1,618).

Асимптотический характер последовательности, ее колебания возле иррационального числа Фибоначчи, имеющие свойство затухать, станут понятнее, если рассмотреть соотношения первых членов этой последовательности. В примере ниже мы рассмотрим числа Фибоначчи приведем отношение второго к первому члену, третьего ко второму и так далее:
1:1 = 1.0000, это меньше фи на 0.6180
2:1 = 2.0000, это больше фи на 0.3820
3:2 = 1.5000, это меньше фи на 0.1180
5:3 = 1.6667, это больше фи на 0.0486
8:5 = 1.6000, это меньше фи на 0.0180
Двигаясь дальше по последовательности Фибоначчи, каждый ее новый член разделит следующий, все более и более приближаясь к недостижимому числу Ф.

Впоследствии мы увидим, что некоторые числа Фибоначчи, составляющие его суммационную последовательность, видны в динамике цен на различные товары; среди методов технического анализа Форекс используются уровни Фибоначчи. Колебания отношений возле 1.615 на ту или иную величину могут быть обнаружены в Волновой Теории Эллиотта, в ней они фигурируют в Правиле чередования. Подсознательно каждый человек ищет пресловутую Божественную пропорцию, которая необходима для удовлетворения стремления к комфорту.

Если мы разделим любой член последовательности Фибоначчи на член, следующий за ним, мы получим обратную к 1.618 величину, то есть 1:1.618. Это тоже достаточно необычное явление, пожалуй, даже замечательное. Исходное соотношение является бесконечной дробью, следовательно, и данное соотношение тоже должно быть бесконечным.

Другой немаловажный факт заключается в следующем. Квадрат любого члена последовательности Фибоначчи равняется числу, которое стоит перед ним в последовательности, умноженному на то число, что идет следом за ним, плюс или минус.
5² = (3 x 8) + 1
8² = (5 x 13) – 1
13² = (8 x 21) + 1
Плюс и минус всегда чередуются, и в этом заключается проявление части Волновой Теории Эллиотта, которая называется Правилом чередования. Это правило гласит: сложные волны коррективного характера перемежаются с простыми, сильные волны импульсного характера – со слабыми волнами коррективного характера, и так далее.

Проявления Божественной пропорции в природе

Обнаруженная математическая последовательность позволяет вычислить бесконечное число постоянных величин. Члены этой последовательности всегда будут проявляться в нескончаемом количестве сочетаний.
С помощью установленной закономерности даётся  математическое толкование природных явлений. В этой связи, открытию математической последовательности принадлежит одно из самых значительных мест в историческом знании.
Мы можем сослаться на целый ряд интересных  теорий, выведенных на основе математической последовательности.

Пирамида в Гизе

Конструкция пирамиды основана на пропорции Ф=1,618. Это открытие было сделано после многочисленных попыток разгадать секреты этой пирамиды. Сама пирамида в Гизе представляется неким посланием потомкам, с тем, чтобы передать определенные знания законов математической последовательности. Во времена возведения пирамиды ее строители не располагали достаточными возможностями для выражения известных им закономерностей. В ту пору не существовала письменность, не использовались ещё и иероглифы. Однако создателям пирамиды удалось с помощью геометрической пропорции своего творения передать свои знания математической закономерности будущим поколениям.

Храмовые жрецы передали Геродоту секрет пирамиды в Гизе. Она выстроена таким образом, что площадь каждой грани равняется квадрату высоты этой грани.
Площадь тpеугольника: 356 x 440 / 2 = 78320
Площадь квадpата: 280 x 280 = 78400
Грань пирамиды в Гизе имеет длину 783.3 фута (238.7 м), ее высота составляет 484.4 фута (147.6 м). Разделив длину грани на высоту, вы придем к соотношению Ф=1.618. Высота 484.4 фута соответствует 5813 дюймам (5-8-13), а это не что иное, как числа последовательности Фибоначчи. Все эти наблюдения приводят нас к выводу, что вся конструкция пирамиды базируется на пропорции Ф=1,618.
– это числа из последовательности Фибоначчи. Эти интересные наблюдения подсказывают, что конструкция пирамиды основана на пропорции Ф=1,618.
Эти сведения дают основание полагать о высоком развитии в те времена  знаний в области математики и астрологии. В строгом соответствии с числом 1.618 возведено это величайшее творение не только рук человека, но и его разума. Сами внутренние и внешние пропорции пирамиды, соблюдённые в строгом соответствии с законом Золотого сечения являются посланием нам, потомкам,  из глубины веков величайшего знания.

Мексиканские пирамиды

Поражает воображение тот факт, что пирамиды в Мексике построены по такому же принципу. Невольно возникает предположение о строительстве мексиканских пирамид в одно время с египетскими, к тому же строители обладали знаниями о математическом законе Золотого сечения.
Поперечное сечение пирамиды обнаруживает форму лестницы. В пеpвом её яpусе 16 ступеней, второй содержит 42 ступени, третий – 68 ступеней. Числа базируются на последовательности Фибначчи по следующей схеме:
16 x 1.618 = 26
16 + 26 = 42
26 x 1.618 = 42
42 + 26 = 68
Число Ф = 1.618 лежит в основе пропорций мексиканской пиpамиды. (Источник: Mysteries of the Mexican Pyramids, by Peter Thomkins /Питеp Томкинс, “Тайны мексиканских пиpамид”/ (New York: Harper & Row, 1976) p. 246, 247.)

Растения

Не менее замечательным является проявление суммарной последовательности Фибоначчи в строении растений.
Такой вывод можно сделать, наблюдая за ростом и развитием стеблей и цветов sneezewort’а. Каждая его новая ветвь, прорастая, дает начало другим ветвям. Рассматривая старые и новые ветви совместно, мы обнаружим число Фибоначчи в каждой из горизонтальных плоскостей. (Источник: The Divine Proportion, by H. E. Huntley /Х. Е. Хантли, “Божественная пpопоpция”/ (New York: Dover, 1970) p. 163.).
В строении соцветий сложноцветных растений вновь проявляется закономерность Золотого сечения:
Иpис имеет 3 лепестка;
Пpимула имеет 5 лепестков;
Амбpозия полыннолистная имеет 13 лепестков;
Hивяник обыкновенный имеет 34 лепестка;
Астpа имеет 55 и 89 лепестков.
Таким образом, суммарной последовательностью Фибоначчи легко можно трактовать закономерность проявлений Золотых чисел, встречаемых в природе. Эти законы действуют в независимости от нашего знания, от чьего-то желания принимать или не принимать их.

+

svikk.biz