Вторник , 19 Ноябрь 2024

Квантовая теория поля для чайников: Квантовая теория поля

Содержание

Квантовая теория поля

Квантовая теория поля


Quantum field theory

    Квантовая теория поля (КТП) – теория релятивистских квантовых явлений, описывающая элементарные частицы, их взаимодействия и взаимопревращения на основе фундаментального и универсального понятия квантованного физического поля. КТП – наиболее фундаментальная физическая теория. Квантовая механика является частным случаем КТП при скоростях, много меньших скорости света. Классическая теория поля следует из КТП, если постоянную Планка устремить к нулю.
    В основе КТП лежит представление о том, что все элементарные частицы являются квантами соответствующих полей. Понятие квантового поля возникло в результате развития представлений о классическом поле и частицах и синтеза этих представлений в рамках квантовой теории. С одной стороны квантовые принципы привели к пересмотру классических взглядов на поле как на непрерывно распределённый в пространстве объект.

Возникло представление о квантах поля. С другой стороны частице в квантовой механике ставится в соответствие волновая функция ψ(x,t), имеющая смысл амплитуды волны, причем квадрат модуля этой амплитуды, т.е. величина |ψ|2 даёт вероятность обнаружить частицу в той точке пространства-времени, которая имеет координаты x, t. В результате с каждой материальной частицей оказалось связано новое поле – поле амплитуд вероятности. Таким образом, на смену полям и частицам – принципиально разным объектам в классической физике – пришли единые физические объекты – квантовые поля в 4-х мерном пространстве-времени, по одному для каждого сорта частиц. Элементарное взаимодействие при этом рассматривается как взаимодействие полей в одной точке или мгновенное превращение в этой точке одних частиц в другие. Квантовое поле оказалось наиболее фундаментальной и универсальной формой материи, лежащей в основе всех её проявлений.


Простейшая диаграмма Фейнмана для рассеяния электронов.

    На основе такого подхода рассеяние двух электронов, испытавших электромагнитное взаимодействие, можно описать следующим образом (см. рисунок). Вначале были два свободных (невзаимодействующих) кванта электронного поля (два электрона), которые двигались навстречу друг другу. В точке 1 один из электронов испустил квант электромагнитного поля (фотон). В точке 2 этот квант электромагнитного поля был поглощён другим электроном. После этого электроны удалялись, не взаимодействуя. В принципе аппарат КТП позволяет рассчитывать вероятности переходов от исходной совокупности частиц к заданной совокупности конечных частиц под влиянием взаимодействия между ними.
    В КТП наиболее фундаментальными (элементарными) полями в настоящее время являются поля, связанные с бесструктурными фундаментальными частицами со спином 1/2, — кварками и лептонами, и поля, связанные с квантами-переносчиками четырёх фундаментальных взаимодействий, т.е.

фотоном, промежуточными бозонами, глюонами (имеющими спин 1) и гравитоном (спин 2), которые называют фундаментальными (или калибровочными) бозонами. Несмотря на то, что фундаментальные взаимодействия и соответствующие им калибровочные поля имеют некие общие свойства, в КТП эти взаимодействия представлены в рамках отдельных полевых теорий: квантовой электродинамики (КЭД), электрослабой теории или модели (ЭСМ), квантовой хромодинамики (КХД), а квантовой теории гравитационного поля пока не существует. Так КЭД – это квантовая теория электромагнитного поля и электронно-позитронного полей и их взаимодействий, а также электромагнитных взаимодействий других заряженных лептонов. КХД – квантовая теория глюонных и кварковых полей и их взаимодействий, обусловленных наличием у них цветовых зарядов.
    Центральной проблемой КТП является проблема создания единой теории, объединяющей все квантовые поля.

См. Также

  1. Квантовая электродинамика
  2. Диаграммы Фейнмана
  3. Аксиомы квантовой механики

Квантовая теория поля простыми словами | Аuriel Astro

Концепции квантовой физики появились в начале ХХ века. Именно она заставила нас по-другому посмотреть на мир частиц, заполняющих собой всё и вся.

Учёные выяснили, что элементарных частиц существует огромное множество, а также подтвердилась гипотеза Эйнштейна о том, что энергия переходит в материю, а материя – в энергию, то есть при столкновении элементарных частиц могут рождаться новые частицы. Понятие точечной частицы заменило другое понятие – понятие квантового поля , из которого соткано всё пространство-время, и кванты этого поля – это и есть элементарные частицы.

Например, у нас есть одна колеблющаяся частица. Если рассматривать её в отдельности, то можно изучить её кинетическую и потенциальную энергию. Если мы возьмём поле, занимающее всю Вселенную, то в каждой точке будут находиться такие колеблющиеся частицы. Они могут быть связанными друг с другом (то есть колебания одной частицы будут влиять на другую) – тогда это будет выглядеть как движущаяся волна, так как одна частица будет влиять на вторую, вторая – на третью и так далее. Трудность заключается в том, что если частица, подобно маятнику, будет колебаться вдоль одной оси, то у неё будет только одна степень свободы. А если она будет колебаться вдоль разных осей (например, вдоль оси Х, У и Z ), то у неё будет уже 3 степени свободы. Получается, что поле, как система таких движущихся частиц, имеет бесконечное число степеней свободы, так как в поле, заполняющем собой всю Вселенную, этих частиц огромное количество. Описать математически это очень сложно – это первая трудность квантовой механики.

Вторая трудность заключается в том, что, если в классической механике число частиц было постоянным, то, согласно квантовой механике, одна частица может породить ещё одну. Дело в том, что классическая физика не рассматривала большой энергетический интервал. А вот при движении частиц на очень высоких скоростях они уже будут обладать и высокими энергиями – об этом нам говорит знаменитое уравнение Альберта Эйнштейна:

Соответственно, если на высокой скорости одна частица сталкивается с другой, то может родиться и третья. Число частиц постоянно меняется – они могут не только рождаться, но и уничтожаться. Как же описать такую сложную систему?

Квантовое поле, которым пронизана вся Вселенная, легко можно сравнить с водой. Например, вы сидите на берегу озера, поверхность которого абсолютно безмятежна, её ничто не тревожит – это поле. Бросьте в воду камень, и пойдёт волна – вы увидите её гребень в форме горки, родившийся в результате взаимодействия с камнем, — это частица. Главная идея квантовой теории поля – это то, что частицы являются элементарными возмущениями полей. Таким образом, наша реальность – это поле, а мы состоим из элементарного возмущения полей. Будучи рожденными этими самыми полями, их кванты содержат в себе все свойства своих прародителей. Такова роль частиц в мире, в котором одновременно существует множество океанов, именуемых полями.

Отсюда вытекает и принцип корпускулярно-волнового дуализма: частицы могут вести себя как волны, а волны – как частицы. Согласно квантовой теории поля, вся Вселенная заполнена не одним, а различными полями из-за того, что частицы могут иметь бесконечное число степеней свободы: это электрические поля, магнитные, гравитационные и другие. При этом, частице соответствует возмущение на этих разных полях.

Например, положительное возмущение электрического поля и гравитационного будут соответствовать протону, так как у него положительный заряд. Если идёт возмущение только гравитационного поля, то виновник этому – нейтрон, так как он нейтрален и имеет массу. Если идёт возмущение электрического и магнитного полей, а гравитационное при этом остаётся спокойным, то мы уже будем иметь дело с фотоном, так как у него нет массы.

Представим, что квантовое поле – это набор энергетических уровней, некая слоистая лестница. Каждая точка в таком пространстве будет описываться определённым значением, соответствующим напряженности электрического, магнитного, гравитационного поля в этой конкретной точке. Когда частица входит в пространство, она изменяет его различные поля в соответствии со своими физическими параметрами (например, в соответствии с электрическим зарядом или массой). Анализируя значения этих полей в данном месте, учёные могут определить, какая частица только что пересекла это пространство.

Когда частицы взаимодействуют друг с другом, передаётся и энергия от одного поля к следующему. Так, например, возмущение электрического поля может передаваться магнитному или гравитационному. Когда пара частица-античастица аннигилирует, масса может быть преобразована в фотон, а значит, в электромагнитную энергию. Но Вселенная не спешит растрачивать свою энергию зря: она всегда сохраняется и может переходить из одного поля в другое. Получается, что ничего не исчезает просто так, и конец одного всегда является началом чего-то нового.

Поневоле задумаешься и о том, что происходит в нашей обычной жизни: замечали вы хоть раз, как, будучи в плохом настроении, у нас всё идёт наперекосяк, что-то не получается, с кем-то человек ссорится, на каждом шагу сплошные неудачи, а ведь он просто вышел из дома в плохом настроении – его негативная энергия стала материальной, он пошёл сеять хаос вокруг себя дальше. Если же взять противоположный пример – положительного, добродушного человека, который стремится совершать благородные и правильные поступки, то его же положительная энергия, отданная им в мир, возвращается к нему в виде помощи других людей, удачи или счастливого стечения обстоятельств? Конечно, это не всегда работает, но в большинстве случаев, «что посеешь, то и пожнёшь». Всё взаимосвязано. Уж не замешана ли и здесь квантовая теория поля?

Читайте больше о нашем мире:

А что, если мы — часть какого-то организма?

Теория струн для чайников

Антропный принцип и поиски иных форм жизни

Теория эфира: «за» и «против»

Пятое фундаментальное взаимодействие

Электромагнитное взаимодействие

Слабое фундаментальное взаимодействие

Сильное фундаментальное взаимодействие

Гравитационное взаимодействие

В.

Гейзенберг. Теория единого поля В. Гейзенберг. Теория единого поля
Эйнштейновский сборник 1969-1970. М.: Наука, 1970. 91-98 C.

Среди многочисленных идей, которые разрабатывал Эйнштейн в связи с общей теорией относительности, фигурирует гипотеза о возможности единой теории поля. Эта идея возбудила живой интерес из-за ее философского значения. Эйнштейн предположил, что, в конечном счете, можно описать все различные феномены, как-то: гравитацию, электромагнетизм, а также и материальные тела — фундаментальным полем или системой полей, что все различные эмпирические законы природы могут быть выражены системой нелинейных уравнений, которым подчиняются компоненты данных полей. С философской точки зрения такая возможность кажется весьма заманчивой. В самом деле, нельзя разобщать такие феномены, как гравитация и электричество. Они обладают способностью взаимно влиять друг на друга так, что законы природы не могут быть совершенно независимыми.

Отсюда единая теория поля охватывала бы эти различные законы и они стали бы частными случаями; одновременно эта теория определяла бы их отношения и, следовательно, структуру природы.

Эйнштейн не смог идти очень далеко в осуществлении этой программы. Его отправной точкой было гравитационное поле, полевые уравнения которого давала общая теория относительности. Поэтому он хотел открыть структуру поля, которая была бы естественным обобщением симметрического тензора (метрического), представляющего гравитацию, и одновременно систему полевых уравнений, соответствующих этой структуре, и представляющую естественное обобщение уравнений чистой гравитации. Прежде всего он попытался охватить ими законы электромагнетизма; что касается материальных тел, то он надеялся, что на последующей стадии разработки теории элементарные частицы могли бы рассматриваться как сингулярности пространства этого универсального поля. Эта надежда основывалась на нелинейном характере полевых уравнений, допускающих такие сингулярности.

Но на этом этапе он игнорировал, можно сказать почти намеренно, квантовую природу элементарных частиц; поэтому оказалось невозможным найти корректное математическое описание их поведения.

До изложения деталей этого вопроса следует упомянуть другую капитальную проблему: связь между системой полевых уравнений и космологической моделью Вселенной. Эйнштейн видел эту связь в свете воззрений Маха. Согласно последнему нет никакого смысла говорить о вращении изолированного тела в пустом пространстве. Следовательно, центробежная сила может появиться лишь тогда, когда пространство не пусто, когда отдаленные массы обусловливают эту силу. Итак, реакция изолированного тела на движение зависит от распределения материи во Вселенной. Это распределение и соответствующая структура пространства-времени не определены однозначно полевыми уравнениями. Но они также не совсем произвольны: они лимитируются полевыми уравнениями и должны соответствовать одному из многочисленных решений этих уравнений.

Поведение изолированной частицы под влиянием местных полей может в известной степени, зависеть от структуры Вселенной. Верно то, что принцип Маха не связан с полевыми уравнениями столь тесно, как это думал Эйнштейн. Но связь между космологической моделью и полевыми уравнениями, применимость этой космологической модели к поведению тел, даже малых, остается существенной чертой любой единой теории поля.

Возвращаясь к квантовой природе элементарных частиц, нужно прежде всего заметить, что сингулярности пространства, обусловленные нелинейным уравнением классического поля, вели бы себя совершенно иначе, чем элементарные частицы в заданном поле сил. Все характеристики, связанные в квантовой теории с кажущимся дуализмом волны-частицы и выражающиеся математической моделью квантовой механики (или волновой механики), не проявлялись бы в поведении сингулярностей. Было бы нереалистично в наше время связывать различные группы естественных феноменов, не учитывая с самого начала квантовую теорию. Более того, многочисленные эксперименты, осуществленные за последние годы с помощью больших ускорителей, сообщили нам множество сведений об элементарных частицах, еще не известных во времена Эйнштейна. Мы знаем теперь, что кроме электромагнитных сил и соответствующих им фотонов, кроме гравитации и соответствующих ей гравитонов, существует большое число различных силовых полей, каждое из которых характеризуется соответствующей частицей (к примеру, ядерные силы). Единая теория поля должна объяснить эти различные поля.

При столкновении двух элементарных частиц очень высокой энергии рождаются многочисленные новые частицы. Было бы плохим описанием этого феномена, если сказать, что частицы разбились на большое число более мелких осколков. Гораздо правильнее сказать, что огромная кинетическая энергия частиц преобразовалась при столкновении по закону Эйнштейна в материю, порождая большое число новых элементарных частиц. В самом деле, независимо от индивидуальной природы частиц, участвующих в столкновении, новые частицы всегда принадлежат хорошо известному спектру элементарных частиц.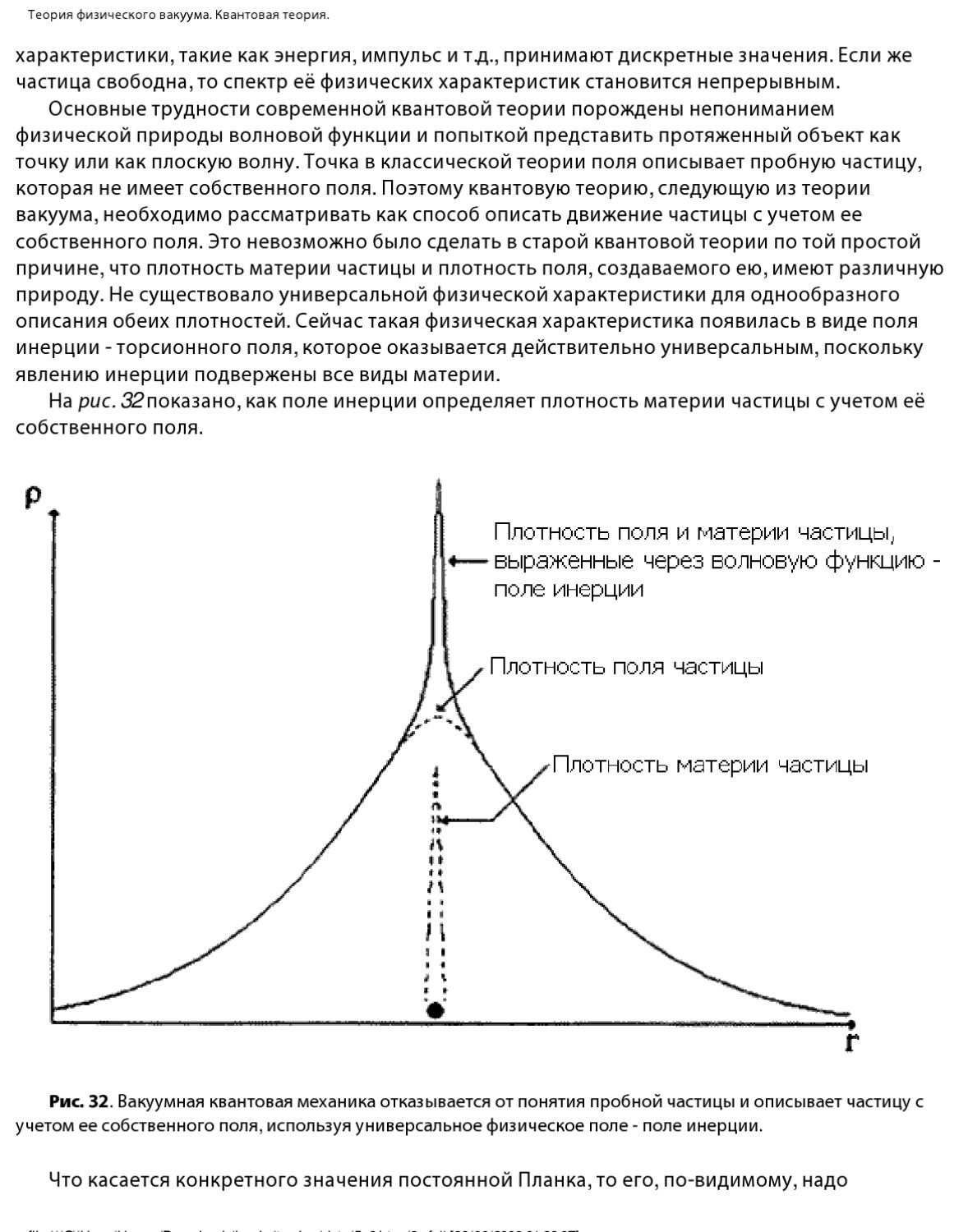 Энергия становится материей, принимая форму элементарной частицы. Спектр элементарных частиц воспроизводит самого себя в процессе столкновения с высокой энергией.

Можно извлечь из этих результатов очень важные заключения. Бросается в глаза, что было бы абсурдным пытаться разработать особую теорию для каждого из этих силовых полей. Единая теория поля могла быть для Эйнштейна предметом спекуляции; для наших дней она абсолютно необходима теоретической физике, если хотят понять элементарные частицы.

Конечно, можно спросить, будет ли эта теория единой теорией поля или, может быть, каким-нибудь другим математическим аппаратом, более пригодным для описания экспериментов. Но эта будущая теория должна быть единой, охватывающей совокупность эмпирических полей.

Эйнштейн полагал, что частицы — сингулярности поля в пространстве. С тех пор квантовая теория поля открыла, что частицы являются сингулярностями (именуемыми полюсами) в пространстве моментов, а не в обычном пространстве.

Для Эйнштейна поле было реальным; оно было последней реальностью, определяющей и геометрию мира и структуру материальных тел. В квантовой теории поле отличает (как и в классической физике) что-то от ничего; но его основная функция — это изменение состояния Вселенной, характеризуемого амплитудой вероятностей, обеспечивающей предсказания о возможностях. Под этим углом зрения позволительно описывать экспериментальные ситуации в физике элементарных частиц, применяя операторы, построенные с учетом действия полевых операторов на основное состояние «Вселенная». Но вряд ли можно считать эти поля реальными и объективными в том смысле, как это сделал Эйнштейн в своей теории поля.

В теории Эйнштейна, так же как и в квантовой теории, формулировка скрытых законов природы дается в последней инстанции уравнением поля. Поэтому основная задача единой теории поля состоит в корректном выборе уравнения поля и сравнении результатов с экспериментальными наблюдениями. В этом отношении любая попытка разработки квантовой теории единого поля имеет большие шансы на успех, чем старая теория Эйнштейна. В настоящее время известно столько вещей о спектре элементарных частиц, об их взаимодействии, о правилах отбора в преобразованиях и т. д., что относительно легко, несмотря на большие математические трудности, проверить, способно ли данное уравнение поля, предложенное в качестве фундаментального закона, дать результаты, соответствующие наблюдениям.

Для открытия фундаментального уравнения поля, вытекающего из анализа экспериментов, нужно обратиться к законам сохранения, правилам отбора и эмпирическим квантовым числам. Уже сорок лет как благодаря математике физики узнали, что эти отношения обязаны симметриям, «групповым свойствам» скрытых законов природы.

Следовательно, эмпирические данные раскроют структуру группы фундаментального уравнения поля, и вполне возможно, что структура группы совместно, может быть, с небольшим количеством других правдоподобных постулатов, определит однозначно это уравнение.

Анализ спектра и правил отбора предоставил бы прямую методику определения структуры группы скрытых законов природы, если все наблюдаемые симметрии были бы точными симметриями. Но это не так. Существуют приблизительные симметрии, как-то: группа изоспина и группы высшего ранга, как SU3, SU6, SU12 и т. д., верных лишь в очень грубом приближении. В этом случае имеется выбор лишь между двумя возможностями: либо предположить, что скрытый закон инвариантен в отношении операций рассматриваемой группы, но затем симметрия нарушается; либо, что симметрия не свойственна скрытому закону, но приблизительная симметрия происходит от динамики системы. Экспериментальный критерий позволит различить указанные две возможности. В первом случае наблюдались бы, согласно одной теореме Гольдстона, бозоны с нулевой массой покоя, ответственные за нарушение симметрии. Во втором случае не должно существовать подобных частиц. Для группы изоспина действительно наблюдаются электромагнитное поле и фотоны с нулевой массой покоя, ответственные за нарушение симметрии. Для групп более высокого ранга SU3, SU6 и т. д. подобные частицы не обнаружены. Считая это окончательным результатом анализа, приходим к следующему заключению: скрытый закон природы должен быть инвариантным относительно операций группы Лоренца, группы изоспина и некоторых других групп (последние соответствуют числам барионов и лептонов, странности и электрическому заряду). Существует лишь одно простое дифференциальное нелинейное уравнение, содержащее эти симметрии, и, следовательно, естественно принять это уравнение за основу теории единого поля. Дифференциальный характер уравнения выпукло выявляет соотношение между причиной и следствием, которое иногда называют релятивистской причинностью. Релятивистская причинность совместима с квантовой теорией, и ее заключения, по-видимому, находятся в хорошем согласии с наблюдениями процесса столкновения.

Исходя из этого нелинейного спинорного уравнения, получают известное число обнадеживающих результатов, делающих вероятным, по моему мнению, что указанное уравнение составляет корректную основу физики элементарных частиц. Я не могу подробнее остановиться на этом пункте. Вместо того чтобы обсуждать очень специфические следствия этой квантовой теории единого поля, я хотел бы сравнить ее общую структуру и результаты с прежней программой Эйнштейна. В центре новой теории оказываются сильные взаимодействия, в которых участвует большинство наиболее элементарных частиц, барионы и мезоны, представляющих полную симметрию уравнения. Эйнштейн в своих попытках единой теории не рассматривал частицы с сильным взаимодействием и соответствующее поле частично потому, что он не мог допустить квантового отношения между полем и частицей и частично потому что в то время были известны лишь некоторые из этих полей и частиц. Поэтому обе теории весьма отличаются в этом отношении.

Все же электромагнитное поле охватывалось в попытке Эйнштейна. В квантовой теории единого поля оно появляется как довольно специфическое поле, вытекающее из асимметрии Вселенной в преобразованиях группы изоспина. На этой стадии новая теория обнаружила очень интересную связь между макроскопической структурой, космологической моделью Вселенной и свойствами элементарных частиц. Эта связь была выражена в некоторой математической форме — теоремой Гольдстона. Если скрытый закон природы инвариантен относительно некоторых преобразований (в данном случае — это преобразование относительно изопространства) и если эта симметрия нарушается асимметрией основного состояния Вселенной, то теорема гласит, что должны появиться бозоны (частицы, подчиняющиеся статистике Возе) с нулевой массой покоя или должны появиться силы с дальним радиусом действия. Эти силы объясняют, почему свойства частиц не могут быть полностью независимыми от макроскопической структуры Вселенной. Действительно, число протонов во Вселенной сильно отличается от числа нейтронов, следовательно, реальный мир не инвариантен относительно вращений изопространства. Мы также знаем, что электромагнитные силы с дальним радиусом действия и соответствующие частицы (фотоны) имеют нулевую массу покоя. Поэтому кажется вполне естественным предполагать, что электромагнитное поле или части этого поля представляют гольдстоново поле и что его существование обязано асимметрии Вселенной в изопространстве.

Этот результат выявляет тесное сходство между инерционными силами (например, центробежными силами) и их космологическим происхождением в теории Эйнштейна, с одной стороны, и с другой — между электромагнитными силами и их космологическим происхождением в квантовой теории единого поля. В том и другом случае качественная гипотеза фундаментальной асимметрии космологической модели достаточна для однозначного количественного определения сил. В общей теории относительности величина центробежных сил получается непосредственно, если известно, что на больших расстояниях метрика стремится к евклидовой. В квантовой теории поля интенсивность электромагнитного поля или элементарный заряд определены, когда известно, что макроскопическая мода асимметрична относительно вращений изопространства. Обнадеживает то, что значение электрического заряда или его эквивалент, значение постоянной тонкой структуры Зоммерфельда, удовлетворительно совпадает с наблюдаемой величиной, как это показали Дюер, Ямамото и Ямасаки. Этот результат, вероятно, наиболее сильный аргумент в пользу нелинейного уравнения поля, предполагаемого нами.

Гравитационное поле находилось в центре единой теории поля Эйнштейна. В квантовой теории единого поля гравитация еще не рассматривалась, и ей наверняка принадлежит весьма малая роль в спектре элементарных частиц. Более того, общая методика учета гравитационного поля кажется довольно ясной. Вряд ли следует, по примеру Эйнштейна, принимать за основу общую риманову геометрию. Тирринг показал в весьма интересной статье, что можно превосходно исходить из уравнения поля, инвариантного относительно преобразований Лоренца, как-то: нелинейного спинорного уравнения. Если фундаментальное уравнение приводит, среди других асимптотических полей, к тензорному полю с дальним радиусом действия, то это асимптотическое поле может обладать всеми свойствами гравитационного поля. Эта сила с дальним радиусом действия способна вновь проявиться в связи с асимметрией основного состояния Вселенной в соответствии с теоремой Гольдстона. Итак, гравитация вновь оказалась бы следствием макроскопической структуры Вселенной, как в теории Эйнштейна.

Более того (это отметил Тирринг), поведение измерительных стержней и часов подвергалось бы влиянию такого гравитационного поля. Если четырехмерная геометрия будет доступной измерению с помощью стержней и часов, то получится риманова геометрия точно такого же типа, которую рассматривал Эйнштейн. Итак, эта геометрия — естественное, но косвенное следствие постулата, утверждающего, что измерительные стержни и часы должны подчиняться универсальному закону, выраженному уравнением поля, и что, как сказал Вайцзекер, теория единого поля должна иметь внутреннюю «семантику», собственные схемы согласованных интерпретаций.

При современном состоянии физики мы еще далеки от полного решения всех этих проблем. Существует множество феноменов в физике элементарных частиц и, возможно, в других разделах, еще не понятных в рамках теории единого поля. Но программа, вытекающая из основной идеи Эйнштейна, сохранила свою философскую мощь вопреки или, лучше сказать, благодаря всем новым экспериментальным данным об элементарных частицах, и эта программа открывает, возможно, самую увлекательную область исследований нашей эпохи.

*Science et synthese. Werner Heisenberg. La theorie du champ unitaire. 38—47. Imprimerie Bussiere, Sanit-Amand (Cher) France. UNESCO, 1967.

Эйнштейновский сборник 1969-1970. М.: Наука, 1983.-408 с.


Используются технологии uCoz

Введение в квантовую теорию поля

Материалы: [Весна 2018] [Весна 2017]
  • Где: 417 ГК
  • Когда: Среда, 10:45 — 12:10
  • Дополнительное время: 122 ЛК, Среда, 12:20 — 15:20
  • Контакты:

Программа

Лекция 1: Введение. Классическая теория поля (Степанов Н.)
15 февраля 2017 г.
  • [обязательно] Материалы лекции
  • [обязательно] Учебник: ПШ — Глава 2.2: Элементы классической теории поля
Лекция 2: «Вторичное квантование» теории Клейна-Гордона (Степанов Н.
) 22 февраля 2017 г.
  • [обязательно] Материалы лекции
  • [обязательно] Учебник: ПШ — Глава 2.3: Поле Клейна-Гордона как набор гармонических осцилляторов
  • [рекомендовано] Учебник: Зи — Глава III.1: Обрезание нашего незнания
Лекция 3: Вторичное квантование и многочастичная квантовая механика (Побойко И.)
1 марта 2017 г.
  • [обязательно] Материалы лекции
  • [рекомендовано] Учебник: Altland, Simons — Глава 2.1: Introduction to second quantization
  • [рекомендовано] Учебник: Ландау — Глава 9: Тождественность частиц
Лекция 4: Модели сильной связи и графен (Степанов Н.
) 15 марта 2017 г.
Лекция 5: Фононы (Степанов Н.)
22 марта 2017 г.
Лекция 6: Функции Грина (Побойко И.)
29 марта 2017 г.
  • [обязательно] Материалы лекции
  • [обязательно] Учебник: ПШ — Глава 2.4: Поле Клейна-Гордона в пространстве-времени
  • [обязательно] Учебник: ПШ — Глава 4.3: Теорема Вика
Лекция 7: Диаграммная техника Фейнмана (Побойко И.)
5 апреля 2017 г.
  • [обязательно] Материалы лекции
  • [обязательно] Учебник: ПШ — Глава 4.2: Разложение корреляционных функций по теории возмущений
  • [обязательно] Учебник: ПШ — Глава 4. 4: Диаграммы Фейнмана
Лекция 8: Функциональный интеграл и квантовая теория поля (Побойко И.)
19 апреля 2017 г.
  • [обязательно] Материалы лекции
  • [обязательно] Учебник: ПШ — Глава 9.2: Функциональное квантование скалярных полей
Лекция 9: Функциональный интеграл в многочастичной квантовой механике (Побойко И.)
26 апреля 2017 г.
  • [обязательно] Материалы лекции
  • [рекомендовано] Учебник: Altland, Simons — Глава 4: Functional field integral
  • [рекомендовано] Учебник: Altland, Simons — Глава 6.3: Bose-Einstein condensation and superfluidity
Лекция 10: Элементы теории Ланду фазовых переходов второго рода (Побойко И.
) 10 мая 2017 г.
  • [обязательно] Материалы лекции
  • [рекомендовано] Учебник: В.В. Лебедев Флуктуационные эффекты в макрофизике

Задания

Таблица с результатами

Литература

  • [обязательно] М.Е. Пескин, Д.В. Шрёдер «Введение в квантовую теорию поля», 2001
  • [рекомендовано] Л.С. Левитов, А.В. Шитов «Функции Грина. Задачи и решения.», ФИЗМАТЛИТ, 2003
  • [рекомендовано] Э. Зи, «Квантовая теория поля в двух словах», 2009
  • [рекомендовано] А.А. Абрикосов, Л.П. Горьков, И.Е. Дзялошинский, «Методы квантовой теории поля в статистической физике», Физматгиз, 1962
  • [рекомендовано] Alexander Altland and Ben Simons, «Condensed Matter Field Theory» (Second Edition), Cambridge University Press, 2010
  • [обязательно] Полное собрание материалов к курсу

почему физики вынуждены искать квантовую теорию гравитации / Хабр

Математику, используемую в науке вообще и в физике в частности, часто сравнивают с языком – а это создаёт впечатление, что в основном она служит секретным кодом для отпугивания чужаков и что это больше неудобство, чем необходимость. И хотя я поддерживаю и высоко ценю популяризацию науки, аккуратное избегание технических терминов и уравнений приводит к тому, что математика воспринимается как нечто необязательное, в лучшем случае – скоропись, а в худшем – инструмент пыток. Но математика – это гораздо большее.

Математика в первую очередь – это дисциплина мыслей. Она очищена от неопределённости языка и служит инструментом вывода последствий из предположений. Она не подвержена человеческим слабостям, не знает жалости и стоит на страже объективности.

Современная теоретическая физика работает, создавая теории на основе набора предположений или аксиом, хотя они не обязательно должны быть чётко установлены и иногда задаются лишь неявно. Тем не менее, будучи сформулированным в математических терминах, эти предположения приводят к гораздо большему набору заключений, навязываемых физикам. Чтобы теория стала допустимой в смысле её применимости ко Вселенной, все эти выводы должны быть как внутренне непротиворечивыми, то есть не порождать противоречий, так и совпадать с наблюдениями.

Для описания самых фундаментальных уровней природы на текущий момент у нас есть две теории – ОТО и Стандартная модель в физике частиц. ОТО – это классическая теория, а Стандартная модель – квантовая теория поля. Первая не подчиняется принципу неопределённости Гейзенберга, вторая подчиняется. Две теории вместе способны описать все существующие наблюдения, хотя некоторые аспекты этих описаний нас не совсем удовлетворяют, например, отсутствующая микроскопическая структура тёмной материи. Комбинация двух теорий совпадает с наблюдениями, но неприятность состоит в том, что между собой они не согласуются.

Это несоответствие лучше всего демонстрирует проблема потери информации в чёрной дыре. Комбинируя ОТО с квантовой теорией поля мы получаем нечто под названием «квантовая теория поля в искривлённом пространстве». Она частично классическая, частично квантовая и поэтому называется «полуклассической гравитацией». В этой комбинированной теории можно подсчитать, что чёрные дыры испускают излучение, называемое «излучением Хокинга», в честь его первооткрывателя.

Излучение Хокинга – спектр чёрного тела без особых примет и без определяющих параметров, за исключением одного: его температуры, зависящей от изначальной массы чёрной дыры. Это значит, что все чёрные дыры с одинаковой начальной массой испаряются, выдавая совершенно одинаковое тепловое излучение, вне зависимости от того, из чего они сформировались. Процесс формирования и последующего испарения чёрной дыры не является обратимым: даже если мы знаем всё о конечном состоянии, мы не можем определить начальное. Информация теряется. Проблема в том, что такой, по сути, необратимый процесс несовместим с квантовой теорией поля, использовавшейся для вывода этого процесса: это внутреннее противоречие, несоответствие – и, следовательно, природа так работать не может. Математика навязала нам это заключение.

Полуклассическая комбинация ОТО и Стандартной модели приводит к другим проблемам. К примеру, нам неизвестно, что происходит с гравитационным полем электрона, проходящего через двойную щель.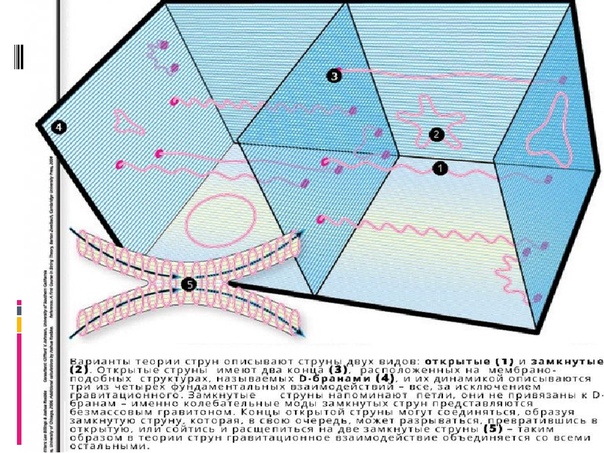 Мы знаем, что волновая функция электрона находится в суперпозиции и проходит через обе щели, создавая статистическое распределение на экране во время измерения. Также мы знаем, что электрон переносит энергию. И мы знаем, что энергия создаёт гравитационное поле. Но поскольку гравитационное поле классическое, оно не может находиться в суперпозиции и проходить через обе щели, как электрон. Что происходит с гравитационным полем электрона? Никто не знает, поскольку оно слишком слабое, чтобы его можно было измерить. Так просто и так обидно!

Третья причина, убеждающая физиков в неполноте комбинации ОТО и СМ состоит в том, что она ведёт к появлению сингулярностей при достаточно обычных обстоятельствах. Сингулярности – объекты с бесконечной плотностью энергии и кривизной. Они не физические и не должны появляться в осмысленной теории. Они также появляются, к примеру, в гидродинамике, при отделении капли воды. Но в последнем случае известно, что сингулярность – артефакт использования приближений в гидродинамике, которая не работает на субатомных расстояниях. На очень коротких расстояниях нужно использовать более фундаментальные теории (то есть, теорию квантовых, отдельных частиц) для описания капли воды и в них нет никаких сингулярностей, чего и следует ожидать.

Считается, что квантификация гравитации решит эти три проблемы, обнажив структуру пространства-времени на сверхмалых расстояниях. К сожалению, гравитацию нельзя квантифицировать, как остальные взаимодействия стандартной модели. Если применить эти методы к гравитации, то мы приходим к теории «эффективной квантовой гравитации», которая не может решить эти проблемы – она всё равно ломается при сильной кривизне. Эта наивным образом («пертурбативно») квантифицированная гравитация не подходит для решения задач с сингулярностями и испарением чёрных дыр, потому что она работает только при слабой гравитации. Она не имеет смысла в качестве фундаментальной теории. Говоря о «квантовой гравитации», физики обычно имеют в виду теорию, которая бы работала вне зависимости от того, насколько сильной будет гравитация.

К квантовой гравитации существует несколько теоретических подходов. Самые известные из них, это асимптотически безопасная гравитация, петлевая квантовая гравитация, теория струн и причинная динамическая триангуляция, а также идеи, которые всерьёз относятся к аналогии с гидродинамикой и считающие гравитацию производным явлением. Пока что нельзя сказать, какой из трёх подходов правильно описывает природу.

По следам измерения поляризации в космическом микроволновом фоновом излучении BICEP (сейчас установлено, что это лишь следствие пыли, находящейся на переднем плане), было сделано заявление, что такое измерение выдаст нам доказательство квантификации гравитации. Это не совсем верно. Во-первых, это относится только к слабым гравитационным полям и значит, не к фундаментальной теории квантовой гравитации. Кроме того, нужно осторожно относиться к предположениям, сделанным ради спора. Действительно, квантовые гравитационные флюктуации в ранней Вселенной должны были оставить отпечаток на фоновом излучении, который в теории можно разглядеть. Однако гораздо сложнее будет доказать, что квантовая гравитация – это единственный способ создать наблюдаемые флюктуации. Для такого заключения потребуется нечто вроде теоремы Белла, доказательства, демонстрирующего, что классическая теория этого не могла бы сделать – а такого доказательства нет.

Квантовая гравитация — не такая большая область для исследований, как, скажем, физика конденсированных сред или исследования рака. Это небольшое сообщество, которое, тем не менее, притягивает большой интерес общественности. И это происходит не зря. Без квантовой гравитации мы не знаем, как ведут себя пространство и время, и не поймём, как началась наша Вселенная. Нам необходима теория квантовой гравитации для объяснения того, как устроен космос и как он возник.

Я также верю, что эта теория даст нам важные уроки о квантификации, которые пригодятся нам на практике. Если послушать приверженцев теории струн, то этот процесс уже пошёл, независимо от того, сможет ли теория струн решить проблему потери информации в чёрной дыре!

Притягательностью квантовая гравитация обязана чистоте задачи и неизбежности математической логики, приводящей к заключению об отсутствии важной части головоломки. Нам предстоит узнать, будет ли достаточно чисто математического подхода для того, чтобы найти эту часть. Если нет, наши заключения останутся двусмысленными, а путеводных данных больше не останется.

Квантовая теория поля при конечной температуре и во внешних полях

Курс посвящён квантовой теории поля в плазме при конечной температуре, а также во внешних электромагнитных полях. Первая часть курса описывает квантовую теорию поля во внешней среде, находящейся в термодинамическом равновесии. Для вычисления физических величин, не зависящих от времени, применяется формализм Мацубары. Согласно ему, средние от статических операторов по каноническому статистическому ансамблю выражаются с помощью квантовой теории поля с евклидовым временем. Для вычисления средних от динамических величин будет используется неравновесная техника Швингера-Келдыша. Температурная теория поля используется как в космологии для описания процессов в ранней Вселенной на горячей стадии (фазовые переходы в квантовой хромодинамике и для хиггсовского поля), так и при изучении продуктов столкновения тяжёлых ионов (кварк-глюонной плазмы и других фаз кварковой материи). Также её методы используются в физике конденсированного состояния.

Во второй части курса вместо внешней среды, находящейся в термодинамическом равновесии, исследуется внешнее электромагнитное поле. Эта область науки начала развиваться ещё в 1930-е годы (уровни Ландау, лагранжиан Эйлера-Гейзенберга). Значительный вклад был в квантовую теорию поля во внешнем поле был сделан во второй половине 20 века как отечественными (Никишов, Ритус, Шабад и др.), так и зарубежными (Швингер и др.) учёными. Тем не менее на текущий момент также активно продолжаются исследования, в основном сконцентрированные на приложениях в двух областях физики: физике сверхсильных световых полей (получаемых на современном поколении лазеров) и в астрофизике (космические лучи, влияние магнитных полей и плазмы на их источники и распространение в межзвёздной среде). В физике сверхсильных световых полей происходит попытка зарегистрировать нелинейные и непертурбативные процессы (рассеяния света на свете, многофотонный процесс Брейта-Уиллера, индуцированный эффект Швингера и др. ) в текущих и будущих лабораторных экспериментах со сверхсильными световыми полями, что подстёгивает и теоретические исследования по этой теме. Для определённых астрофизических и лабораторных процессов необходим одновременный учёт как электромагнитного поля, так и термальной среды.

Ссылка на страницу курса: http://ppc.inr.ac.ru/QFT_in_EF…

Список всех тем лекций

Лекция 1. Введение.
Представление лектора, общий план и особенности курса Обзор Статистическая физика для квантовых полей, некоторые замечания Термальное равновесие Неравновесная теория Обзор применения моделей статистической физики Список литературы Обзор Матрица плотности Новый вид матрицы плотности

Лекция 2. Введение в формализм континуального интеграла.
Введение Формализм континуального интеграла в квантовой механике Континуальный интеграл в термальной квантовой механике Континуальный интеграл в КТП

Лекция 3. Континуальный интеграл. Фермионные поля.
Представления о континуальном интеграле в квантовой и термальной механике Континуальный интеграл в в квантовой механике Матрица плотности для частицы в термальной бане/ Континуальный интеграл в термальной теории Различия между континуальным интегралом в обычной и термальной квантовой механике Континуальный интеграл в квантовой теории поля Статистическая теория в представлениях континуального интеграла Среднее от одного оператора фи Среднее от нескольких операторов фи Корреляторы через производящий функционал, зависящий от источников Вычисление двухточечной функции Грина для свободного скалярного поля для обычной теории поля и термальной теории Вычисление двухточечной функции Грина для свободного скалярного поля для обычной теории поля Вычисление двухточечной функции Грина для свободного скалярного поля для термальной теории поля и ее отличия от обычной теории Фермионные поля Грассман переменные Кратко о теории поля Вывод фермионного пропагатора для термальной теории поля

Лекция 4. Вычисление свободной энергии.
Бозоны и фермионы: отличия. Выражение свободной энергии Вычисление свободной энергии Представление суммы в виде интеграла Вычисление плотности свободной энергии, зависящей от температуры для скалярного поля Вычисление плотности свободной энергии, зависящей от температуры для скалярного поля при p много большем чем m Плотность свободной энергии для фермионного газа

Лекция 5. Континуальный интеграл в теории возмущений.
Свободное скалярное поле Химический потенциал Большой канонический ансамбль Статистический оператор Большой термодинамический потенциал (омега-потенциал) Термодинамический потенциал в лагранжевом формализме Континуальный интеграл в теории возмущений Свободная теория Четырехточечная теория Четырехточечная теория в диаграммах Теория со взаимодействием Выражение для пропагатора Выражение для поправки пропагатора Введение перенормировки массы Вычисление для поправки к массе частицы при T много большем чем m Вычисление свободной энергии Поправки первого порядка Коротко о поправках второго и более высоких порядков Применение теории поля

Лекция 6. Теория возмущений. Поправки второго порядка.
Введение Теория лямбда фи4 Ring и deisy диаграммы n-ного порядка Поправка к эффективной массе

Лекция 7. Эффективный потенциал.
Введение Лямбда фи-4 Массивная теория поля ИК расходимости Потенциал типа «мексиканская шляпа» Эффективная теория Ландау — Гинзбурга Фазовый переход рода рода Отличия между фазовыми переходами 1-го и 2-го родов Зависимость эффективного потенциала от температуры Фазовый переход 2-го порядка Вклад материи в эффективный потенциал Инфракрасная расходимость Выводы

Лекция 8. Безмассовые калибровочные поля.
Термальная масса для скалярного поля Безмассовые калибровочные поля Фотоны Калибровка Лоренца во временной теории поля и псевдокалибровка Лоренца в термальной теории поля Суммирование одночастично приводимых диаграмм с поляризационным оператором Термальная теория поля Мацубаровские частоты для реальных фотонов Кулоновский потенциал в термальной бане Интеграл по d3k в случаях m много больше чем t, m много меньше чем t Скалярный потенциал для статического электромагнитного поля с однопетлевой поправкой

Лекция 9. Квантовая хромодинамика.
Пропагатор Квантовая хромодинамика Классическая хромодинамика Квантование Духи и антидухи Вклад в f от свободного лагранжиана   Поправка f(1) от t Диаграмма   Четвертый порядок  Разложение по малому параметру m/t степени и поправка альфа с в степени 3/2 Эффективные теории и эффективные лагранжианы для квантовой хромодинамики Расстояния L много больше обратной дебаевской массы Dimensiond reduction

Лекция 10. Теория линейного отклика.
Введение Теория линейного отклика на внешние возмущения, зависящие от времени Вывод формулы Кубо Обобщение формулы Кубо (квантовая механика) Вывод временной двухточечной функции Грина в термальной бане Ретардед (запаздывающая функция Грина) Связь между запаздывающим realtime пропагатором и мацубароским пропагатором для подсчета линейных откликов по формуле куба к внешнему взаимодействию/ связь между realtime и термальными пропагаторами Спектральная функция Выражение для спектральной функции Термальный пропагатор

Лекция 11. Применение теории линейного отклика. Техника Келдыша.
Формула Кубо Поправка к поляризационному оператору Возбуждение в плазме на языке квазичастиц Плоская затухающая волна Вклады продольной и поперечной волн Плазменная частота Применение теории линейного отклика Тензор энергии-импульса для идеальной жидкости Тензор энергии-импульса для неидеальной жидкости Формулы Кубо Техника Келдыша Двухточечные корреляторы Построение теории возмущения

Лекция 12. Квантовая теория поля во внешних электромагнитных полях.
Квантовая теория поля во внешних электромагнитных полях Магнитное поле Решение уравнения Дирака в магнитном поле Представление уравнения Дирака в форме уравнения Шрёдингера Стационарное уравнение Шрёдингера Оператор Тo Тау 0 Переход к виду гамильтониана гармонического осциллятора Квантовые «уровни Ландау» Выражение для гамильтониана Выражение Po Уровни энергии Собственные функции Состояние с определенным спином Нулевой уровень Ландау Диаграмма Фейнмана Решение уравнения Дирака для скрещенных полей

Лекция 13. Фейнмановские правила для квантовой электродинамики во внешнем магнитном поле.
Описание процессов в квантовой электродинамики во внешнем магнитном поле Диаграммная техника Фейнмана Поляризационные векторы  Распад фотона на электрон-позитронную пару в сильном поле Волновые функции электрона и позитрона Матричный элемент Квадрат матричного элемента Интегрирование квадрата матричного элемента по импульсам выходящих частиц Пропагатор с однопетлевой поправкой для фотона Мнимая часть поляризационного оператора Метод собственного времени Фока-Швингера

Лекция 14. Методы квантовой механики.
Метод собственного времени Фока-Швингера Пропагатор для комплексных скаляров Пропагатор для электрона во внешнем магнитном поле Решение по Швингеру Решение уравнения для частицы единичной массы во внешнем электромагнитном поле Метод для пропагатора Эффективное действие для электромагнитного поля Интегрирование по частям Второй метод через производящий функционал Анонс следующей лекции

Лекция 15. Лагранжиан Эйлера-Гейзенберга.
Эффективное действие для фотонов и электромагнитного поля След гамма-матриц Гамильтониан в магнитном поле Эффективный лагранжиан Лагранжиан Эйлера- Гейзенберга Разложение по малым е Перенормировка эффективного лагранжиана Полный перенормированный лагранжиан Многофотонные процессы и диаграммы Эффективный лагранжиан в электрическом поле Мнимая часть эффективного лагранжиана

Лекция 16. Эффект Швингера.
Сумма по полюсам Мнимая часть эффективного лагранжиана Производящий функционал z Вероятность того, что вакуум останется вакуумом за промежуток T=tf-ti Эффект Швингера Квантово-механическое туннелирование Согласованная картина эффекта Швингера с описанием эффекта квантово-механического туннелирования Выражение эффективного действия Мнимая часть эффективного действия в представлении функционального интеграла Евклидовый функциональный интеграл Квазиклассика, седловое решение уравнения движения, подстановка решений в показатель экспоненты Седловое уравнение по S Уравнения движения Решения уравнений движения Wordline и больше Подстановка решения в эффективное действие Условия швингеровского рождения пар Распад фотона в электрическом и магнитном поле Электрическое поле Магнитное поле Выводы

Вот почему квантовая теория поля более фундаментальна, чем квантовая механика

Дерек Лайнвебер

Если вы хотите ответить на вопрос о том, что действительно фундаментально во Вселенной, вам нужно будет исследовать материю и энергию в минимально возможных масштабах. Если вы попытаетесь разделить частицы на все меньшие и меньшие составляющие, вы начнете замечать некоторые чрезвычайно забавные вещи, как только вы перейдете на расстояние меньше нескольких нанометров, где все еще применяются классические правила физики.

В еще меньших масштабах реальность начинает вести себя странным, нелогичным образом. Мы больше не можем описывать реальность как состоящую из отдельных частиц с четко определенными свойствами, такими как положение и импульс. Вместо этого мы попадаем в сферу кванта: где правит фундаментальный индетерминизм, и нам нужно совершенно новое описание того, как работает природа. Но даже сама квантовая механика имеет здесь свои недостатки. Они с самого начала обрекли на провал величайшую мечту Эйнштейна — о полном детерминированном описании реальности.Вот почему.

Общие пользователи Викимедиа Майкл Мэггс и (отредактированный) Ричард Бартц

Если бы мы жили в полностью классической неквантовой Вселенной, разобраться в вещах было бы легко. Разделяя материю на более мелкие и мелкие куски, мы никогда не достигнем предела. Не было бы фундаментальных неделимых строительных блоков Вселенной. Вместо этого наш космос будет сделан из непрерывного материала, и если мы построим пресловутый более острый нож, мы всегда сможем разрезать что-то на все меньшие и меньшие куски.

Эту мечту осуществили динозавры в начале 20 века. Эксперименты Планка, Эйнштейна, Резерфорда и других показали, что материя и энергия не могут состоять из непрерывного вещества, а могут быть разделены на дискретные части, известные сегодня как кванты. Первоначальная идея квантовой теории имела слишком много экспериментальных подтверждений: Вселенная в конечном итоге не была классической по своей сути.

Институт периметра

В течение, возможно, первых трех десятилетий 20-го века физики изо всех сил пытались разработать и понять природу Вселенной в этих маленьких, загадочных масштабах. Нужны были новые правила, а для их описания — новые противоречащие интуиции уравнения и описания. Представления об объективной реальности улетучились, заменив их такими понятиями, как:

  • распределения вероятностей, а не предсказуемые результаты,
  • волновые функции, а не положения и импульсы,
  • Отношения неопределенностей Гейзенберга, а не отдельные свойства.

Частицы, описывающие реальность, больше нельзя было описывать исключительно как частицы, подобные. Вместо этого в них были элементы как волн, так и частиц, и они вели себя в соответствии с новым набором правил.

Э. Сигель / пользователь Wikimedia Commons Maschen

Изначально эти описания очень беспокоили физиков. Эти проблемы возникли не просто из-за философских трудностей, связанных с принятием недетерминированной Вселенной или измененным определением реальности, хотя, безусловно, многих беспокоили эти аспекты.

Вместо этого трудности были более серьезными.Специальная теория относительности была хорошо изучена, и все же квантовая механика в том виде, в котором она была первоначально разработана, работала только для нерелятивистских систем. Преобразуя такие величины, как положение и импульс, из физических свойств в квантово-механические операторы — особый класс математических функций — эти странные аспекты реальности можно было бы включить в наши уравнения.

Стив Бирнс / Sbyrnes321 из Wikimedia Commons

Но то, как вы позволяли вашей системе развиваться, зависело от времени, а понятие времени у разных наблюдателей разное. Это был первый экзистенциальный кризис, с которым столкнулась квантовая физика.

Мы говорим, что теория релятивистски инвариантна, если ее законы не меняются для разных наблюдателей: для двух людей, движущихся с разной скоростью или в разных направлениях.Формулировка релятивистски инвариантной версии квантовой механики была проблемой, на преодоление которой величайшие умы физиков потребовалось много лет, и наконец была решена Полем Дираком в конце 1920-х годов.

Пользователь Wikimedia Commons Krea

Результатом его усилий стало то, что теперь известно как уравнение Дирака, которое описывает реалистичные частицы, такие как электрон, а также учитывает:

  • антивещество,
  • собственный угловой момент (он же спин),
  • магнитных моментов,
  • Свойства тонкой структуры материи,
  • и поведение заряженных частиц в присутствии электрического и магнитного полей.

Это был большой скачок вперед, и уравнение Дирака прекрасно описало многие из самых первых известных фундаментальных частиц, включая электрон, позитрон, мюон и даже (в некоторой степени) протон, нейтрон и нейтрино.

Аманда Йохо

Но он не мог учесть всего. Фотоны, например, нельзя полностью описать уравнением Дирака, поскольку они обладают неправильными свойствами частиц. Электрон-электронные взаимодействия были хорошо описаны, а фотонно-фотонные взаимодействия — нет. Объяснение таких явлений, как радиоактивный распад, было совершенно невозможно даже в рамках релятивистской квантовой механики Дирака.Даже при таком огромном прогрессе не хватало главного компонента истории.

Большая проблема заключалась в том, что квантовая механика, даже релятивистская квантовая механика, не была достаточно квантовой, чтобы описать все в нашей Вселенной.

Дж. Белчер в Массачусетском технологическом институте

Подумайте, что произойдет, если поместить два электрона близко друг к другу. Если вы мыслите классически, вы будете думать об этих электронах как о каждом, генерирующем электрическое поле, а также как о магнитном поле, если они находятся в движении. Затем другой электрон, видя поле (я), созданное первым электроном, будет испытывать силу при взаимодействии с внешним полем. Это работает в обоих направлениях, и таким образом происходит обмен силой.

Это будет работать для электрического поля так же хорошо, как и для любого другого типа поля: например, для гравитационного поля. У электронов есть масса, а также заряд, поэтому, если вы поместите их в гравитационное поле, они будут реагировать на основе своей массы так же, как их электрический заряд заставит их реагировать на электрическое поле. Даже в общей теории относительности, где пространство кривых массы и энергии, это искривленное пространство непрерывно, как и любое другое поле.

Рэй Шапп / Майк Лучук; модифицирован Э. Сигелем

Проблема с этим типом формулировки состоит в том, что поля находятся на том же основании, что и положение и импульс при классической трактовке. Поля давят на частицы, расположенные в определенных положениях, и изменяют их импульс. Но во Вселенной, где положения и импульсы неопределенны и должны рассматриваться как операторы, а не как физическая величина со значением, мы сокращаем себя, позволяя нашей трактовке полей оставаться классической.

Это был большой шаг вперед идеи квантовой теории поля или связанного с ней теоретического прогресса: вторичного квантования.Если рассматривать само поле как квантовое, оно также становится квантово-механическим оператором. Внезапно, процессы, которые не были предсказаны (но наблюдаются) во Вселенной, например:

  • создание и уничтожение материи,
  • радиоактивных распадов,
  • квантовое туннелирование для создания электрон-позитронных пар,
  • и квантовые поправки к магнитному моменту электрона,

все имело смысл.

de Carvalho, Vanuildo S. et al. Nucl.Phys. B875 (2013) 738-756

Хотя физики обычно думают о квантовой теории поля с точки зрения обмена частицами и диаграмм Фейнмана, это всего лишь вычислительный и визуальный инструмент, который мы используем, чтобы попытаться добавить некоторый интуитивный смысл к этому понятию.Диаграммы Фейнмана невероятно полезны, но они представляют собой пертурбативный (то есть приближенный) подход к вычислениям, а квантовая теория поля часто дает захватывающие, уникальные результаты, если вы принимаете непертурбативный подход.

Но мотивация для квантования поля более фундаментальна, чем аргумент между сторонниками пертурбативного или непертурбативного подходов. Вам нужна квантовая теория поля, чтобы успешно описывать взаимодействия не только между частицами и частицами или частицами и полями, но также между полями и полями.Благодаря квантовой теории поля и дальнейшему развитию ее приложений все, от фотон-фотонного рассеяния до сильного ядерного взаимодействия, стало теперь объяснимым.

В то же время сразу стало ясно, почему подход Эйнштейна к объединению никогда не сработает. Вдохновленный работой Теодра Калуцы, Эйнштейн был очарован идеей объединить общую теорию относительности и электромагнетизм в единую структуру. Но общая теория относительности имеет фундаментальное ограничение: это классическая теория по своей сути с ее понятием непрерывного неквантованного пространства и времени.

Если вы отказываетесь квантовать свои поля, вы обрекаете себя на упущение важных, внутренних свойств Вселенной. Это было роковой ошибкой Эйнштейна в его попытках объединения и причиной того, что его подход к более фундаментальной теории был полностью (и оправданно) отвергнут.

Национальная лаборатория ускорителей SLAC

Вселенная снова и снова демонстрирует квантовую природу. Эти квантовые свойства проявляются в самых разных приложениях, от транзисторов до светодиодных экранов до излучения Хокинга, которое вызывает распад черных дыр.Причина, по которой квантовая механика фундаментально ошибочна сама по себе, заключается не в странности, которую принесли новые правила, а в том, что она не зашла достаточно далеко. Частицы действительно обладают квантовыми свойствами, но они также взаимодействуют через поля, которые сами по себе являются квантовыми, и все это существует релятивистски-инвариантным образом.

Возможно, мы действительно достигнем теории всего, в которой каждая частица и взаимодействие будут релятивистскими и квантованными. Но эта квантовая странность должна быть частью каждого ее аспекта, даже тех частей, которые мы еще не квантовали.По бессмертным словам Холдейна: «Я лично подозреваю, что Вселенная не только причудливее, чем мы думаем, но и еще причудливее, чем мы можем предположить».

Квантовая теория поля: квантовая физика в плохом настроении

Человечество немного похоже на щенка. Мы провели последние несколько тысячелетий, путешествуя по планете, стремясь исследовать, но из-за отсутствия заботы мы создали ужасный беспорядок. Если бы инопланетная раса предала нас суду за наши преступления (как Q в Star Trek: The Next Generation ), нам пришлось бы сунуть хвост между ног и признать, что мы облажались.

Но можем ли мы предложить что-нибудь в нашу пользу? Есть ли что-то, что мы могли бы преподнести этим инопланетным повелителям, что доказало бы, что, несмотря на наши ошибки, человечество движется в правильном направлении? Я считаю, что нам нужно показать им две вещи. Во-первых, это собрание кинематографических работ Джейсона Стэтхэма, начиная с The Meg (той, где он сражается с акулой-динозавром). Во-вторых, нам необходимо представить наше понимание квантовой теории поля — самого передового научного открытия, которое мы когда-либо делали.

Подробнее о квантовой физике:

Квантовая теория поля не так широко освещается в популярной науке, и если вы откроете какой-нибудь учебник по этому предмету, вы поймете, почему. Это похоже на нечестивую смесь квантовой физики в плохом настроении и каждой кнопки, которую вы никогда не нажимаете на калькуляторе. Идея резюмировать это в 1500 слов или меньше для этой статьи сначала казалась устрашающей (потребовалась целая глава, чтобы охватить это в моей недавней книге), но опять же, если бы мне действительно пришлось представить это жюри инопланетян, я бы не стал ». У меня нет выбора.

Поэтому, ваша честь, я прошу вас уделить мне пять минут вашего межгалактического внимания. В моей презентации может не быть Джейсона Стэтхэма с разворота, ударившего акулу по глазному яблоку, но я попытаюсь оправдать продолжающееся существование человеческой расы. Вот и…

Любой объект можно описать в терминах составляющих его частиц, а любое событие можно описать в терминах взаимодействия этих частиц. Чем больше мы знаем о поведении частиц, тем больше явлений мы можем объяснить.Это цель квантовой физики; чтобы узнать все фундаментальные законы частиц и использовать их, чтобы понять все.

Но все очень быстро усложняется, потому что каждый тип частиц имеет свой собственный набор законов. Квантовые правила, управляющие ядерными взрывами, отличаются от квантовых правил, управляющих мутациями ДНК, поэтому существует не одна версия квантовой физики, а несколько.

Квантовая теория поля — это попытка объединить эти различные наборы законов и сформулировать единую структуру, которая учитывает все сразу, вместо того, чтобы иметь несколько разновидностей одной и той же теории.

Это грандиозная амбиция, но что нам нужно указать инопланетянам, осуждающим нас, так это то, что мы действительно преуспели в этом. Мы действительно открыли объединяющий принцип, который, кажется, объясняет всю квантовую физику, и все, что остается, — это экстраполировать этот принцип на различные сценарии.

Предположительно, конечно, инопланетяне, слушающие нашу просьбу, уже открыли для себя квантовую теорию поля. Следовательно, нам нужно доказать, что мы действительно знаем, что утверждает центральная идея, и именно здесь все становится странно (что также стоит изучить).

Когда мы занимаемся обычной физикой, мы традиционно представляем частицы как маленькие шарики, летающие в пустом пространстве. Это полезный способ изобразить Вселенную, но он не объясняет, почему разные типы частиц подчиняются разным законам. Квантовая теория поля решает загадку, радикально изменив картину: полностью отказаться от идеи частиц, потому что их на самом деле не существует.

Представьте себе смерч, движущийся по воздуху. Хотя мы думаем о нем как о замкнутом объекте, мы знаем, что он на самом деле не является «вещью» сам по себе.Это просто колебание, сотканное из окружающего воздуха. То же самое можно сказать и о волне, колеблющейся по поверхности океана. Он выглядит как отдельный объект, движущийся независимо от спокойной воды вокруг него, но мы знаем, что волна и ее окружение на самом деле сделаны из одного и того же материала. Согласно квантовой теории поля, именно так нам нужно понимать частицы.

Одно из величайших достижений человеческой цивилизации?

В квантовой теории поля пустое пространство на самом деле не пусто.Он наполнен тем, что физики называют «полями» — жидкими субстанциями, которые распространяются во всех направлениях. Точно так же, как вода в нашей аналогии с океаном или воздух в нашей аналогии с торнадо, эти поля обычно бездействуют, но если они будут возбуждены, очаги турбулентности могут пузыриться и перемещаться, как если бы они были отдельными объектами. Мы называем эти маленькие сгустки энергии, появляющиеся в поле, «квантами» или, если хотите, частицами.

Частицы, которые мы используем в обычной физике для описания мира, на самом деле не являются кусками материи, движущимися в космосе, это миниатюрные торнадо, образованные из всепроникающих полей, заполняющих нашу Вселенную.В каком-то смысле частицы — это иллюзия.

Может показаться, что идея о том, что вы на самом деле не созданы из чего-то тревожного, но квантовая теория поля сделала ряд нокаутных предсказаний, от которых трудно отказаться. Например, существование бозона Хиггса. Существование антивещества и нейтрино для другого. Не говоря уже о предсказании так называемой «постоянной тонкой структуры» (мера того, насколько хорошо электроны взаимодействуют со светом) до самого большого числа десятичных знаков, когда-либо зарегистрированных.

Квантовая теория поля также позволила нам собрать под одной крышей различные версии квантовой физики, и почти все, что мы хотим изучать сейчас, от химии продуктов питания до огнеметов, можно понять с одного и того же исходного предположения: Вселенная — это собрание. перекрывающихся полей, и то, что мы думаем как материя, — это просто трехмерные выпуклости, образующиеся в этих полях.

Мы еще не выяснили все детали и не нашли способа использовать ее для объяснения гравитации, но квантовая теория поля — это самое глубокое из того, что мы копали в ткани реальности, и она способна объяснить все, что мы испытываем. .

Итак, если будет угодно космическому суду, я представляю вам самый передовой прорыв, сделанный человечеством на сегодняшний день. Да, мы запекаем нашу атмосферу, обезглавливаем наши тропические леса и топим океаны пластиком, но мы не пропали без вести.

Учитывая, что мы только начали заниматься правильной наукой несколько веков назад и уже раскрыли единственный основной принцип всех физических явлений во Вселенной, я думаю, что это достаточное свидетельство, чтобы показать, что у нас есть потенциал.

Если этого все же недостаточно, вы все равно можете поймать Джейсона Стэтхэма в главной роли в боевике-блокбастере Форсаж: Гоббс и Шоу, только в кинотеатрах.

Фундаментальный: Как квантовая физика и физика элементарных частиц объясняют абсолютно все (кроме гравитации) Тима Джеймса доступен сейчас (13 фунтов стерлингов.99, Маленький Браун)

Следите за Science Focus в Twitter, Facebook, Instagram и Flipboard

Диссипативный подход к квантовой теории поля: концептуальные основы и онтологические последствия

Методологические и метафизические руководящие принципы

Диссипативный подход к QFT построен на основе набора методологических и метафизических руководств, которые мы считаем разумными требованиями для построения последовательной теоретической основы из обоих формальная и онтологическая перспектива.Как уже говорилось, основная цель такого предложения состоит в том, чтобы сформулировать альтернативную эффективную квантовую теорию полей, способную решить основные проблемы, влияющие на ее стандартную формулировку, исходя из четких оснований. Поэтому давайте представим критерии, которые мы принимаем и используем в этом эссе Footnote 3 :

  • Мы считаем математическую непротиворечивость и строгость необходимыми условиями любой устойчивой физической теории. С одной стороны, математическая последовательность — это достоинство, полезное для предложения эмпирически адекватной физической теории, т. Е.е. теоретическая основа, способная воспроизводить статистику наблюдаемых экспериментальных результатов, избегая вычислительных недостатков. С другой стороны, это гарантирует, что теории не приводят к противоречивым результатам. Ссылаясь на это, в этом разделе будет показано, что математическая структура DQFT является последовательной и строгой, поскольку основана на наборе четких понятий и динамических уравнений, основанных на неравновесной термодинамике, которые гарантируют, что используемые формальные механизмы не будут затронуты проблемами. характеризуя стандартную формулировку QFT; Фактически можно сказать, что цель термодинамики состоит в том, чтобы охарактеризовать и сформулировать устойчивые уравнения, которые имеют математический смысл, то есть для которых можно доказать существование и единственность решений.

  • Предполагается фоновое конечное пространство-время Минковского, поскольку физические явления, рассматриваемые с помощью КТП, обычно представляются как события, происходящие в релятивистских условиях пространства-времени. Это предположение влечет за собой несколько математических следствий; например, можно сохранить неоднородные преобразования Лоренца и, следовательно, классификацию Вигнера частиц по массе и спину, рассматривая их как неотъемлемые фундаментальные свойства элементарных частиц (см.Раздел 3). Кроме того, следует подчеркнуть, что DQFT не касается внутренней природы пространства-времени: в дальнейшем мы остаемся агностиками по отношению к его онтологии, рассмотрение которой потребует более глубокой теории относительно QFT. Как следствие, мы рассматриваем последнюю в явном виде как эффективную теорию, справедливую только в определенном диапазоне масштабов энергии и длины. Таким образом, можно рассматривать выбор такого фонового пространства-времени как упрощающее предположение. Сноска 4

  • Переходя к метафизическим принципам, мы стремимся дать реалистичную картину происходящих объектов и процессов в масштабе QFT.Точнее, мы точно определим, каковы теоретические сущности, представляющие реальные объекты в мире и их динамическое поведение в физическом пространстве, избегая метафизической неопределенности, влияющей на стандартную КТП. Пока достаточно заявить, что такая онтология гарантирует, что диссипативная КТП будет иметь точную приверженность существованию четко определенного набора объектов, реальность которого не зависит от каких-либо наблюдений и измерений. Следовательно, мы утверждаем, вопреки широко распространенному мнению в философской литературе, что можно восстановить реалистичную картину физических процессов, происходящих в космосе, также в контексте КТП.

  • Чтобы решить концептуальные и технические проблемы, возникающие из-за различных типов бесконечностей, возникающих в стандартной КТП по построению, мы предполагаем, что в соответствии с диссипативным подходом такие бесконечности считаются только потенциальными, а не актуальными. Следовательно, в настоящей теории мы сохраняем число квантовых частиц всегда конечным и счетным, так что физические состояния могут быть описаны через представление пространства Фока.Как мы увидим в оставшейся части статьи, этот факт поможет нам обойти метафизические последствия бесконечного множества неэквивалентных представлений CCR. Кроме того, мы вводим ограничения, предотвращающие появление расхождений: с одной стороны, мы рассматриваем большие, но конечные объемы пространства, то есть конечную вселенную; этот факт, следовательно, налагает характерный масштаб длины и инфракрасную регуляризацию. С другой стороны, мы принимаем во внимание диссипативный механизм, необходимый для ультрафиолетовой регуляризации.Эти предположения имеют решающее значение для получения эмпирически адекватной и хорошо обоснованной теории. Сноска 5

  • Кроме того, мы предполагаем, что стохастичность естественным образом возникает в КТП, поскольку в такой структуре есть несколько случайных событий, которые нельзя ни механически контролировать, ни точно знать, как, например, флуктуации вакуума, вызывающие спонтанно возникающие и исчезающие электрон-позитронные пары.Существование таких событий и нашу неспособность узнавать и контролировать их следует рассматривать как естественный источник необратимого поведения. Следовательно, этот факт побуждает предложить стохастическую динамику для DQFT. Более того, поскольку последнее основано на аргументах, взятых из неравновесной термодинамики, мы должны подчеркнуть, что в таком контексте случайные флуктуации сопровождаются диссипацией, необратимостью и декогеренцией. Таким образом, кажется естественным, что КТП, основанная на неравновесной термодинамике, реализует стохастическую динамику, что также мотивировано экспериментальными данными и феноменологией квантовой теории полей.

Чтобы завершить эту предварительную иллюстрацию руководящих принципов DQFT, стоит еще раз подчеркнуть, что это явно эффективная теория, имеющая определенный характерный масштаб, лежащий между 10 — 20 м, который является масштабом суперколлайдеров, и 10 — 35 м, что является масштабом Планка. Следовательно, мы моделируем физические воздействия, обусловленные объектами и процессами в более высоких масштабах энергии, через тепловую ванну.Ссылаясь на это, мы в значительной степени полагаемся на современные методы перенормировки — разделяя аргументы в пользу них, изложенные в Уоллесе (2006), — которые являются важными инструментами, введенными для решения уже упомянутых проблем, касающихся бесконечностей и расходимостей, и сохранения нынешней теории формально четко определенной. . Сноска 6

Математическая арена: представление пространства Фока, операторы и поля создания и уничтожения

Пространство Фока \ (\ mathcal {F} \), особый вид комплексного векторного пространства со внутренним произведением, является математической ареной в что имеет место диссипативный подход к КТП.В этом пространстве состояний система независимых квантовых объектов, число которых может меняться во времени, представлена ​​следующим выражением:

$$ \ begin {array} {@ {} rcl @ {}} | n_ {i} \ rangle = | n_ {1}, n_ {2}, \ dots \ rangle. \ end {array} $$

(1)

Состояния в форме, написанной выше, представляют ортонормированный базисный вектор в \ (\ mathcal {F} \), где кет на правой стороне. указывает вектор, в котором n 1 представляет количество объектов в состоянии 1, n 2 представляет количество объектов в состоянии 2 и так далее.Стоит отметить, что уравнение. 1 только подсчитывает количество квантовых объектов, присутствующих в определенном состоянии, он не присваивает им никаких ярлыков, то есть эти объекты не обладают присущей им «таковостью» или «грубостью», выражаясь словами Теллера; иначе говоря, частицы одного и того же вида в одном и том же состоянии абсолютно неотличимы.

Кроме того, для бозонов каждое число заполнения n i является неотрицательным целым числом; для фермионов он должен быть 0 или 1 в силу принципа исключения Паули, который предотвращает возможность для разных фермионов занимать одно и то же состояние. {\ dagger} _ {i} | n_ {1}, n_ {2}, \ dots \ rangle = \ sqrt {n_ {i } +1} | n_ {1}, n_ {2}, \ dots, n_ {i} +1 \ rangle, \ end {array} $$

(2)

наоборот, оператор уничтожения a i уменьшает его на единицу:

$$ \ begin {array} {@ {} rcl @ {}} a_ {i} | n_ {1}, n_ {2}, \ dots \ rangle = \ left \ {\ begin {array} {ll} \ sqrt {n_ {i}} | n_ {1}, n_ {2}, \ dots, n_ {i} -1 \ rangle, \ \ text {for} \ n_ {i}> 0, \\ \\ 0 , \ \ text {for} \ n_ {i} = 0.{\ dagger} _ {v ‘}] = 0 \ end {array} $$

(5)

, где [ A , B ] = A B — B A — коммутатор двух универсальных операторов A , B в \ (\ mathcal {F} \) . Здесь мы не будем рассматривать определение таких операторов для фермионов, поскольку они не имеют строгого отношения к целям настоящего эссе. Footnote 8

В математической и физической литературе хорошо известно, что пространство Фока может быть строго построено, исходя из гильбертова пространства N -частиц. Footnote 9 Основная причина того, что не следует этим путем для определения \ (\ mathcal {F} \) в DQFT, является метафизической по сути, поскольку с симметризацией и антисимметризацией тензорных произведений частицы действительно получают метку, что больше, чем то, что нам действительно нужно для определения нашей онтологии, как подчеркивалось несколькими строками выше. Таким образом, формализм гильбертова пространства «слишком много говорит» о внутренней природе квантовых частиц. Напротив, способ определения пространства Фока, представленный выше, исключает метки частиц, предоставляя нам информацию, касающуюся однозначного числа частиц.

В этой теории, если мы рассматриваем конфигурацию «частиц», состоящую из нескольких разновидностей, каждая из них представлена ​​соответствующим фоковским пространством; Таким образом, общая конфигурация будет представлена ​​единым пространством продукта, полученным путем объединения каждого конкретного пространства Фока отдельных видов частиц. Примечательно, что это последнее пространство будет иметь уникальный вакуум, соответствующий состоянию, в котором нет частиц какого-либо вида. Соответствующие фоковские состояния описывают ансамбль независимых частиц разного сорта; однако не все возможные комбинации состояний имеют физический смысл, как, например, суперпозиции бозонных и фермионных состояний или состояний с разными электрическими зарядами.Такие ограничения известны как правила суперотбора.

Кроме того, стоит подчеркнуть, что операторы создания и уничтожения не имеют онтологического веса как таковые : они являются полезными формальными инструментами, необходимыми (i) для определения переменного числа частиц в \ (\ mathcal {F} \ ), и (ii) для представления физических событий создания и разрушения частиц, происходящих в пространстве-времени. Тем не менее, онтологически первичным в DQFT являются квантовые частицы, которые могут произвольно создаваться и уничтожаться.Таким образом, эти операторы играют важную функциональную роль, то есть математически представляют такие физические события. Как уже упоминалось, в DQFT проблема бесконечного числа представлений канонических соотношений коммутации исчезает по построению, поскольку у нас есть единственное представление таких соотношений, сохраняющее конечным число степеней свободы.

Еще одним шагом к определению DQFT является выбор собственных состояний импульса для представления одночастичных состояний; как следствие, импульсное пространство является фундаментальным представлением физических систем в этой структуре.{d} = \ {\ boldsymbol {{k}} = (z_ {1}, \ dots, z_ {d}) K_ {L} | z_ {j} \ \ text {целое число с} \ | z_ {j} | \ leq N_ {L} \ \ text {для всех} \ j = 1, \ dots, d \}, \ end {array} $$

(6)

, где d — конечное измерение нашего пространства, K L — постоянная решетки в импульсном пространстве, которая мала по предположению, а большое целое число N L ограничивает величина каждого компонента k до N L K L .В приведенном выше уравнении K L , N L — это параметры усечения, которые сохраняют пространство конечным; кроме того, конечное число элементов в K d соответствует метке i общей конструкции пространств Фока. Сноска 10 , Сноска 11

Дальнейшее рассмотрение онтологии DQFT касается роли полей, которые не представляют физические сущности в пространстве-времени в соответствии с настоящей теорией, будучи только математическими инструментами, введенными по эвристическим причинам без прямой физический смысл.{2}} \) — это весовой коэффициент, который представляет собой релятивистское соотношение энергии и импульса для частицы с массой м . Footnote 13 Интересно, что физическое значение фактора \ (1 / \ sqrt {2 \ omega _ {k}} \) становится ясным при реальных вычислениях корреляционных функций соответствующих интересующих величин (см. Раздел 2.4). Однако следует подчеркнуть, что такие факторы не позволяют интерпретировать приведенное выше (7) как переход от собственных состояний импульса к собственным состояниям положения. Этот факт влечет за собой последствия, т. Е.е. непременная трудность для DQFT, чтобы узнать, где частицы расположены в пространстве (эта проблема решена в нерелятивистском случае, когда частицы имеют низкую скорость по сравнению с c , ω k заменяется константой м , так что уравнение 7 можно интерпретировать как собственные состояния положения.Мы вернемся к этому вопросу в разделе 3).

До сих пор мы молчали о том, что такое онтология этой теории, то есть ее фундаментальные сущности, однако, с одной стороны, мы спроектировали пространство Фока таким образом, чтобы можно было учитывать отдельные, дискретные, счетные объекты, число которых могут меняться во времени, с другой стороны, мы заявили, что ни операторы создания и уничтожения, ни поля не имеют онтологического статуса, это только мощные формальные инструменты, появляющиеся в формальном механизме DQFT.

Динамика DQFT

Определив пространство состояний нашей теории, операторы рождения и уничтожения и поля, давайте теперь обсудим два возможных способа описания динамики диссипативного подхода к QFT, первый из которых основан на картине Шредингера. , вторая — о распутывании квантового мастер-уравнения, которое будет введено ниже. Начнем с первого.

Прежде всего, важно подчеркнуть, что полная динамика DQFT, представленная в картине Шредингера, состоит из двух вкладов, обратимого и необратимого.Учитывая обратимый вклад, динамическая эволюция зависящего от времени вектора состояния | ψ t 〉 в гильбертовом пространстве, которое определяется хорошо известным унитарным уравнением Шредингера (SE):

$$ \ begin {array} {@ {} rcl @ {}} \ frac {d} {dt} | \ psi_ {t} \ rangle = -iH | \ psi_ {t} \ rangle \ end {array} $$

(8)

, где H — оператор Гамильтона, спектр которого предполагается ограниченным снизу в контексте DQFT.{\ prime \ prime} \) следует рассматривать как поправочные параметры, причем первый относится к дополнительному вкладу в квадрат массы, а второй относится к постоянной фоновой энергии на единицу объема. Сноска 15 Важно подчеркнуть, что в формуле. 9 импульс сохраняется при столкновениях; этот факт, в свою очередь, подразумевает локальность таких взаимодействий, что, тем не менее, не означает, что DQFT имеет ресурсы, необходимые для строгой локализации частиц в пространстве-времени, как упоминалось выше.

Интересно, что уравнение. 9 может изменять количество отдельных частиц на четную величину: 0, что означает, что количество частиц остается неизменным, ± 2 и ± 4, что означает, что количество частиц может быть увеличено или уменьшено на 2 и 4 соответственно.

Второй динамический вклад DQFT является по своей сути стохастическим, и именно здесь термодинамические аргументы — точнее механизм диссипации — проявляются должным образом. Далее мы описываем наши физические системы в терминах матриц плотности ρ t , которые могут представлять ряд различных физических состояний, возникающих с определенной вероятностью.В этом контексте матрицы плотности являются полезными формальными инструментами, которые позволяют нам обрабатывать ансамбли, образованные идентичными и неотличимыми частицами, поскольку их статистические свойства полностью описываются в терминах ρ t . Стоит отметить, что в DQFT матрицы плотности не представляют физические объекты в пространстве-времени сверх ансамблей частиц, которые они описывают; в этом контексте они играют только функциональную роль в динамике частиц. Таким образом, их не следует сравнивать e.грамм. с функцией ψ в первоначальной теории пилотной волны Бома (см. Bohm 1952), где волновая функция определена в трехмерном пространстве, и это собственное физическое поле, которое направляет движение частиц.

Следуя обычной трактовке диссипативных квантовых систем, мы вводим по своей сути стохастическое основное квантовое уравнение (QME) для матрицы плотности.

$$ \ begin {array} {@ {} rcl @ {}} \ frac {d \ rho_ {t}} {dt} & = & — i [H, \ rho_ {t}] — \ sum \ limits_ {\ boldsymbol {{k}} \ in K ^ {d}} \ upbeta \ gamma_ {k} {{\ int} ^ {1} _ {0}} e ^ {- u \ upbeta \ omega_ {k}} \ left ([a _ {\ boldsymbol {{k}}}, \ rho_ {t} ^ {1-u} [a ^ {\ dagger} _ {\ boldsymbol {{k}}}, \ mu_ {t}]) {\ rho ^ {u} _ {t}}] \ правильно.{-u \ upbeta \ omega _ {k}} \) «производит соответствующие относительные веса для переходов, связанных с рождением и уничтожением свободных частиц» (Öttinger (2017), стр. 65), β = 1/ k B T представляет обратную температуру, γ k обозначает скорость затухания, то есть коэффициент демпфирования, описывающий силу рассеяния, который пренебрежимо мал для малых k и быстро увеличивается для больших к . Сноска 18 Здесь конкретная форма скорости распада Сноска 19 равна γ k = γ 0 + γ k 4 : коэффициент k 2 9025 относится к оператору Лапласа, который вызывает диффузное сглаживание в реальном пространстве, однако наличие двойных коммутаторов в уравнении. 12 предлагает мощность k 4 ; параметр γ 0 добавлен, поскольку состояние с k = 0 может подвергаться диссипации.Стоит отметить, что затухание последнего состояния k = 0 должно быть бесконечно малым, чтобы соответствовать результатам низкоэнергетической КТП. В качестве альтернативы заявлено, поскольку параметр γ обеспечивает отсечку УФ (обратите внимание, что γ 1/3 определяет масштаб длины), этот параметр должен быть достаточно малым, чтобы находиться в физически недоступном диапазоне. В духе процедуры перенормировки и мотивированной стандартной процедурой в КТП, точное значение γ здесь не имеет значения.{-u \ upbeta \ omega _ {k}} \). Как показывает Брейер и Петруччоне (2002), стр. 129 подчеркивают, что необратимая динамика связана с производством энтропии — которая неотрицательна и исчезает при равновесии — в точном смысле, что последнее является «количеством энтропии, произведенной в единицу времени в результате необратимых процессов». Кроме того, как утверждается в Ottinger (2017), pp. 62-63:

[t] мультипликативное разбиение числа ρ t на степени \ ({\ rho _ {t} ^ {u}} \) и \ (\ rho _ {t} ^ {1-u} \) с интегрированием по и вводится, чтобы гарантировать соответствующее взаимодействие с энтропией и, следовательно, надлежащее установившееся состояние или равновесное решение.Структура необратимого члена определяется общими аргументами неравновесной термодинамики или, более формально, модульной динамической полугруппой.

Следовательно, упомянутая выше QME подразумевает сходимость к равновесной матрице плотности. Рассматривая эту конкретную форму QME для матрицы плотности, важно сказать, что температура естественным образом связана с термостатом, который состоит из неразрешенных локальных степеней свободы эффективной теории поля.Повсеместные петли столкновений с участием частиц с большим импульсом, происходящие в течение коротких периодов времени, которые являются источником расхождений в КТП, становятся неразрешимыми из-за наличия диссипации, которая быстро устраняет частицы с большим импульсом и, таким образом, обеспечивает регуляризацию. Подробное обсуждение образовавшихся неразрешимых облаков отдельных частиц, которые можно эффективно видеть с помощью детекторов частиц, можно найти в разделе 3. Ссылаясь на это, стоит отметить, что в этой теории предполагается, что термостат, составляющий окружающую среду, находится в тепловом состоянии. равновесие, поскольку только медленные крупномасштабные степени свободы могут реально ощущать неравновесные эффекты.Этот факт, в свою очередь, следует из фундаментального предположения о разделении масштабов времени в неравновесной термодинамике, которое влечет за собой, что устраненные мелкозернистые степени свободы находятся в равновесии (см. Öttinger 2009 для технических деталей).

Наконец, важно подчеркнуть, что QME является одним из наиболее эффективных способов представления взаимодействия между квантовой системой и термостатом, поскольку точное рассмотрение степеней свободы с высокой энергией потребовало бы решения также сложная система связанных уравнений движения.Во-вторых, эволюция степеней свободы термостата не может быть ни известна, ни механически управляема, поэтому необходимо упростить описание такой физической ситуации, принимая во внимание ограниченный набор соответствующих величин, учитывающих это влияние. Ссылаясь на это, краткосрочные корреляции с термостатом позволяют пренебречь эффектами памяти на динамику и определить стохастический марковский процесс в пространстве состояний системы, учитывая, что такие времена намного меньше, чем характерный временной масштаб эволюция системы, как ясно заявили Брейер и Петруччоне (2002), стр.115-122.

В заключение этого раздела позвольте нам кратко подчеркнуть решающую роль методов ренормгруппы в контексте DQFT. Как неоднократно подчеркивалось, быстрые степени свободы исключены из нашей теории, они образуют среду, с которой взаимодействуют отдельные частицы. Это масштабирование зависит от параметра трения, присутствующего в QME (следовательно, понятие взаимодействующей частицы зависит от такого масштабирования): увеличение масштаба длины эквивалентно увеличению параметра γ k в уравнении.12, что приводит к увеличению скорости производства энтропии.

Наконец, в DQFT объекты, которые могут быть предметом обнаружения и наблюдения, — это облака частиц, возникающие в результате столкновений и взаимодействий более фундаментальных и более быстрых степеней свободы, которые вместо этого недоступны; Следует отметить, что «диссипативная связь с ванной очень слабая, за исключением небольших масштабов длины. Другими словами, диссипативная связь очень быстро стирает мелкомасштабные особенности, в то время как крупномасштабные особенности практически не затрагиваются »(Öttinger 2017, p.29). Кроме того, поскольку нет четкого разделения между различными процессами с высокой и низкой энергией, мы предполагаем самоподобие, что означает, что, хотя более быстрые степени свободы исключаются и не обрабатываются напрямую с помощью DQFT, мы оговариваем, что они ведут себя одинаково. способ относительно более медленных степеней свободы. Строгие аргументы в пользу этого утверждения содержатся в Ottinger (2009). Сноска 20

Интересующие количества

Интересующие количества, которые можно вычислить, зависят от субъективных решений; тем не менее, в этом подразделе мы предоставим наиболее общий класс многократных корреляционных функций, связанных с измеримыми величинами, которые связывают общий абстрактный формализм теории, представленной до сих пор, с экспериментальными данными.{\ dagger} _ {n} \}. \ end {array} $$

(13)

Эту формулу нужно читать изнутри наружу: мы начинаем с матрицы плотности ρ 0 в момент времени t 0 , супероператор эволюции \ (\ mathcal {E} \) имеет вид полученные путем решения QME за определенный интервал времени t , A j представляют линейные операторы, связанные со временами t j с \ (t_ {0} Footnote 22

Распутывание главного квантового уравнения

Другая возможность представить динамику диссипативного подхода к квантовой теории поля основана на идее распутывания главного квантового уравнения. Footnote 23 В частности, вместо формулирования динамики DQFT с использованием квантовых главных уравнений для матриц плотности, можно представить ее в терминах случайного процесса в пространстве состояний системы.Таким образом, основная идея состоит в том, чтобы переписать динамику представленной теории с получением зависящей от времени матрицы плотности ρ t , решая QME как второй момент или ожидание ρ t = E (| ψ t 〉 〈 ψ t |), где | ψ t 〉 представляет собой случайный процесс в соответствующем фоковском пространстве данной открытой системы, состоящий из периодов непрерывной эволюции типа Шредингера, прерываемой случайными квантовыми скачками.Мы подчеркиваем, что распутывания не уникальны, и здесь мы объясняем только самые основные идеи, лежащие в основе распутываний, для простейшего случая невзаимодействующей теории (для более общих разработок см. Оттингер (2017) и ссылки в нем). Сначала мы заполняем некоторые детали описанных выше однопроцессных распутываний, а затем мотивируем и развиваем идею двухпроцессных распутываний. Здесь и для всех обобщений мы рассматриваем распутывания, в которых вектор состояния в любой момент времени t является комплексным кратным одному из базовых векторов \ (\ mathcal {F} \), где взаимодействия должны быть выражены как скачки.Это ограничение, которое можно рассматривать как правило суперотбора, имеет важные последствия: в любой момент времени t система имеет четко определенное содержание частиц, и суперпозиции не играют никакой роли в наших разгадках (см. Также Pashby and Öttinger 2021 ). Практические преимущества этого ограничения для численного моделирования обсуждаются в разделе 3. {\ dagger} _ {k} a_ {k} | \ psi _ {t} \ rangle \).{-2 \ gamma _ {k_ {j}} t}, q_ {j} = 1-p_ {j} \); это изображение взято из Оттингера (2017), стр. 94. NB: эта диаграмма относится к пределу нулевой температуры, что означает, что энергия всегда падает и никогда не увеличивается

Здесь мы рассматриваем распад трехчастичного состояния, затем частицы удаляются до тех пор, пока не будет получен вакуум | 0〉. Интересно, что в любой момент времени t можно вычислить вероятность найти любое состояние, которое может быть сгенерировано удалением одной из частиц из исходного пространства Фока.Глядя на рис. 1, мы начинаем с верхней вершины шестиугольника с тремя частицами, удалив одну из них, мы можем получить три различных состояния, представленных во второй строке; повторяя процесс, мы получаем три различных одночастичных состояния и, в конце концов, можно достичь вакуума, аннигилируя последнюю частицу. Интересно, что следует подчеркнуть, что в любое конечное время можно вычислить вероятность найти любое состояние, которое может быть получено удалением некоторого количества частиц из начального фоковского состояния.Поскольку в КТП мы имеем дело с реальными событиями создания и уничтожения квантовых объектов, мы интерпретируем их распутывание как реальные физические процессы в космосе.

Двухпроцессные распутывания:

В едином процессе распутывание любых изменений в | ψ t 〉 влияет и модифицирует одинаково как бюстгальтер, так и кет-компонент | ψ т 〉 〈 ψ т |.Однако для взаимодействующих теорий или когда нас интересуют более общие корреляционные функции, чем те, которые перечислены в формуле. 13, нам нужно разделить компоненты бюстгальтера и кета. В этом случае следует использовать двухпроцессное распутывание, основанное на следующем представлении матрицы плотности нашей системы: ρ t = E (| ϕ t 〉 〈 ψ t |), где | ϕ t 〉 и | ψ t 〉 — две случайные траектории в пространстве Фока, т.е.е. два разных списка отдельных частиц с потенциально разными прыжками. Footnote 24 Для примера свободной теории при нулевой температуре двухпроцессное распутывание вводит два одновременных скачка:

$$ \ begin {array} {@ {} rcl @ {}} {| \ phi_ {t} \ rangle \ rightarrow \ frac {a_ {k} | \ phi_ {t} \ rangle \ Vert | \ phi_ { t} \ rangle \ Vert} {\ Vert a_ {k} | \ phi_ {t} \ rangle \ Vert}} \\ \\ {| \ psi_ {t} \ rangle \ rightarrow \ frac {a_ {k} | \ psi_ {t} \ rangle \ Vert | \ psi_ {t} \ rangle \ Vert} {\ Vert a_ {k} | \ psi_ {t} \ rangle \ Vert}} \ end {array} $$

со скоростью 2 i k (| ϕ t 〉, | ψ t 〉) γ k

$$ i_ {k} (| \ phi_ {t} \ rangle, | \ psi_ {t} \ rangle) = \ frac {\ Vert a_ {k} | \ phi_ {t} \ rangle \ Vert \ Vert a_ {k} | \ psi_ {t} \ rangle \ Vert} {\ Vert | \ phi_ {t} \ rangle \ Vert \ Vert | \ psi_ {t} \ rangle \ Vert}, $$

и два унитарных уравнения эволюции :

$$ \ begin {array} {@ {} rcl @ {}} {\ frac {d} {dt} | \ phi_ {t} \ rangle = -iH _ {\ text {free}} | \ phi_ {t } \ rangle- \ sum \ limits_ {k} \ gamma_ {k} \ left [a ^ {\ dagger} _ {k} a_ {k} -i_ {k} (| \ phi_ {t} \ rangle, | \ psi_ {t} \ rangle) \ right] | \ phi_ {t} \ rangle} \\ {\ frac {d} {dt} | \ psi_ {t} \ rangle = -iH _ {\ text {free}} | \ psi_ {t} \ rangle- \ sum \ limits_ {k} \ gamma_ {k} \ left [a ^ {\ dagger} _ {k} a_ {k} -i_ {k} (| \ phi_ {t} \ rangle , | \ psi_ {t} \ rangle) \ right] | \ psi_ {t} \ rangle.} \ end {array} $$

В этом случае скачки могут иметь место, только если оба вектора | ϕ t 〉 и | ψ t 〉 содержат частицу с тем же импульсом k .

Двухпроцессное распутывание полезно при вычислении многократных корреляционных функций более общего типа, чем перечисленные в формуле. 13, как показано на Рис. 2 ниже:

Рис. 2

Двухпроцессное разматывание; фотография взята из Öttinger (2017), стр.97

Рассматривая исходный ансамбль состояний | ϕ 0 〉 и | ψ 0 〉, представляющая матрицу плотности системы ρ 0 , они развиваются от времени t 0 до t 1 в соответствии с двухпроцессным распутыванием. Операторы A i , B j затем вводятся с помощью переходов | ϕ j 〉 и | ψ j 〉, временами t j , между этими скачками состояния и их траектории в пространстве Фока эволюционируют согласно двухпроцессному распутыванию.{\ dagger} _ {n} \ bigg \} = E [\ langle \ psi_ {f} | \ phi_ {f} \ rangle].} \ end {array} $$

Это обсуждение может быть расширено включением различных форм распутываний и конкретных примеров, примененных к теории φ 4 ; полностью подробная картина этих процессов дана в Öttinger (2017), раздел 1.2.8. Однако такое техническое обсуждение выходит за рамки вводной части настоящего эссе.

Механизм рассеивания: больше, чем другая схема УФ-регуляризации

В заключение нашего введения в DQFT давайте сыграем роль защитника дьявола.Рассматривая механизм диссипации DQFT, можно было бы рассматривать его просто как еще одну схему ультрафиолетовой регуляризации, такую ​​как, например, решеточная регуляризация, обрезание импульса, размерная регуляризация или регуляризация Паули – Вилларса. Таким образом, можно было бы заключить, что DQFT просто повторяет путь стандартного QFT, чтобы избежать нежелательных результатов, как те, которые резюмированы в разделе 1. Вопреки этому потенциальному возражению, в этом подразделе мы собираемся объяснить, почему диссипация не должна рассматриваться просто как еще одно. формальная схема регуляризации.Далее мы суммируем ряд аргументов, показывающих, что диссипация — это гораздо больше; некоторые из них будут рассмотрены более подробно в следующем разделе.

  1. 1.

    Стоит отметить, что регуляризация глубоко связана с перенормировкой, то есть с исключением степеней свободы. Более того, всякий раз, когда исключаются степени свободы, следует ожидать, что энтропия и диссипация будут играть роль, т.е.е. следует ожидать попадания в область необратимой термодинамики. Возникновение необратимости следует считать естественным, поскольку печально известные расхождения в КТП возникают из-за спонтанного рождения и уничтожения частиц, а процессы, которые находятся далеко за пределами нашего механического контроля, являются слишком быстрыми и слишком локальными. Это мотивация, которая побудила нас предположить, что стохастичность естественным образом возникает в КТП в разделе 2.2.

  2. 2.

    Несмотря на стохастический характер фундаментальных взаимодействий, они описываются с помощью гамильтоновой динамики (без особых критических вопросов), которая имеет чисто обратимую структуру. Уравнения необратимой термодинамики обладают математической структурой, которая обобщает гамильтонову динамику. Неравновесная термодинамика, действительно, не только обеспечивает устойчивые уравнения эволюции, но и важные дополнительные особенности, такие как зависимость флуктуации-диссипация, характеризующая тепловые флуктуации, сопровождающие механизм диссипации при ненулевой температуре (см. Öttinger et al.2021 и ссылки в нем). Следовательно, механизм диссипации кажется более подходящим для представления фундаментальных взаимодействий.

  3. 3.

    В эффективных полевых теориях электрослабых и сильных взаимодействий сила диссипации в DQFT является переменным параметром, очень похожим на шаг решетки или импульсное обрезание, требующий перенормировки.Однако, в отличие от этих чисто вычислительных инструментов, динамическое диссипативное размытие обеспечивает более привлекательный вариант для физической теории в некотором фундаментальном масштабе, а именно в масштабе Планка. Диссипативное размытие можно интерпретировать как источник предела разрешения в масштабе Планка и, следовательно, должно быть связано с гравитацией. Альтернативная теория гравитации, которую можно рассматривать с помощью DQFT, была предложена и развита в Оттингере (2020a, 2020b). Эта теория гравитации с высшими производными эффективно выбирает небольшое подмножество решений из теории Янга-Миллса, основанной на группе Лоренца, с помощью ограничений.В результате все фундаментальные взаимодействия будут объединены DQFT в терминах необратимых динамических уравнений со связями под эгидой теорий Янга-Миллса.

  4. 4.

    Механизм диссипации, появляющийся в QME (12), сформулирован в терминах операторов рождения и уничтожения, связанных со свободным гамильтонианом, и, следовательно, состоит из обмена частицами между системой и ее окружением, где обмен частицами высоких энергий осуществляется сильно одобренный.На наш взгляд, этот необратимый вклад в динамику предполагает онтологию частиц, также в свете феноменологии QFT. Таким образом, формальная структура теории, по-видимому, должным образом отражает экспериментальные данные, полученные от ускорителей частиц.

  5. 5.

    Наконец, как мы видели в этом разделе, формулировка термодинамической КМЭ ДКТП в значительной степени опирается на пространство Фока, связанное с операторами создания собственных состояний импульса свободного гамильтониана, которые мы интерпретируем как частицы.Безчастичный вектор состояния | 0〉 пространства Фока можно интерпретировать как основное и вакуумное состояние свободной теории. Матрицы плотности, полученные из QME (12), в котором полный гамильтониан со всеми взаимодействиями используется при формулировке обратимой динамики, описывают состояния полностью взаимодействующей теории, включая установившееся состояние при заданной температуре. Таким образом, на этой картине состояния вакуума свободной и взаимодействующей теорий имеют четко разные характеры и значение, так что мы получаем новое понимание проблем, поднятых теоремой Хаага.

Решеточная квантовая теория поля — Scholarpedia

Рисунок 1:


Теория поля на решетке — это область теоретической физики, в частности квантовая теория поля, которая занимается теориями поля, определенными на пространственном или решетка пространства-времени.

Теоретическое описание основных составляющих материи и взаимодействие между ними основано на квантовой теории поля. b (x) T_b \, \), компоненты которого являются элементами алгебры Ли компактной Ли группа с образующими \ (T_b \.{n} \ phi (x)) \, \) который является функцией \ (\ phi (x) \) и его производные. Лагранжиан определяет поле уравнения, которые включают взаимодействия. Если сила взаимодействие задается малым параметром \ (g \, \), можно вычислить физических величин приблизительно с удовлетворительной точностью с помощью теория возмущений, которая сводится к разложению в степенной ряд по \ (g \. \). Это, например, случай в квантовой электродинамике (КЭД), где взаимодействие пропорционально постоянной тонкой структуры \ (\ alpha \ приблизительно 1/137 \, \) и многие интересные наблюдаемые могут быть получены в виде степенных рядов по \ (\ альфа \.\) Есть, однако, важные случаи, когда оказалось, что теория возмущений неадекватна для расчета физических количества. Наиболее ярким примером является низкоэнергетический режим квантовой хромодинамики (КХД), теория сильных взаимодействий элементарных частиц.

Не только квантовая хромодинамика, но и другие компоненты Стандартной модели физики элементарных частиц кроме того, теории физики, выходящие за рамки Стандартной модели, снабжают нас непертурбативные задачи.Важным шагом для ответа на такие вопросы является изготовлен К. Вильсоном в 1974 г. (Wilson, 1974). Он представил формулировка квантовой хромодинамики на решетке пространства-времени, которая позволяет применение различных непертурбативных методов. Эта дискретизация будет подробно объяснено ниже. Это приводит к математически четко определенным проблемам, которые (по крайней мере в принципе) разрешимы. Также следует отметить, что введение пространственно-временной решетки может быть взято за отправную точку для математически чистый подход к квантовой теории поля, так называемый конструктивная квантовая теория поля.

В современной квантовой теории поля введение пространственно-временной решетки часть подхода, отличного от операторного формализма. Это решетка теория поля. Его основные ингредиенты:

  • функциональных интегралов,
  • Евклидова теория поля и
  • Пространственно-временная дискретизация полей.

Теория поля на решетке оказалась очень успешной для непертурбативный расчет физических величин. В этой вики введение и обзор основ и методов решетки дается теория поля.Т \! Дт \, L (х, \ точка х) \] является классическим действием для такого пути.

Формально мера интеграла по путям записывается как \ [ \ mathcal {D} х \ эквив \ prod_t dx (t) \] с точностью до коэффициента нормализации. Для частицы в трехмерном пространстве это обобщается на пути \ (x_i (t) \, \), где \ (i \) = 1,2,3, и \ [ \ mathcal {D} x = \ prod_t \ prod_i dx_i (t). \]

Пожалуй, это самая наглядная картина квантовой механики. амплитуда перехода. Его можно записать в виде интеграла по вкладам от всех возможных путей от начальной до конечной точки.Каждый path взвешивается классическим действием, оцениваемым на этом пути.

Для подробного и математически строгого расчета интегралов по путям Заинтересованный читатель отсылается к учебнику (Glimm and Jaffe, 1987). {- \ mathrm { i} Ht}.\] Объектом интереса теории поля являются вакуумные математические ожидания (упорядоченные по времени) произведения полевых операторов, функции Грина: \ [ \ langle 0 | \ varphi (x_1) \ varphi (x_2) \ dots \ varphi (x_n) | 0 \ rangle, \ qquad t_1> t_2> \ точки> t_n. \] Яркие примеры — пропагаторы \ ( \ langle 0 | \ varphi (x) \ varphi (y) | 0 \ rangle. \) Функции Грина по сути содержат всю физическую информацию. В частности, элементы S-матрицы связаны с функциями Грина, например 2-частичные рассеивающие элементы могут быть получены из \ ( \ langle 0 | \ varphi (x_1) \ dots \ varphi (x_4) | 0 \ rangle.\)

Вместо обсуждения функционального интегрального представления для квантовой теории поля с самого начала, мы ограничимся переводом квантово-механические концепции теории поля посредством аналогии. К этому end основные переменные \ (x_i (t) \) переводятся в поля \ (\ phi (\ vec x, t) \. \) Правила перевода: \ [ \ begin {align} x_i (t) \ quad & \ longleftrightarrow \ quad \ phi (\ vec x, t) \\ я \ quad & \ longleftrightarrow \ quad \ vec x \\ \ prod_ {t, i} dx_i (t) \ quad & \ longleftrightarrow \ quad \ prod_ {t, \ vec x} d \ phi (\ vec x, t) \ Equiv \ mathcal {D} \ phi \\ S = \ int \! Dt \ L \ quad & \ longleftrightarrow \ quad S = \ int \! Dt \, d ^ 3x \ \ mathcal {L}, \ end {align} \] где \ (S \) — классическое действие. {\ mathrm {i} S}.\) Эти выражения включают интегралы по всем классическим конфигурациям поля.

Как упоминалось ранее, никаких попыток вывода функциональных интегралов не предпринимается. здесь, а просто мотивация их формы по аналогии. Кроме того, в в случае квантовой механики рассмотрена амплитуда перехода, а теперь формула для функций Грина написана, что немного другой.

Формулы функциональных интегралов вызывают некоторые вопросы. Первый из все, как возникает проекция на основное состояние \ (| 0 \ rangle \)? Во-вторых, эти интегралы содержат осциллирующие подынтегральные выражения из-за мнимые показатели; как насчет их сближения? Более того, есть ли способ оценить их численно?

Далее будет рассмотрено, как введение мнимых времен помогает ответить на эти вопросы.

Евклидова теория поля

Вернемся на мгновение к квантовой механике. Здесь также можно ввести Зеленые функции, например \ [ G (t_1, t_2) = \ langle 0 | X (t_1) X (t_2) | 0 \ rangle, \ qquad t_1> t_2, \] где \ (X (t) \) — оператор положения в картине Гейзенберга. {- \ mathrm {i} H (t_2-t)} | x \ rangle \] для \ (t ‘> t_1> t_2> t \.2 + V (х (\ тау)) \ право \}. \] Функция Грина в реальном времени, которая нас интересовала изначально, можно получить из \ (G_E \) с помощью аналитического продолжения, \ (G (t_1, t_2) = G_E (\ mathrm {i} t_1, \ mathrm {i} t_2) \. \)

Рисунок 3: Вращение фитиля от мнимых координат к реальным временным координатам.

Аналитическое продолжение должно быть сделано таким образом, что все временные аргументы вращаются одновременно против часовой стрелки в комплексной \ (t \) — плоскости. Это так называемое вращение Вика, проиллюстрировано на рисунке 3.

Теперь снова обратимся к теории поля. Функции Грина \ [ G (x_1, \ dots, x_n) = \ langle 0 | T \ varphi (x_1) \ dots \ varphi (x_n) | 0 \ rangle, \] продолжаются до мнимых времен, \ (t = — \ mathrm {i} \ tau \, \) — так называемые швингеровские функции \ [ G_E ((\ vec x_1, \ tau_1), \ точки, (\ vec x_n, \ tau_n)) = G ((\ vec x_1, -i \ tau_1), \ точки, (\ vec x_n, -i \ tau_n)). 4 \ right \}.2, \] которая является метрикой евклидова пространства. Поэтому говорят о евклидовых функций Грина \ (G_E \) и евклидовых функциональных интегралов . Они взяты за отправную точку для непертурбативных исследования полевых теорий и конструктивные исследования.

Возможность аналитического продолжения конкретной теории поля от реальных до мнимых времен и наоборот зависит от определенных условий, которые должны быть выполнены. Для большого класса теорий поля эти условия были проанализированы и сформулированы Остервальдером и Шредером, см. (Osterwalder and Schrader, 1973, 1975).В частности, евклидова теория поля должна удовлетворять так называемой положительности отражения , чтобы соответствовать правильной теории поля в пространстве Минковского.

Поскольку \ (S_E \) реально, интересующие интегралы теперь реальны и не вызывают неприятных ощущений. колебания происходят. Более того, поскольку \ (S_E \) ограничено снизу, множитель \ (\ exp (-S_E) \) в подынтегральном выражении ограничено. Сильно флуктуирующие поля имеют большое евклидово действие \ (S_E \) и, таким образом, подавляются множителем \ (\ exp (-S_E) \.\) (Строго говоря, это утверждение не имеет смысла в поле теории, если не учитывать перенормировку.) Это делает евклидову функциональные интегралы, столь привлекательные по сравнению с их минковскими аналоги.

Можно подумать, что в евклидовой области все нефизично и нет возможности получить физические результаты непосредственно из евклидова Функции зелени. Но это не так. Например, спектр Теорию можно получить следующим образом.{-m_1 \ tau} + \ точки, \] что означает, что можно извлечь массу частицы.

С этого момента мы останемся в евклидовом пространстве и опустим нижний индекс \ (E \, \), так что \ (S \ Equiv S_E \) означает евклидово действие.

Дискретизация решетки

Остается один центральный вопрос: бесконечномерное интегрирование по всем классическим конфигурациям поля, т. е. \ [\ тег {2} \ mathcal {D} \ phi = \ prod_x d \ phi (x), \]

вообще имеет смысл? Как это определяется?

Рисунок 4: 3-мерная решетка

В квантовой механике можно вывести представление интеграла по путям. как предел дискретизации по времени.В качестве в теории поля поля зависят от четырех евклидовых координат вместо единственной временной координаты, теперь мы можем ввести дискретное пространство-время в виде решетки, например гиперкубической решетки, заданной \ [ x _ {\ mu} = a n _ {\ mu}, \ qquad n _ {\ mu} \ in \ mathbf {Z}, \] см. рисунок 4.

Величина \ (a \) по понятным причинам называется шагом решетки . Следует отметить, что шаг решетки, будучи размерной величиной, не является параметром дискретизированной теории, который мог бы e.грамм. быть вставленным в компьютерную программу для оценки интеграла по путям. Размер шага решетки в физических единицах является производной величиной, определяемой динамикой. Это будет объяснено в разделе «Предел сплошности».

Скалярное поле \ [ \ phi (x), \ qquad x \ in \ mbox {решетка}, \] теперь определена только в точках решетки. Частные производные заменяются конечными разностями, \ [ \ partial _ {\ mu} \ phi \ longrightarrow \ Delta _ {\ mu} \ phi (x) \ Equiv \ frac {1} {a} (\ phi (x + a {\ hat {\ mu}}) — \ phi (x)), \] и пространственно-временные интегралы суммами: \ [ \ int \! d ^ 4x \ quad \ longrightarrow \ sum_x a ^ 4 \. {- \ mathrm {i} px} \ \ phi (x).3 T} \ sum_ {l _ {\ mu}}. \] Теперь все функциональные интегралы превратились в регуляризованные и конечные выражения.

Конечно, хотелось бы восстановить физику в непрерывном и бесконечном в конечном итоге пространство-время. Поэтому задача состоит в том, чтобы взять бесконечный объем предел \ [ L, T \ longrightarrow \ infty, \] что в целом является более легкой частью, и принять континуальный предел, \ [ а \ longrightarrow 0. \] Построение континуального предела решеточной теории поля обычно весьма нетривиально, и здесь часто тратится больше всего усилий.{- \ frac {x} {\ xi}} \)

Эта формальная аналогия позволяет использовать хорошо зарекомендовавшие себя методы статистической механика в теории поля и наоборот. Даже терминология обоих поля часто идентичны. Чтобы упомянуть некоторые примеры, в теории поля один использует высокотемпературные разложения и приближения среднего поля, а в В статистической механике применяется ренормализационная группа.

Гамильтонова решеточная теория поля

Альтернатива евклидовой теории поля на решетке, описанная ранее, гамильтонова решеточная теория поля, введенная Когутом и Сасскинд (Когут, Сасскинд, 1975).В этой формулировке только трехмерное пространство дискретизируется на решетке, тогда как время остается непрерывным. Кроме того, время остается реальным и не продолжил евклидову область. Гамильтонова решеточная теория поля допускает применение некоторых аналитических методов, таких как разложения сильной связи и теория возмущений. Поскольку он не подходит для приложения численного метода Монте-Карло, он больше не пользуется внимание, как в начале, и здесь не рассматривается более подробно.

Калибровочная теория на решетке

Теории калибровочных полей также могут быть сформулированы на решетке пространства-времени. Поскольку подробности объясняются в Wiki по решеточным калибровочным теориям, мы просто укажем основные элементы решеточной калибровочной теории для калибровочной группы SU (N). 2} {\ rm Re} ({\ rm Tr} (U (p))).{-S_W}, \] где следует понимать интегрирование \ (dU (b) \) для данного звена \ (b \) как инвариантное интегрирование по групповому многообразию, нормированное на \ [ \ int \! dU = 1. \]

Фермионы на решетке

Переменные Грассмана

Классические бозонные поля являются просто обычными функциями и удовлетворяют \ [ [\ phi (x), \ phi (y)] = 0, \] который можно рассматривать как предел \ (\ hbar \ rightarrow 0 \) квантовой коммутационные отношения.

Статистика Ферми означает, что фермионные квантовые поля обладают хорошо известными равновременные антикоммутационные отношения \ [ \ {\ psi (\ vec x, t), \ psi (\ vec y, t) \} = 0.\] Исходя из этого, можно было бы ввести классический предел, в котором классические фермионные поля удовлетворяют \ [ \ {\ psi (x), \ psi (y) \} \, = 0 \] для всех \ (x, y \. \) Следовательно, классические фермионные поля являются антикоммутирующими переменными, которые также называется переменных Грассмана .

Мы хотели бы отметить, что приведенный выше аргумент является всего лишь эвристическим мотивация. Более строгие подходы можно найти в литературе.

В общем случае комплексная алгебра Грассмана порождается элементами \ (\ eta_i \) и \ (\ bar {\ eta} _i \, \), которые подчиняются \ [ \ begin {align} \ {\ eta_i, \ eta_j \} & = 0 \\ \ {\ eta_i, \ bar {\ eta} _j \} & = 0 \\ \ {\ bar {\ eta} _i, \ bar {\ eta} _j \} & = 0.\ end {align} \] Интегрирование грассмановых переменных можно определить как \ [ \ int \! d \ eta_i \ (a + b \ eta_i) = b \] для произвольных комплексных чисел \ (a, b \. \)

В фермионных теориях поля есть поля Грассмана, которые сопоставляют Переменные Грассмана с каждой точкой пространства-времени. Например, поле Дирака имеет антикоммутирующие переменные \ (\ psi _ {\ alpha} (x) \) и \ (\ bar {\ psi} _ {\ alpha} (x) \, \) где \ (\ alpha \) = 1,2,3,4 — индекс Дирака. Классическое поле Дирака подчиняется \ [ \ {\ psi _ {\ alpha} (x), \ psi _ {\ beta} (y) \} = 0, \ quad \ mbox {и т. д.4х \, \ bar {\ Psi} (x) Q \ Psi (x)} = \ det {Q}. \]

Это знаменитый определитель фермионов. Основная проблема, конечно же, остается а именно для вычисления определителя типично огромной матрицы \ (Q \. \)

При численном моделировании решеточных теорий поля с фермионами расчет \ (\ det {Q} \) оказывается очень утомительным. Поэтому часто используют закаленное приближение, которое рассматривает \ (Q \) как константу. В последние годы разные неутоленные исследования квантовой хромодинамики были проведены и дали оценки ошибок гашения.

Наивные фермионы

Пока нет трудностей с реализацией фермионов на решетке кажется, возникают: все, что нужно сделать, это дискретизировать конфигурации поля известным способом и вычислить функции Грина с некоторыми из методы последнего раздела. Однако есть проблема. Чтобы увидеть это, рассмотрим пропагатор фермиона с массой \ (m \) в качестве примера. Фермионный действие решетки тогда задается \ [ S_F = \ frac {1} {2} \ sum_x \ sum _ {\ mu} \ bar {\ psi} (x) (\ gamma _ {\ mu} \ Delta _ {\ mu} + m) \ psi (x) + h.2}. \] У пропагатора есть полюс для малых \ ​​(k _ {\ mu} \), представляющих физический частицы, но есть дополнительные полюса около \ (k _ {\ mu} = \ pm \ pi \) из-за периодичность знаменателя. Итак, \ (S_F \) действительно описывает 16 вместо 1 частица. Эта проблема — эвфемистически называемая удвоением фермионов — является решающее препятствие для всех решеточных представлений кварковых полей.

Фермионы Вильсона и Стэгджреда

Удвоение фермионов было известно Уилсону еще на заре существования решетки. Квантовая хромодинамика.{(W)} & = S_F — \ frac {r} {2} \ sum_x \ bar {\ psi} (x) \ Box \ psi (x) \\ & = S_F — \ frac {r} {2} \ sum_ {x, \ mu} \ bar {\ psi} (x) \ { \ psi (x + \ hat {\ mu}) + \ psi (x- \ hat {\ mu}) — 2 \ psi (x) \}, \ end {align} \] где \ (0

Фермионы Вильсона имеют серьезный недостаток: даже при исчезающем фермионе масс, киральная симметрия явно нарушается членом Вильсона, и одна имеет проблемы с расчетами, для которых киральная симметрия имеет центральное значение. важность.

Есть альтернативы подходу Вильсона. Один из них, благодаря Когуту и Сасскинда — это так называемые шахматные фермионы. Идея состоит в том, чтобы распространять компоненты \ (\ psi _ {\ alpha} \) поля Дирака в различных точках решетки. Это приводит к снижению фермионов с 16 до 4. Причем для безмассовых фермионы — остаток киральной симметрии в виде киральной U (1) \ (\ otimes \) U (1) -симметрия сохраняется.

Еще лучше с учетом хиральной симметрии и других аспектов формулы для фермионов на решетке, которые подчиняются соотношению Гинспарга-Вильсона .Более подробную информацию можно найти в вики-сайтах по калибровочным теориям на решетке и на решеточные киральные фермионы.

Методы

В предыдущих разделах функциональные интегралы для теорий поля на решетки. Но оценить эти интегралы большой размерности. Расчет в закрытом виде выглядит как вообще невозможно. В этом разделе некоторые методы используются для приближенного вычисления функциональных интегралов.

Теория возмущений

Хотя теория поля на решетке дает возможность изучать непертурбативные аспекты, теория возмущений, тем не менее, очень ценный инструмент на решетке тоже.В частности, его можно использовать для соответствия результаты непертурбативных расчетов к пертурбативным расчетам в регионах, где применимы оба метода.

Теория возмущений сводится к разложению по степеням связи, как в континуум. Решетка обеспечивает внутреннее УФ-обрезание \ (\ pi / a \) для всех импульсы. Кроме того, следует заметить, что пропагаторы и вершины отличаются от континуальных из-за формы решетчатое действие. В частности, возникают глюонные самодействия всех порядков. и не только как трех- и четырехглюонные вершины.2}, \] что является малой величиной при больших голых связях \ (g_0 \. \), поэтому то же, что и при сильном расширении связи. В основном фактор Больцмана расширяется как \ [ \ exp {\ left (\ beta \ frac {1} {N} {\ rm Re} ({\ rm Tr} (U (p))) \ right)} = 1 + \ beta \ frac {1} {N} {\ rm Re} ({\ rm Tr} (U (p))) + \ dots \. \] Полученное расширение можно представить схематически, аналогично Диаграммы Фейнмана теории возмущений. Однако элементы диаграммы плакетки \ (p \) на решетке. Каждая степень \ (\ beta \) вводит еще один плакетка.

В случае скалярных полей соответствующим методом является перескок расширение параметра, которое составляет расширение параметра \ (\ kappa \, \) что мало для больших масс \ (m_0 \. \)

Разложения по параметрам сильной связи и перескока имеют конечный радиус сходимости, в отличие от теории возмущений, которая обычно расходится и в лучшем случае асимптотична.

Другие аналитические методы

Другие аналитические методы доступны для приблизительной оценки функциональные интегралы решеточной калибровочной теории. 4 \).Для калибровочной группы SU (3) это дает 81 920 000 реальных переменных. Это должно быть непреодолимо для обычных квадратуры даже в будущем. Поэтому некоторый статистический метод требуется. Создание калибровочных конфигураций решетки просто случайным образом оказывается быть крайне неэффективным. Ключевой идеей для решения этой проблемы является концепция выборки важности : для заданного действия решетки \ (S \) квадратурные точки \ (x_i \) генерируются с вероятностью \ [ p (x_i) \ sim \ exp \ {- S (x_i) \}. \] Это дает нам большое количество точек в важных регионах. интеграла, значительно повышая точность.{(3)} \ rightarrow \ dots \) ​​с соответствующие вероятности статистическим способом. Конечно, это делается на компьютер. Обновление — это шаг, на котором одна переменная ссылки \ (U_ {x \ mu} \) изменяется, тогда как развертка подразумевает, что один раз проходит через всю решетку, обновляя все переменные ссылки. Часто используемый метод для получение обновлений — это алгоритм Метрополис .

Важной особенностью этого статистического метода оценки является наличие статистических ошибок.{-mL} \, \)

  • большие массы кварков \ [m_q \] в основном слишком велики в расчетах Монте-Карло,
  • замороженное приближение \ [\ det Q = 1 \, \] без учета динамики фермионов.

    • Предел непрерывности

    Поскольку можно выполнять вычисления только при конечном шаге решетки, это важный вопрос, чтобы довести процесс экстраполяции до предела континуума под контролем. Поскольку период решетки является регулятором теории, она может быть полезно применить к этой проблеме методы ренормгруппы.Зная функциональную зависимость голой связи \ (g_0 \) от регулятора, другими словами, решая уравнение ренормгруппы, мы должен знать, как варьировать голое сцепление нашей теории, чтобы достичь континуальный предел. Обсудим эту идею подробнее.

    Рисунок 7: Двумерные решетки с увеличивающейся корреляционной длиной \ (\ xi \)

    Предполагается, что в непрерывном пределе шаг решетки \ (a \) стремится к нулю, в то время как физические массы \ (m \) должны приближаться к конечному пределу.Решетка расстояние, однако, не является безразмерной величиной, поэтому мы должны исправить некоторый масштаб массы \ (m \, \) например некоторая масса частицы, и рассмотрим предел \ (a m \ rightarrow 0 \. \) Обратное этому, \ [ \ frac {1} {am} \ Equiv \ xi, \] можно рассматривать как длину корреляции. В континуальном пределе \ (\ xi \) должна стремиться к бесконечности, что называется критической точкой теории . На рисунке 7 это проиллюстрировано на двумерной решетке с разной корреляционной длиной.

    В чистой калибровочной теории существует единственная безразмерная голая связь \ (g_0 \) и \ (am \), очевидно, является функцией \ (g_0 \.2} \ right) \ cdot (\ dots), \]

    , который показывает непертурбативное происхождение массы \ (m \. \)

    Эти соображения, основанные на пертурбативной \ (\ beta \) — функции, мотивируют следующая гипотеза: континуальный предел калибровочной теории на решетке нужно брать в \ (g_0 \ rightarrow 0 \. \) Более того, мы ожидаем, что он включает массивные взаимодействующие глюболы и статическое удержание кварков.

    Сценарий достижения непрерывного предела выглядит следующим образом. Расчет масс в единицах решетки, т.е.п)) \] для некоторого целого числа \ (p \. \) Такое поведение, \ (m_1 / m_2 \ приблизительно \) const., Называется масштабированием . При численном моделировании масштабирование различных физических величин было установлено для решеточных калибровочных теорий, решеточной КХД и других моделей, тогда как подтверждение асимптотического масштабирования является гораздо более требовательным.

    Список литературы

    • Уилсон, К. (1974). Заключение кварков. Phys. Ред. D 10: 2445.
      • ,
    • , Когут, Дж. И Сасскинд, Л. (1975). Гамильтонова формулировка решеточных калибровочных теорий Вильсона. Phys. Ред. D 11: 395.
    • Остервальдер, К. и Шредер, Р. (1973, 1975). Аксиомы для евклидовых функций Грина. Comm. Математика. Phys. 31 (1973): 83; 42 (1975): 281.

    Дополнительная литература

    • Кройц, Майкл (1985). Кварки, глюоны и решетки. Издательство Кембриджского университета, Кембридж.
    • Montvay, Istvan and Münster, Gernot (1994). Квантовые поля на решетке. Издательство Кембриджского университета, Кембридж.
      • ,
    • Роте, Г. Дж. (2005).Решеточные калибровочные теории: введение. World Scientific, Сингапур.
      • ,
    • Смит, Дж. (2002). Введение в квантовые поля на решетке. Издательство Кембриджского университета, Кембридж.
    • Кройц, Майкл (редактор) (1992). Квантовые поля на компьютере. World Scientific, Сингапур.
    • ДеГранд, Т. и ДеТар, К. (2006). Решеточные методы квантовой хромодинамики. World Scientific, Сингапур.
    • Гаттрингер, С. и Ланг, С. Б. (2010). Квантовая хромодинамика на решетке: вводная презентация.Спрингер, Берлин.
    • Глимм, Джеймс и Джаффе, Артур (1987). Квантовая физика: функционально-интегральная точка зрения. Спрингер, Берлин.

    Внешние ссылки

    Г. Мюнстер, М. Вальцль: Калибровочная теория решеток — краткий учебник, Материалы летней школы по феноменологии калибровочных взаимодействий, 13-19 августа 2000 г., Цуоц, Швейцария, изд. Д. Грауденц, В. Маркушин.

    Р. Гупта: Введение в решеточную КХД, Лекции, прочитанные в летней школе LXVIII Les Houches «Исследование стандартной модели взаимодействия частиц», 28 июля — 5 сентября 1997 г.

    Р.Д. Кенуэй: Теория решеточного поля.

    К. Морнингстар: Метод Монте-Карло в квантовой теории поля.

    U.-J. Визе: Введение в теорию поля решетки.

    См. Также

    Path_integral, Gauge_theories, Lattice_gauge_theories, Квантовая электродинамика, Квантовая_хромодинамика, Асимптотическая_свобода, Решетчатые_хиральные_фермионы, Перенормировка, Renormalization_group

    QFT для семинаров для чайников — Ресурсы

    Ресурсы более высокого уровня для математиков (в основном более продвинутые, чем наша область, но полезные для просмотра)

    Когда я впервые приехал в Штаты, в возрасте 2 лет, моя семья навещала школа Парк-Сити на QFT, где мой отец был участником.Во введении к собранным заметкам была следующая строка:

    «Мы можем с уверенностью утверждать, что физическая интуиция, которую физики используют для решения этих проблем, даже в моделях, актуальность которых для реального мира кажется в лучшем случае незначительной, еще не дошла до все в математику ».

    С тех пор положение дел сильно изменилось. QFT проникла в математику до такой степени, что связанные с QFT тексты, ориентированные на математиков, могут заполнить страницы библиографии.Здесь я перечислю несколько из них, которые мне порекомендовали или которые, по моему мнению, могут быть особенно полезны для выполнения. Я также включаю несколько рекомендованных мной источников для физиков.

    • Упомянутые выше заметки PCMI представляют собой отличный краткий курс Джеффа Рабина.

    • Школа IAS 1996-97 гг. По теории струн содержит безумное количество хороших материалов высокого уровня, включая вводный материал по квантовой механике и теории поля.Рекомендую посмотреть курс Людвига Фаддеева с первого семестра. Книжная версия школы также имеет красивый текст Дэна Фрида и Делиня по классической теории поля.

    • Первые несколько разделов главы 1 этой книги Конна и Марколи содержат очень сжатую, но удобочитаемую версию QFT, предназначенную для математиков. См. Особенно их объяснение интегралов Фейнмана (повернутых по Вику) в элементарном анализе.

    • В этой книге Костелло и Гвильяма изложена, возможно, «современная» математическая точка зрения на квантовую теорию поля с точки зрения строгости и естественности (она включает высшую алгебру).

    • « PCT, Spin and Statistics, and All That » Р. Стритера и А. Уайтмана по ссылкам. Рекомендовано участником: «Это необходимо для математической точки зрения на QFT».

    • Квантовая теория поля в искривленном пространстве-времени Бэра и Фредеденхагена или более короткий «драгоценный камень» Аспекты квантовой теории поля в искривленном пространстве-времени Фуллинг для геометрической перспективы (также рекомендовано участником).

    • Список QFT, предложенный математиками для чтения Питером Войтом.

    Из чего на самом деле состоит Вселенная? Упрощенная квантовая теория поля — Сайт Арвина Эша

    Из чего на самом деле состоит вселенная? Что действительно является фундаментальным в реальности, которую мы воспринимаем?

    В 400 г. до н.э. греческий философ Демокрит высказал идею об атомах как об основных элементах — он считал, что это твердые частицы материи, которые нельзя разделить дальше.

    2300 лет спустя, в 1897 году, Дж. Дж. Томпсон открыл нечто меньшее, чем атом, под названием электрон.А в 1912 году Эрнест Резерфорд обнаружил, что атомы имеют ядра. Затем мы обнаружили, что ядра состоят из протонов и нейтронов. Они считались фундаментальными компонентами, из которых состоит все … до 1960-х годов, когда мы обнаружили, что нейтроны и протоны состоят из еще более мелких вещей, называемых кварками — двух видов: верхние кварки и нижние кварки.

    Сегодня считается, что все, что вы видите вокруг себя, состоит только из этих трех частиц — электронов, верхних и нижних кварков.Это то, из чего сделаны все атомы. Ваш телефон, ваш стол, ваша кожа, трава… все. По крайней мере, это то, чему большинство людей учат на уроках естествознания.

    Проблема только в том, что это неправда. И физики знали это десятилетиями. Эти три частицы на самом деле не фундаментальны.

    Лучшая теория физики говорит нам, что на самом деле частиц вообще нет. Природа состоит из полей. Реальность — это принципиально много разных полей. То, что мы называем частицами, — это просто волны в поле.Но не такое поле.

    Так что, черт возьми, это за поля? А что они говорят нам о природе реальности?

    Идея частиц, даже частиц, о которых я много раз говорил, составляющих стандартную модель, на самом деле не является тем, из чего состоит Вселенная. Частицы — выдумка. Это удобные представления и на самом деле не лучшее понимание Вселенной на сегодняшний день.

    Фундаментальная природа Вселенной — не частицы, а поля.Это жидкие вещества, которые можно возмущать, они могут вибрировать и испытывать возбуждение.

    Что такое поля? Математически поле нечто, что принимает значение в каждой точке пространства. На самом деле они не сделаны ни из чего, кроме того, что строго с точки зрения физики.

    Подумайте об этом так: если у вас есть камин в комнате, температура в каждой точке этой комнаты будет иметь значение. Это будет поле температуры — это аналог фундаментальных полей Вселенной.

    И эти поля в природе есть везде. Вы не можете избежать этого.

    Если вы возьмете прочный металлический ящик и удалите из него все, все газы, все атомы, все фотоны — что останется внутри этого ящика? Это то, что мы называем вакуумом, как вакуум пустого пространства. Но на самом деле этот вакуум изобилует этими полями. И они постоянно движутся и меняются.

    Принцип неопределенности Гейзенберга означает, что квантовое поле не может оставаться на месте. Вместо этого они двигаются, вибрируют и со временем меняют свою ценность.

    Это компьютерная симуляция пустого пространства. Все пузыри, которые вы видите лопающимися и лопающимися, являются возмущениями пустого пространства — в этой пустоте постоянно создаются и разрушаются частицы. Но эти частицы на самом деле являются возбуждением полей, пронизывающих все пространство.

    То, что вы видите в окружающем мире, является возбуждением этих полей. Фактически все, что вы можете увидеть, это возбуждение только четырех полей.

    Вы можете видеть фотоны (или свет), которые являются колебаниями в электромагнитном поле.Электроны — это колебания в электронном поле. Верхние и нижние кварки составляют протоны и нейтроны в ядрах всех атомов, они представляют собой колебания в поле верхнего и нижнего кварков соответственно.

    Удивительно, но все, что вы видите вокруг себя, — телефон, стол, цветы и деревья, землю под ногами. Все состоит только из этих 4 полей.

    Но их больше, чем просто эти 4. Фактически все, что мы обозначили как частицы в стандартной модели, лучшей теории физики, которая у нас есть, на самом деле является возбуждением или колебаниями их собственных полей.

    Общее количество полей будет 17, включая поле Хиггса.
    Обратите внимание, что само пространство-время считается полем, но пока не может быть включено в квантовую теорию поля. Было бы 18-е поле.

    Все так называемые частицы на самом деле являются волнами. И когда я говорю «волна», я не имею в виду волну, подобную океанской. Эти двухмерные модели — всего лишь наглядное пособие, но на самом деле волны будут трехмерными.

    Вы видите какое-либо из этих полей? Не совсем, но когда вы можете получить какое-то представление об этом, соединив магнит с металлическими опилками.Линии, которые вы видите, на самом деле являются линиями магнитного поля, изменяющимися под действием магнита.

    Другой способ визуализировать поля — представить себе объем Вселенной, заполненный водой, как если бы мы жили в океане. А теперь представьте, что вместо воды океан наполнен несколькими жидкостями, примерно 17 различными видами жидкостей. И эти жидкости бывают разных цветов.

    Это может выглядеть действительно впечатляюще и странно, но это в некоторой степени аналогично тому, как на самом деле выглядит наша Вселенная… за исключением того, что вы не можете видеть эти жидкости.

    Почему эта теория лучше, чем идея частиц? Ключевое, что исключает поля, — это идея действия на расстоянии.

    Так, например, в случае ньютоновской гравитации вы должны признать, что гравитация Солнца каким-то образом влияет на Землю, которая находится на расстоянии 120 миллионов километров. Как может что-то повлиять на что-то такое далекое, не касаясь его. Это действие на расстоянии. Даже Ньютон считал действия на расстоянии абсурдными. Он сказал: «Немыслимо, чтобы неодушевленная грубая материя без посредничества чего-то еще, что не является материальным, действовала и влияла на другую материю без взаимного контакта…»

    Общая теория относительности Эйнштейна устранила эту идею действия на расстоянии, заменив пространство чем-то, называемым пространством-временем, которое представляет собой поле, пронизывающее всю реальность.И он математически показал, что гравитация действительно возникает из-за искривления этого поля пространства-времени.

    Все, что происходит с частицей в космосе, определяется тем, что происходит в поле рядом с частицей. Чтобы что-то распространялось на расстояния, оно должно воздействовать на свое поле локально, затем распространяться от локальной точки к другой удаленной точке, а затем воздействовать на поле локально в удаленной точке. Это похоже на то, как волна будет распространяться в воде, если вы бросите в нее камень, от камня к берегу.

    Поля также могут объяснить, как можно создавать и уничтожать частицы. Так, например, когда нейтрон распадается на протон, электрон и антинейтрино — как это происходит? Там прятался электрон? Откуда это.

    Поля обладают свойством отдавать свои вибрации или энергию. Если вы встряхнете поле достаточно сильно, они повлияют на другие поля. Таким образом, в этом распаде энергия кварковых полей нейтрона может быть передана кварковым полям Протона, плюс электронному полю и полям антинейтрино.

    Эти поля влияют на вас каждый день. Когда вы звоните кому-то на свой мобильный телефон, вы вносите возбуждение в поле и влияете на электронику в сотовом телефоне человека, которому вы звоните. На практике это действие на расстоянии, но это не действие на расстоянии. Ваш сотовый телефон создает возбуждение в электромагнитном поле, которое распространяется от вас к вышке сотовой связи и, в конечном итоге, к приемнику на другом конце.

    Но здесь, похоже, возникает дилемма, потому что в школе и из моих видеороликов вы узнали, что квантовая механика касается дискретных вещей — вот почему она называется квантовой.Но поля непрерывны, а не дискретны. Таким образом, здесь возникает конфликт между идеей дискретности частиц, представленной в квантовой механике, и непрерывной природой полей.

    Как согласовываются эти две идеи? Сочетание теории поля с квантовой механикой называется квантовой теорией поля или КТП.

    Итак, по сути, все возбуждения полей происходят только в виде кусков энергии. Энергия волны определяется массой частицы.2.

    Поле просто не принимает энергии ниже определенного порога. Однако, как только вы нажмете на поле достаточно сильно, создается частица. Эта дискретная единица энергии, которую может принять поле, и есть то, что мы называем энергией массы покоя частиц в поле. Это основное количество энергии, которое необходимо добавить к полю, чтобы создать частицу. Некоторые частицы, такие как бозон Хиггса, требуют много энергии для его создания. Вот почему для его обнаружения пришлось построить Большой адронный коллайдер.

    Так, например, один электрон создается, когда электронное поле возбуждается силой 0,511 МэВ (мегаэлектронвольт), что является массой одного электрона. Если вы добавите энергию, эквивалентную 0,4 МэВ, частицы не будут созданы. Если вы вложите энергию 0,7 МэВ, будет создан только один электрон. Если вы вложите 1,1 МэВ, будут созданы два электрона и так далее.

    Рябь в этом электронном поле или 3d-волны в этой жидкости — это маленькие сгустки энергии, проявляющиеся в виде электронов.

    Все электроны в вашем теле и в моем теле являются волнами одного и того же основного поля. Поле фундаментально, электроны — нет. Также в этой комнате и в вашей комнате присутствуют поле верхних и нижних кварков. И все атомы в вашем теле состоят из частиц, которые представляют собой рябь в этих трех полях. Это то же поле, в котором находитесь вы, я и все на Земле. На самом деле это то же поле, в котором находятся все другие планеты и Солнце. Мы в основном состоим из ряби в одних и тех же трех полях по всей Вселенной.

    Нет никаких указаний на то, что рябь на моем поле может взаимодействовать с рябью на вашем поле, но это одно непрерывное поле, и все связано с ним.

    Однако

    Fields не все нам говорят. Он не говорит нам, что такое темная материя, что такое темная энергия, или как произошел Большой взрыв, или почему во Вселенной больше материи, чем антивещества.

    Как волны в поле связаны с волнами вероятности квантовой механики и уравнением Шредингера?

    , когда мы говорим, что электрон — это частица с положением и скоростью, это неверно.И это не потому, что мы не можем измерить его положение и скорость. Это потому, что не существует таких понятий, как положение и скорость. Все, что есть, — это волновая функция. Он разбросан по всему пространству и говорит нам, какими будут положение и скорость, только если мы решим их измерить.

    Так, например, форма электромагнитного поля — это волновая функция фотонов, форма электрического поля — волновая функция электронов и так далее.

    Волновая функция — это то, что действительно существует.Но когда вы наблюдаете за электроном, вы не видите волновую функцию, потому что волновая функция сжалась до дискретного значения. Это можно предсказать с помощью уравнения Шордингера.

    Поля колеблются и модулируются, но когда вы их измеряете, они распадаются на отдельные энергетические пакеты, называемые частицами. У частицы есть место, но поле разбросано повсюду. Итак, квантовая механика утверждает, что реальность отличается от реальности, когда вы ее измеряете, а когда нет.

    Каждая частица во Вселенной — это крошечная рябь лежащего в основе поля, преобразованная в частицу механизмами квантовой механики.

    Квантовые поля, вибрирующие в любом месте пространства и во времени, являются фундаментальными строительными блоками природы.

    Итак, можно ответить на извечный вопрос, является ли свет частицей или волной. Это волны. Частица — это как раз то, что проявляется, когда мы измеряем волну.

    Кто открыл поля? Майкл Фарадей придумал эту идею и фактически использовал слово «поле» в своей записной книжке в 1845 году.

    Действительно ли поля — это просто математические конструкции? Несмотря на то, что поле не состоит из вещества, о котором знают физики, поля считаются реальным, физическим веществом. Это потому, что они существуют в космосе и обладают энергией. Кроме того, их свойства можно рассчитать и точно предсказать по результатам экспериментов.

    Это причина, по которой большинство физиков считают их физической реальностью.

    Являются ли эти поля фундаментальными? Что ж, я думаю, что это фундаментально в том смысле, что это предел нашего понимания.Вполне возможно, что поля — это всего лишь приближение более глубокого уровня реальности.

    Потому что, в конечном счете, должна быть какая-то фундаментальная причина, по которой эти поля обладают теми же свойствами. Все они подчиняются определенным математическим правилам и могут быть предсказаны с помощью математических формул. Почему это так? Почему для электронного поля требуется минимум 0,511 мегаэлектронвольт? Почему он подчиняется математическим правилам? Узнаем ли мы когда-нибудь ответ, в отличие от многих физиков, я думаю, что узнаем.Возможно, мы даже не задаем правильные вопросы.

    По знаменитым словам одного министра обороны, есть известные неизвестные и неизвестные неизвестные. И я думаю, что ответ придет, когда мы, люди, будем знать достаточно, чтобы задать правильный вопрос.

    Квантовая теория поля — обзор

    Введение и предварительные сведения

    Квантовая теория поля (КТП) в искривленном пространстве-времени — это гибридная приближенная теория, в которой предполагается, что квантовые поля материи распространяются в фиксированном классическом фоновом гравитационном поле.Его основное физическое предсказание состоит в том, что сильные гравитационные поля могут поляризовать вакуум и, когда это зависит от времени, привести к созданию пары, так же как сильное и / или зависящее от времени электромагнитное поле может поляризовать вакуум и / или вызвать создание пары заряженных частиц. . Можно ожидать, что это будет хорошее приближение к полной квантовой гравитации при условии, что типичные частоты гравитационного фона намного меньше планковской частоты (c5 / Għ) 1/2 ~ 1043 с-1) и при условии подходящей меры для измерения энергии. , энергия создаваемых частиц намного меньше энергии фонового гравитационного поля или его источников материи.Несомненно, наиболее важным предсказанием теории является эффект Хокинга, согласно которому, скажем, сферически симметричная классическая черная дыра массой M будет излучать тепловое излучение при температуре Хокинга T = (8πM) −1 (здесь и от теперь мы используем единицы Планка, где G, c, ħ и, k (постоянная Больцмана) все принимаются равными 1).

    С математической точки зрения необходимость формулировать законы и вывести общие свойства КТП на неплоских пространствах-временах вынуждает формулировать и доказывать результаты в локальных терминах и, как побочный продукт, тем самым приводит к улучшенному видению КТП с плоским пространством-временем. тоже.Также интересно сформулировать КТП на идеализированном пространстве-времени с определенными глобальными геометрическими особенностями. Таким образом, QFT на пространстве-времени с раздвоенными горизонтами Киллинга тесно связана с эффектом Хокинга; КТП по пространству-времени с замкнутыми времениподобными кривыми тесно связана с вопросом, допускают ли законы физики создание машины времени.

    Как это принято в общей теории относительности, искривленное пространство-время математически моделируется как (паракомпактное, хаусдорфово) многообразие M, снабженное псевдоримановой метрикой g сигнатуры (-, +++) (мы следуем соглашениям стандартный текст Misner et al. (1973)). Мы также будем предполагать, если не указано иное, наше пространство-время будет глобально гиперболическим , то есть, что M допускает глобальную временную координату , под которой мы подразумеваем глобальную координату t , такую, что каждая константа — t поверхность — это гладкая поверхность Коши, т. е. гладкая пространственноподобная 3-поверхность, разрезанная ровно один раз каждой непродолжительной причинной кривой. (Без этого предположения по умолчанию для QFT возникают дополнительные проблемы, о которых мы кратко упомянем в связи с вопросом о «машине времени», который обсуждается позже.) Ввиду этого определения глобально гиперболические пространства-времени явно ориентированы во времени, и мы будем предполагать, что выбор временной ориентации был сделан, чтобы мы могли говорить о направлениях «будущее» и «прошлое». Современные формулировки этого предмета принимают в качестве фундаментальной математической структуры, моделирующей квантовое поле, * -алгебру A (с тождеством I ) вместе с семейством локальных под * -алгебр A (O), помеченных ограниченными открытыми областями O области пространство-время (M, g) и удовлетворяет условию изотонии или net , что из O1⊂O2 следует, что A (O1) является подалгеброй в A (O2), а также условию, что если две ограниченные открытые области O1 и O2 являются пространственноподобно разделены, то коммутируют A (O1) и A (O2).

    Тогда применимы стандартные концепции и методы алгебраической квантовой теории: в частности, состояния определены как положительные (это означает, что ω (A * A) ≥0∀A∈A)) нормализованные (это означает ω ( I ) = 1) линейные функционалы на A. Различают чистых состояний и смешанных состояний, только последние могут быть записаны как нетривиальные выпуклые комбинации других состояний. Каждому состоянию, ω , конструкция GNS связывает представление, ρ ω , A в гильбертовом пространстве Hω вместе с циклическим вектором Ω∈Hω, таким что

    ω (A) = 〈Ω | ρω (A) Ω〉

    (и тройка GNS (ρω, H, Ω) единственна с точностью до эквивалентности).Формулировка * -алгебры как C * -алгебры часто дает технические преимущества. Тогда представление GNS является как всюду определенными ограниченными операторами и неприводимо тогда и только тогда, когда состояние является чистым. Полезная концепция, благодаря Хаагу, — это лист данного состояния ω , который можно определить как набор всех состояний ω σ , которые возникают в форме tr (σρω (⋅)), где σ пробегает операторы плотности (операторы класса следа с единичным следом) на Hω.

    Учитывая состояние ω и автоморфизм α , который сохраняет состояние (т. Е. ω ∘ α = ω ), тогда будет унитарный оператор U на H ω , который реализует α в том смысле, что ρω (α (A)) = U − 1ρω (A) U и U выбирается однозначно из условия U Ω = Ω.

    В стационарном пространстве-времени , то есть таком, которое допускает однопараметрическую группу изометрий, интегральные кривые которых всюду времениподобны, алгебра унаследует однопараметрическую группу (т.е., удовлетворяя α ( t 1 ) ∘ α ( t 2 ) = α ( t 1 + t 2 )) времени- трансляционные автоморфизмы, α ( t ), и, при любом стационарном состоянии (т.е. таком, которое удовлетворяет ω ∘ α ( t ) = ω ∀t∈ R ), они будут реализуется однопараметрической группой унитарных единиц, U ( t ), в ее гильбертовом пространстве GNS, удовлетворяющем условию U ( t ) Ω = Ω.Если U ( t ) строго непрерывен, так что он принимает форму e −i Ht , и если гамильтониан, H , положительный, то ω называется «основным состоянием. . » Обычно ожидается, что основных состояния будут существовать и часто быть уникальными.

    Другой важный класс стационарных состояний для алгебры стационарного пространства-времени — это класс состояний KMS , ω β , при обратной температуре β; они имеют физическую интерпретацию состояний теплового равновесия.В GNS-представлении одного из них автоморфизмы также реализуются сильно непрерывной унитарной группой, e −i Ht , которая сохраняет Ω, но (вместо положительного H ) существует комплексное сопряжение, J , на H ω так, что

    [1] e-βH / 2ρω (A) Ω = Jρω (A *) Ω

    для всех A∈A. Привлекательной особенностью этого предмета является то, что его основные качественные характеристики уже присутствуют в линейных теориях поля и, что необычно по сравнению с другими вопросами в КТП, они допускают прямую явную и строгую математическую формулировку.Фактически, в качестве основного примера в следующем разделе мы приводим конструкцию полевой алгебры для квантованного вещественного линейного уравнения Клейна – Гордона

    [2] (□ g − m2 − V) ϕ = 0

    массы м в глобально гиперболическом пространстве-времени (M, g). Здесь □ g обозначает оператор Лапласа – Бельтрами gab∇a∂b (= (| det (g) |) −1 / 2∂a ((| det (g) | 1 / 2gab∂b)) Мы включаем скалярное внешнее фоновое классическое поле, V , в дополнение к внешнему гравитационному полю, представленному g .В случае, если m равно нулю, если V равно R /6, где R обозначает скаляр Римана, уравнение будет конформно инвариантным .

    Основная новая особенность КТП в искривленном пространстве-времени (уже присутствующая в линейных теориях поля) состоит в том, что в общем (ни плоском, ни стационарном) пространстве-времени не будет какого-либо единственного предпочтительного состояния, а скорее будет семейство предпочтительных состояний, членов которые лучше всего рассматривать как равные друг другу.Именно эта особенность делает приведенную выше алгебраическую структуру особенно подходящей, действительно необходимой для ясной формулировки предмета. Концептуально именно к этой функции нужно привыкнуть. В частности, нужно понимать, что, как мы объясним позже, интерпретация состояния как имеющего определенное «содержание частиц» в целом проблематично, поскольку оно может относиться только к конкретному выбору «вакуумного» состояния и, в зависимости от В интересующем пространстве-времени может быть одно состояние или несколько состояний или, часто, состояния вообще не могут быть названы «вакуумом», и даже когда есть состояния, заслуживающие этого названия, они часто будут определены только в некоторой приблизительной или асимптотической форме. или преходящее чувство, или только в некоторой подобласти пространства-времени.

    Вместе с тем, нельзя ожидать, что глобальные наблюдаемые, такие как «число частиц» или квантовый гамильтониан теории свободного поля плоского пространства-времени, будут обобщены на искривленный контекст пространства-времени, и по этой причине локальные наблюдаемые играют центральную роль в теории. . Квантованный тензор энергии-импульса является особенно естественной и важной такой локальной наблюдаемой, и теория этого явления является центральной для всего предмета. Краткое введение в него дается в следующем разделе.

    За этим следует следующий раздел, посвященный эффектам Хокинга и Унру, а затем краткий раздел, посвященный проблемам расширения теории за пределы установки «по умолчанию» на неглобально гиперболические пространства-времени.Наконец, мы кратко упоминаем ряд других интересных и активных областей предмета, а также выпускаем несколько предупреждений , которые следует иметь в виду при чтении литературы.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *

    Карта сайта
    © Copyright 2019, All Rights Reserved, info @ howtohostel.ru