Фибоначчи и золотое сечение: Золотое сечение Фибоначчи. Божественная мера красоты

Числа Фибоначчи и золотое сечение. А при чем здесь стоматология? |

Эстетическое направление в стоматологии развивается стремительно. Но, как и в любой другой сфере, так или иначе связанной с красотой, здесь тоже есть принципы, над которыми не властно время. Одним из таких принципов является принцип золотого сечения, описанный в XIII веке средневековым математиком Леонардо Фибоначчи. Хотя поначалу этот концепт окружал некий ореол мистицизма, сейчас ни у кого не возникает сомнений по поводу релевантности золотого сечения.

Задолго до Фибоначчи древние греки пользовались этим принципом, чтобы создавать произведения искусства. Сам Леонардо Да Винчи прибегал к золотой пропорции практически во всех своих творениях. Этим же принципом руководствуются и современные автомобильные дизайнеры.

Содержание

Ряд Фибоначчи

Последовательность Фибоначчи встречается в природе практически на каждом шагу – в количестве лепестков розы или кроликов, родившихся за год. Кстати, последний пример особенно волновал Фибоначчи в 1202 году.

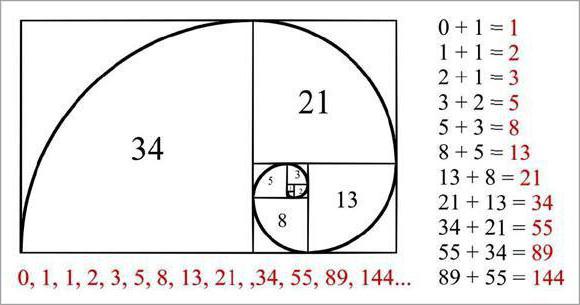
Ряд Фибоначчи представляет собой числовую последовательность, первые значения которого равны 0 или 1, а каждое последующее равно сумме двух предыдущих.

Выглядит это следующим образом: 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13 и т.д.. В конечном счете получается последовательность: 1, 1, 2, 3, 5, 8, 13 …

Золотое сечение

Если поделить одно число из последовательности на предшествующее ему, то получится значение, близкое к 1,618. С развитием последовательности частное, которое еще называют числом Фи, становится все более точным. А его инверсия – 0,618 или число фи – как раз считается золотым сечением.

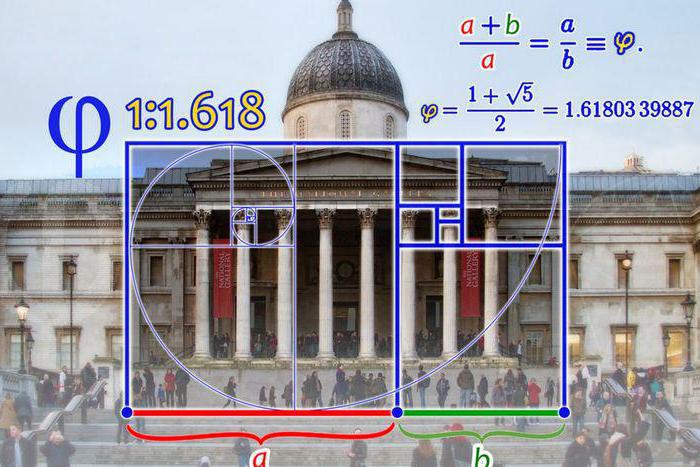
Числа Фибоначчи лежат в основе золотого сечения (1:1,618) и, как следствие, золотой спирали и золотого прямоугольника. Кредитная карта представляет собой идеальный пример золотого прямоугольника. Ее измерения равны 53 мм и 86 мм. Умножив 53 на число Фи или 1,618, получаем 86.

Лучше всего представить себе золотую спираль на примере раковины моллюска наутилуса. Золотая спираль основывается на квадратах из числа последовательности Фибоначчи, начиная с 1×1.

Связь со стоматологией

Золотое сечение используется при определении размера зуба.

Средняя ширина центрального резца составляет примерно 8 мм. Ширина двух центральных резцов будет равняться 16 мм. Если мы хотим определить идеальную эстетическую длину этих самых резцов, мы можем поделить 16 на 1,618 и получится 9,89 мм. Такие расчеты помогают при восстановлении зубов.

Приведем еще один пример. Ширина центральных резцов является хорошей отправной точкой в расчетах. Поэтому допустим, что 8,5 мм является идеальной шириной для конкретного пациента. Ширина обоих центральных резцов составляет 17, а идеальная эстетическая длина — 10,5 мм (17 / 1,618 = 10,5). Если мы разделим ширину этого центрального резца на число Фи, у нас получится результат, с помощью которого можно вернуть идеальную эстетическую визуальную ширину зуба позади него (боковой резец). Следовательно, 8,5 мм / 1,618 = 5,3 мм, и в этом случае это идеальная визуальная ширина бокового резца.

Стоит учитывать, что речь идет именно о визуальной, а не фактической ширине бокового резца. Можно посчитать все еще раз, определяя идеальную ширину клыка: 5,3 мм / 1,618 = 3,3 мм, первого премоляра позади него: 3,3 мм / 1,618 = 2,0 мм, второго премоляра: 2,0 мм / 1,618 = 1,2 мм и т.д..

Таким образом у нас вырисовывается вполне конкретный план реставрации.

Использование золотого сечения — это всего лишь инструмент для создания идеальной эстетической улыбки. Оно может предоставить стоматологу информацию, которая поможет начать разработку новой улыбки пациента. Золотое сечение не является единственным залогом успеха, поскольку есть много других факторов, которые необходимо учитывать.

Поделиться ссылкой:

The following two tabs change content below.

Автор и редактор блога Стомдевайс. Специализируется на стоматологии, медицине и маркетинге. В 2018 году стажировалась в отделе локализации Google. В 2017 и 2018 году стала призером Международной научной конференции молодых ученых в МГУ. С 2015 года профессионально занимается переводами с английского языка.

Числа Фибоначчи и золотое сечение: взаимосвязь

Во вселенной еще много неразгаданных тайн, некоторые из которых ученые уже смогли определить и описать. Числа Фибоначчи и золотое сечение составляют основу разгадки окружающего мира, построения его формы и оптимального зрительного восприятия человеком, с помощью которых он может ощущать красоту и гармонию.

Золотое сечение

Принцип определения размеров золотого сечения лежит в основе совершенства целого мира и его частей в своей структуре и функциях, его проявление можно видеть в природе, искусстве и технике. Учение о золотой пропорции было заложено в результате исследований древними учеными природы чисел.

В основе его лежит теория о пропорциях и соотношениях делений отрезков, которое было сделано еще древним философом и математиком Пифагором. Он доказал, что при разделении отрезка на две части: X (меньшую) и Y (большую), отношение большего к меньшему будет равно отношению их суммы (всего отрезка):

X : Y = Y : X+Y.

В результате получается уравнение: х²– х – 1=0, которое решается как х=(1±√5)/2.

Если рассмотреть соотношение 1/х, то оно равно 1,618…

Свидетельства использования древними мыслителями золотой пропорции приведены в книге Эвклида «Начала», написанной еще в 3 в. до н.э., который применял это правило для построения правильных 5-угольников. У пифагорейцев эта фигура считается священной, поскольку является одновременно симметричной и асимметричной. Пентаграмма символизировала жизнь и здоровье.

Числа Фибоначчи

Знаменитая книга Liber abaci математика из Италии Леонардо Пизанского, который в последующем стал известен, как Фибоначчи, увидела свет в 1202 г. В ней ученый впервые приводит закономерность чисел, в ряду которых каждое число является суммой 2-х предыдущих цифр. Последовательность чисел Фибоначчи заключается в следующем:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 и т.д.

Также ученый привел ряд закономерностей:

Любое число из ряда, разделенное на последующее, будет равно значению, которое стремится к 0,618. Причем первые числа Фибоначчи не дают такого числа, но по мере продвижения от начала последовательности это соотношение будет все более точным.
Если же поделить число из ряда на предыдущее, то результат устремится к 1,618.
Одно число, поделенное на следующее через одно, покажет значение, стремящееся к 0,382.

Применение связи и закономерностей золотого сечения, числа Фибоначчи (0,618) можно найти не только в математике, но и в природе, в истории, в архитектуре и строительстве и во многих других науках.

Спираль Архимеда и золотой прямоугольник

Спирали, очень распространенные в природе, были исследованы Архимедом, который даже вывел ее уравнение. Форма спирали основана на законах о золотом сечении. При ее раскручивании получается длина, к которой можно применить пропорции и числа Фибоначчи, увеличение шага происходит равномерно.

Параллель между числами Фибоначчи и золотым сечением можно увидеть и построив «золотой прямоугольник», у которого стороны пропорциональны, как 1,618:1. Он строится, переходя от большего прямоугольника к малым так, что длины сторон будут равны числам из ряда. Построение его можно сделать и в обратном порядке, начиная с квадратика «1». При соединении линиями углов этого прямоугольника в центре их пересечения получается спираль Фибоначчи или логарифмическая.

История применения золотых пропорций

Многие древние памятники архитектуры Египта возведены с использованием золотых пропорций: знаменитые пирамиды Хеопса и др. Архитекторы Древней Греции широко использовалиих их при возведении архитектурных объектов, таких как храмы, амфитеатры, стадионы. Например, были применены такие пропорции при строительстве античного храма Парфенон, театра Диониса (Афины) и других объектов, которые стали шедеврами древнего зодчества, демонстрирующими гармонию, основанную на математической закономерности.

В более поздние века интерес к золотому сечению поутих, и закономерности были забыты, однако опять возобновился в эпоху Ренессанса вместе с книгой францисканского монаха Л. Пачоли ди Борго «Божественная пропорция» (1509 г.). В ней были приведены иллюстрации Леонардо да Винчи, который и закрепил новое название «золотое сечение». Также были научно доказаны 12 свойств золотой пропорции, причем автор рассказывал о том, как проявляется она в природе, в искусстве и называл ее «принципом построения мира и природы».

Витрувианский человек Леонардо

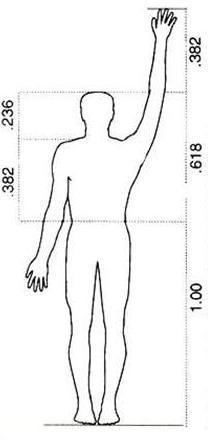
Рисунок, которым Леонардо да Винчи в 1492 г. проиллюстрировал книгу Витрувия, изображает фигуру человека в 2-х позициях с руками, разведенными в стороны. Фигура вписана в круг и квадрат. Этот рисунок принято считать каноническими пропорциями человеческого тела (мужского), описанными Леонардо на основе изучения их в трактатах римского архитектора Витрувия.

Центром тела как равноудаленной точкой от конца рук и ног считается пупок, длина рук приравнивается к росту человека, максимальная ширина плеч = 1/8 роста, расстояние от верха груди до волос = 1/7, от верха груди до верха головы =1/6 и т.д.

С тех пор рисунок используется в виде символа, показывающего внутреннюю симметрию тела человека.

Термин «Золотое сечение» Леонардо использовал для обозначения пропорциональных отношений в фигуре человека. Например, расстояние от пояса до ступней ног соотносится к аналогичному расстоянию от пупка до макушки так же, как рост к первой длине (от пояса вниз). Эти вычисление делается аналогично соотношению отрезков при вычислении золотой пропорции и стремится к 1,618.

Все эти гармоничные пропорции часто используются деятелями искусства для создания красивых и впечатляющих произведений.

Исследования золотого сечения в 16-19 веках

Используя золотое сечение и числа Фибоначчи, исследовательскую работу по вопросу о пропорциях продолжают уже не одно столетие. Параллельно с Леонардо да Винчи немецкий художник Альбрехт Дюрер также занимался разработкой теории правильных пропорций тела человека. Для этого им даже был создан специальный циркуль.

В 16 в. вопросу о связи числа Фибоначчи и золотого сечения были посвящены работы астронома И. Кеплера, который впервые применил эти правила для ботаники.

Новое «открытие» ожидало золотое сечение в 19 в. с опубликованием «Эстетического исследования» немецкого ученого профессора Цейзига. Он возвел эти пропорции в абсолют и объявил о том, что они универсальны для всех природных явлений. Им были проведены исследования огромного количества людей, вернее их телесных пропорций (около 2 тыс.), по итогам которых сделаны выводы о статистических подтвержденных закономерностях в соотношениях различных частей тела: длины плеч, предплечий, кистей, пальцев и т.д.

Были исследованы также предметы искусства (вазы, архитектурные сооружения), музыкальные тона, размеры при написании стихотворений — все это Цейзиг отобразил через длины отрезков и цифры, он же ввел термин «математическая эстетика». После получения результатов выяснилось, что получается ряд Фибоначчи.

Число Фибоначчи и золотое сечение в природе

В растительном и животном мире существует тенденция к формообразованию в виде симметрии, которая наблюдается в направлении роста и движения. Деление на симметричные части, в которых соблюдаются золотые пропорции, — такая закономерность присуща многим растениям и животным.

Природа вокруг нас может быть описана с помощью чисел Фибоначчи, например:

расположение листьев или веток любых растений, а также расстояния соотносятся с рядом приведенных чисел 1, 1, 2, 3, 5, 8, 13 и далее;
семена подсолнуха (чешуя на шишках, ячейки ананаса), располагаясь двумя рядами по закрученным спиралям в разные стороны;
соотношение длины хвоста и всего тела ящерицы;
форма яйца, если провести линию условно через широкую его часть;
соотношение размеров пальцев на руке человека.

И, конечно, самые интересные формы представляют закручивающиеся по спирали раковины улиток, узоры на паутине, движение ветра внутри урагана, двойная спираль в ДНК и структура галактик — все они включают в себя последовательность чисел Фибоначчи.

Использование золотого сечения в искусстве

Исследователи, занимающиеся поиском в искусстве примеров использования золотого сечения, подробно исследуют различные архитектурные объекты и произведения живописи. Известны знаменитые скульптурные работы, создатели которых придерживались золотых пропорций, — статуи Зевса Олимпийского, Аполлона Бельведерского и Афины Парфенос.

Одно из творений Леонардо да Винчи — «Портрет Моны Лизы» — уже многие годы является предметом исследований ученых. Ими было обнаружено, что композиция работы целиком состоит из «золотых треугольников», объединенных вместе в правильный пятиугольник-звезду. Все работы да Винчи являются свидетельством того, насколько глубоки были его познания в строении и пропорциях тела человека, благодаря чему он и смог уловить невероятно загадочную улыбку Джоконды.

Золотое сечение в архитектуре

В качестве примера ученые исследовали шедевры архитектуры, созданные по правилам «золотого сечения»: египетские пирамиды, Пантеон, Парфенон, Собор Нотр-Дам де Пари, храм Василия Блаженного и др.

Парфенон — одно из красивейших зданий в Древней Греции (5 в. до н.э.) — имеет 8 колонн и 17 по разным сторонам, отношение его высоты к длине сторон равно 0,618. Выступы на его фасадах сделаны по «золотому сечению» (фото ниже).

Одним из ученых, который придумал и успешно применял усовершенствование модульной системы пропорций для архитектурных объектов (так называемый «модулор»), — был французский архитектор Ле Корбюзье. В основу модулора положена измерительная система, связанная с условным делением на части человеческого тела.

Русский архитектор М. Казаков, построивший несколько жилых домов в Москве, а также здания сената в Кремле и Голицынской больницы (сейчас 1-я Клиническая им. Н. И. Пирогова), — был одним из архитекторов, которые использовали при проектировании и строительстве законы о золотом сечении.

Применение пропорций в дизайне

В дизайне одежды все модельеры делают новые образы и модели с учетом пропорций человеческого тела и правил золотого сечения, хотя от природы не все люди имеют идеальные пропорции.

При планировании ландшафтного дизайна и создании объемных парковых композиций с помощью растений (деревьев и кустарников), фонтанов и малых архитектурных объектов также могут применяться закономерности «божественных пропорций». Ведь композиция парка должна быть ориентирована на создание впечатления на посетителя, который свободно сможет ориентироваться в нем и находить композиционный центр.

Все элементы парка находятся в таких соотношениях, чтобы с помощью геометрического строения, взаиморасположения, освещения и света, произвести на человека впечатление гармонии и совершенства.

Применение золотого сечения в кибернетике и технике

Закономерности золотого сечения и чисел Фибоначчи проявляются также в переходах энергии, в процессах, происходящих с элементарными частицами, составляющих химические соединения, в космических системах, в генной структуре ДНК.

Аналогичные процессы происходят и в организме человека, проявляясь в биоритмах его жизни, в действии органов, например, головного мозга или зрения.

Алгоритмы и закономерности золотых пропорций широко используются в современной кибернетике и информатике. Одна из несложных задач, которую дают решать начинающим программистам, — написать формулу и определить, сумму чисел Фибоначчи до определенного числа, используя языки программирования.

Современные исследования теории о золотой пропорции

Начиная с середины 20 века, интерес к проблемам и влиянию закономерностей золотых пропорций на жизнь человека, резко возрастает, причем со стороны многих ученых различных профессий: математиков, исследователей этноса, биологов, философов, медицинских работников, экономистов, музыкантов и др.

В США с 1970-хгодов начинает выпускаться журнал The Fibonacci Quarterly, где публикуются работы на эту тему. В прессе появляются работы, в которых обобщенные правила золотого сечения и ряда Фибоначчи используют в различных отраслях знаний. Например, для кодирования информации, химических исследований, биологических и т.д.

числа фибоначчи золотое сечение в природе

Все это подтверждает выводы древних и современных ученых о том, что золотая пропорция многосторонне связана с фундаментальными вопросами науки и проявляется в симметрии многих творений и явлений окружающего нас мира.

Числа Фибоначчи,золотое сечение,последовательность Фибоначчи и Иллюминаты.: kamburina — LiveJournal Леонардо Фибоначчи – один из величайших математиков Средневековья. В одном и своих трудов «Книга вычислений” Фибоначчи описал индо-арабскую систему исчисления и преимущества ее использования перед римской.

Определение

Числа Фибоначчи или Последовательность Фибоначчи — числовая последовательность, обладающая рядом свойств. Например, сумма двух соседних чисел последовательности дает значение следующего за ними (например, 1+1=2; 2+3=5 и т.д.), что подтверждает существование так называемых коэффициентов Фибоначчи, т.е. постоянных соотношений.

Последовательност Фибоначчи начинается так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…

Свойства последовательности Фибоначчи

1. Отношение каждого числа к последующему более и более стремится к 0.618 по увеличении порядкового номера. Отношение же каждого числе к предыдущему стремится к 1.618 (обратному к 0.618). Число 0.618 называют (ФИ).

2. При делении каждого числа на следующее за ним, через одно получается число 0.382; наоборот – соответственно 2.618.

3. Подбирая таким образом соотношения, получаем основной набор фибоначчиевских коэффициентов: … 4.235, 2.618, 1.618, 0.618, 0.382, 0.236.

Связь последовательности Фибоначчи и «золотого сечения»

Последовательность Фибоначчм асимптотически (пpиближаясь все медленнее и медленнее) стpемится к некотоpому постоянному соотношению. Однако, это соотношение иppационально, то есть пpедставляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифp в дpобной части. Его невозможно выразить точно.

Если какой-либо член последовательности Фибоначчи pазделить на пpедшествующий ему (напpимеp, 13:8), pезультатом будет величина, колеблющаяся около иppационального значения 1.61803398875… и чеpез pаз то пpевосходящая, то не достигающая его. Hо даже затpатив на это Вечность, невозможно узнать сотношение точно, до последней десятичной цифpы. Kpаткости pади, мы будем пpиводить его в виде 1.618. Особые названия этому соотношению начали давать еще до того, как Лука Пачиоли (сpедневековый математик) назвал его Божественной пpопоpцией. Cpеди его совpеменных названий есть такие, как Золотое сечение, Золотое сpеднее и oтношение веpтящихся квадpатов. Kеплеp назвал это соотношение одним из «сокpовищ геометpии». В алгебpе общепpинято его обозначение гpеческой буквой фи

Ф=1.618

Представим золотое сечение на примере отрезка.

Рассмотрим отрезок с концами A и B. Пусть точка С делит отрезок AB так что,

AC/CB = CB/AB или

AB/CB = CB/AC.

Представить это можно примерно так: A——C———B

Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.

Отрезки золотой пропорции выражаются бесконечной иррациональной дробью 0,618…, если AB принять за единицу, AC = 0,382.. Kак мы уже знаем числа 0.618 и 0.382 являются коэффициентами последовательности Фибоначчи.

Пропорции Фибоначчи и золотого сечения в природе и истории

Важно отметить, что Фибоначчи как бы напомнил свою последовательность человечеству. Она была известна еще древним грекам и египтянам. И действительно, с тех пор в природе, архитектуре, изобразительном искусстве, математике, физике, астрономии, биологии и многих других областях были найдены закономерности, описываемые коэффициентами Фибоначчи. Просто удивительно, сколько постоянных можно вычислить пpи помощи последовательности Фибоначчи, и как ее члены проявляются в огромном количестве сочетаний. Однако не будет преувеличением сказать, что это не просто игра с числами, а самое важное математическое выражение природных явлений из всех когда-либо открытых.

Пpиводимые ниже примеры показывают некоторые интересные приложения этой математической последовательности.

1. Pаковина закручена по спирали. Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Форма спирально завитой раковины привлекла внимание Архимеда. Дело в том, что отношение измерений завитков раковины постоянно и равно 1.618. Архимед изучал спираль раковин и вывел уравнение спирали. Cпираль, вычерченная по этому уравнению, называется его именем. Увеличение ее шага всегда равномерно. В настоящее время спираль Архимеда широко применяется в технике.

2. Растения и животные. Еще Гете подчеркивал тенденцию природы к спиральности. Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Cпираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Cовместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения. Паук плетет паутину спиралеобразно. Cпиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНK закручена двойной спиралью. Гете называл спираль «кривой жизни».

Cреди придорожных трав растет ничем не примечательное растение — цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий — 38, четвертый — 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.

Ящерица живородящая. В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции — длина ее хвоста так относится к длине остального тела, как 62 к 38.

И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы — симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста. Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого.

Пьер Kюри в начале нашего столетия сформулировал ряд глубоких идей симметрии. Он утверждал, что нельзя рассматривать симметрию какого-либо тела, не учитывая симметрию окружающей среды. Закономерности золотой симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности, как указано выше, есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.

3. Космос. Из истории астрономии известно, что И. Тициус, немецкий астроном XVIII в., с помощью этого ряда (Фибоначчи) нашел закономерность и порядок в расстояниях между планетами солнечной системы

Однако один случай, который, казалось бы, противоречил закону: между Марсом и Юпитером не было планеты. Cосредоточенное наблюдение за этим участком неба привело к открытию пояса астероидов. Произошло это после смерти Тициуса в начале XIX в.

Pяд Фибоначчи используют широко: с его помощью представляют архитектонику и живых существ, и рукотворных сооружений, и строение Галактик. Эти факты — свидетельства независимости числового ряда от условий его проявления, что является одним из признаков его универсальности.

4. Пирамиды. Многие пытались разгадать секреты пирамиды в Гизе. В отличие от других египетских пирамид это не гробница, а скоpее неразрешимая головоломка из числовых комбинаций. Замечательные изобpетательность, мастерство, время и труд аpхитектоpов пирамиды, использованные ими пpи возведении вечного символа, указывают на чрезвычайную важность послания, которое они хотели передать будущим поколениям. Их эпоха была дописьменной, доиероглифической и символы были единственным средством записи открытий. Kлюч к геометро-математическому секрету пирамиды в Гизе, так долго бывшему для человечества загадкой, в действительности был передан Геродоту храмовыми жрецами, сообщившими ему, что пирамида построена так, чтобы площадь каждой из ее граней была равна квадрату ее высоты.

Площадь тpеугольника

356 x 440 / 2 = 78320

Площадь квадpата

280 x 280 = 78400

Длина ребра основания пирамиды в Гизе равна 783.3 фута (238.7 м), высота пирамиды -484.4 фута (147.6 м). Длина ребра основания, деленная на высоту, приводит к соотношению Ф=1.618. Высота 484.4 фута соответствует 5813 дюймам (5-8-13) — это числа из последовательности Фибоначчи. Эти интересные наблюдения подсказывают, что конструкция пирамиды основана на пропорции Ф=1,618. Некоторые современные ученые склоняются к интерпретации, что древние египтяне построили ее с единственной целью — передать знания, которые они хотели сохранить для грядущих поколений. Интенсивные исследования пирамиды в Гизе показали, сколь обширными были в те времена познания в математике и астрологии. Во всех внутренних и внешних пропорциях пирамиды число 1.618 играет центральную роль.

Пирамиды в Мексике. Hе только египетские пиpамиды постpоены в соответствии с совеpшенными пpопоpциями золотого сечения, то же самое явление обнаpужено и у мексиканских пиpамид. Возникает мысль, что как египетские, так и мексиканские пиpамиды были возведены пpиблизительно в одно вpемя людьми общего происхождения.

О последовательности Фибоначчи ордена Иллюминатов.

Это по сути, хранящийся в некогда секретных записях общества Иллюминатов, основанному в 1776 году профессором Адамом Вейсгауптом, последовательность чисел Фибоначчи, записанная в ряд:
58683436563811772030917
98057628621354486227052
60462818902449707207204
18939113748475408807538
68917521266338622235369
31793180060766726354433
38908659593958290563832
26613199282902678806752
08766892501711696207032
22104321626954862629631
36144381497587012203408
05887954454749246185695
36486444924104432077134
49470495658467885098743
39442212544877066478091
58846074998871240076521
70575179788341662562494
07589069704000281210427
62177111777805315317141
01170466659914669798731
76135600670874807101317
95236894275219484353056
78300228785699782977834
78458782289110976250030
26961561700250464338243
77648610283831268330372
42926752631165339247316
71112115881863851331620
38400522216579128667529
46549068113171599343235
97349498509040947621322
29810172610705961164562
99098162905552085247903
52406020172799747175342
77759277862561943208275
05131218156285512224809
39471234145170223735805
77278616008688382952304
59264787801788992199027
07769038953219681986151
43780314997411069260886
74296226757560523172777
52035361393621076738937
64556060605921658946675
95519004005559089502295
30942312482355212212415
44400647034056573479766
39723949499465845788730
39623090375033993856210
24236902513868041457799
56981224457471780341731
26453220416397232134044
44948730231541767689375
21030687378803441700939
54409627955898678723209
51242689355730970450959
56844017555198819218020
64052905518934947592600
73485228210108819464454
42223188913192946896220
02301443770269923007803
08526118075451928877050
21096842493627135925187
60777884665836150238913
49333312231053392321362
43192637289106705033992
82265263556209029798642
47275977256550861548754
35748264718141451270006
02389016207773224499435
30889990950168032811219
43204819643876758633147
98571911397815397807476
15077221175082694586393
20456520989698555678141
06968372884058746103378
10544439094368358358138
11311689938555769754841
49144534150912954070050
19477548616307542264172
93946803673198058618339
18328599130396072014455
95044977921207612478564
59161608370594987860069
70189409886400764436170
93341727091914336501371
57660114803814306262380
51432117348151005590134
56101180079050638142152
70930858809287570345050
78081454588199063361298
27981411745339273120809
28972792221329806429468
78242748740174505540677
87570832373109759151177
62978443284747908176518
09778726841611763250386
12112914368343767023503
71116330725869883258710
33632223810980901211019
89917684149175123313401
52733843837234500934786
04979294599158220125810
45982309255287212413704
36149102054718554961180
87642657651106054588147
56044317847985845397312
86301625448761148520217
06440411166076695059775
78325703951108782308271
06478939021115691039276
83845386333321565829659
77310343603232254574363
72041244064088826737584
33953679593123221343732
09957498894699565647360
07295999839128810319742
63125179714143201231127
95518947781726914158911
77991956481255800184550
65632952859859100090862
18029775637892599916499
46428193022293552346674
75932695165421402109136
30181947227078901220872
87361707348649998156255
47281137347987165695274
89008144384053274837813
78246691744422963491470
81570073525457070897726
75469343822619546861533
12095335792380146092735
10210119190218360675097
30895752895774681422954
33943854931553396303807
29169175846101460995055
06480367930414723657203
98600735507609023173125
01613204843583648177048
48181099160244252327167
21901893345963786087875
28701739359303013359011
23710239171265904702634
94028307668767436386513
27106280323174069317334
48234356453185058135310
85497333507599667787124
49058363675413289086240
63245639535721252426117
02780286560432349428373
01725574405837278267996
03173936401328762770124
36798311446436947670531
27249241047167001382478
31286565064934341803900
41017805339505877245866
55755229391582397084177
29833728231152569260929
95942240000560626678674
35792397245408481765197
34362652689448885527202
74778747335983536727761
40759171205132693448375
29916499809360246178442
67572776790019191907038
05220461232482391326104
32719168451230602362789
35454324617699757536890
41763650254785138246314
65833638337602357789926
72988632161858395903639
98183845827644912459809
37043055559613797343261
34830494949686810895356
96348281781288625364608
42033946538194419457142
66682371839491832370908
57485026656803989744066
21053603064002608171126
65995419936873160945722
88810920778822772036366
84481532561728411769097
92666655223846883113718
52991921631905201568631
22282071559987646842355
20592853717578076560503
67731309751912239738872
24682580571597445740484
29878073522159842667662
57807706201943040054255
01583125030175340941171
91019298903844725033298
80245014367968441694795
95453045910313811621870
45679978663661746059570
00344597011352518134600
65655352034788811741499
41274826415213556776394
03907103870881823380680
33500380468001748082205
91096844202644640218770
53401003180288166441530
91393948156403192822785
48241451050318882518997
00748622879421558957428
20216657062188090578088
05032467699129728721038
70736974064356674589202
58656573978560859566534
10703599783204463363464
85489497663885351045527
29824229069984885369682
80464597457626514343590
50938321243743333870516
65714900590710567024887
98580437181512610044038
14880407252440616429022
47822715272411208506578
88387124936351068063651
66743222327767755797399
27037623191470473239551
20607055039920884426037
08790843334261838413597
07816482955371432196118
95037977146300075559753
79570355227144931913217
25564401283091805045008
99218705121186069335731
53895935079030073672702
33141653204234015537414
42687154055116479611433
23024854404094069114561
39873026039518281680344
82525432673857590056043
20245372719291248645813
33441698529939135747869
89579864394980230471169
67157362283912018127312
91658995275991922031837
23568272793856373312654
79985912463275030060592
56745497943508811929505
68549325935531872914180
11364121874707526281068
69830135760524719445593
21955359610452830314883
91176930119658583431442
48948985655842508341094
29502771975833522442912
57364938075417113739243
76014350682987849327129
97512286881960498357751
58771780410697131966753
47719479226365190163397
71284739079336111191408
99830560336106098717178
30554354035608952929081
84641437139294378135604
82038947912574507707557
51030024207266290018090
42293424942590606661413
32287226980690145994511
99547801639915141261252
57282806643312616574693
88195106442167387180001
10042184830258091654338
37492364118388856468514
31500637319042951481469
42431460895254707203740
55669130692209908048194
52975110650464281054177
55259095187131888359147
65996041317960209415308
58553323877253803272763
29773721431279682167162
34421183201802881412747
44316884721845939278143
54740999990722332030592
62976611238327983316988
25393126200650370288447
82866694044730794710476
12558658375298623625099
98232335971550723383833
24408152577819336426263
04330265895817080045127
88731159355877472172564
94700051636672577153920
98409503274511215368730
09121996295227659131637
09396860727134269262315
47533043799331658110736
96431421719794340563915
51210810813626268885697
48068060116918941750272
29874158699179145349946
24441940121978586013736
60828690722365147713912
68742096651378756205918
54328888341742920901563
13328319357562208971376
56309785015631549824564
45865424792935722828750
60848145335135218172958
79329911710032476222052
19464510536245051298843
08713444395072442673514
62861799183233645983696
37632722575691597239543
83052086647474238151107
92734948369523964792689
93698324917999502789500
06045966131346336302494
99514808053290179029751
82515875049007435187983
51183603272277260171740
45355716588555782972910
61958193517105548257930
70910057635869901929721
79951687311755631444856
48100220014254540554292
73458837116020994794572
08237804368718944805636
89182580244499631878342
02749101533579107273362
53289069334741238022220
11626277119308544850295
41913200400999865566651
77566409536561978978183
80451030356510131589458
90287186108690589394713
68014845700183664956472
03294334374298946427412
55143590584348409195487
01523614031739139036164
40198455051049121169792
00120199960506994966403
03508636929039410070194
50532016234872763232732
44943963048089055425137
97233147518520709102506
36859816795304818100739
42453170023880475983432
34504142584314063612721
09602282423378228090279
76596077710849391517488
73168777135223900911711
73509186006546200990249
75852779254278165970383
49505801062615533369109
37846597710529750223173
07412177834418941184596
58610298018778742744563
86696612772450384586052
64151030408982577775447
41153320764075881677514
97553804711629667771005
87664615954967769270549
62393985709255070274069
97814084312496536307186
65337180605874224259816
53070525738345415770542
92162998114917508611311
76577317209561565647869
54744892713206080635457
79462414531066983742113
79816896382353330447788
31693397287289181036640
83269856988254438516675
86228993069643468489751
48408790396476042036102
06021717394470263487633
65439319522907738361673
89811781242483655781050
34169451563626043003665
74310847665487778012857
79236454185224472361713
74229255841593135612866
37167032807217155339264
63257306730639108541088
68085742838588280602303
34140855039097353872613
45119629264159952127893
11354431460152730902553
82710432596622674390374
55636122861390783194335
70590038148700898661315
39819585744233044197085
66967222931427307413848
82788975588860799738704
47020316683485694199096
54802982493198176579268
29855629723010682777235
16274078380743187782731
82119196952800516087915
72128826337968231272562
87000150018292975772999
35790949196407634428615
75713544427898383040454
70271019458004258202120
23445806303450336581472
18549203679989972935353
91968121331951653797453
99111494244451830338588
41290401817818821376006
65928494136775431745160
54093871103687152116404
05821934471204482775960
54169486453987832626954
80139150190389959313067
03186616706637196402569
28671388714663118919268
56826919952764579977182
78759460961617218868109
45465157886912241060981
41972686192554787899263
15359472922825080542516
90681401078179602188533
07623055638163164019224
54503257656739259976517
53080142716071430871886
28598360374650571342046
70083432754230277047793
31118366690323288530687
38799071359007403049074
59889513647687608678443
23824821893061757031956
38032308197193635672741
96438726258706154330729
63703812751517040600505
75948827238563451563905
26577104264594760405569
50959840888903762079956
63880178618559159441117

В самих записях членов этого секретного общества, данный набор цифр занимает очень важную роль. Но какую? Что скрывали Иллюминаты за этими цифрами?

Дело в том, что по сохранившимся данным Иллюминаты обладали обширными познаниями не только в области оккультных наук, но и математики, астрономии, астрологии, химии и алхимии, медицине и психологии. Также им были доступны некоторые древние источники знаний.

Многие исследователи считают что за этими цифрами может скрываться универсальный код жизни, рецепт филосовского камня и т.п…

Золотое сечение и числа Фибоначчи – Fib0.ru – Суть числа

Иллюстрация Золотого сечения

<div id="yandex_rtb_5" class="lazy lazy-hidden yandex-adaptive classYandexRTB"></div> <script type="text/javascript">if(rtbW>=960){var rtbBlockID="R-A-744187-3";} else{var rtbBlockID="R-A-744187-5";} window.yaContextCb.push(()=>{Ya.Context.AdvManager.render({renderTo:"yandex_rtb_5",blockId:rtbBlockID,pageNumber:5,onError:(data)=>{var g=document.createElement("ins");g.className="adsbygoogle";g.style.display="inline";if(rtbW>=960){g.style.width="580px";g.style.height="400px";g.setAttribute("data-ad-slot","9935184599");}else{g.style.width="300px";g.style.height="600px";g.setAttribute("data-ad-slot","9935184599");} g.setAttribute("data-ad-client","ca-pub-1812626643144578");g.setAttribute("data-alternate-ad-url",stroke2);document.getElementById("yandex_rtb_5").appendChild(g);(adsbygoogle=window.adsbygoogle||[]).push({});}})});window.addEventListener("load",()=>{var ins=document.getElementById("yandex_rtb_5");if(ins.clientHeight =="0"){ins.innerHTML=stroke3;}},true);</script>

Золотое сечение: тайна вселенной

Золотое сечение – это всеобъемлющее проявление структурной гармонии. Оно встречается во всех сферах вселенной в природе, науке, искусстве во всем, с чем может соприкоснуться человек. Однажды познакомившись с золотым правилом, человечество больше ему не изменяло.

Наверняка вам не раз приходилось задумываться, почему Природа способна создавать такие удивительные гармоничные структуры, которые восхищают и радуют глаз. Почему художники, поэты, композиторы, архитекторы создают восхитительные произведения искусства из столетия в столетие. В чем же секрет и какие законы лежат в основе этих гармоничных созданий? Никто не сможет однозначно ответить на этот вопрос, но в нашей книге мы постараемся приоткрыть завесу и рассказать вам об одной из тайн мироздания – Золотом Сечении или, как его еще называют, Золотой или Божественной Пропорцией. Золотое Сечение называется числом PHI (Фи) в честь великого древнегреческого скульптора Фидия (Phidius), который использовал это число в своих скульптурах.

Не одно столетие ученые применяют уникальные математические свойства числа PHI и эти исследования продолжаются и в наши дни. Это число нашло широкое применение во всех областях современной науки, о чем мы так же попытаемся популярно рассказать на страницах нашего сайта Fib0. Также существует ряд и последовательность фибоначчи что это Вы узнаете далее…

Определение золотого сечения

Наиболее простое и ёмкое определение золотого сечения – малая часть относится к большей, как большая – ко всему целому. Приблизительная его величина 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение действует в формах пространства и времени.

Древние видели в золотом сечении отражение космического порядка, а Иоганн Кеплер называл его одним из сокровищ геометрии. Современная наука рассматривает золотое сечение как ассиметричную симметрию, называя его в широком смысле универсальным правилом, отражающим структуру и порядок нашего мироустройства.

Числа фибоначчи в истории

Представление о золотых пропорциях имели древние египтяне, знали о них и на Руси, но впервые научно золотое сечение объяснил монах Лука Пачоли в книге Божественная пропорция, иллюстрации к которой предположительно сделал Леонардо да Винчи. Пачоли усматривал в золотом сечении божественное триединство: малый отрезок олицетворял Сына, большой Отца, а целое Святой дух.

Непосредственным образом с правилом золотого сечения связано имя итальянского математика Леонардо Фибоначчи. В результате решения одной из задач ученый вышел на последовательность чисел, известную сейчас как ряд Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. Отношение соседних чисел ряда Фибоначчи в пределе стремится к Золотому сечению. На отношение этой последовательности к золотой пропорции обратил внимание Кеплер: Устроена она так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член. Сейчас ряд Фибоначчи – это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях.

Леонардо да Винчи также много времени посвятил изучению особенностей золотого сечения, скорее всего, именно ему принадлежит и сам термин. Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.

Со временем правило правило в зависимости от ударения и контекста может обозначать следующее: Правило — требование для исполнения неких условий ( на поведение) всеми участниками какого-либо действия (игры, золотого сечения превратилось в академическую рутину, и только философ Адольф Цейзинг в 1855 году вернул ему вторую жизнь. Он довел до абсолюта пропорции золотого сечения, сделав их универсальными для всех явлений окружающего мира. Впрочем, его математическое эстетство вызывало много критики.

Универсальный код природы

Даже не вдаваясь в расчеты, золотое сечение и Числа фибоначчи можно без труда обнаружить в природе. Так, под него попадают соотношение хвоста и тела ящерицы, расстояния между листьями на ветке, есть золотое сечение и в форме яйца, если условную линию провести через его наиболее широкую часть.

Белорусский ученый Эдуард Сороко, который изучал формы золотых делений в природе, отмечал, что все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм это закручивание по спирали.
Еще Архимед, уделяя внимание спирали, вывел на основе ее формы уравнение, которое и сейчас применяется в технике. Позднее Гете отмечал тяготение природы материальный мир Вселенной, в сущности — основной объект изучения естественных наук к спиральным формам, называя спираль кривой жизни. Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение ДНК и даже структура галактик заключают в себе ряд Фибоначчи.

Формула золотого сечения

Модельеры и дизайнеры одежды все расчеты делают, исходя из пропорций золотого сечения. Человек это универсальная форма может означать: Форма предмета — взаимное расположение границ (контуров) предмета, объекта, а также взаимное расположение точек линии для проверки законов золотого сечения. Конечно, от природы далеко не у всех людей пропорции идеальны, что создает определенные сложности с подбором одежды.

В дневнике Леонардо да Винчи есть рисунок вписанного в окружность обнаженного человека, находящегося в двух наложенных друг на друга позициях. Опираясь на исследования римского архитектора Витрувия, Леонардо подобным образом пытался установить пропорции человеческого тела. Позднее французский архитектор Ле Корбюзье, используя Витрувианского человека Леонардо, создал собственную шкалу гармонических пропорций, повлиявшую на эстетику архитектуры XX века.

Адольф Цейзинг, исследуя пропорциональность человека, проделал колоссальную работу. Он измерил порядка двух тысяч человеческих тел, а также множество античных статуй и вывел, что золотое сечение выражает среднестатистический закон. В человеке живое разумное социальное , субъект общественно-исторической деятельности и культуры ему подчинены практически все части тела, но главный показатель золотого нечто, изготовленное из золота сечения это деление тела В математике: Тело (алгебра) — множество с двумя операциями (сложение и умножение), обладающее определёнными свойствами точкой пупа.
В результате измерений исследователь установил, что пропорции мужского тела 13:8 ближе к золотому сечению многозначный термин, означающий: Сечение в черчении — в отличие от разреза, изображение только фигуры, образованной рассечением тела плоскостью (плоскостями) без изображения частей за этой, чем пропорции женского тела 8:5.

Искусство пространственных форм

Художник Василий Суриков говорил, что в композиции есть непреложный закон, когда в картине нельзя ничего ни убрать, ни добавить, даже лишнюю точку поставить нельзя, это настоящая математика. Долгое время художники следовали этому закону интуитивно, но после Леонардо ди сер Пьеро да Винчи (итал да Винчи процесс создания живописного полотна уже не обходится без решения геометрических задач. Например, Альбрехт Дюрер для определения точек может означать: Точка — абстрактный объект в пространстве, не имеющий никаких измеримых характеристик, кроме координат золотого сечения использовал изобретенный им пропорциональный циркуль.

Искусствовед Ф. В. Ковалев, подробно исследовав картину Николая Ге Александр Сергеевич Пушкин в селе Михайловском, отмечает, что каждая деталь полотна, будь то камин, этажерка, кресло или сам поэт, строго вписаны в золотые пропорции.

Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке Великие пирамиды Гизы, Собор Парижской Богоматери, Храм Василия Блаженного, Парфенон.

И сегодня в любом искусстве пространственных форм стараются следовать пропорциям золотого сечения, так как они, по мнению искусствоведов, облегчают восприятие произведения и формируют у зрителя эстетическое ощущение.

Слово, звук и кинолента

Формы временно?го искусства по-своему демонстрируют нам принцип золотого деления. Литературоведы, к примеру, обратили внимание, что наиболее популярное количество строк в стихотворениях позднего периода творчества Пушкина соответствует ряду Фибоначчи 5, 8, 13, 21, 34.

Действует правило золотого сечения и в отдельно взятых произведениях русского классика. Так кульминационным моментом Пиковой дамы является драматическая сцена Германа и графини, заканчивающаяся смертью последней. В повести 853 строки, а кульминация приходится на 535 строке (853:535=1,6) это и есть точка золотого сечения.

Советский музыковед Э. К. Розенов отмечает поразительную точность соотношений золотого сечения в строгих и свободных формах произведений Иоганна Себастьяна Баха, что соответствует вдумчивому, сосредоточенному, технически выверенному стилю мастера. Это справедливо и в отношении выдающихся творений других композиторов, где на точку золотого сечения обычно приходится наиболее яркое или неожиданное музыкальное решение.

Кинорежиссер Сергей Эйзенштейн сценарий своего фильма Броненосец Потёмкин сознательно согласовывал с правилом золотого сечения, разделив ленту на пять частей. В первых трех разделах действие разворачивается на корабле, а в последних двух в Одессе. Переход на сцены в городе и есть золотая середина фильма.

Гармония Золотого сечения

Научно-технический прогресс имеет длительную историю и прошел в своем историческом развитии несколько этапов (вавилонская и древнеегипетская культура, культура Древнего Китая и Древней Индии, древнегреческая культура, эпоха Средневековья, эпоха Возрождения, промышленная революция 18 в., великие научные открытия 19 в., научно-техническая революция 20 в.) и вошел в 21-й век, который открывает новую эпоху в истории человечества – эпоху Гармонии. Именно в античный период было сделано ряд выдающихся математических открытий, оказавших определяющее влияние на развитие материальной и духовной культуры, среди которых Вавилонская 60-ричная система счисления и позиционный принцип представления чисел, тригонометрия и геометрия Евклида, несоизмеримые отрезки, Золотое Сечение и Платоновы тела, начала теории чисел и теории измерения. И, хотя каждый из этих этапов имеет свою специфику, вместе с тем он обязательно включает содержание предшествующих этапов. В этом и состоит преемственность в развитии науки. Преемственность может осуществляться в различных формах. Одной из сущностных форм ее выражения являются фундаментальные научные идеи, которые пронизывают все этапы научно-технического прогресса и оказывают влияние на различные области науки, искусства, философии и техники.

К разряду таких фундаментальных идей относится идея Гармонии, связанная с Золотым Сечением. По словам Б.Г. Кузнецова, исследователя творчества Альберта Эйнштейна, великий физик свято верил в то, что наука, физика в частности, всегда имела своей извечной фундаментальной целью “найти в лабиринте наблюдаемых фактов объективную гармонию”. О глубокой вере выдающегося физика в существование универсальных законов гармонии мироздания свидетельствует и еще одно широко известное высказывание Эйнштейна: «Религиозность ученого состоит в восторженном преклонении перед законами гармонии».

В древнегреческой философии Гармония противостояла Хаосу и означала организованность Вселенной, Космоса. Гениальный русский философ Алексей Лосев так оценивает основные достижения древних греков в этой области:

“С точки зрения Платона, да и вообще с точки зрения всей античной космологии мир представляет собой некое пропорциональное целое, подчиняющееся закону гармонического деления – Золотого Сечения… Их (древних греков) систему космических пропорций нередко в литературе изображают как курьезный результат безудержной и дикой фантазии. В такого рода объяснениях сквозит антинаучная беспомощность тех, кто это заявляет. Однако понять данный историко-эстетический феномен можно только в связи с целостным пониманием истории, то есть, используя диалектико-материалистическое представление о культуре и ища ответа в особенностях античного общественного бытия».

«Закон золотого деления должен быть диалектической необходимостью. Это – та мысль, которую, насколько мне известно, я провожу впервые», – убежденно высказывался Лосев более полувека назад в связи с анализом культурного наследия древних греков.

А вот еще одно высказывание, касающееся Золотого Сечения. Оно было сделано в 17 веке и принадлежит гениальному астроному Иоганну Кеплеру, автору трех знаменитых «Законов Кеплера». Свое восхищение Золотым Сечением Кеплер выразил в следующих словах:

«В геометрии существует два сокровища – теорема Пифагора и деление отрезка в крайнем и среднем отношении. Первое можно сравнить с ценностью золота, второе можно назвать драгоценным камнем».

Напомним, что старинная задача о делении отрезка в крайнем и среднем отношении, которая упоминается в этом высказывании, – это и есть Золотое Сечение!

Числа Фибоначчи в науке

В современной науке существует много научных групп, профессионально изучающих Золотое Сечение, числа Фибоначчи и их многочисленные приложения в математике, физике, философии, ботанике, биологии, медицине, компьютерной науке. Множество художников, поэтов, музыкантов используют в своем творчестве «Принцип Золотого Сечения». В современной науке сделано ряд выдающихся открытий, основанных на числах Фибоначчи и Золотом Сечении. Открытие “квази-кристаллов”, сделанное в 1982 г. израильским ученым Даном Шехтманом, основанное на Золотом Сечении и “пентагональной” симметрии, имеет революционное значение для современной физики. Прорыв в современных представлениях о природе формообразования биологических объектов, в начале 90-х годов сделан украинским ученым Олегом Боднаром, создавшим новую геометрическую теорию филлотаксиса. Белорусский философ Эдуард Сороко сформулировал «Закон структурной гармонии систем», основанный на Золотом Сечении и играющий важную роль в процессах самоорганизации. Благодаря исследованиям американских ученых Эллиотта, Пректера и Фишера числа Фибоначчи активно вошли в сферу бизнеса и стали основой из оптимальных стратегий в сфере бизнеса и торговли. Эти открытия подтверждают гипотезу американского ученого Д. Винтера, руководителя группы “Планетарные сердцебиения”, согласно которой не только энергетический каркас Земли, но и строение всего живого основаны на свойствах додекаэдра и икосаэдра – двух “Платоновых тел”, связанных с Золотым Сечением. И наконец, самое, пожалуй, главное – структура ДНК генетического кода жизни, представляет собой четырехмерную развертку (по оси времени) вращающегося додекаэдра! Таким образом, оказывается, что вся Вселенная – от Метагалактики и до живой клетки – построена по одному принципу – бесконечно вписываемых друг в друга додекаэдра и икосаэдра, находящихся между собой в пропорции Золотого Сечения!

Украинский профессор и доктор наук Стахов А.П. смог создать некую формулу золотого сечения. Суть этого обобщения предельно проста. Если задаться неотрицательным целым числом р = 0, 1, 2, 3, … и разделить отрезок “AB” точкой С в такой пропорции, чтобы было:

CB/AC=(AB/CB)

То универсальной формулой золотого сечения является выражение:

x^p⁺¹ = x^p + 1

Золотое сечение и пропорции Фибоначчи

Мы уже писали о 10 правилах композиции. Однако есть еще одно правило которое поможет вам улучшить ваши познания в работе с композицией.

Числа Фибоначчи — элементы числовой последовательности, в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени итальянского математика средневековой Европы Леонардо Пизанского по прозвищу Фибоначчи, что обозначает «хороший сын родился».

Числа Фибоначчи так же называют золотым сечением. Не вдаваясь в математику, можно сказать лишь одно — изображения, которые согласуются с золотым сечением и числами Фибоначчи особенно благоприятны для человеческого глаза.

Многие фотографы и дизайнеры придерживаются пропорций 1:1.618 для построения более удачной композиции.

Эта последовательность была хорошо известна в Индии, где применялась в метрических науках. Позже многие исследователи начали замечать эту последовательность в природе и космосе.

Как на практике работать с композицией читайте в статье «9 советов по композиции от Стива Маккарри».

Следующие два видео и последующие за ним изображения помогут вам лучше понять как это работает на практике.

Ниже представлены фотографии, которые сделаны с применением пропорций Фибоначчи.

Число Бога, числа Фибоначчи, Золотое Сечение.: terrao — LiveJournal ,
[more]

«В Божьем творении существует так называемое «Золотое сечение», которое проявляется во множественных формах, числах и схемах – и все это может быть творением только Всемогущего, благого и Всемудрого Бога Писания. Это Золотое сечение, существующее в самых маленьких и самых больших частях природы, свидетельствует о потрясающем мастерстве Бога и Его любви к красоте, функциям и порядку.

Внимательно рассматривая спираль моллюска, вы увидите, что по мере того, как его тело становится больше, оно сохраняет то же самое очертание. Красоту этой формы обычно можно увидеть в разнообразных вещах, таких как: ураганы, спиральные семена, улитка человеческого уха, рог барана, хвост морского конька, растущие листья папоротника, молекула ДНК, волны, ударяющиеся о берег, торнадо, галактики, хвост кометы, вращающейся вокруг Солнца, водоворот, схема расположения семян подсолнуха, маргаритки, одуванчики и т.д.

Эта спираль закручена по строго математической схеме. Сначала рассмотрим спиральную форму в подсолнухах. Внимательно изучив подсолнух, мы увидим два ряда спиралей, которые закручиваются в противоположном направлении. Если посчитать эти спиральные ряды в каждом направлении, то выяснится, что в большинстве случаев соотношение чисел, в зависимости от размера цветка, будет следующим: если цветок маленький, то 34 и 55; если средний, то 55 и 89; если большой, то 89 и 144.

Эти числа являются частью последовательности чисел Фибоначчи, которая была открыта в 1200 г. н.э. Леонардо Пизанским (известен как Фибоначчи). Каждое последующее число является суммой двух предыдущих чисел. Последовательность этих чисел такова: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, и до бесконечности. Когда большее число из этой последовательности разделить на меньшее, расположенное рядом число, то соотношение приблизительно получается 1.618; и если меньшее число разделить на большее число, стоящее рядом, то получается примерно 0.618.

Почему мастера древней Греции и Египта, часто использовали этот коэффициент при создании многих своих произведений искусства? Все потому, что было обнаружено, что при таком коэффициенте человеку наиболее приятно смотреть на предмет дизайна, который образует так называемый Золотой прямоугольник. Если короткая сторона прямоугольника равна 1, то его длинная сторона будет равна 1.618. Эта форма прямоугольника близка к схеме, которая использовалась при создании древнегреческого храма Парфенона, а также многочисленных картин, ваз, дверных проемов, оконных рам, статуй и т.д. Здание ООН – это Золотой прямоугольник. Многие вещи, которыми мы пользуемся, в своей основе имеют приблизительный Золотой прямоугольник: кредитные карточки, игральные карты, открытки, пластинки для электрических выключателей, блокноты, карточки каталога 3 х 5 и 5 х 8 и т.д.

Еще одним чрезвычайно интересным явлением есть то, что последовательность чисел Фибоначчи отмечается в спиральном расположении листьев вокруг стебля растения. Эта спиральная форма хорошо видна, если посмотреть на стебель сверху и увидеть, что угол расхождения листьев от одного к следующему составляет часть окружности, которая является вписанной. В каждом случае угол расхождения следует по ряду чисел Фибоначчи. Примеры: у вяза угол расхождения листьев составляет 1/2 окружности; у березы и лесного ореха — 1/3; у абрикоса и дуба — 2/5; у груши и тополя — 3/8; у миндаля и ивы — 5/13; а у некоторых сосен — либо 5/21, либо 13/34. Почему Бог расположил листья в таком порядке? Такое расположение позволяет каждому листу получить максимальное количество солнечного света и воздуха, при этом каждый лист не затеняет и не сжимает соседние листья.

Такую схему можно обнаружить не только в расположении листьев, но и также в размещении лепестков многих цветов. Примеры: лилия имеет 3 лепестка, фиалка круглолистная — 5, дельфиниум — 8, ромашка непахучая — 13, астра — 21, златоцвет — 34, гелениум — 55, астра новобельгийская — 89. Когда мы понимаем, что информация, необходимая для образования спиралей и чисел в живых организмах, хранится в ДНК, то должно ли нас удивлять, что ширина молекулы ДНК составляет 21 ангстрем, а длина одного полного поворота её спирали равна 34 ангстремам? Молекула ДНК представляет собой одну длинную цепь золотых сечений. Давайте заглянем в мир маленьких и больших вещей. В мире атомов существует четыре основные асимметрии (структура атомного ядра, распределение фрагментов при делении ядра, распределение числа изотопов и распределение излучаемых частиц), и важно то, что «численные значения всех этих асимметрий приблизительно равны «Золотому сечению», и что числа, образующие эти значения, относятся к ряду чисел Фибоначчи или «приближены» к ним. В состояниях изменения количества атомов водорода, когда на последующих энергетических уровнях атомы получают или теряют излучаемую энергию, количественное соотношение изменений атомных электронов имеет в основе последовательность чисел Фибоначчи.

В области очень крупных явлений, если сравнить период времени вращения каждой планеты вокруг Солнца в округленных цифрах с периодом вращения соседней планеты, то получаются коэффициенты Фибоначчи! Начиная с Нептуна, 7 и внутрь, по направлению к Солнцу, соотношения составляют: 1/2, 1/3, 2/5, 3/8, 5/13, 8/21, 13/34. В таком же соотношении спирально расположены листья растений!

То, что периоды вращения планет вокруг Солнца связаны с расположением листьев на стеблях растений, также является удивительным явлением.

Эти формы, числа, спирали и Золотое сечение встречаются во всем Божьем творении. Их можно обнаружить как в живой, так и в неживой природе. Их симметрия, красота и математическая точность присутствуют в каждой сфере природы. И хотя творение лишено полного совершенства (из-за греха Адама), само их присутствие (практически везде и во всем) опровергает мнение о том, что все возникло в результате слепого случая в ходе эволюционных процессов. Можно сделать единственное разумное заключение: Творец Вселенной сотворил все сущее как видимые отпечатки Его невидимого, но все же личностного существования. Это огромный, мудрый, сильный, творческий и независимый Бог творения – Тот Самый Бог Библии, о Котором написано, что Он: «делает дела великие, для нас непостижимые» (Иова 37:5). Он достоин поклонения. И как Его имя? Господь Иисус Христос». ,

http://esotericnews.ru/chislo-boga-chisla-fibonachchi-zolotoe-sechenie.html#comment1280

Золотое сечение и числа последовательности Фибоначчи.Некоторое время назад я обещала прокомментировать утверждение Толкачева о том, что Питер построен по принципу Золотого Сечения, а Москва – по принципу симметрии, и что именно поэтому столь ощутимы различия в восприятии этих двух городов, и именно поэтому петербуржец, приезжая в Москву «заболевает головой», а москвич «заболевает головой», приезжая в Питер. Требуется некоторое время для сонастройки с городом (как при перелете в штаты – требуется сонастройка со временем).

Дело в том, что наш глаз смотрит — ощупывая пространство с помощью определенных движений глаз – саккад (в переводе – хлопок паруса). Глаз совершает «хлопок» и посылает сигнал в мозг «сцепление с поверхностью произошло. Все в порядке. Информация такая-то». И в течение жизни глаз привыкает к определенной ритмике этих саккад. И когда эта ритмика кардинально меняется (с городского пейзажа на лес, с Золотого Сечения на симметрию) – тут то и требуется некоторая работа мозга по перенастройке.

Теперь подробности:
Определение ЗС — это деление отрезка на две части в таком соотношении, при котором большая часть относится к меньшей, как их сумма (весь отрезок) к большей.

То есть, если мы примем весь отрезок c за 1, то отрезок a будет равен 0,618, отрезок b — 0,382. Таким образом, если взять строение, например, храм, построенный по принципу ЗС, то при его высоте скажем 10 метров, высота барабана с куполом будут равны 3,82 см, а высота основания строения будет 6, 18 см. (понятно, что цифры я взяла ровными для наглядности)

Далее можно рассчитать высоту двери, окон, креста. И везде будет просматриваться принцип ЗС.

А какова связь между ЗС и числами Фибоначчи?

Числа последовательности Фибоначчи это:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597…

Закономерность чисел в том, что каждое последующее число равно сумме двух предыдущих чисел.
0 + 1 = 1;
1 + 1 = 2;
2 + 3 = 5;
3 + 5 = 8;
5 + 8 = 13;
8 + 13 = 21 и т.д.,

а отношение смежных чисел приближается к отношению ЗС.
Так, 21 : 34 = 0,617, а 34 : 55 = 0,618.

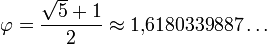
То есть в основе ЗС лежат числа последовательности Фибоначчи.
Вот этот ролик ещё раз наглядно демонстрирует эту связь ЗС и чисел Фибоначчи

Где ещё встречаются принцип ЗС и числа последовательности Фибоначчи?

• Листья у растений описывается последовательностью Фибоначчи. Зерна подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса также располагаются согласно последовательности Фибоначчи.

• Яйцо птицы

• Длины фаланг пальцев человека относятся примерно как числа Фибоначчи. Золотое сечение просматривается в пропорциях лица.

• Эмиль Розенов исследовал ЗС в музыке эпохи Барокко и классицизма на примере произведений Баха, Моцарта, Бетховена.

• Известно, что Сергей Эйзенштейн искусственно построил фильм «Броненосец Потёмкин» по правилам ЗС. Он разбил ленту на пять частей. В первых трёх действие развивается на корабле. В двух последних — в Одессе, где разворачивается восстание. Этот переход в город происходит точно в точке золотого сечения. Да и в каждой части есть свой перелом, происходящий по закону золотого сечения. В кадре, сцене, эпизоде происходит некий скачок в развитии темы: сюжета, настроения. Эйзенштейн считал, что, так как такой переход близок к точке золотого сечения, он воспринимается как наиболее закономерный и естественный.

• Многие элементы декора, а так же шрифты, созданы с использованием ЗС. Например шрифт А.Дюрера (в рисунке буква «А»)

• Считается, что термин «Золотое сечение» ввел Леонардо Да Винчи, который говорил, «пусть никто, не будучи математиком, не дерзнет читать мои труды” и показывал пропорции человеческого тела на своём знаменитом рисунке «Витрувианский человек». “Если мы человеческую фигуру – самое совершенное творение Вселенной – перевяжем поясом и отмерим потом расстояние от пояса до ступней, то эта величина будет относиться к расстоянию от того же пояса до макушки, как весь рост человека к длине от пояса до ступней”.

Знаменитый портрет Моны Лизы или Джоконды (1503) создан по принципу золотых треугольников.

Собственно говоря сама звезда или пентакль представляет собой построение ЗС.

Ряд чисел Фибоначчи наглядно моделируется (материализуется) в форме спирали

А в природе спираль ЗС выглядит вот так:

При этом, спираль наблюдается повсеместно (в природе и не только):
— Семена в большинстве растений расположены по спирали
— Паук плетет паутину по спирали
— Спиралью закручивается ураган
— Испуганное стадо северных оленей разбегается по спирали.
— Молекула ДНK закручена двойной спиралью. Молекулу ДНК составляют две вертикально переплетенные спирали длиной 34 ангстрема и шириной 21 ангстрема. Числа 21 и 34 следуют друг за другом в последовательности Фибоначчи.
— Эмбрион развивается в форме спирали
— Спираль «улитки во внутреннем ухе»
— Вода уходит в слив по спирали
— Спиральная динамика показывает развитие личности человека и его ценностей по спирали.
— Ну и конечно, сама Галактика имеет форму спирали

Таким образом можно утверждать, что сама природа построена по принципу Золотого Сечения, оттого эта пропорция гармоничнее воспринимается человеческим глазом. Она не требует «исправления» или дополнения получаемой картинки мира.

Теперь о Золотом сечении в архитектуре

• Пирамида Хеопса представляет собой пропорции ЗС. (Фотография нравится – с заваленным песком Сфинксом).

• Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции.

Собор «Нотредам де Пари» в Париже, Франция.

Одно из выдающихся строений, выполненных по принципу ЗС – Смольный Собор в Питере. К собору ведут по краям две дорожки и если приближаться по ним к собору, то тот будто приподнимается в воздухе.

В Москве также есть строения выполненные с использованием ЗС. Например, Храм Василия Блаженного

Однако застройка, использующая принципы симметрии преобладает.
Например, Кремль и Спасская башня.

Высота стен Кремля также нигде не отражает принципа ЗС относительно высоты башен, например. Или взять гостиницу Россия, или гостиницу Космос.

При этом здания, построенные по принципу ЗС представляют больший процент в Питере, при этом это здания уличной застройки. Литейный проспект.

Таким образом, Золотое Сечение использует коэффицент 1,68, а симметрия 50/50.
То есть симметричные здания построены по принципу равенства сторон.

Ещё одной важной характеристикой ЗС является её динамичность и стремление к разворачиванию, за счет последовательности чисел Фибоначчи. Тогда как симметрия – наоборот представляет собой стабильность, устойчивость и неподвижность.

Кроме этого, дополнительное ЗС вносит в план Питера обилие водных пространств, расплескавшихся по городу и диктующих подчиненность города их изгибам. Да и сама схема Питера напоминает спираль или зародыш одновременно.

***

Папа, правда, высказал другую версию, отчего у москвичей и питерцев «голова болит» при посещении столиц. Папа относит это к энергиям городов:
Санкт-Петербург – имеет мужской род и соответственно мужские энергии,
Ну а Москва – соответственно – женского рода и обладает женскими энергиями.

Так жителям столиц, настроившимся на свой определенный баланс женского и мужского в своих организмах – сложно перестраиваться при посещении города-соседа, а у кого-то может и сложности какие-то имеются с восприятием одной или другой энергий и оттого город сосед могут и вовсе не любить!

В подтверждение этой версии говорит и то, что все российские императрицы правили именно в Питере, тогда как Москва видела лишь царей мужского пола!

Использованные ресурсы:
Последовательность Фибоначчи, проиллюстрированная природой.
Золотое сечение в живописи и архитектуре.
Золотое сечение и симметрия
Геометрия в архитектуре древнерусского творчества

Что такое последовательность Фибоначчи (она же серия Фибоначчи)?

Леонардо Фибоначчи обнаружил последовательность, сходящуюся на фи.

В 1202 году нашей эры Леонардо Фибоначчи написал в своей книге «Liber Abaci» простую числовую последовательность, которая является основой для невероятных математических отношений, лежащих в основе фи. Эта последовательность была известна еще в VI веке нашей эры индийскими математиками, но именно Фибоначчи представил ее на запад после своих путешествий по всему средиземноморскому миру и Северной Африке.Он также известен как Леонардо Боначчи, поскольку его имя происходит от итальянского языка от слов, означающих «сын Боначи».

Начиная с 0 и 1, каждое новое число в последовательности является просто суммой двух перед ним.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377. , ,

Эта последовательность показана в правом поле страницы в Liber Abaci, где Biblioteca Nazionale di Firenze хранит копию книги. Нажмите, чтобы увеличить.

Отношение последовательности Фибоначчи к золотому сечению таково: отношение каждой последующей пары чисел в последовательности приближается к Фи (1.618 ., так как 5, деленное на 3, составляет 1,666 …, а 8, деленное на 5, составляет 1,60.

В приведенной ниже таблице показано, как соотношения последовательных чисел в последовательности Фибоначчи быстро сходятся на Фи. После 40-го числа в последовательности, соотношение с точностью до 15 знаков после запятой.

1,618033988749895. , ,

Вычислить любое число в последовательности Фибоначчи легко!

Вот два способа, которыми вы можете использовать фи для вычисления n-го числа в последовательности Фибоначчи (f _n).

Если вы считаете, что 0 в последовательности Фибоначчи соответствует n = 0, используйте эту формулу:

f _n = Ph ^ⁿ/5 ^{^½}

Возможно, лучший способ — рассмотреть 0 в последовательности Фибоначчи, чтобы соответствовать 1-му числу Фибоначчи, где n = 1 для 0. Затем вы можете использовать эту формулу, открытую и предоставленную Джорданом Малахи Дантом в апреле 2005 года:

f _n = Ph ^ⁿ / (Phi + 2)

Оба подхода представляют пределы, которые всегда округляются до правильного числа Фибоначчи и приближаются к фактическому числу Фибоначчи при увеличении n.

Соотношение последовательных чисел Фибоначчи сходится на фи

119

Последовательность в последовательности	Итог Фибоначчи номер (сумма двух чисел перед ним)	Отношение каждого номера к номеру до него (по оценкам phi)	Разница от Phi
0	0
1	1
2	1	1.000000000000000	+0,618033988749895
3	2	2.000000000000000	-0,381966011250105
4	3	1,500000000000000	+ 0,118033988749895
5	5	1,666666666666667	-0,048632677916772
6	8	1.600000000000000	+0.018033988749895
7	13	1.625000000000000	-0.006966011250105
8	21	1,615384615384615	+0.002649373365279
9	34	1,61	-0,001013630297724
10	55	1,617647058823529	+0.000386929926365
11	89	1,618181818181818	-0,000147829431923
12	144	1.617977528089888	+0.000056460660007
13	233	1,618055555555556	-0,000021566805661
14	377	1,618025751072961	+0.000008237676933
15	610	1,618037135278515	-0.000003146528620
16	987	1,618032786885246	+0.000001201864649
17	1,597	1.618034447821682	-0,000000459071787
18	2,584	1,618033813400125	+0.000000175349770
19	4 181	1,618034055727554	-0,000000066977659
20	6 765	1,618033963166707	+0.000000025583188
21	10 946	1,618033998521803	-0.000000009771909
22	17 711	1,618033985017358	+0.000000003732537
23	28 657	1,6180339	597	-0,000000001425702
24	46,368	1,618033988205325	+0.000000000544570
25	75 025	1,618033988957902	-0,000000000208007
26	121 393	1.618033988670443	+0,000000000079452
27	196 418	1,618033988780243	-0,000000000030348
28	317 811	1,618033988738303	+0.000000000011592
29	514 229	1,618033988754323	-0,000000000004428
30	832 040	1,618033988748204	+0.000000000001691
31	1 346 269	1,618033988750541	-0,000000000000646
32	2 178 309	1,618033988749648	+0.000000000000247
33	3,524,578	1,618033988749989	-0,000000000000094
34	5 702 887	1,618033988749859	+0.000000000000036
35	9,227,465	1.618033988749909	-0,000000000000014
36	14 930 352	1,618033988749890	+0.000000000000005
37	24 157 817	1,618033988749897	-0,000000000000002
38	39 088 169	1,618033988749894	+0.000000000000001
39	63 245 986	1,618033988749895	-0.000000000000000
40	102,334,155	1,618033988749895	+0.000000000000000

Тауфик Мохаммед отмечает, что число 13, которое некоторые считают несчастливым, находится на позиции номер 7, счастливое число!

Последовательность Фибоначчи и азартные игры или лотереи

Некоторые люди надеются, что числа Фибоначчи дадут преимущество при выборе номеров лотереи или ставок в азартных играх. Правда заключается в том, что результаты азартных игр определяются случайными исходами и не имеют особой связи с числами Фибоначчи.

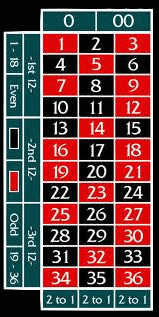Однако существуют системы ставок, используемые для управления размещением ставок, и система Фибоначчи, основанная на последовательности Фибоначчи, представляет собой вариацию прогрессии Мартингейла. В этой системе, часто используемой для казино и онлайн-рулетки, структура ставок соответствует прогрессии Фибоначчи: то есть каждая ставка должна быть суммой двух предыдущих, пока не будет сделан выигрыш. Если число выигрывает, ставка возвращается на два числа в последовательности, потому что их сумма была равна предыдущей ставке.

В системе Фибоначчи ставки остаются ниже, чем прогрессия Мартингейла, которая удваивается каждый раз. Недостатком является то, что в системе рулетки Фибоначчи ставка не покрывает все потери в плохой серии.

Важное предостережение: системы ставок не влияют на основные шансы игры, которые всегда в пользу казино или лотереи. Они могут быть просто полезны для того, чтобы сделать ставки более методичными, как показано в следующем примере:

Раунд	Сценарий 1	Сценарий 2	Сценарий 3
Ставка 1	Ставьте 1 и проигрывайте	Ставьте 1 и проигрывайте	Ставьте 1 и выигрывайте
Ставка 2	Ставьте 1 и проигрывайте	Ставьте 1 и проигрывайте	Ставьте 1 и выигрывайте
Ставка 3	Ставьте 2 и выигрывайте	Ставьте 2 и проигрывайте	Ставьте 1 и проигрывайте
Ставка 4	—	Ставьте 3 и выигрывайте	Ставьте 1 и проигрывайте
Ставка 5	—	—	Ставьте 2 и выигрывайте
Чистый результат	Даже в 0	Вниз на 1	впереди 2

Фибоначчи — Золотое сечение в C?

Переполнение стека

Товары
Клиенты
Случаи использования

Переполнение стека Публичные вопросы и ответы
Команды Частные вопросы и ответы для вашей команды
предприятие Частные вопросы и ответы для вашего предприятия
работы Программирование и связанные с ним технические возможности карьерного роста
Талант Нанимать технический талант
реклама Связаться с разработчиками по всему миру

спиралей и золотое сечение

числа Фибоначчи и Фи связаны со спиральным ростом в природе.

Если вы сложите квадраты любой серии чисел Фибоначчи, они будут равны последнему числу Фибоначчи, использованному в серии, умноженному на следующее число Фибоначчи. Это свойство приводит к спирали Фибоначчи, основанной на следующей прогрессии и свойствах ряда Фибоначчи:

1 ^² + 1 ^² + 2 ^² + 3 ^² + 5 ^² = 5 x 8

1 ^² + 1 ^² +., , + F (n) ^² = F (n) x F (n + 1)

Золотая спираль очень похожа на спираль Фибоначчи, но основана на серии одинаково пропорциональных золотых прямоугольников, каждый из которых имеет золотое отношение 1.618 длины длинной стороны к длине короткой стороны прямоугольника:

Спираль Фибоначчи становится все ближе и ближе к Золотой Спирали, так как она увеличивается в размере из-за отношения каждого числа в ряду Фибоначчи к тому, которое она сходится на Фи, 1.618, по мере того, как серии прогрессируют (например, 1, 1, 2, 3, 5, 8 и 13 дают соотношения 1, 2, 1,5, 1,67, 1,6 и 1,625 соответственно)

Спирали Фибоначчи и Золотые спирали появляются в природе, но не каждая спираль в природе связана с числами Фибоначчи или Фи. Большинство спиралей в природе представляют собой равносторонние спирали, а спирали Фибоначчи и Золотого являются частными случаями более широкого класса спиралей равновероятности. Сама равноугольная спираль — это особый тип спирали с уникальными математическими свойствами, в которой размер спирали увеличивается, но ее форма остается неизменной с каждым последующим вращением ее кривой.Кривая равноугольной спирали имеет постоянный угол между линией от начала координат до любой точки кривой и касательной в этой точке, отсюда и ее название. В природе равноугольные спирали возникают просто потому, что силы, которые создают спираль, находятся в равновесии, и их часто можно увидеть в неживых примерах, таких как спиральные рукава галактик и спирали ураганов. Спирали Фибоначчи, золотые спирали и спирали на основе золотого сечения часто появляются в живых организмах.

Альтернативные спирали в растениях встречаются в числах Фибоначчи.

Наиболее распространенные явления чисел Фибоначчи в природе встречаются у растений, в количестве листьев, расположении листьев вокруг стебля и в расположении листьев, срезов и семян.

Здесь семя подсолнечника иллюстрирует этот принцип, поскольку число спиралей по часовой стрелке равно 55 (отмечено красным, каждая десятая — белым), а число спиралей против часовой стрелки — 89 (отмечено зеленым, каждая десятая — белым).

Сосновые шишки и ананасы иллюстрируют похожие спирали последовательных чисел Фибоначчи, в приведенном ниже примере показан чередующийся рисунок 8 и 13 спиралей в сосновой шишке.

Нажмите на изображение ниже, чтобы увидеть полноразмерные версии каждого изображения выше:

Золотые спирали в морских раковинах

Золотые отношения также иногда встречаются в пропорциях последовательных спиралей морской раковины, как показано ниже.

Спираль оболочки Наутилуса не является золотой спиралью, но часто все еще имеет пропорции золотого сечения.

Оболочка наутилуса часто показана в качестве иллюстрации золотого сечения в природе, но спираль раковины наутилуса НЕ является золотой спиралью, как показано ниже.Наложение золотой спирали обеспечивается программным обеспечением «Золотое сечение» PhiMatrix:

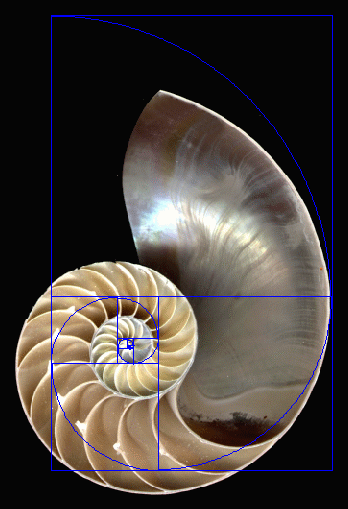
Спираль наутилуса по сравнению с золотой спиралью

Однако спираль Наутилуса, хотя и не является золотой спиралью, часто отображает пропорции своих размеров, близкие к золотому сечению, появляясь в последовательных вращениях оболочки по мере роста Наутилуса. Как и у всех живых организмов, существуют различия в размерах людей, поэтому появление золотого сечения не является универсальным.

См. Также другие примеры и объяснения золотого сечения в спирали наутилуса.

Фи и Фибоначчи в Кеплере и Золотых треугольниках

Создание треугольника на основе Фи (или Пифагор встречает Фибоначчи):

Пифагор обнаружил, что прямоугольный треугольник со сторонами длины a и b и гипотенузой длины c имеет следующее соотношение:

a² + b² = c²

Основополагающее равенство фи имеет аналогичную структуру:

1 + Phi = Phi ^²

^{(1+ 1,618… = 2,618…)}

Взяв квадратный корень каждого члена в этом равенстве, мы получим размеры треугольника, известного как треугольник Кеплера, прямоугольного треугольника, основанного на этом равенстве фи, где:

Длина

Сиде	Длина в квадрате за	, или квадратный корень	длина делится на фи, с = 1
а	1	1	1 / Phi
б	Phi	√ Phi	1 / √ Phi
с	Phi ^²	Phi	1

Этот треугольник показан ниже.Он имеет угол 51,83 ° (или 51 ° 50 ′), который имеет косинус 0,618 или фи.

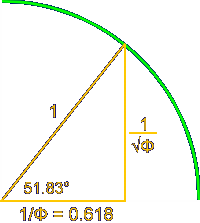
Пифагорейский треугольник 3-4-5 — это единственный прямоугольный треугольник, стороны которого находятся в арифметической прогрессии. 3 + 1 = 4, и 4 плюс 1 = 5. Треугольник Кеплера — единственный прямоугольный треугольник, сторона которого находится в геометрической прогрессии: квадратный корень из числа фи = 1 и 1 раза = =.

Хотя это трудно с уверенностью доказать из-за ухудшения на протяжении веков, некоторые полагают, что этот угол использовался древними египтянами при строительстве Великой пирамиды Хеопса.

Другие треугольники с пропорциями золотого сечения могут быть созданы с отношением Phi (1.618 0339…) к 1 основания и сторон треугольников:

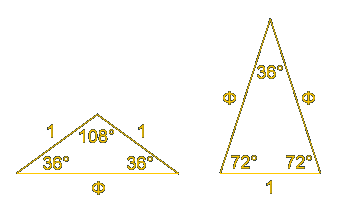
Равнобедренный треугольник справа вверху с основанием в 1 две равные стороны Фи известен как Золотой треугольник. Эти знакомые треугольники найдены воплощенными в пентаграммах и плитках Пенроуза.

Создание треугольника на основе чисел Фибоначчи

Для создания прямоугольного треугольника нельзя использовать три последовательных числа в серии Фибоначчи.Марти Стэндж, однако, предоставил следующие отношения в январе 2007 года: каждая последующая серия из четырех чисел Фибоначчи может быть использована для создания прямоугольного треугольника, при этом основание и гипотенуза определяются вторым и третьим числами, а другая сторона является квадратом корень произведения первого и четвертого чисел. В таблице ниже показано, как работают эти отношения:

серия Фибоначчи				Треугольник Фибоначчи
b ’	a	c	б ”	а²	b’xb ”	a² + b’xb ” = с²
0	1	1	2	1	0	1
1	1	2	3	1	3	4
1	2	3	5	4	5	9
2	3	5	8	9	16	25
3	5	8	13	25	39	64
5	8	13	21	64	105	169
8	13	21	34	169	272	441
13	21	34	55	441	715	1,156
21	34	55	89	1,156	1,869	3 025
34	55	89	144	3 025	4 896	7,921
55	89	144	233	7,921	12 815	20 736
89	144	233	377	20 736	33 553	54 289
144	233	377	610	54 289	87 840	142 129

Таким образом, для иллюстрации, выделенной золотом, в Трактате Штанге о треугольниках Фибоначчи показано, что треугольник со сторонами 5 и квадратным корнем из 39 (e.г., 3 х 13) создаст прямоугольный треугольник с гипотенузой 8.

По мере использования большего числа в ряду треугольник приближается к пропорциям вышеупомянутого треугольника Кеплера на основе фи с отношением гипотенузы к основанию Фи или 1,618…

Фибоначчи и золотое сечение: Золотое сечение Фибоначчи. Божественная мера красоты

Ряд Фибоначчи

Золотое сечение

Связь со стоматологией

Поделиться ссылкой:

Числа Фибоначчи и золотое сечение: взаимосвязь

Золотое сечение

Числа Фибоначчи

Спираль Архимеда и золотой прямоугольник

История применения золотых пропорций

Витрувианский человек Леонардо

Исследования золотого сечения в 16-19 веках

Число Фибоначчи и золотое сечение в природе

Использование золотого сечения в искусстве

Золотое сечение в архитектуре

Применение пропорций в дизайне

Применение золотого сечения в кибернетике и технике

Современные исследования теории о золотой пропорции

Золотое сечение: тайна вселенной

Определение золотого сечения

Числа фибоначчи в истории

Универсальный код природы

Формула золотого сечения

Искусство пространственных форм

Слово, звук и кинолента

Гармония Золотого сечения

Числа Фибоначчи в науке

Золотое сечение и пропорции Фибоначчи

Леонардо Фибоначчи обнаружил последовательность, сходящуюся на фи.

1,618033988749895. , ,

Вычислить любое число в последовательности Фибоначчи легко!

Соотношение последовательных чисел Фибоначчи сходится на фи

Последовательность Фибоначчи и азартные игры или лотереи

Фибоначчи — Золотое сечение в C?

спиралей и золотое сечение

числа Фибоначчи и Фи связаны со спиральным ростом в природе.

Альтернативные спирали в растениях встречаются в числах Фибоначчи.

Золотые спирали в морских раковинах

Спираль оболочки Наутилуса не является золотой спиралью, но часто все еще имеет пропорции золотого сечения.

Фи и Фибоначчи в Кеплере и Золотых треугольниках

Создание треугольника на основе Фи (или Пифагор встречает Фибоначчи):

Создание треугольника на основе чисел Фибоначчи

Добавить комментарий Отменить ответ