Что такое числа Фибоначчи, золотое сечение? ⋆ FutureNow
Последовательность Фибоначчи – одна из самых известных формул математики. Так, что такое числа Фибоначчи, золотое сечение и какая их интересная стория?
Что такое числа Фибоначчи?Каждое число в последовательности Фибоначчи – это сумма двух чисел, предшествующих ему.
Итак, последовательность выглядит так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и т. Математическое уравнение, описывающее число Фибоначчи: Xn + 2 = Xn + 1 + Xn
Фибоначчи числа иногда называют “секретным кодом природы” и “общем правилом природы”. Говорят, что данная последовательность руководит размерами всего сущего, в том числе обьясняет Великую пирамиду в Гизе, так и многие вещи, с которыми мы сталкиваемся каждый день.
Числа Фибоначчи: богатая историяПоэтому какова реальная история стоит за этой знаменитой последовательностью?
Многие источники утверждают, что ее впервые обнаружил или “изобрел” Леонардо Фибоначчи.
Итальянский математик, родился около 1170 года нашей эры и первоначально был известен как Леонардо из Пизы. Лишь в 19 веке историки придумали прозвище Фибоначчи, чтобы отличить математика от другого известного Пизарського Леонардо.
Но Леонардо из Пизы на самом деле не изобрел последовательность. Ее впервые упоминают древние санскритские тексты, в которых использовалась индуистско-арабская система числения, еще много веков до Леонардо Пизы.
Однако в 1202 Леонардо из Пизы опубликовал большой том “Liber Abaci,” книгу по математике “о том, как производить вычисления”. “Liber Abaci”, написанная для торговцев, где изложена индуистско-арабский арифметика, которая является полезной для отслеживания прибыли, убытков, остатков по кредитам и тому подобное.
ЧТО ТАКОЕ ШАРОВАЯ МОЛНИЯ: СУЩЕСТВУЕТ ЛИ ОНА?
В книге Леонардо из Пизы вводит последовательность с задачей о кроликах. Проблема заключается в следующем: начнем с самца и самки кролика.
“Liber Abaci” впервые представила эту последовательность западному миру. Но после нескольких скудных абзацев о разведении кроликов Леонардо из Пизы больше никогда не вспоминал ее.
На самом деле эти числа Фибоначчи были забыты до 19 века, когда математики подробнее изучили математические свойства последовательности. В 1877 году французский математик Эдуард Лукас официально назвал задачу о кроликах “последовательностью Фибоначчи”.
Мы узнали что такое числа Фибоначчи, но какое же значение имеет последовательность Фибоначчи?
Кроме как учебный инструмент, она проявляется во многих случаях в природе. Однако, это не какой-то секретный код, который руководит архитектурой Вселенной.
Однако, это не какой-то секретный код, который руководит архитектурой Вселенной.
Это правда, что последовательность Фибоначчи тесно связана с тем, что сейчас известно как “золотое сечение”. Проще говоря, отношение чисел в последовательности, поскольку последовательность идет к бесконечности, приближается к золотому сечению, который составляет +1,6180339887498948482 … Оттуда математики могут вычислить то, что называется золотой спиралью, или логарифмической спирали, коэффициент роста которой равен золотому сечению.
Золотое сечение объясняет рост некоторых растений. Например, спиральное расположение листьев или лепестков на некоторых растениях соответствует золотому сечению. Но есть также растения, которые не соблюдают этого правила.
Мистификации и выдумкиКогда люди начинают связывать человеческое тело, искусство и архитектуру, много вымышленных теорий и мистификаций ссылаются на последовательность Фибоначчи.
“Понадобится большая книга, чтобы задокументировать всю дезинформацию о золотом сечении, многие из которой – это просто повторение одних и тех же фантазий разных авторов”, – написал Джордж Марковский, математик из университета Мэн в 1992 году.
Значительная часть этой дезинформации может быть отнесена к книге 1855 года немецкого психолога Адольфа Зейзинга. Он утверждал, что пропорции человеческого тела основана на золотом сечении.
Золотое соотношение проросло в “золотые прямоугольники”, “золотые треугольники” и всевозможные теории об этих знаковых размерах.
С тех пор люди говорят, что золотое соотношение или золотое сечение можно найти в размерах Пирамиды в Гизе, Парфеноне, “Витрувийським человеке” Леонардо да Винчи и ренессансных сооружениях.
Под сомнение можно поставить и беспрекословное утверждение о том, что золотое сечение является “однозначно приятным” для человеческого глаза – на чем часто настаивают фотографы.
Часто все эти утверждения, когда их проверяют, являются ошибочными. Люди часто выдают желаемое за действительное.
Источник: www.livescience.com/
Золотое сечение в дизайне
Говорят, что “божественная пропорция” заложена в природе, и во многих вещах вокруг нас.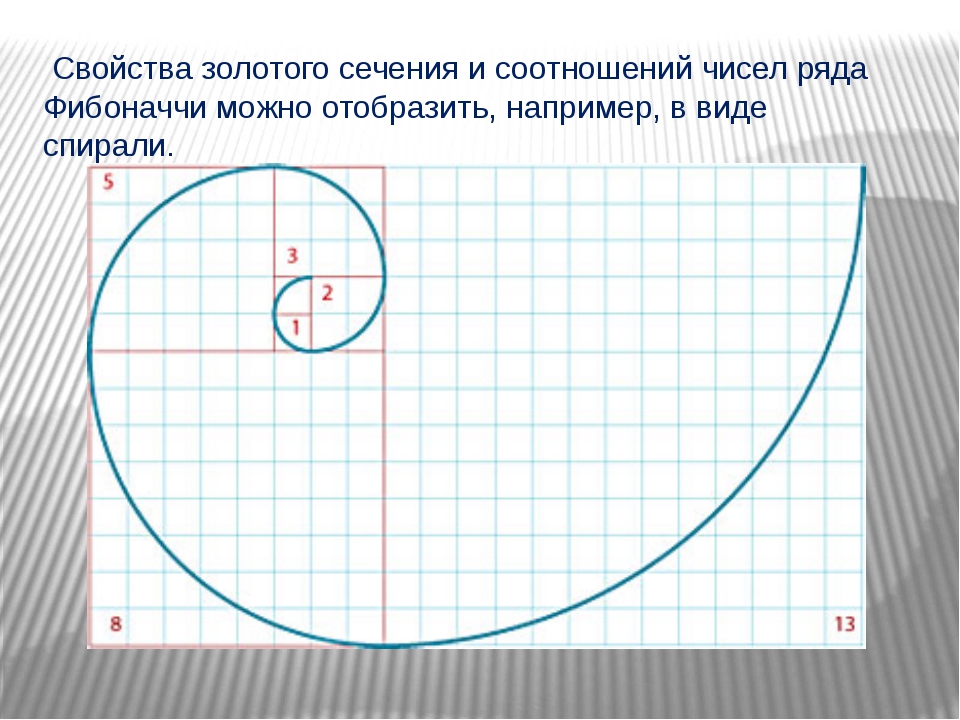 Вы можете найти ее в цветах, ульях, морских раковинах, и даже нашем теле.
Вы можете найти ее в цветах, ульях, морских раковинах, и даже нашем теле.
Эта божественная пропорция, также известная как золотое сечение, божественное сечение, или золотая пропорция может быть применена к различным видам искусства и обучения. Ученые утверждают, что чем ближе объект к золотому сечению, тем лучше человеческий мозг воспринимает его.
С тех пор как это соотношение было открыто, многие художники и архитекторы применяли его в своих работах. Вы можете найти золотое сечение в нескольких шедеврах эпохи Возрождения, архитектуре, живописи, и многом другом. В результате – красивый и эстетически приятный шедевр.
Немногие знают, в чем заключается тайна золотого сечения, что так радует наши глаза. Многие полагают, что то, что она появляется везде и является “универсальной” пропорцией, заставляет нас принять ее как что-то логическое, гармоничное и органичное. Другими словами, оно просто “чувствует” то, что нам нужно.
Итак, что такое золотое сечение?
Золотое сечение, также известное как “фи” по-гречески, это математическая константа. Оно может быть выражено уравнением a/b=a+b/a=1,618033987, где a больше, чем b. Это также можно объяснить последовательностью Фибоначчи, другой божественной пропорцией. Последовательность Фибоначчи начинается с 1 (некоторые говорят с 0) и добавляет к нему предыдущее число, чтобы получить последующее (т.е. 1, 1, 2, 3, 5, 8, 13, 21 …)
Оно может быть выражено уравнением a/b=a+b/a=1,618033987, где a больше, чем b. Это также можно объяснить последовательностью Фибоначчи, другой божественной пропорцией. Последовательность Фибоначчи начинается с 1 (некоторые говорят с 0) и добавляет к нему предыдущее число, чтобы получить последующее (т.е. 1, 1, 2, 3, 5, 8, 13, 21 …)
Если вы попытаетесь найти частное от деления двух последующих чисел Фибоначчи (т.е. 8/5 или 5/3), результат очень близок к золотому сечению 1,6 или φ (фи).
Золотая спираль создается с помощью золотого прямоугольника. Если у вас есть прямоугольник из квадратов 1, 1, 2, 3, 5 и 8 соответственно, как показано на рисунке выше, вы можете приступить к строительству золотого прямоугольника. Используя сторону квадрата, как радиус, вы создаете дугу, которая касается точек квадрата по диагонали. Повторите эту процедуру с каждым квадратом в золотом треугольнике, и в конечном итоге вы получите золотую спираль.
Где мы можем увидеть его в природе
Золотое сечение и последовательность Фибоначчи можно найти в лепестках цветов. У большинства цветков количество лепестков сводится к двум, трем, пяти или больше, что походит на золотое сечение. Например, у лилий 3 лепестка, у лютиков 5, у цветков цикория 21, а у ромашек 34. Вероятно, семена цветков также следуют золотому сечению. Например, семена подсолнечника прорастают из центра и растут к внешней стороне, заполняя головку семени. Обычно они спиралевидные и имеют сходство с золотой спиралью. Более того, количество семян, как правило, сводится к числам Фибоначчи.
У большинства цветков количество лепестков сводится к двум, трем, пяти или больше, что походит на золотое сечение. Например, у лилий 3 лепестка, у лютиков 5, у цветков цикория 21, а у ромашек 34. Вероятно, семена цветков также следуют золотому сечению. Например, семена подсолнечника прорастают из центра и растут к внешней стороне, заполняя головку семени. Обычно они спиралевидные и имеют сходство с золотой спиралью. Более того, количество семян, как правило, сводится к числам Фибоначчи.
Руки и пальцы также являются примером золотого сечения. Посмотрите ближе! Основание ладони и кончик пальца разделен частями (костьми). Соотношение одной части в сравнении к другой всегда 1,618! Даже предплечья с руками находятся в таком же соотношении. И пальцы, и лицо, и можно продолжать список…
Применение в искусстве и архитектуре
Парфенон в Греции, как утверждается, был построен с использованием золотых пропорций. Считается, что размерные соотношения высоты, ширины, колонн, расстояния между столбами, и даже размер портика близки к золотому сечению. Это возможно потому, что здание выглядит пропорционально идеально, и оно было таким с древних времен.
Это возможно потому, что здание выглядит пропорционально идеально, и оно было таким с древних времен.
Леонардо Да Винчи был также поклонником золотого сечения (и многих других любопытных предметов, собственно говоря!). Дивная красота Мона Лизы может быть связана с тем, что ее лицо и тело представляют собой золотое сечение, как и реальные человеческие лица в жизни. Кроме того, цифры в картине “Тайная вечеря” Леонардо Да Винчи расположены в порядке, который используется в золотом сечении. Если начертить золотые прямоугольники на холсте, Иисус окажется как раз в центральной доле.
Применение в дизайне логотипов
Неудивительно, что вы также можете найти использование золотого сечения во многих современных проектах, в частности, дизайне. Сейчас давайте сосредоточимся на том, как это может быть использовано в дизайне логотипа. Во-первых, рассмотрим некоторые из самых известных в мире брендов, которые использовали золотое сечение для совершенствования своих логотипов.
Видимо, Apple использовал круги из чисел Фибоначчи, соединив и обрезав формы для получения логотипа Apple. Неизвестно, было ли это сделано намеренно или нет. Тем не менее, в результате получился идеальный и визуально эстетичный дизайн логотипа.
Логотип Toyota использует соотношение a и b, формируя сетку, в которой образуются три кольца. Обратите внимание, как этот логотип использует прямоугольники вместо кругов для создания золотого сечения.
Логотип Pepsi создан двумя пересекающимися кругами, один больше другого. Как показано на рисунке выше, больший круг пропорционален в соотношении к меньшему – вы уже догадались! Их последний нерельефный логотип – простой, эффектный и красивый!
Кроме Toyota и Apple, логотипы некоторых других компаний, таких как, BP, iCloud, Twitter, и Grupo Boticario, как полагают, также использовали золотое сечение. И мы все знаем, насколько известны эти логотипы – все потому, что изображение сразу всплывает в памяти!
Как вы можете применить его в своих проектах?
Создайте эскиз золотого прямоугольника, как показано выше желтым цветом. Этого можно достичь путем построения квадратов с высотой и шириной из чисел, принадлежащих золотому сечению. Начните с одного блока и поместите другой рядом с ним. А другой квадрат, чья площадь равна тем двум, поместите над ними. Вы автоматически получите сторону из 3 блоков. После построения этой конструкции из трех блоков, в конечном итоге у вас будет сторона из 5 четырехугольников, из которой можно сделать другую (площадью в 5 блоков) коробку. Это может продолжаться сколько угодно, пока вы не найдете тот размер, который вам нужен!
Этого можно достичь путем построения квадратов с высотой и шириной из чисел, принадлежащих золотому сечению. Начните с одного блока и поместите другой рядом с ним. А другой квадрат, чья площадь равна тем двум, поместите над ними. Вы автоматически получите сторону из 3 блоков. После построения этой конструкции из трех блоков, в конечном итоге у вас будет сторона из 5 четырехугольников, из которой можно сделать другую (площадью в 5 блоков) коробку. Это может продолжаться сколько угодно, пока вы не найдете тот размер, который вам нужен!
Прямоугольник может перемещаться в любом направлении. Выделите мелкие прямоугольники и используйте каждый из них, чтобы собрать макет, который будет служить в качестве сетки дизайна логотипа.
Если логотип более округлый, то вам потребуется круговая версия золотого прямоугольника. Вы можете добиться этого начертанием кругов, пропорциональных числам Фибоначчи. Создайте золотой прямоугольник, используя только круги (это означает, что самый большой круг будет иметь диаметр 8, а у круга поменьше будет диаметр 5, и так далее). Теперь разделите эти круги и разместите их так, чтобы вы могли сформировать основную схему для вашего логотипа. Вот пример логотипа Twitter:
Теперь разделите эти круги и разместите их так, чтобы вы могли сформировать основную схему для вашего логотипа. Вот пример логотипа Twitter:
Примечание: Вам не обязательно чертить все круги или прямоугольники золотого сечения. Вы также можете использовать один размер неоднократно.
Как применять его в дизайне текста
Это проще, чем проектирование логотипа. Простое правило для применения золотого сечения в тексте заключается в том, что последующий больший или меньший текст должен соответствовать Фи. Давайте разберем этот пример:
Если размер моего шрифта – 11, то подзаголовок должен быть написан в более крупном шрифте. Умножаю шрифт текста на число золотого сечения, чтобы получить большее число (11*1,6=17). Значит подзаголовок должен быть написан в 17 размере шрифта. А теперь заголовок или название. Умножу подзаголовок на пропорцию и получу 27 (1*1,6=27). Вот так! Ваш текст теперь пропорционален золотому сечению.
Как применить его в веб-дизайне
А здесь немного сложнее. Вы можете оставаться верными золотому сечению даже в веб-дизайне. Если вы опытный веб-дизайнер, вы уже догадались, где и как ее можно применить. Да, мы можем эффективно использовать золотое сечение и применить его к сеткам наших веб-страниц и макетам пользовательского интерфейса.
Вы можете оставаться верными золотому сечению даже в веб-дизайне. Если вы опытный веб-дизайнер, вы уже догадались, где и как ее можно применить. Да, мы можем эффективно использовать золотое сечение и применить его к сеткам наших веб-страниц и макетам пользовательского интерфейса.
Возьмите общее число сетки пикселей за ширину или высоту и используйте его для построения золотого прямоугольника. Разделите наибольшую ширину или длину для получения меньших чисел. Это может быть шириной или высотой вашего основного контента. То, что осталось, может быть боковой панелью (или нижней панелью, если вы применили его к высоте). Теперь продолжайте использовать золотой прямоугольник для дальнейшего применения его к окнам, кнопкам, панелям, изображениям и тексту. Вы также можете построить полную сетку, основанную на маленьких версиях золотого прямоугольника расположенных как горизонтально, так и вертикально для создания более маленьких объектов интерфейса, которые пропорциональны золотому прямоугольнику. Для получения пропорций вы можете использовать этот калькулятор.
Для получения пропорций вы можете использовать этот калькулятор.
Спираль
Вы также можете использовать золотую спираль, чтобы определить, где разместить контент на вашем сайте. Если ваша домашняя страница загружается с графическим контентом, как, например, на веб-сайте онлайн магазина или блога фотографий, вы можете воспользоваться золотым методом спирали, который используют многие художники в своих работах. Задумка в том, чтобы поместить наиболее ценный контент в центре спирали.
Контент со сгруппированным материалом тоже может быть размещен при помощи золотого прямоугольника. Это означает, что чем ближе спираль движется к центральным квадратам (к одному квадратному блоку), тем “плотнее” там содержимое.
Вы можете использовать эту технику, чтобы обозначить расположение вашего заголовка, изображений, меню, панели инструментов, окна поиска и других элементов. Twitter славится не только использованием золотого прямоугольника в дизайн логотипа, но и задействовал его в веб-дизайне.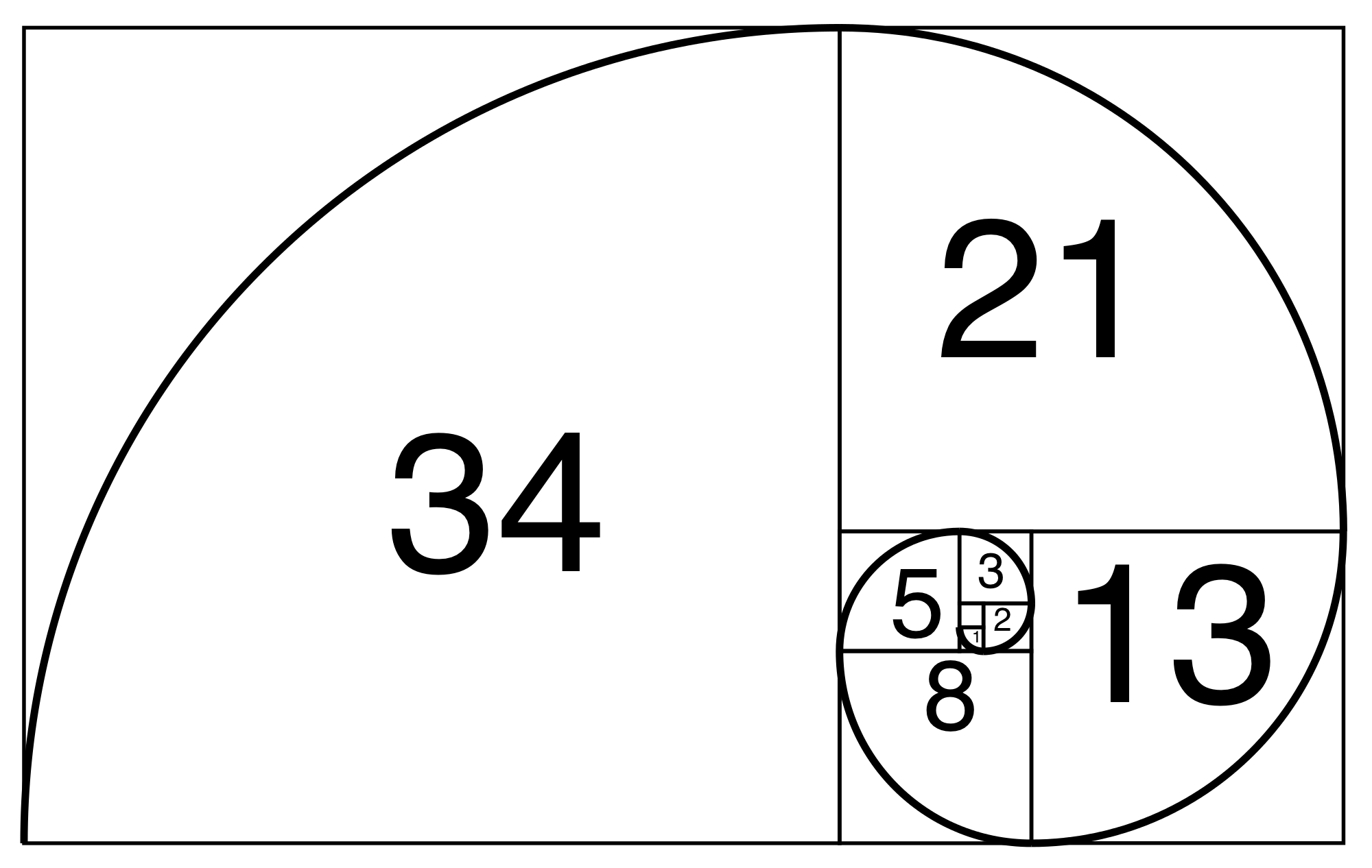 Как? Благодаря использованию золотого прямоугольника, или, другими словами концепцией золотой спирали, в странице профиля пользователей.
Как? Благодаря использованию золотого прямоугольника, или, другими словами концепцией золотой спирали, в странице профиля пользователей.
Но нелегко будет проделать такое на платформах CMS, где автор материала определяет расположение вместо веб-дизайнера. Золотое сечение подходит WordPress и другим дизайнам блога. Это, вероятно, потому, что боковая панель почти всегда присутствует в дизайне блога, который хорошо вписывается в золотой прямоугольник.
Правило третей
Для тех, кто не очень понимает язык математики, есть более простой способ. Он известен как правило третей. Оно не включает в себя точные математические вычисления, но помогает достигнуть правильных пропорций.
Все, что требуется – это разделить первоначальный эскиз на девять равных частей:
Точки, где встречаются линии в сетке, будут основными точками вашего дизайна, от которых вы будете в дальнейшем отталкиваться. Вы можете поместить ключевую тему или основные элементы на одну или все точки пересечения. Фотографы также используют эту концепцию.
Фотографы также используют эту концепцию.
Если Вы разделите каждую колонку в сетке так, чтобы получились две равные половины, то Вы получите сетку для работы с дизайном сайта. Например, Вы можете разместить эмблему или логотип в верхнем правом квадрате в левой части. Менее важная информация, которая будет располагаться вертикально сверху вниз, может брать свое начало верхнем правом квадрате.
Чем ближе прямоугольники к соотношению 1:1,6, тем приятнее воспринимается картина человеческим мозгом (так как это ближе к золотому сечению). Если вы не любите математику и не хотите считать, то достаточно использовать отношение 3:5 при расчете золотого отношения. Результат будет не таким точным, но он будет близок к пропорциям, которые применяются в работе с дизайном.
Пример того, как можно использовать сечение в веб-дизайне, описан ниже.
Золотое сечение на примере
Ширина вашего макета может быть фиксированная или гибкая, но прежде чем применить золотое отношение, вам нужно определить число, чтобы начать с ним работать. Для веб-дизайна это число будет равно числу пикселей в ширине лэйаута.
Для веб-дизайна это число будет равно числу пикселей в ширине лэйаута.
Если вы, например, работаете на лэйауте в 1200 пикселей, то нужно разделить это число на Phi. Для упрощения задачи, число Phi можно сократить до 1.62. При делении 1200 на 1.62, Вы получаете ширину основной колонны, что в нашем случае составит 740 пикселей.
Чтобы определить ширину второй колонки, просто вычтите ширину главной колонки от общей ширины. В этом примере получается 460 пикселей.
Теперь у вас есть две колонки в 740 пикселей и 460. При помощи этого простого вычисления, вы всегда сможете определить идеальные пропорции для колонок вашего сайта.
Для гибкого лэйаута нужно брать расчеты в процентах. Делим 100% на 1.62 и получаем основную колонку, которая займет 62%, а вторая – 38% соответственно. Далее вы сможете работать исходя из этого соотношения.
Золотое отношение может эффективно использоваться, при создании маленьких прямоугольников в пределах общего дизайна. Это пространство может быть использовано для кнопок навигации, заголовков изображений, пространства для объявлений или для текста, который располагается вокруг изображения. Как бы их не использовали, эти мини золотые прямоугольники будут пропорциональны и законченный вид дизайна, будет приятным завершением работы.
Это пространство может быть использовано для кнопок навигации, заголовков изображений, пространства для объявлений или для текста, который располагается вокруг изображения. Как бы их не использовали, эти мини золотые прямоугольники будут пропорциональны и законченный вид дизайна, будет приятным завершением работы.
Золотое сечение – не панацея
Использование золотого сечения в дизайне не гарантирует успех вашего лендинга.
В то же время изображения, блоки текста и врезок могут быть хорошо представлены в маленьких золотых прямоугольниках, которые формируют красивый, сбалансированный вид, но число прямоугольников на каждой странице должно быть ограниченным. Ничто в веб-дизайне не должно быть в слишком большом количестве.
Также важно помнить о том, что есть много других факторов, которые нужно учитывать при создании дизайна, и которые будут соответствовать общей цели проекта.
Инструменты для дизайнеров
Калькулятор Phi
Когда вы вводите число в этот веб-инструмент, он рассчитывает результат, необходимый для золотого сечения. Этот сервис бесплатный и очень простой в использовании.
Этот сервис бесплатный и очень простой в использовании.
Типографический калькулятор Pearsonified
Это онлайн инструмент с кнопкой ‘Set My Type’. Вы просто нажимаете на нее после того, как введете ширину контента и/или размер шрифта, и сервис сам подберет лучшее типографическое решение. У Вас также есть возможность ввести значение CPL. Он оптимизирует размер знаков по линиям.
Сервис золотого отношения UX Triggers
Вы можете проверить любой сайт с помощью этого бесплатного сервиса и быстро определить использована ли последовательность Фибоначчи в дизайне.
Заключительные мысли
Веб-страницы выглядят более гармонично, когда они сделаны с использованием принципов золотого сечения. Это единственное соотношение, которое использовалось еще две тысячи лет назад, для тех же целей, что и сегодня. Посетителя интуитивно будут чувствовать комфорт гармоничного интерфейса, потому что им уже знакомы классические пропорции архитектурных строений и других произведений искусства.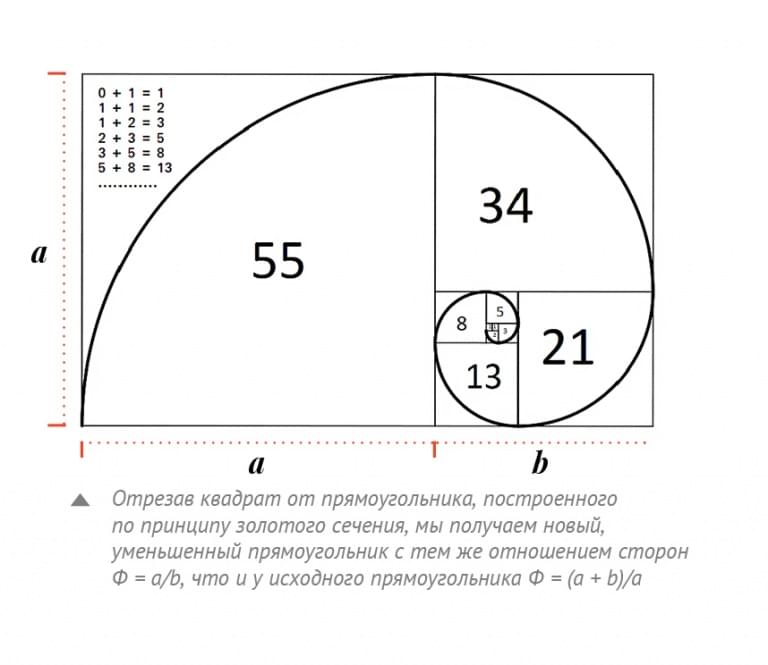
Использование золотых прямоугольников дает чувство упорядоченности вашему лендингу. Но вы должны быть аккуратны, и избегать злоупотребления ими. Слишком большое их количество произведет обратный эффект и сделает дизайн приторным и менее привлекательным.
Сочетание математических вычислений и органической структуры в веб-дизайне может дать отличный результат. Необязательно, чтобы весь дизайн опирался на все упомянутые принципы, иногда достаточно правила третей, которое поможет вам правильно соблюсти пропорции и расположить элементы на свои места.
Готовы проверить полученные знания на лендинге? Вы можете выбрать подходящий шаблон и настроить его под себя в конструкторе LPgenerator, или, если у вас нет времени разбираться в тонкостях лендостроения, но при этом вам нужна уникальная страница с гарантированно высокой конверсией, подать заявку на индивидуальный дизайн.
Он будет выполнен с учетом всех ваших пожеланий, подчеркнет особенности оффера и позиционирование бренда, а еще — легко масштабируется по мере необходимости.
Высоких конверсий!
12-03-2016
Числа Фибоначчи и золотое сечение окружают нас повсюду. Вот примеры | Хакнем Школа
Дэн Браун «Код да Винчи»#хакнем_математика 👈 рубрика, содержащая интересный, познавательный контент по математике как для школьников, так и для взрослых 🥳
Недавно, читая роман Дэна Брауна «Код да Винчи», я по-новому посмотрела на известные со школы: последовательность чисел Фибоначчи, «золотое сечение» и число Фи. Герой романа использует в качестве кода несколько чисел этого ряда.
Своими новыми для себя открытиями я решила поделиться с нашими читателями.
Удивительную последовательность чисел открыл итальянский математик Леонардо Пизанский, более известный под именем Фибоначчи (родился около 1170 — умер после 1228).
Числа, образующие последовательность:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, … называются «числами Фибоначчи», а сама последовательность — последовательностью Фибоначчи. Что же в них такого удивительного?
Что же в них такого удивительного?
1) В этой последовательности первые два числа равны либо 1 и 1, либо 0 и 1, а каждое последующее число получается из суммы двух предыдущих чисел: 1 = 0 +1, 2 = 1 + 1, 3 = 1 +2, 5 = 2 + 3, 8 = 3 +5, и т. д.
2) Ещё одна особенность в том, что при делении любого числа из последовательности на число, стоящее перед ним в ряду, результатом будет величина, колеблющаяся около иррационального значения 1.61803398875… и через раз то — превосходящая, то — не достигающая его. После 13-ого числа этот результат деления становится постоянным до бесконечности ряда.
Именно это постоянное число деления в средние века было названо Божественной пропорцией, а в наши дни именуется, как золотое сечение. В алгебре это число обозначается греческой буквой фи (φ).
Итак, Золотая пропорция = 1 : 1,618
233 / 144 = 1,618
377 / 233 = 1,618
610 / 377 = 1,618 и т. д., можете проверить сами…
д., можете проверить сами…
Но самое интересное, что меня поразило, это то, что золотая пропорция есть как в нашем теле, так и в природе.
Тело человека и золотое сечение«Витрувиа́нский человек» — изображение, созданное Леонардо да ВинчиОказывается, художники, учёные, модельеры и дизайнеры делают свои расчёты, чертежи или наброски, исходя из соотношения золотого сечения, так как пропорции различных частей нашего тела составляют число, очень близкое к золотому сечению.
Если эти пропорции совпадают с формулой золотого сечения, то внешность или тело человека считается идеально сложенным.
Несколько основных золотых пропорций нашего тела:
· расстояние от кончиков пальцев до запястья равно 1:1,618;
· расстояние от уровня плеча до макушки головы и размера головы равно 1:1,618;
· расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы равно 1:1,618;
· расстояние от кончика подбородка до кончика верхней губы и от кончика верхней губы до ноздрей равно 1:1,618 и др.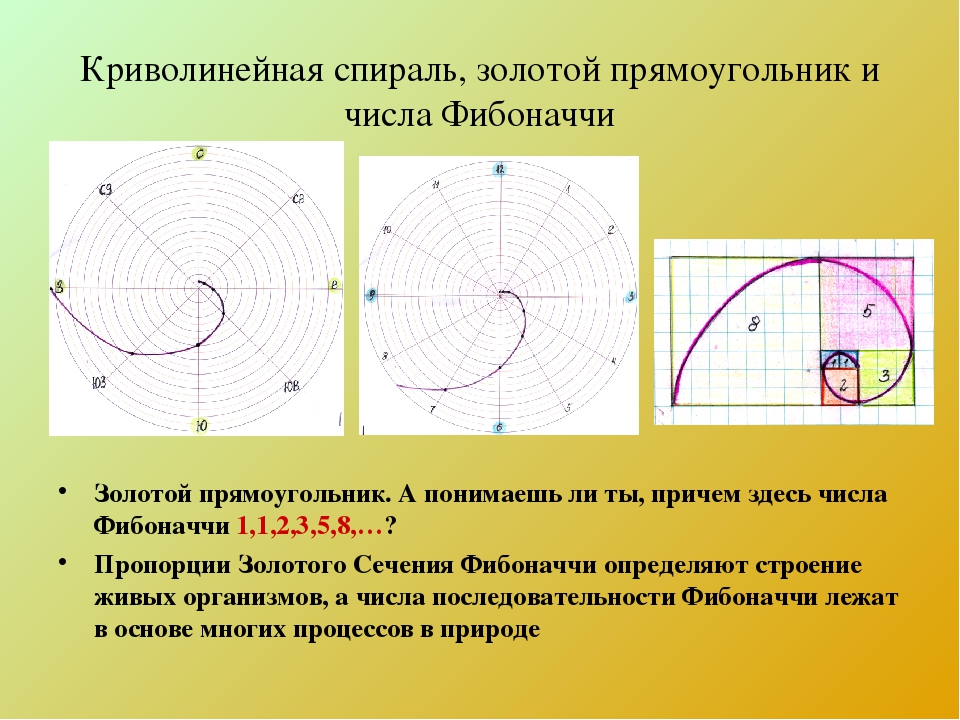
Формулу золотого сечения можно найти в других частях тела человека: и в руках человека, и ушах, и в строении лёгких и даже в строении молекулы ДНК (если интересно, можно найти информацию самостоятельно).
Золотой прямоугольникЗолотой прямоугольникВ геометрии есть такой прямоугольник, который называют золотым прямоугольником, его длинные стороны соотносятся с короткими сторонами в соотношении 1,168:1.
Он обладает удивительными свойствами — отрезав от золотого прямоугольника квадрат, строна которого равна меньшей стороны прямоугольника, мы снова получим золотой прямоугольник, но меньшего размера. Продолжая отрезать квадраты, мы будем получать всё меньшие и меньшие золотые прямоугольники.
Причём, располагаться они будут по логарифмической спирали, имеющей важное значение в математических моделях природных объектов (например, раковинах улиток).
ПРИРОДАИдеальную пропорцию создала сама природаВ природе, лежащее в основе строения спирали, правило золотого сечения встречается в природе очень часто в бесподобных по красоте творениях:
- числа спиралей на большинстве шишек и ананасах равны числам Фибоначчи;
- расположение листьев и ветвей на стеблях многих растений соответствуют числам Фибоначчи;
- семена в центре подсолнуха организованы в два набора спиралей — короткие, идущие по часовой стрелке от центра, и более длинные — против часовой стрелки;
- у большинства улиток, которые обладают раковинами, раковина растёт в форме логарифмической спирали.

Оказывается, числа Фибоначчи повсюду вокруг нас!
#хакнем_математика 👈 подпишись на этот хэштег, чтобы получать новый интересный и познавательный контент по математике 🥳
Автор: #ирина_чудневцева 41 год, город Ярославль, мама 16-летнего подростка.
Разметчик Фибоначчи
Разметчик Фибоначчи — это устройство, позволяющее вам всегда иметь под рукой соотношениие размеров для ваших изделий, удовлетворяющее принципам Золотого Соотношения. Если вы хотите, чтоб мебель, которую вы делаете, была не только функциональна, но и по-настоящему красива, то начинать нужно с пропорций предмета в целом и его частей. Если эти пропорции правильны, ваше произведение будет радовать глаз, иначе — может быть ужасным. Разметчик Фибоначчи — отличное подручное средство для проектирования красивых изделий.
|
Разметчик Фибоначчи, специальный инструмент, назван по имени итальянского математика Фибоначчи, жившего в XIII веке. «Фибоначчи» у этого учёного — это псевдоним, происхождение которого не известно он же — Fibonacci, он же — Леона́рдо Пиза́нский, он же — Leonardo Pisano. В честь учёного назван и числовой ряд, в котором каждое последующее число равно сумме двух предыдущих. Эта числовая последовательность носит название чисел Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, … Хотя этот ряд и был известен ещё в Древней Индии, т.е. задолго до рождения умного Фибоначчи, но, тем не менее, своё нынешнее название числа Фибоначчи получили благодаря исследованию свойств этих чисел, проведённому именно этим учёным в его труде «Книга абака» (Издательство РИМГНИЗ «Римское Государственное Народное Издательство», 1202 г.). Ряды Фибоначчи, спирали Фибоначчи, уровни Фибоначчи — об этом много можно прочитать. |
К чёму всё это? Одна закономерность упомянута, но можно заметить и другую — деление числа в ряду Фибоначчи на предыдущее даёт практически постоянный результат — 1,618 — проверьте, если не лень. С этими последовательностями много чего связано — от биржевых котировок до рубежей разграничения развития человечества на отдельные этапы, которые иногда называют временными ступенями эволюции. Короче говоря, замечательная последовательность. Ну и к чему же это, нам то, с шипорезками, пилами и стамесками, зачем всё это? Есть в этом большой смысл и для нас, читаем дальше.
С этими последовательностями много чего связано — от биржевых котировок до рубежей разграничения развития человечества на отдельные этапы, которые иногда называют временными ступенями эволюции. Короче говоря, замечательная последовательность. Ну и к чему же это, нам то, с шипорезками, пилами и стамесками, зачем всё это? Есть в этом большой смысл и для нас, читаем дальше.
Даже если вы одарены превосходным видением, не так-то просто спроектировать предмет мебели без использования основополагающих принципов для определения размеров этого предмета мебели и, главное, пропорций между его элементами. Будет ли это подход к проектированию, который передаётся от мастера к ученику или ваше врожденное чувство равновесия и гармонии, которым обладают лишь некоторые одарённые люди, в любом случае без такой совокупности знаний и опыта вы не сможете создать совершенное изделие, которое будет радовать ваш глаз и вызывать восхизение окружающих и ваших друзей. Можно создать изделие, которое будет прочно и функционально адекватно, но не будет радовать и вызывать приятные чувства. Предмет мебели, который не учитывает проверенные веками правила построения может выглядеть неуклюжим, неуравновешенным или даже ужасным.
Предмет мебели, который не учитывает проверенные веками правила построения может выглядеть неуклюжим, неуравновешенным или даже ужасным.
Главным среди множества совокупностей фундаментальных установок, сложившихся за сотни лет представлений и понятий, которые разработчики предметов мебели использовали и продолжают использовать для обеспечения баланса и хороших пропорций в дизайне мебели является золотая пропорция или соотношение (также называемое золотой серединой или золотым сечением). Обозначается эта пропорция греческой буквой ∳ (фи). Золотое соотношение может быть выражено уравнением ∳ (фи)= [1 + √ 5] / 2. Для простоты практического применения, мы можем взять лишь результирующее значение ∳ (фи), равное 1,618. Т.е. одно значение к другому должно относится как 1 к 1,618. Одна длина, к другой, например.
Один из многих замечательных принципов золотой пропорции является то, что коротий отрезок прямой линии по отношению к длинному отрезку этой же линии относится так же, как длинный отрезок линии относится к общей длине линии, и это соотношение равно ∳ (фи) = 1,618:
Именно это соотношение заложено в самой конструкции замечательного разметочного инструмента — Разметчика Фибоначчи:
Исходя из описанного принципа, Золотым (или гармоничным) Прямоугольником является такой, стороны в котором соотносятся как 1 : 1,618, т. е. длина большей стороны прямоугольника равна длине меньшей стороны прямоугольника, умноженной на ∳ (фи)=1,618:
е. длина большей стороны прямоугольника равна длине меньшей стороны прямоугольника, умноженной на ∳ (фи)=1,618:
Узнаёте? Это же столешница гармоничного стола! Или фасад тумбы и много чего ещё.
Аналогично, Золотым (или гармоничным) Параллелепипедом является тот, стороны в котором тоже соотносятся как 1 : 1,618, т.е. длина большей стороны параллелепипеда равна высоте параллелепипеда, умноженной на ∳ (фи)=1,618, а ширина параллелепипеда равна высоте параллелепипеда, поделённой на ∳ (фи)=1,618:
Узнаёте? Это же мебельная тумба, пристенный стол (консоль) и т.д.
Золотая Пропорция лежит в основе многих (если не всех) естественных соотношений и даже построения нашей Вселенной. Примеры есть в изобилии на каждом уровне, от размножения кроликов, расположения семян в подсолнухе и орешков в шишке, до астрофизики и квантовой механики. Планетарные орбиты и даже структура человеческой фигуры являются ещё одним подвержедния соблюдения этой замечательной пропорции.
Соотношение между соседними фалангами пальцев — это ∳ (фи) = 1,618, Соотношение между локтем и кистью — это ∳ (фи) = 1,618, соотношение расстояния от макушки до глаз и растояния от глаз до подбородка — это ∳ (фи) = 1,618, соотношение расстояния от макушки до пупка и растояния от пупка до пяток — это опять-таки ∳ (фи) = 1,618:
Дистанции между солнцем и первыми пяти планетами в солнечной системе так же соотносятся (примерно) как ∳ (фи) = 1,618, поэтому, как безусловно известно, астронометрия использует золотое соотношение при определении планет на их орбитах:
Будучи столь фундаментальным и столь широко распространённым в природе, это отношение просто призывает нас на подсознательном уровне как абсолютно правильное, которому надо следовать. Как таковое, это соотношение было использовано на протяжении веков дизайнерами и архитекторами, от пирамид до мебельных шедевров.
Большая пирамида в Гиза, как теперь понятно, тоже построена в соответствии с Золотым Сечением: высота стороны пирамиды равна длине основания стороны пирамиды, умноженной на всё ту же величину ∳ (фи) = 1,618:
При строительстве Парфенона (древнегреческий храм, расположенный на афинском Акрополе, главный храм в древних Афинах) использовалось соотношение ∳ (фи) = 1,618 при определении внешних размеров и соотношения его частей:
Достоверно не известно, применялись ли при построении Парфенона калькуляторы или Разметчики Фибоначчи, но соотношение точно применялось. Более подробно о соотношении ∳ (фи) = 1,618 в конструкции этого памятника архитектуры сказано в видеоролике, начиная с 48-й секунды:
Более подробно о соотношении ∳ (фи) = 1,618 в конструкции этого памятника архитектуры сказано в видеоролике, начиная с 48-й секунды:
В вышеприведённом ролике, наконец-то, дело дошло и до предмета мебели, пусть и простого. Главное — соотношение всё то же — ∳ (фи) = 1,618.
В одном из видов комода с множеством ящиков называемом в разных изданиях как Highboy или Popadour («Высокий парень» или «Помпадур»), сделанном в Филадельфии в промежутке между 1762 и 1790 годами, используется Золотая Пропорция в соотношении размеров многих из его элементов. Каркас — это Золотой прямоугольник, положение сужения («талии» шкафа) определяется делением общей высоты шкафа на ∳ (фи) = 1,618. Высоты нижних ящиков так же соотносятся как ∳ (фи) = 1,618:
Высоты нижних ящиков так же соотносятся как ∳ (фи) = 1,618:
Золотое Сечение применяется при изготовлении мебели чаще всего в качестве некоего прямоугольника, который строится с помощью ∳ (фи) = 1,618 для двух его измерений, т.е. уже упоминаемого Золотого прямоугольника, где длина в 1,618 раз больше ширины (или наоборот). Эти пропорции могут быть использованы для определения габаритных размеров мебели, а также деталей интерьера, таких как двери и ящики. Можно применять рассчёты, деля и умножая на такое «круглое» и удобное число, как 1,618, но можно просто использовать Разметчик Фибоначчи, просто снимая размеры бОльшего предмета и откладывая после этого размер меньшего предмета. Или наоборот. Быстро, просто и удобно.
Предметы мебели являются трехмерными и Золотое Соотношение может быть применено ко всем трем измерениям, т.е. предмет мебели становится Золотым Параллелепипедом, если сделать его по правилам Золотого Соотношения. К примеру, в простом случае, глядя на предмет мебели сбоку, его высота может быть наибольшим измерением в Золотом Прямоугольнике.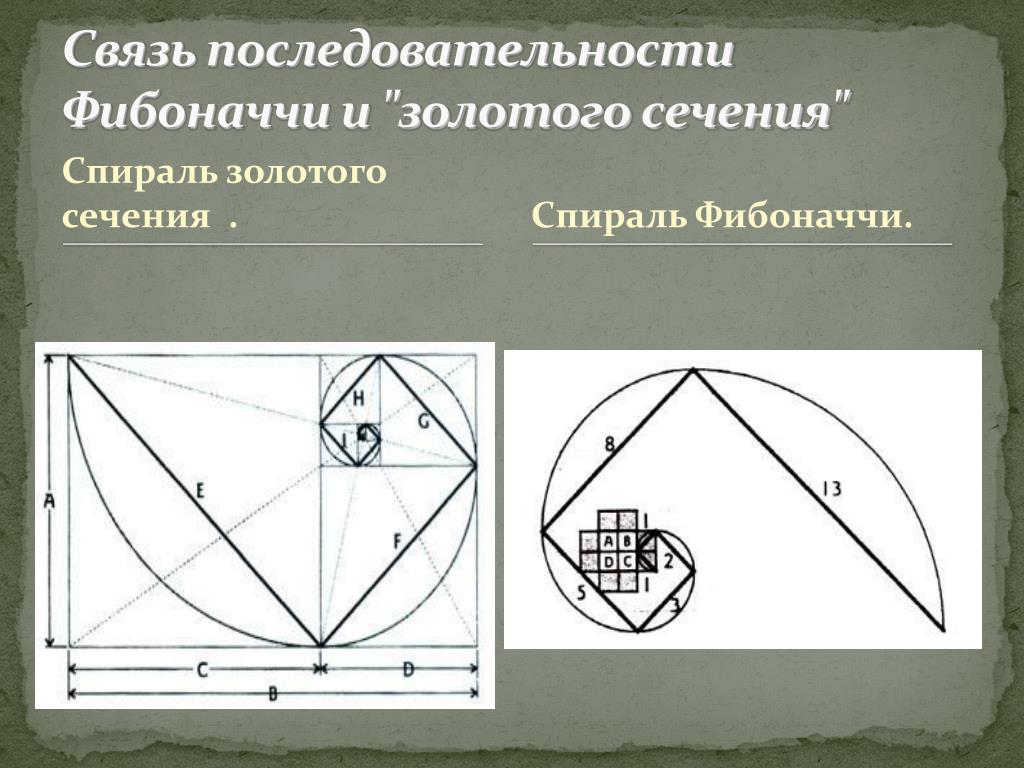 Однако, если смотреть на тот же предмет мебели спереди, та же высота может быть коротким измерением в Золотом Прямоугольнике.
Однако, если смотреть на тот же предмет мебели спереди, та же высота может быть коротким измерением в Золотом Прямоугольнике.
Необходимо отметить, однако, что форма предмета должна следовать за его функцией. Даже превосходные пропорции мебели могут оказаться быть бессмысленными, если этот предмет не может быть использован, например потому, что он слишком маленький или слишком большой или по другим причинам не может быть использован с комфортом. Следовательно, практические соображения должны быть на первом месте. В самом деле, большинство проектов мебели требуют, чтоб вы начали проектирование с некоторых заданных размеров: стол должен быть определенной высоты, шкаф возможно, придется приноравливать к конкретному пространству, а в книжном шкафу может потребоваться определенное количество полок. Но почти наверняка вы вынуждены будете определять множество других размеров, в отношении которых можно применить правильные пропорции. Но результат будет стоит затраченных усилий, чтоб в результате увидеть, как Золотое Соотношение может работать для всех этих элементов.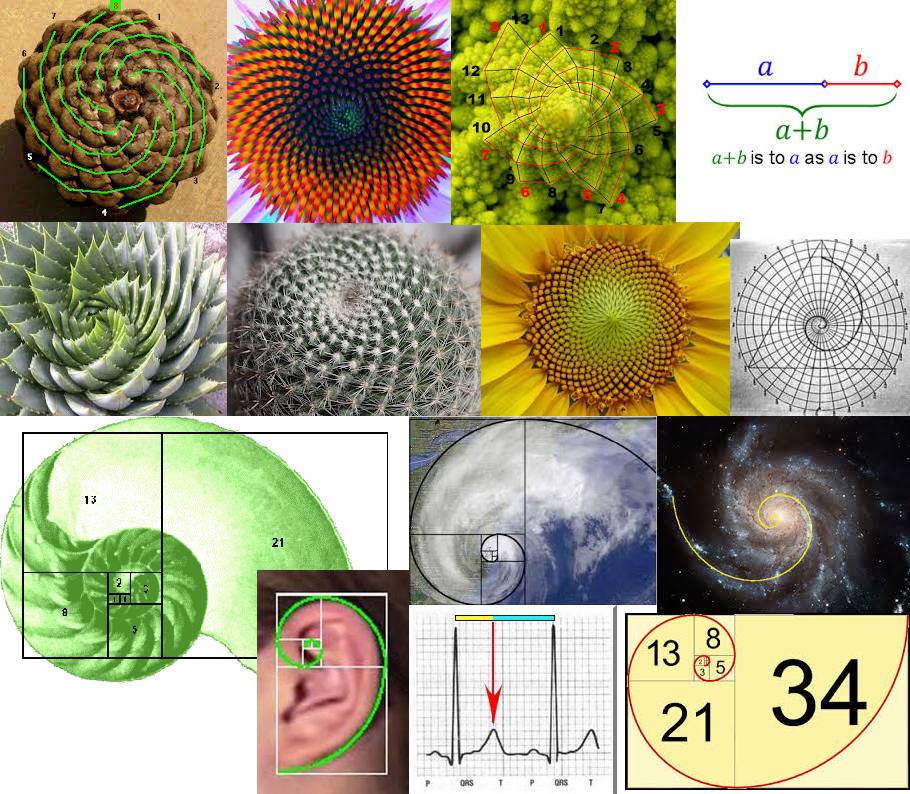 Принятие решения о размерах «на глаз» или, что еще хуже, исходя из имеющихся заготовок, не позволит вам получить отлично сбалансированный, с красивыми пропорциями отдельных частей и предмета мебели в целом.
Принятие решения о размерах «на глаз» или, что еще хуже, исходя из имеющихся заготовок, не позволит вам получить отлично сбалансированный, с красивыми пропорциями отдельных частей и предмета мебели в целом.
Итак, размеры отдельных частей мебели должны быть пропорциональны в соответствии с Золотым Соотношением. Такие элементы, как ножки стола, относительные размеры элементов каркаса, такие как вертикальные и горизонтальные части фасадов, проноги, царги и т.д., могут быть рассчитаны с применением Золотой Пропорции. Золотое сечение также предлагает один из способов решение проблемы проектирования ящиков в комоде с ступенчатым увеличением высоты ящиков. С помощью Разметчика Фибоначчи легко осуществить такую разметку — надо просто взять размер бОльшего ящика и по разметчику отложить размеры двух соседних ящиков и т.д. После этого, взяв размер ящика, по разметчику отложить расстояние от верха ящика до места расположения его ручки.
Такой метод использования Разметчика Фибоначчи, как инструмента для практического применения Золотого Соотношения будут эффективен для определения и других размеров, таких, как положение полок в шкафу, разделителей между ящиками и т. д. Любые размеры предмета мебели, изначально, определяются функциональными и структурными требованиями, но множество поправок может быть сделано путём применения Золотого Соотношения, что, несомненно, добавит в предмет гармонию. Использование Золотого Соотношения при проектировании мебели позволит вам сделать гармоничным не только предмет в целом, но и позволит вам быть уверенным в том, что все составные части — дверные панели, ящики, ножки, царги и т.д. принципиально, гармонично связаны между собой.
д. Любые размеры предмета мебели, изначально, определяются функциональными и структурными требованиями, но множество поправок может быть сделано путём применения Золотого Соотношения, что, несомненно, добавит в предмет гармонию. Использование Золотого Соотношения при проектировании мебели позволит вам сделать гармоничным не только предмет в целом, но и позволит вам быть уверенным в том, что все составные части — дверные панели, ящики, ножки, царги и т.д. принципиально, гармонично связаны между собой.
Спроектировать что-то с абсолютно совершенными пропорциями редко удается в реальности. Почти каждый предмет мебели или дерева придётся соотносить с ограничениями, накладываемыми функциональностью, возможностями столярных соединений или экономией средств. Но даже попытка приблизиться к совершенству, которое может быть определено как размеры, в точности соответствующие Золотому Соотношению гарантирет вам получение лучшего результата по сравнению с разработкой без внимания к этим основополагающим принципам.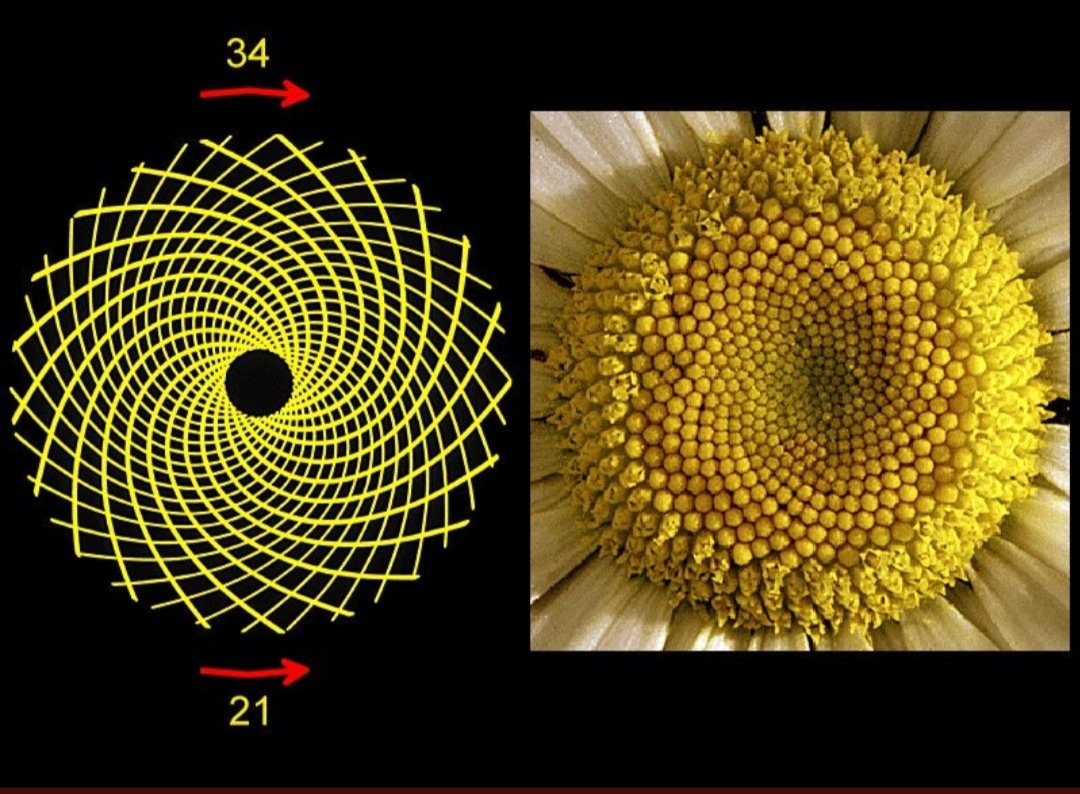 Даже если вы приблизились к идеальным пропорциям, то глаз зрителя сгладит небольшие недостатки и сознание заполнит некоторые пробелы в дизайте. Желательно, но не обязательно, чтоб всё было идеально и соответственно формуле. Но если предмет вашей мебели абсолютно не соответствует правильным пропорциям, без сомнения, он будет некрасив. Поэтому стремиться к правильным пропорциям необходимо.
Даже если вы приблизились к идеальным пропорциям, то глаз зрителя сгладит небольшие недостатки и сознание заполнит некоторые пробелы в дизайте. Желательно, но не обязательно, чтоб всё было идеально и соответственно формуле. Но если предмет вашей мебели абсолютно не соответствует правильным пропорциям, без сомнения, он будет некрасив. Поэтому стремиться к правильным пропорциям необходимо.
Наконец, мы часто корректируем вещи на глаз, чтобы сделать предмет легче и лучше сбалансированным, и делаем мы это с помощью методов, которые являются повседневными в деревообработке. Эти методы включают в себя учёт изменения размеров заготовки, исходя из направления волокон древесины, учёт рисунка древесины, с помощью которого можно предмет мебели сделать более привлекательным, отделку краёв и углов, которая создаст впечатление большей или меньшей толщины элемента изделия, использование молдингов для более точного соответствия изделия Золотому Прямоугольнику или Параллелепипеду, использование сужающихся ножек, чтобы сделать ощущение большего приближения предмета мебели к идеальной пропорции, и, в конце концов, смешивание всех этих методов для достижения идеального дизайна. Использование Золотого Сечения и инструмента для его применения — Разметчика Фибоначчи — начало этого стремления к совершенству.
Использование Золотого Сечения и инструмента для его применения — Разметчика Фибоначчи — начало этого стремления к совершенству.
В статье использованы материалы главы «A Guide to Good Design» из книги «Practical Furniture Design», написанной Graham Blackburn — признанным мебельным мастером, популяризатором деревообработки и издателем.
Евгений Фукс
технический консультант
LeighJigs.ru
[email protected]
Золотое сечение как объяснение пропорций красоты
Над чем работают лучшие умы современной стоматологической науки? Над идеальной улыбкой, воплотившей в себе красоту и здоровье.
Что такое «красота»? Почему лицо и облик одного человека нам нравится, а другого — нет?
На эти вопросы пытались ответить учёные ещё тогда, когда не было ни только стоматологии как направления медицины, но и сама медицина находилась в стадии зарождения.
Оказывается, наше лицо и тело имеет определённые пропорции, кажущиеся на первый взгляд почти мистическими.
Хотя в наш просвещённый век многому можно найти научное и даже математическое объяснение.
Принято считать, что впервые закономерности соотношение размеров тела человека и отдельных его частей обобщил и сформулировал в 1855 г. немецкий исследователь Цейзинг в своём научном труде «Эстетические исследования». За основу своей теории он взял учение о «золотом сечении».
Ещё в VI веке до н.э. древнегреческий философ и математик Пифагор ввёл в научный обиход понятие «золотое деление». «Золотое деление» — это пропорциональное деление отрезка на неравные части. При этом меньший отрезок так относится к большему, как больший отрезок относится ко всему отрезку. a : b = b : c или с : b = b : а.
Так что же особенного в этом соотношении?
Оказывается, что всегда меньший отрезок относится к большему, как 0,382: к 0,618:
То есть, если АВ принять за единицу, АЕ/ЕВ=0,62/0,32 (в практических целях используют приближённые значения).
Один из примеров «золотого деления», с которым наверняка все знакомы, это — пентаграмма и, как представители её, так любимые людьми старшего поколения, «знак качества» и «звезда».
Все диагонали пятиугольника (пятиугольная звезда) делят друг друга на отрезки, связанные между собой «золотой пропорцией».
В настоящее время эта математическая закономерность носит название «золотое сечение», которое ввел в обиход ещё Леонардо да Винчи, который проводил сечения стереометрического тела, образованного правильными пятиугольниками. И каждый раз он получал соотношение сторон в «золотом делении». Он дал этому делению название «золотое сечение», принятое до сих пор.
Но не Пифагор впервые обнаружил закономерность «золотого сечения». Ещё древние египтяне и вавилоняне использовали эти знания в строительстве пирамид и изготовлении предметов обихода. Древние греки при проектировании своих зданий использовали пропорции «золотого сечения». В эпоху возрождения интерес к «золотому сечению» усилился.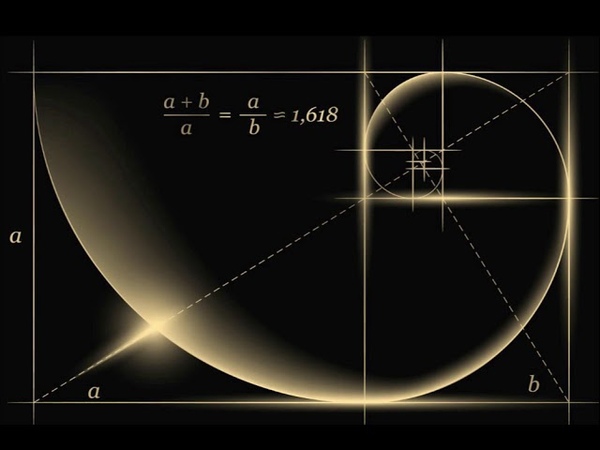 Художники нашли применение ему в искусстве. Учение о «золотом сечении» связано с именем гениального итальянского математика и монаха Луки Пачоли. В 1509 г. Была издана его книга «Божественная пропорция» с иллюстрациями Леонардо да Винчи (предположительно). Он причислял золотую пропорцию к «божественной сути» через триединство: бог сын, бог отец и святой дух, находящихся между собой в «золотой пропорции».
Художники нашли применение ему в искусстве. Учение о «золотом сечении» связано с именем гениального итальянского математика и монаха Луки Пачоли. В 1509 г. Была издана его книга «Божественная пропорция» с иллюстрациями Леонардо да Винчи (предположительно). Он причислял золотую пропорцию к «божественной сути» через триединство: бог сын, бог отец и святой дух, находящихся между собой в «золотой пропорции».
История «золотого сечения» связана ещё с одним известным итальянским математиком Фибоначчи. До наших времён дошёл ряд чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д., известный, как ряд Фибоначчи.
Особенность последовательности данных чисел заключается в том, что каждый её член, начиная с третьего, равен сумме двух предыдущих (2+3=5, 3+5=8), а отношение смежных чисел ряда приближается к отношению «золотого сечения» (21:34=0,617, а 34:55=0,618). В последствии все исследователи «золотого сечения» в растительном и животном мире, искусстве и анатомии приходили к этому ряду, как арифметическому выражению закона золотого деления.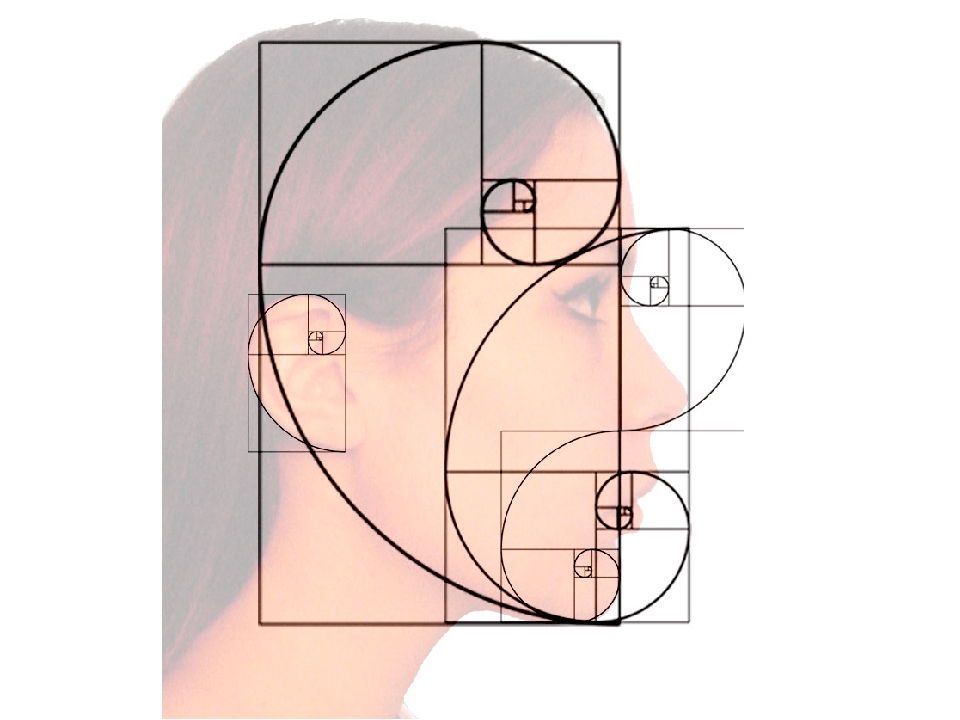 Интересно, что свой закон Фибонначи вывел, подсчитывая количество рождённых кроликов от пары кроликов за год.
Интересно, что свой закон Фибонначи вывел, подсчитывая количество рождённых кроликов от пары кроликов за год.
Так в чём же ореол таинственности «золотого сечения»?
Всё, что растёт и приобретает какую-либо форму в живом мире нашей планеты — растёт вверх или закручивается по спирали. Спираль (например, морская раковина) — пример соотношения в пропорциях «золотого сечения». Спирали прослеживаются в расположении семян в шишках хвойных деревьев, в семенах подсолнечника и др.
Паук плетёт паутину по спирали, ДНК человека закручено по спирали.
А рост вверх? Растение живёт по тем же законам «золотого сечения». Самый большой участок стебля — до первого листочка. Затем следующие сегменты уменьшаются в пропорции «золотого сечения»: с : в = в : а
Удивительно то, что и человек в соотношении отдельных частей тела и расстояний между ними, подчиняется законам «золотого сечения».
Немецкий учёный Альберт Дюрер доказал, что рост человека делится в золотых пропорциях линией, проходящей через пупок и линией, проходящей через кончики средних пальцев опущенных рук.
Его труды продолжил Цейзинг. Он выяснил, что пропорции мужского тела колеблются в пределах 13 : 8 = 1, 625.
А пропорции женского тела в среднем находятся в соотношении 8 : 5 = 1,6.
Пропорции «золотого сечения» проявляются в отношении длины плеча, предплечья, кисти и пальцев и т.д.
Поразительно, но в лице человека можно проследить множество пропорций, подчиненных «золотому сечению». Причем, чем больше в лице человека соотношений в этой пропорции, тем красивее нам он кажется. Есть лица, при характеристике которых употребляют выражение «правильные черты лица». У этих людей основные пропорции наиболее близки к соотношению 1, 618: или 62 : 38.
Какие же пропорции в лице человека стремятся к «золотому сечению»?
Прежде всего, у людей с красивыми лицами наблюдается:
- Идеальная пропорция между расстояниями от медиального угла глаза до крыла носа и от крыла носа до подбородка. Это соотношение называется «динамической симметрией» или «динамическим равновесием».

- Соотношение высоты верхней и нижней губы будет 1,618.
- Высота надгубной складки (расстояние между верхней губой и нижней границей носа) и высота губ будут составлять соотношение 62 : 38.
- Ширина одной ноздри суммарно с шириной переносицы относится к ширине другой ноздри в пропорции «золотого сечения».
- Ширина ротовой щели также относится к ширине между наружными краями глаз, а расстояние между наружными уголками глаз — к ширине лба на уровне линии бровей, как все пропорции «золотого сечения».
- Расстояние между линии смыкания губ до крыльев носа относится к расстоянию от линии смыкания губ до нижней точки подбородка, как 38 : 62: И к расстоянию от крыльев носа до зрачка — как 38 : 62 = 0.
- Расстояние между линией верхней части лба до линии зрачков и расстояние между линией зрачков и линией смыкания губ имеет пропорцию «золотого сечения».
Можно продолжить этот список соотношения размеров гармоничного лица. Получается, правильную красоту можно математически просчитать и даже прибегнуть к хирургической корректировке с целью совершенствования внешности.
Получается, правильную красоту можно математически просчитать и даже прибегнуть к хирургической корректировке с целью совершенствования внешности.
В настоящее время стоматология, наряду с пластической хирургией, занимается не только лечением заболеваний полости рта, но и эстетической медициной.
Удивительно, но и в стоматологии можно проследить пропорции «золотого сечения».
Красивая улыбка — это не только белоснежные здоровые ровные зубы, но и их правильное соотношение и расположение. И здесь мы опять сталкиваемся с закономерность «золотого сечения».
Вот некоторые примеры соотношений размеров и расстояний между зубами:
- Ширина верхнего центрального резца относится к ширине нижнего центрального резца, как 62 : 38, т.е. 1, 618:, в соотношении «золотого сечения».
- В этой же пропорции находится ширина двух верхних резцов к ширине двух нижних.
- Расстояние между премолярами верхней челюсти относится к ширине четырёх верхних резцов, как 62 : 38.

- Расстояние между дистальными поверхностями нижних клыков и щечными фиссурами моляров — пропорция 38 : 62.
И этот список можно продолжить.
Как же на практике можно использовать знание о «золотом сечении» и его влиянии на параметры в стоматологии?
Разумеется, искать применение золотых пропорций в эстетической стоматологии.
Расположение, размер и взаимное соотношение зубов в полости рта — всё это подчинено общему закону — «золотому сечению».
Вольно или невольно, осознанно или неосознанно врач использует эти пропорции при восстановлении коронковой части зуба, при протезировании или ортодонтических мероприятиях. Лучше, конечно, чтобы врач применял математическую составляющую в формировании вашей красоты и здоровья.
А мы теперь знаем, что человек — только часть живого мира на нашей планете, подчиняющийся общим законам мироздания. И доказательство тому — учение о «золотом сечении», дошедшее до нас уже даже не из предыдущего тысячелетия.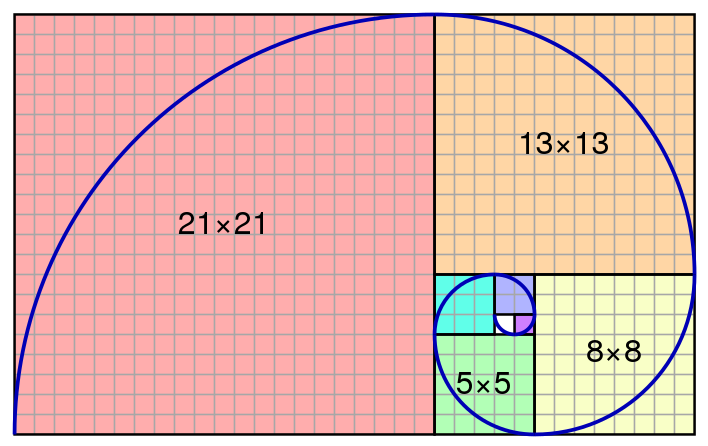
Время работы
| Пн-Пт | 10:00 — 22:00 |
| Сб-Вс | 10:00 — 20:00 |
Хохлова Елена Александровна Врач-стоматолог терапевт, эндодонтист
Золотое сечение в архитектуре: принцип проектирования зданий
Почему нас так привлекают строения древней архитектуры, при виде которых мы испытываем гармонию и умиротворение? Все они были построены на основе золотого сечения, данная зависимость прослеживается и в средневековье, и в современном мире. Математическая пропорция встречается повсеместно: это и ракушки моллюсков, и знаменитые картины художников, и строение человеческого тела, и даже египетские пирамиды. Сегодня об обзоре редакции Homius.ru расскажем простыми словами, как и, самое главное, зачем нужно использовать божественную гармонию чисел, и как она поможет в строительстве собственного дома и оформлении интерьера.
Содержание статьи
Просто о сложном: что это такое – правило золотого сечения
Золотое сечение –это правило общей пропорции, которая создает универсальную композицию. Математики называют её формулой божественной гармонии или асимметричной симметрией.
Это интересно! Общее определение правила ЗС –меньшая величина относится к большей, как большая к целому. Было рассчитано приблизительное число, равное 1,6180339887, это и есть коэффициент золотого сечения. Если смотреть в процентном соотношении, то в одном целом меньшая величина занимает 38%, большая – 62%.
Признано считать, что ЗС пришло к нам еще с древней Греции, но есть и такое мнение, что его греки подсмотрели у египтян. Если проанализировать архитектуру Египта того времени, можно чётко проследить соблюдение математической гармонии. Необычные свойства числовой зависимости стали причиной мистического отношения к золотому сечению:
- практически все живые организмы можно привести к принципу числовой зависимости.
 Например, тело человека, количество семечек в подсолнухе, структуру ДНК, произведения искусства и вирусную бактерию;
Например, тело человека, количество семечек в подсолнухе, структуру ДНК, произведения искусства и вирусную бактерию; - данная зависимость чисел характерна только для биологических существ и кристаллов, все остальные неживые объекты природы крайне редко обладают золотой пропорцией;
- именно математическая пропорция в строении биологических объектов оказалась оптимальной для выживания.
Экскурс в историю: кто придумал золотое сечение
Представление о золотой пропорции имели и древние греки, и египтяне, известно было о ней и на Руси. Но впервые ещё в 1509 году в книге «Божественная Пропорция», иллюстрации к которой принадлежат Леонардо да Винчи, монах Лука Пачоли дал научное определение правилу. Он видел в золотом сечении божественное единство:
- маленький отрезок – это сын;
- большой – отец;
- весь отрезок – это святой дух.
Это интересно! Историки присваивают Леонардо да Винчи определение термина ЗС, поскольку он долгое время изучал божественную закономерность и воплощал её принцип в своих творениях.
Вторую жизнь ЗС получило в 1855 году благодаря философу Адольфу Цейзингу. Он доработал теорию до абсолютного идеала, и она стала универсальной для всех проявлений. Все это он описал в своей книге «Математическое Эстетство», на которое в свое время обрушилось много негатива и критики.
Золотое сечение в божественной пропорцииПринцип расчета и построения золотого сечения
Примеры пропорции золотого сечения можно видеть при строительстве многих архитектурных сооружений, только нужно знать, как правильно его увидеть. Для этого достаточно посмотреть на строение всего 5 минут.
Как определить число золотого сечения
С пропорцией ЗС связывают астронома из Италии Фибоначчи, он вывел ряд чисел, в котором значение каждого последующего равно сумме двух предыдущих. Сегодня эта закономерность известна как ряд Фибоначчи:
- 0, 1,1 (0+1), 2 (1+1), 3 (1+2), 5 (2+3), 8 (3+5), 13 (5+8), 21 (8+13), 34 (13+21), 55 (21+34), 89 (34+55) и так до бесконечности;
- если выполнить деление последующего числа на предыдущее – получится коэффициент ЗС.

Данную формулу применяют для расчета пропорций золотого сечения в любой отрасли, на практике чаще всего используют округленные значения 0,62 и 0,38.
Ряд Фибоначчи в церкви Покрова на НерлиКак рассчитать золотое сечение на простейшем примере
Проще всего объяснить гармонию ЗС можно на примере обычного куриного яйца, точнее на удалении всех точек скорлупы от центра тяжести. Именно форма оболочки, а не её прочность, обеспечила выживаемость птиц столь долгое время и в любых условиях.
Если взять обычный отрезок, который состоит из нескольких маленьких, их длины относятся к большей величине как 0,62. Это показывает, как можно разбить целую линию для получения идеальной пропорции.
Простой пример золотого сечения в курином яйцеКак построить золотое сечение на примере прямоугольника и спирали
Если построить золотой прямоугольник, используя ряд Фибоначчи, он будет выглядеть как единое целое. Рассмотрим зависимость на примере:
- нужно нарисовать квадрат со стороной 1 и рядом ещё один аналогичный;
- над ними разместить квадрат со стороной 2;
- слева гармонично помещается квадрат с гранью 3;
- ниже – квадрат со стороной 5;
- справа пространство займет квадрат с гранью 8;
- площадь прямоугольника 8×13, в котором 13 — это следующее число ряда;
- если разделить на калькуляторе следующее число на предыдущее, получится значение золотого сечения 1,62, причём, чем больше числа, тем меньшая погрешность в их отношении;
- если по этому принципу построить спираль, каждую четверть витка она будет расширяться именно на значение ЗС.

На видео можно более подробно узнать про магию чисел Фибоначчи:
Божественная гармония золотого сечения в архитектуре: фото древних построек и примеры современного строительства
Многие древние здания, которые сохранились до наших времен, подтверждают мнение, что они были построены по правилам идеальной пропорции. Это резиденции королей, церкви, общественные сооружения. Рассмотрим на примерах принцип золотого сечения в разных странах.
Тайны древнеегипетской архитектуры
В архитектуре Древнего Египта по правилам золотой пропорции была построена пирамида Хеопса. Глядя на творение строителей, можно увидеть треугольник с прямым углом, один катет которого является высотой, второй – половиной длины основания. Если взять отношение гипотенузы к меньшей стороне, получим идеальное значение 1,61950 или 1,62.
Это интересно! Форма пирамиды имеет ещё одно неоспоримое свойство.
В нём сталь становится прочнее, вода дольше сохраняет свежий вкус, и быстрее растут живые растения. Много лет ученые пытаются разгадать этот феномен, но пока его научное решение не найдено.
Было замечено, что пирамида улучшает психоэмоциональное состояние человека, в её области уменьшаются вредоносные излучения, пропадают геопатогенные зоны.
Идеальная пропорция золотого сечения в пирамидеИдеальные пропорции в древней Греции
Идеальная пропорциональность делает архитектурные объекты запоминающимися. Яркий представитель ЗС из древней Греции – Парфенон, который возведен в 5 веке до нашей эры. Если взять отношение его высоты к ширине, получится практически идеальное число 0,618.
Ученые определили, что для абсолютного золотого числа нужно отнять от высоты 14 см и прибавить их к ширине. Учитывая строение сооружения, очень похоже, что это было сделано древними архитекторами Иктином и Калликратом намеренно, поскольку фасад немного сужается в верхней части и отклоняется от золотого прямоугольника. Но общие пропорции ЗС соблюдены.
Но общие пропорции ЗС соблюдены.
Принцип идеальной пропорции в древнегреческом Парфеноне:
Памятники архитектуры средневековья
Прекрасным памятником истории архитектуры средневековья, сохранившимся до нашего времени, является собор Парижской Богоматери или Нотр-Дам де Пари.
В здании очень заметно желание архитектора соблюсти гармонию и целостностьАнализируя строение, принцип ЗС можно видеть на нескольких участкахАрхитектура России
Ряд Фибоначчи – это своеобразная матрица, с помощью которой анализируют любое архитектурное сооружение. Чтобы было проще ориентироваться, можно построить на принципе золотого сечения циркуль Фибоначчи.
Разметчик Фибоначчи построен по правилу золотого сеченияИспользовать циркуль можно практически на любом архитектурном сооруженииЧтобы исследовать большие объекты, нужно отойти на некоторое расстояние и приложить циркульЗолотое сечение в архитектуре Москвы
Выдающееся здание МГУ на Воробьевых горах было построено в послевоенное время.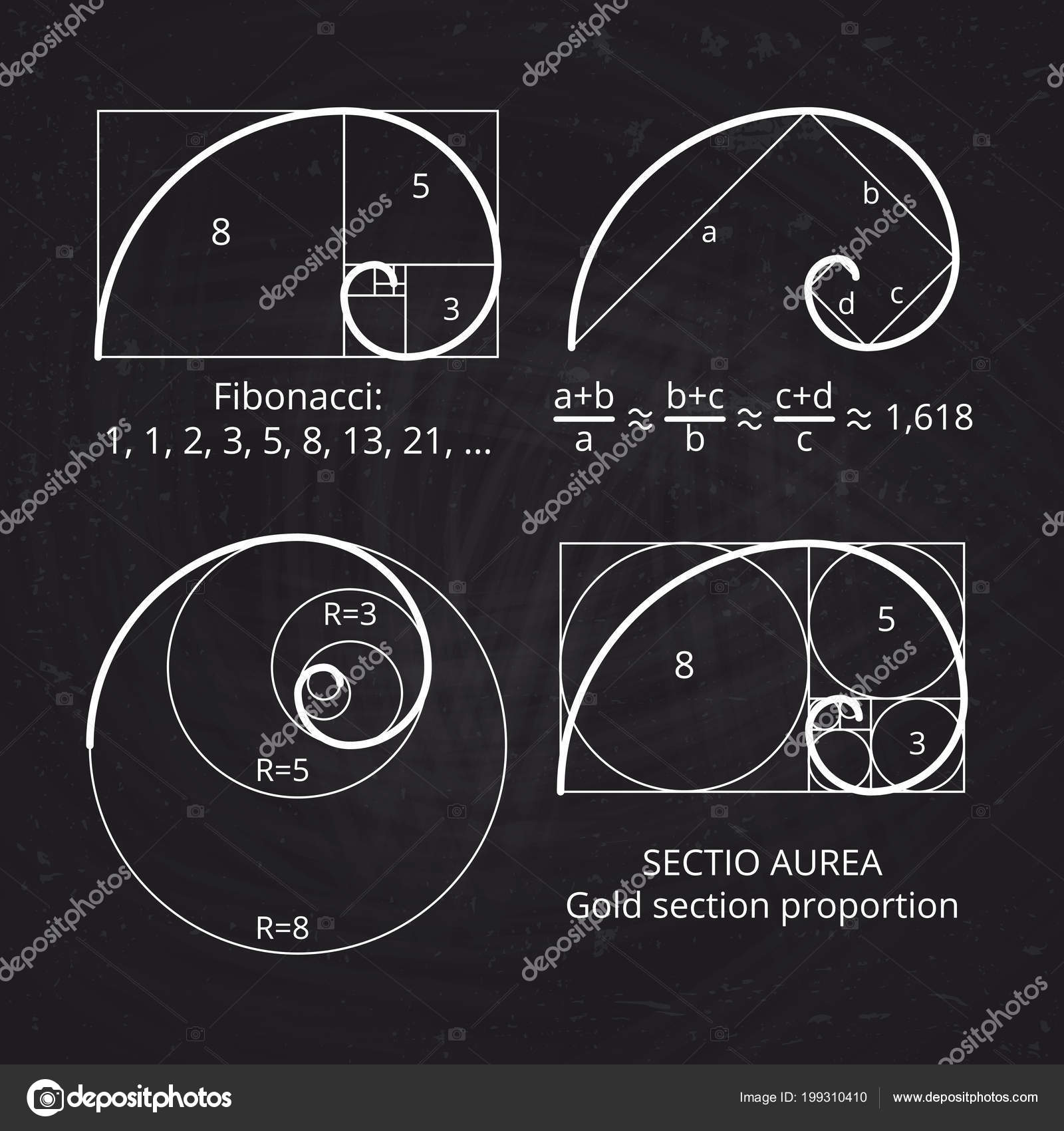 В те годы это было самое высокое строение, состоящее из пяти композиционных групп, которые венчает центральная башня. Здесь чётко прослеживается треугольник с прямым углом, гипотенуза которого захватывает пристройки и проходит через угол здания.
В те годы это было самое высокое строение, состоящее из пяти композиционных групп, которые венчает центральная башня. Здесь чётко прослеживается треугольник с прямым углом, гипотенуза которого захватывает пристройки и проходит через угол здания.
Золотые пропорции прослеживаются и в работах русского зодчего Матвея Казакова.
Кремлевское здание сенатаПречистенский дворецГолицынская больницаДом союзов — благородное собраниеИспользовал это прием и архитектор Василий Баженов, его здания причислены к историческим памятникам
Дом ПашковаАрхитектура в Санкт-Петербурге
Живым примером золотого сечения является Исаакиевский собор.
ЗС в Исаакиевском собореВ первую очередь можно проанализировать его ширину, равную 400 единицам:
- при делении числа 400 на значение золотого сечения получим приблизительно 248;
- при дальнейшем делении 248/1,618=153;
- основная часть собора вписывается в золотой прямоугольник, длинная сторона которого равна 400, ширина – 248.

По высоте здания ЗС можно видеть у купола, благодаря этому внешнее восприятие памятника архитектуры становится гармоничным.
На фото чётко прослеживаются золотой треугольник и прямоугольник в Исаакиевском собореПриведем ещё несколько примеров золотого сечения в архитектуре Санкт-Петербурга.
Кунсткамера
Кунсткамера была построена ещё в 1718 году, руководил строительством немецкий архитектор Георг Маттарнови. Она представляет собой 2 корпуса по 3 этажа, между ними возведена куполообразная многоярусная конструкция в виде башни.Золотое сечение в соотношении сторон можно наблюдать в длине корпусов и в высотах разных уровней.
В башне по всей высоте четко прослеживается равнобедренный треугольник, а это значит, что Кунсткамера построена по общему принципу ЗСТорговый дом Эсдерс и Схейфальс
ЗС в здании, возведенном в 1907 году, наблюдается в следующих размерах:
- 671, 414, 256, 98, 60, 37 и 23.
Композиция смотрится гармонично благодаря золотому соблюдению высотных величин.
Дом Советов
Дом Советов был возведен по проекту Троцкого в 1941 году, основной акцент выполняют портик по центру с 14 колоннами и скульптурный ансамбль. По обе стороны расположены два корпуса высотой в 5 этажей. Длина здания – 1472 единицы, если разделить его на значение Ф = 1,618, получим размерный ряд:
- 1472, 909, 562, 347, 214, 132, 81, 50. К ним относятся высота входа, всего сооружения, различных элементов.
Золотой прямоугольный треугольник идеально вписывается в центр здания, его вершина совпадает с вершиной Дома Советов, а гипотенуза заканчивается в конце бокового крыла. Если построить равнобедренный золотой треугольник, его грани будут проходить через точки в верхней части основного входа.
Очевидная пропорциональность Дома СоветовПримеры золотого сечения в современной архитектуре
В современной архитектуре формула расчёта золотого сечения позволяет проектировать уникальные формы, которые несут прочность, спокойствие и красоту.
Правило золотого сечения при строительстве частного дома
Многие архитекторы, которые разрабатывают проекты частных домов, используют правило золотого сечения. У клиентов создается ощущение, что все детали проработаны для максимально комфортного проживания. При грамотном выборе площадей жильцы на психологическом уровне ощущают умиротворение и успокоение.
Что нужно знать при проектировании фасада
В современном строительстве при проектировании домов кроме ряда Фибоначчи используют ещё один метод, основоположником которого был архитектор из Франции Ле Корбюзье. Он принимал за основу рост будущих владельцев усадьбы и, исходя их этого, рассчитывал параметры строения и комнат. Благодаря такому подходу дом получался не только гармоничный, но и максимально комфортный с индивидуальными чертами хозяев.
Идеальные пропорции частного домаЗолотое сечение в оформлении интерьера
Даже если дом возведен по типовому проекту, можно внутри его создать интерьер, максимально приближенный к идеальной пропорции 1:1,62. Например, благодаря дополнительным перегородкам или расположению мебельных групп, а также можно изменить дверные или оконные проемы, чтобы соотношение ширины к высоте было в золотом сечении.
Например, благодаря дополнительным перегородкам или расположению мебельных групп, а также можно изменить дверные или оконные проемы, чтобы соотношение ширины к высоте было в золотом сечении.
Аналогичная ситуация и с цветовым оформлением интерьера, здесь действует упрощенное правило:
- 60% — основная палитра;
- 30% — дополнительный оттенок;
- 10% — близкий тон, который усиливает восприятие основного и дополнительного.
Правило 1/1,62 в интерьере должно сопровождаться во всем: в соотношении мебели к общей площади, в ее высоте по отношению к параметрам комнаты.
Заключение
Принцип золотого сечения не является новым в архитектуре, поскольку в прежние времена здания строились не по типовым проектам, а с учетом индивидуальных особенностей будущих владельцев. Такие строения выглядят даже спустя многие года гармоничными и привлекательными. Интерьер, оформленный по правилам идеальной пропорции, позволяет грамотно использовать все площади.
Теперь вы сможете самостоятельно и правильно применить божественную гармонию математических цифр, планируя строительство дома или оформляя свой интерьер. Более того, интересную комбинацию цифр можно использовать и в экономике, и в расчете инвестиций и во всех деталях, с которыми соприкасается человек ежедневно.
Если у вас ещё остались вопросы, предлагаем посмотреть видео, в котором простыми словами разъяснен принцип действия золотого сечения:
Предыдущая
Новинки рынкаОт теории к практике: самостоятельная регулировка окон к зиме
СледующаяНовинки рынкаБалкон и лоджия: в чём разница, о каких нюансах стоит знать, если вы решились на переделку?
Понравилась статья? Сохраните, чтобы не потерять!
ТОЖЕ ИНТЕРЕСНО:
ВОЗМОЖНО ВАМ ТАКЖЕ БУДЕТ ИНТЕРЕСНО:
Фибоначчи повсюду!. Числа Фибоначчи названы в честь… | by Сергей Базанов | Paradox Review
Числа Фибоначчи и золотое сечение
Как известно, последовательность Фибоначчи начинается с 1 и 1, после чего каждое новое число является результатом сложения двух предыдущих чисел:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Если разделить два последовательных числа в этом ряду, например 144/89, в конечном итоге получится число 1,618, которое называется «Золотое число» или «Золотое сечение».
Пропорция золотого сечения считается эстетически приятной и из-за этого многие художники и архитекторы, в том числе Сальвадор Дали и Ле Корбюзье использовали её в своих работах.
Последовательность Фибоначчи и Золотое сечение тесно взаимосвязаны. Отношение последовательных чисел Фибоначчи сходится и приближается к золотому сечению, а выражение замкнутой формулы для последовательности Фибоначчи включает Золотое сечение.
Золотой прямоугольник (розовый) с длинной стороной a и короткой стороной b, и находящийся рядом с ним квадрат со стороной длиной a, создадут подобный золотой прямоугольник с длинной стороной а + b и короткой стороной a. Это изобажение иллюстрирует взаимосвязь отношений (a+b)/a = a/b.Спираль Фибоначчи или золотая спираль — это последовательность соединенных четвертей окружностей, вписанных внутри массивов квадратов со сторонами равными числам Фибоначчи.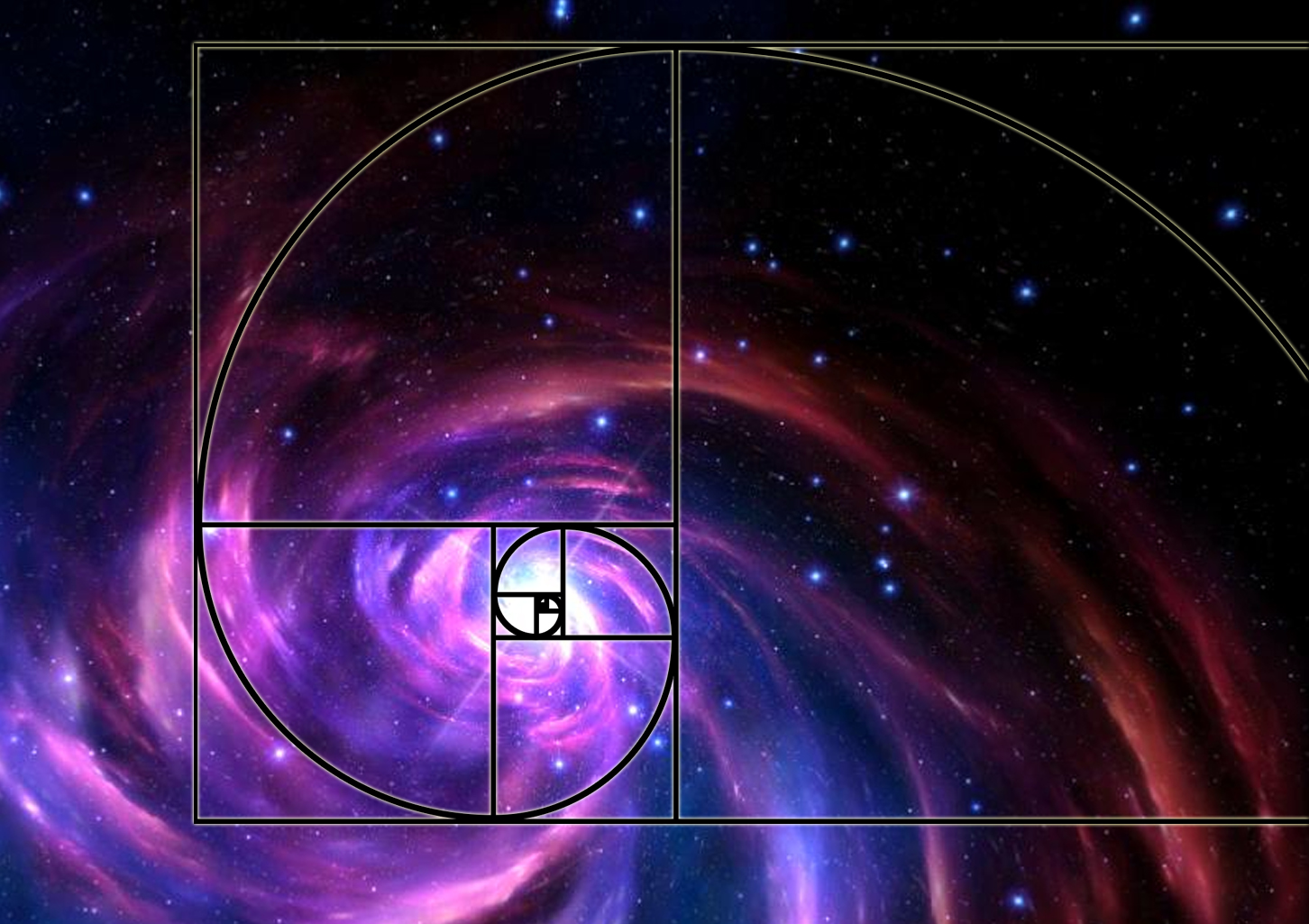 Квадраты идеально подходят друг к другу из-за природы последовательности Фибоначчи, в которой следующее число равно сумме двух перед ним (см.предыдущий рисунок). Любые два последовательных числа Фибоначчи имеют отношение, очень близкое к золотому сечению, которое составляет примерно 1.618034. Чем больше пара чисел Фибоначчи, тем ближе это приближение. Спираль и результирующий прямоугольник называются золотым прямоугольником.
Квадраты идеально подходят друг к другу из-за природы последовательности Фибоначчи, в которой следующее число равно сумме двух перед ним (см.предыдущий рисунок). Любые два последовательных числа Фибоначчи имеют отношение, очень близкое к золотому сечению, которое составляет примерно 1.618034. Чем больше пара чисел Фибоначчи, тем ближе это приближение. Спираль и результирующий прямоугольник называются золотым прямоугольником.
Страница не найдена
- Образование
Общий
- Словарь
- Экономика
- Корпоративные финансы
- Рот ИРА
- Акции
- Паевые инвестиционные фонды
- ETFs
- 401 (к)
Инвестирование / Торговля
- Основы инвестирования
- Фундаментальный анализ
- Управление портфелем ценных бумаг
- Основы трейдинга
- Технический анализ
- Управление рисками
- Рынки
Новости
- Новости компании
- Новости рынков
- Торговые новости
- Политические новости
- Тенденции
Популярные акции
- Яблоко (AAPL)
- Тесла (TSLA)
- Amazon (AMZN)
- AMD (AMD)
- Facebook (FB)
- Netflix (NFLX)
- Симулятор
- Твои деньги
Личные финансы
- Управление благосостоянием
- Бюджетирование / экономия
- Банковское дело
- Кредитные карты
- Домовладение
- Пенсионное планирование
- Налоги
- Страхование
Обзоры и рейтинги
- Лучшие онлайн-брокеры
- Лучшие сберегательные счета
- Лучшие домашние гарантии
- Лучшие кредитные карты
- Лучшие личные займы
- Лучшие студенческие ссуды
- Лучшее страхование жизни
- Лучшее автострахование
- Советники
Ваша практика
- Управление практикой
- Продолжая образование
- Карьера финансового консультанта
- Инвестопедия 100
Управление благосостоянием
- Портфолио Строительство
- Финансовое планирование
- Академия
Популярные курсы
- Инвестирование для начинающих
- Станьте дневным трейдером
- Торговля для начинающих
- Технический анализ
Курсы по темам
- Все курсы
- Курсы трейдинга
- Курсы инвестирования
- Финансовые профессиональные курсы
Представлять на рассмотрение
Извините, страница, которую вы ищете, недоступна.
 Вы можете найти то, что ищете, используя наше меню или параметры поиска. дом
Вы можете найти то, что ищете, используя наше меню или параметры поиска. дом- О нас
- Условия эксплуатации
- Словарь
- Редакционная политика
- Рекламировать
- Новости
- Политика конфиденциальности
- Свяжитесь с нами
- Карьера
- Уведомление о конфиденциальности Калифорнии
- #
- А
- B
- C
- D
- E
- F
- грамм
- ЧАС
- я
- J
- K
- L letter-m»> M
- N
- О
- п
- Q
- р
- S
- Т
- U
- V
- W
- Икс
- Y
- Z
Страница не найдена
- Образование
Общий
- Словарь
- Экономика
- Корпоративные финансы
- Рот ИРА
- Акции
- Паевые инвестиционные фонды
- ETFs
- 401 (к)
Инвестирование / Торговля
- Основы инвестирования
- Фундаментальный анализ
- Управление портфелем ценных бумаг
- Основы трейдинга
- Технический анализ
- Управление рисками
- Рынки
Новости
- Новости компании
- Новости рынков
- Торговые новости
- Политические новости
- Тенденции
Популярные акции
- Яблоко (AAPL)
- Тесла (TSLA)
- Amazon (AMZN)
- AMD (AMD)
- Facebook (FB)
- Netflix (NFLX)
- Симулятор
- Твои деньги
Личные финансы
- Управление благосостоянием
- Бюджетирование / экономия
- Банковское дело
- Кредитные карты
- Домовладение
- Пенсионное планирование
- Налоги
- Страхование
Обзоры и рейтинги
- Лучшие онлайн-брокеры
- Лучшие сберегательные счета
- Лучшие домашние гарантии
- Лучшие кредитные карты
- Лучшие личные займы
- Лучшие студенческие ссуды
- Лучшее страхование жизни
- Лучшее автострахование
- Советники
Ваша практика
- Управление практикой
- Продолжая образование
- Карьера финансового консультанта
- Инвестопедия 100
Управление благосостоянием
- Портфолио Строительство
- Финансовое планирование
- Академия
Популярные курсы
- Инвестирование для начинающих
- Станьте дневным трейдером
- Торговля для начинающих
- Технический анализ
Курсы по темам
- Все курсы
- Курсы трейдинга
- Курсы инвестирования
- Финансовые профессиональные курсы
Представлять на рассмотрение
Извините, страница, которую вы ищете, недоступна.
 Вы можете найти то, что ищете, используя наше меню или параметры поиска. дом
Вы можете найти то, что ищете, используя наше меню или параметры поиска. дом- О нас
- Условия эксплуатации
- Словарь
- Редакционная политика
- Рекламировать
- Новости
- Политика конфиденциальности
- Свяжитесь с нами
- Карьера
- Уведомление о конфиденциальности Калифорнии
- #
- А
- B
- C
- D
- E
- F
- грамм
- ЧАС
- я
- J
- K
- L letter-m»> M
- N
- О
- п
- Q
- р
- S
- Т
- U
- V
- W
- Икс
- Y
- Z
Страница не найдена
- Образование
Общий
- Словарь
- Экономика
- Корпоративные финансы
- Рот ИРА
- Акции
- Паевые инвестиционные фонды
- ETFs
- 401 (к)
Инвестирование / Торговля
- Основы инвестирования
- Фундаментальный анализ
- Управление портфелем ценных бумаг
- Основы трейдинга
- Технический анализ
- Управление рисками
- Рынки
Новости
- Новости компании
- Новости рынков
- Торговые новости
- Политические новости
- Тенденции
Популярные акции
- Яблоко (AAPL)
- Тесла (TSLA)
- Amazon (AMZN)
- AMD (AMD)
- Facebook (FB)
- Netflix (NFLX)
- Симулятор
- Твои деньги
Личные финансы
- Управление благосостоянием
- Бюджетирование / экономия
- Банковское дело
- Кредитные карты
- Домовладение
- Пенсионное планирование
- Налоги
- Страхование
Обзоры и рейтинги
- Лучшие онлайн-брокеры
- Лучшие сберегательные счета
- Лучшие домашние гарантии
- Лучшие кредитные карты
- Лучшие личные займы
- Лучшие студенческие ссуды
- Лучшее страхование жизни
- Лучшее автострахование
- Советники
Ваша практика
- Управление практикой
- Продолжая образование
- Карьера финансового консультанта
- Инвестопедия 100
Управление благосостоянием
- Портфолио Строительство
- Финансовое планирование
- Академия
Популярные курсы
- Инвестирование для начинающих
- Станьте дневным трейдером
- Торговля для начинающих
- Технический анализ
Курсы по темам
- Все курсы
- Курсы трейдинга
- Курсы инвестирования
- Финансовые профессиональные курсы
Представлять на рассмотрение
Извините, страница, которую вы ищете, недоступна.
 Вы можете найти то, что ищете, используя наше меню или параметры поиска. дом
Вы можете найти то, что ищете, используя наше меню или параметры поиска. дом- О нас
- Условия эксплуатации
- Словарь
- Редакционная политика
- Рекламировать
- Новости
- Политика конфиденциальности
- Свяжитесь с нами
- Карьера
- Уведомление о конфиденциальности Калифорнии
- #
- А
- B
- C
- D
- E
- F
- грамм
- ЧАС
- я
- J
- K
- L letter-m»> M
- N
- О
- п
- Q
- р
- S
- Т
- U
- V
- W
- Икс
- Y
- Z
Страница не найдена
- Образование
Общий
- Словарь
- Экономика
- Корпоративные финансы
- Рот ИРА
- Акции
- Паевые инвестиционные фонды
- ETFs
- 401 (к)
Инвестирование / Торговля
- Основы инвестирования
- Фундаментальный анализ
- Управление портфелем ценных бумаг
- Основы трейдинга
- Технический анализ
- Управление рисками
- Рынки
Новости
- Новости компании
- Новости рынков
- Торговые новости
- Политические новости
- Тенденции
Популярные акции
- Яблоко (AAPL)
- Тесла (TSLA)
- Amazon (AMZN)
- AMD (AMD)
- Facebook (FB)
- Netflix (NFLX)
- Симулятор
- Твои деньги
Личные финансы
- Управление благосостоянием
- Бюджетирование / экономия
- Банковское дело
- Кредитные карты
- Домовладение
- Пенсионное планирование
- Налоги
- Страхование
Обзоры и рейтинги
- Лучшие онлайн-брокеры
- Лучшие сберегательные счета
- Лучшие домашние гарантии
- Лучшие кредитные карты
- Лучшие личные займы
- Лучшие студенческие ссуды
- Лучшее страхование жизни
- Лучшее автострахование
- Советники
Ваша практика
- Управление практикой
- Продолжая образование
- Карьера финансового консультанта
- Инвестопедия 100
Управление благосостоянием
- Портфолио Строительство
- Финансовое планирование
- Академия
Популярные курсы
- Инвестирование для начинающих
- Станьте дневным трейдером
- Торговля для начинающих
- Технический анализ
Курсы по темам
- Все курсы
- Курсы трейдинга
- Курсы инвестирования
- Финансовые профессиональные курсы
Представлять на рассмотрение
Извините, страница, которую вы ищете, недоступна.
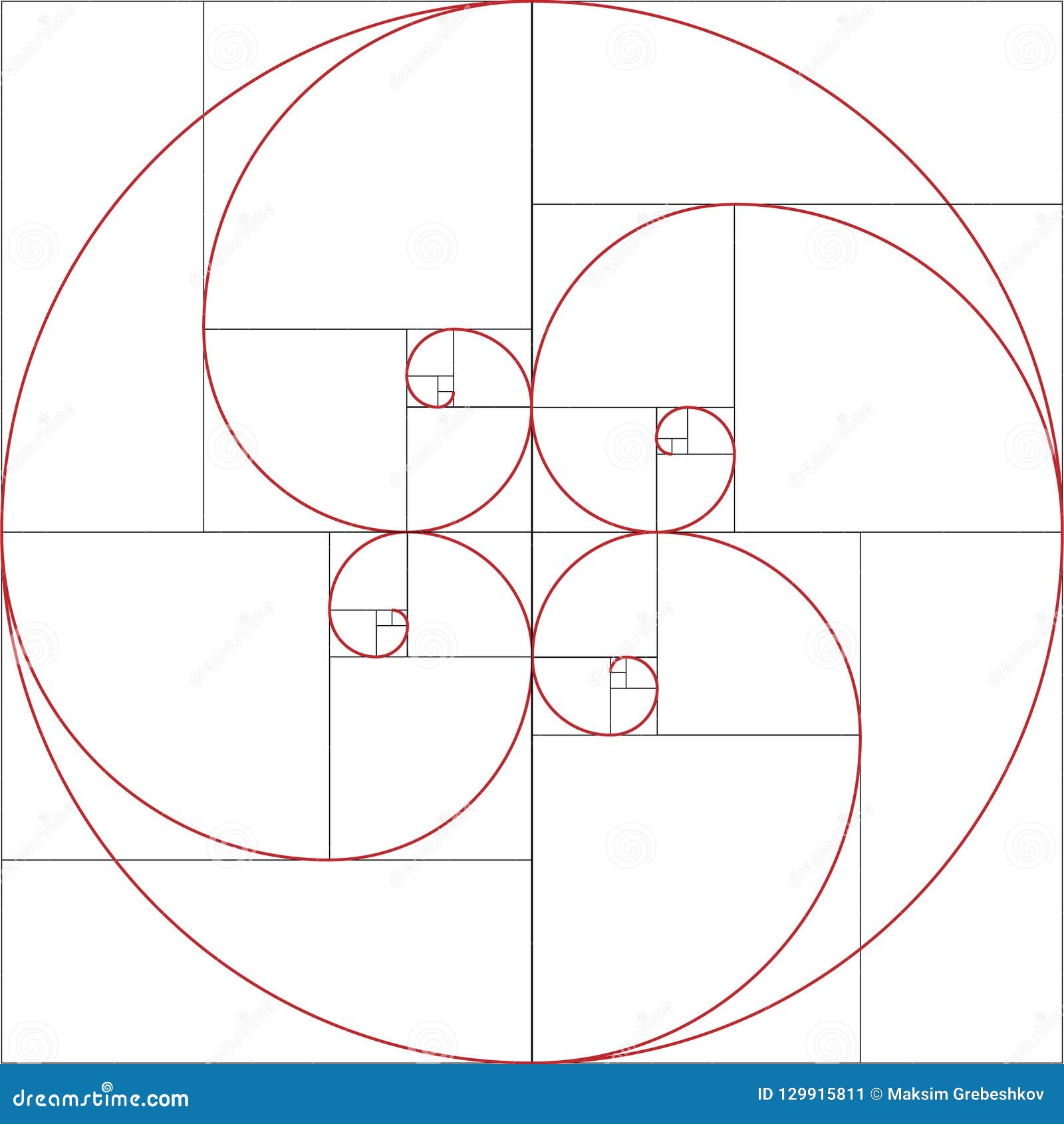 Вы можете найти то, что ищете, используя наше меню или параметры поиска. дом
Вы можете найти то, что ищете, используя наше меню или параметры поиска. дом- О нас
- Условия эксплуатации
- Словарь
- Редакционная политика
- Рекламировать
- Новости
- Политика конфиденциальности
- Свяжитесь с нами
- Карьера
- Уведомление о конфиденциальности Калифорнии
- #
- А
- B
- C
- D
- E
- F
- грамм
- ЧАС
- я
- J
- K
- L letter-m»> M
- N
- О
- п
- Q
- р
- S
- Т
- U
- V
- W
- Икс
- Y
- Z
φ Золотое сечение ★ Фибоначчи
Это отрывок из книги «Мастер Фибоначчи: человек, изменивший математику». Все цитаты занесены в каталог на странице «Цитаты».
ЗОЛОТОЕ СООТНОШЕНИЕ
(Предыдущий раздел: Phi )
Купить сейчас на Амазонке Древнее соотношение Евклида на протяжении веков описывалось многими именами, но впервые было названо «золотым сечением» в девятнадцатом веке. Не очевидно, что Фибоначчи установил какую-либо связь между этим соотношением и последовательностью чисел, которую он нашел в задаче о кролике («Евклид»).Только в конце семнадцатого века связь между числами Фибоначчи и золотым сечением была доказана (и даже тогда не полностью) шотландским математиком Робертом Симсоном (1687-1768) (Livio 101).
Не очевидно, что Фибоначчи установил какую-либо связь между этим соотношением и последовательностью чисел, которую он нашел в задаче о кролике («Евклид»).Только в конце семнадцатого века связь между числами Фибоначчи и золотым сечением была доказана (и даже тогда не полностью) шотландским математиком Робертом Симсоном (1687-1768) (Livio 101).
Греческая буква тау (Ττ) на протяжении сотен лет представляла золотое сечение в математике, но недавно (в начале 20-го века) американскому математику Марку Барру, который выбрал первое, присвоил этому соотношению символ фи ( Φ ). Греческая буква в имени великого скульптора Фидия (ок.490–430 гг. До н.э.), потому что считалось, что он использовал золотое сечение в своих скульптурах и в дизайне Парфенона (Доннеган; Ливио 5). [Правдивость этих и других утверждений (например, о том, что золотое сечение встречается в картинах, египетских пирамидах и измерениях пропорций человеческого тела) рассматривается в «Фибоначчи в искусстве и музыке». ] Немецкий математик Мартин Ом (брат физика Георга Симона Ома, в честь которого назван закон Ома) впервые использовал термин «золотое сечение» для описания этого отношения во втором издании своей книги Die Reine Elementar-Mathematik (Чистая элементарная математика) (1835).Он писал: «Это разделение произвольной линии на две такие части обычно называют« золотым сечением »». Однако он не изобретал этот термин, поскольку сказал «обычно называет», указывая на то, что этот термин является общепринятым. принял тот, который использовал сам (Livio 6).
] Немецкий математик Мартин Ом (брат физика Георга Симона Ома, в честь которого назван закон Ома) впервые использовал термин «золотое сечение» для описания этого отношения во втором издании своей книги Die Reine Elementar-Mathematik (Чистая элементарная математика) (1835).Он писал: «Это разделение произвольной линии на две такие части обычно называют« золотым сечением »». Однако он не изобретал этот термин, поскольку сказал «обычно называет», указывая на то, что этот термин является общепринятым. принял тот, который использовал сам (Livio 6).
Число золотого сечения для phi (φ) составляет 0,61803 39887…, что коррелирует с соотношением, вычисляемым при делении числа в ряду Фибоначчи на его последующее число, например. n) / (x — (1-x)), где x = (1 + sqrt 5) / 2 ~ 1,618.
n) / (x — (1-x)), где x = (1 + sqrt 5) / 2 ~ 1,618.
Другой способ написать уравнение:
Следовательно, phi = 0,618 и 1 / Phi. Сила фи — это отрицательная сила фи. Одна из причин, по которой последовательность Фибоначчи очаровывала людей на протяжении веков, заключается в этой тенденции соотношения чисел в рядах падать либо на фи, либо на фи [после F (8)]. Другие обсуждали, может ли существовать сверхъестественное объяснение того, что кажется невероятным математическим совпадением.
Спираль Фибоначчи
Границы квадратов последовательных чисел Фибоначчи создают спираль, известную как спираль Фибоначчи; он следует за поворотами под постоянным углом, который очень близок к золотому сечению. В результате ее часто называют золотой спиралью (Леви 121).
Золотая спираль Настоящая золотая спираль образована серией золотых прямоугольников с одинаковыми пропорциями, поэтому она не совсем такая же, как спираль Фибоначчи, но очень похожа. По мере увеличения размера спирали Фибоначчи она приближается к углу золотой спирали, потому что отношение каждого числа в ряду Фибоначчи к числу до того, как оно сходится к Phi , 1,618 , по мере развития ряда (Meisner, «Spirals »).
По мере увеличения размера спирали Фибоначчи она приближается к углу золотой спирали, потому что отношение каждого числа в ряду Фибоначчи к числу до того, как оно сходится к Phi , 1,618 , по мере развития ряда (Meisner, «Spirals »).
Многие природные явления (например, вращение ураганов и спиральные рукава галактик) и объекты в природе, кажется, существуют в форме золотых спиралей; например, раковина наутилуса с камерами (Nautilus pompilius) и расположение семян в головке подсолнечника, очевидно, расположены по спирали, как и чешуйки шишек сосновых шишек (Knott, Brief; Livio 8).Спирали Фибоначчи, золотые спирали и спирали, основанные на золотом сечении, часто появляются в живых организмах. Однако не каждая спираль в природе связана с числами Фибоначчи или Фи; некоторые из этих спиралей являются равноугольными спиралями, а не спиралями Фибоначчи или золотыми спиралями. Равноугольная спираль имеет уникальные математические свойства, при которых размер спирали увеличивается, но объект сохраняет форму кривой при каждом последующем повороте. Числа Фибоначчи чаще всего встречаются в природе в количестве и расположении листьев вокруг стеблей растений, а также в расположении листьев, частей и семян цветов и других растений (Мейснер, «Спирали»).
Числа Фибоначчи чаще всего встречаются в природе в количестве и расположении листьев вокруг стеблей растений, а также в расположении листьев, частей и семян цветов и других растений (Мейснер, «Спирали»).
Многие наблюдатели находят паттерны спиралей Фибоначчи и золотых спиралей эстетически более привлекательными, чем другие паттерны. Поэтому некоторые историки и изучающие математику придают исключительную ценность тем объектам и видам деятельности в природе, которые, кажется, следуют паттернам Фибоначчи.
7.2: Золотое сечение и последовательность Фибоначчи
В этом разделе мы обсудим очень особое число, называемое золотым сечением. Это иррациональное число, немного больше единицы.6, и он (несколько удивительно) имел огромное значение в мире науки, искусства и музыки. Также было обнаружено, что это число имеет удивительную связь с так называемой последовательностью Фибоначчи, первоначально изученной в контексте биологии много веков назад. Эта неожиданная связь между алгеброй, биологией и искусством предполагает математическое единство мира и иногда также обсуждается в философии.
Золотое сечение
Для одного числа \ (a \) и другого меньшего числа \ (b \) соотношение этих двух чисел находится путем их деления.Их соотношение равно \ (a / b \). Другое соотношение получается сложением двух чисел \ (a + b \) и делением их на большее число \ (a \). Новое соотношение — \ ((a + b) / a \). Если эти два соотношения равны одному и тому же числу, то это число называется золотым соотношением. Греческая буква \ (\ varphi \) (фи) обычно используется для обозначения золотого сечения.
Например, если \ (b = 1 \) и \ (a / b = \ varphi \), то \ (a = \ varphi \). Второе соотношение \ ((a + b) / a \) тогда будет \ ((\ varphi + 1) / \ varphi \). Поскольку эти два соотношения равны, это правда:
\ [\ varphi = \ dfrac {\ varphi + 1} {\ varphi} \ nonumber \]
(Это уравнение имеет два решения, но только положительное решение называется золотым сечением \ (\ varphi \)).
Один из способов написать это число —
\ [\ varphi = \ dfrac {1+ \ sqrt {5}} {2} \ nonumber \]
\ (\ sqrt {5} \) — положительное число, которое при умножении само на себя дает \ (5: \ sqrt {5} \ times \ sqrt {5} = 5 \).
Золотое сечение — иррациональное число. Если человек попытается записать его десятичное представление, оно никогда не остановится и никогда не создаст шаблон, но начнется так: 1.6180339887 … Интересная особенность этого числа заключается в том, что вы можете вычесть из него 1 или разделить 1 по нему, и результат будет таким же.
\ [\ varphi-1 = 1,6180339887 \ ldots-1 = 0,6180339887 \ nonumber \]
\ [1 / \ varphi = \ frac {1} {1.6180339887} = 0,6180339887 \ nonumber \]
Золотой прямоугольник
Если длина прямоугольника, деленная на его ширину, равна золотому сечению, то прямоугольник называется «золотым прямоугольником». Если квадрат отрезан от одного конца золотого прямоугольника, то другой конец будет новым золотым прямоугольником. На картинке большой прямоугольник (синий и розовый вместе) является золотым прямоугольником, потому что \ (a / b = \ varphi \).{2} \). Тогда мы получим \ (\ dfrac {a} {b} = \ dfrac {b} {a-b} \). Обе стороны: \ (\ varphi \) .
Последовательность Фибоначчи
Последовательность Фибоначчи — это список чисел. Начните с 1, 1, а затем вы сможете найти следующее число в списке, сложив два последних числа вместе. Результирующая (бесконечная) последовательность называется последовательностью Фибоначчи. Поскольку мы начинаем с 1, 1, следующее число будет 1 + 1 = 2. Теперь у нас есть 1, 1, 2. Следующее число 1 + 2 = 3. Теперь у нас есть 1, 1, 2, 3. Следующее число 2 + 3 = 5.Следующее — 3 + 5 = 8 и так далее. Каждое из этих чисел называется числом Фибоначчи. Первоначально Фибоначчи (Леонардо Пизанский, живший около 800 лет назад) придумал эту последовательность для изучения популяций кроликов! Он, вероятно, понятия не имел, что произойдет, если вы разделите каждое число Фибоначчи на предыдущее, как показано ниже.
Число Фибоначчи | делится на число до | соотношение |
|---|---|---|
1 | ||
1 | 1/1 | = 1. |
2 | 2/1 | = 2,0000 |
3 | 3/2 | = 1,5000 |
5 | 5/3 | = 1.6667 |
8 | 8/5 | = 1,6000 |
13 | 13/8 | = 1,6250 |
21 | 21/13 | = 1. |
34 | 34/21 | = 1,6190 … |
55 | 55/34 | = 1,6177 … |
89 | 89/55 | = 1.6182 … |
… | . | … |
= 1,6180 … |
Вот очень удивительный факт:
Примечание
Отношение двух последовательных чисел Фибоначчи приближается к золотому сечению.
Оказывается, числа Фибоначчи довольно часто встречаются в природе. Некоторые примеры — узор листьев на стебле, части ананаса, цветение артишока, распускание папоротника и расположение сосновой шишки. Числа Фибоначчи также встречаются в генеалогическом древе пчел.
Между тем, многие художники и исследователи музыки изучали художественные произведения, в которых золотое сечение играет важную роль. К ним относятся работы Микеланджело, Да Винчи и Моцарта. Заинтересованные читатели могут найти в Интернете множество ресурсов и видео. Возможно, неудивительно, что числа вроде 3, 5, 8 и 13 очень важны в теории музыки; просто взгляните на клавиши пианино!
Заинтересованные читатели могут найти в Интернете множество ресурсов и видео. Возможно, неудивительно, что числа вроде 3, 5, 8 и 13 очень важны в теории музыки; просто взгляните на клавиши пианино!
Номер ссылки
- Список литературы (17)
Авторы и указание авторства
Фибоначчи
ФибоначчиЭнди Нортон
Отделение Математическое образование
Университет Джорджии
* см. Другие примеры
Фибоначчи и золотое сечение
Связь между последовательностью Фибоначчи и Золотое сечение удивительно.У нас есть два, казалось бы, не связанных между собой темы, производящие такое же точное количество. Учитывая, что это число (или золотое сечение) нерационально, происшествие выходит за рамки совпадение. Это требует дальнейшего изучения …Золотое сечение = (sqrt (5) + 1) / 2 или около 1,618 Золотое сечение, пожалуй, лучше всего отображается визуально.
 в золотом прямоугольнике. Этот прямоугольник обладает тем свойством, что
его длина находится в соотношении Голена с шириной. Как следствие,
мы можем разделить этот прямоугольник на квадрат и прямоугольник меньшего размера
что похоже на первое.Пусть следующий набросок GSP проиллюстрирует:
в золотом прямоугольнике. Этот прямоугольник обладает тем свойством, что
его длина находится в соотношении Голена с шириной. Как следствие,
мы можем разделить этот прямоугольник на квадрат и прямоугольник меньшего размера
что похоже на первое.Пусть следующий набросок GSP проиллюстрирует:Последовательность Фибоначчи — это последовательность, в которой определяется каждый член. как сумма двух предыдущих условий: Мы можем легко создать эту последовательность в электронной таблице, используя формулу выше. Это было сделано в центральной колонке. таблицы ниже:
| 1 | 1 | |
| 2 | 1 | 1 |
| 3 | 2 | 2 |
| 4 | 3 | 1.5 |
| 5 | 5 | 1.66666666666667 |
| 6 | 8 | 1,6 |
| 7 | 13 | 1,625 |
| 8 | 21 | 1,61538461538462 |
| 9 | 34 | 1,6112 |
| 10 | 55 | 1.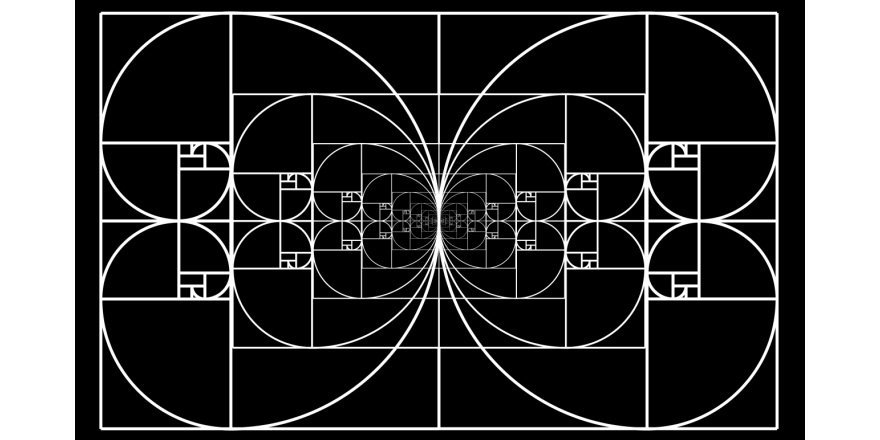 61764705882353 61764705882353 |
| 11 | 89 | 1,61818181818182 |
| 12 | 144 | 1,61797752808989 |
| 13 | 233 | 1.61805555555556 |
| 14 | 377 | 1.61802575107296 |
| 15 | 610 | 1.61803713527851 |
| 16 | 987 | 1.61803278688525 |
| 17 | 1597 | 1.61803444782168 |
| 18 | 2584 | 1.61803381340013 |
| 19 | 4181 | 1.61803405572755 |
| 20 | 6765 | 1.61803396316671 |
| 21 | 10946 | 1.6180339985218 |
| 22 | 17711 | 1.61803398501736 |
| 23 | 28657 | 1. 6180339 6180339 |
| 24 | 46368 | 1.61803398820533 |
| 25 | 75025 | 1.6180339889579 |
| 26 | 121393 | 1.61803398867044 |
| 27 | 196418 | 1.61803398878024 |
| 28 | 317811 | 1.6180339887383 |
| 29 | 514229 | 1.61803398875432 |
| 30 | 832040 | 1.6180339887482 |
| 31 | 1346269 | 1.61803398875054 |
| 32 | 2178309 | 1.61803398874965 |
| 33 | 3524578 | 1.61803398874999 |
| 34 | 5702887 | 1.61803398874986 |
| 35 | 9227465 | 1. 61803398874991 61803398874991 |
| 36 | 14930352 | 1.61803398874989 |
| 37 | 24157817 | 1.6180339887499 |
| 38 | 3 | 1.61803398874989 |
| 39 | 63245986 | 1.6180339887499 |
| 40 | 102334155 | 1.61803398874989 |
| 41 | 165580141 | 1.6180339887499 |
| 42 | 267 6 | 1.6180339887499 |
| 43 | 433494437 | 1.6180339887499 |
| 44 | 701408733 | 1.6180339887499 |
| 45 | 1134 | 1.6180339887499 |
| 46 | 1836311903 | 1.6180339887499 |
| 47 | 2971215073 | 1.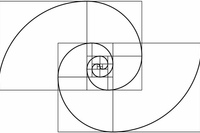 6180339887499 6180339887499 |
| 48 | 4807526976 | 1.6180339887499 |
| 49 | 7778742049 | 1.6180339887499 |
| 50 | 12586269025 | 1.6180339887499 |
Понимание отношений Помните, теперь золотой прямоугольник можно разделить в квадрат и еще один золотой прямоугольник. Фактически, мы можем повторить этот процесс снова и снова. Предположим, мы начинаем с прямоугольника длиной Y и шириной X. Когда мы разделим этот прямоугольник на квадрат и новый золотой прямоугольник, получаем длину X и ширину Y-X для нового прямоугольника. Поскольку стороны прямоугольников равны в той же пропорции (а именно 1.618 …), получаем: Теперь вернемся к последовательности Фибоначчи.

 Как открыть хостел | HowToHostel Как открыть хостел …
Как открыть хостел | HowToHostel Как открыть хостел … 


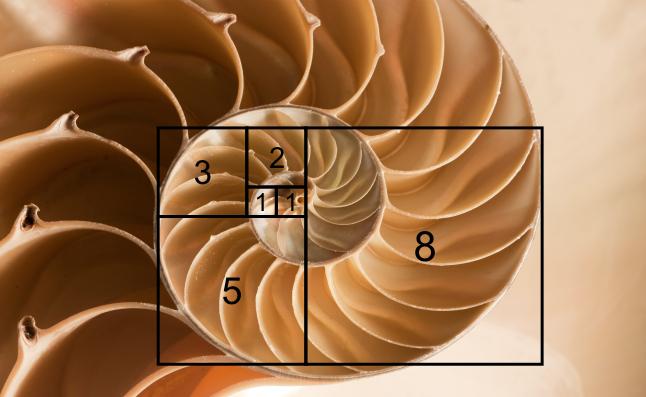

 Например, тело человека, количество семечек в подсолнухе, структуру ДНК, произведения искусства и вирусную бактерию;
Например, тело человека, количество семечек в подсолнухе, структуру ДНК, произведения искусства и вирусную бактерию;


 В нём сталь становится прочнее, вода дольше сохраняет свежий вкус, и быстрее растут живые растения. Много лет ученые пытаются разгадать этот феномен, но пока его научное решение не найдено.
В нём сталь становится прочнее, вода дольше сохраняет свежий вкус, и быстрее растут живые растения. Много лет ученые пытаются разгадать этот феномен, но пока его научное решение не найдено.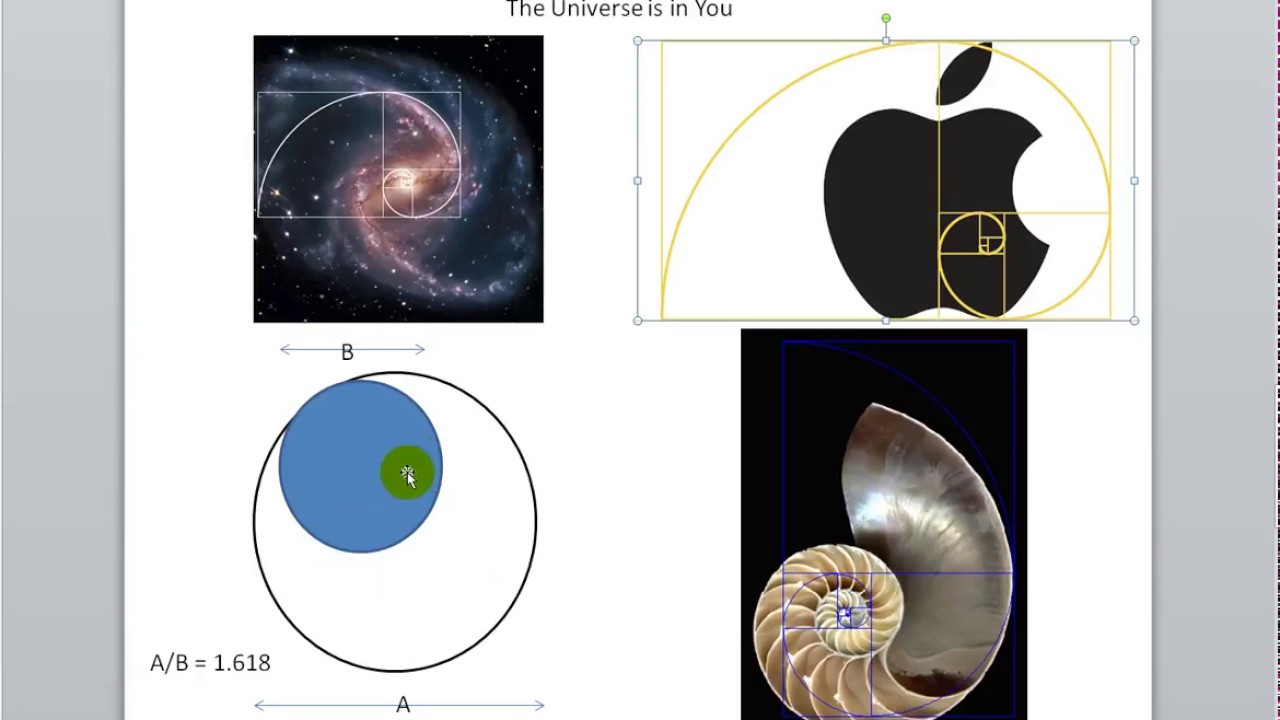
 0000
0000 6154 …
6154 …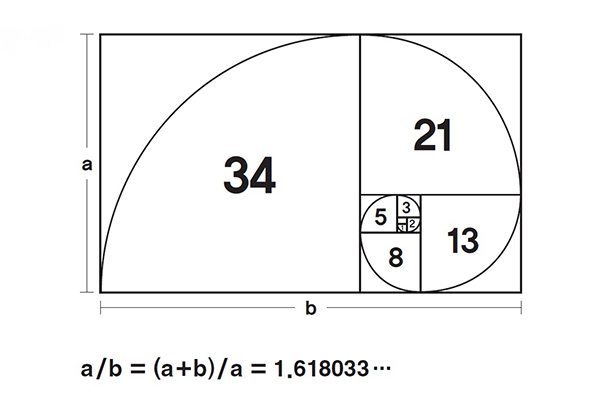 ..
..